
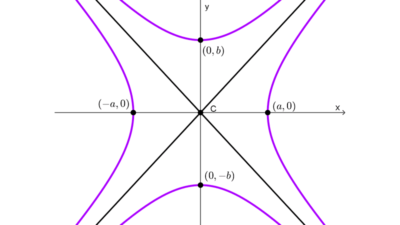
Vértices de la hipérbola
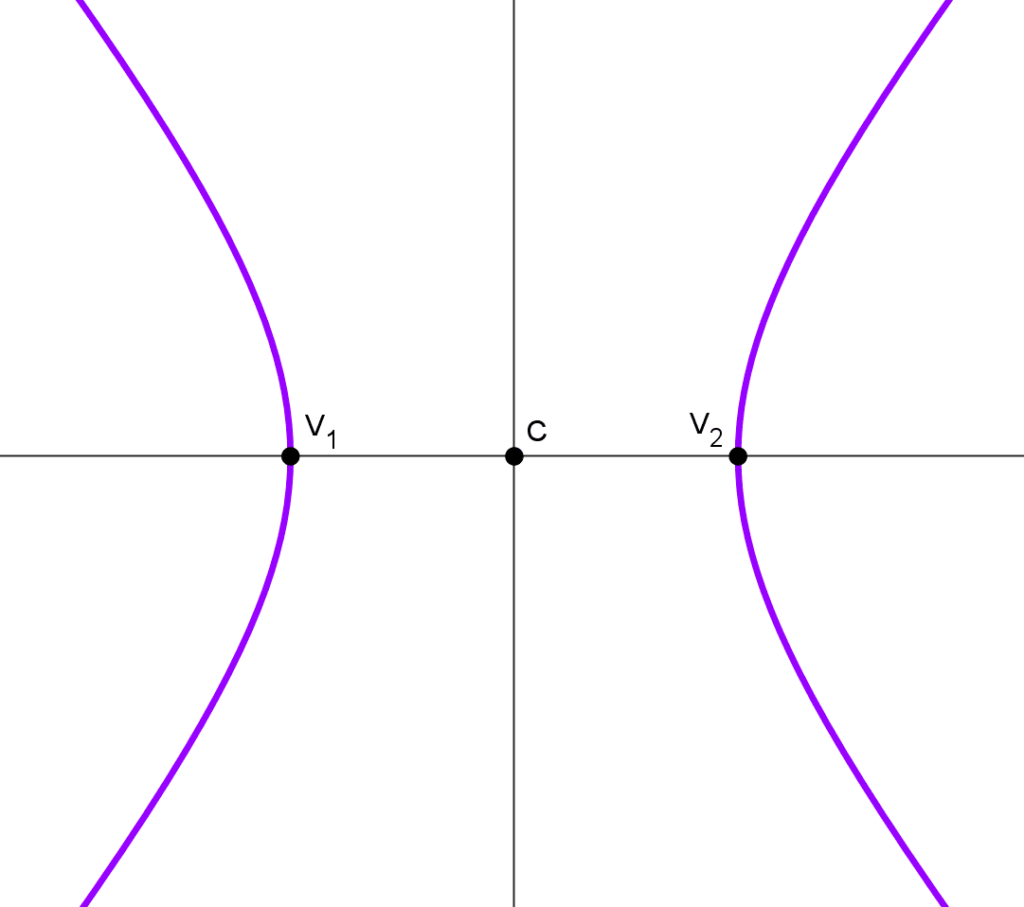
Los vértices de la hipérbola son los dos puntos de la misma que están más cerca del centro, ambos se encuentran sobre el eje focal y el segmento que los une se llama eje transversal. Los vértices se encuentran separados por una distancia 2a (la longitud del eje transversal).
A continuación, veremos cómo calcular los vértices de una hipérbola paso a paso. Si aún no conoces el significado de la hipérbola en matemáticas, te invito a revisar antes el artículo principal donde explicamos su concepto, definición, fórmulas y propiedades.
Cómo hallar los vértices de la hipérbola
Las coordenadas de los vértices se pueden obtener conociendo el centro y la longitud del semieje transversal, datos que pueden obtenerse de la ecuación canónica.
| Ecuación canónica | Eje transversal | Centro | Vértices |
|---|---|---|---|
| *\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1* | Sobre el eje x | (0, 0) | (a, 0) (-a, 0) |
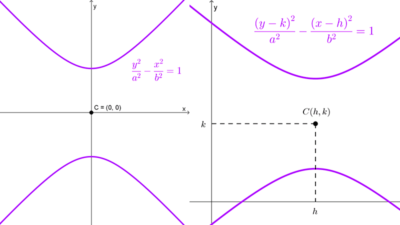
| *\dfrac{y^2}{a^2}-\dfrac{x^2}{b^2}=1* | Sobre el eje y | (0, 0) | (0, a) (0, -a) |
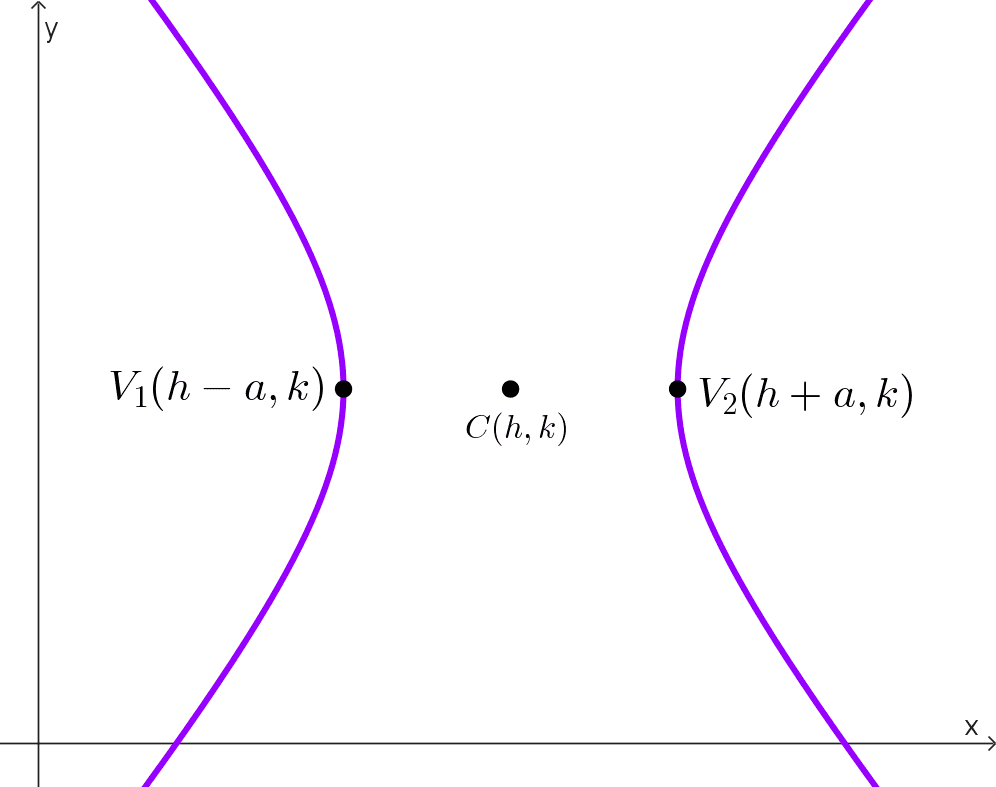
| *\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1* | Paralelo al eje x | (h, k) | (h + a, k) (h - a, k) |
| *\dfrac{(y-k)^2}{a^2}-\dfrac{(x-h)^2}{b^2}=1* | Paralelo al eje y | (h, k) | (h, k + a) (h, k - a) |
Ejercicios resueltos
Ejercicio 1
Calcular los vértices de la hipérbola *\dfrac{x^2}{4}-\dfrac{y^2}{9}=1*
Solución: podemos observar que se trata de una hipérbola con eje transversal horizontal, ya que el término con x2 es positivo. Además, el centro es el origen de coordenadas (0, 0).
Recordemos que una hipérbola con estas características, los vértices se encuentran a una distancia “a” del centro hacia la izquierda y la derecha, es decir, en los puntos (±a, 0), donde a es la longitud del semieje transversal.
De la ecuación extraemos *a^2=4,* de donde se obtiene que *a=\sqrt{4}=2.* Por lo tanto, los vértices de la hipérbola están en los puntos (2, 0) y (-2, 0). Estos corresponden a los extremos del eje transversal.
Ejercicio 2
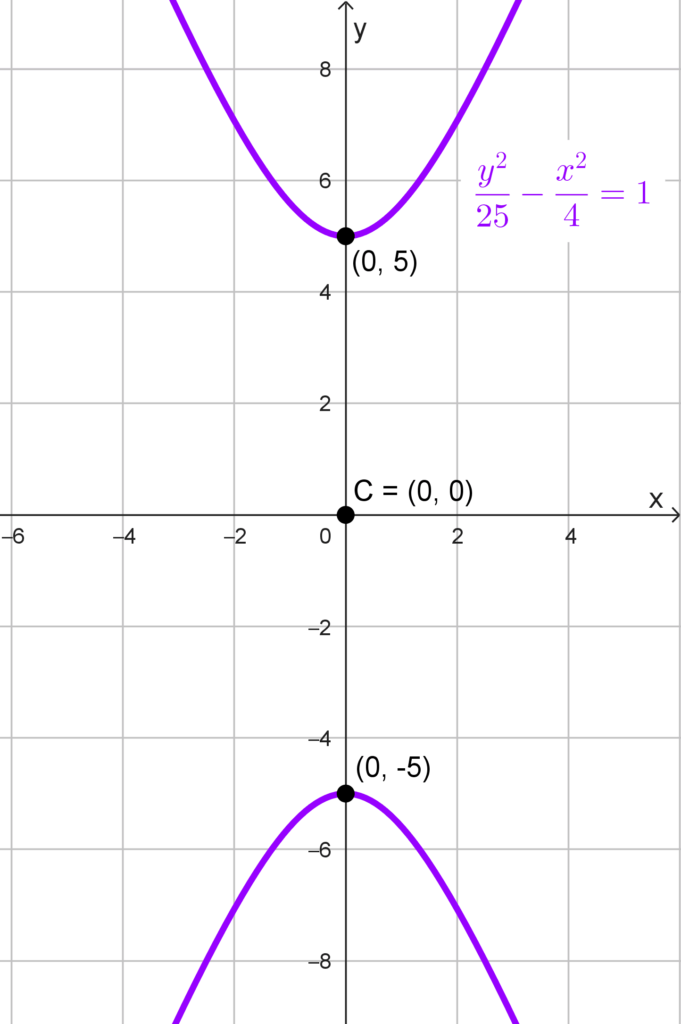
Dada la ecuación de la hipérbola *\dfrac{y^2}{25}-\dfrac{x^2}{4}=1* determinar sus vértices.
Solución: empezamos observando que se trata de una hipérbola con eje transversal vertical, ya que el término positivo está asociado a y2 . Además, el centro de la hipérbola es el origen de coordenadas (0, 0).
Para una hipérbola con estas características, los vértices se encuentran a una distancia “a” del centro hacia arriba y hacia abajo, es decir, en los puntos (0, ±a), donde a es la longitud del semieje transversal.
De la ecuación dada, identificamos que *a^2=25,* de donde podemos sacar *a=\sqrt{25}=5.* Por lo tanto, los vértices de la hipérbola están en los puntos (0, 5) y (0, -5).
Ejercicio 3
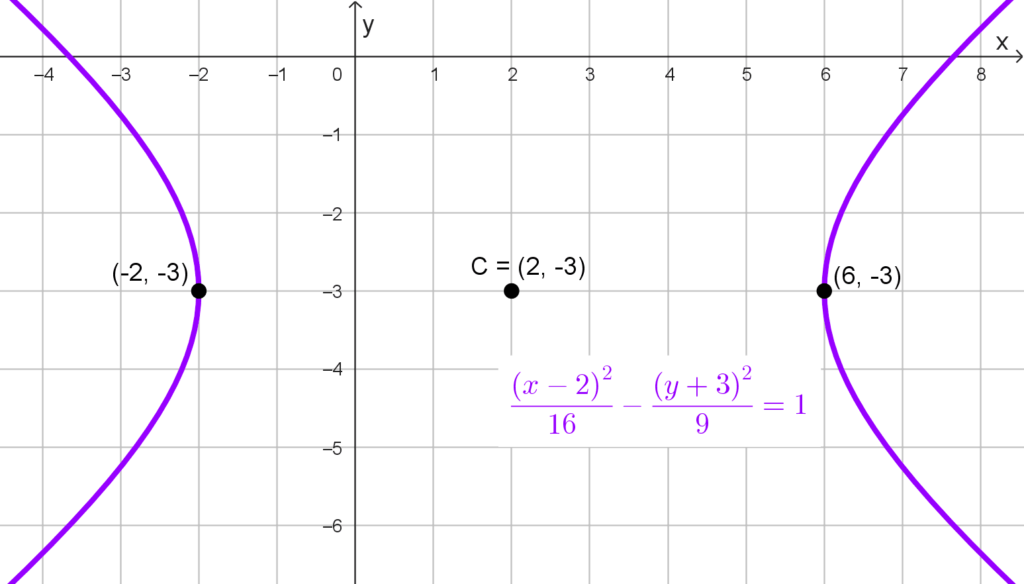
Hallar las coordenadas de los vértices de la hipérbola *\dfrac{(x-2)^2}{16}-\dfrac{(y+3)^2}{9}=1*
Solución: observamos que se trata de una hipérbola horizontal, ya que el término positivo está asociado a *(x-2)^2.* Además, el centro de la hipérbola no está en el origen, sino en el punto (2, -3).
Para una hipérbola con eje transversal horizontal, los vértices se encuentran a una distancia “a” del centro hacia la izquierda y la derecha, es decir, en los puntos (h ± a, k), donde (h, k) es el centro y a es la longitud del semieje transversal.
De la ecuación dada podemos identificar que *a^2=16,* de donde *a=\sqrt{16}=4.* Por lo tanto, los vértices de la hipérbola están en los puntos (2+4, -3) y (2-4, -3), es decir, en (6, -3) y (-2, -3).
Ejercicio 4
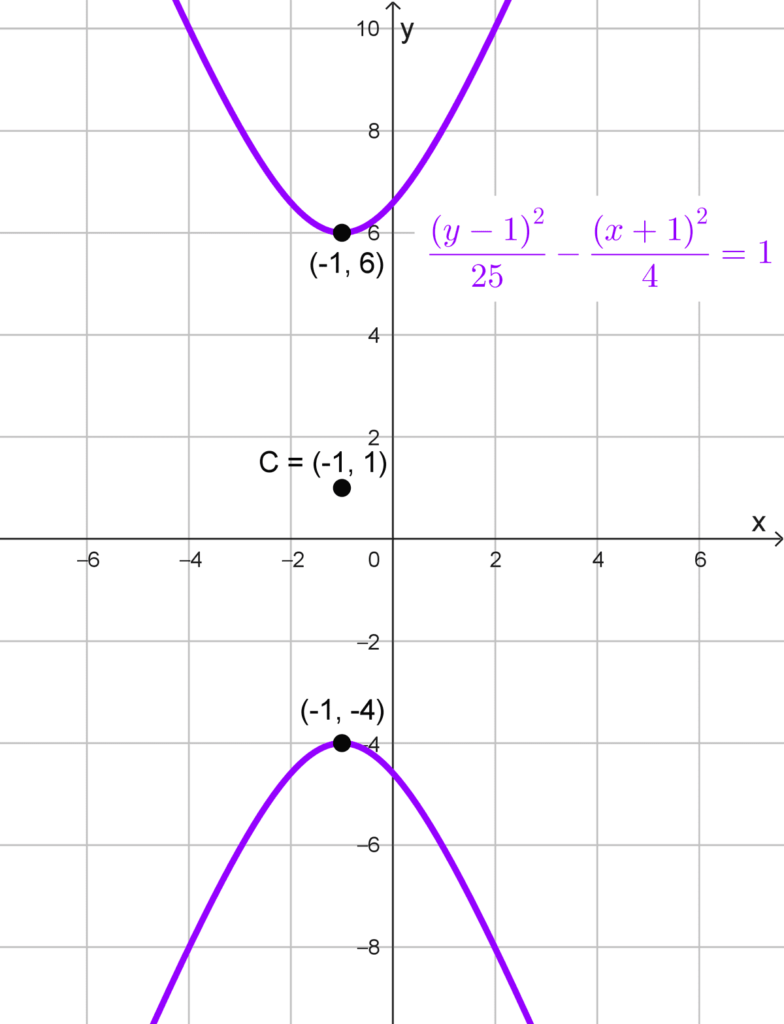
Obtener los vértices de la hipérbola de ecuación *\dfrac{(y-1)^2}{25}-\dfrac{(x+1)^2}{4}=1*
Solución: observamos por la ecuación que se trata de una hipérbola vertical, ya que el término positivo está asociado a *(y-1)^2.* Además, el centro de la hipérbola no está en el origen, sino en el punto (-1, 1).
Para una hipérbola con estas características, los vértices se encuentran a una distancia a del centro hacia arriba y hacia abajo, es decir, en los puntos (h, k ± a), donde (h, k) es el centro y a es la longitud del semieje transversal.
De la ecuación, identificamos que *a^2=25,* de donde *a=\sqrt{25}=5.* Por lo tanto, los vértices de la hipérbola están en los puntos (-1, 1+5) y (-1, 1-5), es decir, en (-1, 6) y (-1, -4).
Ejercicio 5
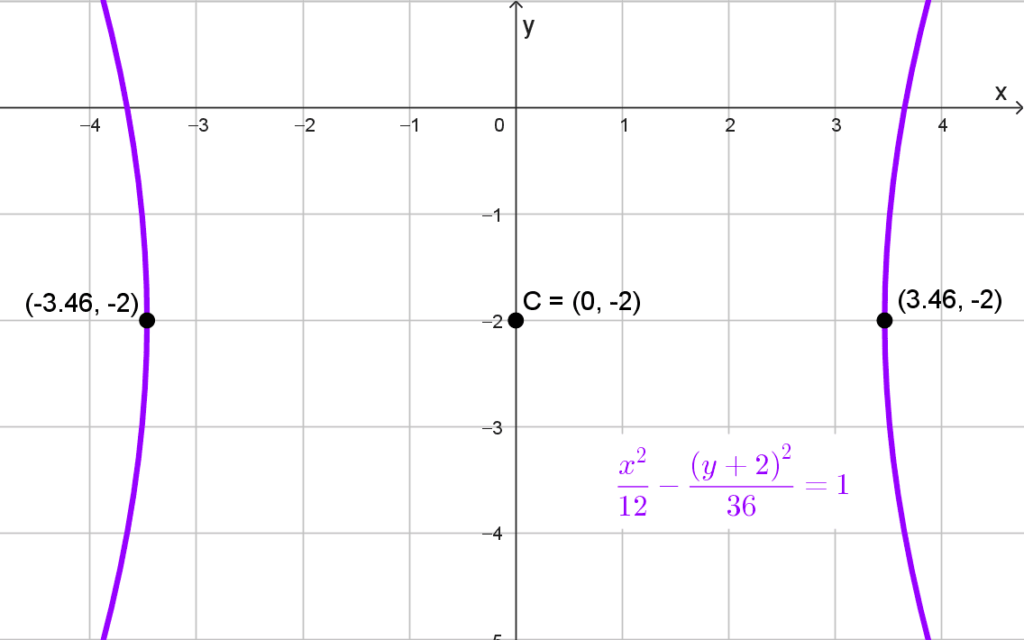
Encontrar los dos vértices de la hipérbola *3x^2-y^2-4y-40=0*
Solución: la ecuación no está en forma canónica sino general, así que no podemos obtener directamente los datos necesarios. Si completamos los cuadrados, encontramos una forma equivalente:
*\dfrac{x^2}{12}-\dfrac{(y+2)^2}{36}=1*
Aquí observamos que se trata de una hipérbola horizontal, ya que el término positivo está asociado a x2. Además, el centro de la hipérbola se encuentra en el punto (0, -2), indicado por la traslación en y.
Para una hipérbola con eje transversal horizontal, los vértices se encuentran a una distancia “a” del centro hacia la izquierda y la derecha, es decir, en los puntos (h ± a, k), donde (h, k) es el centro y a es la longitud del semieje transversal.
De la ecuación dada, identificamos que *a^2=12,* de donde *a=\sqrt{12}=2\sqrt{3}.* Por lo tanto, los vértices de la hipérbola están en los puntos *(0+2\sqrt{3}, -2)* y *(0-2\sqrt{3}, -2),* es decir, en *(2\sqrt{3}, -2) ~~y~~ (-2\sqrt{3}, -2).*
Utilizando redondeo, los vértices están aproximadamente en (3,46; -2) y (-3,46; -2).
Bibliografía
- Engler, A. y otros. (2020). Geometría Analítica. Universidad Nacional del Litoral.
- Fuller, G. y Tarwater, D. (1995). Geometría Analítica (7ma edición). Pearson Educación.
- Lehmann, C. (1989). Geometría Analítica. Limusa.
- Leithold. L. (1992). Álgebra y Trigonometría con Geometría Analítica. Oxford University Press.
- Mora, W., y Figueroa, G. (2009). Cónicas. Revista Digital Matemática, Educación e Internet.
- Márquez, A. y otros. (2009). Geometría Analítica. Prentice Hall.
- Raichman, S. y Totter, E. (2016). Geometría Analítica para Ciencias e Ingeniería. Universidad Nacional de Cuyo.
- Sullivan, M. (2006). Álgebra y Trigonometría. Pearson Educación.
- Swokowski, E. y Cole, J. (2009). Álgebra y Trigonometría con Geometría Analítica. Cengage Learning.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta

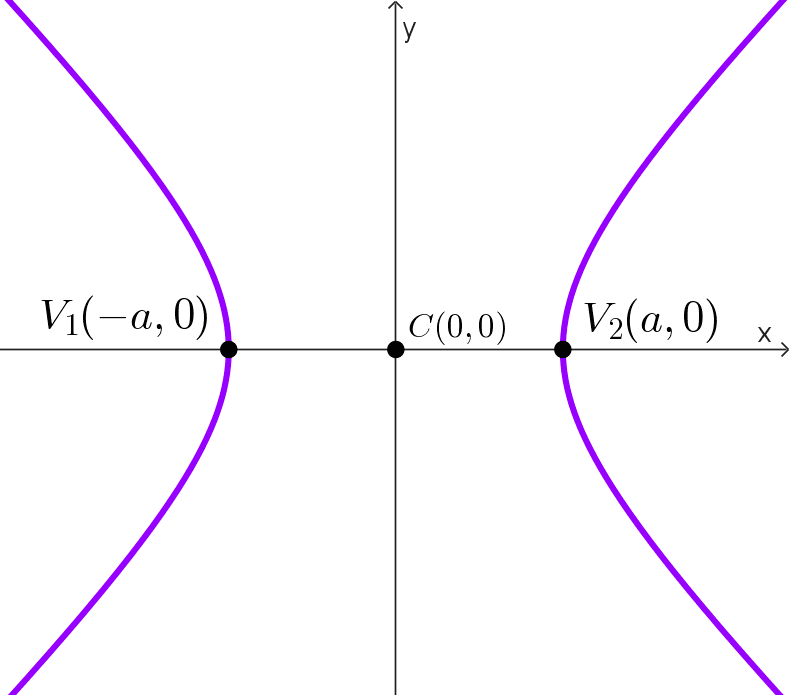
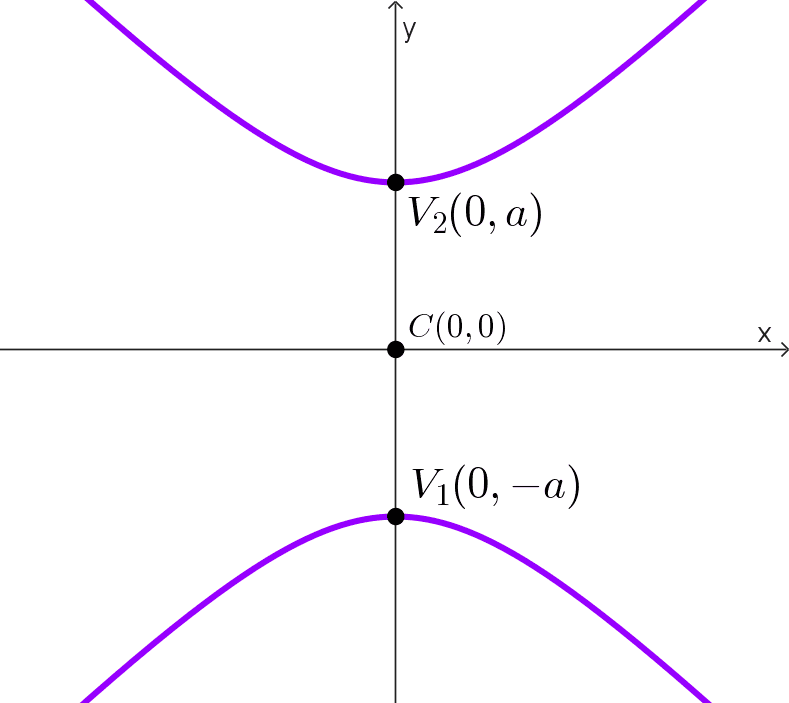
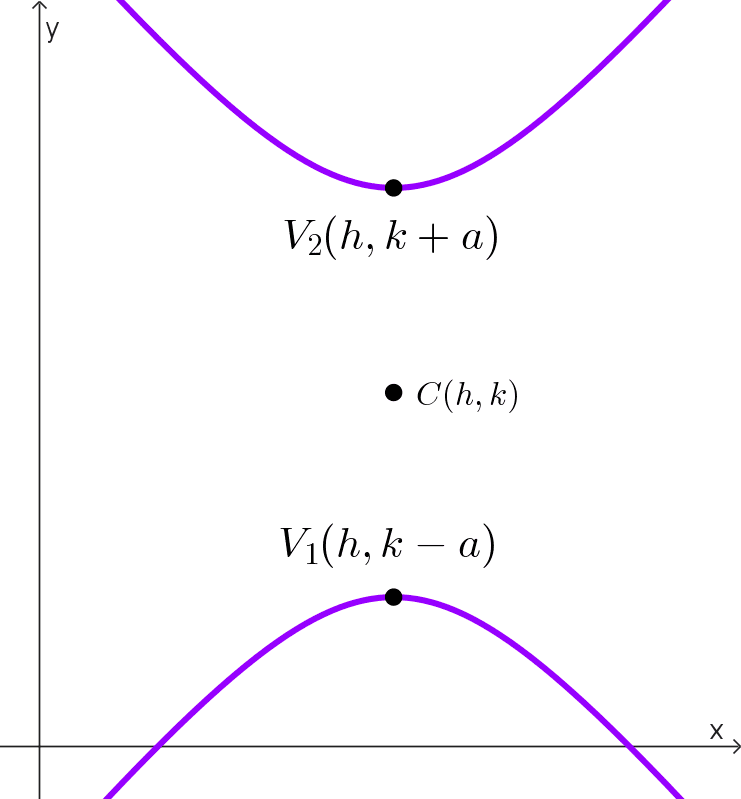
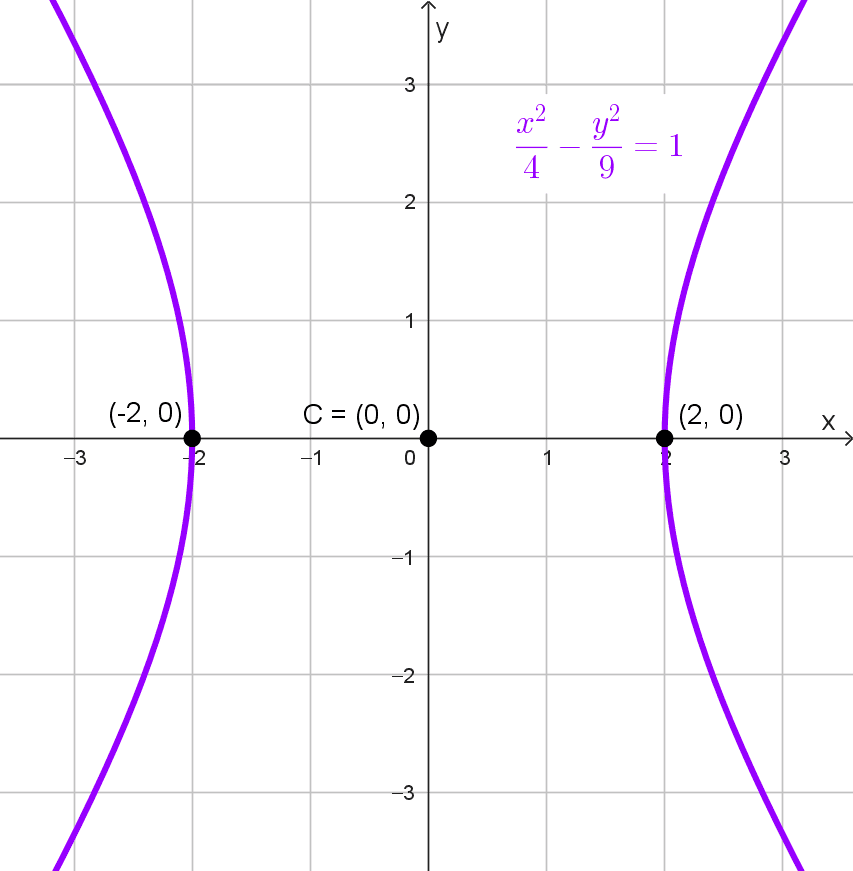
Otros artículos que pueden interesarte