Centro de una elipse
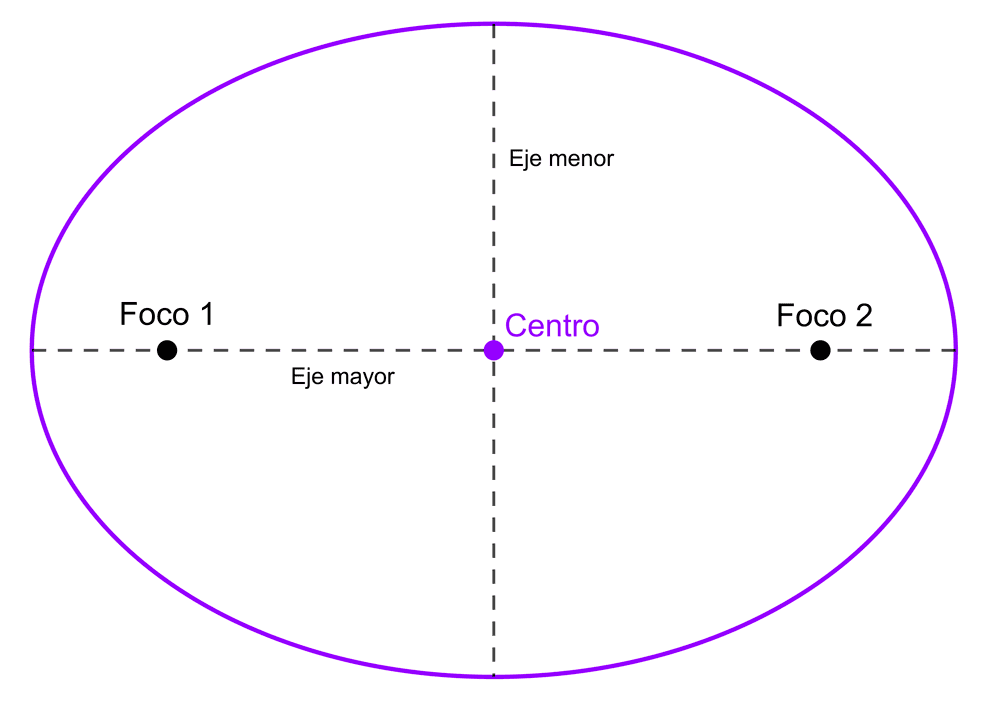
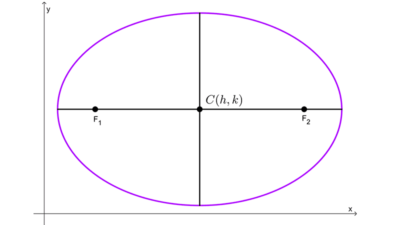
El centro de una elipse es el punto medio del segmento que une sus focos, también es el punto donde se cortan el eje mayor y el eje menor.
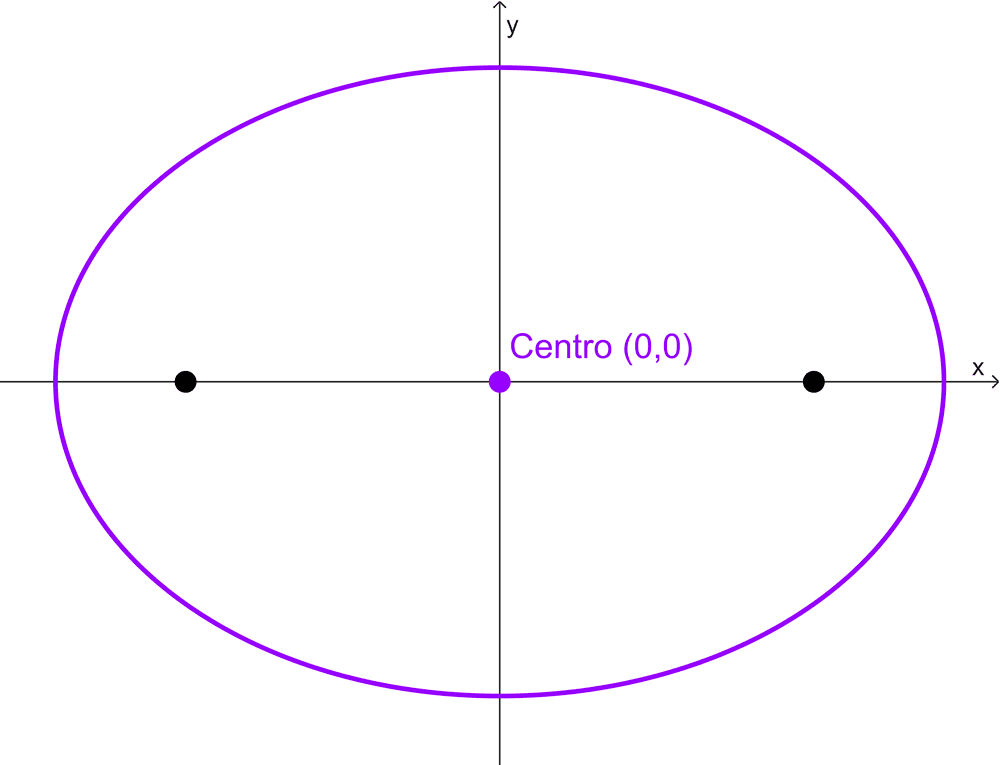
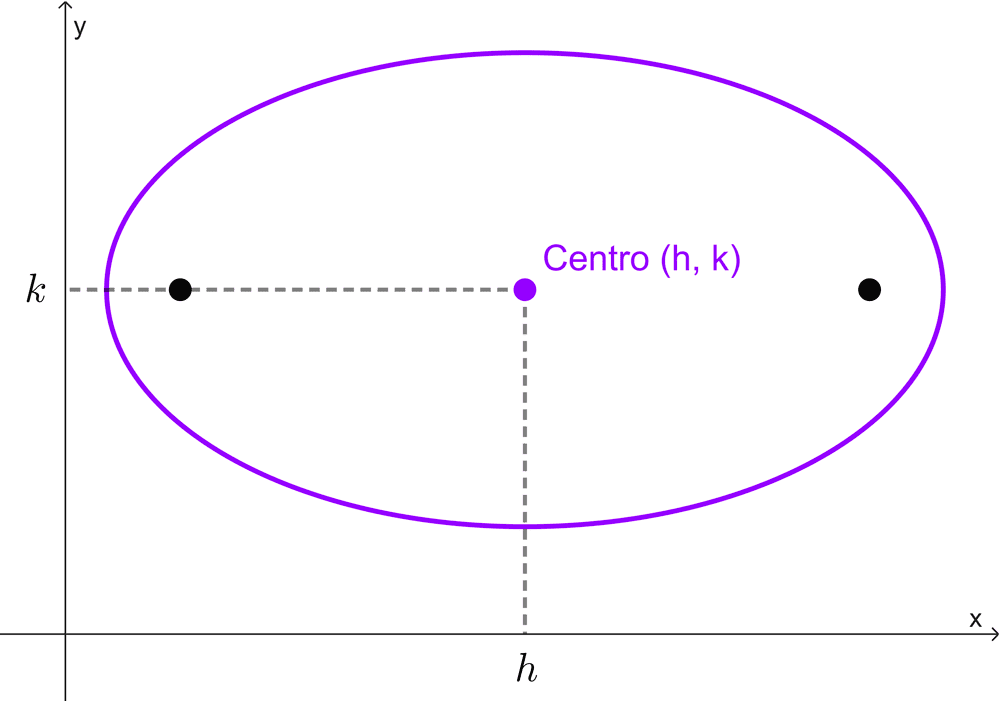
El centro puede estar en el origen de coordenadas (0, 0) o en cualquier otro punto del plano, generalmente simbolizado como (h, k). En el segundo caso, la elipse se traslada h unidades en forma horizontal y k unidades en forma vertical.
Para saber si el centro está en el origen o fuera del origen, podemos fijarnos en la ecuación canónica, la cual cambia según cada caso. También la ecuación general luce diferente dependiendo del centro. Esto puede verse en la siguiente tabla:
| Centro | Ecuación canónica u ordinaria | Ecuación general |
|---|---|---|
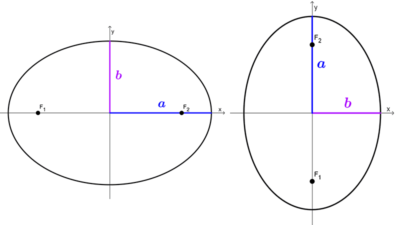
| En el origen, punto (0, 0) | *\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1* *\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1* | Ax² + Cy² + F = 0 A y C tienen el mismo signo. |
| Fuera del origen, punto (h, k) | *\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1* *\dfrac{(x-h)^2}{b^2}+\dfrac{(y-k)^2}{a^2}=1* | Ax² + Cy² + Dx + Ey + F = 0 A y C tienen el mismo signo. |
La ecuación ordinaria de la elipse con centro en el origen tiene las dos variables elevadas al cuadrado, mientras que si el centro es el punto (h, k), esas coordenadas aparecen restándose a la variable correspondiente. También, la ecuación general de la elipse con centro fuera del origen posee términos lineales (Dx y Ey), distinto al caso de cuando el centro es el origen, donde esos términos no existen.
Si los focos de una elipse coinciden con el centro, entonces la elipse es una circunferencia y los semiejes pasan a tener la misma longitud, igual al radio.
A continuación, veremos distintas formas de obtener el centro de la elipse si se tiene la ecuación, los focos, los vértices o la gráfica.
Importante: en este artículo tratamos solo un elemento de la elipse. Si aún no estás familiarizado con sus conceptos básicos, te recomiendo revisar antes el artículo principal, donde explicamos su definición, fórmulas, partes, tipos y características.
Índice
¿Cómo hallar el centro?
Existen distintas formas de hallar el centro dependiendo de los datos que se tengan.
A partir de la ecuación
Encontrar el centro de una elipse a partir de su ecuación requiere una inspección de la misma. Pueden seguirse los siguientes pasos:
- Si la ecuación no está en forma canónica, operar algebraicamente para que lo esté.
- Identificar el valor h, el cual aparece en el binomio con la variable x.
- Identificar el valor k, el cual aparece en el binomio con la variable y.
- El centro de la elipse es el punto C(h, k).
Si en la ecuación ordinaria las variables aparecen en la forma x2 e y2, entonces el centro es el origen de coordenadas.
Ejemplo 1
Hallar el centro de la elipse con ecuación *\dfrac{x^2}{16}+\dfrac{y^2}{9}=1*
Solución: la ecuación está en forma canónica y puede verse que las variables aparecen elevadas al cuadrado y no están dentro de paréntesis con otros valores. Por esto, el centro de la elipse es el origen de coordenadas: C(0, 0).
Ejemplo 2
Determinar el centro de la elipse *\dfrac{(x-1)^2}{9}+\dfrac{(y+2)^2}{25}=1*
Solución: la ecuación está en forma canónica y podemos notar que no es como la anterior, pues el centro no es el origen. Podemos obtener las coordenadas h y k del centro a partir de los binomios x - 1 y y + 2 igualándolos a la forma genérica:
*x-h=x-1 → -h=-1 → h=1*
*y-k=y+2 → -k=2 → k=-2*
Otra forma de verlo es cambiando de signo al número que aparece junto a cada variable. Por ejemplo, en x - 1 la variable aparece junto a un -1, entonces h = 1; en y + 2 la variable aparece junto a un +2, por tanto cambiando de signo se obtiene que k = -2.
En conclusión, el centro de la elipse es C(1, -2).
Ejemplo 3
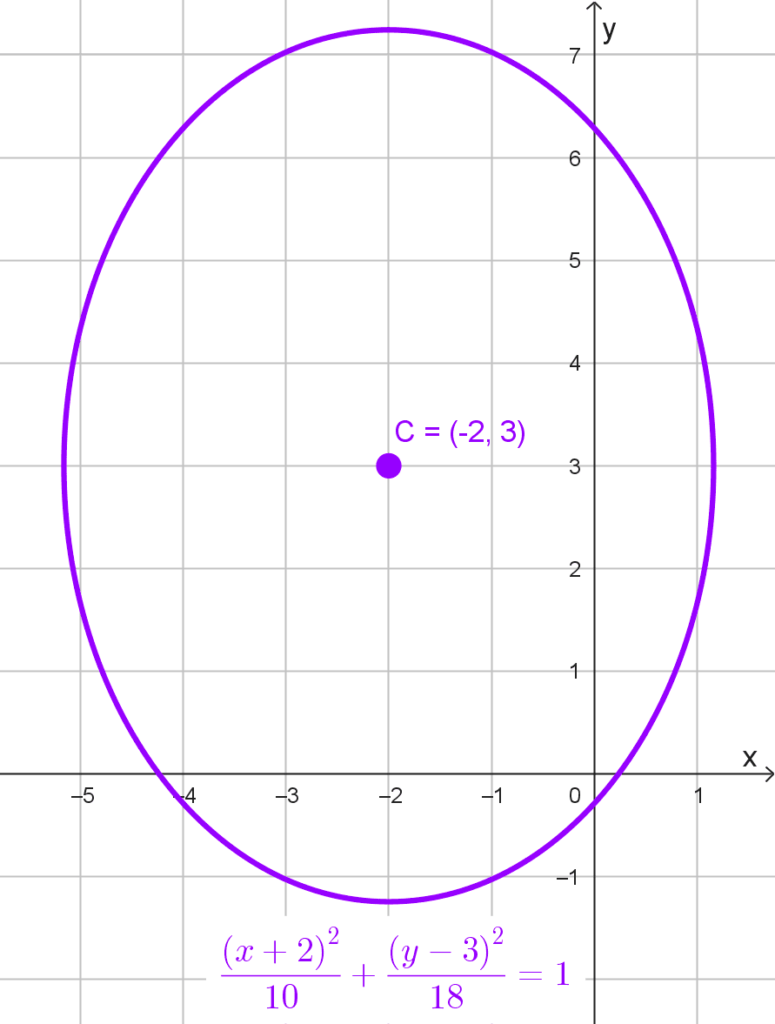
Calcular el centro de la elipse *\dfrac{(x+2)^2}{10}+\dfrac{(y-3)^2}{18}=1*
Solución: la elipse está en forma canónica, identificamos de la ecuación las coordenadas del centro:
*x-h=x+2 → -h=2 → h=-2*
*y-k=y-3 → -k=-3 → k=3*
Por tanto, el centro es el punto C(-2, 3)
Ejemplo 4
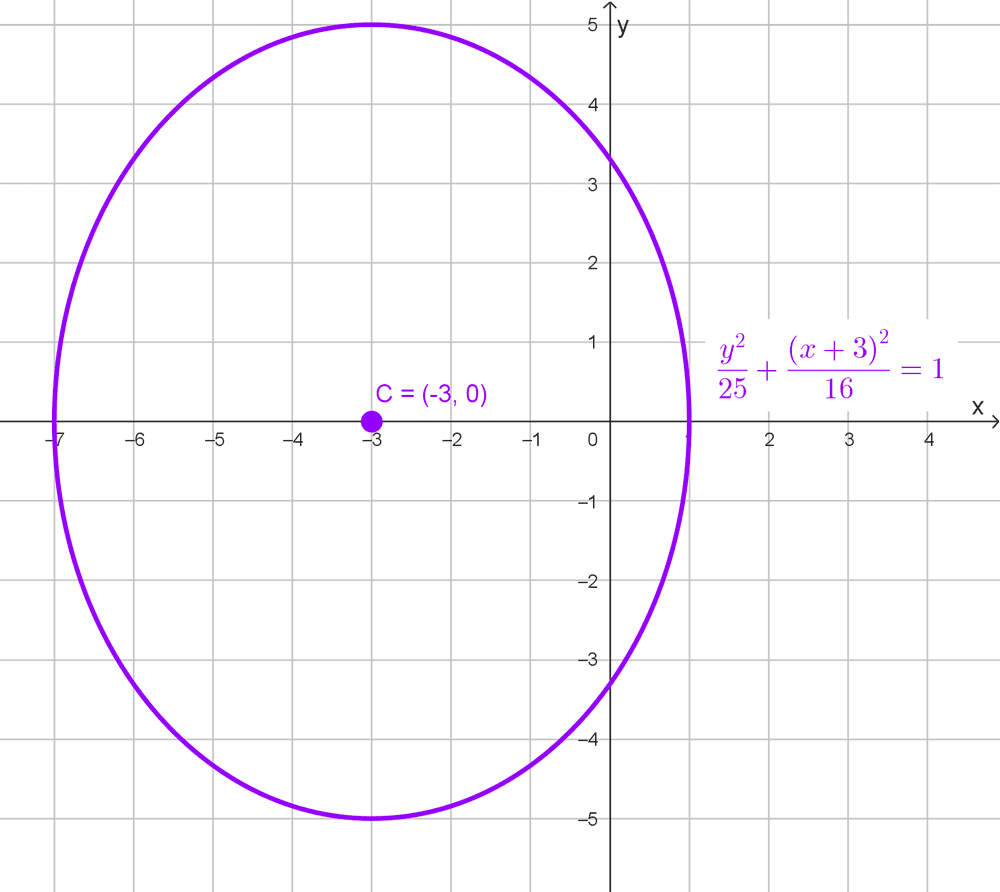
Encontrar el centro de *\dfrac{y^2}{25}+\dfrac{(x+3)^2}{16}=1*
Solución: la ecuación está en forma canónica, sin embargo se observa que la variable x aparece dentro de un binomio y la variable y no. Podemos proceder como hicimos antes:
*x-h=x+3 → -h=3 → h=-3*
*y-k=y → -k=0 → k=0*
Por lo tanto, el centro es el punto C(-3, 0) que está sobre el eje x.
Ejemplo 5
Obtener el centro de la elipse *2x^2+4x+7y^2-28y-40=0*
Solución: la elipse no está en forma canónica sino general, para sacar el centro primero debemos completar los cuadrados hasta llegar a la forma ordinaria. Si hacemos esto obtenemos que la expresión equivalente es:
*\dfrac{(x+1)^2}{35}+\dfrac{(y-2)^2}{10}=1*
De aquí se extrae que h = -1 y k = -(-2) = 2, por tanto el centro de la elipse es el punto C(-1, 2).
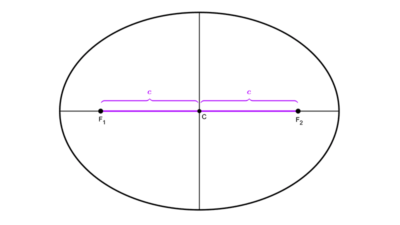
A partir de los focos
Si se tienen los focos de la elipse F1(x1, y1) y F2(x2, y2), entonces el centro es por definición el punto medio entre ellos y sus coordenadas pueden obtenerse con la fórmula del punto medio, que consiste en sumar las coordenadas homólogas de los focos y dividir entre dos, así:
*C\left(\dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2}\right)*
Ejemplo 1
Una elipse tiene focos en (2, 4) y (-2, 4), obtener las coordenadas de su centro.
Solución: como el centro es el punto medio entre los focos, usamos la fórmula que vimos antes:
*C\left(\dfrac{2+(-2)}{2}, \dfrac{4+4}{2}\right) → C\left(\dfrac{0}{2}, \dfrac{8}{2}\right) → C(0, 4)*
Por tanto, el centro es el punto C(0, 4).
Ejemplo 2
Los focos de una elipse tienen coordenadas (1, 5) y (1, -1), calcular el centro.
Solución: aplicando la fórmula del punto medio:
*C\left(\dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2}\right)→C\left(\dfrac{1+1}{2}, \dfrac{5+(-1)}{2}\right)→C\left(\dfrac{2}{2}, \dfrac{4}{2}\right) → C(1, 2)*
En conclusión, el centro es el punto C(1, 2)
La fórmula aplicada también funciona en una elipse rotada, es decir, aquella que presenta una inclinación de su eje mayor con respecto a los ejes coordenados.
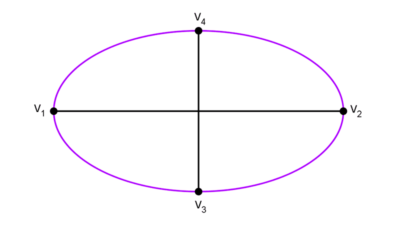
A partir de los vértices
Los vértices están a la misma distancia del centro, al igual que los focos, así que puede usarse la fórmula del punto medio para hallar el centro teniendo los vértices, ya sean los principales (extremos del eje mayor) o los secundarios (extremos del eje menor).
Dados los dos vértices principales o secundarios V1(x1, y1) y V2(x2, y2) de una elipse, el centro está es el siguiente punto:
*C\left(\dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2}\right)*
Ejemplo
Los vértices principales de una elipse tienen coordenadas (-1, 3) y (9, 3), determinar su centro.
Solución: aplicando la fórmula del punto medio podemos sacar el centro:
*C\left(\dfrac{-1+9}{2}, \dfrac{3+3}{2}\right) → C\left(\dfrac{8}{2}, \dfrac{6}{2}\right) → C(4, 3)*
Por lo tanto, el centro es el punto C(4, 3).
Si en lugar de tener las coordenadas de los dos vértices principales o los dos secundarios se tienen uno y uno, entonces no se puede usar la fórmula del punto medio, en cambio se pueden obtener las coordenadas del centro de la siguiente forma.
Si se tiene un vértice principal VP (xP, yP) y un vértice secundario VS (xS, yS) y la elipse es horizontal (|xP - xS| > |yP - yS|) entonces el centro es: C(xS, yP). Si, en cambio, la elipse es vertical (|xP - xS| < |yP - yS|), el centro es C(xP, yS). Esto se puede ver mejor si se grafican los puntos en el plano cartesiano.
A partir de la gráfica
Si se dispone de la gráfica de la elipse donde se muestran los ejes, los focos o los vértices, el centro puede obtenerse como la intersección de los ejes o el punto medio entre los focos o los vértices.
Ejemplo
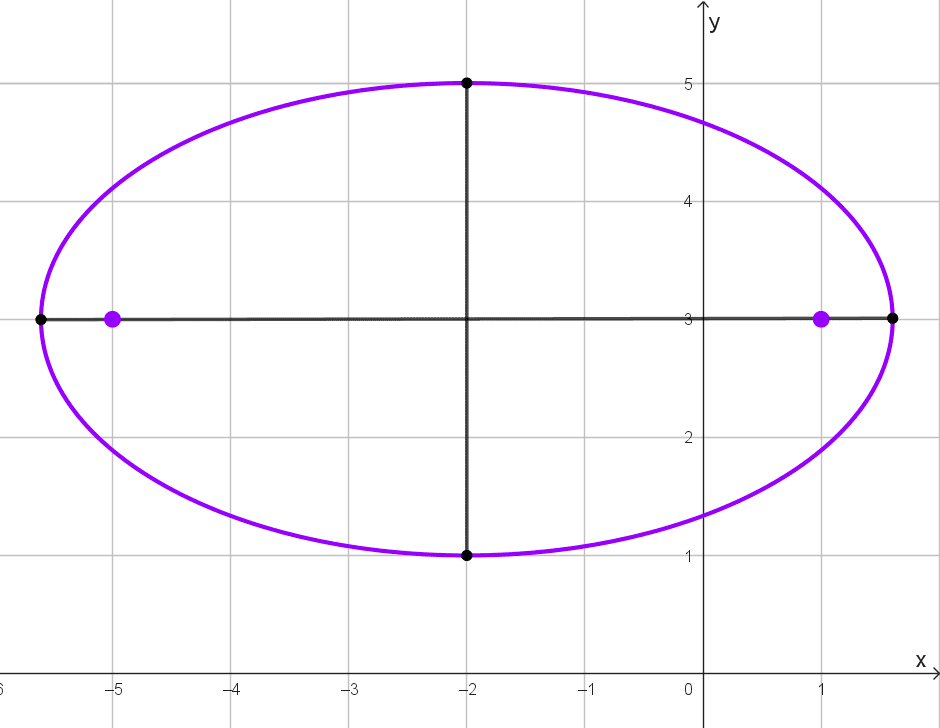
A continuación se grafica una elipse, ¿cuál es su centro?
La intersección de los ejes de la elipse ocurre en el punto (-2, 3), por tanto, ese es su centro.
Recursos adicionales
Los siguientes videos pueden ayudarte a la hora de determinar el centro de una elipse:
Bibliografía
- Engler, A. y otros. (2020). Geometría Analítica. Universidad Nacional del Litoral.
- Fuller, G. y Tarwater, D. (1995). Geometría Analítica (7ma edición). Pearson Educación.
- Lehmann, C. (1989). Geometría Analítica. Limusa.
- Leithold. L. (1992). Álgebra y Trigonometría con Geometría Analítica. Oxford University Press.
- Mora, W., y Figueroa, G. (2009). Cónicas. Revista Digital Matemática, Educación e Internet.
- Márquez, A. y otros. (2009). Geometría Analítica. Prentice Hall.
- Raichman, S. y Totter, E. (2016). Geometría Analítica para Ciencias e Ingeniería. Universidad Nacional de Cuyo.
- Sullivan, M. (2006). Álgebra y Trigonometría. Pearson Educación.
- Swokowski, E. y Cole, J. (2009). Álgebra y Trigonometría con Geometría Analítica. Cengage Learning.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta


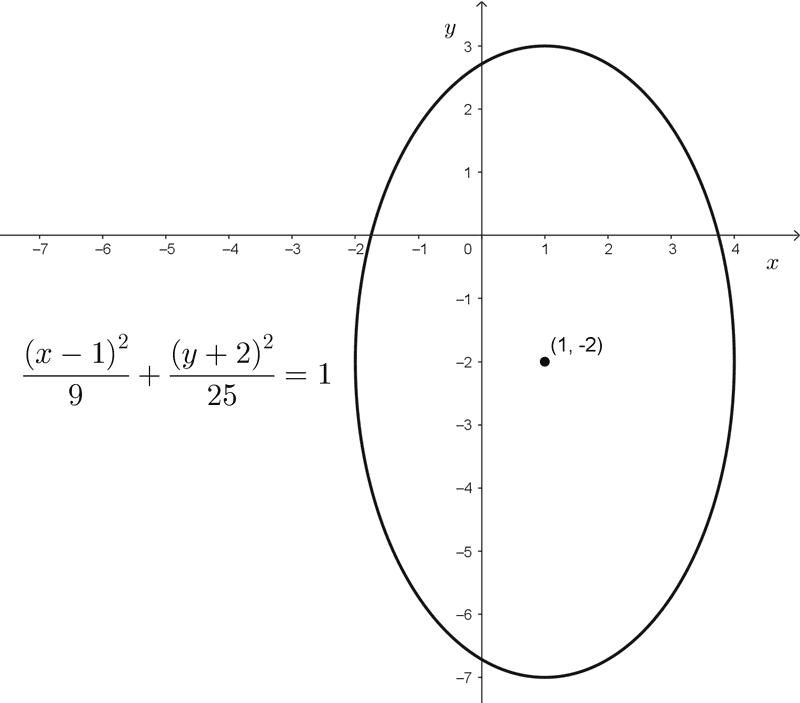



Otros artículos que pueden interesarte