
Elipse: qué es, ecuación, elementos y ejemplos
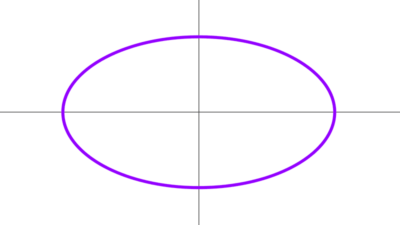
Una elipse es una curva plana, cerrada y simple que se define como el lugar geométrico de todos los puntos de un plano tales que la suma de sus distancias a dos puntos fijos llamados focos es constante.
La elipse también es una sección cónica que resulta del corte de un cono circular recto con un plano que pasa por todas sus generatrices pero no es perpendicular al eje del cono. La orientación y la inclinación del plano determinan la forma de la elipse resultante.
A continuación, explicaremos más aspectos sobre la elipse en matemáticas: sus elementos, ecuaciones, ejemplos, características y usos, entre otras cosas.
Índice
Elementos
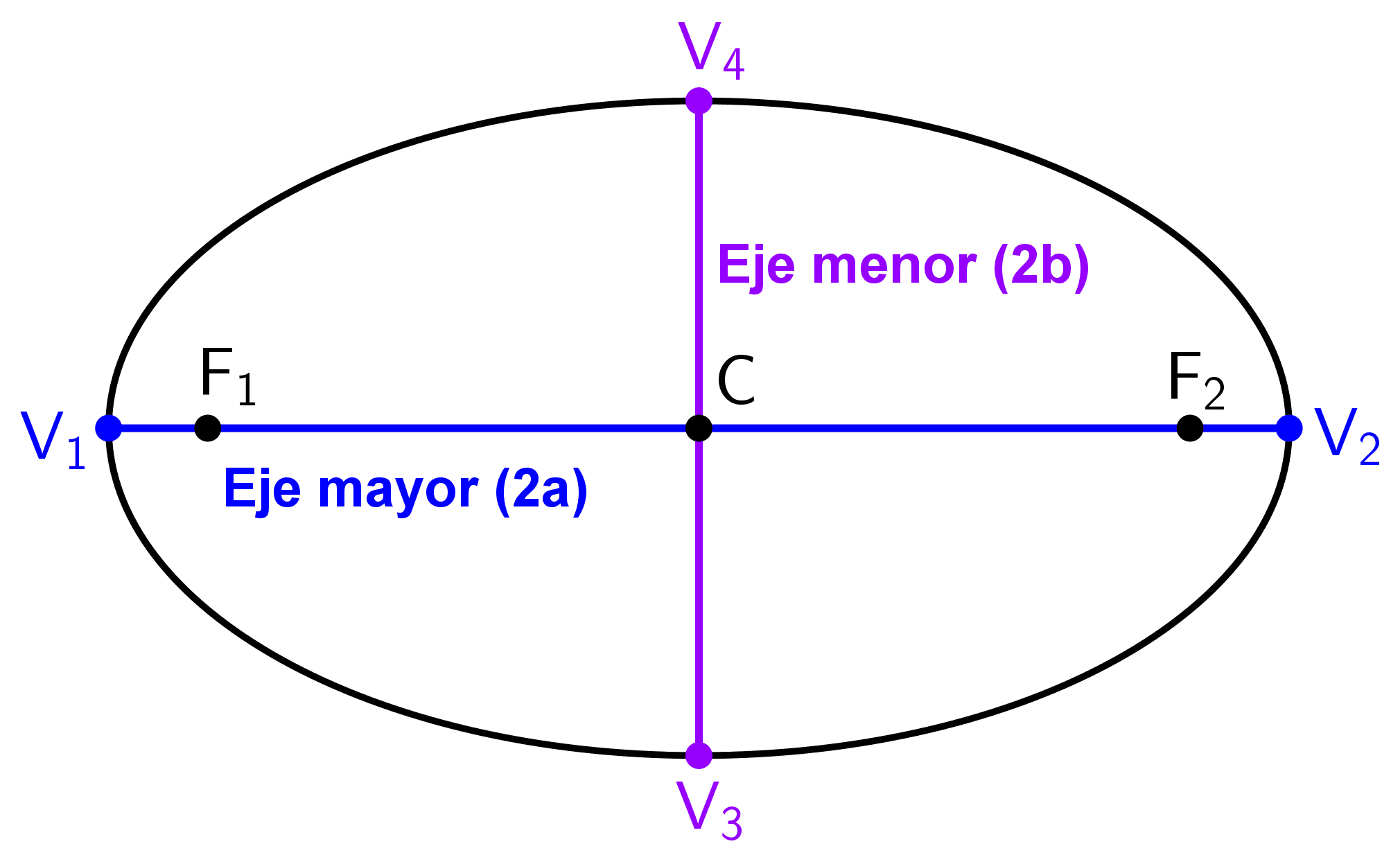
La elipse tiene elementos característicos que permiten definirla, analizar su geometría y comprender sus propiedades. Las partes fundamentales de una elipse son:
- Focos (F1 y F2): son dos puntos fijos del plano. La característica fundamental de una elipse es que la suma de las distancias desde cualquier punto de la elipse a estos dos focos es constante.
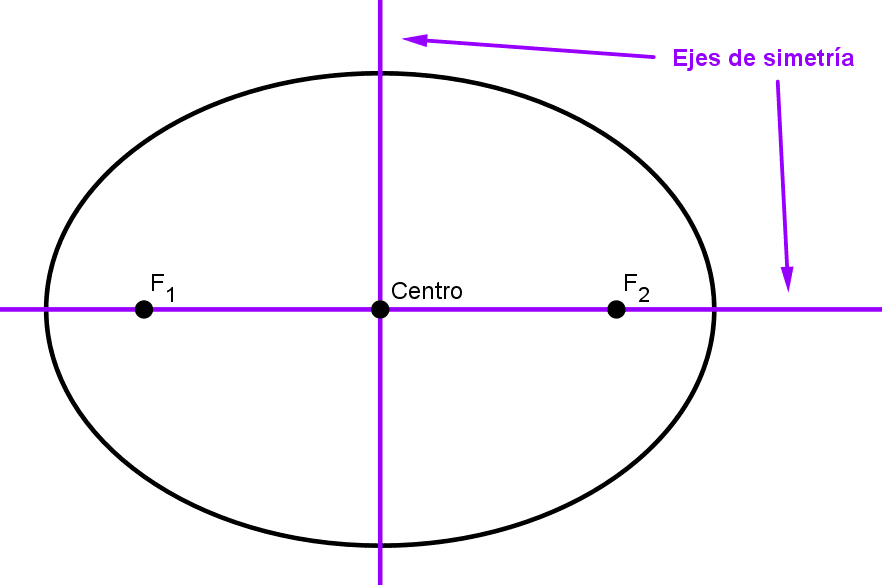
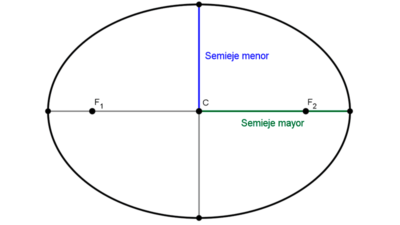
- Centro (C): es el punto medio del segmento que une los focos y coincide con el centro de simetría de la figura.
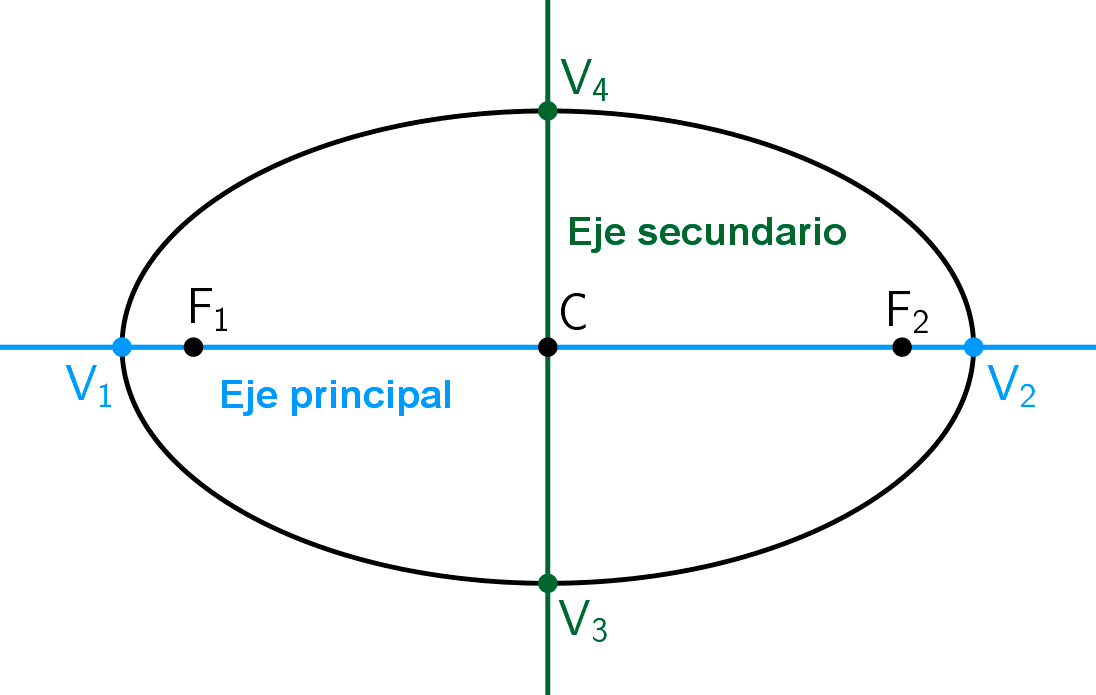
- Eje focal o principal: es la recta que pasa por los focos y el centro, es un eje de simetría de la figura.
- Eje secundario o normal: es la recta que pasa por el centro de la elipse y es perpendicular al eje focal, es el segundo eje de simetría.
- Eje mayor (2a): es el segmento de mayor longitud que pasa por el centro y los focos, y se extiende hasta los extremos de la curva. Representa la mayor distancia entre dos puntos opuestos de la elipse y su longitud se denota como 2a. La mitad de este segmento recibe el nombre de semieje mayor (a). El eje mayor está contenido en el eje focal.
- Eje menor (2b): es el segmento perpendicular al eje mayor que pasa por el centro y se extiende hasta los extremos de la curva en esa dirección. Representa la menor distancia entre dos puntos opuestos de la elipse y su longitud se denota como 2b. La mitad de este segmento recibe el nombre de semieje menor (b). El eje menor está contenido en el eje secundario.
- Radios vectores: son los segmentos que unen un punto cualquiera P de la elipse con cada uno de los focos. La suma de las longitudes de los radios vectores es siempre igual a una constante: la longitud del eje mayor (2a), así: d(P, F1) + d(P, F1) = 2a.
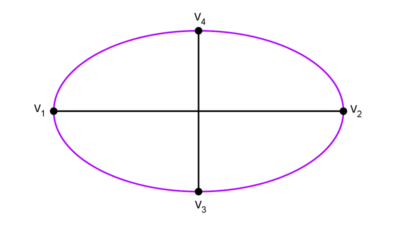
- Vértices: son los cuatro puntos de intersección de la elipse con sus ejes. Se representan con las letras V1, V2, V3 y V4. Los que están sobre el eje mayor se llaman vértices principales y los que están sobre el menor se llaman vértices secundarios o covértices.
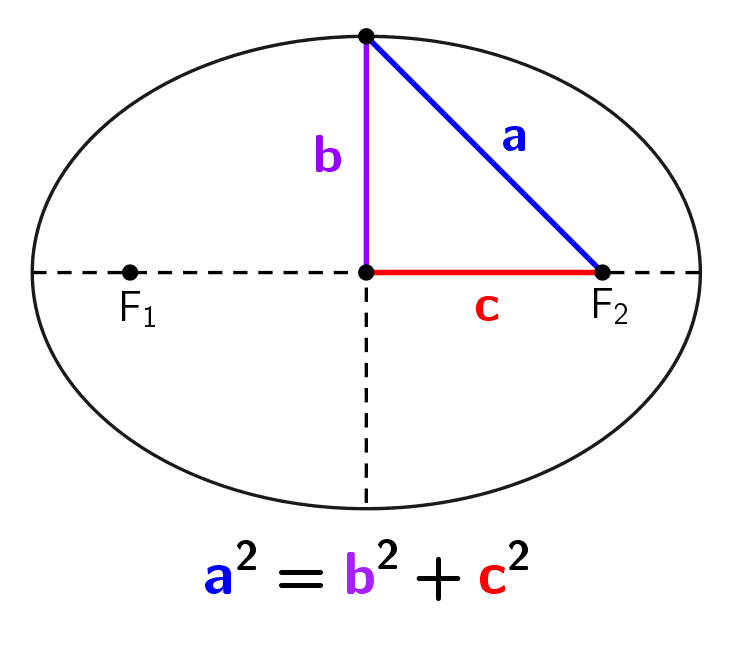
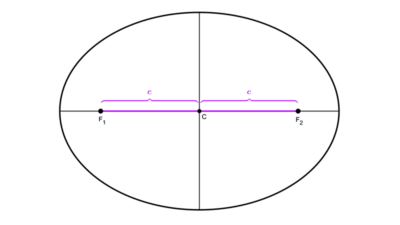
- Distancia focal (2c): es la distancia entre los focos, denotada como 2c, donde c es la distancia desde el centro hasta uno de los focos, conocida como semidistancia focal. Esta última se relaciona con los semiejes a través de la ecuación c2 = a2 - b2.
- Excentricidad (e o ε): es el cociente entre la distancia del centro al foco y la distancia del centro a un vértice principal: e = c / a. Este número mide el grado de "redondez" o "aplastamiento" de la elipse y siempre es menor que 1 (0 ≤ e < 1).
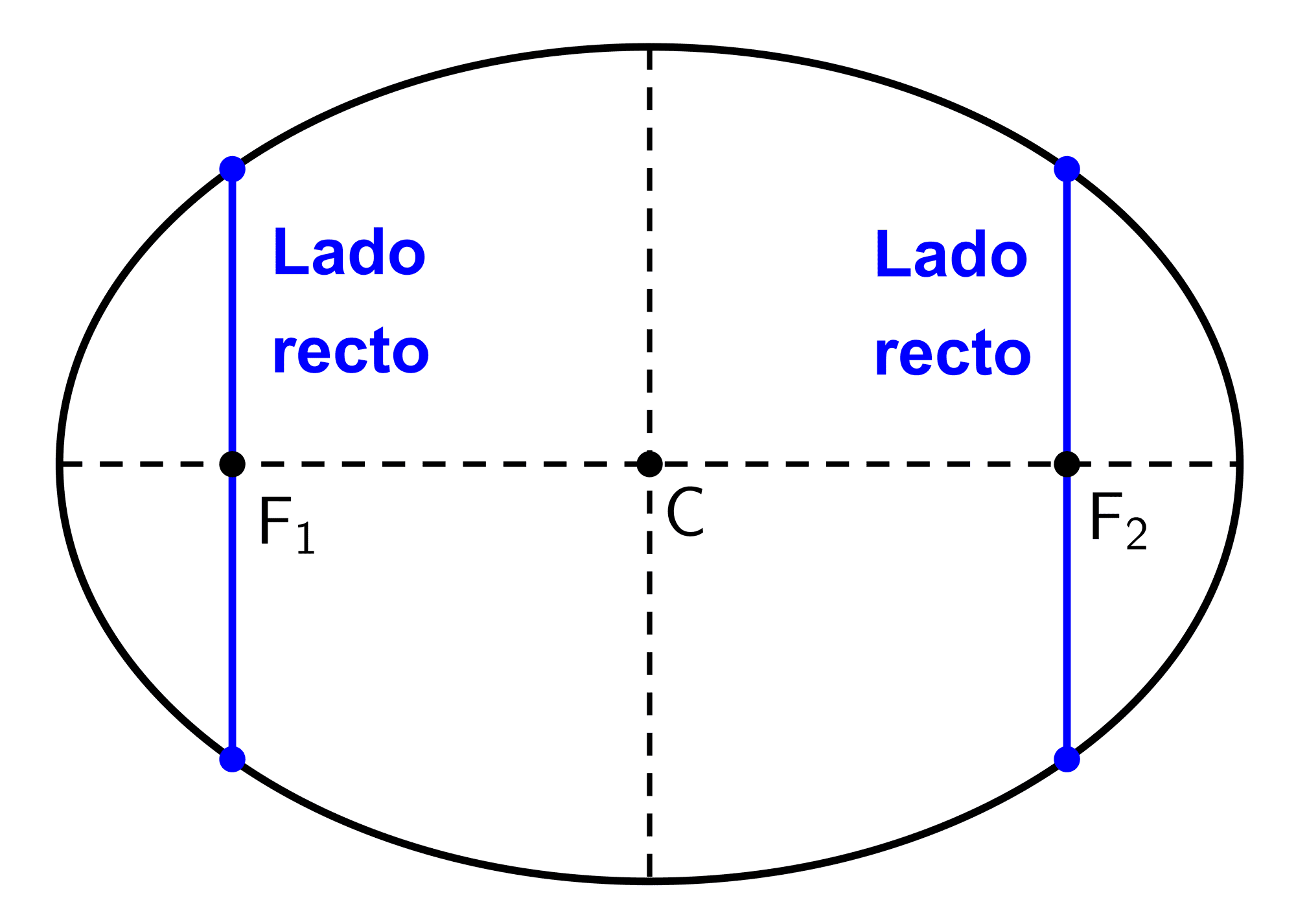
- Lado recto: es un segmento que une dos puntos de la elipse, es perpendicular al eje mayor y pasa por uno de los focos. Toda elipse tiene dos lados rectos cuyas longitudes son LR = 2b2 / a.

Una elipse, al igual que las demás secciones cónicas, puede describirse mediante distintas ecuaciones (general, paramétrica, polar, entre otras). Entre todas ellas, la más utilizada es la llamada ecuación canónica (también llamada ordinaria o reducida), que se expresa en coordenadas cartesianas y permite identificar de manera directa los elementos principales de la elipse.
Llamamos ecuación canónica a la forma más simple y estandarizada de una curva, aquella que resalta de inmediato sus características esenciales. En el caso de la elipse, su ecuación canónica incluye las coordenadas del centro y las longitudes de sus semiejes al cuadrado, lo que nos da la información clave para representarla gráficamente y analizar sus propiedades geométricas.
A continuación, veremos en detalle la ecuación canónica de la elipse. Más adelante en este artículo estudiaremos la ecuación general, la paramétrica y la polar.
Ecuación canónica
La ecuación canónica u ordinaria de una elipse cambia dependiendo del centro y de la orientación que tenga el eje mayor de la elipse.
1) Si el centro es el origen de coordenadas (0, 0), las ecuaciones son:
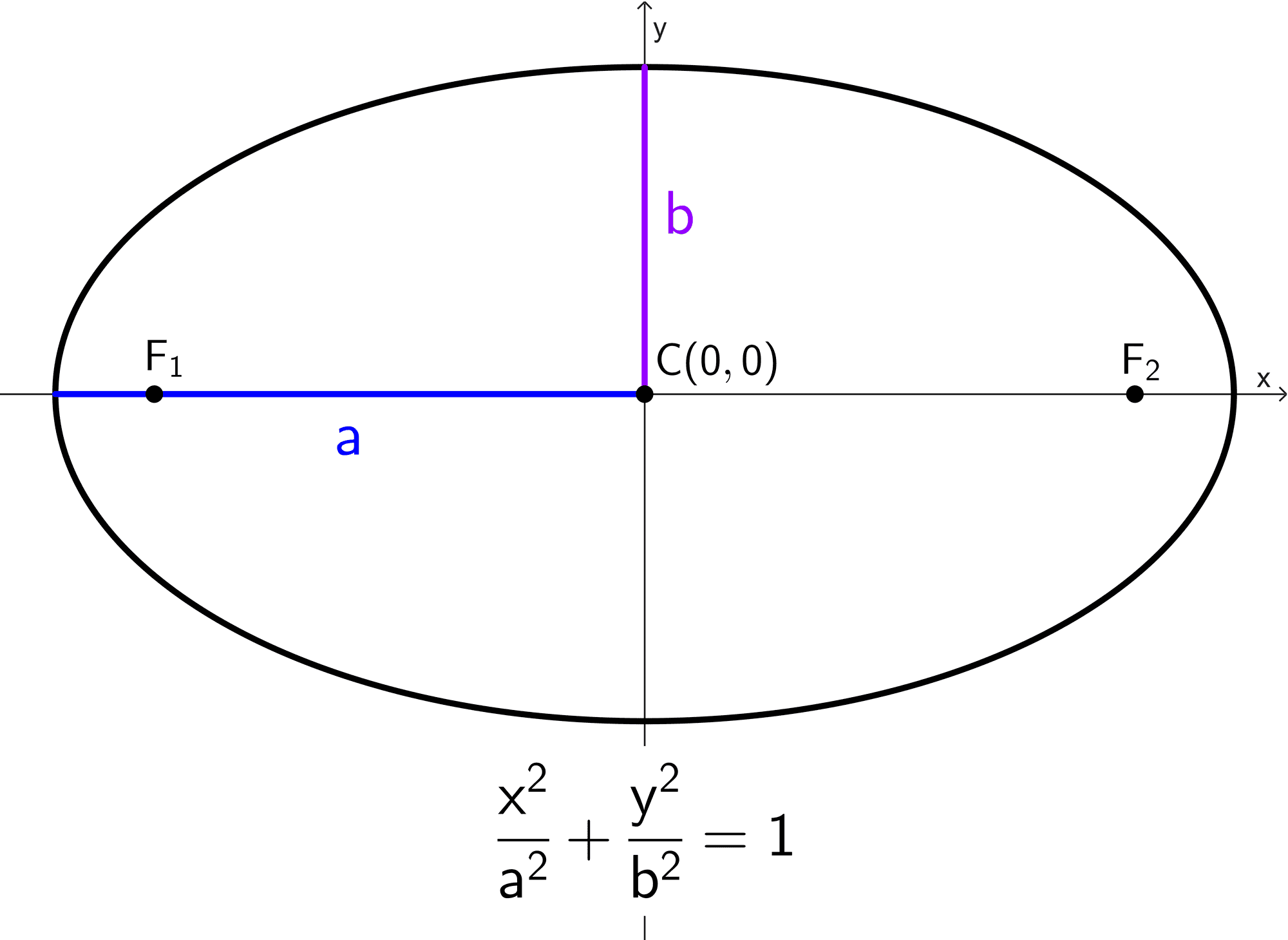
- Elipse horizontal (eje mayor sobre el eje X): *\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1*
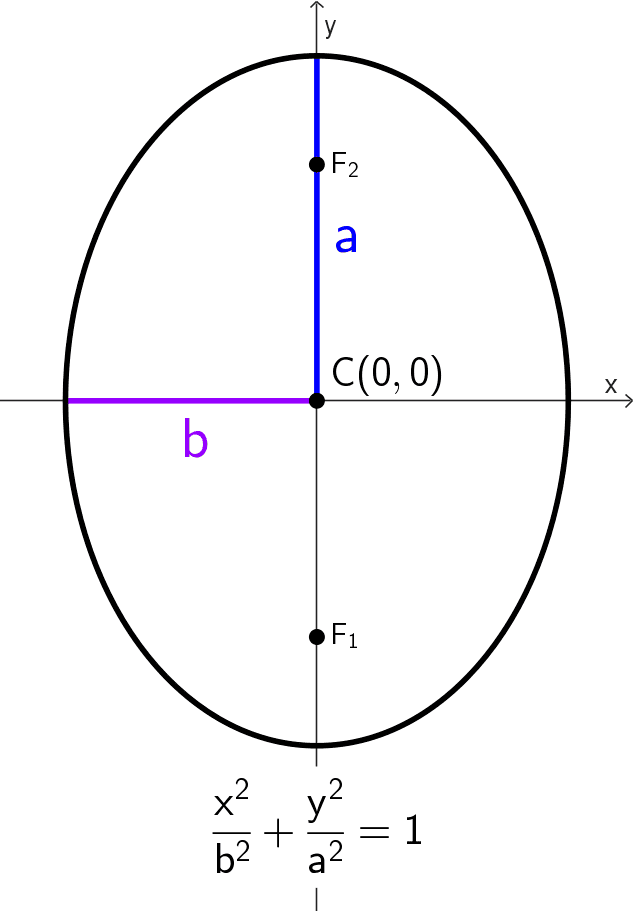
- Elipse vertical (eje mayor sobre el eje Y: *\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1*
2) Si el centro es un un punto (h, k) del plano cartesiano:
- Elipse horizontal (eje mayor paralelo al eje X): *\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1*
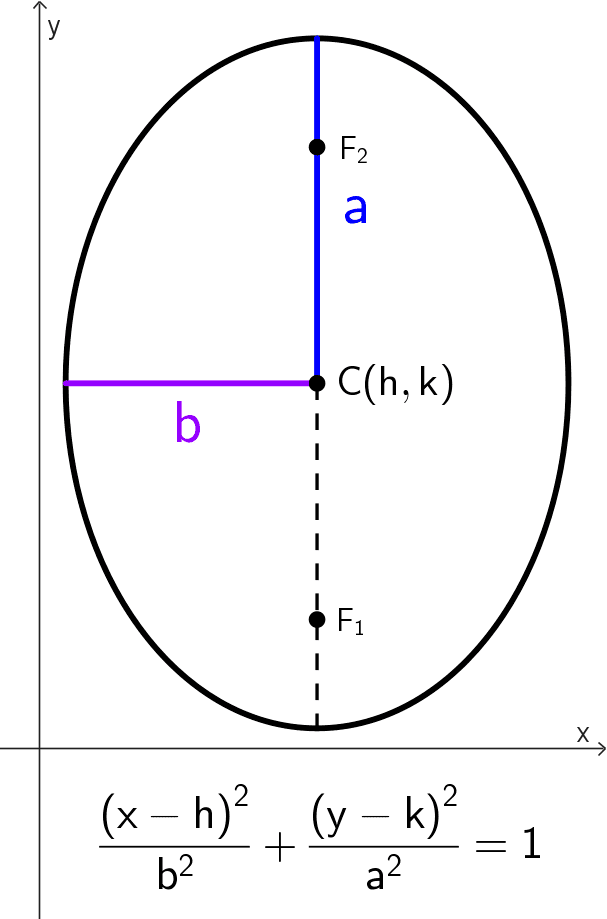
- Elipse vertical (eje mayor paralelo al eje Y): *\dfrac{(x-h)^2}{b^2}+\dfrac{(y-k)^2}{a^2}=1*
En los cuatro casos, a es la longitud del semieje mayor, b es la longitud del semieje menor y a > b. Las demostraciones de estas fórmulas se harán más adelante en este artículo. A continuación, vemos la gráfica de cada caso.
Cómo identificar los elementos a partir de la ecuación
- La orientación de la elipse depende de dónde se encuentre el denominador mayor: si está debajo de la variable x2, la elipse es horizontal; en cambio, si está debajo de y2, la elipse es vertical.
- Los semiejes se obtienen extrayendo la raíz cuadrada de los denominadores. El mayor de los dos corresponde al semieje mayor (a) y el menor al semieje menor (b).
- El centro de la elipse se identifica observando los términos que acompañan a cada variable dentro de la ecuación. La coordenada en x (abscisa) aparece junto a la variable x, y la coordenada en y (ordenada) aparece junto a la variable y. Ambas coordenadas aparecen cambiadas de signo. Si no aparece ningún número junto a la variable, significa que la coordenada correspondiente es cero. En el caso de que ni x ni y estén acompañadas por un número, el centro está en el origen de coordenadas.
Los focos y los vértices de la elipse también pueden extraerse de su ecuación canónica, y lo vemos en la siguiente tabla. Recordemos que la semidistancia focal (c) se calcula a partir de la relación fundamental: *c=\sqrt{a^b-b^2}.*
| Ecuación | Eje mayor | Centro | Focos | Vértices |
|---|---|---|---|---|
| *\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1* | Sobre el eje x | (0, 0) | (±c, 0) | (±a, 0) (0, ±b) |
| *\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1* | Sobre el eje y | (0, 0) | (0, ±c) | (0, ±a) (±b, 0) |
| *\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1* | Paralelo al eje x | (h, k) | (h ± c, k) | (h ± a, k) (h, k ± b) |
| *\dfrac{(x-h)^2}{b^2}+\dfrac{(y-k)^2}{a^2}=1* | Paralelo al eje y | (h, k) | (h, k ± c) | (h, k ± a) (h ± b, k) |
Ejemplos
Veremos algunos ejemplos de elipses con sus ecuaciones, cómo obtener sus elementos principales y sus gráficas.
Ejemplo 1
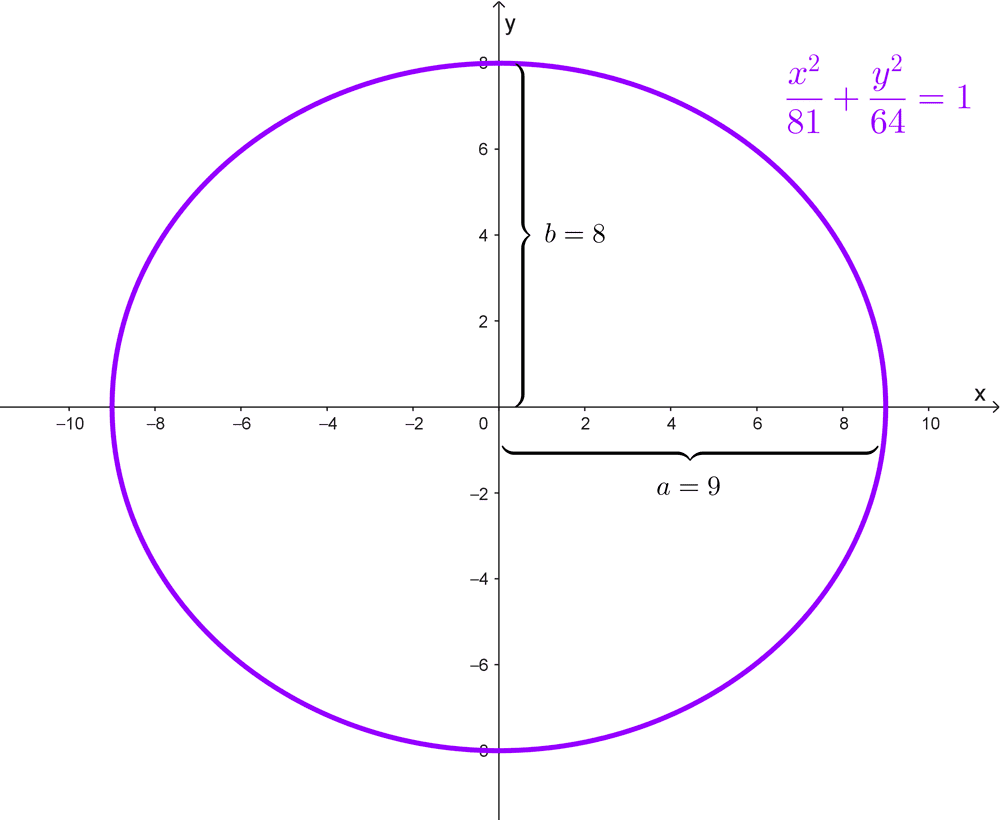
*\dfrac{x^2}{81}+\dfrac{y^2}{64}=1*
La ecuación corresponde a una elipse centrada en el origen, porque las variables aparecen solas en los numeradores. Los denominadores son 81 y 64, debido a que el denominador de x2 es mayor al de y2, la elipse tiene una orientación horizontal (eje mayor sobre el eje x).
Extraemos las longitudes de los semiejes sacando raíz cuadrada a los denominadores. El más grande corresponderá al semieje mayor (a) y el más pequeño al semieje menor (b):
*a=\sqrt{81}=9*
*b=\sqrt{64}=8*
Por tanto, la elipse es horizontal, tiene semiejes *a=9,* *b=8* y centro en el origen de coordenadas (0, 0). Podemos ver su gráfica a continuación.
Ejemplo 2
*\dfrac{x^2}{4}+\dfrac{y^2}{25}=1*
La ecuación corresponde a una elipse centrada en el origen, por la misma razón que el ejemplo anterior. Los denominadores son 4 y 25; como el denominador de y2 es mayor que el de x2, la elipse tiene una orientación vertical (su eje mayor está sobre el eje y).
Obtenemos las longitudes de sus semiejes:
*a=\sqrt{25}=5*
*b=\sqrt{4}=2*
Por tanto, la elipse es vertical, con semiejes *a=5, b=2* y centro en el origen de coordenadas.
Ejemplo 3
*\dfrac{x^2}{16}+\dfrac{y^2}{9}=1*
Se trata de una elipse con centro en el origen. En este caso, los denominadores son 16 y 9. Dado que el denominador de x2 es mayor que el de y2, el eje mayor se encuentra sobre el eje x, por lo que la elipse es horizontal.
Calculamos los semiejes tomando la raíz cuadrada de cada denominador:
*a=\sqrt{16}=4, \quad b=\sqrt{9}=3*
En consecuencia, la elipse es horizontal, con semiejes *a=4*, *b=3* y centro en el origen (0, 0).
Ejemplo 4
*\dfrac{(x-1)^2}{9}+\dfrac{(y+2)^2}{25}=1*
Identificamos que la ecuación tiene la forma de una elipse centrada fuera del origen. Observamos que los denominadores son 9 y 25. Como el mayor está bajo y2, el eje mayor es paralelo al eje y, de modo que la elipse es vertical.
Ahora identificamos el centro. Recordemos que en la ecuación aparece *(x-h)^2* y *(y-k)^2.* En este caso tenemos *(x-1)^2* y *(y+2)^2.* Al comparar, se obtiene:
*x-h=x-1 \quad → \quad h=1*
*y-k=y+2 \quad → \quad k=-2*
Por lo tanto, el centro es C(1, -2).
Finalmente, calculamos los semiejes extrayendo raíz cuadrada a los denominadores:
*a=\sqrt{25}=5, \quad b=\sqrt{9}=3*
En conclusión, la elipse es vertical, con centro en *(1,-2),* semieje mayor *a=5* y semieje menor *b=3.*
Ejemplo 5
*\dfrac{(x+3)^2}{36}+\dfrac{(y-4)^2}{16}=1*
Observando los denominadores, 36 y 16, vemos que el mayor está bajo x2. Por lo tanto, el eje mayor es paralelo al eje x y la elipse es horizontal. Ahora determinamos el centro:
*x-h=x+3 \quad → \quad h=-3*
*y-k=y-4 \quad → \quad k=4*
El centro está entonces en el punto (-3, 4).
Finalmente, obtenemos los semiejes tomando la raíz cuadrada de los denominadores:
*a=\sqrt{36}=6, \quad b=\sqrt{16}=4*
Así, la elipse es horizontal, con centro en *(-3, 4),* semieje mayor *a=6* y semieje menor *b=4.*
Ejemplo 6
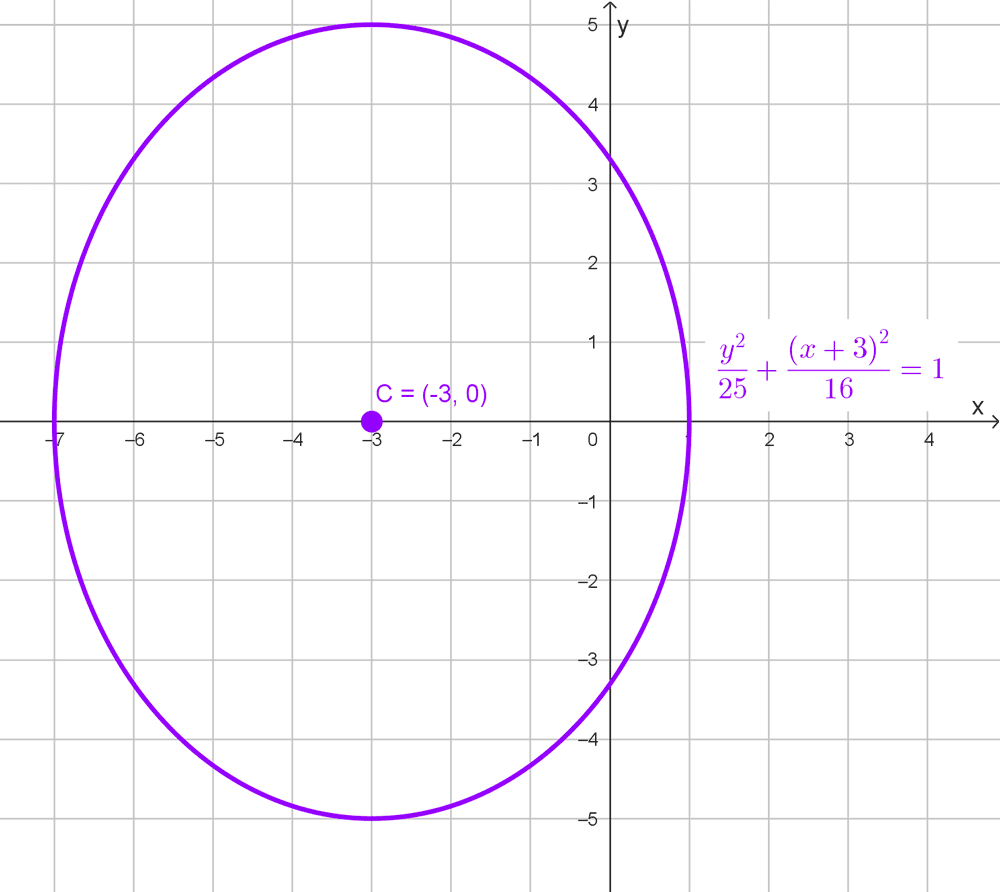
*\dfrac{y^2}{25}+\dfrac{(x+3)^2}{16}=1*
Identificamos que la ecuación tiene la forma de una elipse centrada fuera del origen. Observamos los denominadores 25 y 16. Como el mayor está bajo *y^2,* el eje mayor es paralelo al eje *y,* de modo que la elipse es vertical.
Ahora determinamos el centro. Recordemos que en la ecuación aparece *(x-h)^2* y *(y-k)^2.* En este caso tenemos *(x+3)^2* y *y^2,* que equivale a *(y-0)^2.* Al comparar, obtenemos:
*x-h=x+3 \quad \rightarrow \quad h=-3*
*y-k=y-0 \quad \rightarrow \quad k=0*
Por lo tanto, el centro es *C(-3, 0),* un punto que se encuentra sobre el eje x.
Finalmente, calculamos los semiejes extrayendo raíz cuadrada a los denominadores:
*a=\sqrt{25}=5*
*b=\sqrt{16}=4*
En conclusión, la elipse es vertical, con centro en *(-3, 0),* semieje mayor *a=5* y semieje menor *b=4.*
Ejemplo 7
*\dfrac{(x+1)^2}{35}+\dfrac{(y-2)^2}{10}=1*
Observamos los denominadores 35 y 10. Como 35 > 10 y el mayor está bajo *(x+1)^2,* el eje mayor es paralelo al eje x, por lo que la elipse es horizontal.
Ahora determinamos el centro comparando con la forma estándar:
*x-h=x+1 \quad \rightarrow \quad h=-1*
*y-k=y-2 \quad \rightarrow \quad k=2*
Por lo tanto, el centro es *C(-1, 2).*
Finalmente, calculamos los semiejes extrayendo la raíz cuadrada de los denominadores.
*a=\sqrt{35} ≈ 5,92*
*b=\sqrt{10} ≈ 3,16*
En conclusión, la elipse es horizontal, con centro en *(-1, 2),* semieje mayor *a=\sqrt{35} ≈ 5,916* y semieje menor *b=\sqrt{10} ≈ 3,162.* Ambos semiejes tienen valores irracionales.
Ejemplo 8
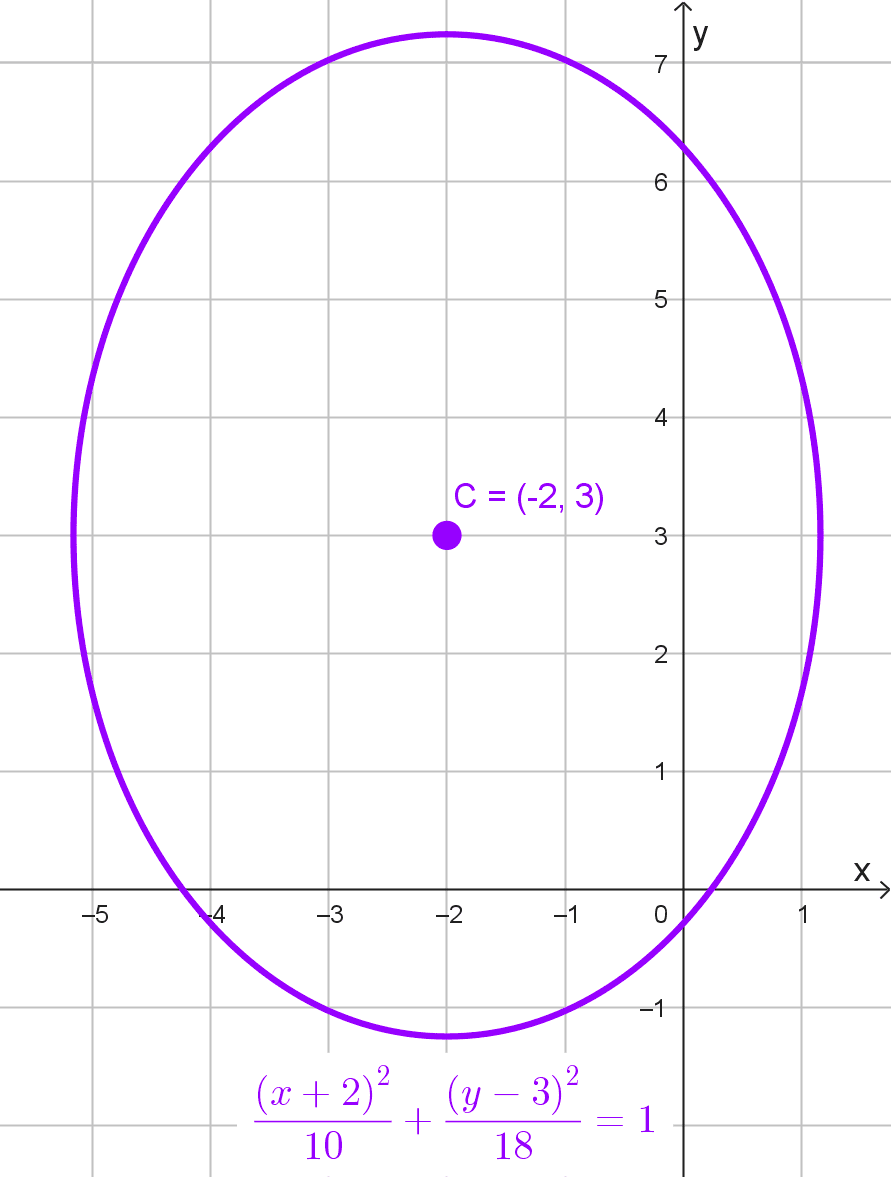
*\dfrac{(x+2)^2}{10}+\dfrac{(y-3)^2}{18}=1*
Observamos que los denominadores son 10 y 18. Como 18 > 10 y el mayor está bajo *(y-3)^2,* el eje mayor es paralelo al eje y, por lo que la elipse es vertical.
Ahora determinamos el centro comparando con la forma estándar:
*x-h=x+2 \quad \rightarrow \quad h=-2*
*y-k=y-3 \quad \rightarrow \quad k=3*
Por lo tanto, el centro es *(-2, 3).*
Finalmente, calculamos los semiejes:
*a=\sqrt{18} ≈ 4,24*
*b=\sqrt{10} ≈ 3,16*
En conclusión, la elipse es vertical, con centro en *(-2, 3),* semieje mayor *a=\sqrt{18}* y semieje menor *b=\sqrt{10}.*
A partir de los datos de la ecuación se pueden obtener los demás elementos de la elipse (focos, vértices, excentricidad, etc), para ver cómo hacerlo puedes visitar el artículo de ejercicios de elipse:
Nota: la ecuación de la elipse se parece mucho a la de la hipérbola, pero hay una diferencia fundamental:
- En la elipse, todos los términos son positivos: *\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1*
- En la hipérbola, uno de los términos aparece con signo negativo: *\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1*
Esa diferencia en el signo es lo que cambia por completo la forma de la curva: en lugar de una figura cerrada (elipse), obtenemos dos ramas abiertas (hipérbola).
Ecuación general
La ecuación general de una elipse (o de cualquier cónica) es una ecuación de segundo grado en dos variables:
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0
donde A, B, C, D, E y F son números reales. Para que represente una cónica de tipo elipse debe cumplirse esta condición: el número B2 - 4AC (llamado discriminante) debe ser negativo. Es decir:
B2 - 4AC < 0
Cuando esto se cumple, la ecuación puede corresponder a una elipse propiamente dicha, a una elipse degenerada (que se reduce a un punto) o a una elipse imaginaria (sin puntos reales).
Si los ejes de la elipse son paralelos a los ejes cartesianos, el término mixto Bxy no aparece en la ecuación (B = 0). En este caso la forma general se reduce a:
Ax2 + Cy2 + Dx + Ey + F = 0
Para que la ecuación represente una cónica de tipo elipse debe ocurrir que A y C tengan el mismo signo, ambos positivos o ambos negativos (esto se deriva de B2 - 4AC < 0 → -4AC < 0 → AC > 0). Si la ecuación representa una elipse real, entonces:
- Si A < C, la elipse es horizontal (eje mayor paralelo al eje X).
- Si C < A, la elipse es vertical (eje mayor paralelo al eje Y).
- Si A = C, la elipse es una circunferencia.
- Si D = 0 y E = 0, el centro está en el origen de coordenadas (0, 0).
- Si D = 0 pero E ≠ 0, entonces hay traslación vertical y el centro se encuenta sobre el eje Y.
- Si E = 0 pero D ≠ 0, hay traslación horizontal y el centro se encuentra sobre el eje X.
- Si E ≠ 0 y D ≠ 0, entonces el centro está desplazado del origen vertical y horizontalmente.
Cuando los ejes de la elipse no son paralelos a los ejes coordenados, aparece el término mixto Bxy (B ≠ 0). En este caso hablamos de una elipse rotada.
Algunos ejemplos de elipses en su forma general son:
- *3x^2+4y^2-12=0*
- *25x^2+16y^2-400=0*
- *4x^2+9y^2-16x-32=0*
- *16x^2+9y^2-64x-54y+1=0*
- *8x^2+25y^2-48x+50y+47=0*
- *36x^2+25y^2+72x-200y-464=0*
- *2x^2+4x+7y^2-28y-40=0*
La ecuación general no siempre es la más cómoda para trabajar, porque no permite identificar a simple vista los elementos de la elipse. Por eso, en la práctica, se busca transformarla en la ecuación canónica. El procedimiento consiste en completar cuadrados en los términos de x y de y, reorganizando después la ecuación.
Ejemplo
Transformar esta ecuación a una forma canónica: *8x^2+25y^2-48x+50y+47=0.*
Solución
Lo que haremos será agrupar los términos con las mismas variables y completar cuadrados. Primero, reordenamos la ecuación agrupando los términos en x y en y:
*(8x^2-48x)+(25y^2+50y)=-47*
Factorizamos los coeficientes de los términos cuadráticos para facilitar la completación de cuadrados. Para los términos en x, factorizamos 8; para los de y, 25.
*8(x^2-6x)+25(y^2+2y)=-47*
Ahora, completamos cuadrados dentro de cada paréntesis. Para *x^2-6x,* tomamos la mitad del coeficiente lineal (-6), que es -3, y lo elevamos al cuadrado, obteniendo 9. Así, *x^2-6x+9=(x-3)^2.* De manera similar, para *y^2+2y,* la mitad del coeficiente lineal (2) es 1, y al elevarlo al cuadrado obtenemos 1, por lo que *y^2+2y+1=(y+1)^2.*
Añadimos estos valores dentro de los paréntesis, pero debemos compensar con los mismos términos multiplicados por los coeficientes respectivos para mantener la igualdad. Para los términos en x, sumamos 9 dentro del paréntesis, lo que equivale a sumar *8 \times 9=72* en total. Para los términos en y, sumamos 1 dentro del paréntesis, lo que equivale a sumar *25 \times 1=25.* Para equilibrar, sumamos estos mismos valores en el lado derecho de la ecuación:
*8(x^2-6x+9)+25(y^2+2y+1)=-47+72+25*
Simplificamos ambos lados:
*8(x-3)^2+25(y+1)^2=50*
Para obtener la ecuación ordinaria de la elipse, dividimos ambos lados entre 50:
*\dfrac{8(x-3)^2}{50}+\dfrac{25(y+1)^2}{50}=1*
Simplificamos las fracciones:
*\dfrac{(x-3)^2}{50/8}+\dfrac{(y+1)^2}{50/25}=1*
*\dfrac{(x-3)^2}{25/4}+\dfrac{(y+1)^2}{2}=1*
Esta es la ecuación de una elipse horizontal centrada en *(3,-1),* con semieje mayor *a=\sqrt{25/4}=5/2* y semieje menor *b=\sqrt{2}.*
Si quisiéramos hacer el proceso contrario, es decir, de la ecuación canónica llegar a la general, basta con desarrollar los cuadrados de los numeradores y simplificar hasta obtener la forma polinómica igualada a cero.
Excentricidad
La excentricidad de una elipse es un concepto fundamental que mide el grado de "achatamiento" de la curva, indicando qué tan alargada o qué tan cercana a un círculo es. Se representa por e o ε (épsilon) y no debe confundirse con la constante e, base de los logaritmos naturales.
Por definición, la excentricidad se calcula como el cociente entre la semidistancia focal (c) y el semieje mayor (a):
*e=\dfrac{c}{a}*
Otra forma de calcularla, derivada de la relación pitagórica *a^2=b^2+c^2,* es:
*e=\sqrt{\dfrac{a^2-b^2}{a^2}}=\sqrt{1-\dfrac{b^2}{a^2}}.*
En cuanto a sus valores, la excentricidad de una elipse siempre satisface 0 ≤ e < 1. Esto ocurre porque necesariamente 0 ≤ c < a, lo que implica que 0 ≤ c/a <1. La interpretación de este número es sencilla:
- Si la excentricidad se acerca a 0 (e → 0), la elipse se hace más circular, ya que los focos tienden a coincidir con el centro. En el caso límite e = 0, la elipse se convierte en una circunferencia, y los semiejes tienen la misma longitud.
- Si la excentricidad se acerca a 1 (e → 1), la elipse se hace más alargada, aproximándose a un segmento de recta.
Características y propiedades
La elipse tiene una serie de propiedades importantes que veremos a continuación.
Relación fundamental
Existe una relación entre el semieje mayor (a), el semieje menor (b) y la semidistancia focal (c). Se cumple la fórmula:
a2 = b2 + c2
Con esta ecuación se puede obtener uno de estos valores a partir de los otros dos. Para recordar la fórmula, es útil visualizar un triángulo rectángulo en el que a es la hipotenusa, mientras que b y c corresponden a los catetos.
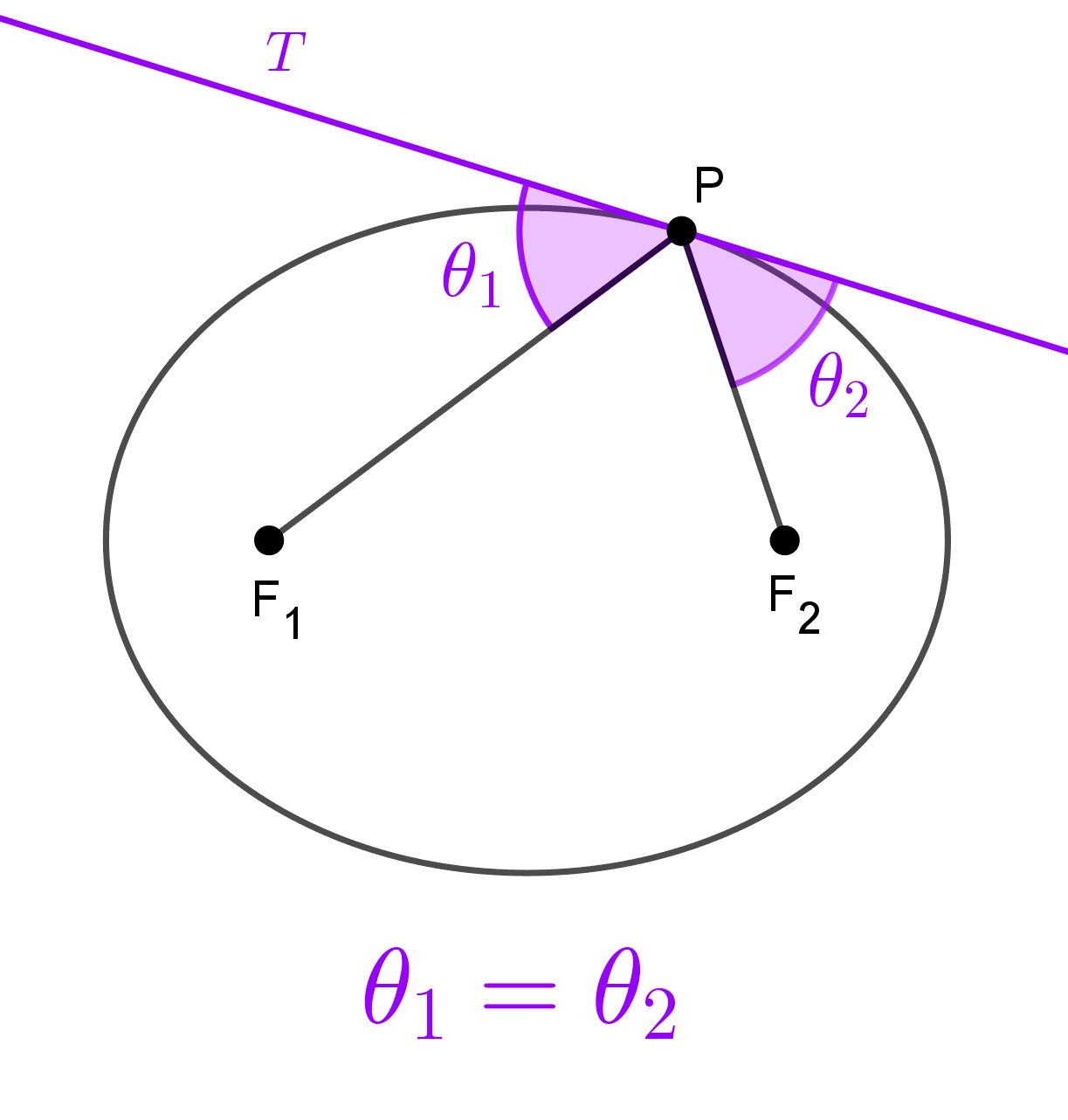
Propiedad reflectiva
La elipse tiene una propiedad acústica y óptica importante: si una onda (sonora o luminosa) se emite desde uno de los focos, al reflejarse en cualquier punto de la curva pasará necesariamente por el otro foco.
En términos matemáticos, esta propiedad expresa que, para cualquier punto de la curva, los radios vectores que lo unen con los focos forman ángulos iguales con la recta tangente en dicho punto. Es decir, dado un punto P de la elipse con focos F1 y F2, si θ1 es el ángulo entre la tangente en P y PF1,
y θ2 es el ángulo entre la tangente en P y PF2, entonces: θ1 = θ2.
Esta propiedad es utilizada en la vida real, por ejemplo:
- Galerías de susurros: en algunas construcciones con forma elíptica (como la cúpula de la Catedral de San Pablo en Londres), una persona que susurre en un foco puede ser escuchada claramente por alguien ubicado en el otro foco, incluso a gran distancia.
- Medicina: existe un tratamiento para romper cálculos renales en donde se usan elipses reflectivas para concentrar ondas de choque en el cálculo (que se coloca en un foco), evitando dañar otros tejidos.
Simetrías
La elipse tiene dos ejes de simetría que son perpendiculares entre sí: el eje principal o focal (recta que contiene a los focos, el centro y los vértices principales) y el eje secundario o normal (recta que pasa por el centro y los vértices secundarios). Además, el centro de simetría de la figura es el centro de la elipse.
Área
Él área encerrada por una elipse puede calcularse con la siguiente fórmula que depende de los semiejes mayor (a) y menor (b):
A = π ⋅ a ⋅ b
Si ambos semiejes son iguales (a = b = r), la elipse se convierte en una circunferencia y la fórmula se reduce al área del círculo:
A = π ⋅ r2
Perímetro
Calcular de manera exacta el perímetro de una elipse es un problema que no tiene una solución elemental como en el caso de la circunferencia. La expresión rigurosa implica trabajar con integrales elípticas de segunda especie, cuyo tratamiento es bastante complicado. También existen desarrollos en forma de series infinitas, como la serie de Gauss-Kummer, pero su uso es más teórico que práctico debido a la dificultad de los cálculos.
Ante esta situación, los matemáticos han ideado diferentes fórmulas de aproximación que permiten obtener valores muy cercanos al real. Dentro de ellas, las propuestas de Srinivasa Ramanujan son las más difundidas, ya que logran un equilibrio entre precisión y sencillez de aplicación.
Una de las expresiones más utilizadas es la llamada primera aproximación de Ramanujan, que funciona bien siempre que los semiejes a y b no difieran demasiado. La fórmula se expresa como:
*P ≈ \pi \left[ 3(a+b)-\sqrt{(3a+b)(a+3b)} \right]*
Su mayor ventaja es la simplicidad, y ofrece resultados muy aceptables en el caso de elipses con excentricidad baja, es decir, aquellas que son casi circulares. Para mejorar esta aproximación, Ramanujan propuso una versión más precisa que se conoce como Ramanujan II. En este caso interviene un parámetro auxiliar h:
*h=\dfrac{(a-b)^2}{(a+b)^2}*
Este valor permite refinar el cálculo con la siguiente expresión:
*P ≈ \pi (a+b)\left(1+\dfrac{3h}{10+\sqrt{4-3h}} \right)*
Este método es confiable para muchos casos de elipses, aunque en situaciones extremas, cuando la excentricidad es muy alta (e → 1), pierde algo de exactitud.
Para cubrir esos casos, el matemático David W. Cantrell desarrolló una versión corregida de la segunda fórmula de Ramanujan que ajusta los errores en el caso de elipses muy alargadas. Esta modificación reduce el margen de error a apenas 0,00145%, convirtiéndola en la opción más precisa y práctica disponible para cualquier valor de la excentricidad.
La fórmula modificada de Ramanujan por Cantrell es:
*P ≈ \pi(a+b)\left(1+\dfrac{3h}{10+\sqrt{4-3h}}+\left(\dfrac{4}{\pi}-\dfrac{14}{11}\right)h^{12}\right)*
siendo *h=\dfrac{(a-b)^2}{(a+b)^2}*
En la práctica, la elección de la fórmula depende de la forma de la elipse:
- Si se trata de una elipse casi circular, la aproximación sencilla de Ramanujan (primera aproximación) es más que suficiente.
- Para elipses de proporciones intermedias conviene aplicar la segunda aproximación de Ramanujan (Ramanujan II).
- Cuando la figura es muy alargada, la mejor alternativa es la modificación de Cantrell.
Origen cónico de la elipse
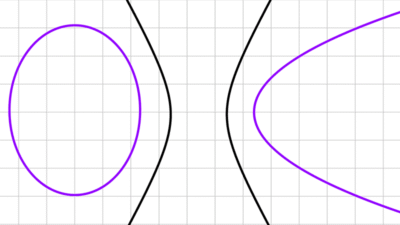
Dijimos al principio que la elipse es una sección cónica, estas son curvas que se obtienen al intersectar un cono circular recto (imaginado como un doble cono que se extiende hacia arriba y hacia abajo) con un plano. El tipo de curva que aparece depende exclusivamente de la inclinación del plano respecto del cono y de si el plano pasa o no por el vértice.
Llamemos α al ángulo de apertura del cono (el ángulo entre el eje y una generatriz) y φ al ángulo entre el plano de corte y el eje. La elipse surge cuando el plano corta una sola hoja del cono y la intersección es cerrada. Geométricamente, esto ocurre cuando el ángulo del plano cumple α < φ ≤ 90° y el plano no contiene al vértice. Si φ = 90°, el corte es perpendicular al eje del cono y se obtiene una circunferencia, que es un caso particular de la elipse con excentricidad nula.
Cuando cambiamos la inclinación del plano, ocurre lo siguiente:
- Si el plano es paralelo a una generatriz del cono (φ = α), la intersección deja de ser cerrada y se obtiene una parábola.
- Si el plano está más "vertical" que una generatriz (φ < α), corta a ambas hojas del doble cono y resulta una hipérbola.
Cuando el plano contiene el vértice, la sección resulta en una cónica degenerada.
Ecuación paramétrica
En lugar de describir una curva únicamente mediante una relación entre x e y, es posible hacerlo a través de una tercera variable auxiliar llamada parámetro. Así se obtiene lo que se conoce como ecuación paramétrica, donde ambas coordenadas se expresan como funciones de un mismo valor t.
Con el objetivo de parametrizar una elipse, partimos de la ecuación canónica centrada en el origen:
*\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1*
Observamos su similitud con la identidad trigonométrica *\cos^2(t)+\sin^2(t)=1,* lo que nos sugiere hacer la correspondencia:
*\dfrac{x}{a}=\cos(t), \quad \dfrac{y}{b}=\sin(t)*
Esto conduce directamente a las ecuaciones paramétricas de la elipse:
*x=a \cos(t), \quad y=b \sin(t),\quad \text{donde } 0≤t≤2\pi*
Si el centro de la elipse no está en el origen, sino en un punto (h, k), basta con sumar estas coordenadas a las ecuaciones para desplazarla:
*x=h+a \cos(t), \quad y=k+b \sin(t), \quad 0≤t≤2\pi*
De este modo, al recorrer t dentro de ese intervalo, se generan todos los puntos de la elipse. En el caso particular en que a = b = r, la parametrización describe una circunferencia:
*x=r \cos(t), \quad y=r \sin(t),\quad 0 ≤t≤2\pi*
La representación paramétrica resulta sumamente práctica en geometría analítica y aplicaciones físicas porque permite calcular puntos de la curva de manera directa, facilita el análisis de áreas y longitudes de arco mediante integrales, y además describe de forma natural la trayectoria de un punto en movimiento sobre la elipse, lo que explica su uso en astronomía y en la modelización de órbitas planetarias.
Ecuación en coordenadas polares
En el plano cartesiano representamos los puntos mediante dos coordenadas, x e y, que indican cuánto nos alejamos de los ejes horizontal y vertical. En cambio, en el sistema de coordenadas polares la ubicación de un punto se describe con un par (r, θ), donde r es la distancia desde el origen (llamado polo) hasta el punto, y θ es el ángulo que forma el segmento que los une con el eje polar, que coincide con el semieje positivo de x. Así, mientras que en cartesianas los desplazamientos son rectos y ortogonales, en polares los puntos se localizan a partir de un radio y un giro.
Para deducir la ecuación de una elipse en este sistema conviene recurrir a otra definición de cónica distinta a la habitual con centro y ejes. Una cónica es el lugar geométrico de los puntos cuya distancia a un foco fijo guarda una proporción constante con la distancia a una recta fija llamada directriz. Esa proporción es la excentricidad e. Cuando e < 1 se obtiene una elipse.
Colocando el foco en el polo y eligiendo de forma conveniente la posición de la directriz, la ecuación polar de la elipse puede escribirse como:
*r=\dfrac{ep}{1±e \cos \theta} \quad \text{o} \quad r=\dfrac{ep}{1±e \sin \theta}*
donde p es la distancia desde el polo hasta la directriz y e es la excentricidad de la elipse. El signo y la función trigonométrica dependen de la orientación de esa recta:
- Si la directriz es perpendicular al eje polar, aparece el término con cos θ. El signo positivo corresponde a una directriz ubicada a la derecha del polo y el signo negativo a una directriz ubicada a la izquierda.
- Si la directriz es paralela al eje polar, aparece el término con sin θ. En este caso, el signo positivo se usa cuando la directriz está por encima del polo y el signo negativo cuando está por debajo.
Método de construcción
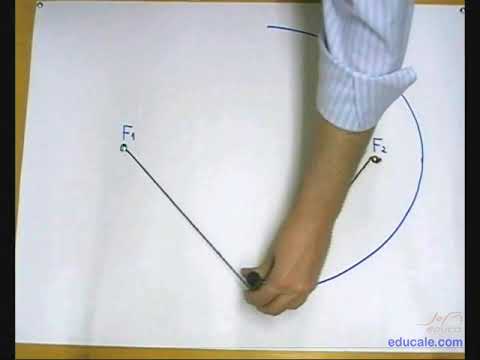
Existen distintos métodos para construir una elipse, algunos basados en propiedades geométricas y otros en procedimientos más técnicos o algebraicos. Entre ellos, uno de los más sencillos e intuitivos es el conocido como método del jardinero, utilizado desde hace siglos tanto en matemáticas como en arquitectura y paisajismo.
Este procedimiento se fundamenta directamente en la definición geométrica de la elipse: el conjunto de todos los puntos cuya suma de distancias a dos puntos fijos (llamados focos) es constante. Aprovechando esta idea, se utiliza una cuerda y dos estacas para convertir la definición en un trazo físico.
Los pasos a seguir son los siguientes:
- Marcar en la superficie los dos focos de la elipse (por ejemplo, con clavos, estacas o chinchetas).
- Tomar una cuerda cuya longitud es igual al eje mayor de la elipse (2a).
- Atar los extremos de la cuerda a los dos focos.
- Con un lápiz, tensar la cuerda y desplazarla alrededor de los focos, manteniéndola estirada en todo momento.
De este modo, el lápiz va describiendo la curva de la elipse. La razón por la que funciona es simple: en cualquier posición, la suma de las dos longitudes de cuerda (desde el lápiz hasta cada foco) siempre es constante e igual a 2a, cumpliendo la condición que define a la elipse.
Este método recibe el nombre de “elipse del jardinero” porque es comúnmente empleado para diseñar jardines y plazas con formas elípticas, incluso en escalas muy grandes. Si bien el procedimiento se explica fácilmente en palabras, resulta mucho más claro al verlo en acción. A continuación encontrarás un video demostrativo de este método.
Aplicaciones
Las elipses tienen varias aplicaciones en la vida cotidiana y en la ciencia, veremos algunas de ellas a continuación.
Astronomía y mecánica celeste
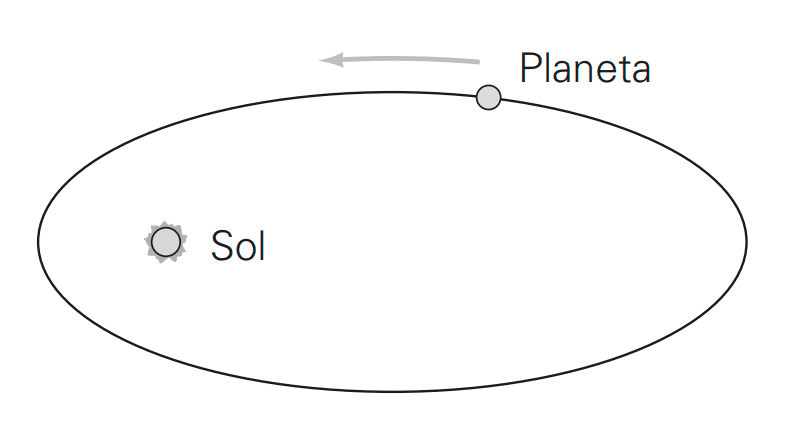
Durante siglos se pensó que los planetas giraban alrededor del Sol en órbitas circulares, pero fue Johannes Kepler, a comienzos del siglo XVII, quien demostró que estas trayectorias eran en realidad elípticas, con el Sol ubicado en uno de los focos. Este hallazgo se conoce como la Primera Ley de Kepler y marcó un antes y un después en la astronomía.
Una consecuencia directa de este descubrimiento es que la distancia entre un planeta y el Sol no es constante, sino que varía a lo largo de la órbita. Así, existen puntos de máxima cercanía (perihelio) y de máxima lejanía (afelio).
La importancia de las elipses no se limita a los planetas. En 1705, Edmond Halley demostró que el cometa que lleva su nombre seguía también una órbita elíptica alrededor del Sol, lo que permitió predecir con exactitud su regreso. De hecho, en la mecánica celeste clásica se demuestra que cuando dos cuerpos interactúan únicamente por la gravedad, y su órbita es cerrada, la trayectoria resultante siempre es una elipse (o un círculo como caso particular).
El estudio de las elipses también se relaciona con la Segunda Ley de Kepler, que dice que un planeta no se mueve siempre a la misma velocidad. Cuando está más cerca del Sol (perihelio) avanza más rápido, y cuando está más lejos (afelio) lo hace más despacio. Lo interesante es que, aunque cambie su rapidez, el área que recorre la línea imaginaria que une al planeta con el Sol en un mismo intervalo de tiempo siempre resulta igual.
En conjunto, las Leyes de Kepler y el concepto geométrico de la elipse constituyen la base de la mecánica celeste, permitiendo describir y predecir la dinámica de planetas, satélites y cometas.
Arquitectura y diseño
La elipse ha dejado una huella profunda en el arte y diseño. Su forma elegante y armónica ha sido aprovechada desde la antigüedad para resolver problemas estructurales y, al mismo tiempo, generar espacios con gran valor estético y simbólico.
Uno de los ejemplos más impresionantes se encuentra en la antigua Roma con el Coliseo. Su planta está formada por elipses concéntricas que organizan desde la fachada exterior hasta la arena central. Gracias a esta disposición, el edificio puede albergar a decenas de miles de espectadores manteniendo una visibilidad óptima desde cualquier punto.
Durante el Renacimiento y el Barroco, la elipse adquirió un papel aún más destacado. El arquitecto Gian Lorenzo Bernini diseñó la iglesia de Sant’Andrea al Quirinale en Roma con una planta elíptica. Esta elección no fue casual: la forma otorga dinamismo al interior del templo y resalta la importancia simbólica del altar, situado en uno de los ejes principales de la elipse, generando un efecto de centralidad y recogimiento espiritual.
La elipse también se utilizó en las estructuras de ingeniería, como demuestra el Puente de Santa Trinidad en Florencia, construido en el siglo XVI por Bartolomeo Ammanati. Fue el primer puente en emplear arcos elípticos, que ofrecían mayor esbeltez y elegancia que los tradicionales arcos semicirculares. Aunque fue destruido en la Segunda Guerra Mundial, se reconstruyó en 1958 siguiendo fielmente el diseño original.
Acústica
Las propiedades reflectivas de la elipse se aprovechan en el campo de la acústica. Una de sus características más notables es que las ondas emitidas desde uno de los focos se reflejan en la superficie elíptica y convergen en el otro foco. Esto significa que un sonido débil en un punto puede escucharse con gran nitidez en otro lugar específico, aunque ambos estén separados por cierta distancia.
Un ejemplo célebre de este fenómeno es la Galería de los Susurros en la Catedral de San Pablo, en Londres. Allí, un susurro pronunciado en un extremo de la cúpula se transmite claramente hasta el otro extremo, como si los dos interlocutores estuvieran al lado, mientras que las personas situadas en el resto de la sala apenas perciben el sonido.
La elipse también ha tenido un papel fundamental en el diseño de salas de conciertos y teatros. Gracias a su forma, las ondas sonoras pueden concentrarse o distribuirse de manera uniforme hacia el público, lo que mejora la calidad acústica del espacio. Esta misma propiedad se utiliza en la fabricación de reflectores y espejos acústicos, que permiten dirigir el sonido hacia un punto focal, logrando que la voz o la música lleguen con claridad incluso a largas distancias.
Curiosidades
Un ejemplo fácil para observar una elipse ocurre cuando inclinamos un vaso cilíndrico con agua. La superficie del agua, que en reposo es siempre plana y horizontal, al inclinarse se proyecta como una elipse sobre las paredes del vaso. Es una forma natural que surge de la intersección entre un plano y un cilindro, tal como ocurre en la definición geométrica de las secciones cónicas.
Otro caso curioso se da con una linterna que ilumina una pared inclinada. Aunque el haz de luz salga en forma circular, al chocar con una superficie oblicua la mancha luminosa se transforma en una elipse. Este fenómeno se debe al mismo principio: un cono de luz que intersecta un plano inclinado siempre genera una figura elíptica.
Existen mesas de billar elípticas que aprovechan la propiedad reflectiva de la elipse: si una bola se lanza desde un foco, tras rebotar en los bordes siempre terminará en dirección al otro foco. De este modo, se puede diseñar una mesa con un agujero ubicado en un foco y garantizar que cualquier tiro iniciado desde el otro llegue directamente a ese punto, como se muestra en el siguiente video.
Demostración de las ecuaciones
Aquí se presentan las demostraciones de las fórmulas de la elipse que vimos hasta ahora.
Demostración de la ecuación canónica
Para deducir la ecuación canónica de la elipse, consideraremos un caso especial con centro en el origen y eje mayor sobre el eje x.
Los focos tienen coordenadas F1(-c, 0) y F2(c, 0), los vértices principales están en (a, 0) y (-a, 0), los vértices secundarios en (0, b) y (0, -b), el centro es (0, 0). P(x, y) es un punto cualquiera de la elipse. Aplicando la definición, de debe cumplir que:
*d(F_1, P)+d(F_2, P)=k*
Para calcular k, consideramos los vértices de la elipse, que son puntos de la misma, por lo que cumplen con la definición dada. Llamemos V2 al vértice principal ubicado en (a, 0). Entonces tenemos que:
*d(V_2, F_1)=a+c*
*d(V_2, F_2)=a-c*
Donde a es la distancia desde el centro de la elipse hasta el vértice, y c es la distancia desde el centro hasta uno de los focos. Entonces, la suma de las distancias desde V2 hasta los focos es:
*d(V_2,F_1)+d(V_2,F_2)=(a+c)+(a-c)=a+c+a-c=2a*
Por lo tanto, la constante k es igual a 2a. Esto significa que para cualquier punto P(x, y) en la elipse, la suma de las distancias a los focos es 2a, que no es otra cosa que la longitud del eje mayor. Reemplazando en la definición:
*d(F_1,P)+d(F_2,P)=2a*
Utilizamos la fórmula de la distancia que surge de aplicar el Teorema de Pitágoras:
*\sqrt{(x+c)^2+y^2}+\sqrt{(x-c)^2+y^2}=2a*
Aislamos un radical:
*\sqrt{(x+c)^2+y^2}=2a-\sqrt{(x-c)^2+y^2}*
Elevamos ambos lados al cuadrado:
*(\sqrt{(x+c)^2+y^2})^2=(2a-\sqrt{(x-c)^2+y^2})^2*
Eliminamos el paréntesis:
*(x+c)^2+y^2=4a^2-4a\sqrt{(x-c)^2+y^2}+(x-c)^2+y^2*
Simplificamos y aislamos el radical.
*x^2+2cx+c^2+y^2=4a^2-4a\sqrt{(x-c)^2+y^2}+x^2-2cx+c^2+y^2*
*4cx-4a^2=-4a\sqrt{(x-c)^2+y^2}*
Dividimos ambos lados entre 4.
*cx-a^2=-a\sqrt{(x-c)^2+y^2}*
Elevamos de nuevo ambos lados al cuadrado.
*(cx-a^2)^2=a^2[(x-c)^2+y^2]*
Eliminamos el paréntesis.
*c^2x^2-2a^2cx+a^4=a^2(x^2-2cx+c^2+y^2)*
Reordenamos los términos.
*c^2x^2-a^2x^2+a^2y^2=a^2c^2-a^4*
Multiplicamos por -1 ambos lados y factorizamos el lado derecho.
*(a^2-c^2)x^2+a^2y^2=a^2(a^2-c^2)*
Para obtener puntos de la elipse que no se encuentren sobre el eje x, debemos considerar que a > c, ya que la suma de la longitud de los lados del triángulo es mayor que la longitud del tercer lado:
*d(F_1,P)+d(F_2,P)>d(F_1,F_2)*
*2a>2c*
*a>c*
Puesto que a>c, también se tiene *a^2>c^2,* entonces *a^2-c^2>0.* Hagamos *b^2=a^2-c^2, b>0.* Reemplazamos en la ecuación:
*b^2x^2+a^2y^2=a^2b^2*
Dividiendo ambos lados entre *a^2b^2* se obtiene:
*\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1*
Esta última es la ecuación canónica de la elipse con centro en (0, 0), focos en (-c, 0) y (c, 0), eje mayor sobre el eje x y vértices en (-a, 0) y (a, 0). La longitud del semieje mayor es a y la del eje menor es b.
Con un proceso análogo demostramos que si el eje mayor está sobre el eje y, la ecuación se transforma en:
*\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1*
Para el caso en que el centro está desplazado del origen y tiene coordenadas (h, k), utilizamos la fórmula de transformación de coordenadas, reemplazando x por x-h e y por y-k en ambas ecuaciones. Así obtenemos:
Elipse con eje mayor horizontal: *\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1*
Elipse con eje mayor vertical: *\dfrac{(x-h)^2}{b^2}+\dfrac{(y-k)^2}{a^2}=1*
Demostración de la ecuación general
Para llegar a la ecuación general partimos de la ecuación reducida de la elipse:
*\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1*
Primero, eliminamos los denominadores multiplicando ambos lados por *a^2b^2:*
*b^2(x-h)^2+a^2(y-k)^2=a^2b^2*
Desarrollamos los términos y ordenamos:
*b^2(x^2-2hx+h^2)+a^2(y^2-2ky+k^2)=a^2b^2*
Expandiendo y agrupando:
*b^2x^2-2b^2hx+b^2h^2+a^2y^2-2a^2ky+a^2k^2=a^2b^2*
Reorganizamos para formar la ecuación general de segundo grado:
*b^2x^2+a^2y^2-2b^2hx-2a^2ky+b^2h^2+a^2k^2-a^2b^2=0*
Finalmente, reescribimos esta ecuación en la forma estándar:
*Ax^2+Cy^2+Dx+Ey+F=0*
donde:
- *A=b^2*
- *C=a^2*
- *D=-2b^2h*
- *E=-2a^2k*
- *F=b^2h^2+a^2k^2-a^2b^2*
Si tenemos la ecuación general y queremos pasar a la canónica, es necesario manipular algebraicamente la expresión y algunas veces se requerirá completar los cuadrados. El siguiente artículo contiene ejercicios resueltos sobre el pasaje entre ecuación general y canónica:
Recursos adicionales
Lás fórmulas de la elipse se resumen en la siguiente imagen.
Con el siguiente recurso podrás interactuar con una elipse modificando su excentricidad y visualizar en tiempo real cómo cambia su forma.
Para graficar una elipse puedes utilizar algún graficador de cónicas, particularmente yo recomiendo GeoGebra, es gratuito y sencillo de usar.
En el siguiente video se explica qué es una elipse y sus elementos:
En el siguiente video se explica cómo dibujar una elipse utilizando un compás, un método muy utilizado en dibujo técnico.
Lecturas recomendadas:
- Engler, A. y otros. (2020). Geometría Analítica. Universidad Nacional del Litoral.
- Fuller, G. y Tarwater, D. (1995). Geometría Analítica (7ma edición). Pearson Educación.
- Lehmann, C. (1989). Geometría Analítica. Limusa.
- Leithold. L. (1992). Álgebra y Trigonometría con Geometría Analítica. Oxford University Press.
- Márquez, A. y otros. (2009). Geometría Analítica. Prentice Hall.
- Raichman, S. y Totter, E. (2016). Geometría Analítica para Ciencias e Ingeniería. Universidad Nacional de Cuyo.
- Sullivan, M. (2006). Álgebra y Trigonometría. Pearson Educación.
- Swokowski, E. y Cole, J. (2009). Álgebra y Trigonometría con Geometría Analítica. Cengage Learning.
Preguntas frecuentes
¿Una elipse y un óvalo son lo mismo?
No, una elipse y un óvalo no son lo mismo. La elipse es una figura geométrica definida matemáticamente, simétrica y con propiedades específicas, mientras que el óvalo es un término más general para describir cualquier figura curva cerrada similar a un huevo, sin una definición matemática estricta.
¿Una elipse y un elipsoide son lo mismo?
No, una elipse y un elipsoide no son lo mismo. Una elipse es una figura plana, mientras que un elipsoide es su versión tridimensional, parecido a una esfera achatada o alargada, que surge de rotar una elipse alrededor de uno de sus ejes.
¿Cuál es la diferencia entre círculo, circunferencia y elipse?
Toda circunferencia es una elipse con excentricidad cero, pero no toda elipse es una circunferencia. Un círculo es la región del plano delimitada por una circunferencia, incluyendo todos los puntos en su interior.
¿Cómo saber si un punto pertenece a una elipse?
Para saber si un punto del plano pertenece a una elipse, se pueden reemplazar sus coordenadas en la ecuación canónica o general. Si se cumple la igualdad, el punto pertenece a la elipse, si no, no pertenece.
Otros contenidos sobre elipses
-
quiero su respuesta del vértice y de foco V1 (6,1) , V2 (-2,1) y F1 (7,6), F2 (7,6) nose como hacer
-
Super bien la pagina, te ayuda a entender todo bien resumido y entendible
2 Comentarios
Deja una respuesta



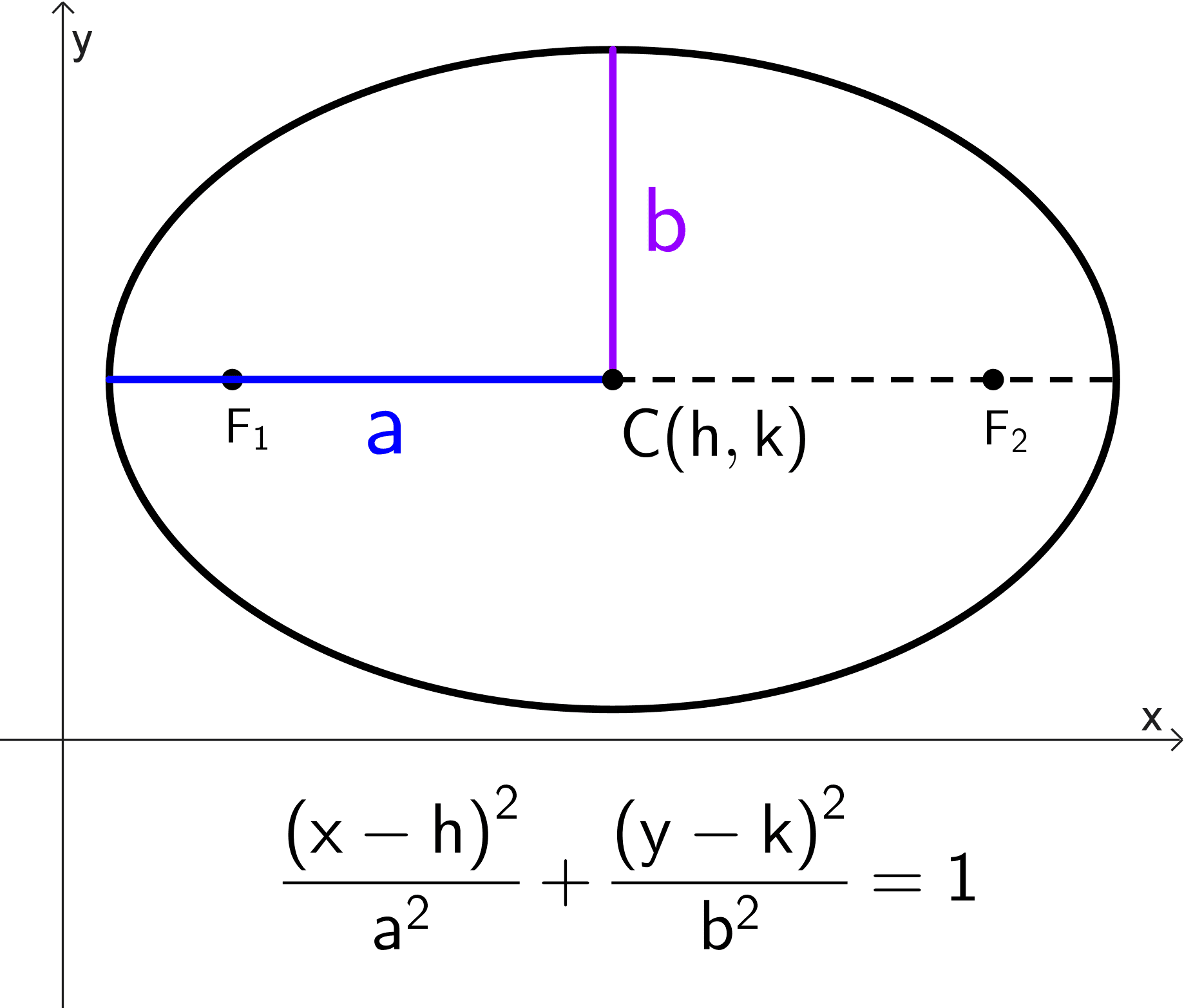


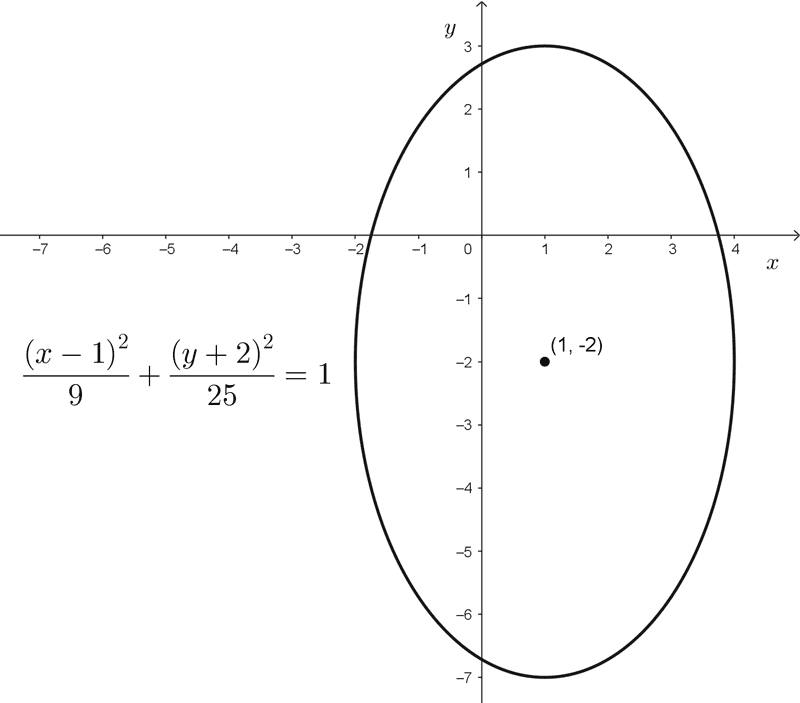















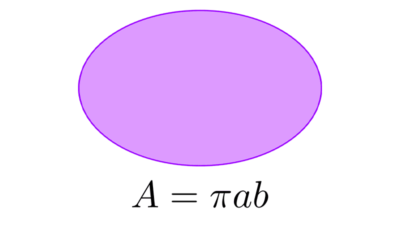


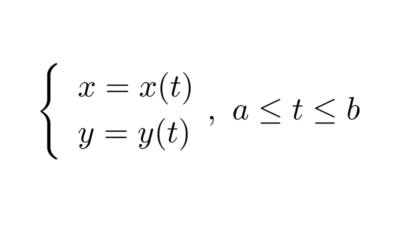
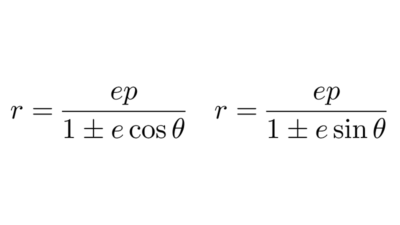
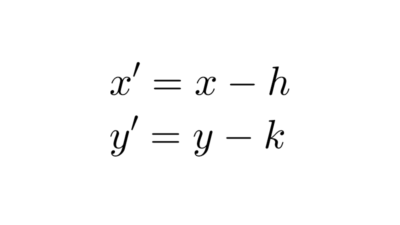
Otros artículos que pueden interesarte