
Ejes y semiejes de la hipérbola
Los ejes de la hipérbola son rectas o segmentos de rectas que nos dan información sobre la misma. Existen distintos ejes en una hipérbola:
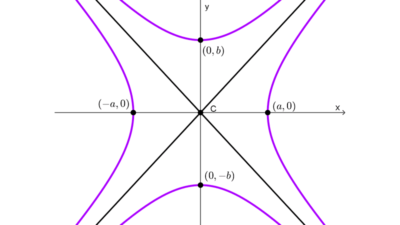
- Eje transversal: es el segmento que une los vértices de la hipérbola y pasa por el centro, su longitud es 2a donde a es la distancia del centro a un vértice. Este segmento también es llamado eje transverso o real y a su mitad se le llama semieje transversal.
- Eje conjugado: es un segmento perpendicular al eje transversal que pasa por el centro y tiene longitud 2b. Sirve como guía para trazar las asíntotas y la mitad de este eje se llama semieje conjugado.
- Eje focal o principal: es una recta que pasa por los focos, los vértices y el centro de la hipérbola, contiene al eje transversal y es un eje de simetría de la gráfica.
- Eje imaginario o secundario: es una recta perpendicular al eje focal que pasa por el centro, contiene al eje conjugado y es un eje de simetría de la hipérbola.
Nótese que los ejes transverso y conjugado son segmentos de rectas, mientras que los ejes focal e imaginario son rectas. Toda hipérbola tiene dos ejes de simetría: el eje focal y el eje imaginario.
Una hipérbola es horizontal o vertical dependiendo de la orientación del eje transversal. La siguiente propiedad relaciona a las longitudes de los semiejes transversal (a) y conjugado (b) con la semidistancia focal (c):
c2 = a2 + b2
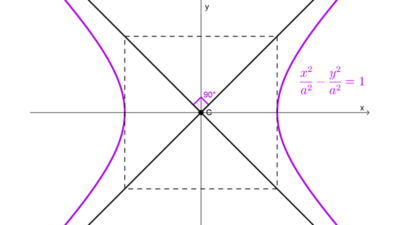
El eje transverso y el conjugado pueden tener la misma longitud, en tal caso la hipérbola se llama equilátera.
Importante: si aún no conoces el significado de la hipérbola en matemáticas, te recomiendo revisar antes el artículo principal donde explicamos su concepto, definición, fórmulas y propiedades.
Cómo hallar los ejes de una hipérbola
Las longitudes de los semiejes aparecen en la ecuación canónica de la hipérbola elevados al cuadrado y como los denominadores de las variables.
| Orientación | Ecuación canónica | Ejes y semiejes | Centro | Ejes de simetría |
|---|---|---|---|---|
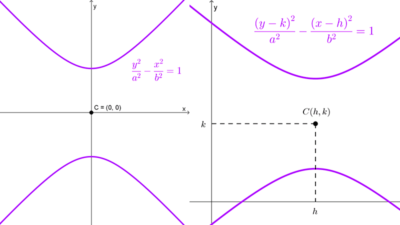
| Hipérbola horizontal | *\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1* | El semieje transversal es a. El semieje conjugado es b. El eje transversal mide 2a. El eje conjugado mide 2b. | (h, k) | Eje focal: y = k Eje imaginario: x = h |
| Hipérbola vertical | *\dfrac{(y-k)^2}{a^2}-\dfrac{(x-h)^2}{b^2}=1* | El semieje transversal es a El semieje conjugado es b. El eje transversal mide 2a. El eje conjugado mide 2b. | (h, k) | Eje focal: x = h Eje imaginario: y = k |
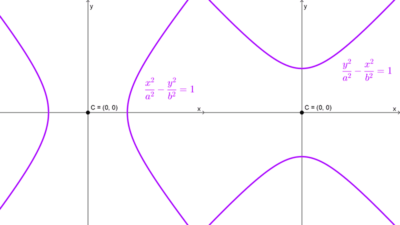
El término positivo en la ecuación canónica determina la orientación del eje transversal:
- Si el término positivo es el que contiene a la variable x, el eje transversal es paralelo al eje x, resultando en una hipérbola horizontal.
- Si el término positivo es el que contiene a la variable y, el eje transversal es paralelo al eje y, resultando en una hipérbola vertical.
El denominador del término positivo permite extraer la longitud del semieje transversal (a), mientras que mediante el denominador del término negativo podemos obtener la longitud del semieje conjugado (b). Es necesario extraer la raíz cuadrada de los denominadores.
Si la ecuación no está en forma canónica, podemos operar algebraicamente para conseguir que lo esté. Multiplicando por dos los valores de a y b se obtienen las longitudes del eje transverso y conjugado, respectivamente.
Ejercicios resueltos
Ejercicio 1
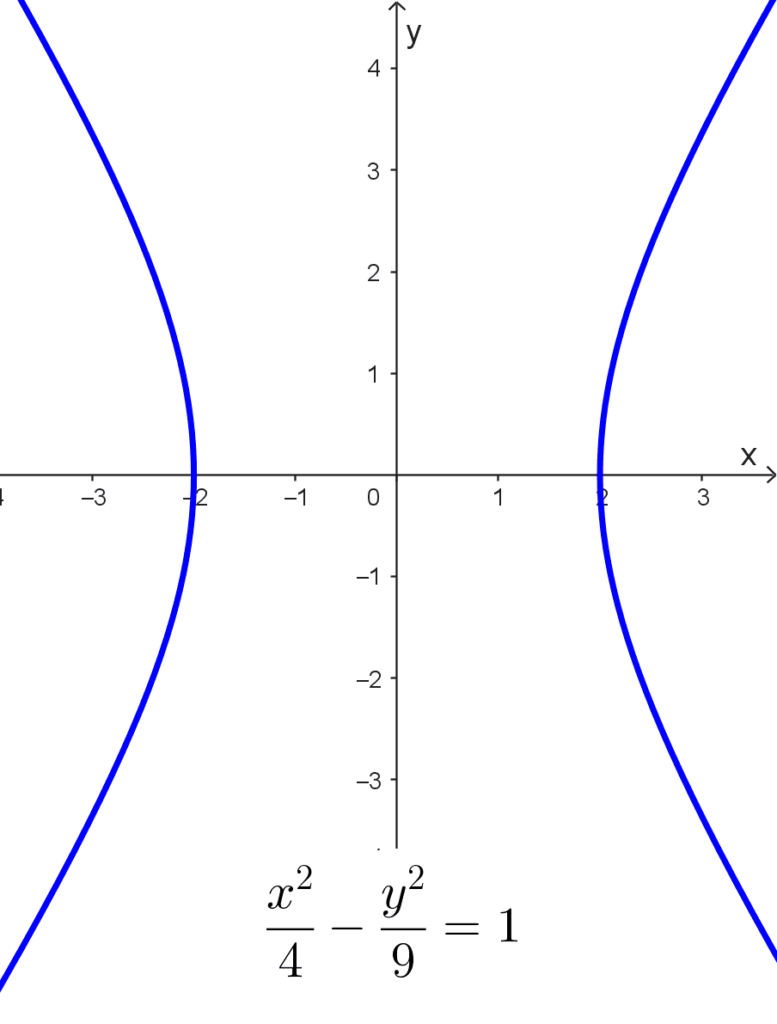
Obtener los ejes transverso y conjugado de la hipérbola *\dfrac{x^2}{4}-\dfrac{y^2}{9}=1*
Solución: la ecuación está en forma canónica así que podemos extraer los datos necesarios, como la hipérbola es horizontal (el término positivo está asociado a la variable x), el eje transverso (de longitud 2a) es horizontal. Las longitudes de los semiejes se pueden obtener sacando raíz cuadrada a los denominadores.
El denominador del término positivo es 4, por tanto:
*a^2=4→a=\sqrt{4}=2*
El denominador del término negativo es 9, por tanto:
*b^2=9→b=\sqrt{9}=3*
Calculamos las longitudes de cada eje multiplicando los valores anteriores por 2:
- Eje transversal: *2a=2\cdot 2=4*
- Eje conjugado: *2b=2\cdot 3=6*
Ejercicio 2
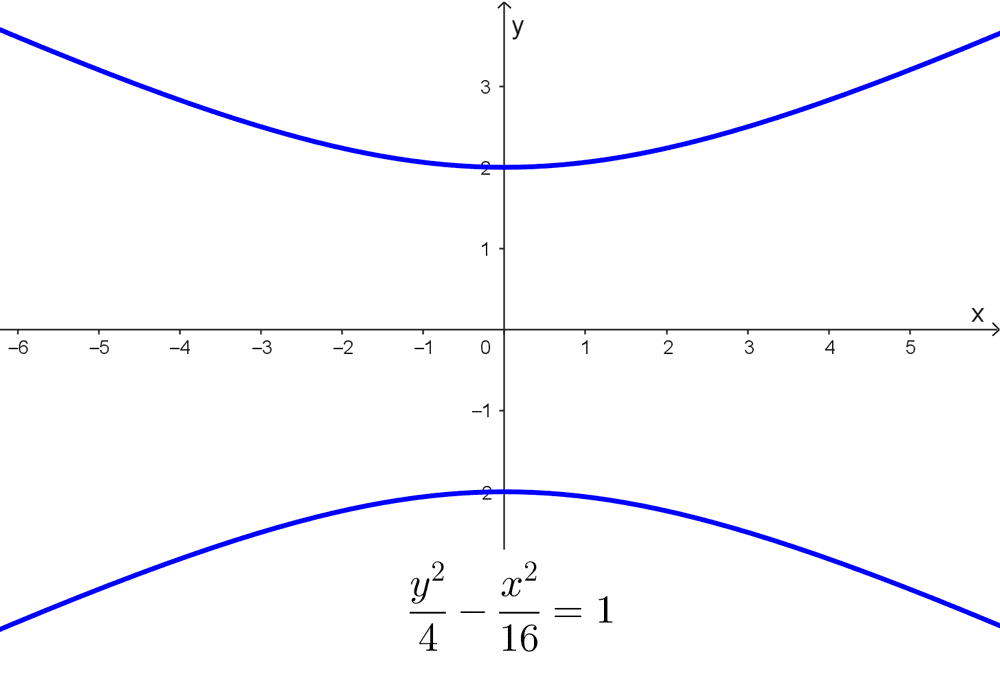
Calcular los ejes transversal, conjugado y los ejes de simetría de la hipérbola *\dfrac{y^2}{25}-\dfrac{x^2}{16}=1*
Solución: la hipérbola está en forma estándar y observamos que tiene orientación vertical pues el término positivo tiene la variable y. Procedemos a sacar los valores de los semiejes:
Del término positivo: *a^2=25→a=\sqrt{25}=5*
Del término negativo: *b^2=16→b=\sqrt{16}=4*
Ahora calculamos los ejes completos multiplicando por dos:
- Eje transverso: *2a=2\cdot 5=10*
- Eje conjugado: *2b=2\cdot 4=8*
De la ecuación se identifica que el centro de la hipérbola es el origen de coordenadas, por tanto los ejes de simetría son los ejes cartesianos. Sus ecuaciones son:
- Eje focal: *x=0*
- Eje imaginario: *y=0*
Ejercicio 3
Dada la ecuación de la hipérbola *\dfrac{(x-2)^2}{19}-\dfrac{(y+3)^2}{9}=1,* determinar sus ejes principales y de simetría.
Solución: de la ecuación canónica reconocemos que la hipérbola es horizontal y está centrada fuera del origen. Sacamos las longitudes de los semiejes de los denominadores:
*a^2=19→a=\sqrt{19}*
*b^2=9→b=\sqrt{9}=3*
Ahora calculamos los ejes multiplicando por dos:
- Eje transversal: *2a=2\cdot \sqrt{19}≈8,72*
- Eje conjugado: *2b=2\cdot 3=6*
De la ecuación obtenemos el centro que es el punto (h, k) = (2, -3). Los ejes de simetría tienen la forma x = h, y = k, por tanto son:
- Eje imaginario: *x=2*
- Eje focal: *y=-3*
Ejercicio 4
Hallar los semiejes a y b de la hipérbola *y^2-2y-2x^2-9=0*
Solución: en este caso tenemos la ecuación general de la hipérbola y no podemos obtener directamente los datos necesarios. Sin embargo, si completamos los cuadrados encontramos una forma equivalente:
*\dfrac{(y-1)^2}{10}-\dfrac{x^2}{5}=1*
De aquí podemos identificar que la hipérbola es vertical y su centro está desplazado del origen. De los denominadores obtenemos los datos para resolver el problema:
*a^2=10→a=\sqrt{10}*
*b^2=5→b=\sqrt{5}*
Entonces:
- Semieje transversal: *a=\sqrt{10}≈3,16*
- Semieje conjugado: *b=\sqrt{5}≈2,24*
Bibliografía
- Engler, A. y otros. (2020). Geometría Analítica. Universidad Nacional del Litoral.
- Fuller, G. y Tarwater, D. (1995). Geometría Analítica (7ma edición). Pearson Educación.
- Lehmann, C. (1989). Geometría Analítica. Limusa.
- Leithold. L. (1992). Álgebra y Trigonometría con Geometría Analítica. Oxford University Press.
- Mora, W., y Figueroa, G. (2009). Cónicas. Revista Digital Matemática, Educación e Internet.
- Márquez, A. y otros. (2009). Geometría Analítica. Prentice Hall.
- Raichman, S. y Totter, E. (2016). Geometría Analítica para Ciencias e Ingeniería. Universidad Nacional de Cuyo.
- Sullivan, M. (2006). Álgebra y Trigonometría. Pearson Educación.
- Swokowski, E. y Cole, J. (2009). Álgebra y Trigonometría con Geometría Analítica. Cengage Learning.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta





Otros artículos que pueden interesarte