Secciones cónicas
Las secciones cónicas son figuras geométricas que resultan de la intersección de un plano con un cono de dos hojas. Dependiendo del ángulo entre el plano y el eje del cono se pueden obtener diferentes tipos de cónicas: circunferencia, elipse, parábola e hipérbola.
Las cónicas pueden definirse como lugares geométricos en el plano, es decir, conjuntos de puntos que cumplen ciertas condiciones matemáticas. A partir de esta definición podemos deducir, a través del álgebra, las ecuaciones que describen con precisión cada una de estas curvas.
Cada tipo de sección cónica tiene elementos y propiedades particulares que pueden analizarse desde su gráfica o su ecuación algebraica. A lo largo de este artículo, veremos cómo se originan estas curvas, sus definiciones formales, cómo se expresan mediante ecuaciones, ejemplos y algunas de sus aplicaciones más importantes.
Índice
Cómo se forman las cónicas
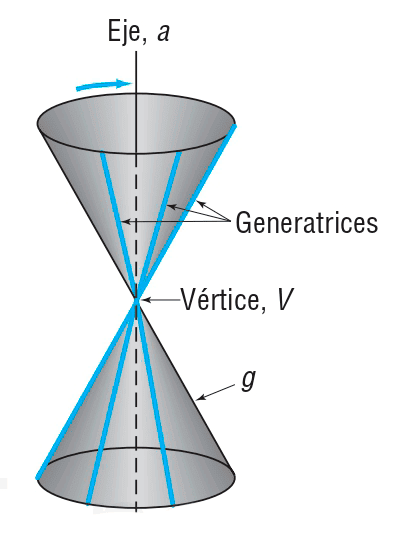
La palabra cónica proviene de cono, una figura geométrica tridimensional que se forma de la siguiente manera: consideramos que e y g son dos rectas distintas que se intersecan en un punto V. La recta e permanece fija mientras que la recta g gira alrededor de e, manteniendo el mismo ángulo entre ambas. La colección de puntos que genera la recta g se llama cono circular recto.
La recta fija se denomina eje, y las rectas que pasan por V y forman el mismo ángulo que g con e se llaman generatrices del cono. Cada generatriz es una recta que se encuentra completamente sobre el cono. El cono se divide en dos partes, llamadas hojas, que se intersecan en el vértice.
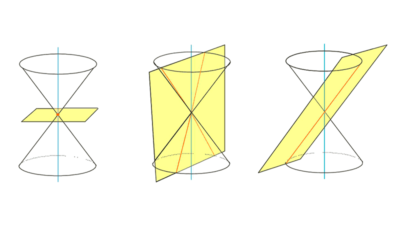
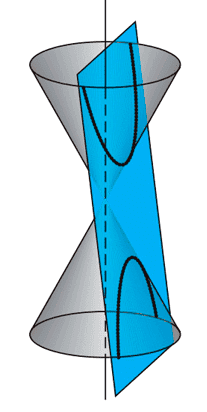
Las secciones cónicas son curvas que se obtienen al intersectar un cono circular recto con un plano. Imaginemos el plano como un cuchillo que atraviesa el cono en diferentes ángulos y posiciones. Dependiendo de la orientación del plano respecto al cono, se obtienen diferentes tipos de secciones cónicas:
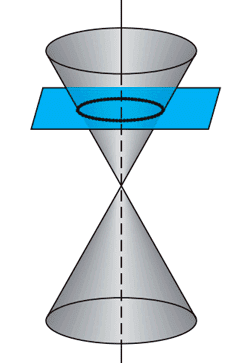
- Circunferencia: cuando el plano es perpendicular al eje del cono y corta todas las generatrices.
- Elipse: cuando el plano está ligeramente inclinado, corta todas las generatrices pero solo una hoja del cono.
- Parábola: cuando el plano es paralelo a una generatriz y corta solo una hoja del cono.
- Hipérbola: cuando el plano corta ambas hojas.
Si el plano incluye el vértice, la intersección del plano y el cono es un punto, una recta o un par de rectas que se cruzan. Estos casos se denominan cónicas degeneradas.
El concepto de cónicas aparece desde los estudios de los antiguos griegos, pero fue a partir del siglo XVII que se formalizó y se estudiaron sus propiedades algebraicas. La geometría euclidiana proporciona una comprensión intuitiva y visual de las cónicas, mientras que la geometría analítica permite estudiar las cónicas a través de sus ecuaciones, lo que proporciona herramientas para el análisis y la resolución de problemas geométricos mediante el álgebra.
Las figuras cónicas tienen numerosas aplicaciones en ciencia, tecnología y diseño. Las elipses modelan órbitas planetarias y optimizan la acústica y la distribución de cargas; las parábolas se usan en antenas, reflectores y trayectorias balísticas; y las hipérbolas permiten localizar objetos por señales, enfocar ondas y describir trayectorias espaciales.
Circunferencia
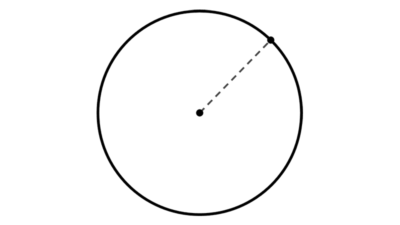
Una circunferencia se obtiene cuando un plano corta a un cono de manera perpendicular al eje del cono. Se define como el conjunto de puntos que están a una distancia fija, llamada radio, de un punto fijo, llamado centro.
Los elementos fundamentales de la circunferencia son:
- Centro: es un punto fijo ubicado en el interior de la circunferencia al cual equidistan todos los puntos de esta.
- Radio: es la distancia entre el centro y todos los puntos de la circunferencia.
El radio puede ser cualquier número positivo. En un plano cartesiano, el centro de la circunferencia puede ser cualquier punto. Existe otro elemento, llamado diámetro, cuya longitud es el doble del radio y se trata de un segmento que une dos puntos de la circunferencia y pasa por el centro.
La ecuación canónica de la circunferencia con centro en el origen de coordenadas es:
x2 + y2 = r2
donde x e y son las coordenadas de un punto genérico P(x, y) de la circunferencia y r es el radio.
Si en lugar de el origen de coordenadas queremos de centro a un punto cualquiera (h, k), la ecuación se transforma en:
(x - h)2 + (y - k)2 = r2
Ejemplos
- x2 + y2 = 4 representa una circunferencia con centro en (0, 0) y radio 2.
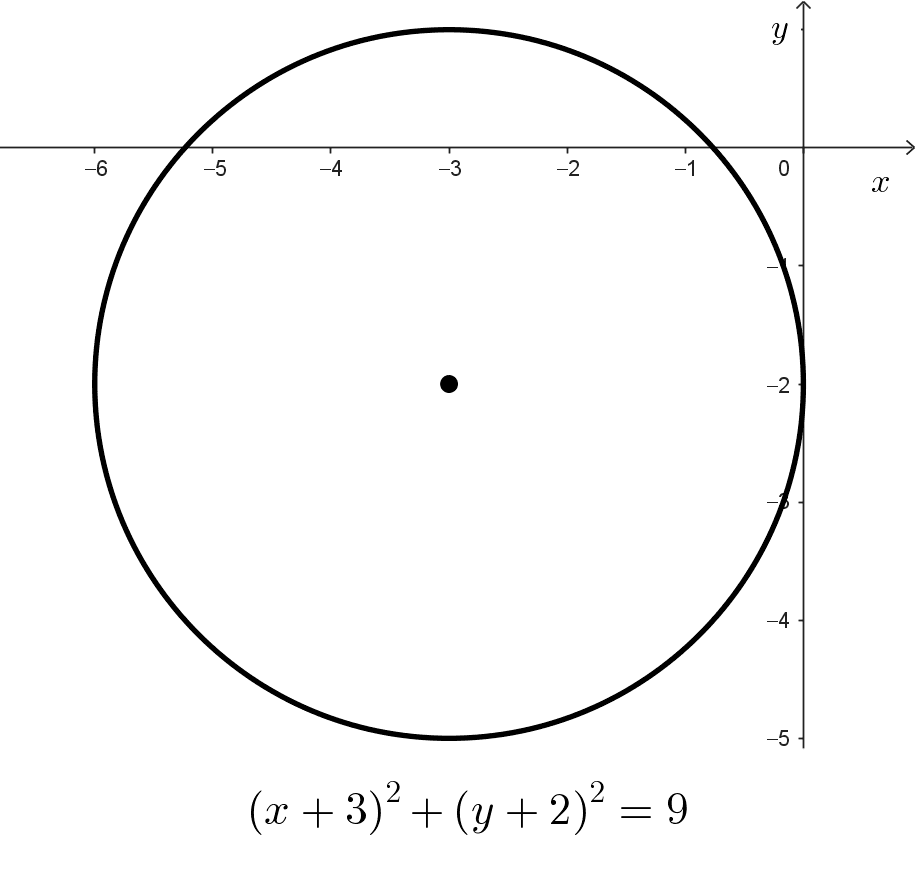
- (x+3)2 + (y+2)2 = 9 es la ecuación de una circunferencia con centro en (-3, -2) y radio 3.
- x2 + (y - 1)2 = 5 es la ecuación de una circunferencia con centro en (0, 1) y radio √5≈2,24.
Algunas propiedades de la circunferencia son:
- Cualquier recta que pase por el centro divide la circunferencia en dos mitades iguales.
- La longitud de la circunferencia (perímetro) se relaciona con su radio mediante la fórmula: P= 2πr, donde π es aproximadamente 3,141592.
- El área encerrada por la circunferencia se calcula con la fórmula: A = πr2.
Frecuentemente se confunde a la circunferencia con el círculo, pero son conceptos diferentes. El círculo es la figura geométrica completa que incluye la circunferencia y el área interior, mientras que la circunferencia es solo el borde o contorno del círculo.
La circunferencia tiene aplicaciones en el diseño de engranajes, ruedas, estructuras arquitectónicas y cálculos físicos, gracias a su forma simétrica que permite un movimiento uniforme, una distribución eficiente de cargas y precisión en sistemas mecánicos y estructurales.
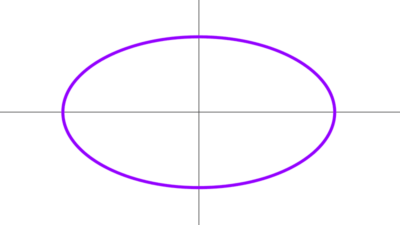
Elipse
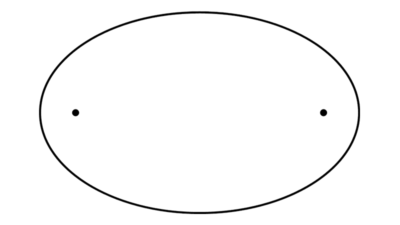
Una elipse se obtiene cuando un plano ligeramente inclinado corta a un cono en una sola hoja del mismo, pero el plano no llega a ser paralelo a ninguna generatriz. La elipse también se define como el conjunto de puntos para los cuales la suma de las distancias a dos puntos fijos, llamados focos, es constante.
Los elementos fundamentales de la elipse son:
- Focos: son dos puntos fijos situados en el interior de la elipse. La suma de las distancias desde cualquier punto de la elipse a los dos focos es constante.
- Centro: es el punto medio del segmento que une los focos.
- Eje mayor: es el segmento más largo que pasa por los focos y tiene sus extremos en la elipse. La longitud del eje mayor se representa como 2a es la distancia máxima entre dos puntos de la elipse. La mitad de este eje se llama semieje mayor, su longitud es a.
- Eje menor: es el segmento más corto que pasa por el centro y es perpendicular al eje mayor. La longitud del eje menor se simboliza como 2b es la distancia mínima entre dos puntos de la elipse. La mitad de este eje se llama semieje menor, su longitud es b.
La ecuación de la elipse varía dependiendo de la orientación del eje mayor (horizontal o vertical) y del centro (el origen de coordenadas u otro punto). Los cuatro formas canónicas se muestran en la siguiente tabla:
| Ecuación canónica | Orientación del eje mayor | Centro |
|---|---|---|
| \(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\) | Horizontal | (0, 0) |
| \(\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1\) | Vertical | (0, 0) |
| \(\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1\) | Horizontal | (h, k) |
| \(\dfrac{(x-h)^2}{b^2}+\dfrac{(y-k)^2}{a^2}=1\) | Vertical | (h, k) |
En todos los casos, a es la longitud del semieje mayor, b es la longitud del semieje menor, y a > b. Cuando la orientación es horizontal, las elipse es más ancha que alta; en cambio, cuando la orientación es vertical, la elipse es más alta que ancha.
¿Te está sirviendo este artículo? ¡Por favor, califícalo!
4,5 / 5 — 23 votos
Ejemplos
- La ecuación \(\dfrac{x^2}{16}+\dfrac{y^2}{9}=1\) representa una elipse horizontal con centro en el origen donde el semieje mayor mide 4 y el semieje menor mide 3.
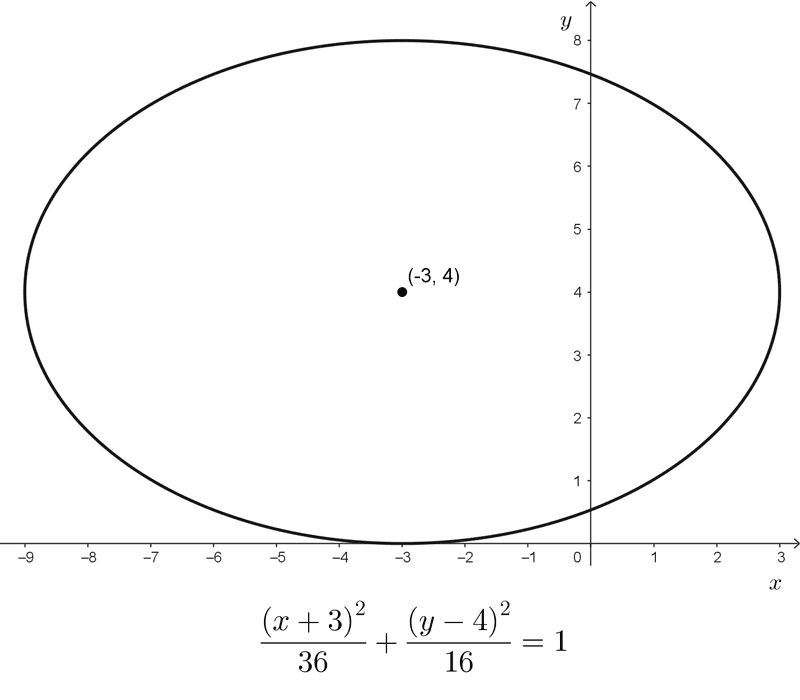
- \(\dfrac{(x+3)^2}{36}+\dfrac{(y-4)^2}{16}=1\) es una elipse con eje mayor horizontal, centro en (-3, 4), semiejes mayor a = 6 y menor b = 4.
- La ecuación \(\dfrac{(x-1)^2}{9}+\dfrac{(y+2)^2}{25}=1\) representa una elipse vertical con centro en (1,-2) donde el semieje mayor mide 5 y el menor mide 3.
Se puede considerar a una circunferencia como un caso particular de elipse cuando los focos son el mismo punto.
Las elipses tienen aplicaciones clave en campos como la astronomía, la ingeniería, la arquitectura y la óptica, donde su forma única permite describir órbitas planetarias, distribuir cargas en estructuras, optimizar la acústica y concentrar luz o sonido con precisión.
Parábola
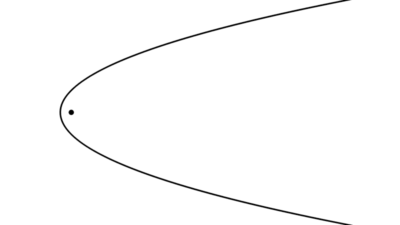
Una parábola se obtiene cuando un cono es cortado por un plano paralelo a una generatriz. Se define como el conjunto de puntos que están a una distancia igual de un punto fijo, llamado foco, y de una línea recta fija, llamada directriz.
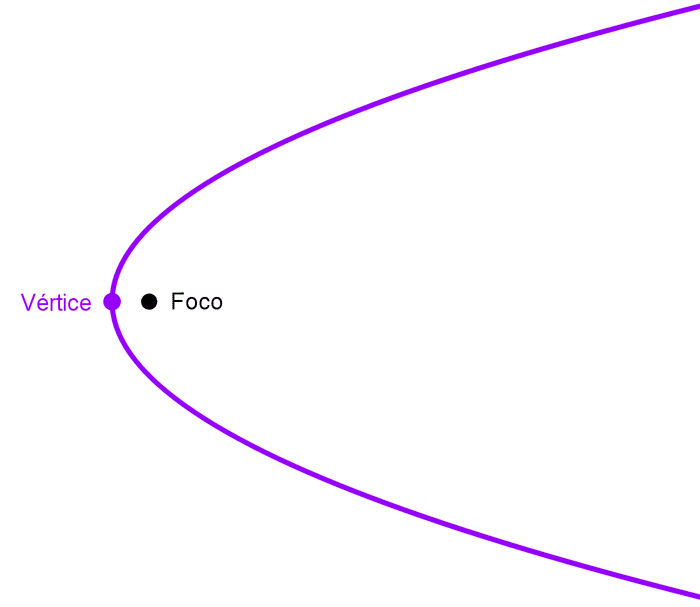
Los elementos fundamentales de la parábola son:
- Foco: es el punto fijo del plano.
- Directriz: es una línea fija que no pasa por el foco. La distancia desde cualquier punto de la parábola a la directriz es igual a la distancia de ese punto al foco.
- Vértice: es el punto de la parábola que está más cercano tanto al foco como a la directriz.
- Distancia focal: es la distancia entre el foco y el vértice o entre el vértice y la directriz. Su valor es |p|, donde p es un parámetro que aparece en la ecuación.
La parábola puede abrirse hacia arriba, hacia abajo, hacia la derecha o hacia la izquierda, dependiendo de la orientación de la directriz y el foco.
La ecuación estándar de la parábola con vértice en el origen y que se abre hacia la izquierda o la derecha es:
\(y^2=4px\)
donde |p| es la distancia focal. Cuando p > 0, la curva abre hacia la derecha y cuando p < 0, la curva abre hacia la izquierda.
Si la parábola se abre hacia arriba o hacia abajo, la ecuación es:
\(x^2=4py\)
Cuando p > 0, la curva abre hacia arriba y cuando p < 0, la curva abre hacia abajo.
Para una parábola con vértice en un punto cualquiera (h, k), la ecuación se transforma en:
- \((y-k)^2=4p(x-h)\) para parábolas que abren hacia izquierda o derecha.
- \((x-h)^2=4p(y-k)\) para parábolas que abren hacia arriba o hacia abajo.
Ejemplos
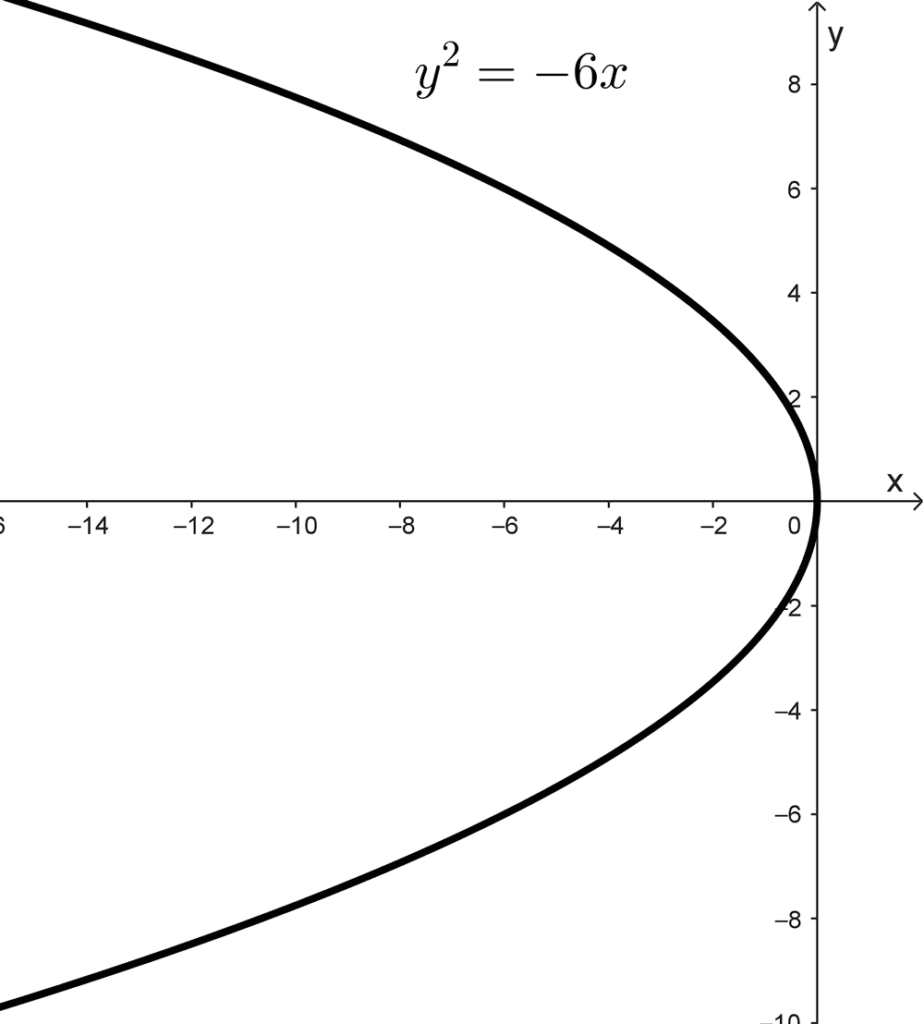
- La ecuación \(y^2=-6x\) representa una parábola con vértice en (0, 0) donde la distancia del foco al vértice es 1,5. La curva abre hacia la izquierda.
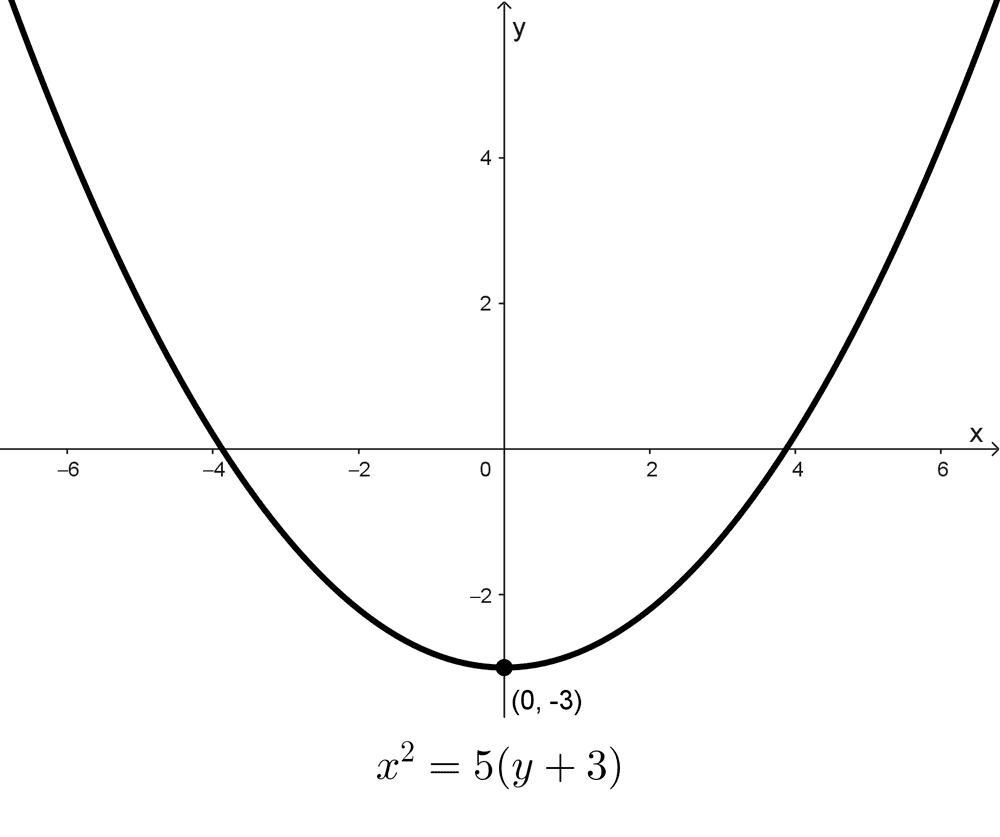
- La ecuación \(x^2=5(y+3)\) representa una parábola con vértice en (0, -3) donde la distancia del foco al vértice es 5/4. La curva se abre hacia arriba.
- La ecuación \((y-1)^2=2(x+2)\) representa una parábola con vértice en (-2, 1) donde la distancia del foco al vértice es 1/2. La curva se abre hacia la derecha.
La parábola tiene múltiples aplicaciones en ciencia y tecnología gracias a su capacidad para concentrar luz, sonido o cargas, siendo esencial en antenas parabólicas, dispositivos ópticos, acústicos y telescopios. También se utiliza para la modelización de trayectorias balísticas y fenómenos económicos, entre otras cosas.
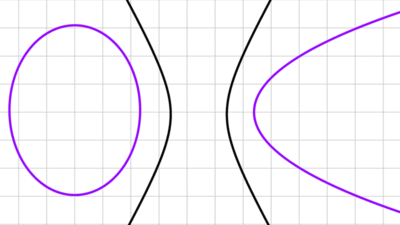
Hipérbola
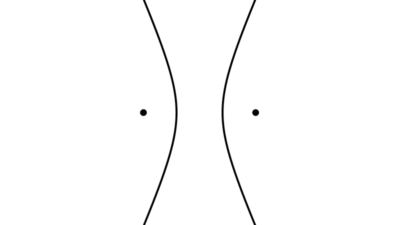
Una hipérbola se obtiene cuando un plano corta las dos hojas de un cono. También se define como el conjunto de puntos para los cuales la diferencia de las distancias a dos puntos fijos, llamados focos, es constante en valor absoluto.
Los elementos fundamentales de la hipérbola son:
- Focos: son los dos puntos fijos en el plano, se ubican sobre una recta llamada eje focal. La diferencia de las distancias desde cualquier punto de la hipérbola a estos dos focos es constante.
- Centro: es el punto medio del segmento que une a los focos.
- Vértices: son dos puntos de la hipérbola que se encuentran sobre el eje focal y a la misma distancia del centro.
- Eje transversal: es el segmento que une los vértices, su longitud es 2a. A la mitad de este eje se le llama semieje transversal y su longitud es a.
- Eje conjugado: es el segmento perpendicular al eje focal y pasa por el centro de la hipérbola, su longitud es 2b. A la mitad de este eje se le llama semieje conjugado y su longitud es b.
La hipérbola tiene dos ramas que se abren en direcciones opuestas. La orientación de la apertura depende de la disposición de los focos y los ejes.
La ecuación ordinaria de la hipérbola es muy parecida a la de la elipse, la diferencia es que tiene un término cuadrático negativo en el primer miembro. La ecuación varía dependiendo de la orientación del eje transversal (horizontal o vertical) y la posición del centro (en el origen de coordenadas u otro punto).
| Ecuación canónica | Orientación del eje transversal | Centro |
|---|---|---|
| \(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\) | Horizontal | (0, 0) |
| \(\dfrac{y^2}{a^2}-\dfrac{x^2}{b^2}=1\) | Vertical | (0, 0) |
| \(\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1\) | Horizontal | (h, k) |
| \(\dfrac{(y-k)^2}{a^2}-\dfrac{(x-h)^2}{b^2}=1\) | Vertical | (h, k) |
En los cuatro casos, a es la longitud del semieje transversal, b es la longitud del semieje conjugado y, a diferencia de la elipse, aquí sí puede ocurrir que b sea mayor que a. Cuando la orientación es horizontal, las ramas se abren hacia la izquierda y la derecha; cuando es vertical, las ramas se abren hacia arriba y hacia abajo.
Ejemplos
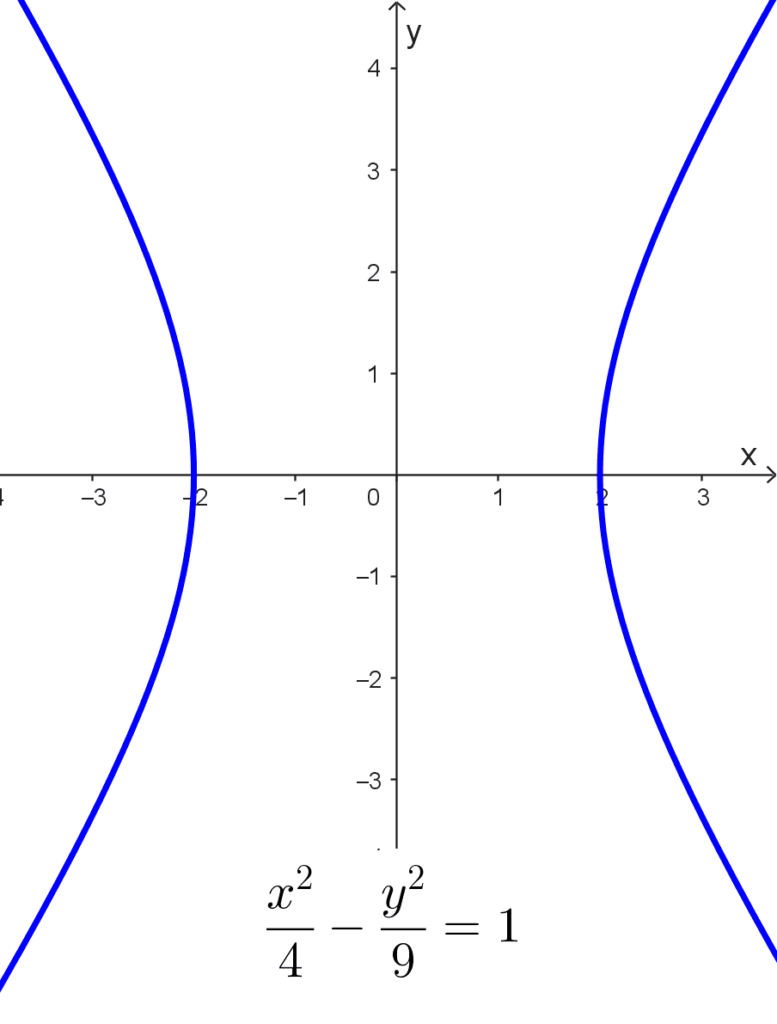
- La ecuación \(\dfrac{x^2}{4}-\dfrac{y^2}{9}=1\) representa una hipérbola horizontal con centro en el origen donde el semieje transversal mide 2 y el conjugado mide 3.
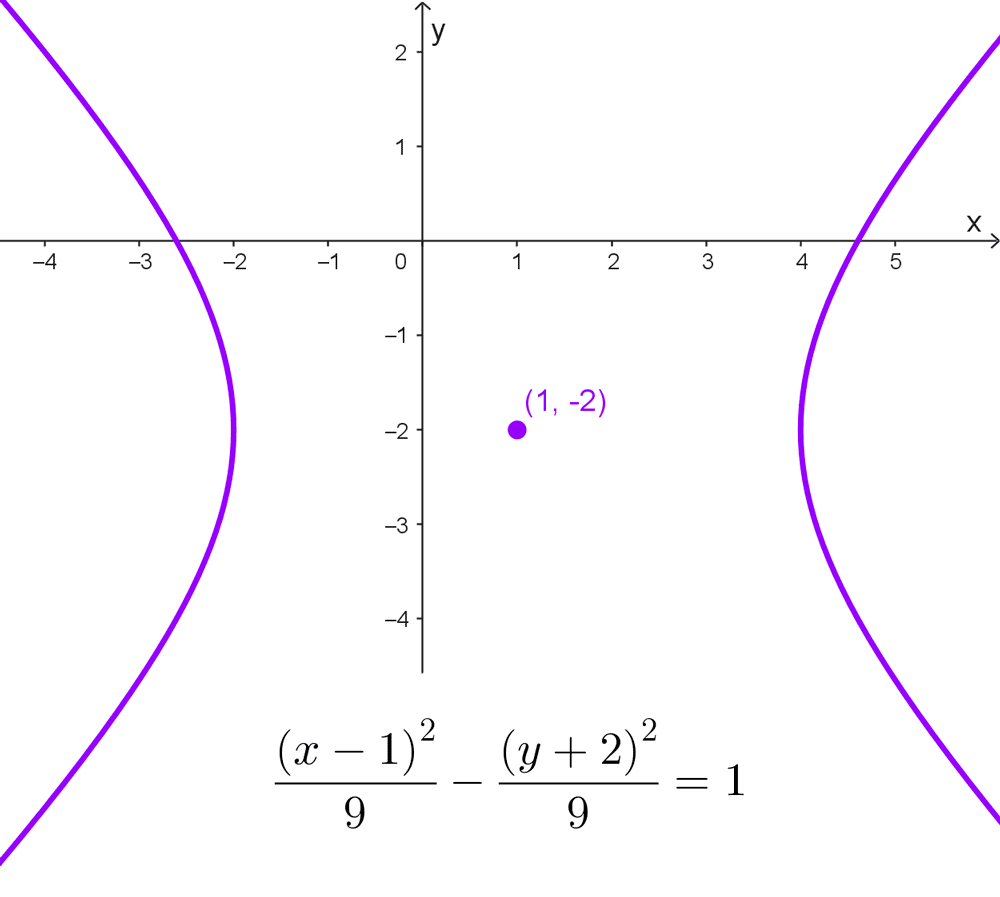
- La ecuación \(\dfrac{(x-1)^2}{9}-\dfrac{(y+2)^2}{9}=1\) representa una hipérbola con eje transversal horizontal y centro en (1, -2). Las longitudes de los semiejes son iguales: a = b = 3.
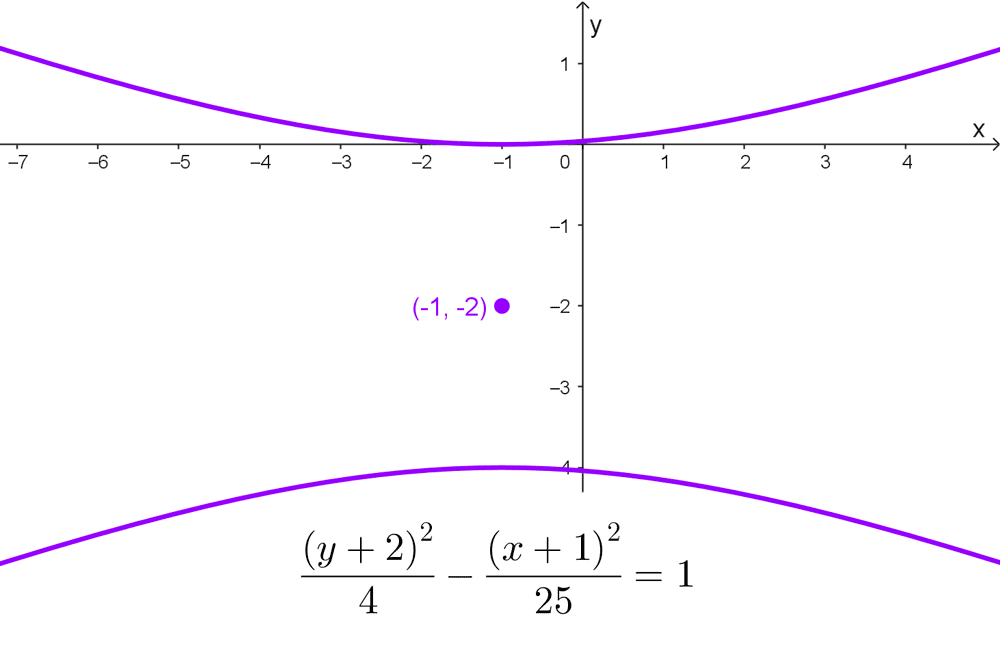
- La ecuación \(\dfrac{(y+2)^2}{4}-\dfrac{(x+1)^2}{25}=1\) representa una hipérbola vertical con centro en (-1, -2) donde el semieje tranversal mide 2 y el conjugado 5.
La hipérbola tiene aplicaciones clave en navegación, localización por señales, óptica, acústica y astronomía, destacando en sistemas similares al GPS, antenas y telescopios, donde su forma permite enfocar señales y calcular posiciones con gran precisión.
Resumen de ecuaciones
Los elementos fundamentales y las fórmulas de cada cónica se resumen en la siguiente tabla.
| Cónica | Elementos importantes | Ecuación canónica |
|---|---|---|
| Circunferencia | -Radio (r). -Centro (h, k). | \((x-h)^2+(y-k)^2=r^2\) |
| Elipse | -Centro (h, k). -Semieje mayor (a). -Semieje menor (b). | Horizontal \(\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1\) Vertical \(\dfrac{(x-h)^2}{b^2}+\dfrac{(y-k)^2}{a^2}=1\) |
| Parábola | -Foco. -Directriz. -Vértice (h, k). -Distancia focal, |p|. | Horizontal \((y-k)^2=4p(x-h)\) Vertical \((x-h)^2=4p(y-k)\) |
| Hipérbola | -Centro (h, k). -Semieje transversal (a). -Semieje conjugado (b). | Horizontal \(\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1\) Vertical \(\dfrac{(y-k)^2}{a^2}-\dfrac{(x-h)^2}{b^2}=1\) |
Nota: la ecuación canónica (también llamada estándar, ordinaria o reducida) de una cónica es una forma simplificada que permite identificar fácilmente sus características principales. Por ejemplo, en la circunferencia se puede leer directamente el centro y el radio; en la elipse y la hipérbola podemos obtener el centro, los semiejes y la orientación; y en la parábola, la orientación y la distancia focal. Existe una forma más general que abarca todas las cónicas, la explicamos en este artículo: ecuación general de las cónicas.
Recursos adicionales
En el siguiente video se explica cómo se forman las secciones cónicas:
El estudio de las figuras cónicas requiere de muchos gráficos, por lo que es fundamental contar con herramientas que faciliten la visualización y el análisis. Para esto, recomiendo utilizar GeoGebra o Desmos, dos plataformas accesibles en línea y gratuitas.
GeoGebra permite dibujar cónicas y otras figuras geométricas de manera interactiva, ya sea manipulando elementos o con ecuaciones. Por ejemplo, puedes dibujar una elipse indicando dos puntos como focos y un punto de la curva. Desmos, por otro lado, se especializa en la graficación de curvas a partir de sus ecuaciones, por lo que será necesario contar con ellas.
En el siguiente video podrás ver cómo graficar cónicas usando GeoGebra:
En la siguiente animación podrás ver cómo se genera un cono a partir del giro de una recta alrededor de otra fija:
Bibliografía consultada
- Engler, A., Müller, D., Vrancken, S. y Hecklein, M. (2020). Geometría analítica. Universidad Nacional del Litoral.
- Fuller, G. y Tarwater, D. (1995). Geometría analítica (7.ª ed.). Pearson Educación.
- Lehmann, C. (1989). Geometría analítica. Limusa.
- Leithold. L. (1992). Álgebra y trigonometría con geometría analítica. Oxford University Press.
- Márquez, A., Vázquez, F., Ruiz, H., Villegas, M. y Figueroa, M. (2009). Geometría analítica. Prentice Hall.
- Raichman, S. y Totter, E. (2016). Geometría analítica para ciencias e ingeniería. Universidad Nacional de Cuyo.
- Sullivan, M. (2006). Álgebra y trigonometría. Pearson Educación.
- Swokowski, E. y Cole, J. (2009). Álgebra y trigonometría con geometría analítica. Cengage Learning.
Más contenido sobre cónicas

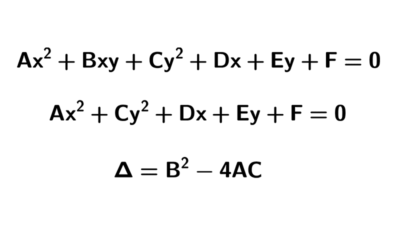
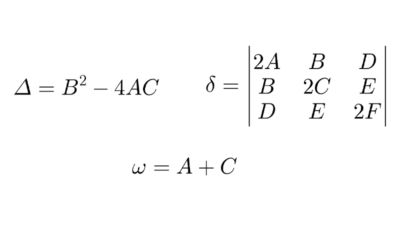




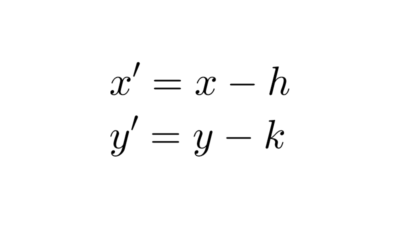
¿Te ha servido este contenido? ¡Califícalo!
4,5 / 5 — 23 votos
CÓMO CITAR ESTE ARTÍCULO
Machado, D. (2025, 10 de mayo). Secciones cónicas. Exponty. https://exponty.com/secciones-conicas
12 Comentarios
Deja una respuesta



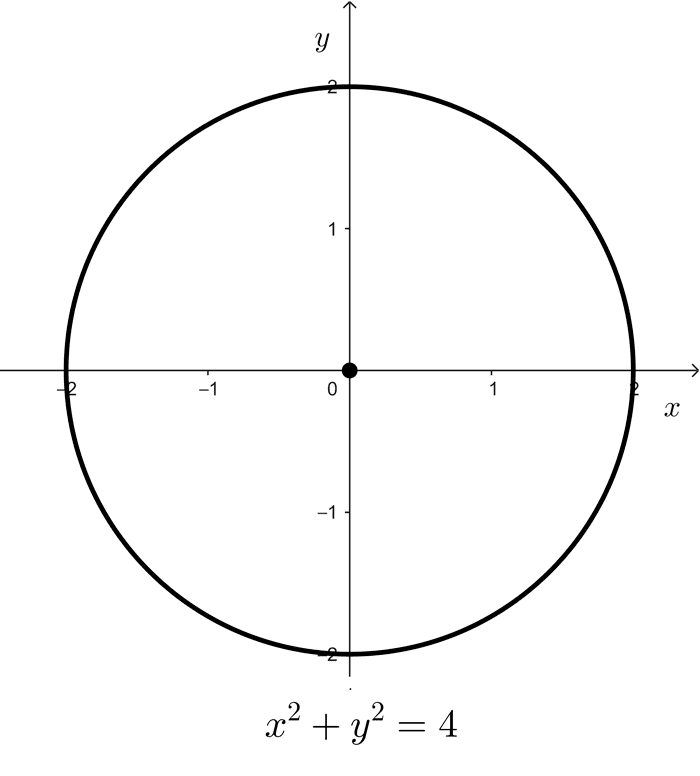
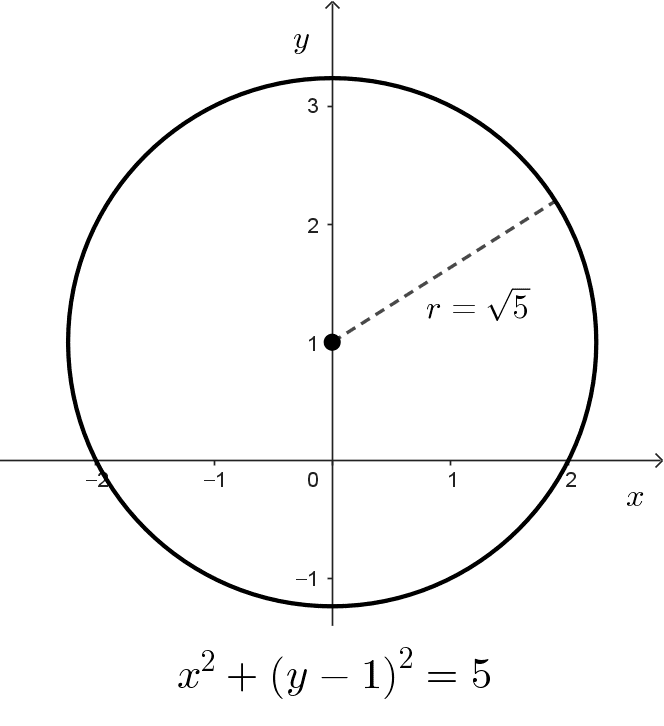



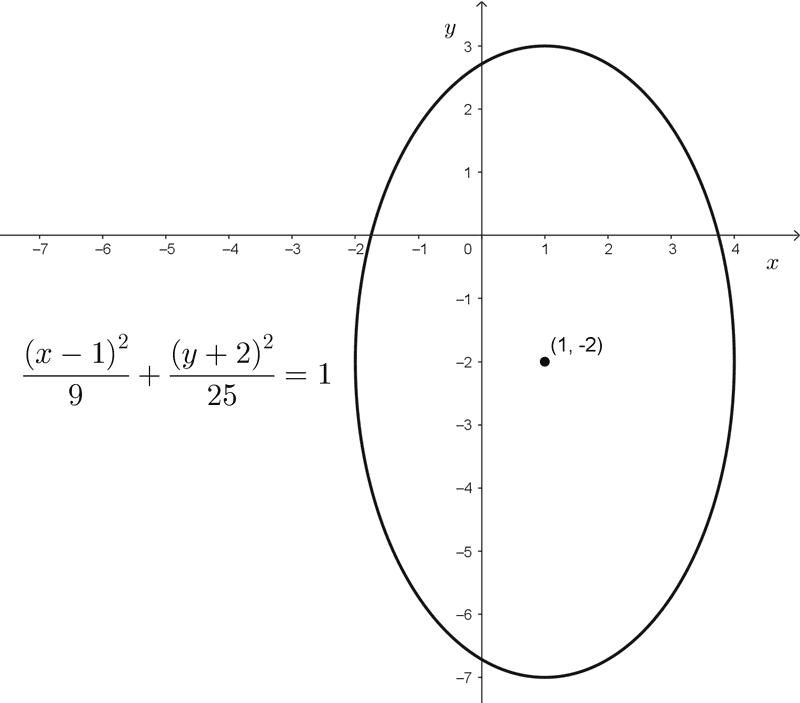

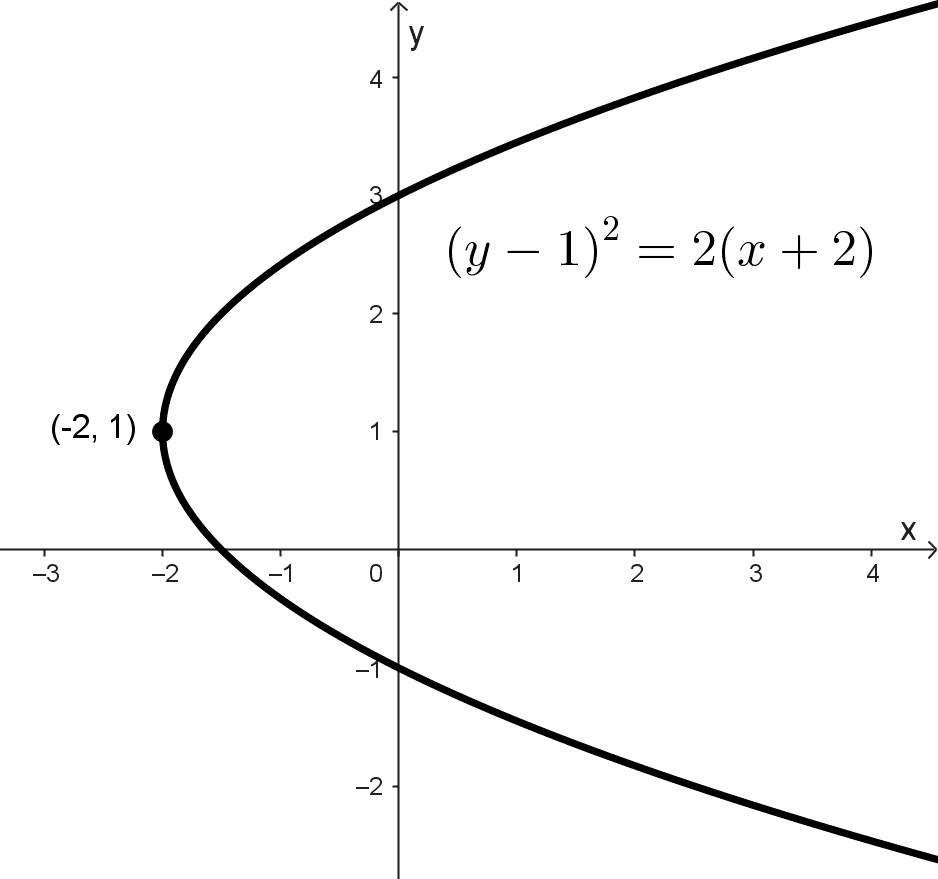



Hola prof cuestión en el ejemplo 2
para la ecuación (x+3)2 + (y+2)2 = 9 sus coordenadas correctas serian (-3,-2) con radio de 3 tal como lo grafica en la circunferencia 2
si las coordenadas fueran (3,2) con radio de 3 entonces la ecuación sería (x-3)2 + (y-2)2 = 9 en negativos estando la circunferencia más cercana al cuadrante uno ¿no es así? si estoy mal corríjame.
Como comentario realmente me gustó mucho mucho su forma de explicar, facilita demasiado el análisis matemático.