Elipses horizontales y verticales
Una elipse puede tener distintas orientaciones dependiendo de la posición del eje mayor con respecto a los ejes coordenados. Cuando el eje mayor es paralelo al eje x, la elipse se considera horizontal; si, en cambio, es paralelo al eje y, la elipse es vertical.
A continuación, explicaremos las elipses horizontales y verticales y cómo identificar cada caso a partir de la ecuación canónica o la general. Si aún no conoces el significado de la elipse en matemáticas, te recomiendo revisar antes el artículo principal, donde explicamos su definición, fórmulas, partes y características.
Índice
Elipse horizontal
Una elipse horizontal es aquella cuyo eje mayor es paralelo al eje x o está sobre el mismo. La ecuación canónica cambia dependiendo de si el centro es el origen de coordenadas u otro punto:
Centro en (0, 0): \(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\)
Centro en (h, k): \(\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1\)
donde:
- a > b
- La longitud del eje mayor es 2a.
- La longitud del eje menor es 2b.
En una elipse horizontal, el denominador del término que contiene la variable x es más grande que el del término que contiene la variable y. Si el centro es el origen, el eje mayor está sobre el eje x; si el centro es otro punto, el eje mayor es horizontal, paralelo al eje x.
Los elementos de una elipse horizontal pueden extraerse a partir de la ecuación canónica, como se muestra en la siguiente tabla:
| Ecuación | Eje mayor | Centro | Focos | Vértices |
|---|---|---|---|---|
| \(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\) | Sobre el eje x | (0, 0) | (±c, 0) donde c = √(a2 - b2) | (±a, 0) (0, ±b) |
| \(\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1\) | Paralelo al eje x | (h, k) | (h ± c, k) donde c = √(a2 - b2) | (h ± a, k) (h, k ± b) |
Ejemplos
Los siguientes son ejemplos de fórmulas de elipses con eje mayor horizontal:
- \(\dfrac{x^2}{16}+\dfrac{y^2}{9}=1\)
- \(\dfrac{x^2}{36}+\dfrac{y^2}{16}=1\)
- \(\dfrac{(x-5)^2}{25}+\dfrac{(y+2)^2}{9}=1\)
- \(\dfrac{(x+1)^2}{35}+\dfrac{(y-2)^2}{10}=1\)
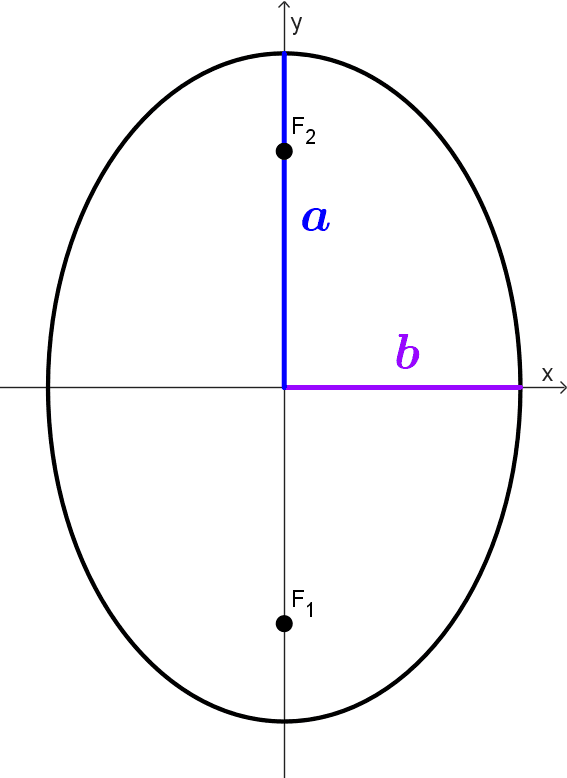
Elipse vertical
Una elipse vertical es aquella cuyo eje mayor es paralelo al eje y o se encuentra sobre el mismo. La ecuación canónica es diferente dependiendo del centro de la elipse:
Centro en (0, 0): \(\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1\)
Centro en (h, k): \(\dfrac{(x-h)^2}{b^2}+\dfrac{(y-k)^2}{a^2}=1\)
donde:
- a > b
- La longitud del eje mayor es 2a.
- La longitud del eje menor es 2b.
En una elipse vertical, el denominador del término que contiene la variable y es más grande que el del término que contiene la variable x. Si el centro es el origen, el eje mayor está sobre el eje y; si el centro es otro punto, el eje mayor es vertical, paralelo al eje y.
Los elementos de una elipse vertical se pueden extraer de la ecuación ordinaria, como se muestra en la siguiente tabla:
| Ecuación | Eje mayor | Centro | Focos | Vértices |
|---|---|---|---|---|
| \(\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1\) | Sobre el eje y | (0, 0) | (0, ±c) donde c = √(a2 - b2) | (0, ±a) (±b, 0) |
| \(\dfrac{(x-h)^2}{b^2}+\dfrac{(y-k)^2}{a^2}=1\) | Paralelo al eje y | (h, k) | (h, k ± c) donde c = √(a2 - b2) | (h, k ± a) (h ± b, k) |
Ejemplos
Los siguientes son ejemplos de fórmulas de elipses con eje mayor vertical:
- \(\dfrac{x^2}{4}+\dfrac{y^2}{25}=1\)
- \(\dfrac{y^2}{30}+\dfrac{x^2}{10}=1\)
- \(\dfrac{(x-1)^2}{9}+\dfrac{(y+2)^2}{25}=1\)
- \(\dfrac{(x+1)^2}{25}+\dfrac{(y-4)^2}{36}=1\)
Cómo saber si una elipse es horizontal o vertical
Saber la orientación de una elipse es relativamente sencillo si se tiene la ecuación canónica, en ella se deben identificar los denominadores de las variables:
- Si el denominador del término que contiene a la variable x es mayor que el término que contiene la variable y, entonces se trata de una elipse horizontal, su eje mayor y su eje focal son paralelos al eje x.
- Si el denominador del término que tiene y es mayor que el término que tiene x, entonces se trata de una elipse vertical, cuyos eje mayor y eje focal son paralelos al eje y.
Si en lugar de la ecuación ordinaria se tiene la fórmula general, será necesario completar los cuadrados y acomodar la expresión hasta que se alcance la forma canónica.
Ejercicios resueltos
Determinar a partir de la ecuación si las siguientes elipses son horizontales o verticales:
- \(\dfrac{x^2}{31}+\dfrac{y^2}{32}=1\)
- \(9x^2+4y^2=25\)
- \(4x^2+9y^2=36\)
- \(16x^2+9y^2=144\)
- \(16x^2+25y^2=100\)
- \(36x^2+25y^2+72x-200y-464=0\)
- \(2x^2+4x+7y^2-28y-40=0\)
- \(x^2+3y^2-6x+6y=0\)
Soluciones
Ecuación 1
\(\dfrac{x^2}{31}+\dfrac{y^2}{32}=1\)
El denominador de y2 es 32, el de x2 es 31, como 32 > 31, el denominador más grande lo tiene el término con la variable y, por tanto la elipse es vertical.
Ecuación 2
\(9x^2+4y^2=25\)
Dividiendo los dos miembros entre 25 y simplificando se obtiene la forma canónica:
\(\dfrac{9x^2+4y^2}{25}=\dfrac{25}{25}\)
\(\dfrac{9x^2}{25}+\dfrac{4y^2}{25}=1\)
\(\dfrac{x^2}{25/9}+\dfrac{y^2}{25/4}=1\)
Como 25/9 ≈ 2,78 y 25/4 = 6,25, el denominador más grande lo tiene y2, por tanto la elipse tiene orientación vertical.
Ecuación 3
\(4x^2+9y^2=36\)
Dividiendo ambos miembros entre 36 y simplificando:
\(\dfrac{4x^2}{36}+\dfrac{9y^2}{36}=\dfrac{36}{36}\)
\(\dfrac{x^2}{9}+\dfrac{y^2}{4}=1\)
Como 9 > 4, el denominador del término que tiene x es más grande al del término con y, por tanto la elipse es horizontal.
Ecuación 4
\(16x^2+9y^2=144\)
Dividiendo los dos lados de la ecuación entre 144 y simplificando, se obtiene la ecuación canónica:
\(\dfrac{16x^2}{144}+\dfrac{9y^2}{144}=\dfrac{144}{144}\)
\(\dfrac{x^2}{9}+\dfrac{y^2}{16}=1\)
Como 16 > 9, el denominador más grande está bajo y2, por tanto la elipse es vertical.
Ecuación 5
\(16x^2+25y^2=100\)
Dividiendo ambos miembros entre 100 y simplificando los coeficientes, se obtiene:
\(\dfrac{16x^2}{100}+\dfrac{25y^2}{100}=\dfrac{100}{100}\)
\(\dfrac{x^2}{25/4}+\dfrac{y^2}{4}=1\)
Como 25/4 = 6,25 es mayor a 4, el denominador más grande se encuentra bajo x2, por tanto la elipse es horizontal.
Ecuación 6
\(36x^2+25y^2+72x-200y-464=0\)
Si completamos los cuadrados se obtiene la siguiente expresión equivalente en forma canónica:
\(\dfrac{(x+1)^2}{25}+\dfrac{(y-4)^2}{36}=1\)
Como 36 > 25, el denominador más grande se encuentra bajo el término que contiene a la variable y, por tanto la elipse es vertical.
Para ver ejemplos de cómo completar los cuadrados visita el siguiente artículo:
Ecuación 7
\(2x^2+4x+7y^2-28y-40=0\)
Completando los cuadrados se obtiene la forma canónica:
\(\dfrac{(x+1)^2}{35}+\dfrac{(y-2)^2}{10}=1\)
Como 35 > 10, el denominador mayor se encuentra en el término con la variable x, resultando en una elipse horizontal.
Ecuación 8
\(x^2+3y^2-6x+6y=0\)
Completando los cuadrados se obtiene:
\(\dfrac{(x-3)^2}{12}+\dfrac{(y+1)^2}{4}=1\)
Como 12 > 4, el denominador mayor está en el término con la variable x, por tanto la elipse tiene su eje mayor horizontal.
Recursos adicionales
El siguiente video explica las elipses horizontales y verticales:
Bibliografía consultada
- Engler, A., Müller, D., Vrancken, S. y Hecklein, M. (2020). Geometría analítica. Universidad Nacional del Litoral.
- Fuller, G. y Tarwater, D. (1995). Geometría analítica (7.ª ed.). Pearson Educación.
- Lehmann, C. (1989). Geometría analítica. Limusa.
- Leithold. L. (1992). Álgebra y trigonometría con geometría analítica. Oxford University Press.
- Márquez, A., Vázquez, F., Ruiz, H., Villegas, M. y Figueroa, M. (2009). Geometría analítica. Prentice Hall.
- Raichman, S. y Totter, E. (2016). Geometría analítica para ciencias e ingeniería. Universidad Nacional de Cuyo.
- Sullivan, M. (2006). Álgebra y trigonometría. Pearson Educación.
- Swokowski, E. y Cole, J. (2009). Álgebra y trigonometría con geometría analítica. Cengage Learning.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta




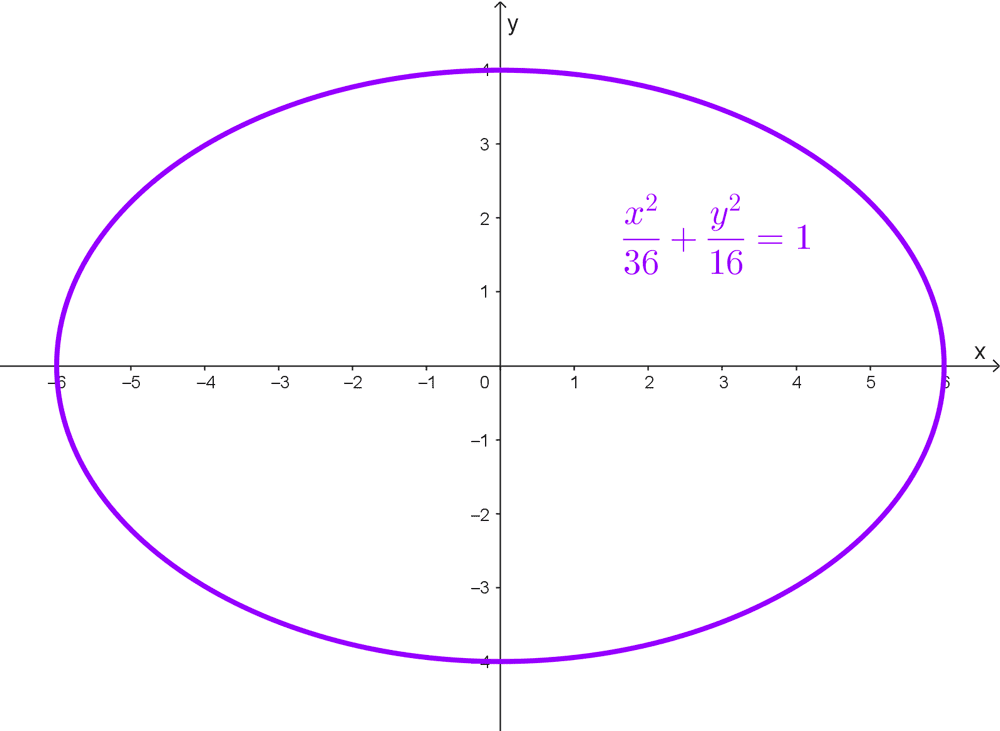

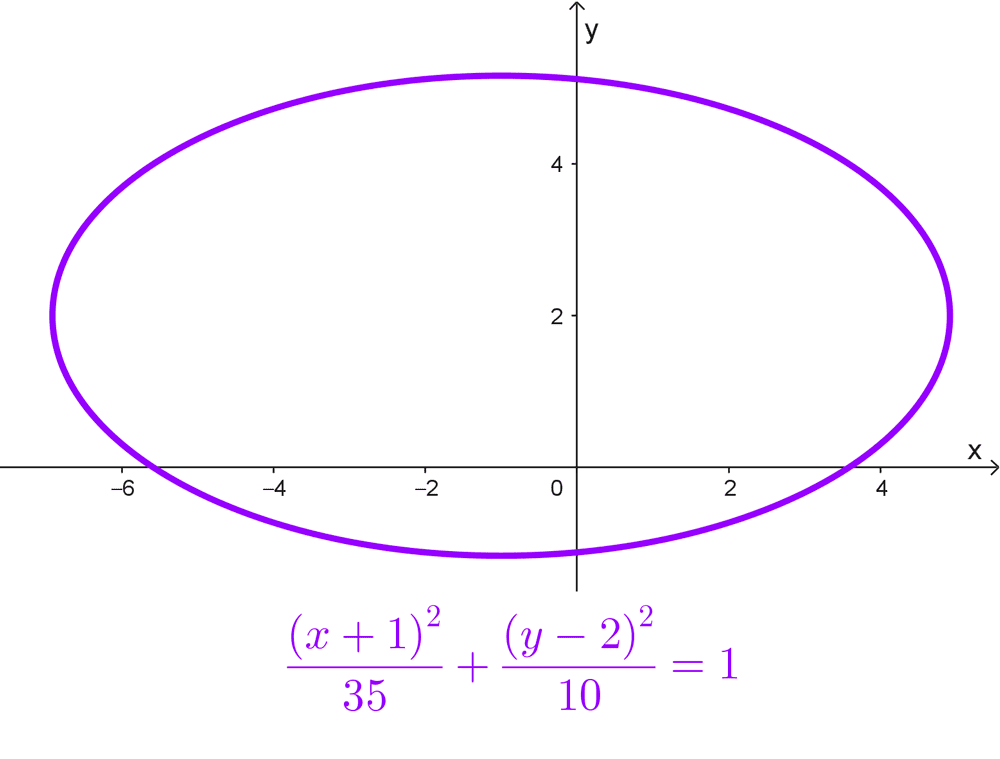

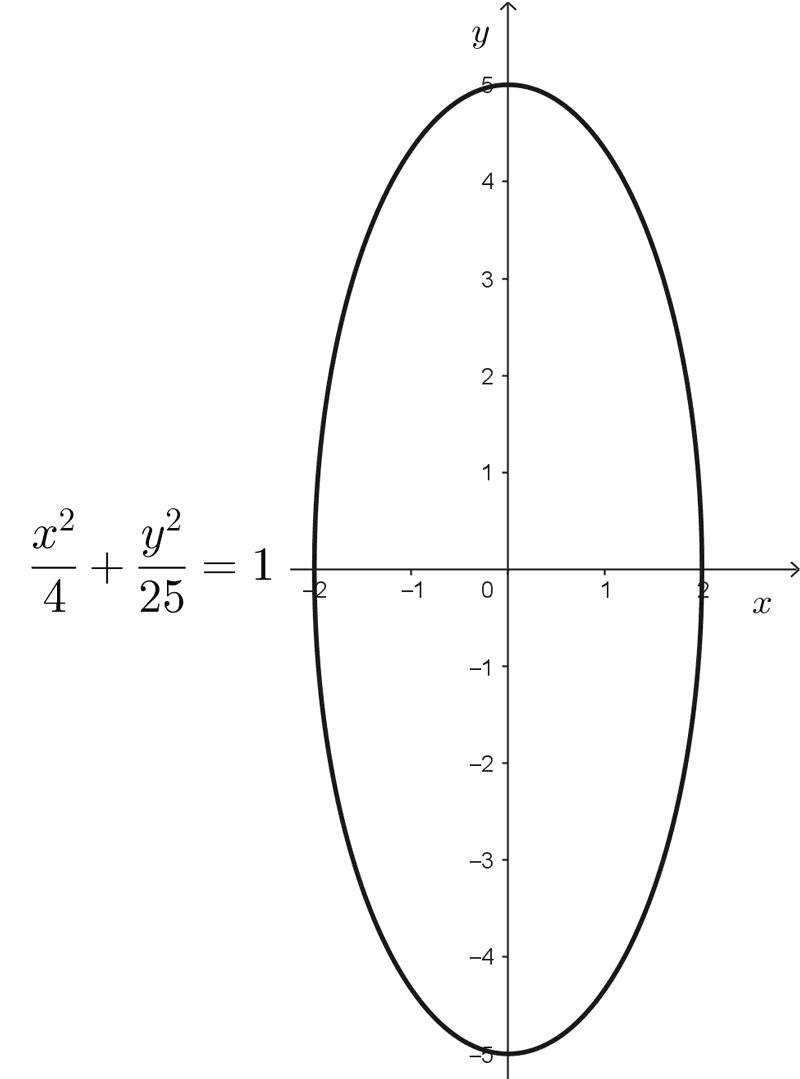
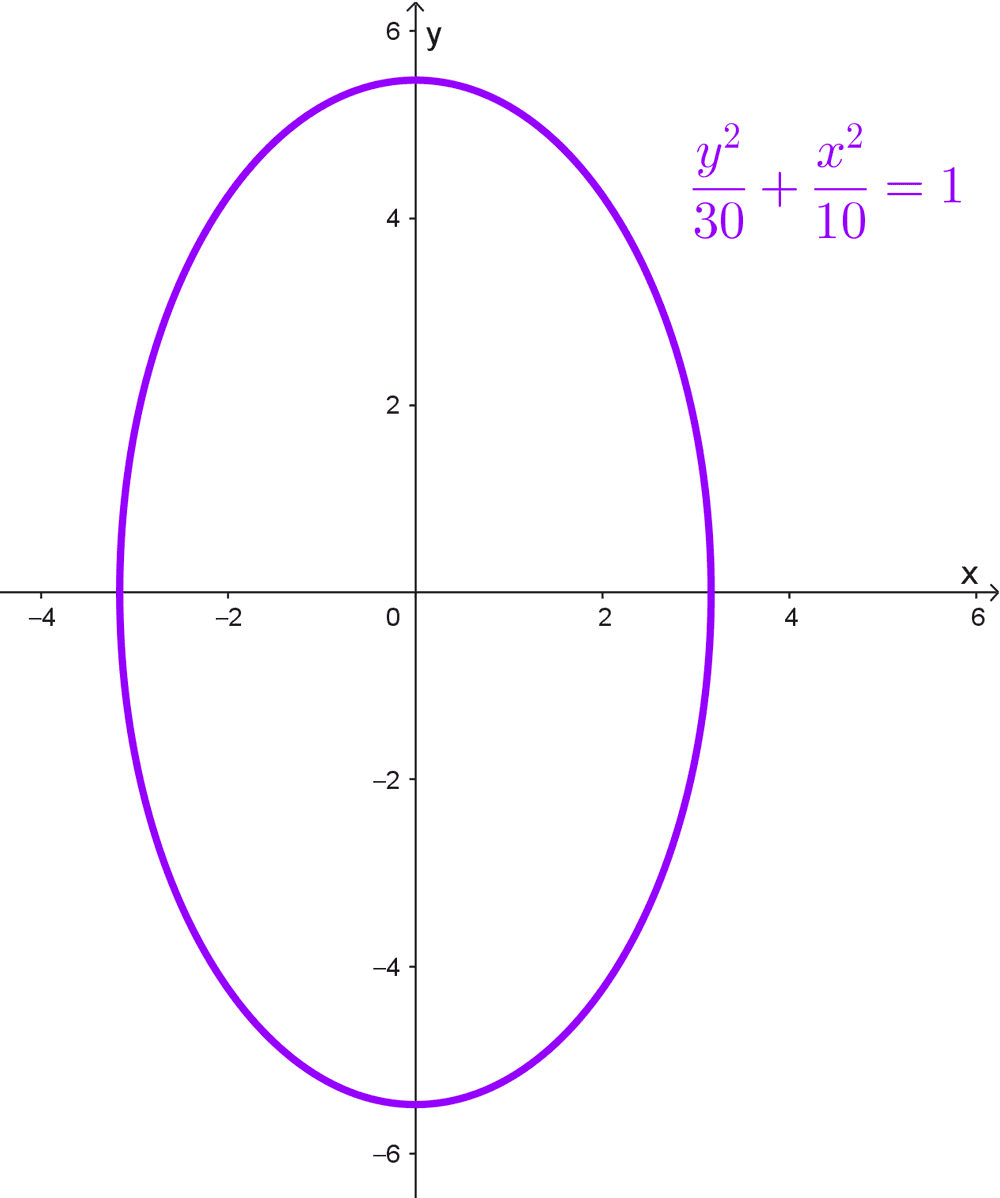
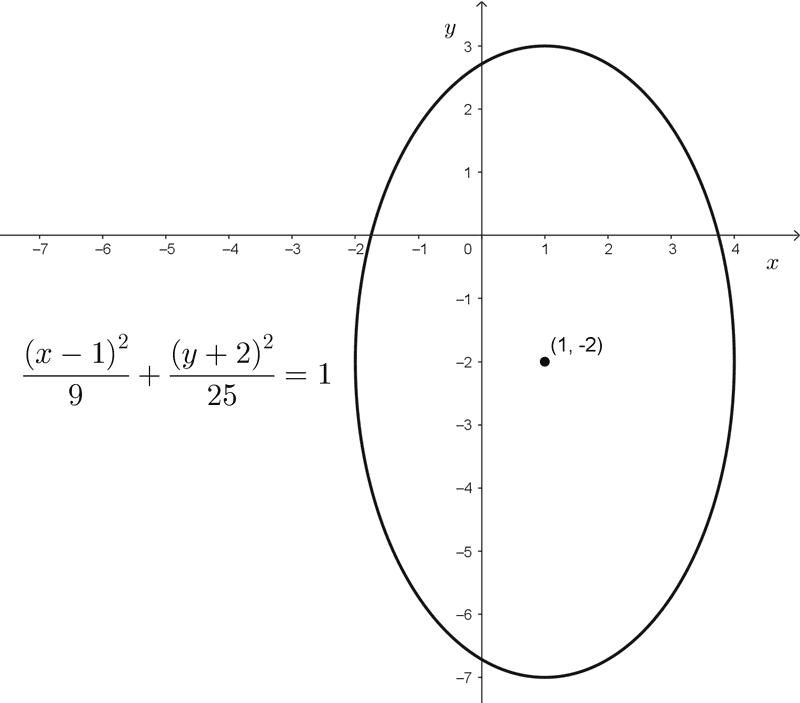
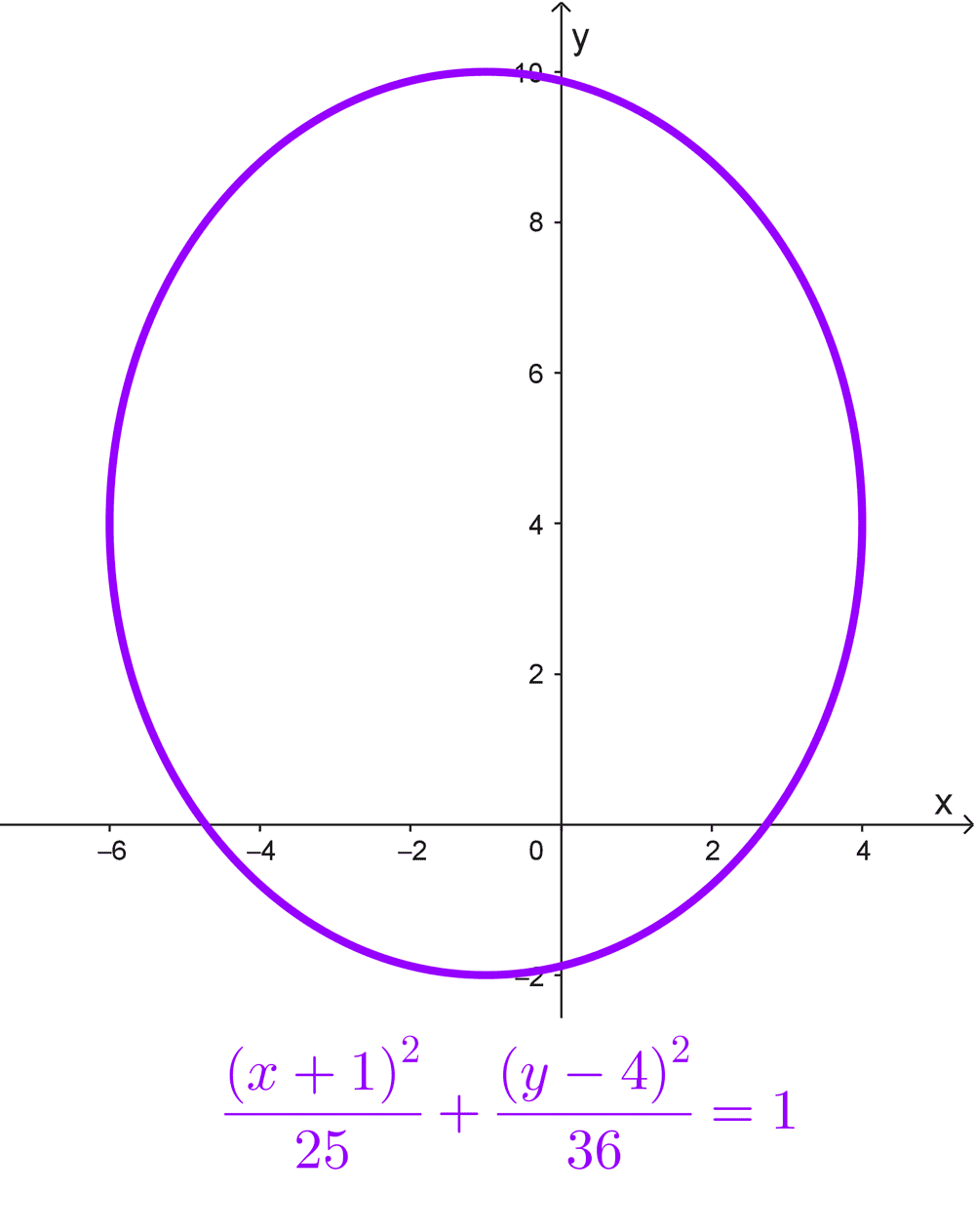

Otros artículos que pueden interesarte