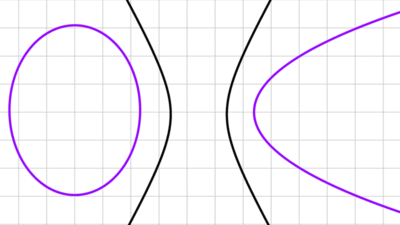
Excentricidad de las cónicas

En este artículo explicamos qué es la excentricidad en las secciones cónicas y cómo calcularla en cada caso con ejemplos.

¿Qué es la excentricidad?

La excentricidad de una cónica es un número que mide la forma y la desviación de la cónica respecto a una circunferencia. Este valor se simboliza como “e” o “ε (epsilon)” y que describe cuán "estirada" o "aplanada" es una cónica.

Elipse 

Debido a que en toda elipse ocurre que c < a, la excentricidad no supera el valor 1, es decir, está comprendida entre cero y uno (0 ≤ e < 1). 

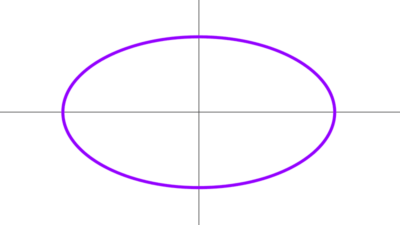
• Cuando la excentricidad es cercana a cero, la elipse se parece cada vez más a una circunferencia. Cuando e = 0, la elipse se convierte en una circunferencia perfecta. En este caso, los focos son el mismo punto y coinciden en el centro, por lo que c = 0. También puede interpretarse como que los semiejes son iguales.
• Cuando la excentricidad se acerca a 1, los focos se alejan cada vez más del centro y la elipse se alarga y se aplasta. 

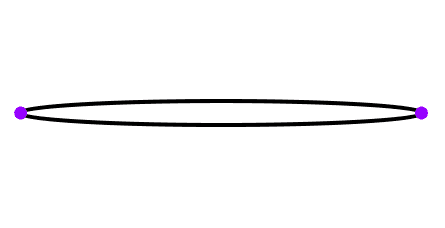
La excentricidad nunca puede llegar al valor 1, porque esto significaría que los focos son al mismo tiempo vértices de la elipse, cosa que no puede ocurrir. Sin embargo, mientras más se acerque al 1, más plana será la gráfica de la elipse, llegando a parecerse a un segmento.

Ejemplos

A continuación, se resuelven paso a paso algunos ejercicios sobre hallar la excentricidad de una elipse.

Ejemplo 1

Dada la siguiente elipse determinar su excentricidad: *\dfrac{x^2}{64}+\dfrac{y^2}{9}=1*

Solución: tenemos dos caminos para calcular la excentricidad, usar la fórmula con la semidistancia focal o la que solo involucra los semiejes, usaremos el primer camino.

Primero, extraemos de la ecuación que *a^2=64 → a=8* y *b^2=9,* lo que significa que la elipse es horizontal. Ahora determinamos la semidistancia focal usando la siguiente fórmula:

*c=\sqrt{a^2-b^2}*

*c=\sqrt{64-9}*

*c=\sqrt{55}*

*c≈7,42*

Ahora usamos la fórmula de la excentricidad:

*e=\dfrac{c}{a}=\dfrac{\sqrt{55}}{8}*

*e≈0,93*

Ejemplo 2

Obtener la excentricidad de la siguiente elipse: *\dfrac{y^2}{25}+\dfrac{x^2}{16}=1*

Solución: de la ecuación extraemos que se trata de una elipse vertical donde a² = 25 y b² = 16. Calcularemos la excentricidad usando la fórmula alternativa:

*e= \sqrt{1-\dfrac{b^2}{a^2}}*

*e=\sqrt{1-\dfrac{16}{25}}*

*e=\sqrt{\dfrac{9}{25}}*

*e=\dfrac{3}{5}≈0,6*

Ejemplo 3

Encontrar la excentricidad de elipse *\dfrac{(x-1)^2}{15}+\dfrac{y^2}{14}=1*

Solución: en este caso notamos que se trata de una elipse horizontal donde a² = 15 y b² = 14. Sacaremos la excentricidad con la segunda fórmula ya que requiere menos pasos:

*e=\sqrt{1-\dfrac{b^2}{a^2}}*

*e=\sqrt{1-\dfrac{14}{15}}*

*e=\sqrt{\dfrac{1}{15}}*

*e≈0,26*

Ejemplo 4

Calcular la excentricidad de *2x^2+4x+7y^2-28y-40=0*

Solución: la ecuación no está en forma canónica así que no puede calcularse directamente la excentricidad, sino que es necesario manipular algebraicamente la ecuación hasta obtener la forma estándar.

Completando los cuadrados se puede llegar a que la ecuación dada se puede escribir en forma canónica:

*\dfrac{(x+1)^2}{35}+\dfrac{(y-2)^2}{10}=1*

De aquí extraemos que *a^2=35* y *b^2=10,* tratándose de una elipse con eje mayor horizontal. Calculamos la excentricidad:

*e=\sqrt{1-\dfrac{b^2}{a^2}}*

*e=\sqrt{1-\dfrac{10}{35}}*

*e=\sqrt{\dfrac{5}{7}}*

*e≈0,85*

Parábola

Toda parábola tiene excentricidad igual a 1 independientemente de su forma. 

Ejemplos

Determinar la excentricidad de las siguientes parábolas:

1. *3y+4=(x-2)^2-5*
2. *x+5=-2(y-1)^2+3*
3. *y=-\dfrac{1}{2}(x+3)^2+4*

Solución: todas las parábolas tienen excentricidad e=1.

Hipérbola 

Al igual que en la elipse, se puede calcular usando la distancia del centro a un foco (c) y la del centro al vértice (a):

e = c / a

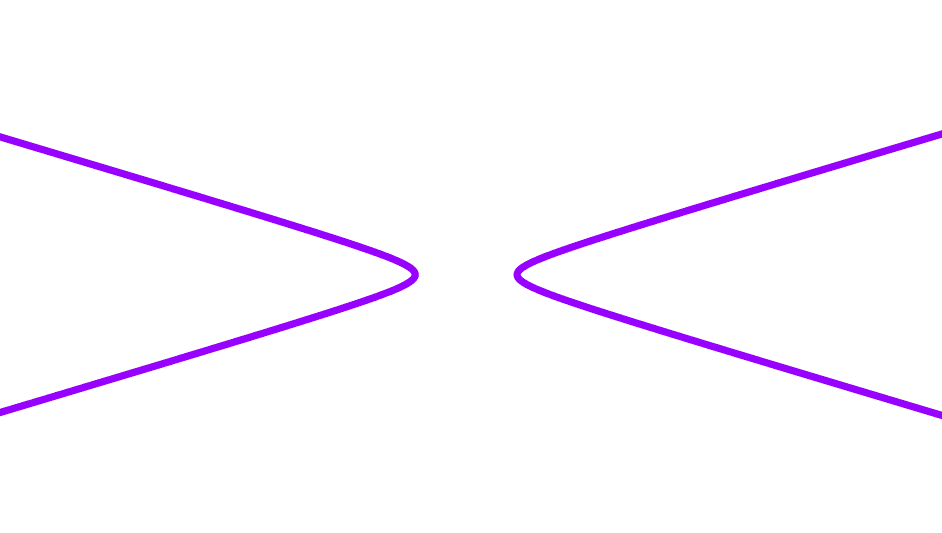
En una hipérbola, la excentricidad es siempre mayor que 1, ya que los focos están más lejos del centro que los vértices, lo que implica que c > a. A medida que la excentricidad aumenta, las ramas de la hipérbola se hacen más "abiertas" y más parecidas a rectas paralelas. Cuánto más cerca de uno, más “achatadas” están las ramas. 

Ejemplos

Calcular la excentricidad de las siguientes hipérbolas.

1. *\dfrac{(x-3)^2}{4}-(y+2)^2=1*
2. *\dfrac{(y-1)^2}{9}-\dfrac{(x+5)^2}{16}=1*
3. *\dfrac{x^2}{7}-\dfrac{(y-4)^2}{8}=1*

Soluciones

1) De *(x-3)^2-\dfrac{(y+2)^2}{4}=1* extraemos que *a^2=1* y *b^2=4* porque el término positivo es el que tiene el valor de a. 

Con estos valores calculamos la excentricidad:

*e=\sqrt{1+\dfrac{b^2}{a^2}}=\sqrt{1+\dfrac{4}{1}}=\sqrt{5}≈2,24*

2) En la ecuación *\dfrac{(y-1)^2}{9}-\dfrac{(x+5)^2}{16}=1* identificamos los valores que necesitamos. En esta ecuación, el término positivo es el que contiene a y, por lo que *a^2=9* y *b^2=16.*

Calculamos la excentricidad:

*e=\sqrt{1+\dfrac{b^2}{a^2}}=\sqrt{1+\dfrac{16}{9}}=\sqrt{\dfrac{25}{9}}=\dfrac{5}{3}\approx 1.67*

3) En la ecuación *\dfrac{x^2}{7}-\dfrac{(y-4)^2}{8}=1,* el término positivo es *\dfrac{x^2}{7},* por lo que *a^2=7* y *b^2=8.*

Calculamos la excentricidad:

*e=\sqrt{1+\dfrac{b^2}{a^2}}=\sqrt{1+\dfrac{8}{7}}=\sqrt{\dfrac{15}{7}}\approx 1.46*

Como es de esperarse, todas las excentricidades son mayores a 1. 

Resumen de fórmulas

Sección cónica	Excentricidad	Fórmulas
Circunferencia	e = 0	-
Elipse	0 ≤ e < 1	e = c / a *e=\sqrt{1-\dfrac{b^2}{a^2}}*
Parábola	e = 1	-
Hipérbola	e > 1	e = c / a *e=\sqrt{1+\dfrac{b^2}{a^2}}*

Preguntas frecuentes