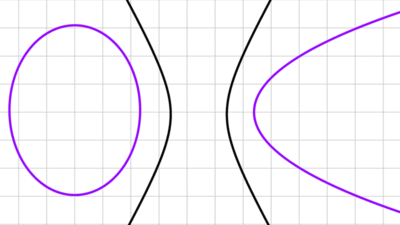
Aplicaciones de las cónicas

Las cónicas están presentes en múltiples aspectos de nuestra vida diaria: las antenas parabólicas y los telescopios, que usan la parábola para enfocar señales y luz; las órbitas elípticas de los satélites, esenciales para las comunicaciones globales; la arquitectura, que emplea formas hiperbólicas y elípticas en estructuras; las trayectorias parabólicas de los objetos lanzados; los faros de autos, diseñados para proyectar la luz de manera eficiente; entre otras cosas.

Además de su forma estética, las cónicas poseen una propiedad reflexiva que se relaciona con cómo se comportan los rayos de luz u ondas de sonido cuando inciden sobre ellas. Esta propiedad es especialmente notable en la elipse, la parábola y la hipérbola.

En las elipses e hipérbolas, cualquier rayo de luz que emana de uno de sus focos se refleja hacia el otro foco. En una parábola, un rayo de luz que proviene de su foco se reflejará paralelamente al eje de simetría de la parábola. De manera inversa, si un rayo incide paralelamente al eje de simetría, se reflejará hacia el foco. Esta propiedad es la base del diseño de antenas parabólicas y reflectores, que concentran señales o luz en un único punto.

A continuación hablaremos de la importancia de las cónicas y cómo son utilizadas en distintos campos.

Arquitectura y diseño

Las cónicas han desempeñado un papel importante en la arquitectura a lo largo de los siglos, siendo utilizadas tanto por su valor estético como por sus propiedades estructurales. Entre estas, la elipse ha sido especialmente valorada debido a su forma única y la relativa facilidad para trazarla mediante métodos geométricos, como el método del jardinero. 

Un ejemplo icónico del uso de la elipse en la arquitectura es el Coliseo de Roma, una de las maravillas del mundo antiguo. La planta del Coliseo está compuesta por elipses perfectas concéntricas, desde su perímetro exterior hasta la arena central. 

Coliseo de Roma

La elipse no solo servía como una solución estética, sino que también permitía una disposición eficiente de los asientos y una mejor distribución del sonido, mejorando la experiencia de los espectadores durante los espectáculos. Este diseño innovador fue replicado en muchos anfiteatros romanos a lo largo del Imperio.

En el Renacimiento y el Barroco, la elipse continuó siendo una forma predominante en la arquitectura. Por ejemplo, el Puente de Santa Trinidad en Florencia, construido en el siglo XVI por Bartolomeo Ammanati, fue el primer puente en utilizar un arco elíptico. Esta innovación permitió una estructura más esbelta y elegante en comparación con los arcos semicirculares tradicionales. Aunque el puente fue destruido durante la Segunda Guerra Mundial, fue reconstruido en 1958 respetando su diseño original, lo que destaca su importancia histórica y arquitectónica.

Otro ejemplo notable de la elipse en la arquitectura barroca es la iglesia de Sant'Andrea al Quirinale en Roma, diseñada por Gian Lorenzo Bernini. Esta iglesia utiliza una planta elíptica que no solo añade dinamismo al espacio interior, sino que también refuerza la importancia simbólica del altar central, alineado con uno de los ejes principales de la elipse.

La aplicación de las cónicas en la arquitectura no se limita solo a la estructura y el diseño visual; también tiene importantes aplicaciones en la acústica. Por ejemplo, la Galería de los Susurros en la Catedral de San Pablo en Londres es un fascinante ejemplo de cómo una cúpula elíptica puede manipular el sonido. 

Debido a su forma, un susurro pronunciado en uno de los focos de la elipse se transmite claramente al otro foco, permitiendo una comunicación inaudible para quienes se encuentren fuera de estos puntos. Esta misma propiedad se encuentra en otros espacios, como el Salón de las Estatuas del Capitolio de Washington D.C donde la cúpula elíptica ha sido aprovechada para efectos estéticos.

Ingeniería

Las secciones cónicas ofrecen soluciones innovadoras y eficientes en diversas áreas de la ingeniería. Un ejemplo destacado es el uso de arcos parabólicos en el diseño de puentes y estructuras. Estos arcos, debido a su capacidad para distribuir las cargas de manera uniforme, permiten construir puentes que son no solo estéticamente atractivos, sino también estructuralmente eficientes. 

La parábola también se encuentra en el diseño de reflectores parabólicos, utilizados en antenas y sistemas de iluminación. La propiedad matemática de la parábola, que hace que todos los rayos paralelos a su eje se reflejen hacia un único punto focal, es aprovechada para concentrar señales o luz en un solo punto, mejorando la eficiencia de estos sistemas. 

Un caso similar es el de los hornos parabólicos, dispositivos que utilizan la energía solar para cocinar alimentos, concentrando los rayos del sol en un punto focal a través de un reflector en forma de parábola. Este diseño permite alcanzar temperaturas superiores a los 200°C, lo que facilita la cocción rápida de alimentos, siendo una opción ecológica y sostenible, ideal para áreas donde no se dispone de electricidad o combustibles fósiles.

Las elipses se utilizan en la fabricación de hornos diseñados para concentrar calor en un punto específico, aprovechando las propiedades geométricas de esta figura. En estos hornos elípticos, la fuente de calor se coloca en uno de los focos de la elipse, mientras que el objeto o material a calentar se sitúa en el otro foco. 

Este diseño permite que la energía térmica se concentre de manera eficiente en el material, lo que es particularmente útil en procesos industriales como la fabricación de cristales de alta pureza, donde se requiere un calentamiento uniforme y preciso. 

Las órbitas de satélites también dependen de las propiedades de las secciones cónicas, en este caso, principalmente de las elipses. Los satélites orbitan la Tierra siguiendo trayectorias elípticas, donde la Tierra ocupa uno de los focos. En aviación, las trayectorias de vuelo a menudo siguen curvas parabólicas para optimizar el consumo de combustible y la eficiencia del viaje, especialmente durante maniobras complejas como los ascensos y descensos.

Por otro lado, las formas elípticas e hiperbólicas tienen aplicaciones esenciales en el diseño de engranajes y mecanismos de transmisión. Las elipses permiten diseñar engranajes que cambian la velocidad angular de rotación de manera suave y controlada, lo que es fundamental en maquinaria de precisión. 

Las hipérbolas, por su parte, se utilizan en el diseño de engranajes cónicos hipoides, que permiten transmitir movimiento entre ejes que no se cruzan y que no están alineados, algo crucial en sistemas como los diferenciales de vehículos.

Además, en la construcción de grandes infraestructuras, como las torres de enfriamiento de centrales nucleares, se utiliza la forma hiperbólica debido a su eficiencia estructural. La geometría hiperbólica no solo proporciona estabilidad ante fuertes vientos, sino que también maximiza la eficiencia en la disipación de calor, lo que es vital en la operación segura de estas plantas.

En los faros de los automóviles, la bombilla se coloca en el foco del reflector parabólico. Cuando la luz emitida por la bombilla golpea la superficie interna del reflector, es dirigida hacia adelante en un haz de luz que permite iluminar la carretera de manera efectiva. 

Este principio no solo se aplica en los faros de los autos, sino también en otros dispositivos como linternas, faros de búsqueda y antenas parabólicas. En estas últimas, cuando una señal electromagnética, como una onda de radio o microondas, llega a la superficie de la antena, esta señal es reflejada hacia el foco con alta precisión. 

Es en este punto focal donde se encuentra el receptor, comúnmente llamado LNB (Low-Noise Block), que capta y convierte la señal reflejada en información útil, como datos de televisión o internet. La forma parabólica asegura que todas las señales, independientemente del ángulo en el que lleguen, se concentren en el mismo punto, maximizando la intensidad y calidad de la recepción.

Física

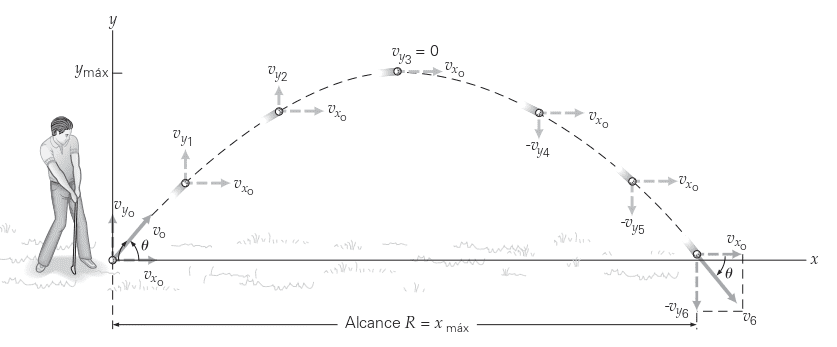
Las trayectorias de proyectiles y objetos bajo la influencia de la gravedad siguen una curva parabólica, un fenómeno fundamental en la física balística y con aplicaciones en diversos campos como la ingeniería y la defensa. 

Cuando un objeto es lanzado, su movimiento horizontal, combinado con la constante aceleración hacia abajo debido a la gravedad, lo hace seguir una trayectoria que puede describirse matemáticamente mediante una parábola. Esto es observable, por ejemplo, al lanzar una pelota al aire, donde su altura aumenta hasta un punto máximo antes de descender nuevamente.

La ecuación de la trayectoria parabólica es clave para predecir el comportamiento de proyectiles en distintas situaciones, lo cual es particularmente útil en aplicaciones prácticas como el cálculo de la trayectoria de misiles o el diseño de ángulos de lanzamiento óptimos para alcanzar objetivos. 

Astronomía

La comprensión de las cónicas en astronomía ha sido un proceso evolutivo que ha transformado nuestra visión del universo. Durante la antigüedad y hasta la Edad Media, se creía que las órbitas de los cuerpos celestes eran perfectos círculos. Esta idea, respaldada por figuras como Platón y Ptolomeo, dominó el pensamiento astronómico durante siglos, ya que el círculo se consideraba la figura geométrica más perfecta.

Sin embargo, en el siglo XVII, esta concepción cambió radicalmente gracias a los trabajos de Johannes Kepler. Kepler, utilizando las detalladas observaciones de su mentor Tycho Brahe, llegó a la conclusión de que las órbitas planetarias no eran circulares, sino elípticas. Este descubrimiento fue fundamental en la historia de la astronomía. 

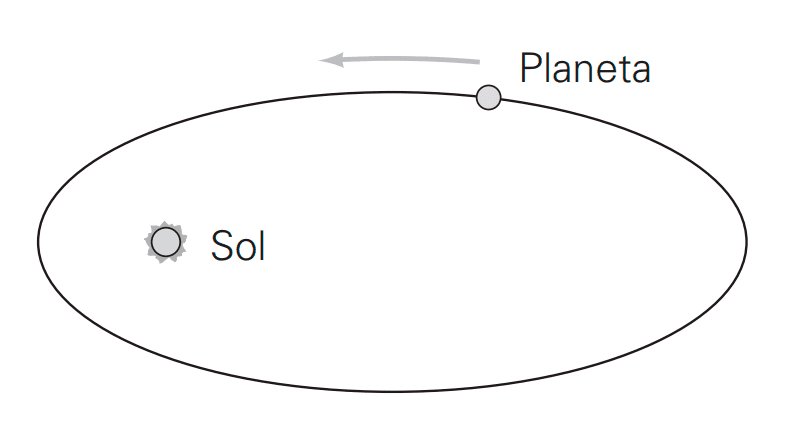
En su primera ley, Kepler estableció que los planetas se mueven en órbitas elípticas alrededor del Sol, con el Sol ocupando uno de los focos de la elipse, mientras que el otro foco permanece vacío y no influye en el movimiento del planeta. Este hallazgo fue revolucionario, ya que proporcionó un ajuste mucho más preciso a las observaciones astronómicas que el modelo circular anterior.

Kepler también se interesó por los cometas, que presentan trayectorias mucho más diversas. Algunos cometas, como el famoso Halley, siguen órbitas elípticas y retornan periódicamente al Sistema Solar. Sin embargo, otros cometas tienen trayectorias hiperbólicas, lo que implica que pasan una vez cerca del Sol y luego se alejan para no regresar jamás. 

En el campo de la óptica astronómica, la comprensión de las cónicas ha sido fundamental para el desarrollo de instrumentos de observación avanzados. Los telescopios reflectores modernos, como los utilizados por la NASA y otras agencias espaciales, emplean espejos parabólicos para enfocar la luz de manera eficiente. 

Este diseño elimina las aberraciones esféricas presentes en otros sistemas ópticos, permitiendo capturar imágenes extremadamente nítidas y detalladas del universo. La forma parabólica de los espejos asegura que los rayos de luz paralelos converjan exactamente en un punto focal, lo que es esencial para estudiar fenómenos astronómicos distantes con alta precisión y contribuye significativamente a descubrimientos en campos como la cosmología y la exploración planetaria.

Telecomunicaciones

Antes de la aparición del GPS, uno de los sistemas de navegación más avanzados fue el LORAN (Long Range Navigation), que utilizaba principios geométricos basados en las hipérbolas para determinar la posición de un receptor. 

Este sistema, desarrollado durante la Segunda Guerra Mundial, se basaba en la diferencia de tiempo en que las señales de radio llegaban a un receptor desde dos o más estaciones transmisoras ubicadas en posiciones conocidas. Estas diferencias de tiempo se convertían en diferencias de distancia, y cuando se trazaban sobre un mapa, el resultado era una serie de curvas hiperbólicas. La intersección de varias de estas curvas permitía determinar con precisión la ubicación del receptor.

El uso de las hipérbolas no se limitó a la navegación, sino que también jugó un papel crucial en la guerra para determinar la posición del enemigo mediante la detección del sonido de los disparos. Este método, conocido como triangulación acústica, implicaba la colocación de varios micrófonos en diferentes ubicaciones para captar el sonido de un disparo. 

Dado que el sonido viaja a una velocidad constante, la diferencia en el tiempo en que el sonido llegaba a los micrófonos se podía utilizar para calcular la distancia del punto de origen del disparo a cada micrófono. Al igual que en el LORAN, estas diferencias se trazaban como hipérbolas en un mapa. La intersección de las hipérbolas de diferentes pares de micrófonos permitía determinar la posición exacta del enemigo.

Medicina

Las elipses tienen aplicaciones en la eliminación de cálculos renales mediante la litotricia extracorpórea por ondas de choque (LEOC). Este procedimiento aprovecha las propiedades geométricas de las elipses para dirigir ondas de choque con precisión.

La litotricia funciona gracias a la forma elíptica de ciertas estructuras utilizadas en el proceso. Una fuente de ondas de choque se coloca en uno de los focos de una estructura elíptica, mientras que el cálculo renal se posiciona en el otro foco. Las ondas de choque generadas viajan a través del agua en la que el paciente está parcialmente sumergido, y se concentran en el cálculo, fragmentándolo en pequeños trozos que pueden ser expulsados del cuerpo a través de la orina.

Este método es particularmente efectivo para cálculos de tamaño moderado, con tasas de éxito que varían entre el 70% y el 90%, dependiendo de la composición y el tamaño del cálculo. A diferencia de otros métodos más invasivos, como la cirugía abierta o la ureteroscopia, la litotricia extracorpórea por ondas de choque es mucho menos invasiva, generalmente se realiza de manera ambulatoria, y permite una recuperación más rápida, con menos dolor postoperatorio y complicaciones. 

Bibliografía consultada

• Alegría, P. (s.f.). Las cónicas y sus aplicaciones.
• Có, P. (2018). Álgebra y Geometría Analítica: Secciones cónicas. Universidad Nacional de Rosario.
• Engler, A. y otros. (2020). Geometría Analítica. Universidad Nacional del Litoral.
• Mora, W., y Figueroa, G. (2009). Cálculo superior. Revista Digital Matemática, Educación e Internet.
• Muñoz González, A. (2015). Curvas cónicas desde su origen hasta sus aplicaciones en la actualidad. Universidad de Valladolid.
• Pérez Gutiérrez, I. (2012). Estudio de las aplicaciones de las cónicas mediado por la modelación desde una visión analítica. Universidad Nacional de Colombia.
• Sullivan, M. (2006). Álgebra y Trigonometría. Pearson Educación.
• Swokowski, E. y Cole, J. (2009). Álgebra y Trigonometría con Geometría Analítica. Cengage Learning.