Posiciones relativas de una recta y una circunferencia

Una recta puede tener tres posiciones relativas respecto a una circunferencia, determinadas por el número de puntos que comparten. Estas posiciones son: exterior (ningún punto en común), tangente (un punto en común) y secante (dos puntos en común).   

Recta exterior

Una recta se considera exterior a una circunferencia si no tiene ningún punto en común con ella. En este caso, la distancia desde el centro de la circunferencia hasta la recta es mayor que la longitud del radio de la circunferencia.   

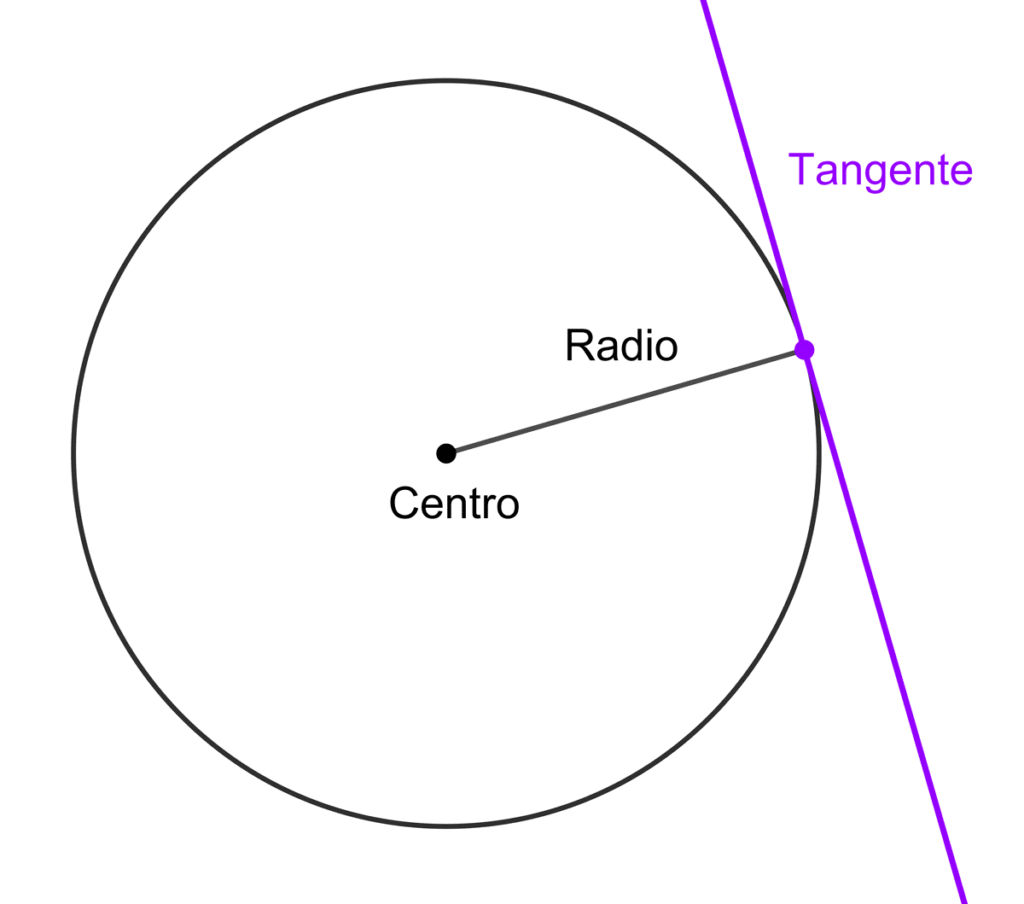
Recta tangente

Una recta es tangente a una circunferencia si comparte solamente un punto con ella, denominado punto de tangencia. La distancia desde el centro de la circunferencia hasta la recta tangente es igual a la longitud del radio.   

Una característica fundamental de la recta tangente es que es perpendicular al radio de la circunferencia en el punto de tangencia.

Cómo hallar la recta tangente a una circunferencia

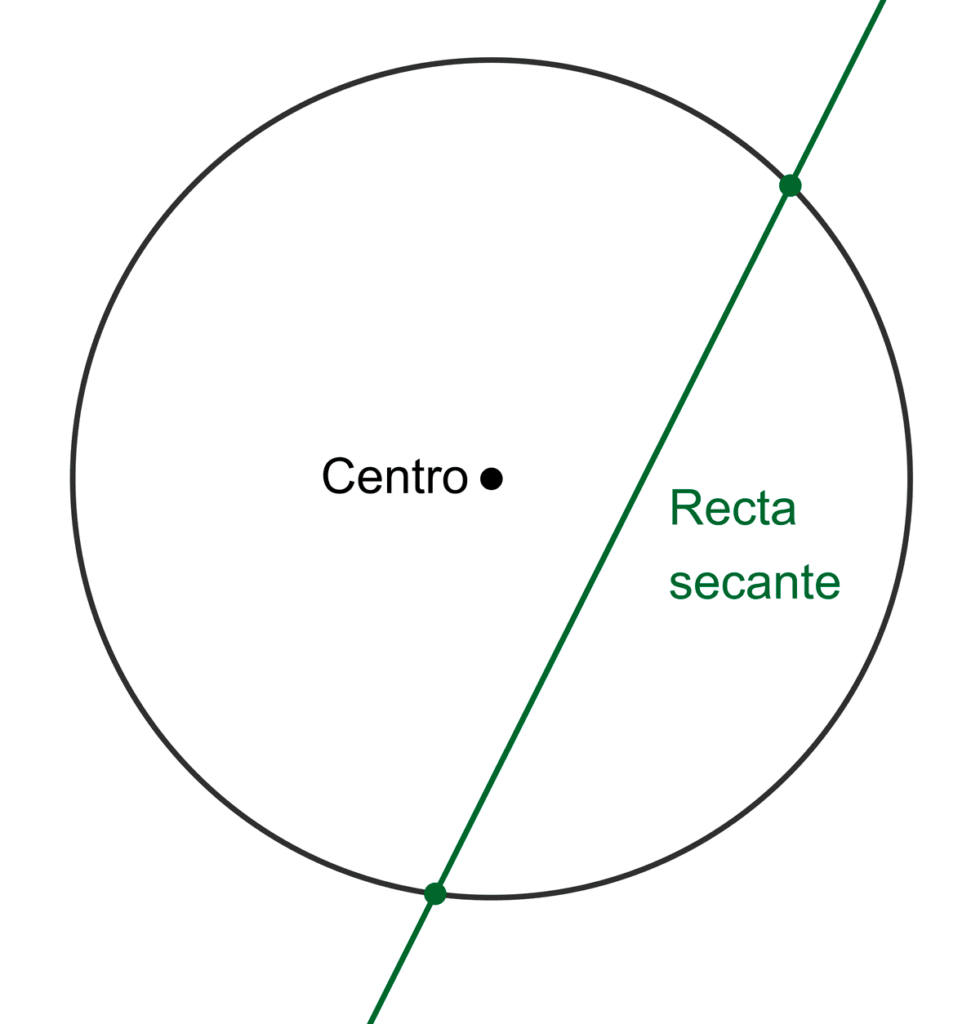
Recta secante

Una recta es secante a una circunferencia si la intersecta en dos puntos distintos. En este caso, la distancia desde el centro de la circunferencia hasta la recta es menor que la longitud del radio. El segmento de la recta comprendido entre estos dos puntos de intersección se denomina cuerda de la circunferencia. 

Cómo determinar la posición relativa

Existen distintos métodos para saber la posición relativa de una recta y una circunferencia teniendo las ecuaciones de ambas. Veremos dos de estas formas a continuación.

Método 1: comparar la distancia a la recta con el radio

Dada una circunferencia con centro en C(a, b) y radio r, y una recta de ecuación general Ax + By + C = 0, se calcula la distancia del centro a la recta con la fórmula:

*d=\dfrac{|Aa+Bb+C|}{\sqrt{A^2+B^2}}*

Luego se compara d con r:

• Si d < r, la recta es secante.
• Si d = r, la recta es tangente.
• Si d > r, la recta es exterior.

Ejemplos

Determinar la posición relativa entre la circunferencia y la recta dada:

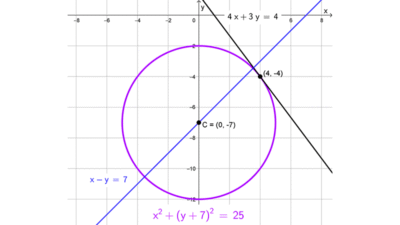
1. Circunferencia *x^2+y^2=9;~~* recta *4x+3y+20=0*
2. Circunferencia *(x-2)^2+(y-3)^2=16;~~* recta *x=6*
3. Circunferencia *(x+5)^2+(y-1)^2=12;~~* recta *x+y=0*

Solución 1

Analizamos la circunferencia *x^2+y^2=9* y la recta *4x+3y+20=0*. El centro de la circunferencia es *(0, 0)* y su radio *r=\sqrt{9}=3*. Calculamos la distancia *d* del centro a la recta usando la fórmula:

*d=\dfrac{|4(0)+3(0)+20|}{\sqrt{4^2+3^2}}=\dfrac{20}{5}=4*

Como *d=4>3=r*, la recta es exterior a la circunferencia.

Solución 2

Estudiamos la circunferencia *(x-2)^2+(y-3)^2=16* y la recta vertical *x=6*. El centro está en *(2, 3)* y el radio es *r=4*. La distancia del centro a la recta es la diferencia horizontal:

*d=|6-2|=4*

Dado que *d=4=r*, la recta es tangente a la circunferencia.

Solución 3

Examinamos la circunferencia *(x+5)^2+(y-1)^2=12* y la recta *x+y=0*. El centro es *(-5, 1)* y el radio *r=2\sqrt{3} ≈ 3,464*. Calculamos la distancia:

*d=\dfrac{|(-5)+1|}{\sqrt{1^2+1^2}}=\dfrac{4}{\sqrt{2}} ≈ 2,828*

Como *d ≈ 2,828<3,464 ≈ r*, la recta es secante y corta la circunferencia en dos puntos.

Método 2: resolver un sistema de ecuaciones

Para determinar algebraicamente la posición de una recta con respecto a una circunferencia, consideramos el sistema de ecuaciones formado por la ecuación de la recta y la ecuación de la circunferencia. Si el sistema no tiene solución, la recta es exterior; si tiene una única solución, la recta es tangente; si tiene dos soluciones, la recta es secante.

Paso 1

Comenzamos con las ecuaciones correspondientes:

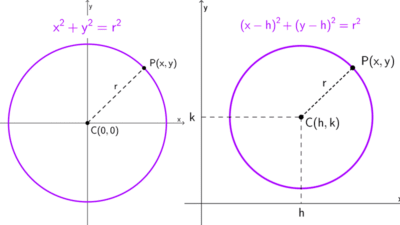
• Circunferencia: *(x-h)^2+(y-k)^2=r^2*
• Recta: *y=mx+b*

Si la recta está dada en forma general, reescribirla despejando la variable y para obtener la forma explícita, esto hará que las sustituciones sean más sencillas. 

Con esto, planteamos el sistema de ecuaciones:

*\begin{cases} (x - h)^2 + (y - k)^2 = r^2 \\ y = mx + b \end{cases}*

Paso 2

Para resolver el sistema, sustituimos la ecuación de la recta en la circunferencia:

*(x-h)^2+(mx+b-k)^2=r^2*

Expandimos ambos términos:

*x^2-2hx+h^2+m^2x^2+2m (b-k) x+(b-k)^2=r^2*

Agrupamos términos semejantes:

*(1+m^2) x^2+(-2h+2m (b-k)) x+(h^2+(b-k)^2-r^2)=0*

Esta es una ecuación cuadrática en *x*:

*Ax^2+Bx+C=0*

donde:

• *A=1+m^2*
• *B=-2h+2m (b-k)*
• *C=h^2+(b-k)^2-r^2*

Al ser una ecuación cuadrática, podemos resolverla mediante la fórmula de Bhaskara:

*x = \dfrac{ -B \pm \sqrt{B^2 - 4AC} }{2A}*

El discriminante *\Delta=B^2-4AC* nos dirá si la ecuación no tiene solución, tiene una solución o dos soluciones.

Paso 3

Analizamos el discriminante *\Delta=B^2-4AC* para determinar la posición relativa:

• Si Δ > 0 hay dos soluciones reales, por tanto, la recta es secante (corta en dos puntos).
• Si Δ = 0 hay una única solución real (raíz doble), por lo tanto, la recta es tangente (corta en un punto).
• Si Δ < 0 no hay soluciones reales, por lo tanto la recta es exterior (no corta en ningún punto).

Si, además de determinar la posición relativa, se desean conocer las coordenadas de los puntos de intersección de la recta con la circunferencia, podemos reemplazar la o las raíces halladas en la ecuación original de la circunferencia o de la recta, con esto hallaremos la coordenada y correspondiente a cada raíz.

Los pasos de este procedimiento se pueden resumir así:

1. Formar el sistema de ecuaciones entre la circunferencia y la recta.
2. Sustituir la ecuación de la recta en la de la circunferencia y desarrollarla.
3. Analizar el discriminante de la ecuación cuadrática para determinar la posición relativa.

Ejemplos

Determinar la posición relativa entre la circunferencia *(x-2)^2+y^2=25* y las siguientes rectas:

1. *3x+4y-6=0*
2. *3x+4y-31=0*
3. *3x+4y-60=0*

Además, hallar el o los puntos de intersección, si existen.

Solución 1

Analizamos la circunferencia *(x-2)^2+y^2=25* y la recta *3x+4y-6=0.* El sistema a resolver es: 

*\begin{cases} (x-2)^2+y^2=25 \\ 3x+4y-6=0 \end{cases}*

Primero, despejamos *y* de la recta para sustituir en la circunferencia:

*y=\dfrac{6-3x}{4}*

Sustituyendo en la ecuación de la circunferencia:

*(x-2)^2+\left(\dfrac{6-3x}{4}\right)^2=25*

Desarrollamos y simplificamos:

*(x^2-4x+4)+\dfrac{(36-36x+9x^2)}{16}=25*

Multiplicamos todo por 16 para eliminar denominadores:

*16x^2-64x+64+36-36x+9x^2=400*

Agrupamos términos:

*25x^2-100x-300=0 \quad → \quad x^2-4x-12=0*

Calculamos el discriminante:

*\Delta=(-4)^2-4(1)(-12)=16+48=64 > 0*

Como *\Delta>0*, la recta es secante y corta la circunferencia en dos puntos. Hallamos las coordenadas resolviendo para *x*:

*x=\dfrac{4 \pm \sqrt{64}}{2}=\dfrac{4 \pm 8}{2} \quad → \quad x=6~ \text{ o }~ x=-2*

Sustituyendo en la ecuación de la recta para obtener *y*:

Para *x=6*: *y=\dfrac{6-18}{4}=-3*

Para *x=-2*: *y=\dfrac{6+6}{4}=3*

Puntos de intersección: *(6, -3)* y *(-2, 3)*

Solución 2

Analizamos la circunferencia *(x-2)^2+y^2=25* y la recta *3x+4y-31=0.* Primero establecemos el sistema de ecuaciones:

*\begin{cases} (x-2)^2+y^2=25 \\  3x+4y=31 \end{cases}*

Para resolverlo, despejamos *y* de la ecuación de la recta:

*y=\dfrac{31-3x}{4}*

Sustituimos esta expresión en la ecuación de la circunferencia:

*(x-2)^2+\left(\dfrac{31-3x}{4}\right)^2=25*

Desarrollamos los términos al cuadrado:

*x^2-4x+4+\dfrac{961-186x+9x^2}{16}=25*

Multiplicamos toda la ecuación por 16 para eliminar denominadores:

*16x^2-64x+64+961-186x+9x^2=400*

Agrupamos términos semejantes:

*25x^2-250x+1025=400*

*25x^2-250x+625=0*

Simplificamos dividiendo entre 25:

*x^2-10x+25=0*

Calculamos el discriminante para determinar la naturaleza de las soluciones:

*\Delta=(-10)^2-4(1)(25)=100-100=0*

Como el discriminante es cero, la recta es tangente a la circunferencia. Resolvemos para *x*:

*x=\dfrac{10 \pm \sqrt{0}}{2}=5*

Finalmente, sustituimos *x=5* en la ecuación de la recta para encontrar *y*:

*y=\dfrac{31-3(5)}{4}=\dfrac{31-15}{4}=\dfrac{16}{4}=4*

Punto de tangencia: *(5, 4)*.

Solución 3

Evaluamos ahora la recta *3x+4y-60=0.* El sistema a resolver es:

*\begin{cases} (x-2)^2+y^2=25 \\ 3x+4y-60=0 \end{cases}*

Despejamos *y*:

*y=\dfrac{60-3x}{4}*

Sustituyendo en la circunferencia:

*(x-2)^2+\left(\dfrac{60-3x}{4}\right)^2=25*

Tras simplificar, obtenemos:

*25x^2-100x+900=0 \quad → \quad x^2-4x+36=0*

El discriminante es:

*\Delta=(-4)^2-4(1)(36)=16-144=-128 < 0*

Como *\Delta<0*, la recta es exterior y no hay puntos de intersección.

Recursos adicionales

Con el siguiente recurso de GeoGebra puedes modificar dinámicamente las ecuaciones de la circunferencia y la recta para comprobar la posición relativa y ver los puntos de intersección (si existen):

Bibliografía consultada

• Lehmann, C. (1989). Geometría Analítica. Limusa.
• Raichman, S. y Totter, E. (2016). Geometría Analítica para Ciencias e Ingeniería. Universidad Nacional de Cuyo.