
Directriz de una parábola
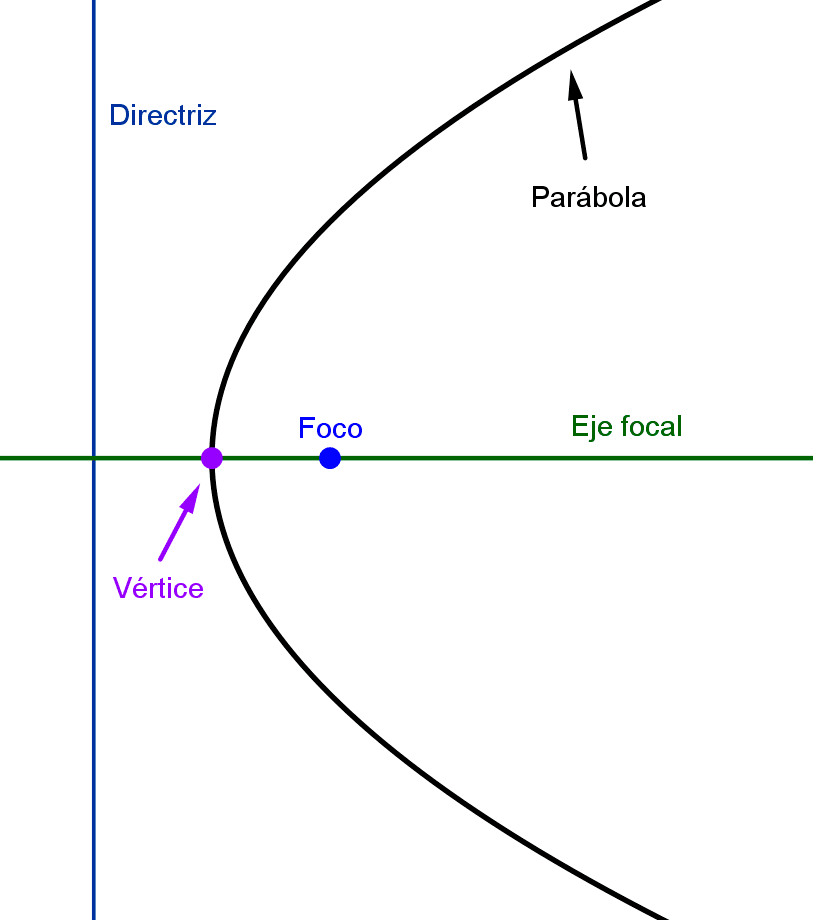
La directriz de una parábola es una línea recta que es perpendicular a su eje de simetría y que no toca la parábola. Esta recta aparece en la definición de la cónica, ya que una parábola es el conjunto de puntos que están a igual distancia de una recta llamada directriz y de un punto llamado foco.
Nota: este artículo se centra en un elemento específico de la parábola. Si todavía no conoces los conceptos fundamentales de esta cónica, te recomiendo empezar por el artículo principal donde los explicamos detalladamente:
Índice
Ecuación de la directriz
Si la parábola es vertical, su directriz es horizontal; si la parábola es horizontal, su directriz es vertical. La distancia del vértice a la directriz es igual a |p| (valor absoluto de p), donde p es el parámetro que aparece en la ecuación canónica de la parábola. Podemos utilizar este valor para determinar la ecuación de la directriz, ya que esta siempre se encontrará a |p| unidades del vértice.
Vértice en el origen
Si el vértice es el origen, tenemos dos casos posibles:
- La ecuación y2 = 4px representa una parábola horizontal cuyo eje de simetría es el eje x, las ramas abren hacia la derecha si p > 0 y hacia la izquierda si p < 0. La directriz en este caso tiene ecuación x = -p.
- La ecuación x2 = 4py es de una parábola vertical que abre hacia arriba si p > 0 y hacia abajo si p < 0, el eje focal es el eje y. La ecuación de la directriz es y = -p.
Las ecuaciones se resumen en la siguiente tabla.
| Ecuación de la parábola | Orientación | Apertura | Ecuación de la directriz |
|---|---|---|---|
| y2 = 4px | Horizontal | Hacia la derecha si p > 0 Hacia la izquierda si p < 0 | x = -p |
| x2 = 4py | Vertical | Hacia arriba si p > 0 Hacia abajo si p < 0 | y = -p |
Ejemplo 1
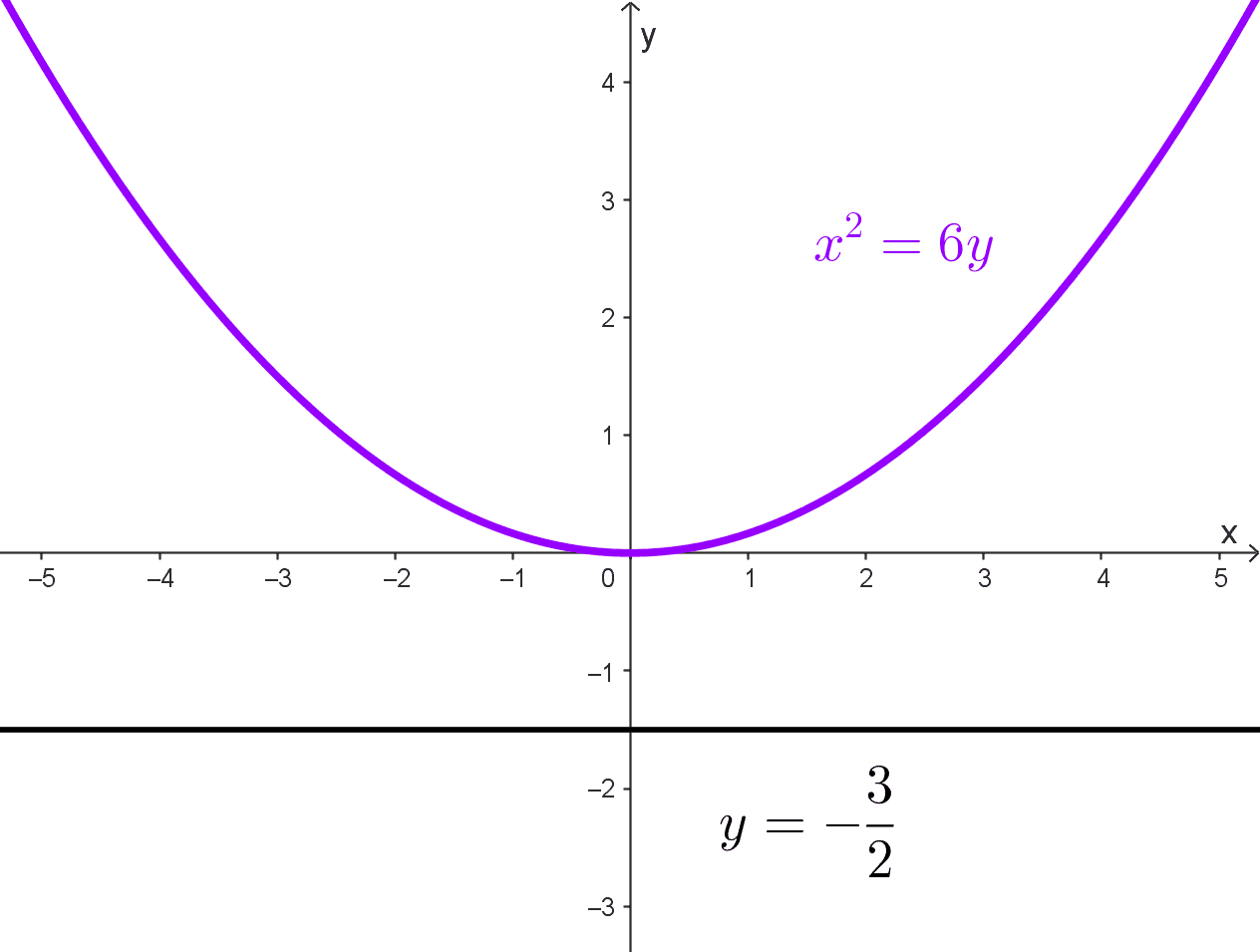
Obtener la ecuación de la directriz de la parábola \(x^2=6y\)
Solución
Comenzamos identificando que la ecuación proporcionada se asemeja a la forma estándar \(x^2=4py,\) correspondiente a una parábola vertical con vértice en el origen.
Comparando ambas ecuaciones, observamos que \(4p=6,\) lo que nos permite despejar \(p\) para encontrar el valor del parámetro. Haciendo esto, obtenemos \(p=\dfrac{6}{4}=\dfrac{3}{2}.\)
Con esto, llegamos al segundo paso donde determinamos la ecuación de la directriz. Para una parábola vertical que abre hacia arriba, la directriz es una recta horizontal ubicada a una distancia \(p\) por debajo del vértice. Por lo tanto, su ecuación es \(y=-p.\) Sustituyendo el valor de \(p,\) la ecuación de la directriz resulta ser:
\(y=-\dfrac{3}{2}\)
Ejemplo 2
Hallar la ecuación de la directriz de la parábola horizontal \(x=-10y^2\)
Solución
Como primer paso, reescribimos la ecuación en su forma estándar para identificar los parámetros clave. La ecuación dada es \(x=-10y^2,\) que puede expresarse como:
\(x=-10y^2 \quad → \quad y^2=-\dfrac{1}{10}x\)
Esta forma corresponde a una parábola horizontal que abre hacia la izquierda, ya que el parámetro p es negativo.
Ahora podemos compararla con la forma estándar de una parábola horizontal:
\(y^2=4px\)
Igualando las dos expresiones, tenemos:
\(4p=-\dfrac{1}{10} \quad → \quad p=-\dfrac{1}{40}\)
La directriz de una parábola horizontal tiene como ecuación:
\(x=-p\)
Por tanto, la ecuación de la recta directriz es:
\(x=-\left(-\dfrac{1}{40}\right)=\dfrac{1}{40}\)
Vértice fuera del origen
Si el vértice no está en origen de coordenadas sino en un punto (h, k), para obtener la ecuación de la directriz, el valor h se suma al lado derecho de la ecuación en las parábolas horizontales; y en parábolas verticales se suma el valor k. Las fórmulas y ecuaciones se resumen en la siguiente tabla:
| Ecuación de la parábola | Orientación | Apertura | Ecuación de la directriz |
|---|---|---|---|
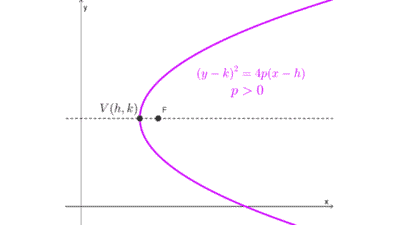
| (y - k)2 = 4p (x - h) | Horizontal | Hacia la derecha si p > 0 Hacia la izquierda si p < 0 | x = h - p |
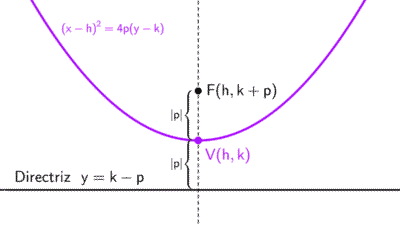
| (x - h)2 = 4p (y - k) | Vertical | Hacia arriba si p > 0 Hacia abajo si p < 0 | y = k - p |
Ejemplo 1
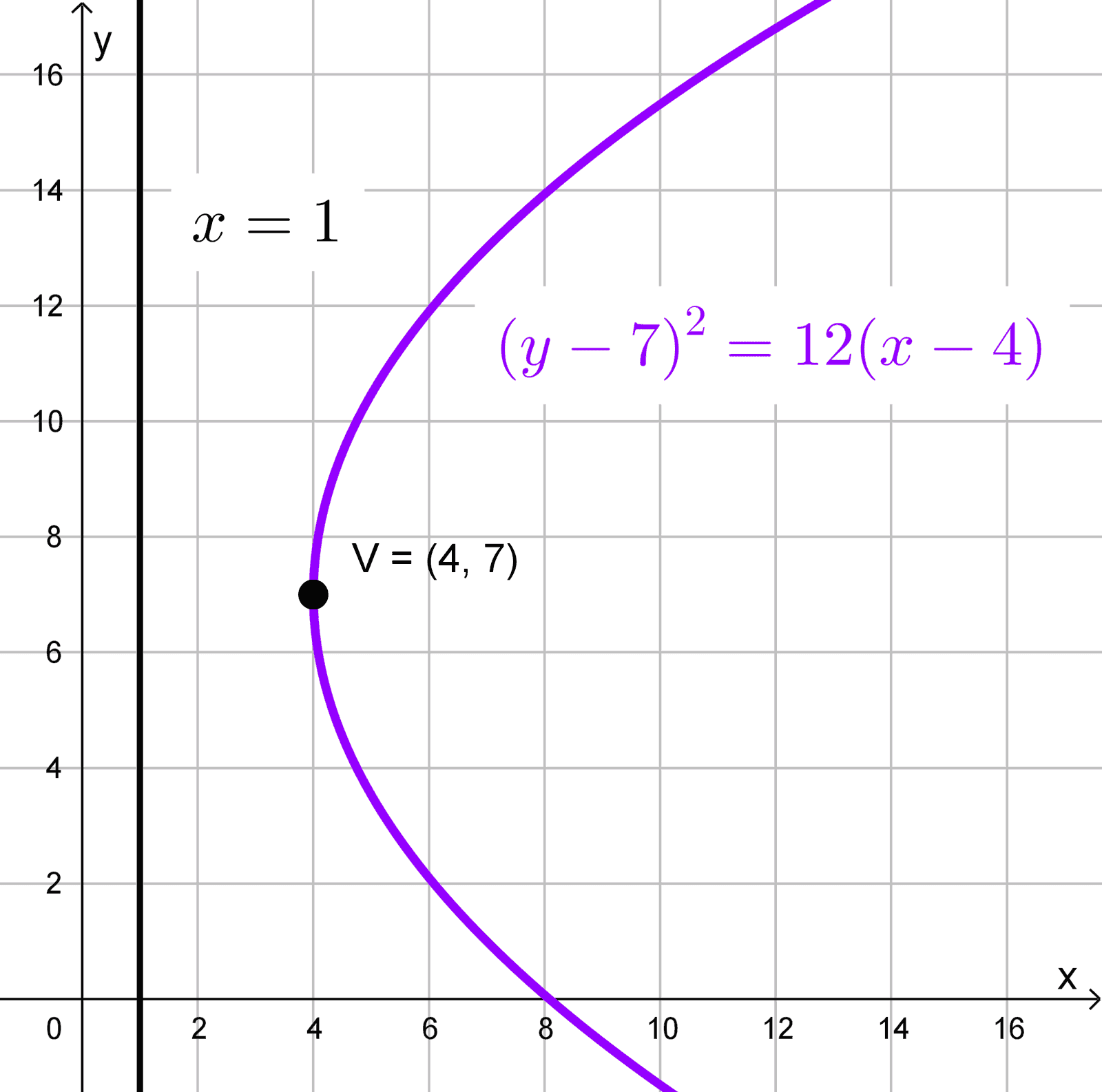
Hallar la directriz de una parábola cuya ecuación es \((y-7)^2=12(x - 4).\)
Solución
Comparando la ecuación dada con la canónica de una parábola horizontal \((y-k)^2=4p (x-h),\) deducimos que el vértice de la parábola es \((4, 7).\) Además, al igualar \(4p\) con el coeficiente del término lineal en \(x,\) obtenemos \(4p=12,\) lo que implica que \(p=3.\)
Dado que la ecuación tiene la forma \((y-k)^2=4p (x-h),\) sabemos que la parábola abre hacia la derecha si el parámetro p es positivo y hacia la izquierda si es negativo. En este caso, como \(p=3>0,\) la parábola abre hacia la derecha. Por lo tanto, la directriz será una recta vertical ubicada a |p| unidades a la izquierda del vértice.
La ecuación de la directriz para este caso es \(x=h-p.\) Sustituyendo los valores conocidos, obtenemos: \(x=4-3=1\)
Finalmente, concluimos que la directriz de la parábola es la recta vertical dada por la ecuación
\(x=1\)
Ejemplo 2
Si una parábola tiene un eje de simetría vertical con vértice en (1, 4) y su foco en (1, 2), encuentre la ecuación de la directriz.
Solución
Observamos que tanto el vértice como el foco tienen la misma coordenada \(x=1,\) lo que confirma que el eje de simetría es vertical. Como el foco está en \((1, 2)\) y el vértice en \((1, 4),\) la parábola se abre hacia abajo, ya que el foco está por debajo del vértice.
El parámetro p será negativo y lo calculamos como:
\(p=y_{\text{foco}}-y_{\text{vértice}}=2-4=-2\)
Por lo tanto, \(p=-2.\)
Para una parábola vertical que abre hacia abajo, la directriz es una recta horizontal ubicada a una distancia \(p\) por encima del vértice. Su ecuación general es:
\(y=y_{\text{vértice}}-p\)
Sustituyendo los valores conocidos:
\(y=4-(-2)=4+2=6\)
Así, la ecuación de la directriz es:
\(y=6\)
Ejemplo 3
Calcular la directriz de la parábola \((y+3)^2=-8(x+2)\)
Solución
Comenzamos reconociendo que expresión tiene la forma estándar de una parábola horizontal: \((y-k)^2=4p (x-h).\)
Primero, identificamos el vértice \((h, k).\) Comparando con la forma estándar, observamos que:
\(h=-2, \quad k=-3\)
Además, el valor \(-8\) corresponde a \(4p,\) por lo que:
\(4p=-8 \quad → \quad p=-2\)
Dado que p es negativo, la parábola abre hacia la izquierda. La directriz es una recta vertical ubicada a |p| unidades del vértice en la dirección opuesta a la apertura. Su ecuación es:
\(x=h-p\)
Sustituyendo los valores conocidos:
\(x=-2-(-2) \quad → \quad x=-2+2=0\)
Finalmente, concluimos que la recta directriz de la parábola está dada por la ecuación:
\(x=0\)
Ejemplo 4
Determinar la ecuación de la recta directriz de la parábola \(x^2-4y+28=0\)
Solución
Comenzamos por reescribir la ecuación en su forma canónica. Primero, despejamos el término cuadrático y los términos lineales:
\(x^2=4y-28\)
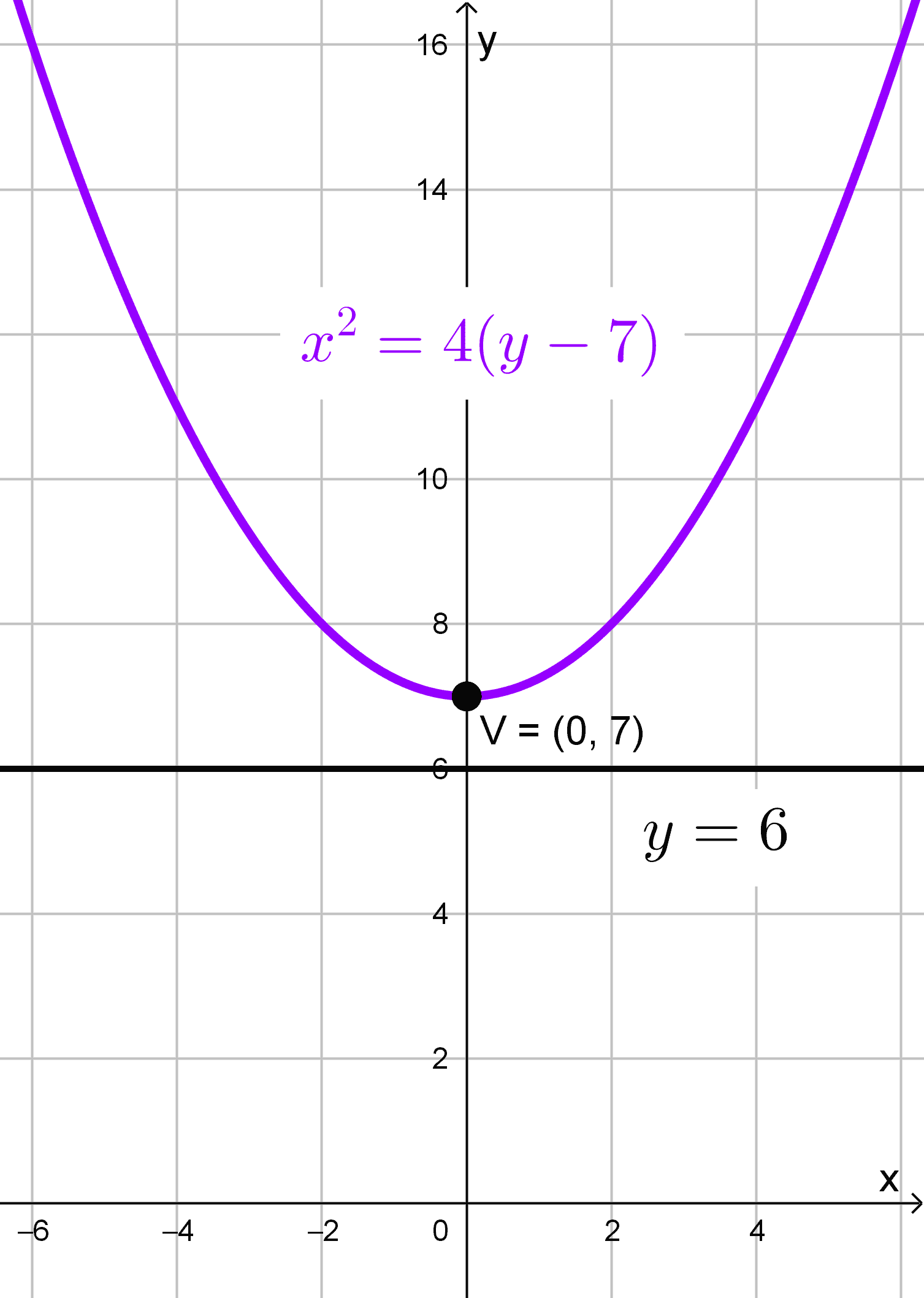
\(x^2=4 (y-7)\)
Ahora, al comparar esta ecuación con la forma canónica de una parábola vertical \((x-h)^2=4p (y-k),\) identificamos que el vértice \((h, k)\) corresponde a \((0, 7).\) Además, igualando el coeficiente del término lineal en \(y\) con \(4p,\) obtenemos \(4p=4,\) lo que implica \(p=1.\)
Como p > 0, la parábola abre hacia arriba. La directriz será una recta horizontal ubicada |p| unidades por debajo del vértice, su ecuación es \(y=k-p.\) Sustituyendo los valores conocidos, resulta:
\(y=7-1\)
\(y=6\)
Finalmente, concluimos que la directriz de la parábola es la recta horizontal dada por la ecuación:
\(y=6\)
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta





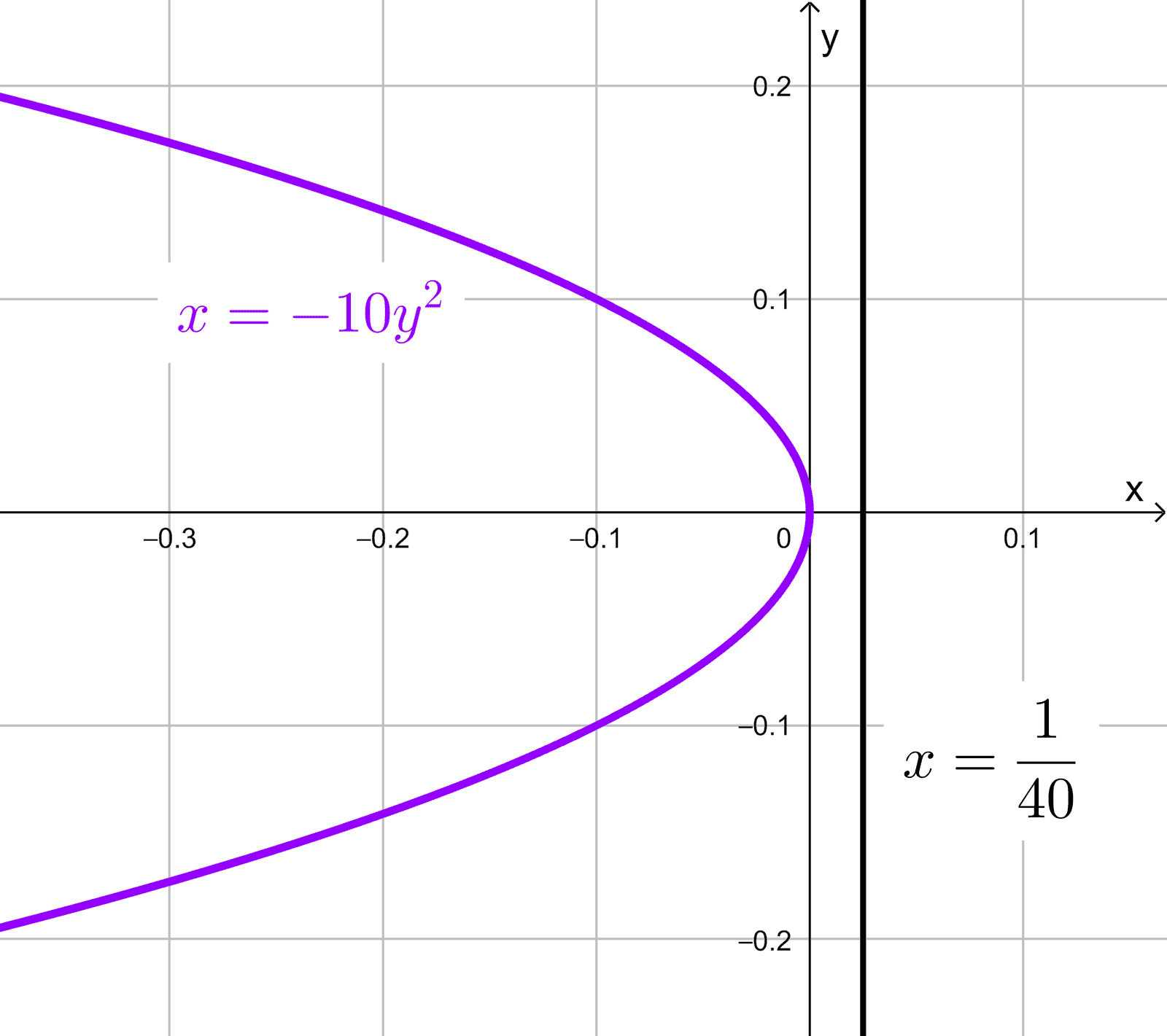
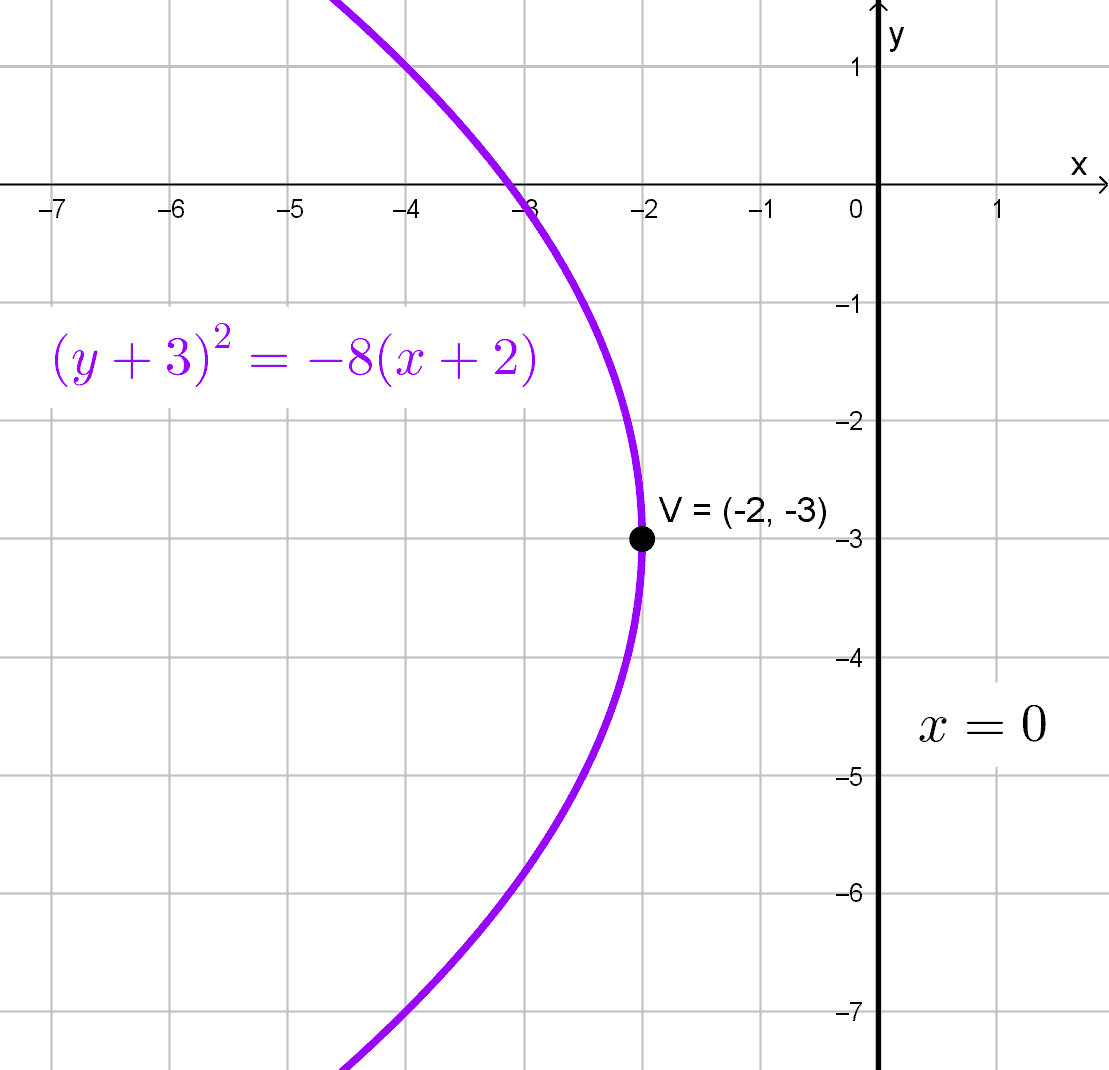


Otros artículos que pueden interesarte