Parábola: qué es, elementos, ecuaciones y ejemplos
Una parábola es una curva abierta y continua cuyos puntos están a la misma distancia de un punto fijo, llamado foco, y de una línea recta fija, llamada directriz. La parábola también puede definirse como una sección cónica que resulta de la intersección de un cono circular recto con un plano paralelo a una de sus generatrices.
A continuación, explicaremos más aspectos sobre la parábola en matemáticas: sus elementos, ecuaciones, ejemplos, propiedades y aplicaciones, entre otras cosas.
Índice
Elementos
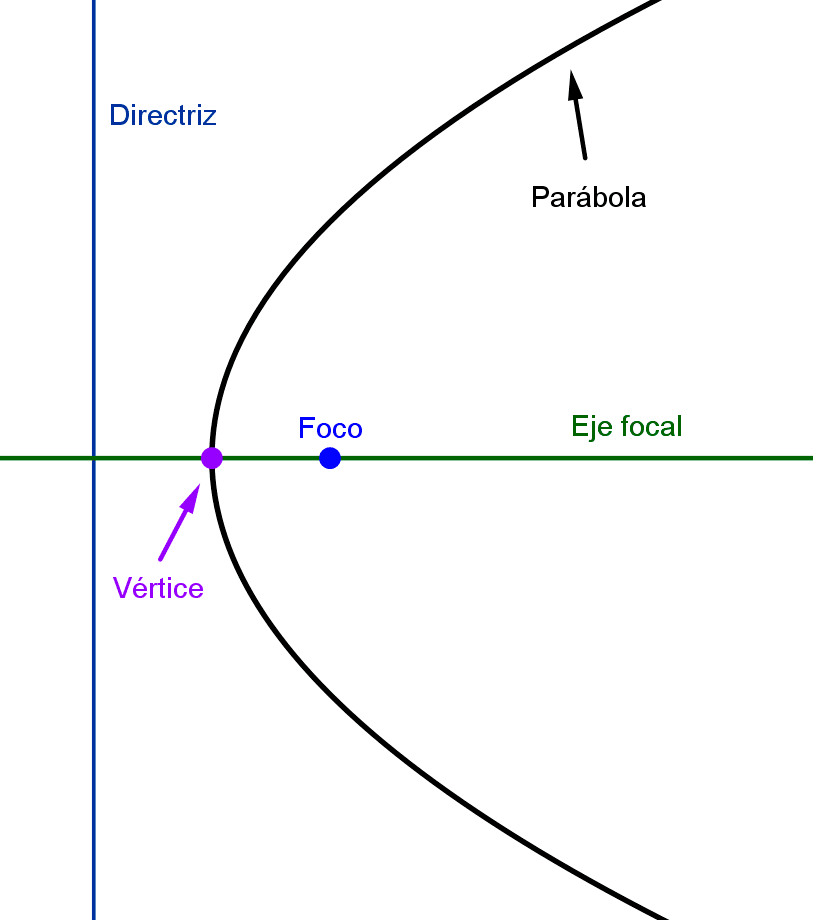
Las partes más importantes de la parábola son:
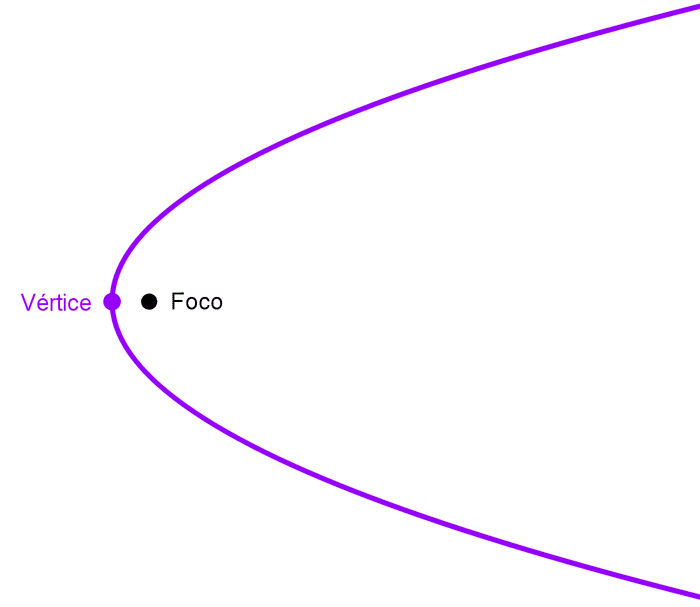
- Foco: es el punto fijo del plano que se menciona en la definición.
- Directriz: es la línea fija utilizada en la definición de la parábola. Cada punto de la parábola está a una distancia igual del foco y de la directriz.
- Vértice: es el punto de la parábola que está más cercano tanto al foco como a la directriz.
- Distancia focal: es la distancia entre el vértice y el foco.
- Eje de simetría: también conocido como eje focal, es la línea que pasa por el foco y el vértice y es perpendicular a la directriz. Divide a la parábola en dos partes simétricas.
- Lado recto: es el segmento que une dos puntos de la parábola, pasa por el foco y es perpendicular al eje focal. Su longitud es L = |4p|, donde |p| es la distancia del vértice al foco.
Ecuación canónica
La ecuación canónica u ordinaria de la parábola en coordenadas cartesianas varía dependiendo del tipo de parábola, que se clasifica según la orientación del eje de simetría (horizontal o vertical) y la posición del vértice (en el origen o fuera de él).
Parábolas con vértice en el origen (0, 0)
1) Eje de simetría horizontal: y2 = 4px
- Si p > 0, la parábola abre hacia la derecha.
- Si p < 0, la parábola abre hacia la izquierda.
2) Eje de simetría vertical: x2 = 4py
- Si p > 0, la parábola abre hacia arriba (es convexa).
- Si p < 0, la parábola abre hacia abajo (es cóncava).
En los cuatro casos, p se llama parámetro de la ecuación y su valor absoluto, |p|, es la distancia focal, es decir, la distancia que hay entre el vértice y el foco o entre el vértice y la directriz. Las demostraciones de estas fórmulas se harán más adelante en este artículo.
Ejemplos
Algunos ejemplos de parábolas con vértice en el origen son:
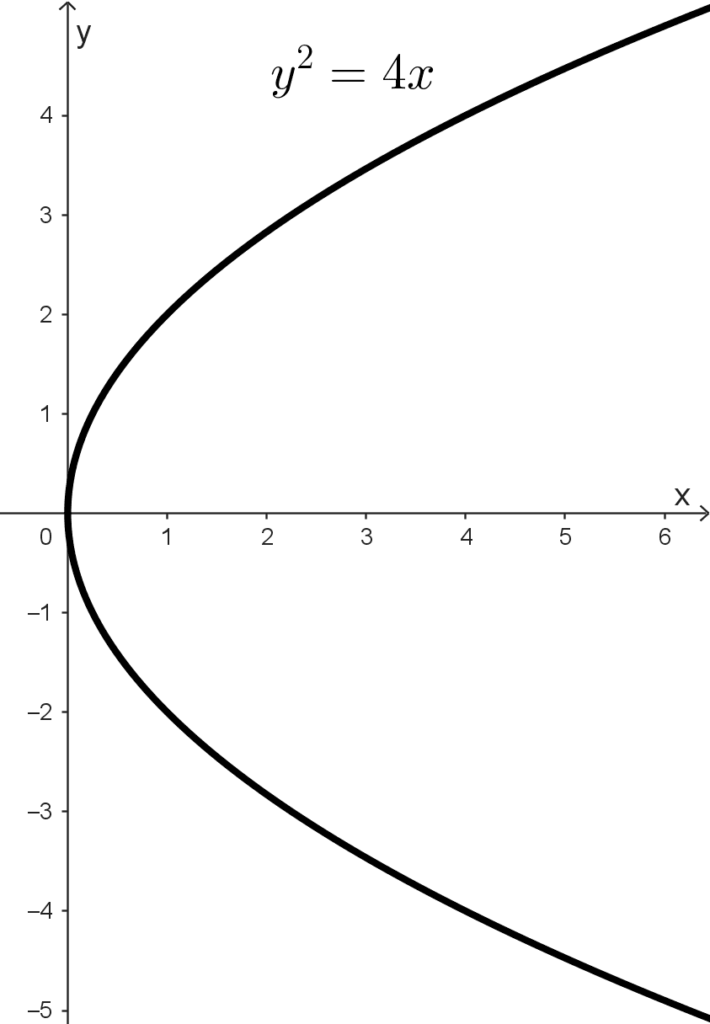
- y2 = 4x es una parábola horizontal que abre hacia la derecha.
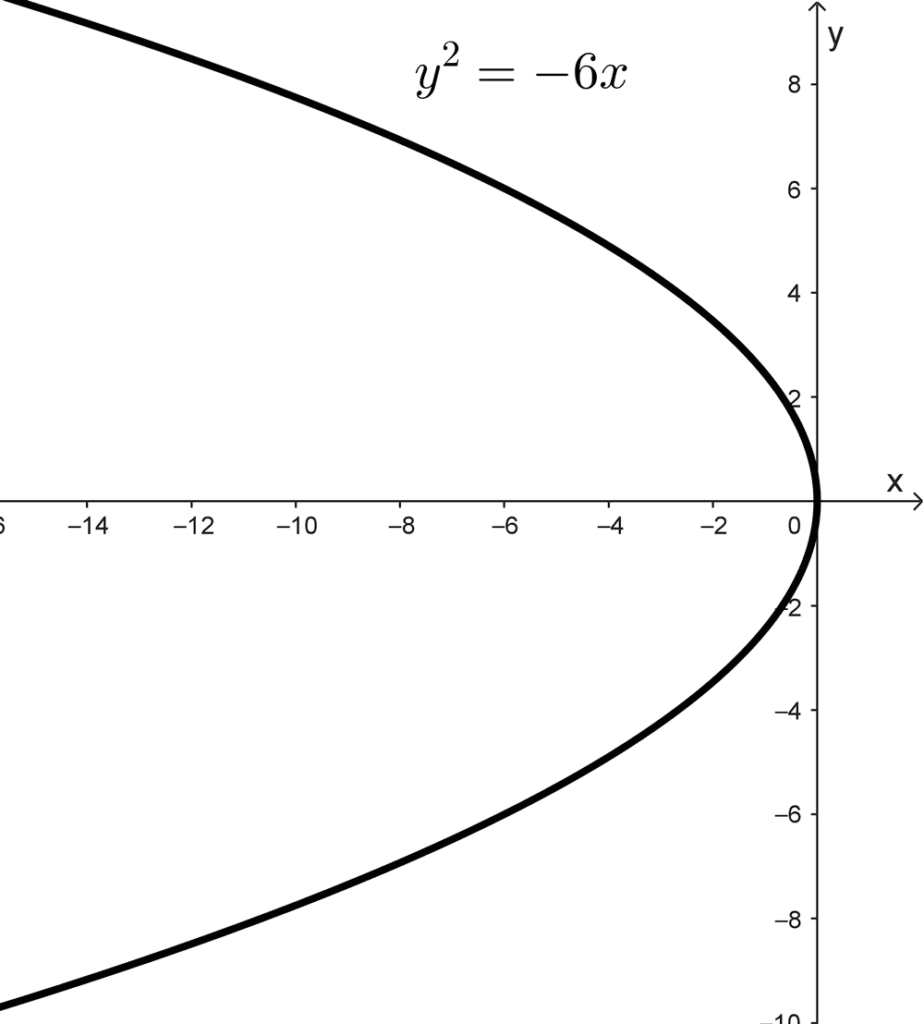
- y2 = -6x es una parábola horizontal que abre hacia la izquierda.
- x2 = 8y es una parábola vertical abierta hacia arriba.
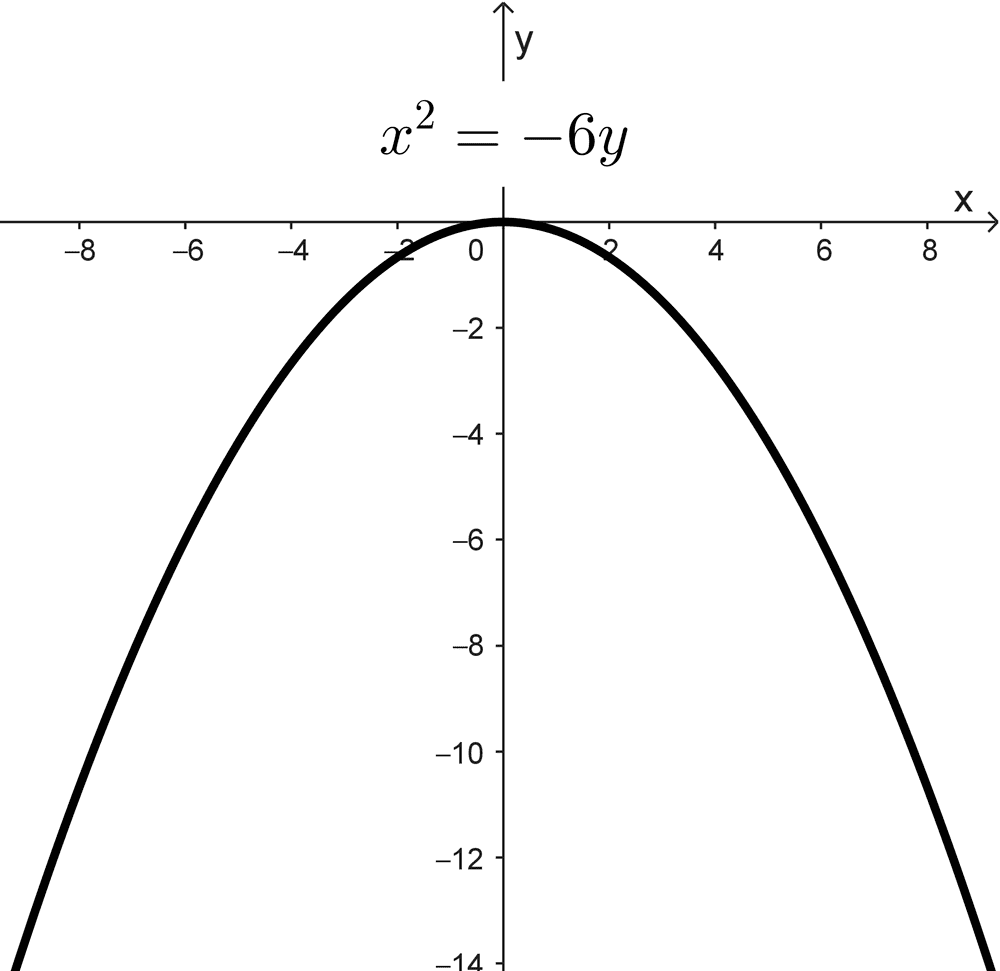
- x2 = -6y es una parábola vertical que abre hacia abajo.
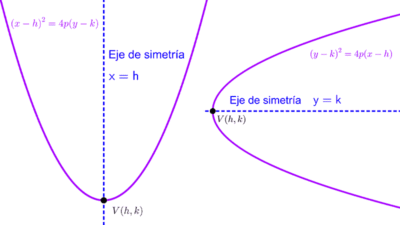
Parábolas con vértice fuera del origen en coordenadas (h, k)
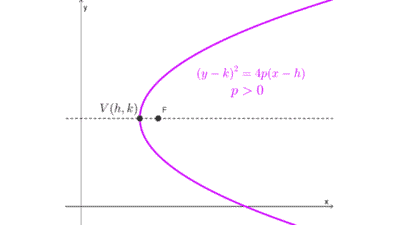
1) Eje de simetría horizontal: (y - k)2 = 4p (x - h)
- Si p > 0, la parábola abre hacia la derecha.
- Si p < 0, la parábola abre hacia la izquierda.
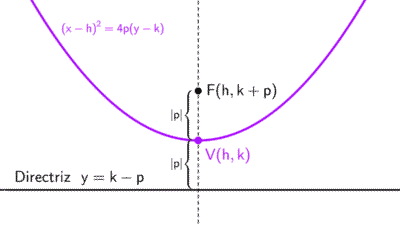
2) Eje de simetría vertical: (x - h)2 = 4p (y - k)
- Si p > 0, la parábola abre hacia arriba (convexa).
- Si p < 0, la parábola abre hacia abajo (cóncava).
Ejemplos
Algunos ejemplos de parábolas con vértice fuera del origen son:
- (y - 1)2 = 2 (x + 2) es una parábola horizontal con vértice en (-2, 1) abierta hacia la derecha.
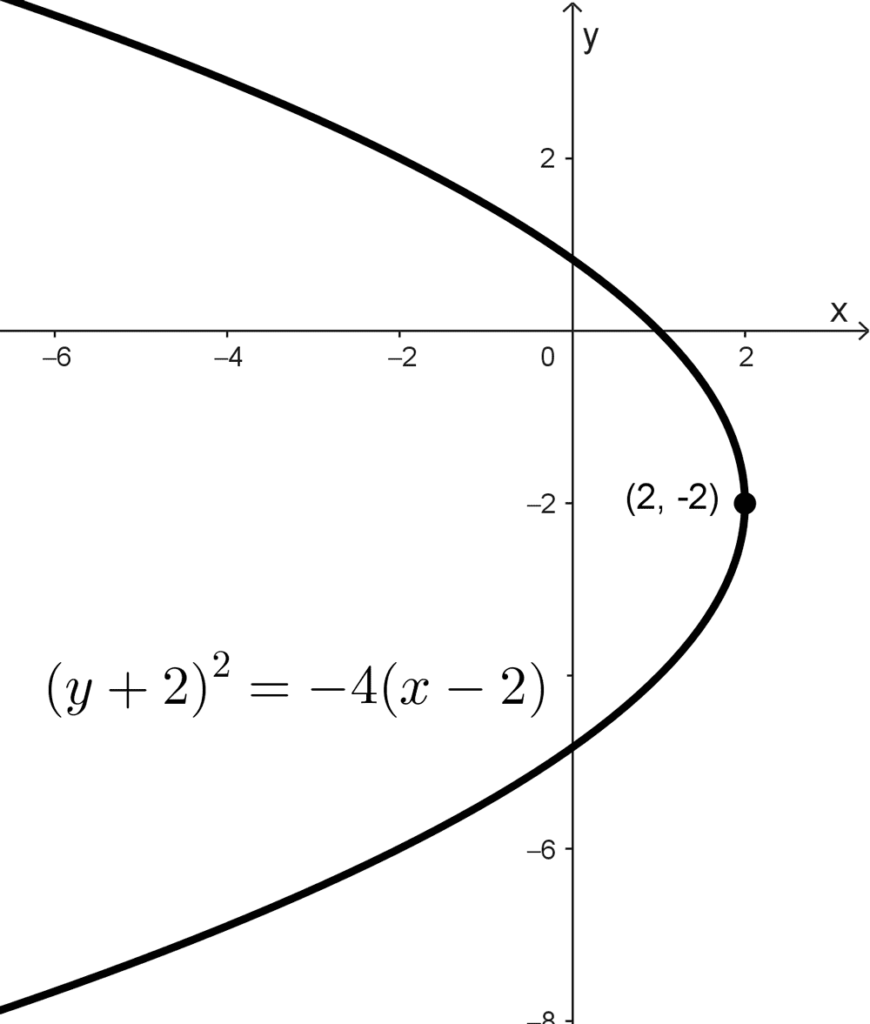
- (y + 2)2 = -4 (x - 2) es una parábola horizontal con vértice en (2, -2) y abierta hacia la izquierda.
- x2 = 5 (y + 3) es una parábola vertical convexa con vértice en (0, -3).
- (x - 1)2 = -4 (y - 2) representa una parábola vertical cóncava con vértice en (1, 2).
Los elementos de la parábola (vértice, foco, directriz, eje de simetría y lado recto) pueden obtenerse a partir de su ecuación canónica. Puedes ver cómo hacerlo en el artículo de ejercicios de parábola:
Propiedades
Las parábolas tienen las siguientes características:
- Simetría: toda parábola es simétrica respecto a un eje que pasa por el vértice y el foco, y que es perpendicular a la directriz. Cada punto de la parábola tiene un punto simétrico al otro lado del eje, a la misma distancia.
- Vértice: es el punto medio entre el foco y el punto donde el eje de simetría intersecta a la directriz. En parábolas verticales, el vértice representa el punto máximo (si abre hacia abajo) o mínimo (si abre hacia arriba). En parábolas horizontales, corresponde al punto con abscisa máxima o mínima, según la orientación de la curva (izquierda o derecha, respectivamente).
- Excentricidad: la excentricidad de toda parábola es igual a 1, lo que significa que la distancia de cualquier punto de la parábola al foco es igual a su distancia a la directriz.
- Lado recto: la longitud del lado recto (o cuerda focal perpendicular al eje) es igual a |4p|, donde |p| es la distancia entre el vértice y el foco. Este segmento es útil para trazar la parábola y entender su apertura.
- Propiedad reflectiva: cualquier rayo que incide paralelamente al eje de simetría se refleja pasando por el foco, y viceversa: un rayo que parte del foco se refleja saliendo paralelo al eje. Esta propiedad es clave en el diseño de antenas parabólicas, faros y concentradores solares, ya que permite concentrar o distribuir energía (luz, sonido, ondas) de forma eficiente gracias a la geometría de la curva.
Aplicaciones
La parábola tiene diversos usos en la vida real y en ciencias que aprovechan sus propiedades geométricas:
- Óptica: los reflectores parabólicos se utilizan en dispositivos como faros, antenas parabólicas y telescopios debido a su capacidad para reflejar rayos paralelos hacia un punto focal. Esta propiedad permite enfocar luz o señales electromagnéticas con alta precisión, maximizando su intensidad.
- Acústica: los micrófonos parabólicos aprovechan la propiedad reflectiva de la parábola para concentrar el sonido en su foco. Esto mejora la claridad y el volumen del audio captado, siendo ideales para registrar sonidos lejanos o en entornos ruidosos.
- Astronomía: los telescopios parabólicos usan espejos con forma de parábola para concentrar la luz proveniente de cuerpos celestes en un único punto. Esto permite observaciones más nítidas y detalladas, fundamentales para la investigación astronómica.
- Ingeniería y arquitectura: las curvas parabólicas se integran en el diseño estructural de puentes y otras construcciones por su eficiencia en la distribución de cargas. Esta geometría mejora la estabilidad y durabilidad de las obras, especialmente en estructuras como puentes colgantes o arcos.
- Balística y física: en ausencia de resistencia del aire, la trayectoria de un proyectil bajo la acción de la gravedad describe una parábola. Este principio es clave en la física y se aplica en cálculos de alcance y dirección en contextos militares o deportivos.
- Economía y negocios: algunas curvas de oferta y demanda se modelan con funciones cuadráticas, que representan parábolas. Estas funciones ayudan a analizar cómo varían precios y cantidades según diferentes factores del mercado.
Ecuación general
La ecuación general de la parábola es Ax2 + Cy2 + Dx + Ey + F = 0 donde el producto de los coeficientes A y C es igual a cero: A ⋅ C = 0 y el eje de simetría es paralelo a un eje coordenado. Si el eje de la parábola presenta una rotación respecto a los ejes cartesianos, la ecuación general es Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 donde se debe cumplir que B2 - 4AC = 0.
La razón de que el producto AC deba ser cero es porque solo puede existir un término cuadrático en la ecuación. En los casos donde uno de estos coeficientes es cero y no hay rotación de eje (B = 0), obtenemos una parábola con un eje de simetría específico:
- Si A = 0, C ≠ 0 y D ≠ 0, la ecuación se simplifica a una forma que incluye el término y2 pero no el término x2, o sea Cy2 + Dx + Ey + F = 0. Esto indica que la parábola tiene su eje de simetría paralelo al eje x, abriéndose hacia la derecha o hacia la izquierda.
- Si C = 0, A ≠ 0 y E ≠ 0, la ecuación se simplifica a una forma que incluye el término x2 pero no el término y2, o sea Ax2 + Dx + Ey + F = 0. Esto indica que la parábola tiene su eje de simetría paralelo al eje y, abriéndose hacia arriba o hacia abajo.
Ejemplos de parábolas en forma general:
- *y^2-8x=0*
- *x^2-4x-4y+16=0*
- *y^2-4y-4x+8=0*
- *x^2-10x+6y+19=0*
- *y^2-12x-10y+73=0*
- *x^2-8x+10y+66=0*
Resumen de ecuaciones
| Ecuación canónica | Eje de simetría | Apertura | Vértice | Foco | Directriz |
|---|---|---|---|---|---|
| y2 = 4px | El eje x | Hacia la derecha si p > 0 Hacia la izquieda si p < 0 | (0, 0) | (p, 0) | x = -p |
| x2 = 4py | El eje y | Hacia arriba si p > 0 Hacia abajo si p < 0 | (0, 0) | (0, p) | y = -p |
| (y - k)2 = 4p (x - h) | Paralelo al eje x y = k | Hacia la derecha si p > 0 Hacia la izquieda si p < 0 | (h, k) | (h + p, k) | x - h = -p |
| (x - h)2 = 4p (y - k) | Paralelo al eje y x = h | Hacia arriba si p > 0 Hacia abajo si p < 0 | (h, k) | (h, k + p) | y - k = -p |
Demostraciones de las ecuaciones
Aquí se presentan las demostraciones de las fórmulas de la parábola que vimos hasta ahora.
Demostración de la ecuación canónica
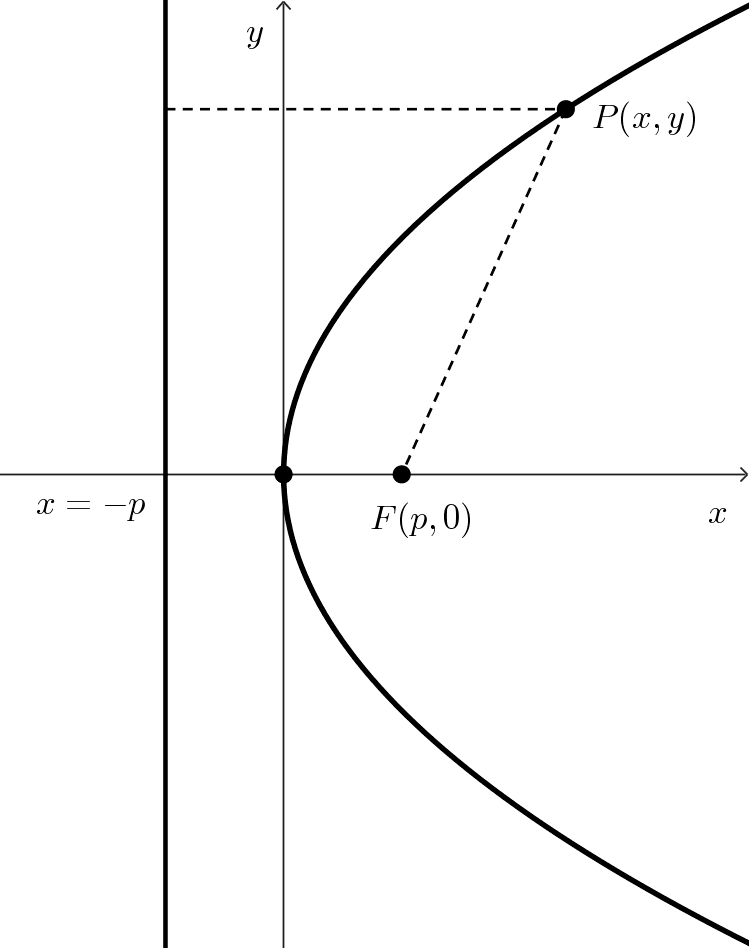
Para hallar la ecuación de la parábola, consideramos un caso sencillo con la parábola abierta hacia la derecha, vértice en el origen y eje focal sobre el eje x.
Supongamos que el foco está en el punto F(p, 0) y la directriz es la línea vertical x = -p.
La distancia de P(x, y) al foco F(p, 0): *\sqrt{(x-p)^2+y^2}*
La distancia de P(x, y) a la directriz x=-p es: *|x+p|*
Por la definición de parábola, para cualquier punto P(x, y) de la misma se cumple que la distancia al foco F(p, 0) es igual a la distancia a la directriz x = -p:
*\sqrt{(x-p)^2+y^2}=|x+p|*
El valor absoluto se elimina considerando que x+p es positivo, ya que la parábola abre hacia la derecha.
*\sqrt{(x-p)^2+y^2}=x+p*
Elevamos al cuadrado para eliminar la raíz:
*(x-p)^2+y^2=(x+p)^2*
Expandimos ambos lados:
*x^2-2px+p^2+y^2=x^2+2px+p^2*
Cancelamos *x^2* y *p^2* de ambos lados:
*-2px+y^2=2px*
*y^2=4px*
Por lo tanto, la ecuación de una parábola horizontal con vértice en el origen y eje focal sobre el eje x, es:
*y^2=4px*
Cuando p es positivo, la parábola abre hacia la derecha, cuando p es negativo la parábola abre hacia la izquierda. Para los casos donde la parábola abre hacia arriba o hacia abajo, el procedimiento es similar, pero invertimos la variable que está elevada al cuadrado.
Parábola que abre hacia arriba o hacia abajo: *x^2=4py*
Esta deducción se puede extender para parábolas con vértices en puntos diferentes al origen, ajustando las coordenadas del vértice y del foco en consecuencia. Para simplificar, podemos usar las fórmulas de la transformación de coordenadas, reemplazando x por x - h e y por y - k en las ecuaciones antes halladas.
Demostración de la ecuación general
Para encontrar la ecuación general de la parábola, partiremos de las ecuaciones canónicas con vértice en (h, k). La ecuación de una parábola horizontal es:
*(y-k)^2=4p(x-h)*
Desarrollando esta ecuación, obtenemos:
*y^2-2ky+k^2=4px-4ph*
Reordenando los términos:
*y^2-2ky+k^2-4px+4ph=0*
*y^2-2ky-4px+(k^2+4ph)=0*
Esta expresión corresponde a la ecuación general de segundo grado con dos variables del tipo:
*Ax^2+Cy^2+Dx+Ey+F=0*
donde:
- *A=0*
- *C=1*
- *D=-4p*
- *E=-2k*
- *F=k^2+4ph*
La ecuación canónica de una parábola vertical es: *(x-h)^2=4p(y-k),* desarrollando esta ecuación, obtenemos:
*x^2-2hx-4py+(h^2+4pk)=0*
Esta expresión corresponde a la ecuación general de segundo grado con dos variables del tipo:
*Ax^2+Cy^2+Dx+Ey+F=0*
donde:
- *A=1*
- *C=0*
- *D=-2h*
- *E=-4p*
- *F=h^2+4pk*
Recursos adicionales
Para graficar parábolas y otras cónicas, recomiendo GeoGebra, una herramienta matemática gratuita e interactiva. Te permite crear gráficos precisos y explorar las propiedades de las figuras de manera intuitiva.
En la siguiente animación verás cómo se forma una parábola a partir del foco y la directriz. Podrás modificar parámetros como la posición del foco y de la directriz.
En el siguiente video se explica cómo graficar una parábola a mano en el contexto del dibujo técnico usando el foco y la directriz. Se muestra cómo trazar el eje, localizar el vértice, y obtener puntos usando distancias específicas, para luego unirlos y formar la curva.
En este video, se ofrece una lección acerca del uso de parábolas en proyectos de ingeniería, enfocándose particularmente en la construcción de puentes. Se detalla el proceso para diseñar un puente parabólico, establecer su ecuación fundamental y calcular segmentos precisos del puente mediante el uso de coordenadas y formulaciones matemáticas.
La ecuación de una parábola con eje de simetría vertical se puede desarrollar y expresar en la forma *y=ax^2+bx+c,* que es una función cuadrática de x cuya gráfica es la parábola.
No todas las parábolas son gráficas de funciones, sino solo aquellas cuyo eje de simetría es vertical. Esto se debe a que, para que una relación sea una función, cada valor de x debe corresponder a un único valor de y. Las parábolas con un eje de simetría horizontal no cumplen esta condición, ya que para algunos valores de x existen dos valores de y.
Para una parábola escrita en la forma *y=f(x)=ax^2+bx+c,* las coordenadas del vértice se pueden encontrar utilizando la fórmula: *\left(-\dfrac{b}{2a},f\left(-\dfrac{b}{2a}\right)\right)*
La ecuación del eje de simetría es *x=-\dfrac{b}{2a}.*
El valor del coeficiente a determina la dirección en la que abre la parábola. Si a > 0, se abre hacia arriba, pero si a < 0, se abre hacia abajo. La anchura de la curva está determinada por el valor absoluto de a; un valor absoluto más alto hace que sea más estrecha, mientras que un menor valor absoluto la hace más ancha.
Las raíces de la función cuadrática, o los puntos donde la parábola cruza el eje x, se calculan utilizando la fórmula general para resolver ecuaciones cuadráticas:
*x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}*
El discriminante *b^2-4ac* determina la naturaleza de las raíces: si es positivo, hay dos raíces reales y distintas; si es cero, hay una raíz real doble; y si es negativo, no hay raíces reales.
Lecturas recomendadas:
- Lehman, C. (1989). Geometría Analítica. Limusa.
- Sullivan, M. (2006). Álgebra y Trigonometría. Pearson Educación.
- Swokowski, E. y Cole, J. (2009). Álgebra y Trigonometría con Geometría Analítica. Cengage Learning.
Más contenidos sobre la parábola
Última actualización del contenido: 06/05/2025
Graficadores de cónicas online
Ecuaciones paramétricas de las cónicas
Cónicas en coordenadas polares
Traslación de secciones cónicas
Propiedades de las secciones cónicas
-
Felicidad Montemayor dice: Maestro: No soy una experta en matemáticas y sinceramente no las entiendo. Mi interés es relacionar las parábolas matemáticas con las PARÁBOLAS DE JESÚS. Podría ser tan amable, lo cual se lo agradecería profundamente, explicarme en forma, lo más sencilla posible, la relación que existe entre las dos?
Gracias por la atención a mi mensaje.-
¡Hola! Las parábolas matemáticas y las parábolas de Jesús no están relacionadas, ya que pertenecen a campos distintos. La parábola en matemáticas es una curva con ciertas propiedades geométricas, mientras que las parábolas de Jesús son relatos con enseñanzas morales y espirituales. Solo comparten el nombre, pero su significado es diferente. ¡Saludos!
-
2 Comentarios
Felicidad Montemayor 
Deja una respuesta
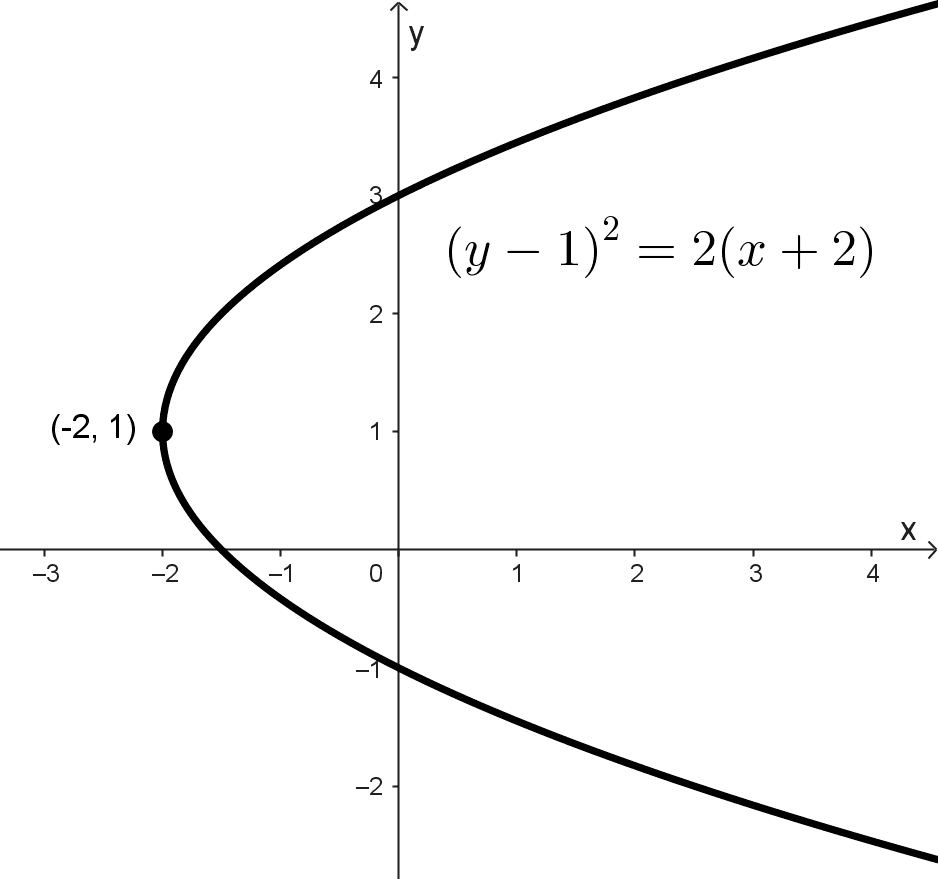
Otros artículos que pueden interesarte