
Parábola horizontal
Una parábola horizontal es aquella cuyo eje de simetría es paralelo o coincidente con el eje x. Sus ramas pueden abrirse hacia la izquierda o hacia la derecha.
La ecuación canónica de una parábola horizontal con vértice en el origen es:
y2 = 4px
donde |p| es la distancia entre el vértice y el foco. Si p tiene signo positivo, las ramas de la parábola abren hacia la derecha; si p es negativo, las ramas abren hacia la izquierda.
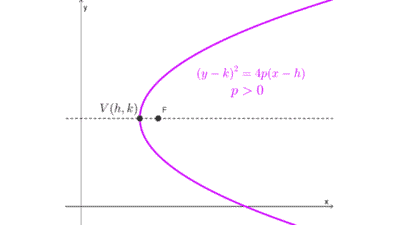
Si el vértice no es el origen sino un punto (h, k), la ecuación canónica es:
(y - k)2 = 4p (x - h)
Del mismo modo que antes, el signo de p indica hacia donde abren las ramas.
Podemos reconocer la ecuación de una parábola con eje horizontal fijándonos cuál variable está elevada al cuadrado. En las parábolas horizontales es la variable y, mientras que en las verticales es la variable x.
Para saber si una parábola horizontal se abre hacia la derecha o la izquierda, es necesario mirar el signo del parámetro p. Si p > 0, la parábola abre hacia la derecha; si p < 0, abre hacia la izquierda.
Nota: aquí nos enfocamos solo en un tipo de parábola. Si no estás familiarizado con los fundamentos de esta cónica, te sugiero leer primero el artículo general donde los desarrollamos a fondo:
Índice
Elementos
Las ecuaciones junto con los elementos de las parábolas se resumen en la siguiente tabla:
| Ecuación | Vértice | Apertura | Eje de simetría | Foco | Directriz |
|---|---|---|---|---|---|
| y2 = 4px | (0, 0) | Hacia la derecha si p > 0 Hacia la izquierda si p < 0 | y = 0 | (p, 0) | x = -p |
| (y - k)2 = 4p (x - h) | (h, k) | Hacia la derecha si p > 0 Hacia la izquierda si p < 0 | y = k | (h + p, k) | x = h - p |
La deducción de la ecuación se realizó en este artículo sobre la parábola.
Ejemplos
Los siguientes son ejemplos de ecuaciones de parábolas con eje focal horizontal:
- \(y^2=8x\)
- \(y^2=-9(x+1)\)
- \((y-2)^2=4(x-1)\)
- \(-8(x+2)=(y+3)^2\)
Ecuación general
La ecuación general de una parábola horizontal es:
Cy2 + Dx + Ey + F = 0
A diferencia de una parábola vertical, la variable elevada al cuadrado es y.
Podemos llegar a esta forma general desarrollando la ecuación canónica con vértice en (h, k):
\((y-k)^2=4p (x-h)\)
Primero expandimos ambos miembros:
\(y^2-2ky+k^2=4px-4ph\)
Igualamos la ecuación a cero pasando todos los términos al mismo lado:
\(y^2-2ky+k^2-4px+4ph=0\)
Agrupamos los términos para obtener la forma general:
\(y^2-4px-2ky+(k^2+4ph)=0\)
De aquí puede verse que:
- \(C=1\)
- \(D=-4p\)
- \(E=-2k\)
- \(F=k^2+4ph\)
Ejemplos
Las siguientes son ecuaciones generales de parábolas horizontales:
- \(3y^2+20x-3=0\)
- \(x=2y^2-5x\)
- \(2x+6y^2-3y=0\)
- \(6y^2-2y-3=x\)
¿Una parábola horizontal es una función?
Una parábola horizontal no es una función porque no cumple con el postulado de unicidad, ya que para un mismo valor de x puede haber dos valores de y.
Por ejemplo, en \(y^2=x,\) se puede despejar \(y=\pm \sqrt{x}.\) Al valor \(x=4\) le corresponde tanto el valor \(y=2\) como el \(y=-2,\) lo cual no puede pasar en una función. Dicho de otro modo, una parábola horizontal no pasa la prueba de la recta vertical para ser una función.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta





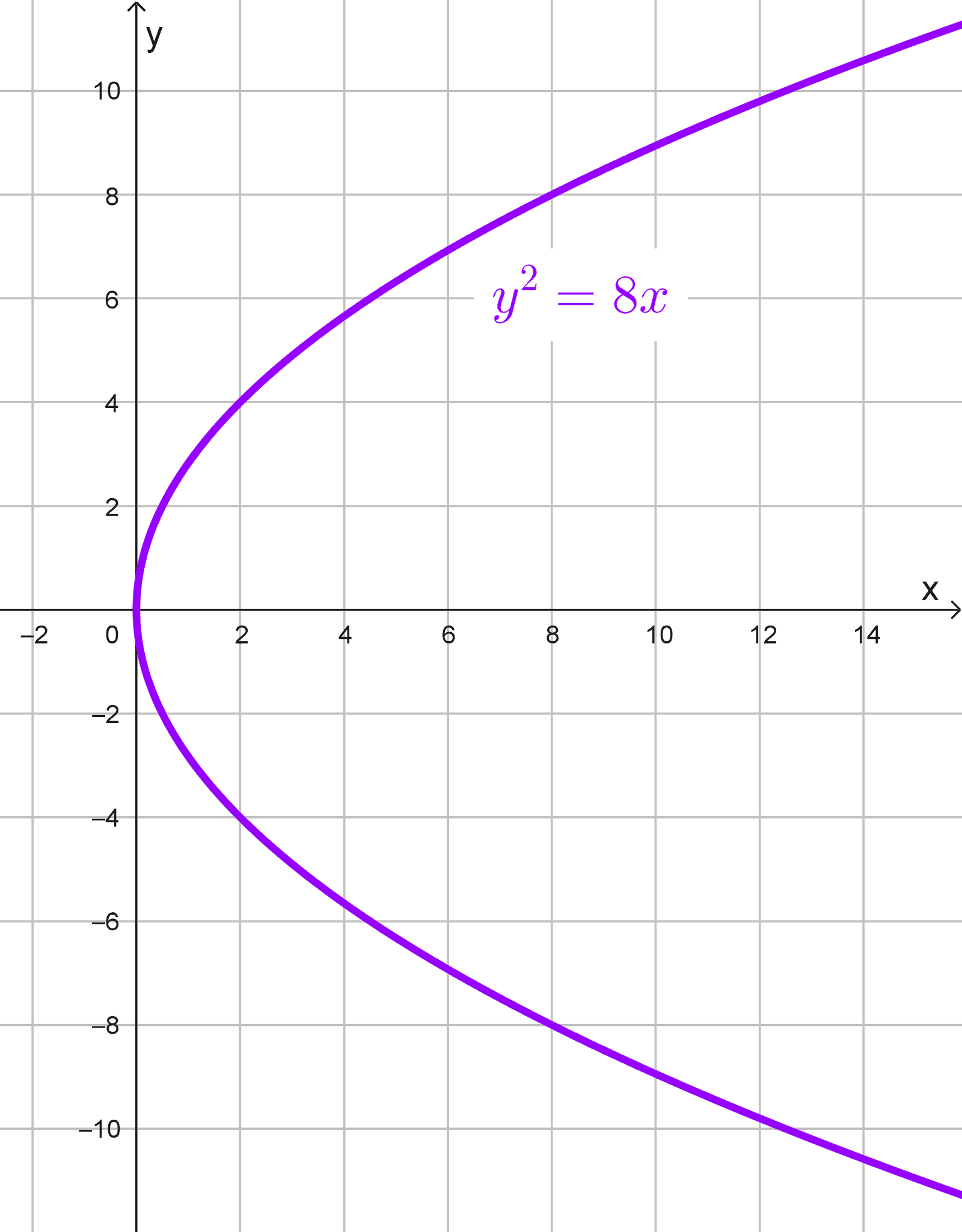
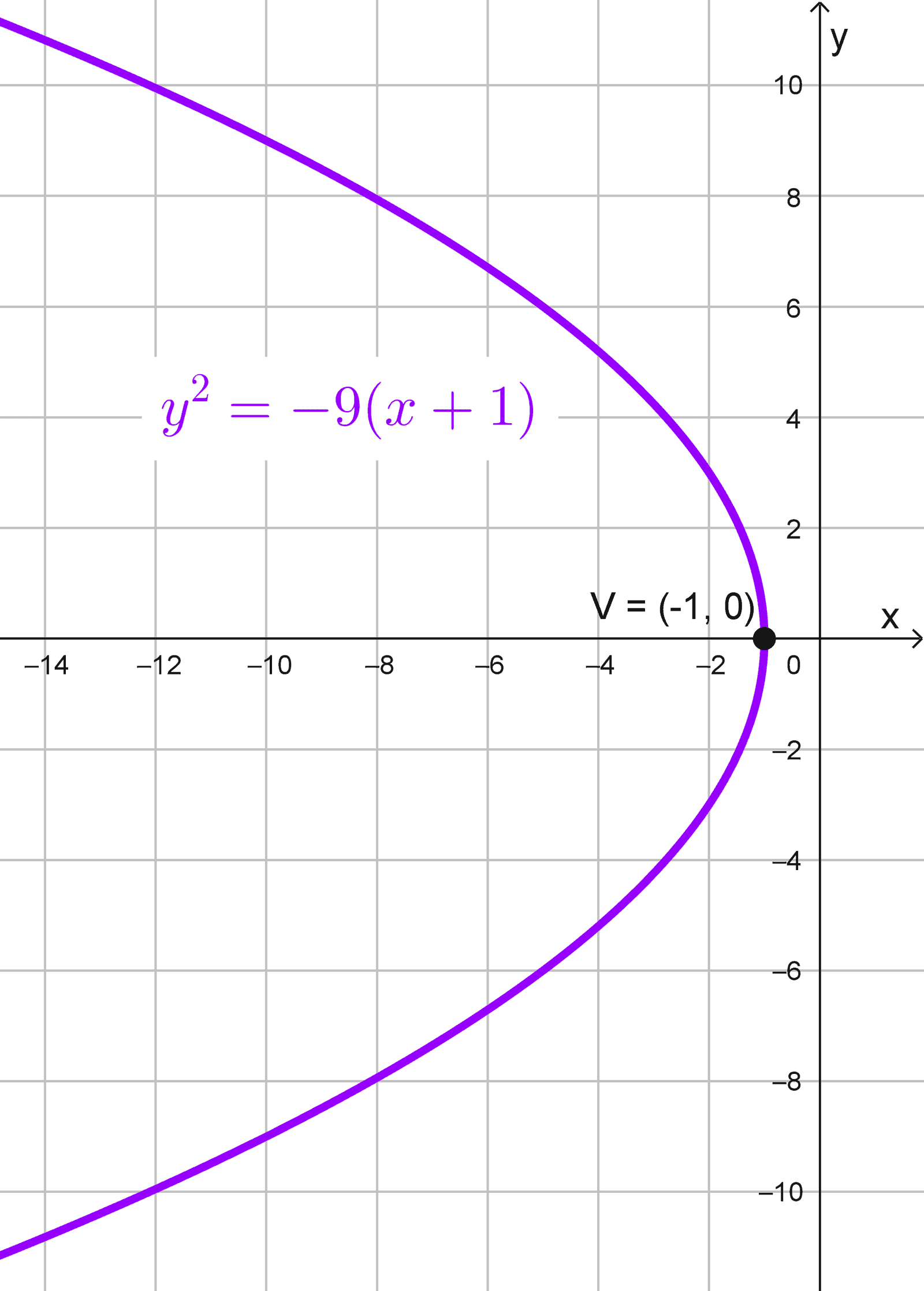
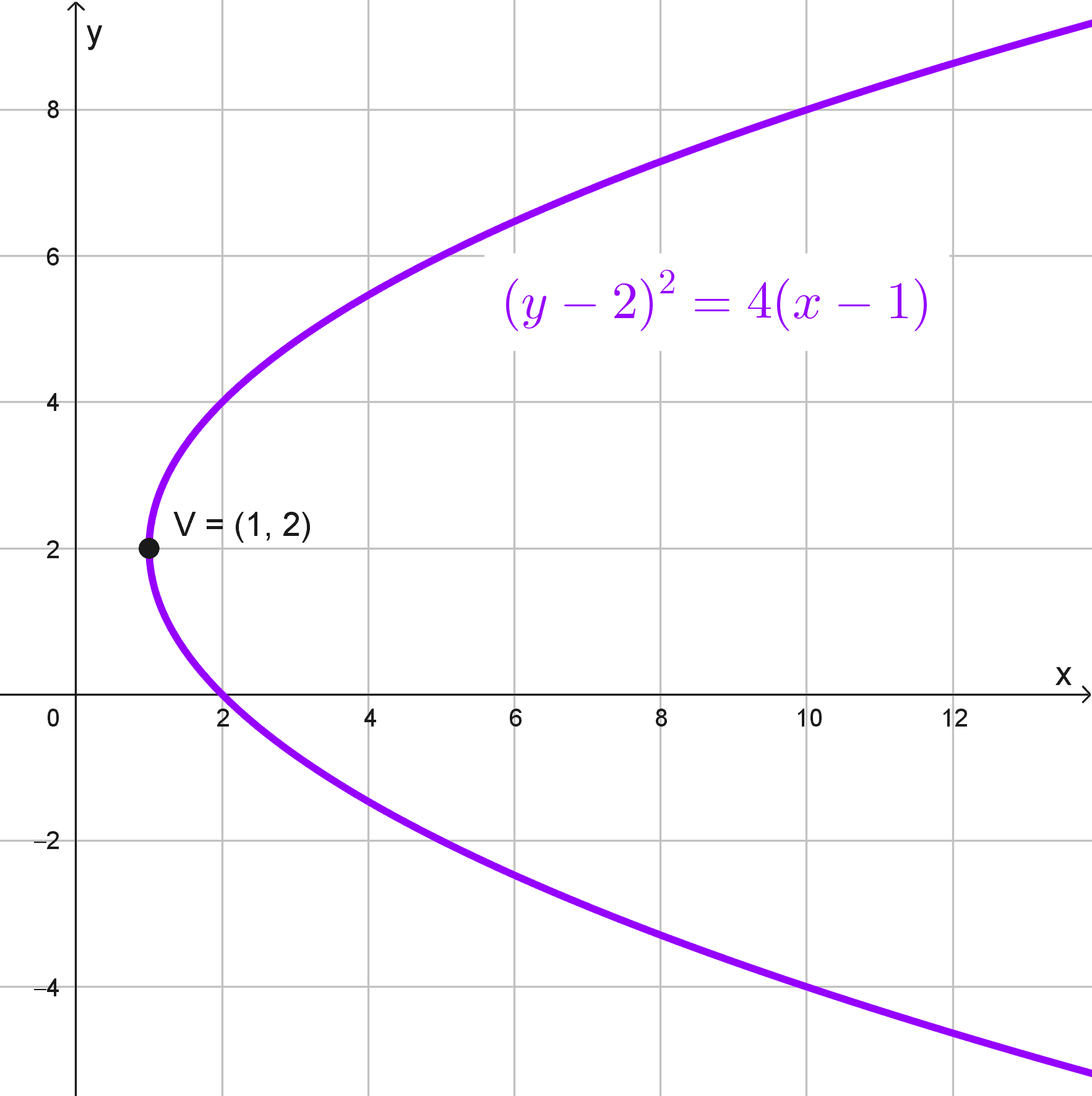



Otros artículos que pueden interesarte