Circunferencia: definición, elementos y ecuaciones
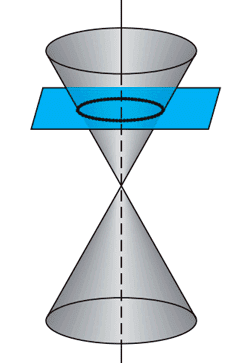
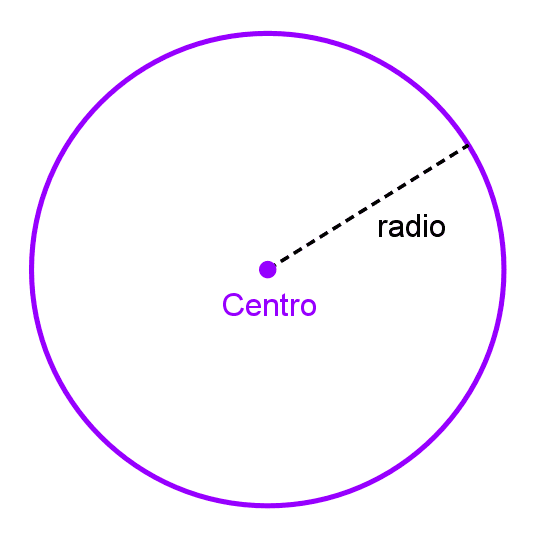
Una circunferencia es una figura geométrica plana cuyos puntos están a una distancia fija, llamada radio, de un punto fijo llamado centro. Su gráfica es una curva suave, continua y cerrada. La circunferencia también puede definirse como una sección cónica, la cual resulta de cortar un cono circular recto con un plano perpendicular a su eje.
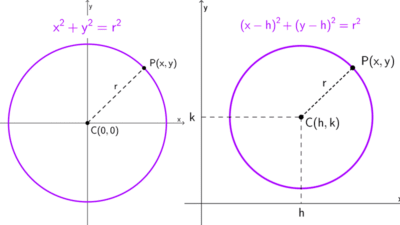
La ecuación canónica de una circunferencia con centro en el origen (0, 0) y radio r es:
x2 + y2 = r2
Si el centro no está en el origen de coordenadas sino en un otro punto (h, k) del plano cartesiano, la ecuación canónica se convierte en:
(x - h)2 + (y - k)2 = r2
La demostración de estas ecuaciones se realiza más adelante de este artículo.
A continuación, explicaremos más aspectos sobre la circunferencia en matemáticas: ejemplos, sus partes, la obtención de sus ecuaciones, características y propiedades de la misma, entre otras cosas.
Índice
Ejemplos
Algunos ejemplos de circunferencias con sus gráficas son:
- (x + 2)2 + (y - 1)2 = 16 es una circunferencia con centro en (-2, 1) y radio 4 (recuerda que el radio está elevado al cuadrado en la ecuación).
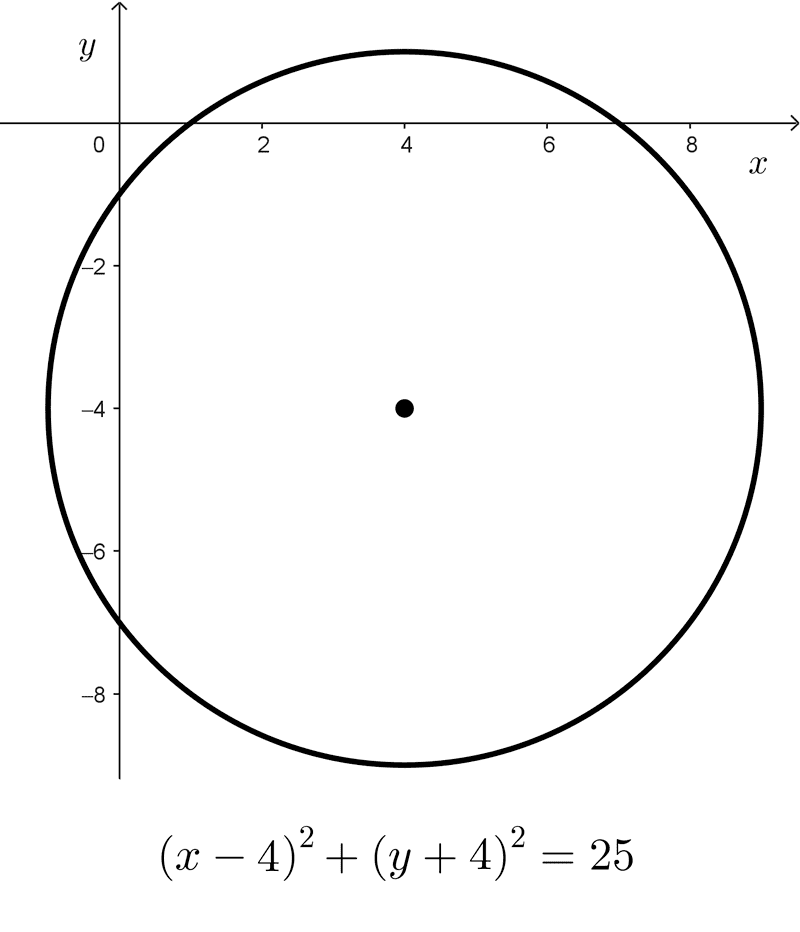
- (x - 4)2 + (y + 4)2 = 25 es una circunferencia con centro en (4, -4) y radio 5.
- (x - 1)2 + y2 = 9 es una circunferencia con centro en (1, 0) y radio 3.
- x2 + y2 = 4 es una circunferencia con centro en (0, 0) y radio 2.
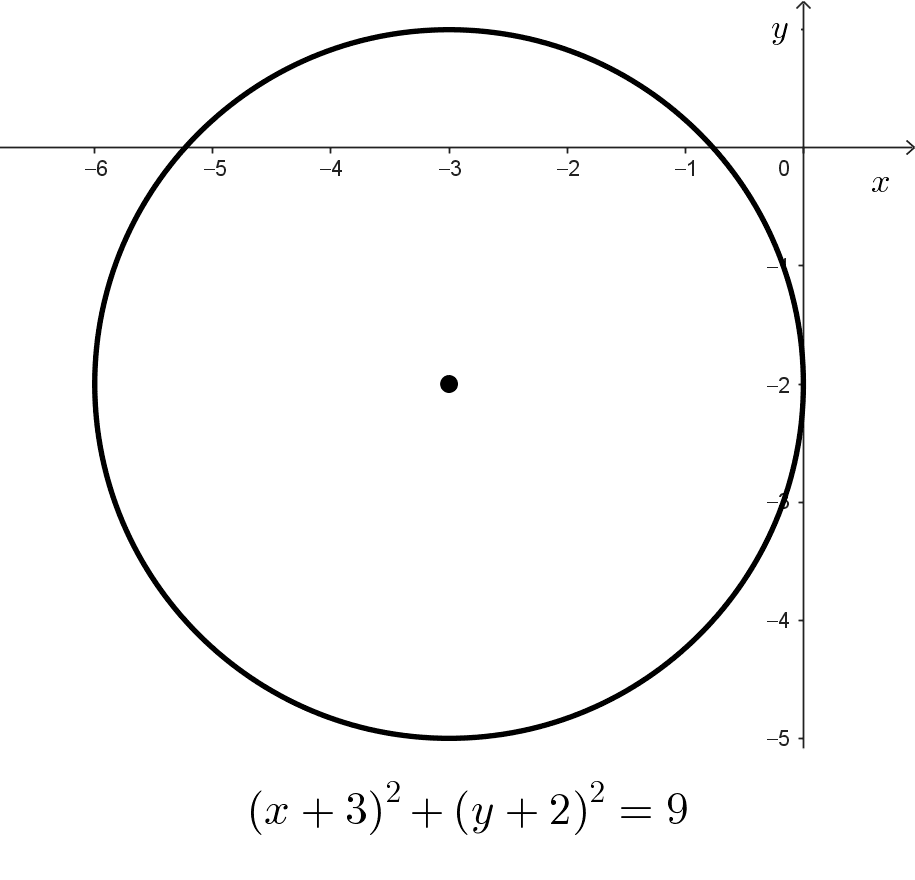
- (x + 3)2 + (y + 2)2 - 9 = 0, si la reordenamos es (x+3)2 + (y+2)2 = 9, una circunferencia con centro en (-3, -2) y radio 3.
- x2 + y2 = 1 es una circunferencia con centro en (0, 0) y radio 1, también conocida como la circunferencia unitaria o goniométrica.
- x2 + (y - 1)2 = 5 es una circunferencia con centro en (0, 1) y radio √5≈2,24.
- (x - 2)2 + y2 = 10 es una circunferencia con centro en (2, 0) y radio √10≈3,16.
Elementos
Las partes principales de una circunferencia son:
- Centro: es el punto fijo equidistante a todos los puntos de la circunferencia. Se representa con la letra C y su ubicación se describe por sus coordenadas (h, k) en el plano cartesiano.
- Radio: es la distancia desde el centro de la circunferencia hasta cualquier punto de ella. Es una cantidad positiva y constante que se representa con la letra r.
Se los considera los elementos principales porque son suficientes para describir una única circunferencia.
Otras partes de la circunferencia son:
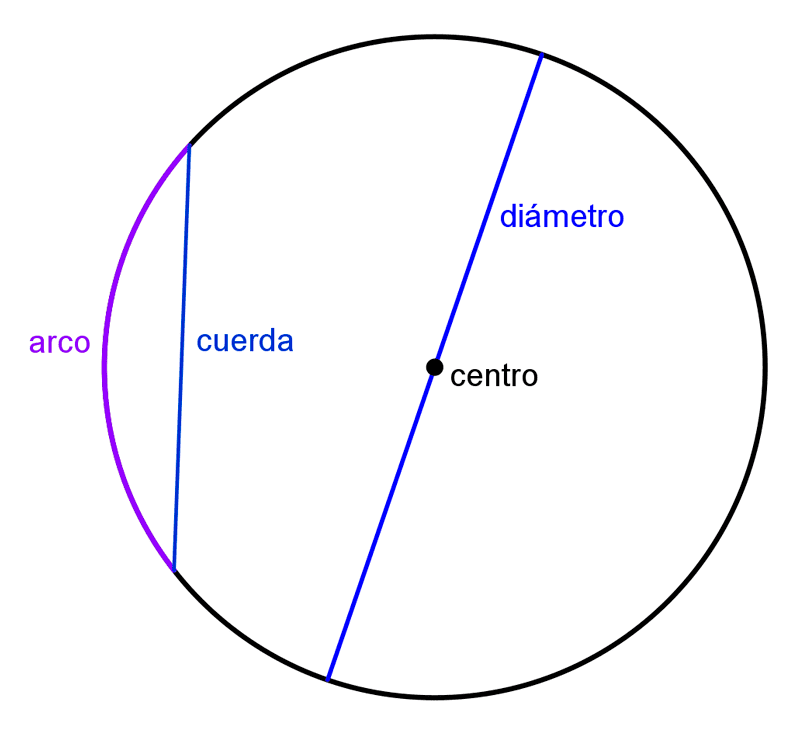
- Diámetro: es el segmento que pasa por el centro y une dos puntos de la circunferencia. Se representa con la letra "d" y su longitud es el doble del radio, es decir, d=2r. Cada diámetro divide a la circunferencia en dos partes iguales, conocidas como semicircunferencias.
- Perímetro: es la longitud total de la curva, está relacionada con el radio y con el número pi por la siguiente fórmula: P=2πr.
- Cuerda: es un segmento que une dos puntos de la circunferencia, pero no necesariamente pasa por el centro. El diámetro es la cuerda más larga.
- Arco: es una porción de la circunferencia comprendida entre dos puntos.
- Sector circular: es la región del plano limitada por dos radios y el arco comprendido entre ellos.
¿Te está sirviendo este artículo? ¡Por favor, califícalo!
4,8 / 5 — 5 votos
Si ocurre que el radio es cero, la circunferencia se convierte en un único punto (el centro), y se considera un caso de cónica degenerada. El radio nunca puede ser negativo.
En geometría euclidiana, las circunferencias se simbolizan indicando su centro y su radio, por ejemplo, una circunferencia con centro O y radio r se simboliza como C(O, r). En geometría analítica, las circunferencias se describen mediante ecuaciones en el plano cartesiano.
Ecuación general
La ecuación general de la circunferencia es x2 + y2 + Dx + Ey + F = 0, donde se cumple que D2 + E2 - 4F > 0.
Podemos llegar a la fórmula general a partir de desarrollar y reacomodar la ecuación canónica. Por ejemplo:
- La ecuación \((x+2)^2+(y-1)^2=16\) es en forma general: \(x^2+y^2+4x-2y-11=0.\)
- Desarrollando \(x^2+(y-4)^2=5,\) llegamos a la ecuación general \(x^2+y^2-8y+11=0.\)
- La circunferencia \((x-3)^2+(y+4)^2=25\) tiene fórmula general \(x^2+y^2-6x+8y=0.\)
Cómo pasar de la fórmula canónica a la general y viceversa
- Para pasar de la fórmula ordinaria a la ecuación general, desarrollamos los cuadrados y reorganizamos los términos, como hemos visto anteriormente.
- Para convertir la ecuación general a la ecuación canónica, debemos completar cuadrados y reorganizar los términos, identificando así el centro (h, k) y el radio r a partir de los coeficientes D, E y F.
No todas las ecuaciones de la forma x2 + y2 + Dx + Ey + F = 0 representan una circunferencia. Para que sí lo hagan, se deben cumplir la condición antes dicha: D2 + E2 - 4F > 0. Si no se cumple esta condición, la ecuación no representa a una circunferencia en el plano real.
Características
Las siguientes son las propiedades fundamentales de una circunferencia:
- Equidistancia del centro: todos los puntos que la componen la circunferencia están a la misma distancia del centro, esta distancia se denomina radio.
- Congruencia: todas las circunferencias que tienen el mismo radio son congruentes entre sí. Esto significa que pueden coincidir exactamente si se superponen.
- Relación entre radio y diámetro: el diámetro es igual al doble del radio. d=2r.
- Longitud de la circunferencia: el perímetro se calcula utilizando la fórmula L=2πr, donde π es una constante aproximadamente igual a 3,14159.
- Área del círculo: el área de la región encerrada por una circunferencia se determina con la fórmula A=πr2.
Fórmulas importantes
Resumimos a continuación las fórmulas de la circunferencia que son de utilidad al trabajar con ella.
| Ecuación | Centro | Radio |
|---|---|---|
| x² + y² = r² | (0, 0) | r |
| (x - h)² + (y - k)² = r² | (h, k) | r |
- Longitud de la circunferencia: L = 2πr
- Diámetro: d = 2r
- Área del círculo: A = πr2
Circunferencias en la vida cotidiana
La circunferencia tiene múltiples aplicaciones prácticas en la vida diaria y en el diseño de diversos objetos. Algunos ejemplos son:
- Diseño de engranajes: los engranajes tienen dientes distribuidos uniformemente a lo largo de una circunferencia, lo que permite transmitir movimiento y fuerza de forma suave y constante entre distintas partes de una máquina.
- Diseño de ruedas: la forma circular de las ruedas asegura un movimiento uniforme y sin saltos, fundamental para el funcionamiento eficiente de vehículos y maquinaria industrial. Las fórmulas que incluyen π (pi) permiten calcular con precisión el perímetro y el área del círculo, facilitando el dimensionamiento correcto de los componentes.
- Movimientos circulares en física: cuando un objeto se desplaza en una trayectoria circular, describe una circunferencia. Conceptos como la velocidad angular, la aceleración centrípeta y el período de rotación se basan en las propiedades de la circunferencia.
- Arquitectura: muchos diseños arquitectónicos emplean secciones de circunferencias en arcos y cúpulas, que además de su valor estético, proporcionan estabilidad estructural y una eficiente distribución de cargas.
- Ingeniería estructural: en la construcción de puentes, túneles y otras estructuras, se utilizan principios geométricos basados en la circunferencia para distribuir las tensiones de forma uniforme, lo que reduce puntos de tensión y mejora la resistencia global de la estructura.
Demostraciones de las ecuaciones
Demostración de la ecuación canónica
La definición de circunferencia se puede hacer en términos más formales de la siguiente manera:
Una circunferencia es el lugar geométrico de los puntos del plano que están a una distancia fija r de un punto fijo C(h, k).
Para deducir la ecuación, llamaremos P(x, y) a un punto genérico de la circunferencia.
Planteando simbólicamente la definición, tenemos que:
\(d(P, C)=r\)
Usamos la fórmula de distancia entre dos puntos para reescribir el primer miembro:
\(\sqrt{(x-h)^2+(y-k)^2}=r\)
Elevando al cuadrado ambos miembros nos queda:
\((x-h)^2+(y-k)^2=r^2\)
Esta última es conocida como la ecuación canónica u ordinaria de una circunferencia con centro en (h, k) y radio r.
A partir de esta podemos deducir la ecuación en el caso particular de que el centro sea el origen de coordenadas, es decir, el punto (0, 0). Si hacemos h=0 y k=0 en la ecuación canónica, nos queda:
\(x^2+y^2=r^2\)
que es la ecuación canónica de una circunferencia centrada en el origen con radio r.
Cómo identificar el centro y el radio
- Centro: en la ecuación (x-h)2 + (y-k)2 = r2, el centro es el punto (h, k), los valores de h y k son los números que se encuentran dentro de los paréntesis y cambian de signo. Por ejemplo, si la ecuación es (x+2)2 + (y-3)2 =16, entonces h=-2 y k=3. Así, el centro es (-2, 3).
- Radio: el término r2 en la ecuación representa el cuadrado del radio. Para encontrar el radio real, debemos tomar la raíz cuadrada de este valor. Por ejemplo, si la ecuación es (x+2)2 + (y-3)2 =16, entonces r2=16. El radio es r=√16=4.
Demostración de la ecuación general
Para deducir la ecuación general de la circunferencia, partimos de la fórmula canónica con centro en (h, k) y radio r:
\((x-h)^2+(y-k)^2=r^2\)
Desarrollando los cuadrados de esta expresión, obtenemos:
\(x^2-2hx+h^2+y^2-2ky+k^2=r^2\)
Reorganizamos los términos:
\(x^2+y^2-2hx-2ky+h^2+k^2=r^2\)
Ahora, agrupamos las constantes en un solo término:
\(x^2+y^2-2hx-2ky+(h^2+k^2-r^2)=0\)
Para simplificar, designamos las constantes de la siguiente manera: \(D=-2h,\) \(E=-2k,\) y \(F=h^2+k^2-r^2.\) Así, obtenemos la ecuación general de la circunferencia: \(x^2+y^2+Dx+Ey+F=0.\)
Recursos adicionales
Diferencia entre círculo y circunferencia
Es importante distinguir entre los términos "circunferencia" y "círculo", ya que aunque a menudo se utilizan indistintamente en el lenguaje cotidiano, no son lo mismo.
La circunferencia se refiere exclusivamente al perímetro del círculo. Es decir, es la línea curva continua que forma el borde exterior del círculo. Un ejemplo de circunferencia en la vida real es la rueda de una bicicleta; la circunferencia sería el borde exterior del neumático.
Por otro lado, el círculo incluye tanto la circunferencia como todo el espacio contenido dentro de ella. Un ejemplo común es un plato; el borde del plato representa la circunferencia, mientras que la superficie completa del plato es el círculo.

Matemáticamente, la circunferencia solo tiene perímetro, no área. Su longitud se calcula con la fórmula: L=2πr donde r es el radio del círculo. El círculo, en cambio, posee tanto perímetro como área, este último se calcula con la fórmula: A=πr2.
Cómo graficar una circunferencia
Manualmente
Para graficar una circunferencia de manera manual, necesitarás un compás, un lápiz, una regla y un papel. Primero, decide dónde estará el centro de la circunferencia y márcalo en el papel. Este punto será el eje desde donde medirás el radio. A continuación, determina la longitud del radio abriendo el compás a la distancia deseada.
Una vez que tengas el compás ajustado, coloca la punta en el punto central previamente marcado. Asegúrate de mantener el compás firme y, con el lápiz en el otro extremo, gira lentamente el compás en un movimiento circular completo para trazar la circunferencia.
Utilizando software
Para graficar una circunferencia mediante software, tienes disponibles dos herramientas gratuitas: GeoGebra y Desmos.
GeoGebra permite graficar la circunferencia a partir del centro y un punto y también desde sus ecuaciones. Es una herramienta muy versátil que ofrece dinamismo, precisión y flexibilidad. En Desmos, por otro lado, para graficar una circunferencia necesitarás contar con la ecuación en forma estándar o general. Una vez escrita, el gráfico se mostrará en la pantalla en un sistema de ejes cartesianos.
Videos y recursos interactivos
En el siguiente video se explica a la circunferencia y su ecuación:
Con el siguiente recurso podrás modificar los parámetros de centro y radio de una circunferencia y ver cómo cambia el gráfico en tiempo real:
Bibliografía
- Engler, A., Müller, D., Vrancken, S. y Hecklein, M. (2020). Geometría analítica. Universidad Nacional del Litoral.
- Fuller, G. y Tarwater, D. (1995). Geometría analítica (7.ª ed.). Pearson Educación.
- Lehmann, C. (1989). Geometría analítica. Limusa.
- Leithold. L. (1992). Álgebra y trigonometría con geometría analítica. Oxford University Press.
- Márquez, A., Vázquez, F., Ruiz, H., Villegas, M. y Figueroa, M. (2009). Geometría analítica. Prentice Hall.
- Raichman, S. y Totter, E. (2016). Geometría analítica para ciencias e ingeniería. Universidad Nacional de Cuyo.
- Sullivan, M. (2006). Álgebra y trigonometría. Pearson Educación.
- Swokowski, E. y Cole, J. (2009). Álgebra y trigonometría con geometría analítica. Cengage Learning.
Contenidos sobre la circunferencia
¿Te ha servido este contenido? ¡Califícalo!
4,8 / 5 — 5 votos
CÓMO CITAR ESTE ARTÍCULO
Machado, D. (2025, 11 de abril). Circunferencia: definición, elementos y ecuaciones. Exponty. https://exponty.com/circunferencia
-
Muchas gracias, me facilito bastante en exámen. Una explicación exelente. 😁
-
Gracias por su explicación
-
Gracias por una buena explicación que a servido de enseñanzas 👍👍👍👍😁
6 Comentarios
Deja una respuesta


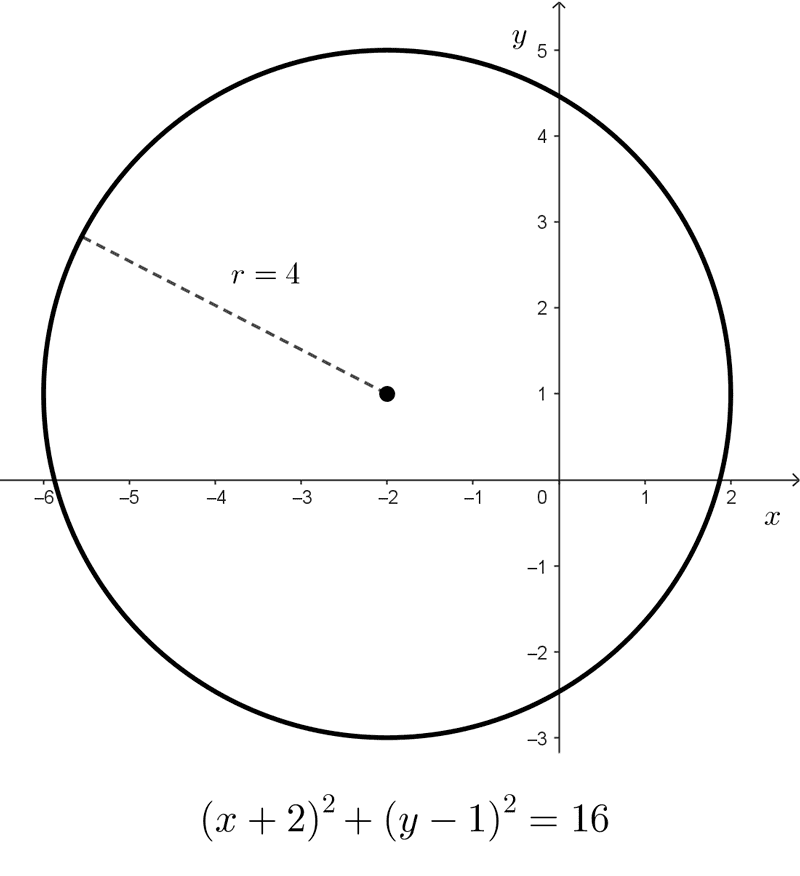
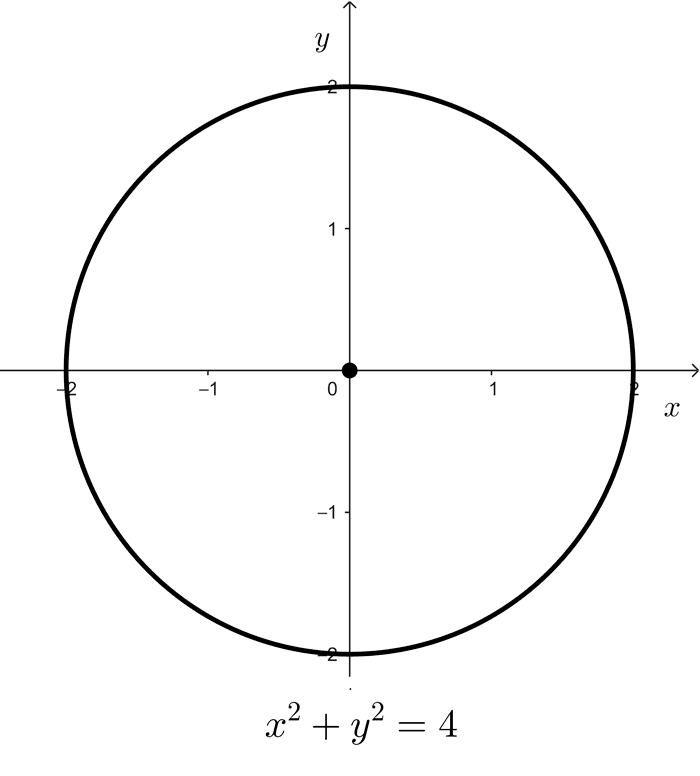
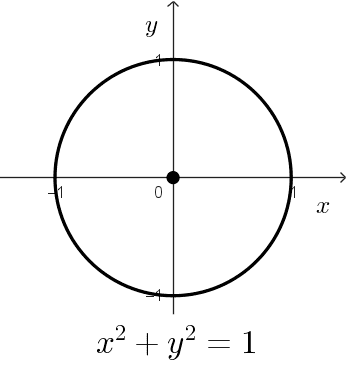
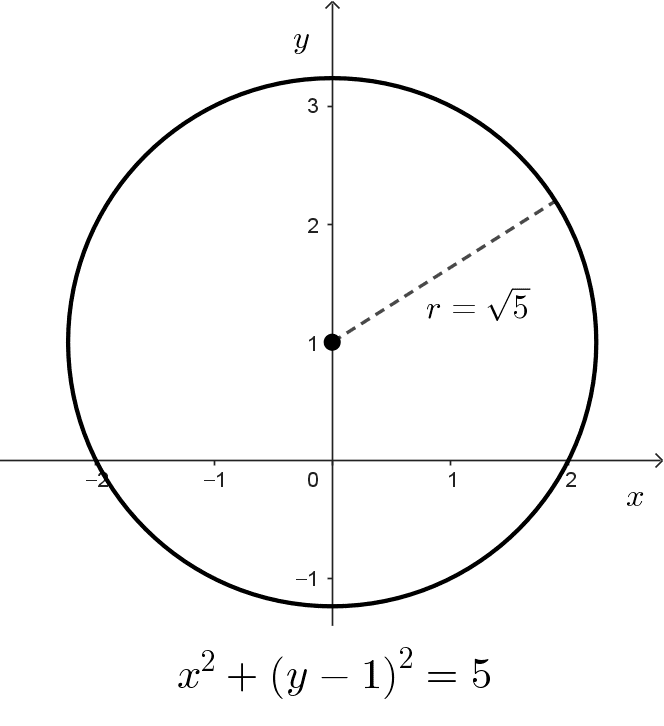
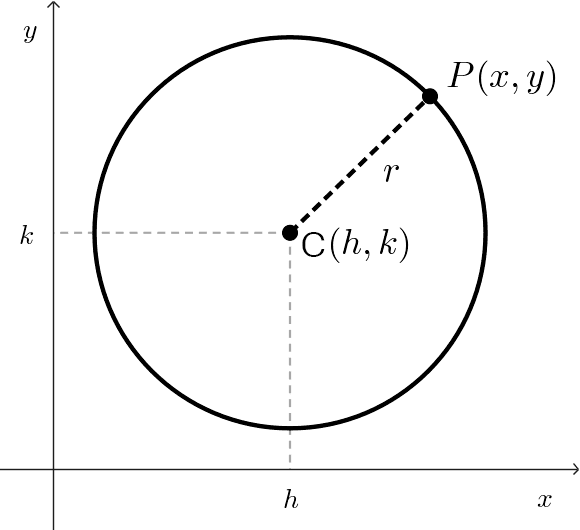






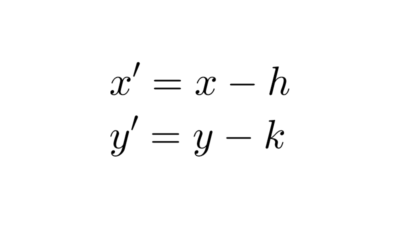
Otros artículos que pueden interesarte