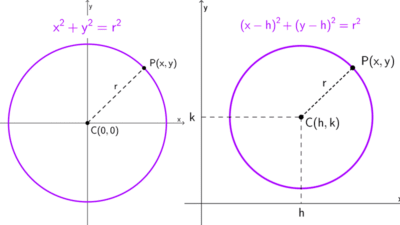
Ejercicios de circunferencia
En este artículo veremos ejercicios de circunferencia desarrollados paso a paso con gráficas. Si aún no conoces sus conceptos fundamentales, te recomiendo primero revisar el artículo principal donde tratamos la teoría básica:
Índice
Ejercicios generales




Encontrar la ecuación de una circunferencia a partir de datos
Determinar la ecuación ordinaria de la circunferencia que cumple las condiciones dadas en cada caso y graficarla.
- Centro en el origen y diámetro 2√11.
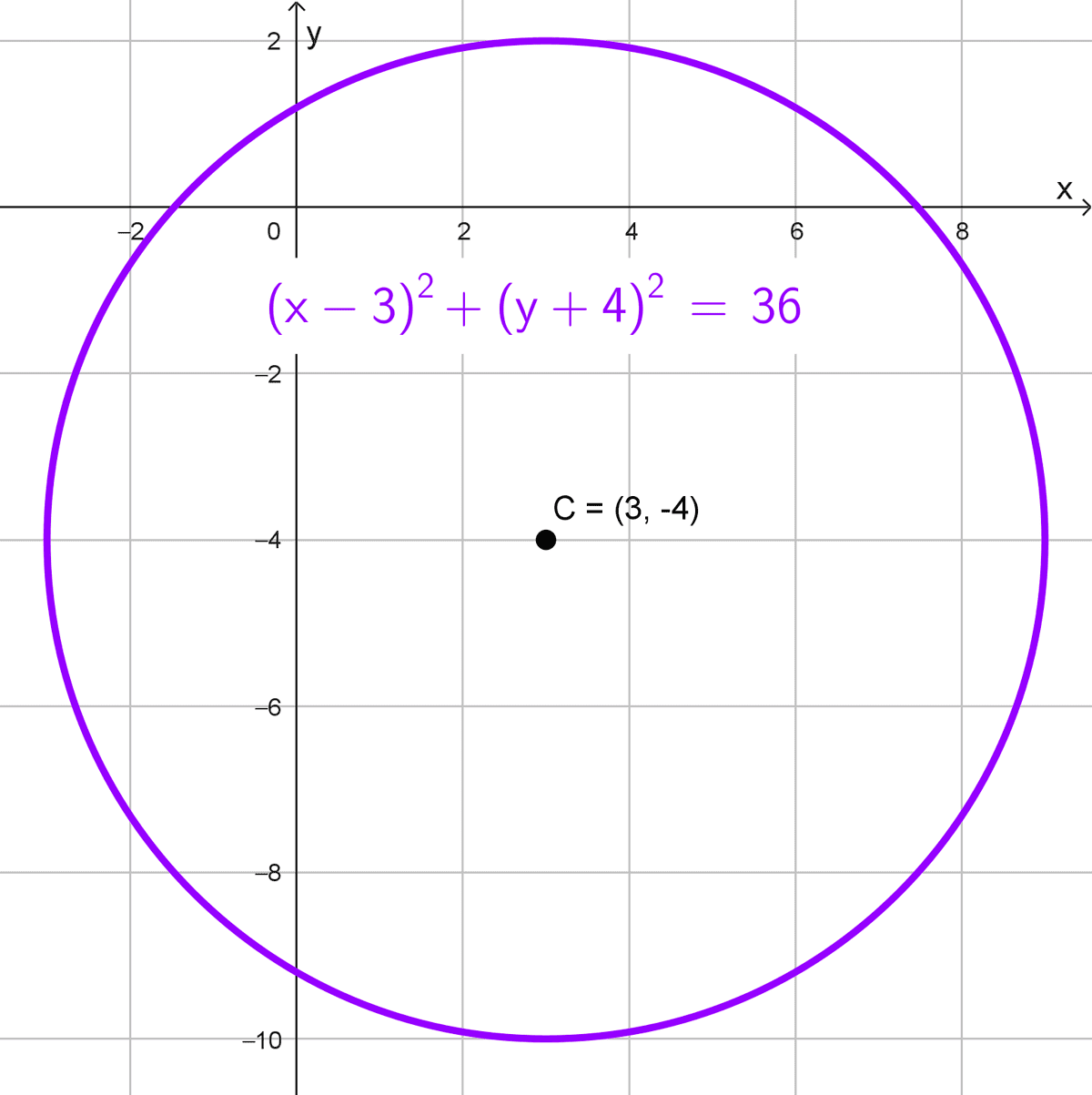
- Centro (3, -4), radio 6.
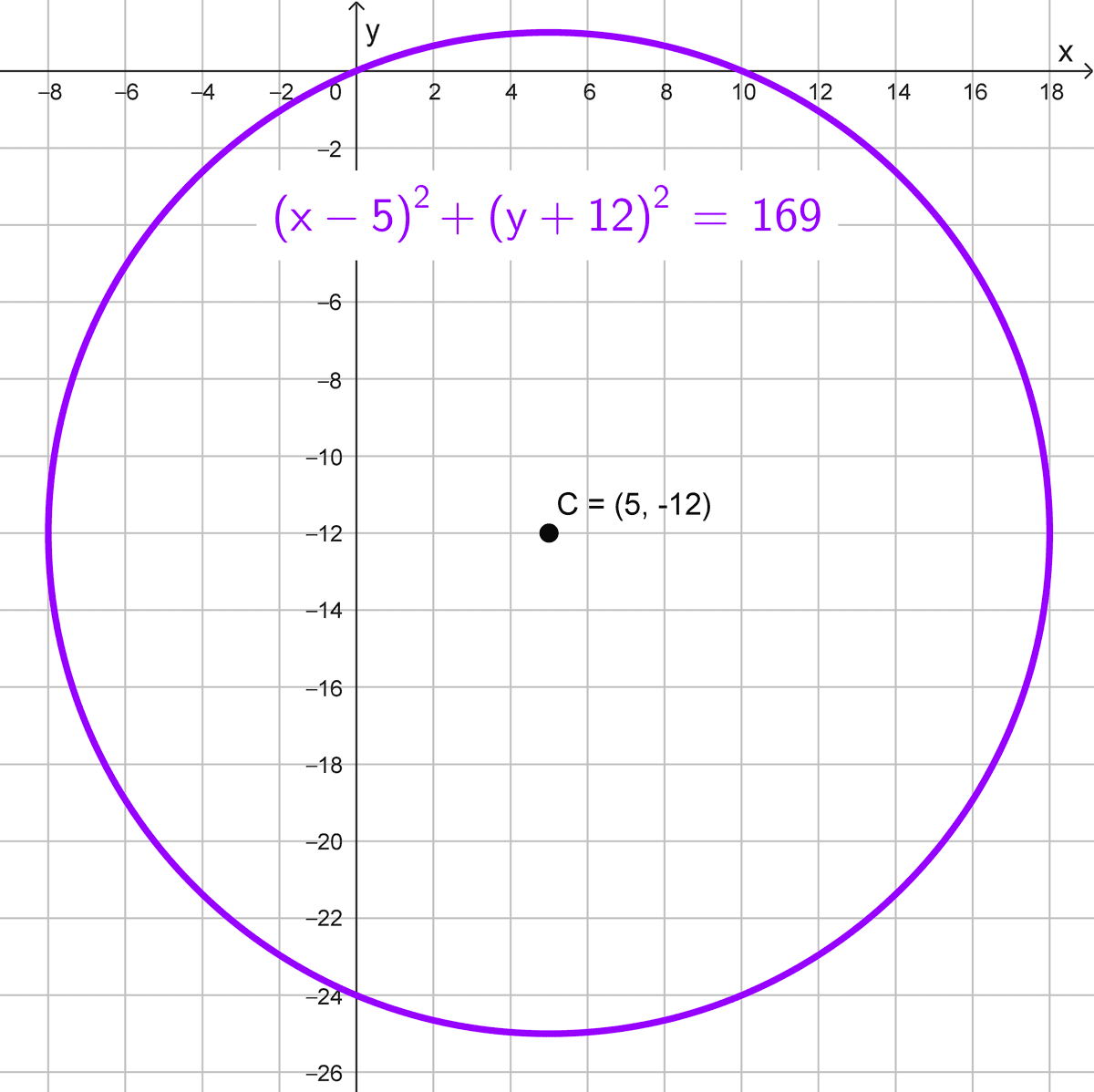
- Centro (5, -12), radio 13.
- Centro (5, -3), radio √6.
- Centro (π, -1/12), radio √17.
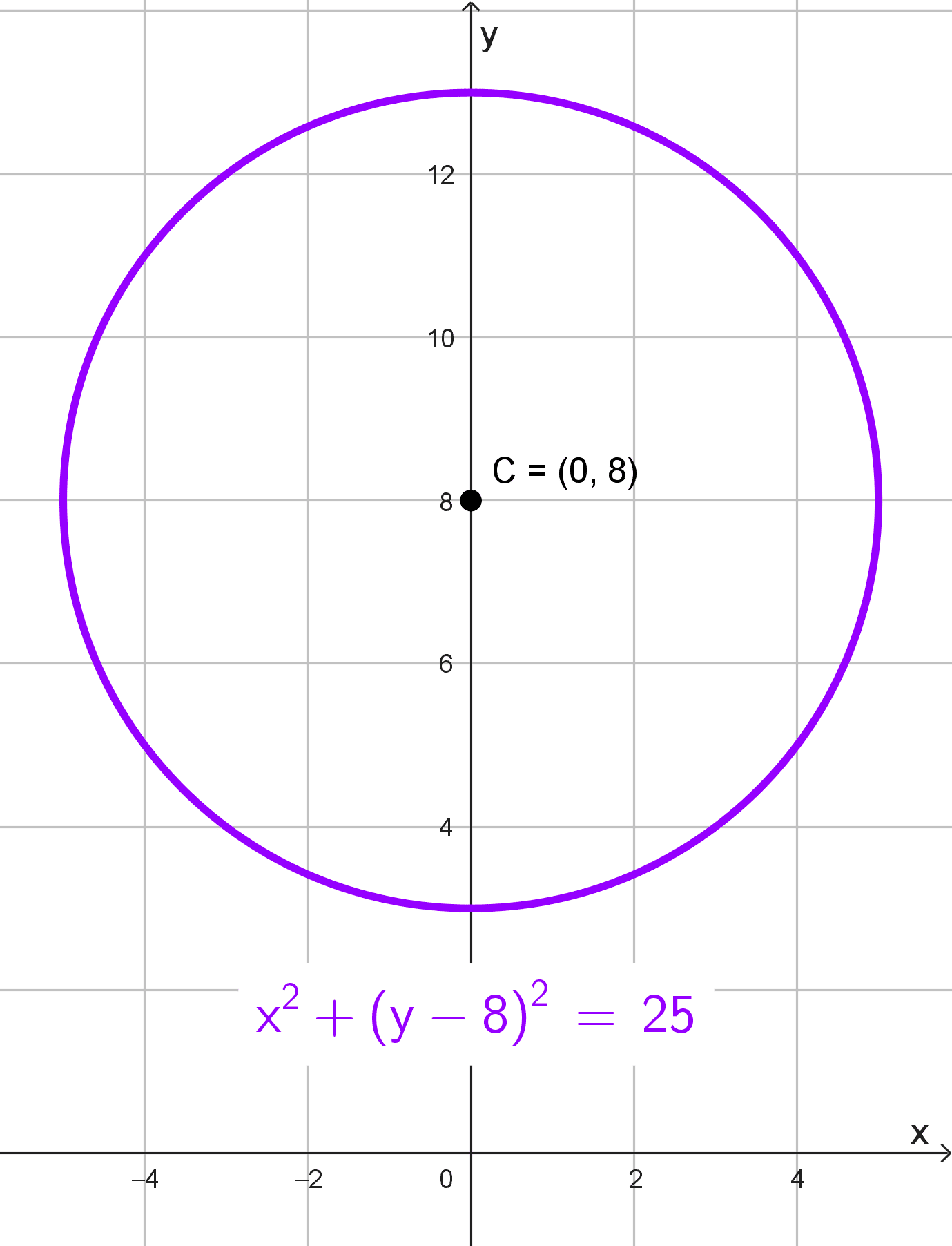
- Centro (0, 8), radio 5.
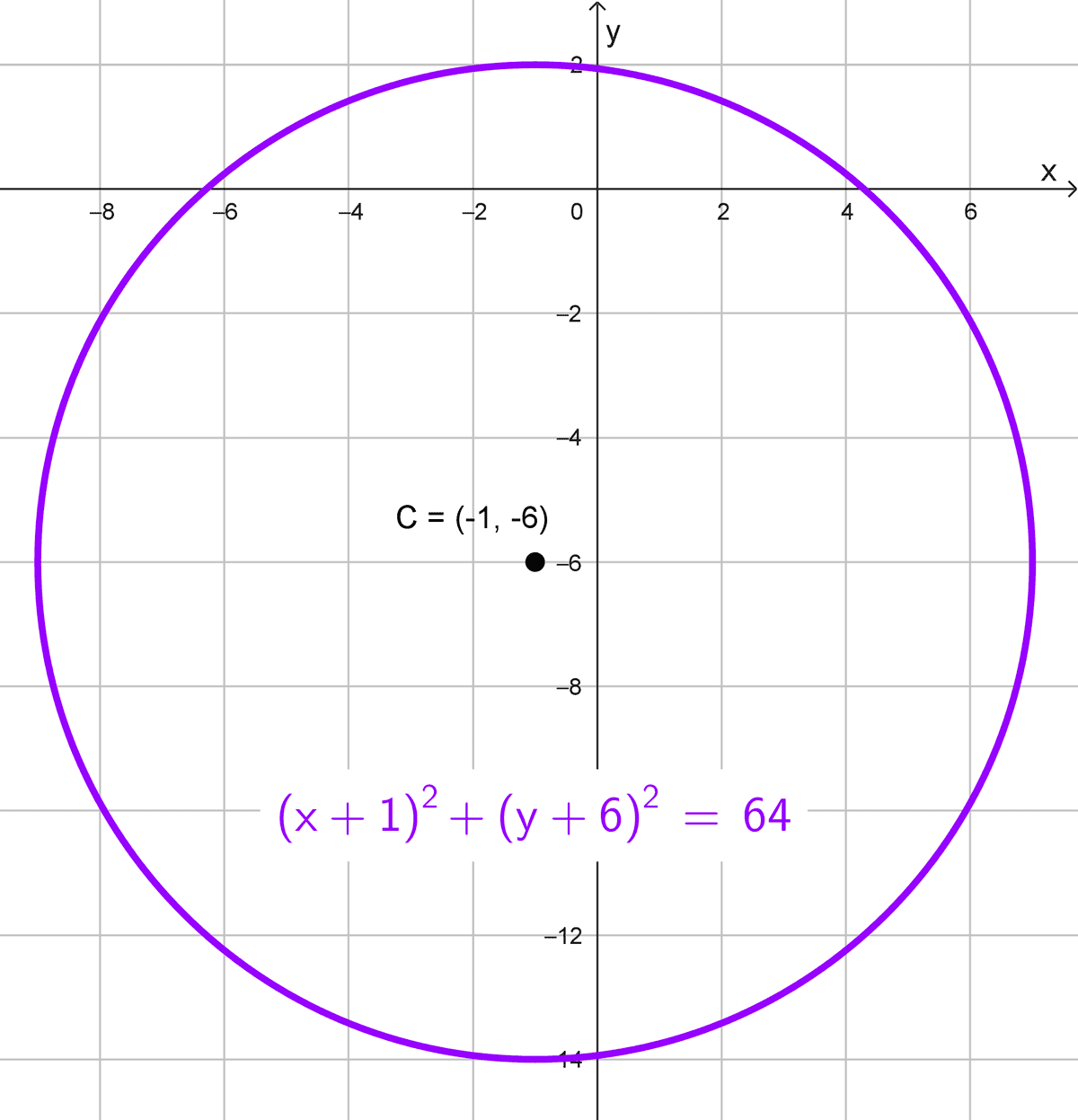
- Centro (-1,-6), radio 8.
- Centro (3/5; 1/3), radio √10.
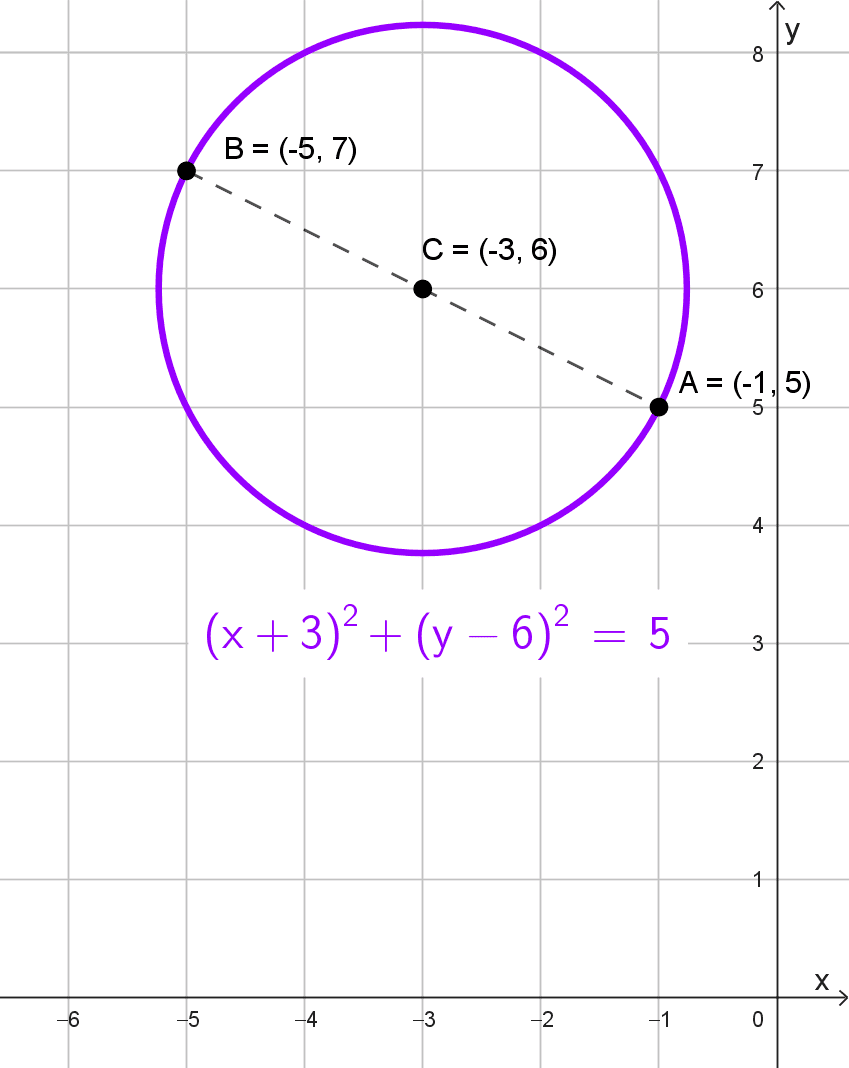
- El segmento que une A(-1, 5) y B(-5, 7) es un diámetro.
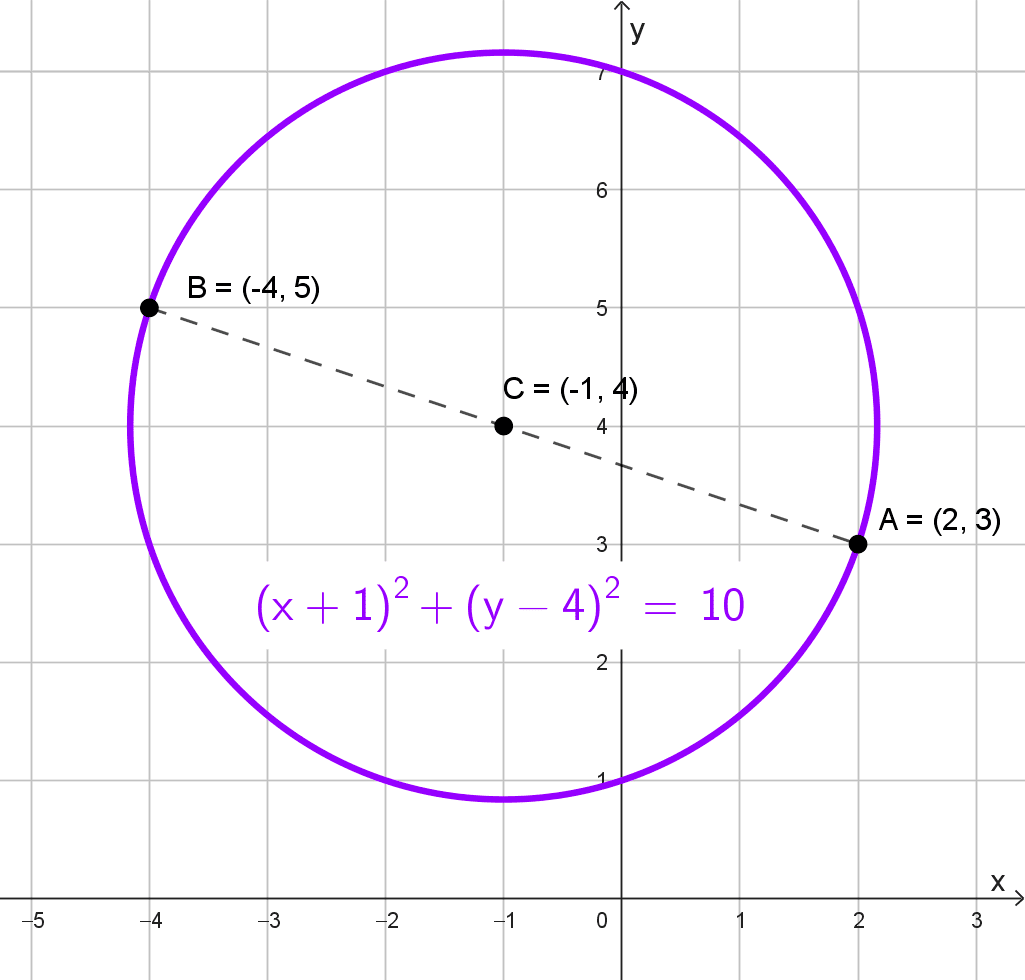
- Los extremos de un diámetro son los puntos A(2, 3) y B(-4, 5).
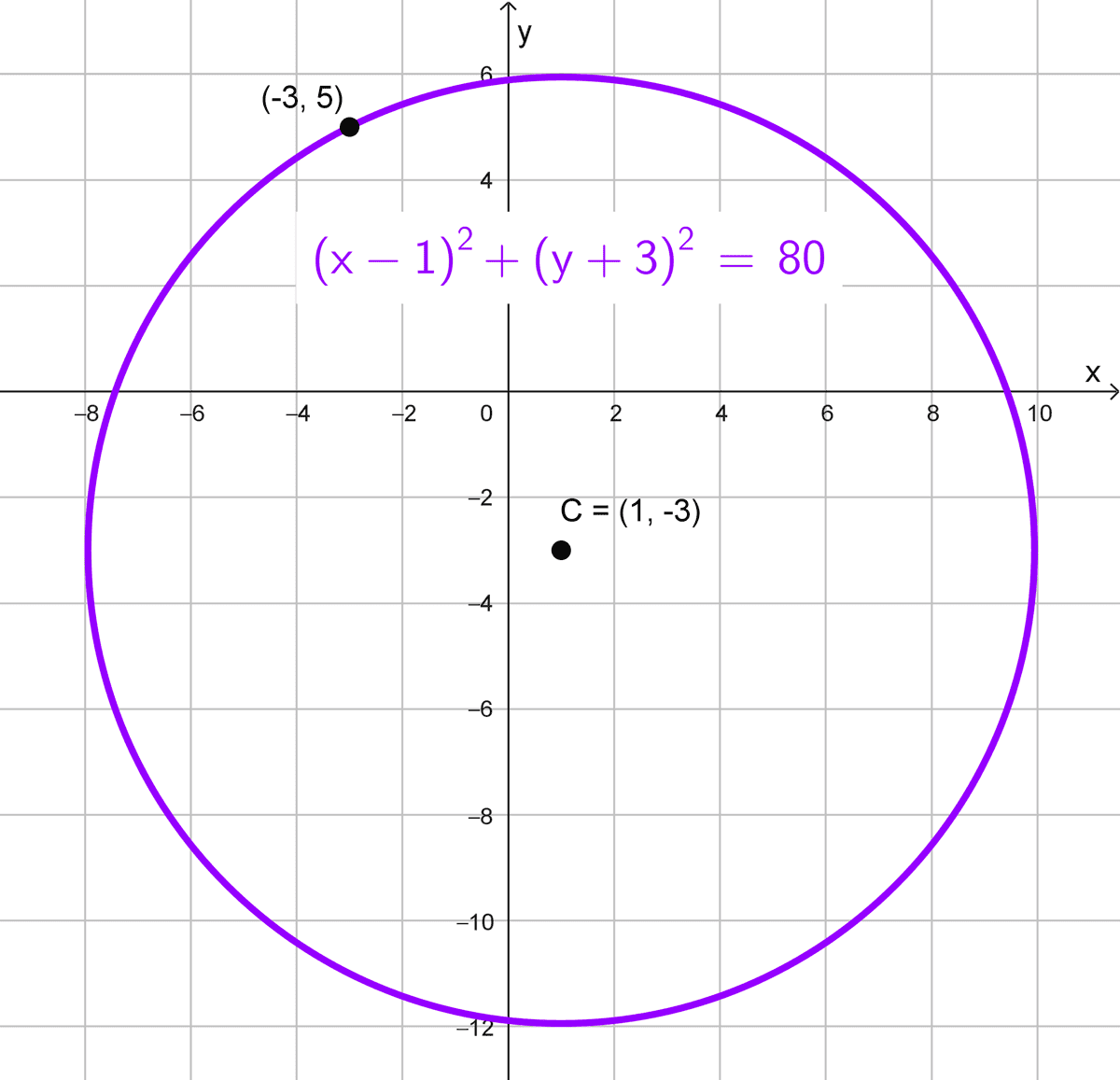
- El centro está en (1, -3) y la circunferencia pasa por (-3, 5).
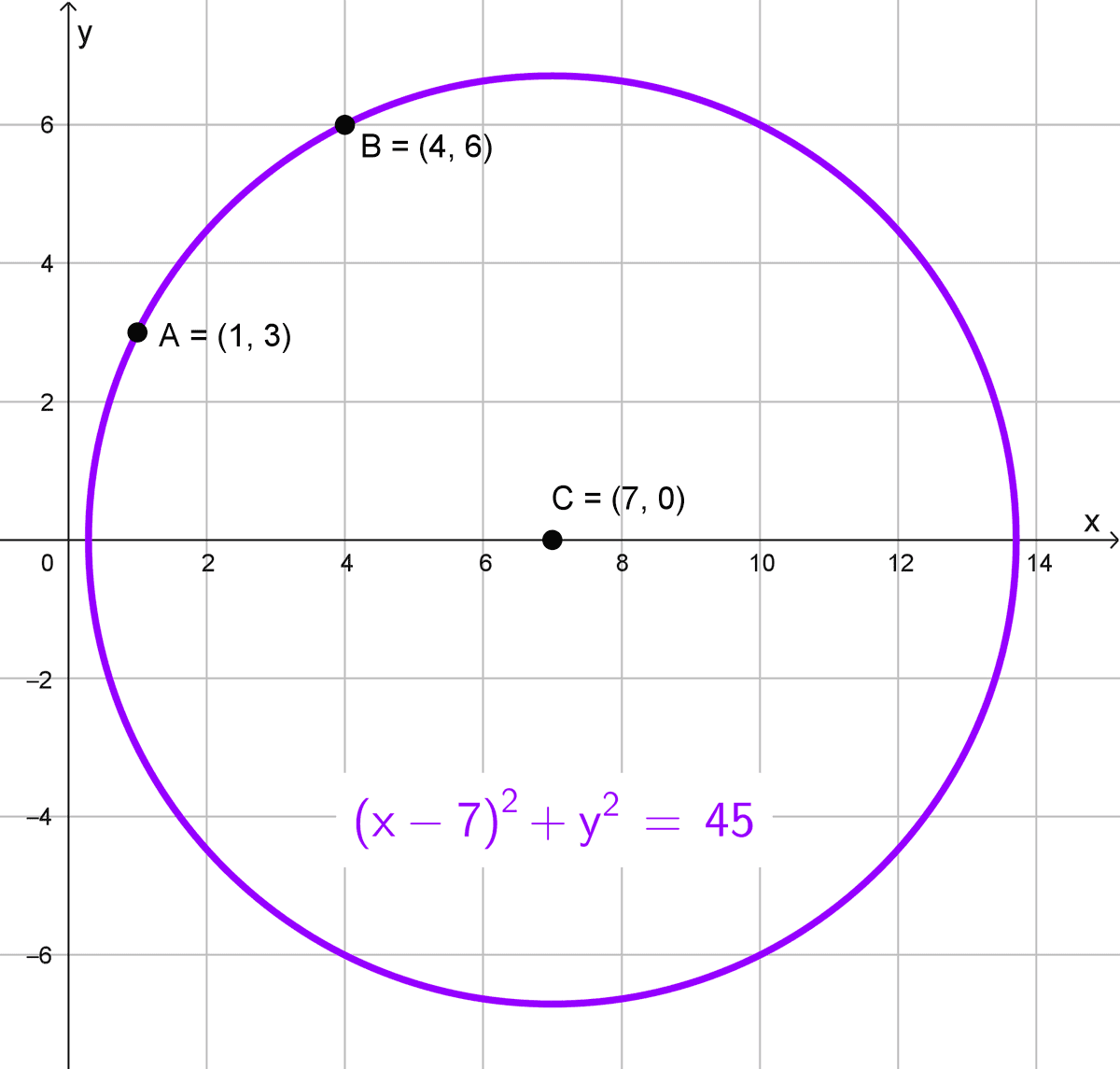
- Su centro está sobre el eje X y pasa por los dos puntos A(1, 3) y B(4, 6).
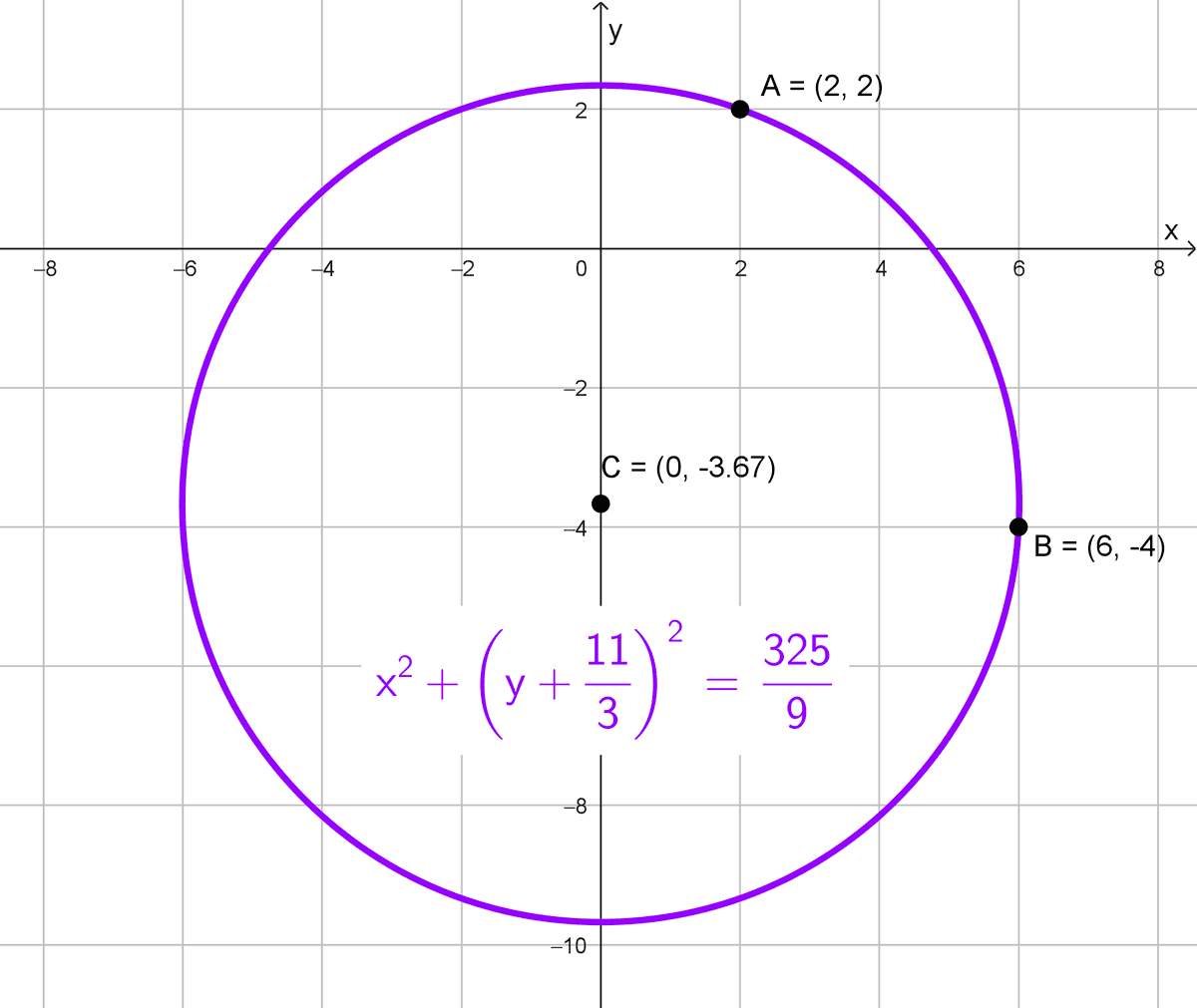
- Su centro está sobre el eje Y y pasa por los puntos A(2, 2) y B(6, -4).
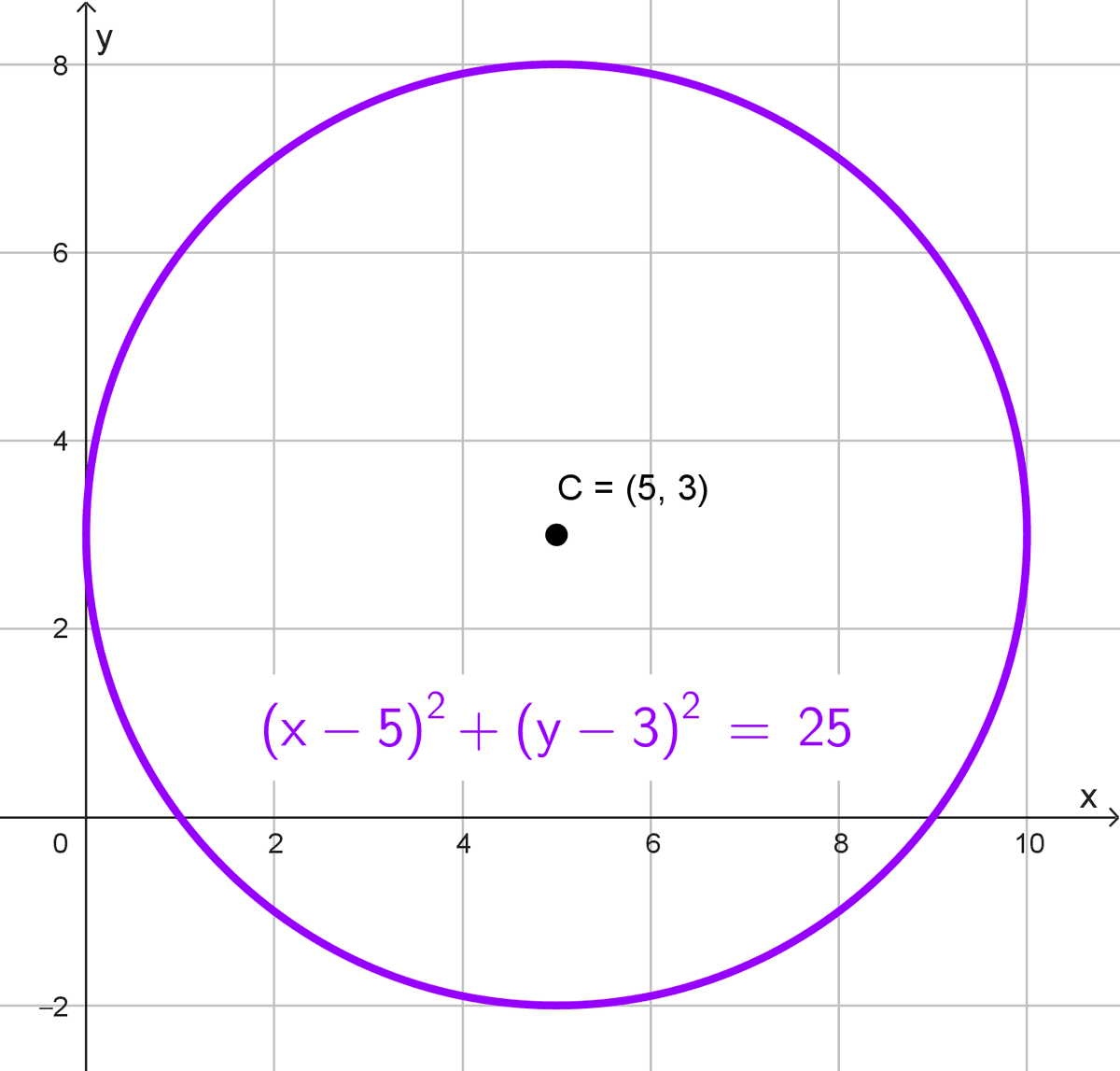
- La circunferencia es tangente al eje y y el centro está en (5, 3).
- Es tangente a los dos ejes, tiene radio 5 y se encuentra en el tercer cuadrante.
- La circunferencia es tangente a la recta 3x + 4y = 16 y el centro está en (-3, -4).
- La circunferencia es tangente a la recta 5x - 12y = 24 y el centro está en (5, -5).
- La circunferencia es tangente a la recta x - y = 2 en el punto (4, 2) y el centro está en el eje x.
- La circunferencia es tangente a la recta x + 2y = 3 en el punto (-1, 2) y el centro está en el eje y.
- La circunferencia es tangente a la recta 4x + 3y = 4 en el punto (4, -4) y el centro está en la recta x - y = 7
Soluciones
Solución 1
La ecuación ordinaria de una circunferencia con centro en el origen (0, 0) es \(x^2+y^2=r^2,\) donde r es el radio. Dado que el diámetro es \(2\sqrt{11},\) el radio es la mitad de este valor:
\(r=\dfrac{2\sqrt{11}}{2}=\sqrt{11}\)
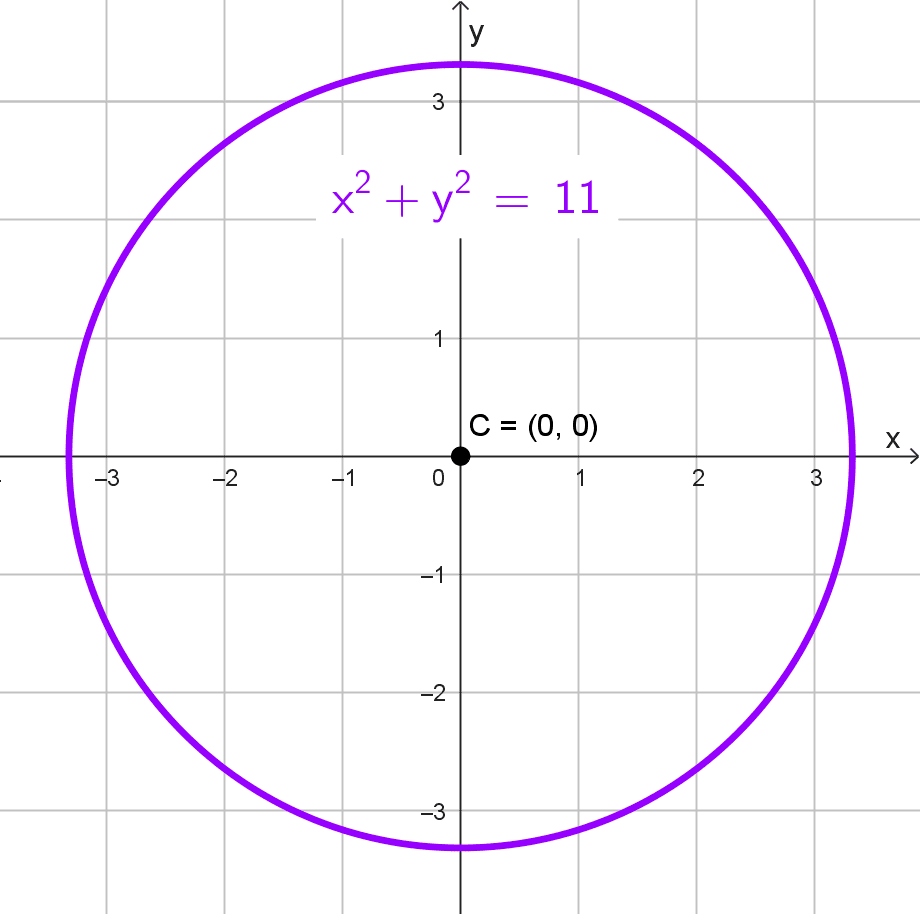
Sustituyendo en la ecuación, obtenemos:
\(x^2+y^2=(\sqrt{11})^2 → x^2+y^2=11\)
Solución 2
Solución 3
Solución 4
Solución 5
Solución 6
Solución 7
Solución 8
Solución 9
Datos: Extremos del diámetro en \(A(-1, 5)\) y \(B(-5, 7).\)
Calculamos el centro como el punto medio del segmento AB:
\(h=\dfrac{-1+(-5)}{2}=-3, \quad k=\dfrac{5+7}{2}=6\)
El radio es la mitad de la distancia entre A y B:
\(\text{Distancia } AB=\sqrt{(-5-(-1))^2+(7-5)^2}=\sqrt{16+4}=\sqrt{20}=2\sqrt{5}\)
\(r=\dfrac{2\sqrt{5}}{2}=\sqrt{5}\)
La ecuación ordinaria es:
\((x+3)^2+(y-6)^2=5\)
Solución 10
Datos: Extremos del diámetro en \(A(2, 3)\) y \(B(-4, 5).\)
Hallamos el centro (punto medio):
\(h=\dfrac{2+(-4)}{2}=-1, \quad k=\dfrac{3+5}{2}=4\)
Calculamos el radio como la mitad de la distancia \(AB:\)
\(\text{Distancia } AB=\sqrt{(-4-2)^2+(5-3)^2}=\sqrt{36+4}=\sqrt{40}=2\sqrt{10}\)
\(r=\dfrac{2\sqrt{10}}{2}=\sqrt{10}\)
La ecuación canónica resulta:
\((x+1)^2+(y-4)^2=10\)
Solución 11
Solución 12
Datos: Centro sobre el eje X (es decir, \(k=0\)) y pasa por A(1, 3) y B(4, 6).
Como el centro \((h, 0)\) equidista de \(A\) y \(B,\) planteamos:
\(\sqrt{(1-h)^2+(3-0)^2}=\sqrt{(4-h)^2+(6-0)^2}\)
Simplificando y elevando al cuadrado:
\((1-h)^2+9=(4-h)^2+36\)
Resolviendo:
\(1-2h+h^2+9=16-8h+h^2+36\)
\(-2h+10=-8h+52 → 6h=42 → h=7\)
El centro es \((7, 0).\) Calculamos el radio con \(A(1, 3):\)
\(r=\sqrt{(1-7)^2+(3-0)^2}=\sqrt{36+9}=\sqrt{45}=3\sqrt{5}\)
La ecuación canónica queda:
\((x-7)^2+y^2=45\)
Solución 13
Datos: Centro sobre el eje \(Y\) (es decir, \(h=0\)) y pasa por \(A(2, 2)\) y \(B(6,-4).\)
Como el centro \((0, k)\) equidista de \(A\) y \(B,\) planteamos:
\(\sqrt{(2-0)^2+(2-k)^2}=\sqrt{(6-0)^2+(-4-k)^2}\)
Simplificando y elevando al cuadrado:
\(4+(2-k)^2=36+(-4-k)^2\)
Resolviendo:
\(4+4-4k+k^2=36+16+8k+k^2\)
\(8-4k=52+8k →-12k=44 → k=-\dfrac{11}{3}\)
El centro es \(\left(0,-\dfrac{11}{3}\right).\) Calculamos el radio con \(A(2, 2):\)
\(r=\sqrt{(2-0)^2+\left(2-\left(-\dfrac{11}{3}\right)\right)^2}=\sqrt{4+\left(\dfrac{17}{3}\right)^2}=\sqrt{4+\dfrac{289}{9}}=\sqrt{\dfrac{325}{9}}\)
La ecuación ordinaria es:
\(x^2+\left(y+\dfrac{11}{3}\right)^2=\dfrac{325}{9}\)
Solución 14
Datos: Centro en (5, 3) y tangente al eje Y.
Como la circunferencia es tangente al eje Y, la distancia del centro a dicho eje es igual al radio. La distancia de (5, 3) al eje Y (recta x = 0) es:
\(r=|5-0|=5\)
Usando la forma reducida de la circunferencia con centro (h, k) = (5, 3):
\((x-5)^2+(y-3)^2=r^2\)
Sustituyendo el radio:
\((x-5)^2+(y-3)^2=5^2\)
Obtenemos la ecuación canónica:
\((x-5)^2+(y-3)^2=25\)
Solución 15
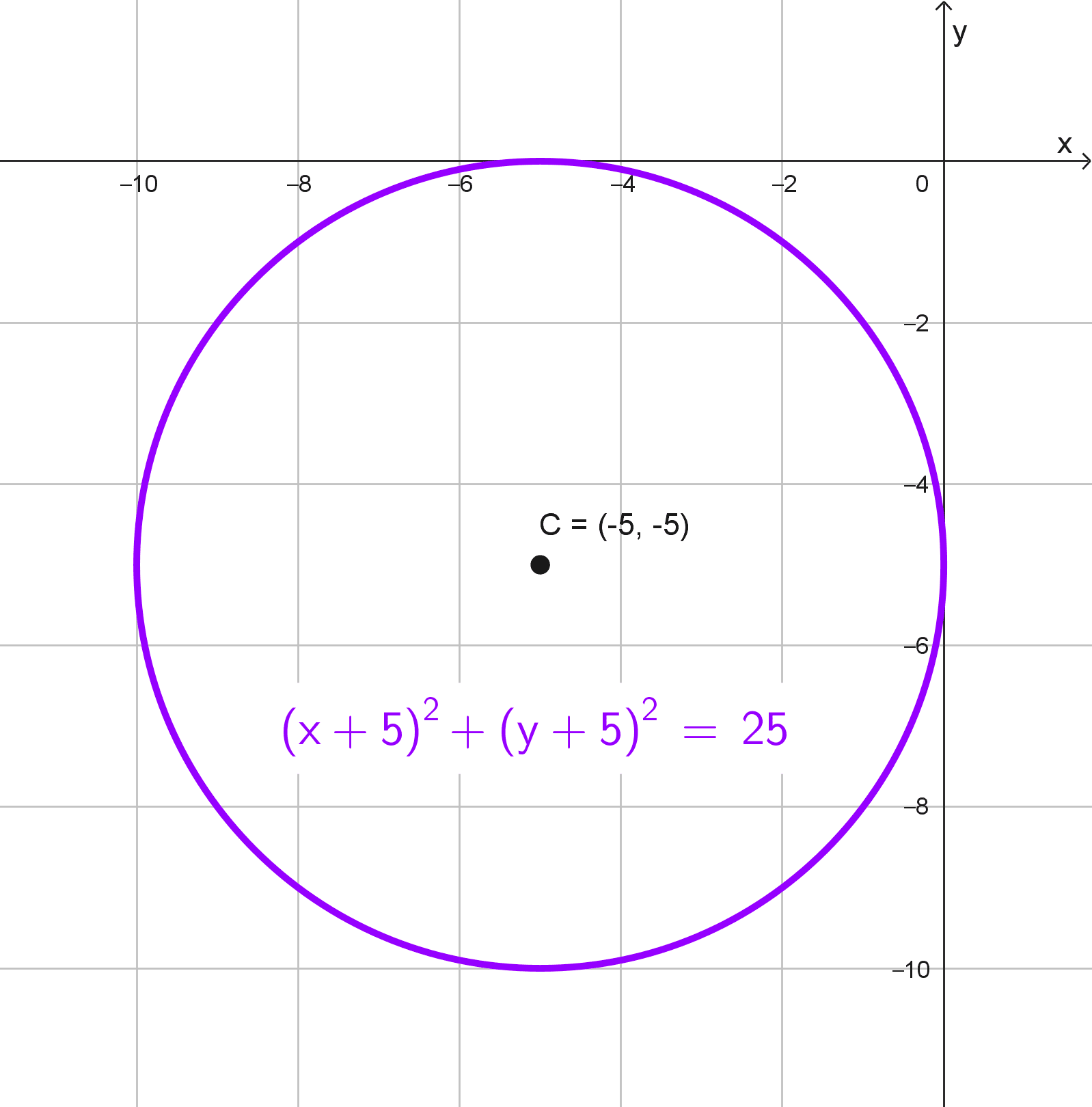
Datos: Tangente a ambos ejes, radio 5 y ubicada en el tercer cuadrante.
En el tercer cuadrante, tanto x como y son negativas. Al ser tangente a ambos ejes:
\(|h|=r \quad \text{y} \quad |k|=r\)
Como está en el tercer cuadrante:
\(h=-5, \quad k=-5\)
La ecuación ordinaria es:
\((x+5)^2+(y+5)^2=5^2\)
Desarrollando:
\((x+5)^2+(y+5)^2=25\)
Solución 16
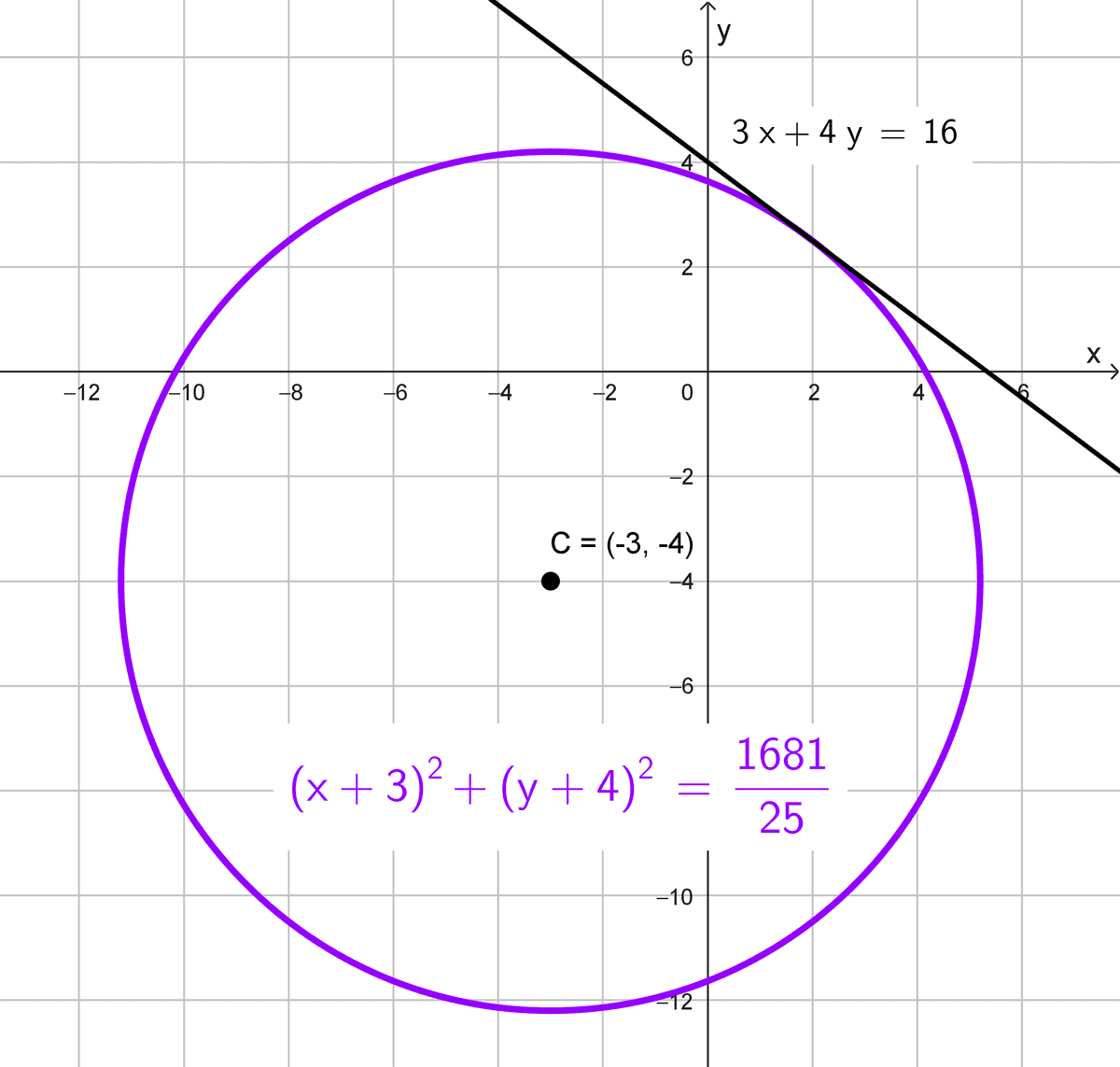
Datos: Centro en (-3, -4) y tangente a la recta 3x + 4y = 16.
El radio es la distancia del centro a la recta tangente. Usamos la fórmula de distancia de punto a recta:
\(r=\dfrac{|3(-3)+4(-4)-16|}{\sqrt{3^2+4^2}}=\dfrac{|-9-16-16|}{5}=\dfrac{41}{5}\)
La ecuación reducida con centro (h, k) = (-3, -4):
\((x+3)^2+(y+4)^2=r^2\)
Sustituyendo el radio:
\((x+3)^2+(y+4)^2=\left(\dfrac{41}{5} \right)^2\)
Quedando la ecuación canónica:
\((x+3)^2+(y+4)^2=\dfrac{1681}{25}\)
Solución 17
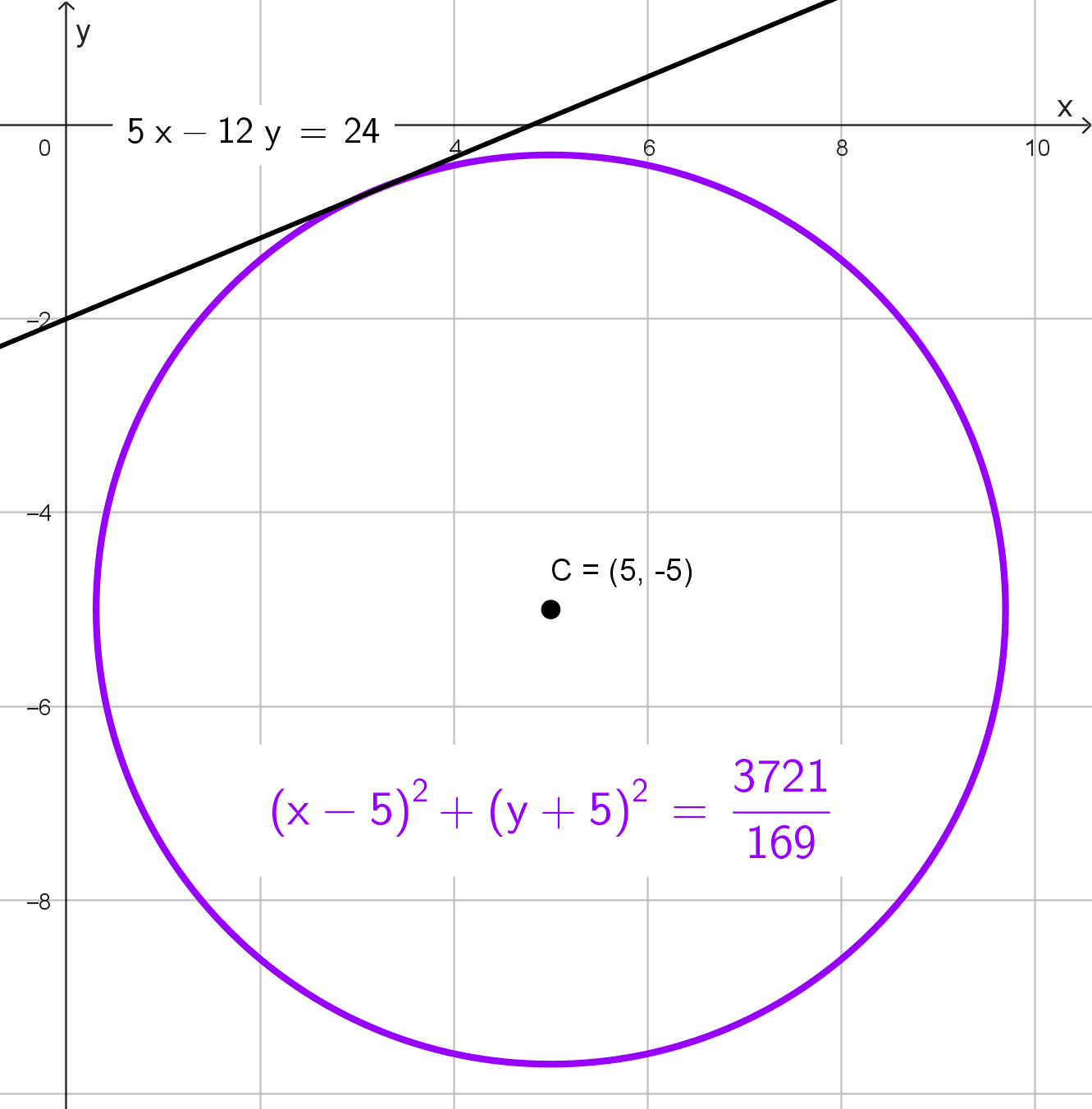
Datos: Centro en (5, -5) y tangente a la recta 5x - 12y = 24.
Calculamos el radio como distancia del centro a la recta:
\(r=\dfrac{|5(5)-12(-5)-24|}{\sqrt{5^2+(-12)^2}}=\dfrac{|25+60-24|}{13}=\dfrac{61}{13}\)
Usando la forma ordinaria con centro (5, -5):
\((x-5)^2+(y+5)^2=r^2\)
Sustituimos el radio:
\((x-5)^2+(y+5)^2=\left(\dfrac{61}{13} \right)^2\)
Obtenemos la ecuación ordinaria:
\((x-5)^2+(y+5)^2=\dfrac{3721}{169}\)
Solución 18
Datos: Centro sobre el eje x y tangente a la recta x - y = 2 en el punto (4, 2).
Dado que el centro de la circunferencia está en el eje x, su coordenada es \((h, 0).\) La circunferencia es tangente a la recta \(x-y=2\) en el punto \((4, 2).\) La distancia del centro \((h, 0)\) a la recta \(x-y-2=0\) debe ser igual al radio \(r,\) que también es la distancia entre \((h, 0)\) y \((4, 2).\)
Calculamos la distancia del centro a la recta:
\(\dfrac{|h-0-2|}{\sqrt{1^2+(-1)^2}}=\dfrac{|h-2|}{\sqrt{2}}\)
La distancia entre \((h, 0)\) y \((4, 2)\) es:
\(\sqrt{(h-4)^2+(0-2)^2}=\sqrt{(h-4)^2+4}\)
Igualando ambas expresiones:
\(\dfrac{|h-2|}{\sqrt{2}}=\sqrt{(h-4)^2+4}\)
Elevando al cuadrado y resolviendo:
\(\dfrac{(h-2)^2}{2}=(h-4)^2+4 → (h-2)^2=2(h-4)^2+8\)
Expandiendo:
\(h^2-4h+4=2h^2-16h+32+8 →-h^2+12h-36=0\)
Resolviendo la ecuación cuadrática:
\(h=\dfrac{-12±\sqrt{144-144}}{-2}=6\)
El centro es \((6, 0).\) Calculamos el radio:
\(r=\sqrt{(6-4)^2+(0-2)^2}=\sqrt{4+4}=2\sqrt{2}\)
La ecuación canónica es:
\((x-6)^2+y^2=8\)
Solución 19
Datos: Tangente a la recta x + 2y = 3 en el punto (-1, 2) y el centro está en el eje y.
El centro está en el eje Y, por lo que su coordenada es \((0, k).\) La circunferencia es tangente a la recta \(x+2y=3\) en \((-1, 2).\) La distancia del centro \((0, k)\) a la recta \(x+2y-3=0\) es igual al radio \(r,\) que también es la distancia entre \((0, k)\) y \((-1, 2).\)
Calculamos la distancia del centro a la recta:
\(\dfrac{|0+2k-3|}{\sqrt{1^2+2^2}}=\dfrac{|2k-3|}{\sqrt{5}}\)
La distancia entre \((0, k)\) y \((-1, 2)\) es:
\(\sqrt{(0+1)^2+(k-2)^2}=\sqrt{1+(k-2)^2}\)
Igualando ambas expresiones:
\(\dfrac{|2k-3|}{\sqrt{5}}=\sqrt{1+(k-2)^2}\)
Elevando al cuadrado y resolviendo:
\(\dfrac{(2k-3)^2}{5}=1+(k-2)^2 → 4k^2-12k+9=5+5k^2-20k+20\)
Simplificando:
\(-k^2+8k-16=0 → k^2-8k+16=0 → (k-4)^2=0 → k=4\)
El centro es \((0, 4).\) Calculamos el radio:
\(r=\sqrt{1+(4-2)^2}=\sqrt{5}\)
La ecuación ordinaria es:
\(x^2+(y-4)^2=5\)
Solución 20
Datos: Tangente a la recta 4x + 3y = 4 en el punto (4, -4) y el centro está en la recta x - y = 7
El centro \((h, k)\) está en la recta \(x-y=7,\) por lo que \(h-k=7.\) La circunferencia es tangente a la recta \(4x+3y=4\) en \((4,-4).\) La distancia del centro a la recta \(4x+3y-4=0\) es igual al radio \(r,\) que también es la distancia entre \((h, k)\) y \((4,-4).\)
Calculamos la distancia del centro a la recta:
\(\dfrac{|4h+3k-4|}{\sqrt{4^2+3^2}}=\dfrac{|4h+3k-4|}{5}\)
La distancia entre \((h, k)\) y \((4,-4)\) es:
\(\sqrt{(h-4)^2+(k+4)^2}\)
Igualando ambas expresiones y usando \(h=k+7:\)
\(\dfrac{|4(k+7)+3k-4|}{5}=\sqrt{(k+3)^2+(k+4)^2}\)
Simplificando el numerador:
\(\dfrac{|7k+24|}{5}=\sqrt{2k^2+14k+25}\)
Elevando al cuadrado y resolviendo:
\(\dfrac{49k^2+336k+576}{25}=2k^2+14k+25 → 49k^2+336k+576=50k^2+350k+625\)
Obtenemos:
\(-k^2-14k-49=0 → k^2+14k+49=0 → (k+7)^2=0 → k=-7\)
Entonces \(h=0.\) El centro es \((0,-7).\) Calculamos el radio:
\(r=\sqrt{(0-4)^2+(-7+4)^2}=5\)
La ecuación canónica es:
\(x^2+(y+7)^2=25\)
Determinar elementos de una circunferencia a partir de su ecuación
A partir de las siguientes ecuaciones de circunferencias determinar su centro y radio, luego graficarla.
- \(x^2+y^2=25\)
- \(x^2+y^2+6x-4x-12=0\)
- \(x^2+y^2+4x+12y+36=0\)
- \(x^2+y^2-8x-2y+1=0\)
- \(x^2+y^2-10x+4y-7=0\)
- \(x^2+y^2-10x-24y+25=0\)
- \(2x^2+2y^2+12x-2y-3=0\)
- \(3x^2+3y^2-6x+5y=0\)
¿Te está sirviendo este artículo? ¡Por favor, califícalo!
0,0 / 5 — 0 votos
Soluciones
Solución 1
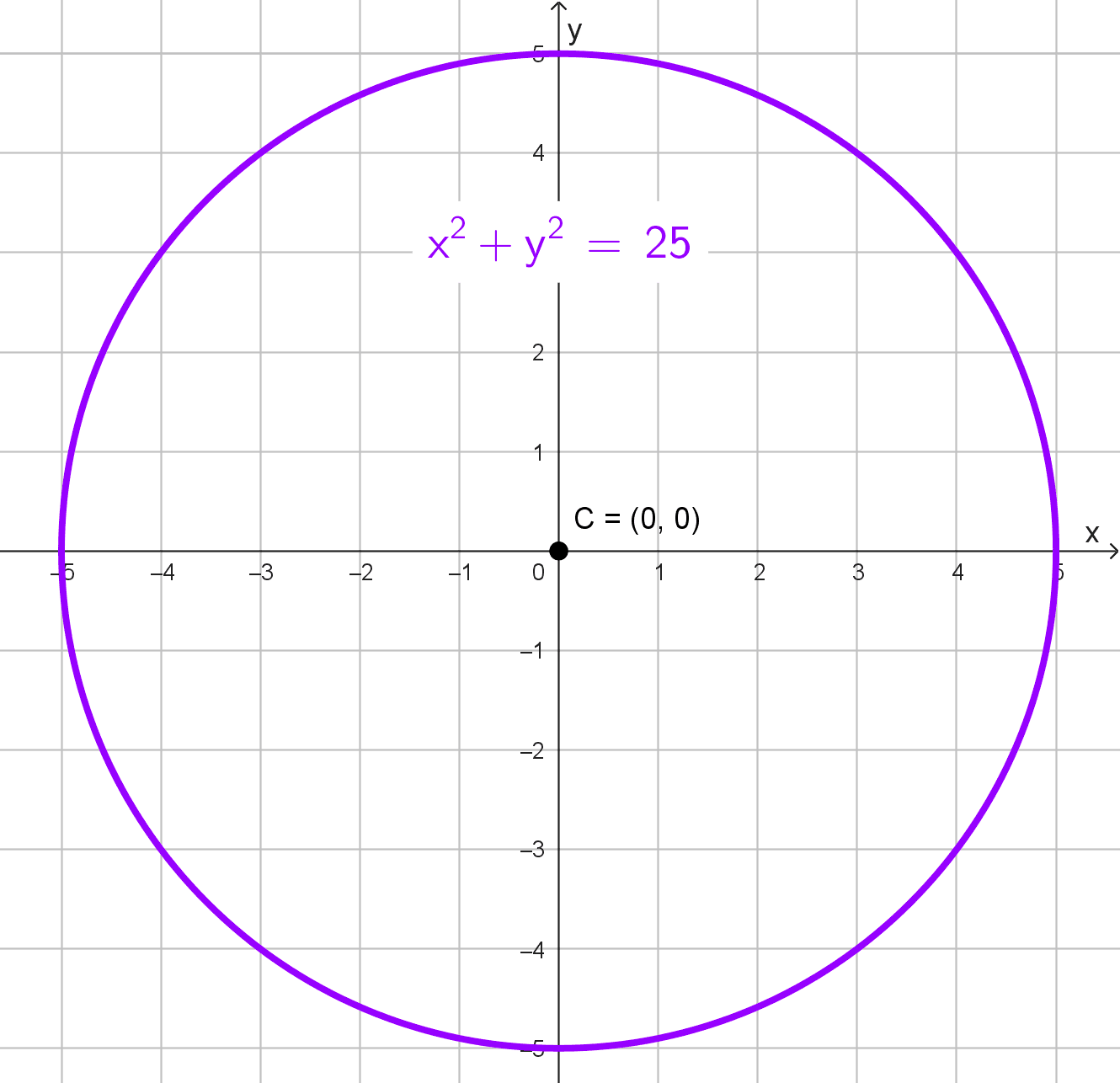
Ecuación dada: \(x^2+y^2=25.\)
Esta ecuación corresponde a la forma estándar de una circunferencia centrada en el origen \((h, k)=(0, 0).\) Comparando con la ecuación general \((x-h)^2+(y-k)^2=r^2,\) deducimos que el radio al cuadrado es \(r^2=25.\) Por lo tanto, el radio es \(r=\sqrt{25}=5.\)
Elementos:
- Centro (0; 0)
- Radio: 5.
Solución 2
Ecuación dada: \(x^2+y^2+6x-4x-12=0\)
Completando los cuadrados (véase los ejercicios de ecuación general a canónica) se obtiene:
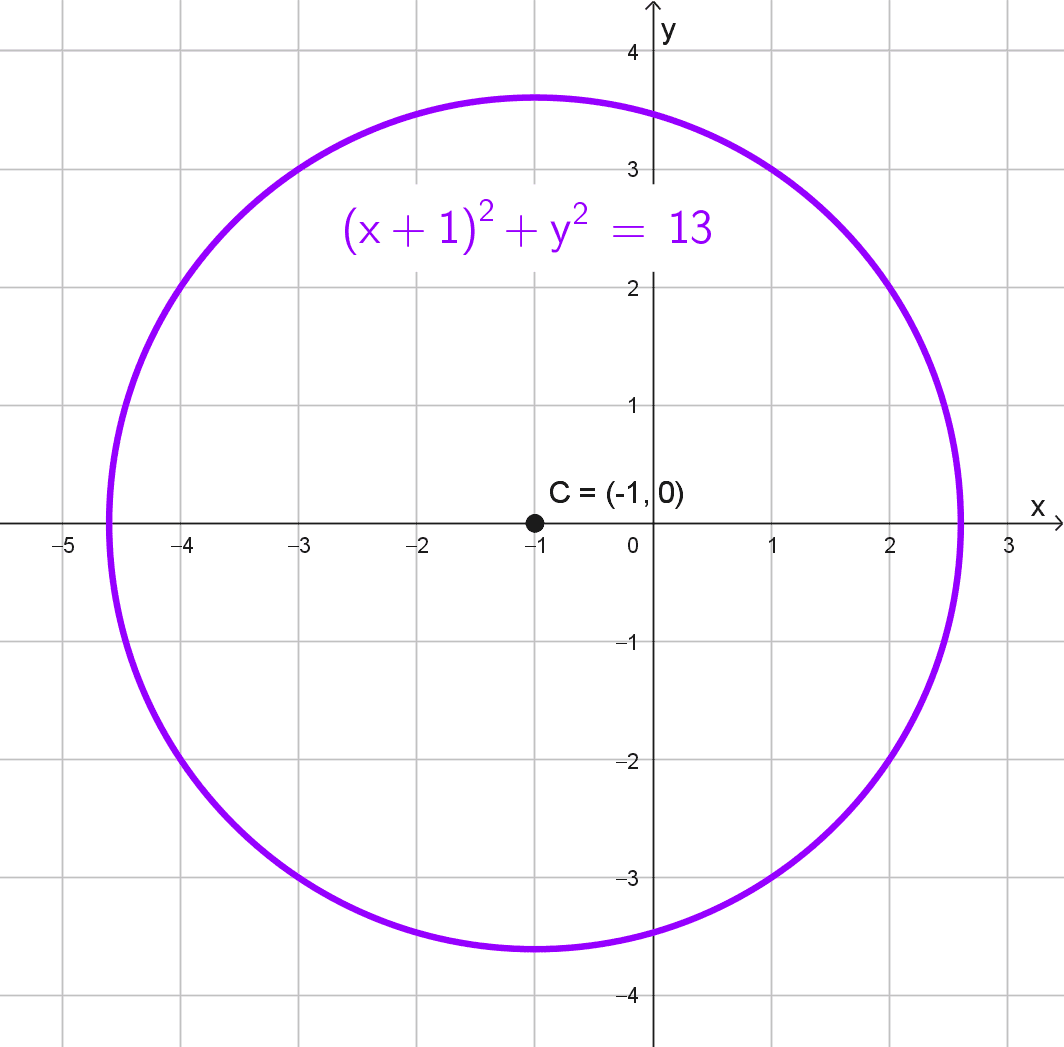
\((x+1)^2+y^2=13\)
Identificamos la ecuación de una circunferencia centrada fuera del origen: \((x-h)^2+(y-k)^2=r^2.\) Reescribimos la ecuación para identificar el centro y el radio. Observamos que \((x+1)^2\) puede expresarse como \((x-(-1))^2,\) lo que indica que la coordenada \(h\) del centro es \(-1.\) La coordenada \(k\) es \(0\) porque no hay término en \(y.\) Así, el centro es \((-1; 0).\) El radio se obtiene de \(r^2=13,\) por lo que \(r=\sqrt{13} ≈ 3,61.\)
Elementos:
- Centro: (-1; 0)
- Radio: \(\sqrt{13}≈ 3,61\)
Solución 3
Solución 4
Solución 5
Solución 6
Solución 7
Solución 8
Determinar si una ecuación representa a una circunferencia
Determine cuáles de las siguientes ecuaciones representan una circunferencia o un punto, o no tienen gráfica.
- \(x^2+y^2-2x+4y+5=0\)
- \(x^2+y^2-6x+2y+36=0\)
- \(x^2+y^2+4x-8y-5=0\)
- \(x^2+y^2+10y=0\)
- \(x^2+y^2-x=0\)
- \(x^2+y^2+8x+15=0\)
- \(x^2+y^2-4x-4y+9=0\)
- \(x^2+y^2+7x+5y+16=0\)
Soluciones
Solución 1
Analizamos la ecuación dada \(x^2+y^2-2x+4y+5=0.\) Completamos cuadrados para los términos en x e y:
Para x:
\(x^2-2x\) se completa como \((x^2-2x+1)-1=(x-1)^2-1\)
Para y:
\(y^2+4y\) se completa como \((y^2+4y+4)-4=(y+2)^2-4\)
Sustituyendo en la ecuación original:
\((x-1)^2-1+(y+2)^2-4+5=0\)
Simplificamos los términos constantes:
\((x-1)^2+(y+2)^2-1-4+5=0 → (x-1)^2+(y+2)^2=0\)
La ecuación resultante \((x-1)^2+(y+2)^2=0\) solo se cumple cuando ambos cuadrados son cero, es decir:
\(x-1=0 \quad \text{y} \quad y+2=0 → x=1, \quad y=-2\)
Por lo tanto, la ecuación representa un único punto en el plano: \((1; -2).\) No corresponde a una circunferencia ni carece de gráfica.
Solución 2
Dada la ecuación \(x^2+y^2-6x+2y+36=0,\) completamos cuadrados:
Para \(x:\)
\(x^2-6x\) se completa como \((x^2-6x+9)-9=(x-3)^2-9\)
Para \(y:\)
\(y^2+2y\) se completa como \((y^2+2y+1)-1=(y+1)^2-1\)
Sustituyendo en la ecuación original:
\((x-3)^2-9+(y+1)^2-1+36=0\)
Simplificamos los términos constantes:
\((x-3)^2+(y+1)^2-9-1+36=0 \rightarrow (x-3)^2+(y+1)^2=-26\)
El lado derecho es negativo, lo cual es imposible para una suma de cuadrados. Por lo tanto, la ecuación no tiene gráfica.
Solución 3
Analizamos la ecuación \(x^2+y^2+4x-8y-5=0.\) Completamos cuadrados:
Para \(x:\)
\(x^2+4x\) se completa como \((x^2+4x+4)-4=(x+2)^2-4\)
Para \(y:\)
\(y^2-8y\) se completa como \((y^2-8y+16)-16=(y-4)^2-16\)
Sustituyendo en la ecuación original:
\((x+2)^2-4+(y-4)^2-16-5=0\)
Simplificamos los términos constantes:
\((x+2)^2+(y-4)^2-4-16-5=0 \rightarrow (x+2)^2+(y-4)^2=25\)
La ecuación representa una circunferencia con centro en \((-2; 4)\) y radio \(5.\)
Solución 4
Dada la ecuación \(x^2+y^2+10y=0,\) completamos cuadrados solo para \(y\) (no hay términos lineales en \(x\)):
\(y^2+10y\) se completa como \((y^2+10y+25)-25=(y+5)^2-25\)
Sustituyendo en la ecuación original:
\(x^2+(y+5)^2-25=0 \rightarrow x^2+(y+5)^2=25\)
La ecuación representa una circunferencia con centro en \((0;-5)\) y radio \(5.\)
Solución 5
Analizamos la ecuación \(x^2+y^2-x=0.\) Completamos cuadrados para \(x:\)
\(x^2-x\) se completa como \(\left(x^2-x+\dfrac{1}{4}\right)-\dfrac{1}{4}=\left(x-\dfrac{1}{2}\right)^2-\dfrac{1}{4}\)
Sustituyendo en la ecuación original:
\(\left(x-\dfrac{1}{2}\right)^2-\dfrac{1}{4}+y^2=0 \rightarrow \left(x-\dfrac{1}{2}\right)^2+y^2=\dfrac{1}{4}\)
La ecuación representa una circunferencia con centro en \(\left(\dfrac{1}{2}; 0\right)\) y radio \(\dfrac{1}{2}.\)
Solución 6
Dada la ecuación \(x^2+y^2+8x+15=0,\) completamos cuadrados para \(x:\)
\(x^2+8x\) se completa como \((x^2+8x+16)-16=(x+4)^2-16\)
Sustituyendo en la ecuación original:
\((x+4)^2-16+y^2+15=0 \rightarrow (x+4)^2+y^2=1\)
La ecuación representa una circunferencia con centro en \((-4; 0)\) y radio \(1.\)
Solución 7
Analizamos la ecuación \(x^2+y^2-4x-4y+9=0.\) Completamos cuadrados:
Para \(x:\)
\(x^2-4x\) se completa como \((x^2-4x+4)-4=(x-2)^2-4\)
Para \(y:\)
\(y^2-4y\) se completa como \((y^2-4y+4)-4=(y-2)^2-4\)
Sustituyendo en la ecuación original:
\((x-2)^2-4+(y-2)^2-4+9=0 \rightarrow (x-2)^2+(y-2)^2=-1\)
El lado derecho es negativo, por lo tanto, la ecuación no tiene gráfica.
Solución 8
Dada la ecuación \(x^2+y^2+7x+5y+16=0,\) completamos cuadrados:
Para \(x:\)
\(x^2+7x\) se completa como \(\left(x^2+7x+\dfrac{49}{4}\right)-\dfrac{49}{4}=\left(x+\dfrac{7}{2}\right)^2-\dfrac{49}{4}\)
Para \(y:\)
\(y^2+5y\) se completa como \(\left(y^2+5y+\dfrac{25}{4}\right)-\dfrac{25}{4}=\left(y+\dfrac{5}{2}\right)^2-\dfrac{25}{4}\)
Sustituyendo en la ecuación original:
\(\left(x+\dfrac{7}{2}\right)^2-\dfrac{49}{4}+\left(y+\dfrac{5}{2}\right)^2-\dfrac{25}{4}+16=0\)
Simplificamos los términos constantes:
\(\left(x+\dfrac{7}{2}\right)^2+\left(y+\dfrac{5}{2}\right)^2-\dfrac{49}{4}-\dfrac{25}{4}+16=0 \rightarrow \left(x+\dfrac{7}{2}\right)^2+\left(y+\dfrac{5}{2}\right)^2=\dfrac{5}{2}\)
La ecuación representa una circunferencia con centro en \(\left(-\dfrac{7}{2};-\dfrac{5}{2}\right)\) y radio \(\sqrt{\dfrac{5}{2}}.\)
Ecuación general a canónica
Dadas las siguientes ecuaciones generales de circunferencias, obtener su forma canónica u ordinaria.
- \(x^2+y^2+6x-4x-12=0\)
- \(x^2+y^2+4x+12y+36=0\)
- \(x^2+y^2-8x-2y+1=0\)
- \(x^2+y^2-10x+4y-7=0\)
- \(x^2+y^2-10x-24y+25=0\)
- \(x^2+y^2+4x+12y+3=0\)
- \(x^2+y^2-3x-4y=0\)
- \(2x^2+2y^2+12x-2y-3=0\)
- \(3x^2+3y^2-6x+5y=0\)
Soluciones
Solución 1
Partimos de la ecuación general:
\(x^2+y^2+6x-4x-12=0\)
Observamos que hay dos términos en \(x\) (\(6x\) y \(-4x\)), así que los combinamos:
\(x^2+y^2+(6x-4x)-12=0\)
\(x^2+y^2+2x-12=0\)
Movemos el término independiente al otro lado y agrupamos términos con x:
\((x^2+2x)+y^2=12\)
Queremos expresar \(x^2+2x\) como un binomio cuadrado perfecto. Para ello, tomamos el coeficiente de \(x\) (que es \(2\)) y lo dividimos entre \(2:\)
\(\dfrac{2}{2}=1\)
Elevamos este resultado al cuadrado:
\(1^2=1\)
Sumamos y restamos este valor dentro del paréntesis (para mantener la igualdad):
\((x^2+2x+1-1)+y^2=12\)
Dejamos solo el valor positivo y pasamos el otro al segundo miembro:
\((x^2+2x+1)+y^2=12+1\)
\((x+1)^2+y^2=13\)
Finalmente, la forma canónica es \((x+1)^2+y^2=13\)
Solución 2
Primeramente analizamos la ecuación \(x^2+y^2+4x+12y+36=0\) y reorganizamos los términos para agrupar las variables \(x\) y \(y,\) trasladando el término independiente al otro lado de la igualdad:
\((x^2+4x)+(y^2+12y)=-36\)
Para completar el cuadrado en x, tomamos el coeficiente lineal 4, lo dividimos entre 2 obteniendo 2, y luego elevamos al cuadrado, lo que nos da 4. Este valor se suma y resta dentro del paréntesis para mantener el equilibrio de la ecuación, quedando:
\((x^2+4x+4-4)+(y^2+12y)=-36\)
De manera similar, para el término en y, el coeficiente 12 se divide entre 2 resultando 6, y al elevarlo al cuadrado obtenemos 36. Sumamos y restamos este valor dentro del segundo paréntesis:
\((x^2+4x+4-4)+(y^2+12y+36-36)=-36\)
Dejamos solo los términos positivos dentro de los paréntesis y el otro lo pasamos al segundo miembro. Los cuadrados perfectos quedan evidentes y los términos independientes se combinan con el lado derecho:
\((x^2+4x+4)+(y^2+12y+36)=-36+4+36\)
Finalmente, expresamos los trinomios como binomios al cuadrado y simplificamos el término derecho:
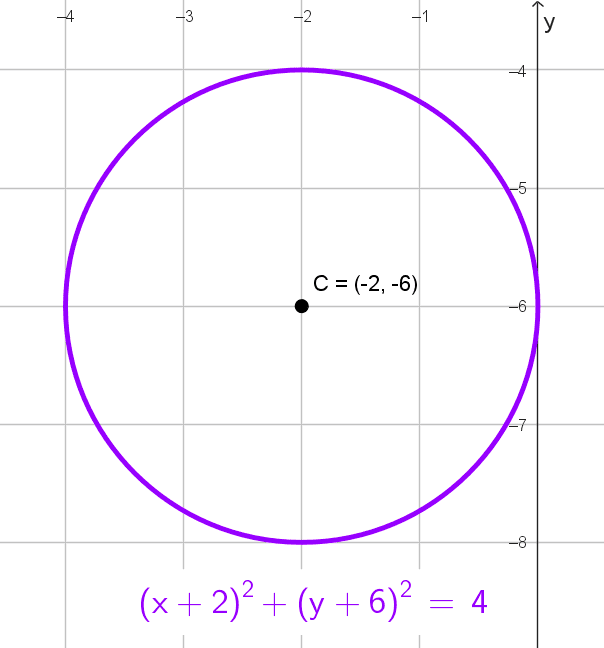
\((x+2)^2+(y+6)^2=4\)
Por lo tanto, la forma ordinaria es \((x+2)^2+(y+6)^2=4.\)
Solución 3
Para \(x^2+y^2-8x-2y+1=0,\) agrupamos:
\((x^2-8x)+(y^2-2y)=-1\)
Completamos cuadrados:
\((x^2-8x+16)+(y^2-2y+1)=-1+16+1\)
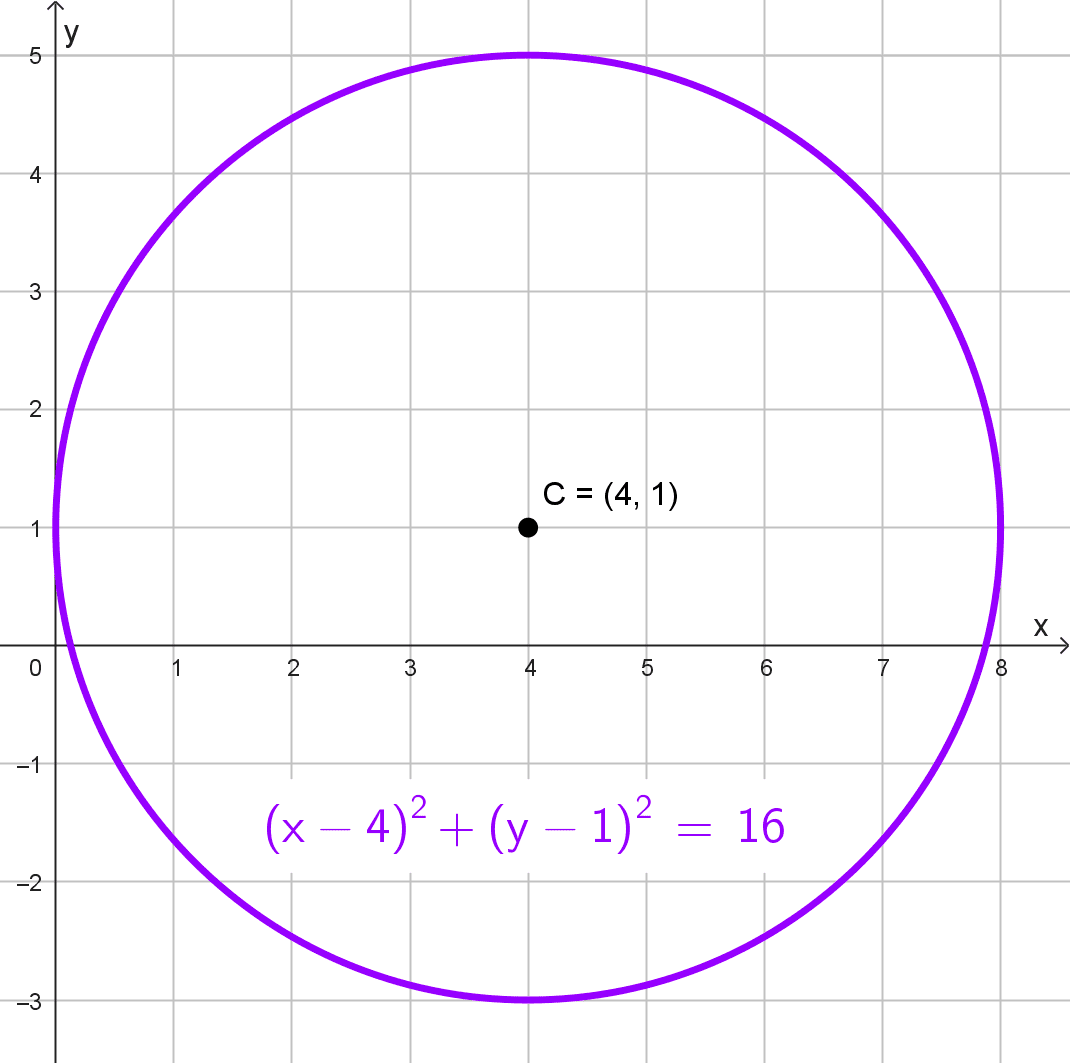
\((x-4)^2+(y-1)^2=16\)
La ecuación canónica es \((x-4)^2+(y-1)^2=16.\)
Solución 4
Partimos de \(x^2+y^2-10x+4y-7=0\) y agrupamos:
\((x^2-10x)+(y^2+4y)=7\)
Completamos cuadrados:
\((x^2-10x+25)+(y^2+4y+4)=7+25+4\)
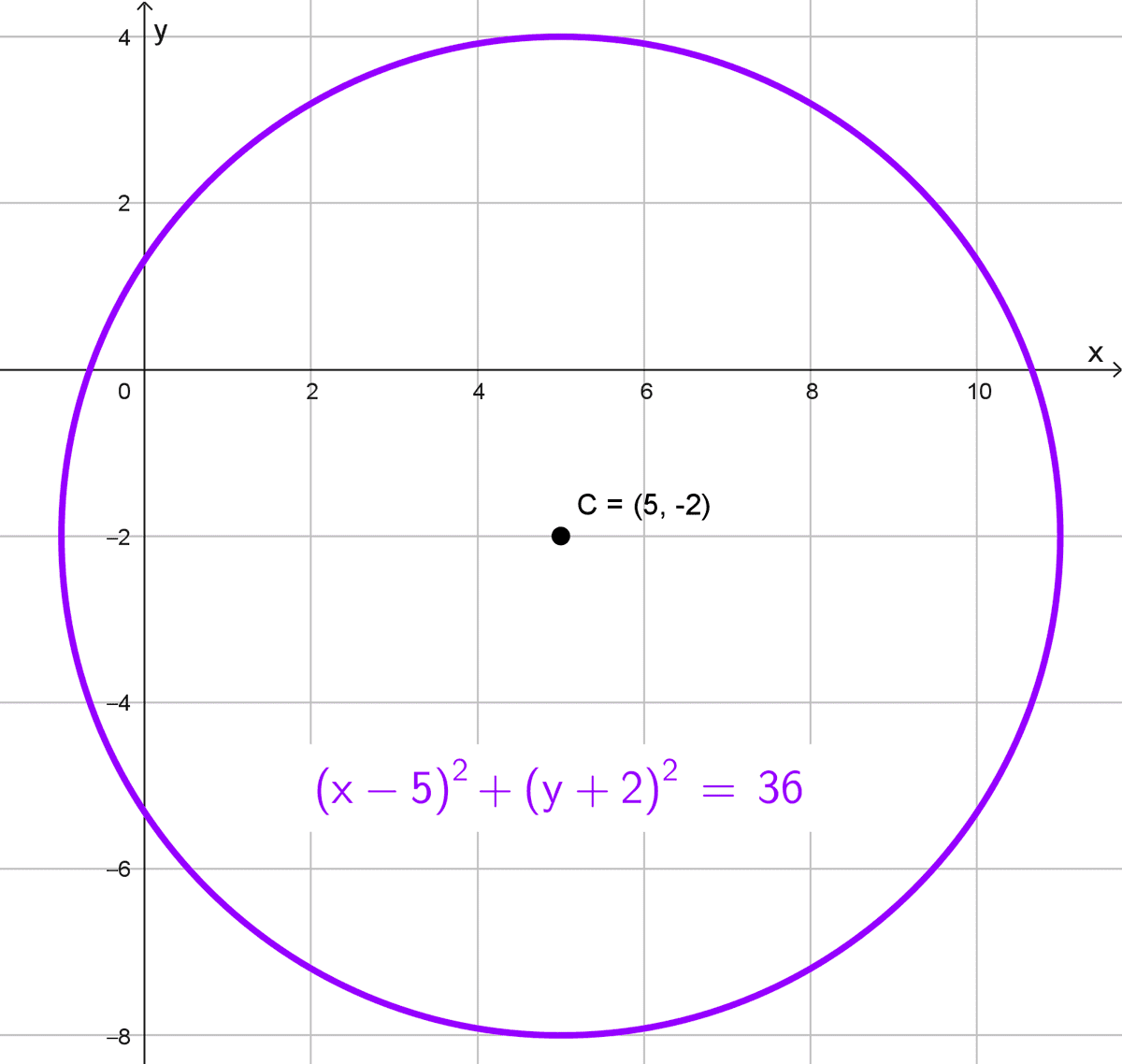
\((x-5)^2+(y+2)^2=36\)
La ecuación ordinaria es \((x-5)^2+(y+2)^2=36.\)
Solución 5
Dada \(x^2+y^2-10x-24y+25=0,\) agrupamos:
\((x^2-10x)+(y^2-24y)=-25\)
Completamos cuadrados:
\((x^2-10x+25)+(y^2-24y+144)=-25+25+144\)
\((x-5)^2+(y-12)^2=144\)
La forma reducida es \((x-5)^2+(y-12)^2=144.\)
Solución 6
Para \(x^2+y^2+4x+12y+3=0,\) agrupamos:
\((x^2+4x)+(y^2+12y)=-3\)
Completamos cuadrados:
\((x^2+4x+4)+(y^2+12y+36)=-3+4+36\)
\((x+2)^2+(y+6)^2=37\)
La ecuación reducida es \((x+2)^2+(y+6)^2=37.\)
Solución 7
Partimos de \(x^2+y^2-3x-4y=0\) y agrupamos:
\((x^2-3x)+(y^2-4y)=0\)
Completamos cuadrados:
\((x^2-3x+2,25)+(y^2-4y+4)=0+2,25+4\)
\((x-1,5)^2+(y-2)^2=6,25\)
La ecuación canónica es \((x-1,5)^2+(y-2)^2=6,25.\)
Solución 8
Dada \(2x^2+2y^2+12x-2y-3=0,\) dividimos toda la ecuación por 2:
\(x^2+y^2+6x-y=1,5\)
Agrupamos términos:
\((x^2+6x)+(y^2-y)=1,5\)
Completamos cuadrados:
\((x^2+6x+9)+\left(y^2-y+0,25\right)=1,5+9+0,25\)
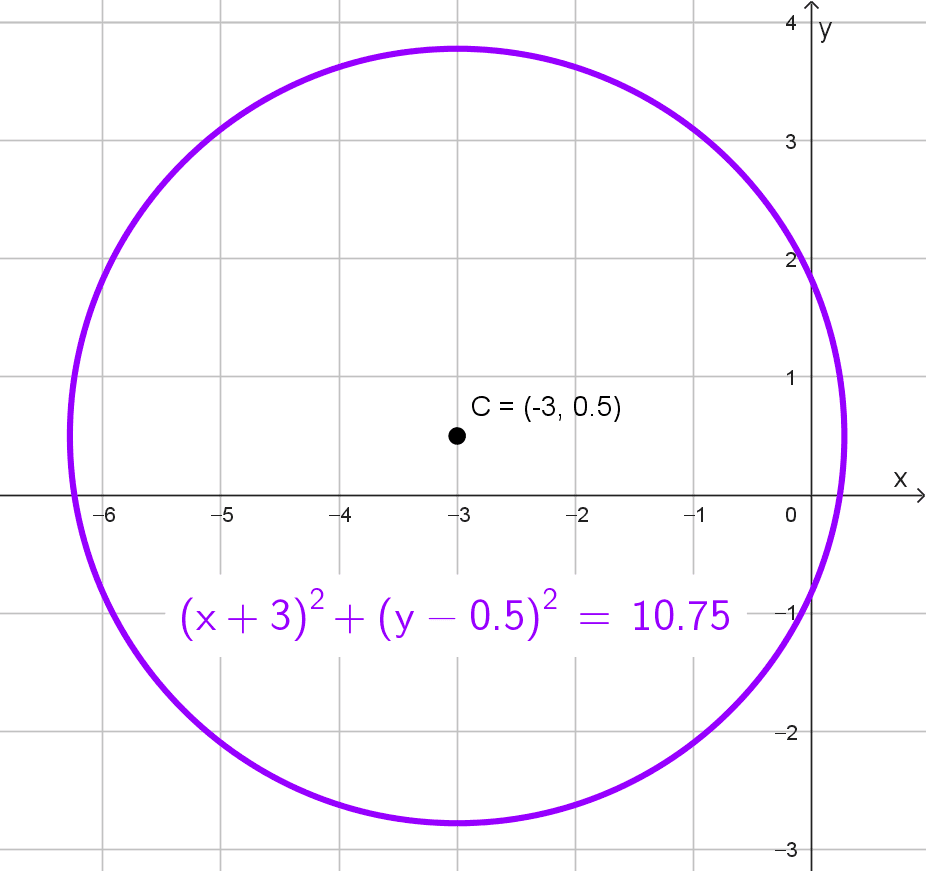
\((x+3)^2+\left(y-0,5\right)^2=10,75\)
La forma ordinaria es \((x+3)^2+\left(y-0,5\right)^2=10,75.\)
Solución 9
Partimos de \(3x^2+3y^2-6x+5y=0\) y dividimos por 3:
\(x^2+y^2-2x+\dfrac{5}{3}y=0\)
Agrupamos términos:
\((x^2-2x)+\left(y^2+\dfrac{5}{3}y\right)=0\)
Completamos cuadrados:
\((x^2-2x+1)+\left(y^2+\dfrac{5}{3}y+\dfrac{25}{36}\right)=0+1+\dfrac{25}{36}\)
\((x-1)^2+\left(y+\dfrac{5}{6}\right)^2=\dfrac{61}{36}\)
La forma reducida es \((x-1)^2+\left(y+\dfrac{5}{6}\right)^2=\dfrac{61}{36}.\)
Ecuación canónica a general
A partir de las siguientes ecuaciones canónicas de circunferencias, encuentre su forma general.
- \((x-3)^2+(y+2)^2=9\)
- \((x+1)^2+y^2=\dfrac{25}{4}\)
- \((x-4)^2+(y+3)^2=\dfrac{1}{9}\)
Soluciones
Solución 1
Partimos de la ecuación canónica \((x-3)^2+(y+2)^2=9.\) Desarrollamos los cuadrados de los binomios:
\(x^2-6x+9+y^2+4y+4=9\)
Agrupamos los términos y trasladamos la constante al primer miembro:
\(x^2+y^2-6x+4y+13-9=0\)
Simplificamos para obtener la forma general:
\(x^2+y^2-6x+4y+4=0\)
Solución 2
La ecuación canónica dada es \((x+1)^2+y^2=\dfrac{25}{4}.\) Desarrollamos el cuadrado del primer binomio:
\(x^2+2x+1+y^2=\dfrac{25}{4}\)
Multiplicamos toda la ecuación por 4 para eliminar el denominador:
\(4x^2+8x+4+4y^2=25\)
Reorganizamos los términos y simplificamos:
\(4x^2+4y^2+8x-21=0\)
La última ecuación es válida, pero podemos dividir entre 4 para normalizar:
\(x^2+y^2+2x-\dfrac{21}{4}=0\)
Solución 3
Comenzamos con la ecuación \((x-4)^2+(y+3)^2=\dfrac{1}{9}.\) Desarrollamos los cuadrados:
\(x^2-8x+16+y^2+6y+9=\dfrac{1}{9}\)
Multiplicamos por 9 para eliminar la fracción:
\(9x^2-72x+144+9y^2+54y+81=1\)
Agrupamos y simplificamos:
\(9x^2+9y^2-72x+54y+224=0\)
Dividimos entre 9 para obtener la forma general normalizada:
\(x^2+y^2-8x+6y+\dfrac{224}{9}=0\)
Calcular área y perímetro
Hallar la longitud (perímetro) y el área encerrada por las siguientes circunferencias.
- \(x^2+y^2=25\)
- \(x^2+y^2+6x-4x-12=0\)
- \(x^2+y^2+4x+12y+36=0\)
- \(x^2+y^2-8x-2y+1=0\)
- \(x^2+y^2-10x+4y-7=0\)
Soluciones
Solución 1
Partimos de la ecuación dada de la circunferencia: \(x^2+y^2=25.\) Esta ecuación está en la forma estándar \(x^2+y^2=r^2,\) donde \(r\) es el radio. Al comparar ambas expresiones, identificamos que \(r^2=25,\) por lo que el radio es \(r=\sqrt{25}=5.\)
Para calcular la longitud (perímetro) de la circunferencia, usamos la fórmula \(L=2\pi r.\) Sustituyendo el valor del radio, obtenemos:
\(L=2\pi \cdot 5=10\pi \text{ unidades.}\)
El área encerrada por la circunferencia se determina con la fórmula \(A=\pi r^2.\) Reemplazando el radio:
\(A=\pi \cdot 5^2=25\pi \text{ unidades cuadradas.}\)
Así, la longitud es \(10\pi\) y el área es \(25\pi.\)
Solución 2
La ecuación dada es \(x^2+y^2+6x-4x-12=0.\) Si completamos los cuadrados (véase los ejercicios de ecuación general a canónica) obtenemos:
\((x+1)^2+y^2=13\)
Esta corresponde a la forma estándar \((x-h)^2+(y-k)^2=r^2,\) donde \((h, k)\) es el centro y \(r\) el radio. Identificamos que \(h=-1\), \(k=0\) y \(r^2=13,\) por lo que el radio es \(r=\sqrt{13}.\)
Calculamos la longitud de la circunferencia:
\(L=2\pi \cdot \sqrt{13}=2\sqrt{13}\pi \text{ unidades.}\)
El área del círculo se obtiene con:
\(A=\pi \cdot (\sqrt{13})^2=13\pi \text{ unidades cuadradas.}\)
Por lo tanto, la longitud es \(2\sqrt{13}\pi\) y el área es \(13\pi.\)
Solución 3
La ecuación es \(x^2+y^2+4x+12y+36=0,\) completando los cuadrados obtenemos:
\((x+2)^2+(y+6)^2=4\)
Identificamos el centro en \((-2;-6)\) y \(r^2=4,\) por lo que el radio es \(r=2.\)
El perímetro de la circunferencia es:
\(L=2\pi \cdot 2=4\pi \text{ unidades.}\)
El área del círculo es:
\(A=\pi \cdot 2^2=4\pi \text{ unidades cuadradas.}\)
La longitud es \(4\pi\) y el área es \(4\pi.\)
Solución 4
Dada la ecuación \(x^2+y^2-8x-2y+1=0,\) completamos cuadrados para obtener:
\((x-4)^2+(y-1)^2=16\)
Reconocemos el centro en \((4; 1)\) y \(r^2=16,\) lo que implica un radio \(r=4.\)
Calculamos la longitud del perímetro:
\(L=2\pi \cdot 4=8\pi \text{ unidades.}\)
El área del círculo es:
\(A=\pi \cdot 4^2=16\pi \text{ unidades cuadradas.}\)
En conclusión, la longitud es \(8\pi\) y el área es \(16\pi.\)
Solución 5
La ecuación dada es \(x^2+y^2-10x+4y-7=0,\) completando cuadrados obtenemos:
\((x-5)^2+(y+2)^2=36\)
Esta circunferencia tiene centro en \((5;-2)\) y \(r^2=36,\) por lo que el radio es \(r=6.\)
La longitud de la circunferencia es:
\(L=2\pi \cdot 6=12\pi \text{ unidades.}\)
El área encerrada es:
\(A=\pi \cdot 6^2=36\pi \text{ unidades cuadradas.}\)
Por lo tanto, la longitud es \(12\pi\) y el área es \(36\pi.\)
Problemas de la vida real
Los siguientes ejercicios son aplicaciones de la circunferencia a problemas de la vida cotidiana o las ciencias.
Ejercicio 1
Una rueda de bicicleta tiene un diámetro de 70 cm. ¿Cuántos metros recorre en 50 vueltas completas sin patinar?
Solución
Para determinar la distancia recorrida por la rueda en 50 vueltas, primero calculamos la circunferencia de la rueda, que corresponde a la distancia recorrida en una vuelta completa. La fórmula de la circunferencia \(C\) es:
\(C=\pi \times d\)
donde \(d\) es el diámetro. Dado que el diámetro es \(70\,\text{cm},\) sustituimos:
\(C=\pi \times 70\,\text{cm} ≈ 219,91~\text{cm}\)
Ahora, multiplicamos la circunferencia por el número de vueltas (50) para obtener la distancia total en centímetros:
\(\text{Distancia total}=50 \times 219,91\,\text{cm} ≈ 10 995,5~\text{cm}\)
Finalmente, convertimos centímetros a metros dividiendo entre 100:
\(10 995,5~\text{cm}=109,955~\text{m}\)
Por lo tanto, la rueda recorre aproximadamente 109,96 metros en 50 vueltas.
Ejercicio 2
En un evento, cada mesa redonda tiene un diámetro de 1,5 m y se colocan manteles circulares que sobresalen 20 cm por cada lado. ¿Cuál es el área de tela que se necesita para cada mantel?
Solución
Para determinar el área de tela necesaria para cada mantel, comenzamos analizando las dimensiones proporcionadas. El diámetro de la mesa es de 1,5 metros, lo que implica un radio de \(r_{\text{mesa}}=\dfrac{1,5}{2}=0,75\) metros. El mantel sobresale 20 centímetros (equivalentes a 0,2 metros) por cada lado, lo que significa que el radio del mantel será la suma del radio de la mesa y el exceso:
\(r_{\text{mantel}}=r_{\text{mesa}}+0,2=0,75+0,2=0,95 \text{ metros}\)
El área \(A\) de un círculo se calcula mediante la fórmula \(A=\pi r^2.\) Aplicando esto al mantel:
\(A=\pi (0,95)^2=\pi \times 0,9025 ≈ 2,835 \text{ m}^2\)
Por lo tanto, se requieren aproximadamente 2,835 metros cuadrados de tela para cada mantel.
Ejercicio 3
Un cartel publicitario tiene forma circular y un área de 15,7 m². ¿Cuál es el radio del cartel?
Solución
Para hallar el radio del cartel circular, partimos de la fórmula del área de un círculo:
\(A=\pi r^2\)
Donde \(A=15,7 \, \text{m}^2.\) Despejamos el radio \(r:\)
\(r^2=\dfrac{A}{\pi}=\dfrac{15,7}{\pi}\)
Aproximando \(\pi ≈ 3,14,\) calculamos:
\(r^2=\dfrac{15,7}{3,14}=5\)
Finalmente, obtenemos el radio tomando la raíz cuadrada:
\(r=\sqrt{5} ≈ 2,24 ~ \text{m}\)
El radio del cartel es aproximadamente 2,24 metros.
Ejercicio 4
Una tapa de alcantarilla circular tiene un radio de 0,3 m. ¿Qué cantidad de pintura se necesita para pintarla por completo si se le dan dos manos y cada litro cubre 3 m²?
Solución
Primero, calculamos el área de la tapa circular utilizando la fórmula del área de un círculo:
\(A=\pi r^2\)
Donde \(r=0,3 ~ \text{m}.\) Sustituyendo:
\(A=\pi (0,3)^2=\pi \times 0,09 ≈ 0,2827 ~ \text{m}^2\)
Como se aplicarán dos manos de pintura, el área total a cubrir es:
\(A_{\text{total}}=2 \times 0,2827 ≈ 0,5655 ~ \text{m}^2\)
Sabemos que 1 litro de pintura cubre 3 m², por lo que la cantidad de pintura necesaria se obtiene con una regla de tres:
\(\text{Pintura requerida}=\dfrac{0,5655}{3} ≈ 0,1885 ~ \text{litros}\)
Se necesitan aproximadamente 0,19 litros de pintura para cubrir la tapa con dos manos.
Ejercicio 5
Un sistema de riego automático cubre un área circular de 12 m de radio. ¿Qué superficie cubre en total? ¿Cuánto se reduce el área si se disminuye el radio a 10 m?
Solución
Para determinar la superficie cubierta por el sistema de riego, utilizamos la fórmula del área de una circunferencia:
\(A=\pi r^2\)
Donde \(r=12 ~ \text{m}.\) Sustituyendo:
\(A=\pi (12)^2=144\pi ~ \text{m}^2\)
El área total cubierta es \(144\pi ~ \text{m}^2≈314,16~ \text{m}^2 \)
Si el radio se reduce a \(10 ~ \text{m},\) calculamos la nueva área:
\(A'=\pi (10)^2=100\pi ~ \text{m}^2\)
La reducción del área se obtiene restando ambas áreas:
\(\Delta A=144\pi-100\pi=44\pi ~ \text{m}^2\)
Por lo tanto, el área se reduce en \(44\pi ~ \text{m}^2≈138,23 ~ \text{m}^2\)
Respuestas:
- Superficie total con \(r=12 ~ \text{m}:\) \(144\pi ~ \text{m}^2≈314,16~ \text{m}^2 \)
- Reducción al disminuir a \(r=10 ~ \text{m}:\) \(44\pi ~ \text{m}^2≈138,23 ~ \text{m}^2\)
Ejercicio 6
Una plaza tiene una fuente circular en el centro y un camino también circular rodeándola. Si el diámetro de la fuente es de 6 m y el del camino externo es de 12 m, ¿cuál es el área disponible para caminar?
Solución
Tenemos dos circunferencias concéntricas: la fuente y el camino. La fuente tiene un diámetro de 6 m, por lo que su radio r es la mitad, es decir, \(r=3\) m. El camino externo tiene un diámetro de 12 m, así que su radio R es \(R=6\) m.
El área disponible para caminar corresponde a la región anular entre las dos circunferencias. Calculamos esta área restando el área de la fuente del área del camino:
\(\text{Área del camino}=\pi R^2-\pi r^2=\pi (R^2-r^2)\)
Sustituyendo los valores conocidos:
\(\text{Área del camino}=\pi (6^2-3^2)=\pi (36-9)=27\pi ~ \text{m}^2≈84,82 ~ \text{m}^2\)
Por lo tanto, el área disponible para caminar es \(27\pi≈84,82\) metros cuadrados.
Ejercicio 7
Una antena de telefonía celular tiene un alcance circular de 10 km. Si dos antenas están separadas por 15 km, ¿habrá alguna zona entre ellas donde no haya cobertura de ninguna de las dos?
Solución
La cobertura de cada antena puede modelarse como una circunferencia con radio \(r=10\) km. La condición que interesa es si las regiones cubiertas por ambas antenas se solapan por completo, parcialmente o si quedan zonas sin cubrir.
Coloquemos una antena en el punto \(A(0; 0).\) Su área de cobertura está dada por la circunferencia:
\(x^2+y^2=100\)
Ubicamos la segunda antena en el punto \(B(15; 0),\) ya que están separadas por 15 km en línea recta. Su cobertura está definida por:
\((x-15)^2+y^2=100\)
Para saber si existe una zona sin cobertura entre ambas, debemos analizar si las circunferencias se intersectan. Dos circunferencias de igual radio \(r\) se intersectan si la distancia entre sus centros \(d\) es menor que \(2r,\) se tocan externamente si \(d=2r,\) y no se tocan si \(d>2r.\)
En este caso, la distancia entre los centros es de 15 km y el doble del radio es \(2 \times 10=20\) km. Como \(15<20,\) las circunferencias se intersectan, por lo tanto, hay una zona entre ambas antenas que está cubierta por ambas señales.
Dado que su cobertura se superpone, no existe ninguna región entre ambas antenas que quede sin cobertura. Cada punto entre ellas está al menos a 7,5 km de una de las antenas, y como su alcance es de 10 km, todos esos puntos están dentro del rango de alguna de las dos.
Por lo tanto, no hay ninguna zona entre ellas sin cobertura.
Ejercicio 8
Un satélite de comunicaciones orbita la Tierra a una altura constante de 600 km sobre la superficie. Si el radio de la Tierra es aproximadamente 6378 km, ¿cuál es la longitud de la órbita del satélite en un día?
Solución
La órbita del satélite puede considerarse circular, con un radio igual a la suma del radio terrestre y la altura a la que se encuentra el satélite. Dado que la Tierra tiene un radio de aproximadamente 6378 km, y el satélite está a una altura de 600 km, el radio de la órbita es:
\(r=6378+600=6978 \text{ km}\)
La longitud de una circunferencia se calcula con la fórmula:
\(L=2\pi r\)
Sustituyendo el valor del radio:
\(L=2\pi \cdot 6978\)
\(L ≈ 2 \cdot 3,1416 \cdot 6978 ≈ 43844,1 \text{ km}\)
Por lo tanto, la longitud de la órbita del satélite en un día es de aproximadamente 43844,1 km.
Bibliografía
- Engler, A., Müller, D., Vrancken, S. y Hecklein, M. (2020). Geometría analítica. Universidad Nacional del Litoral.
- Fuller, G. y Tarwater, D. (1995). Geometría analítica (7.ª ed.). Pearson Educación.
- Lehmann, C. (1989). Geometría analítica. Limusa.
- Leithold. L. (1992). Álgebra y trigonometría con geometría analítica. Oxford University Press.
- Márquez, A., Vázquez, F., Ruiz, H., Villegas, M. y Figueroa, M. (2009). Geometría analítica. Prentice Hall.
- Raichman, S. y Totter, E. (2016). Geometría analítica para ciencias e ingeniería. Universidad Nacional de Cuyo.
- Sullivan, M. (2006). Álgebra y trigonometría. Pearson Educación.
- Swokowski, E. y Cole, J. (2009). Álgebra y trigonometría con geometría analítica. Cengage Learning.
¿Te ha servido este contenido? ¡Califícalo!
0,0 / 5 — 0 votos
CÓMO CITAR ESTE ARTÍCULO
Machado, D. (2025, 26 de junio). Ejercicios de circunferencia. Exponty. https://exponty.com/ejercicios-circunferencia
Deja una respuesta

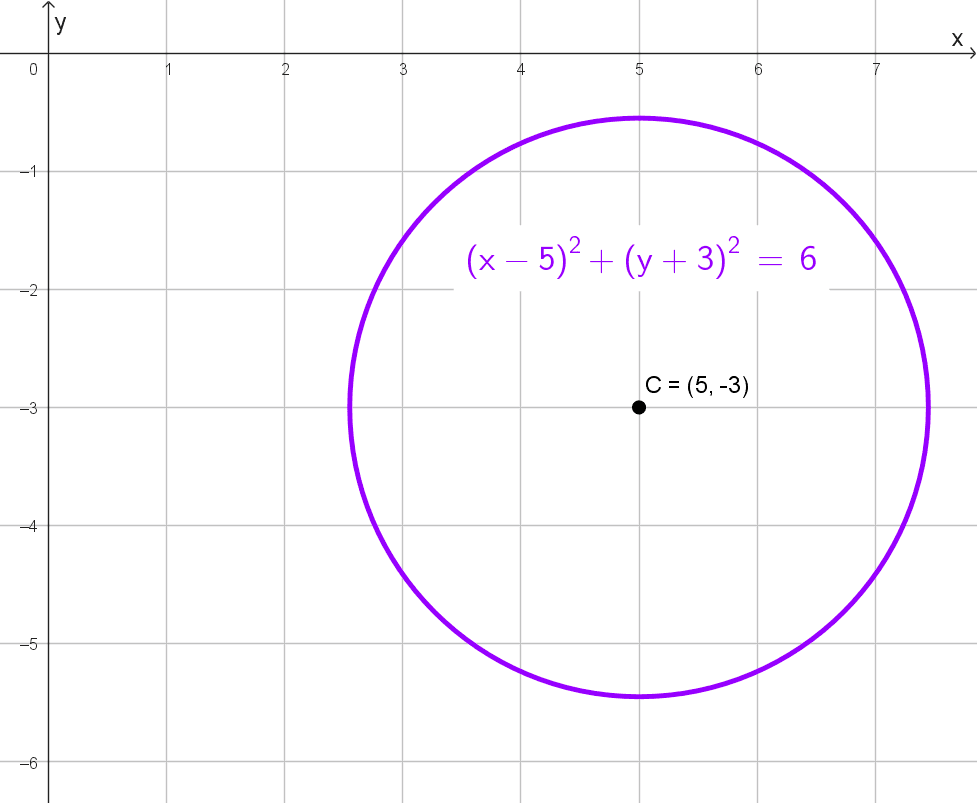
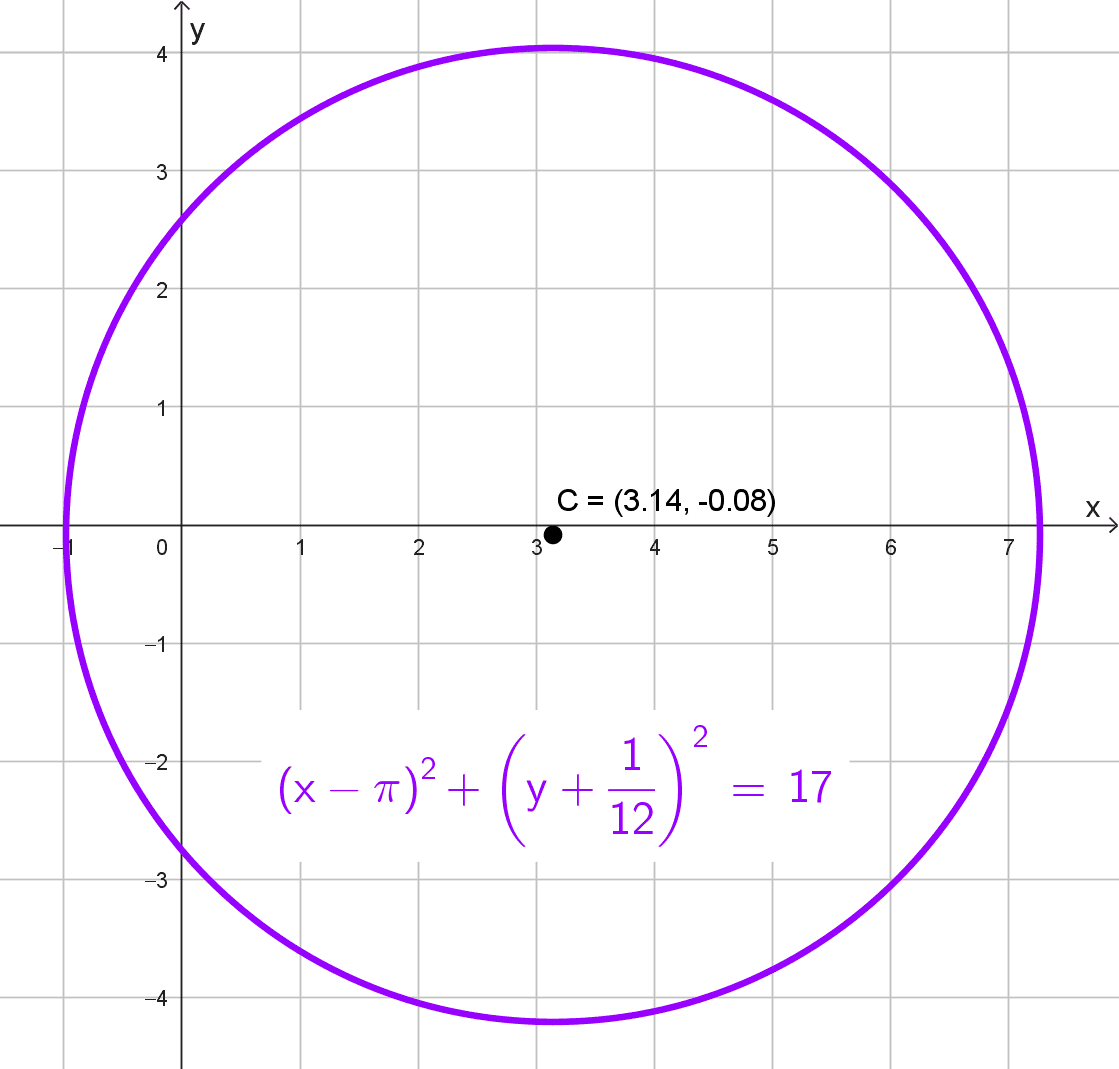
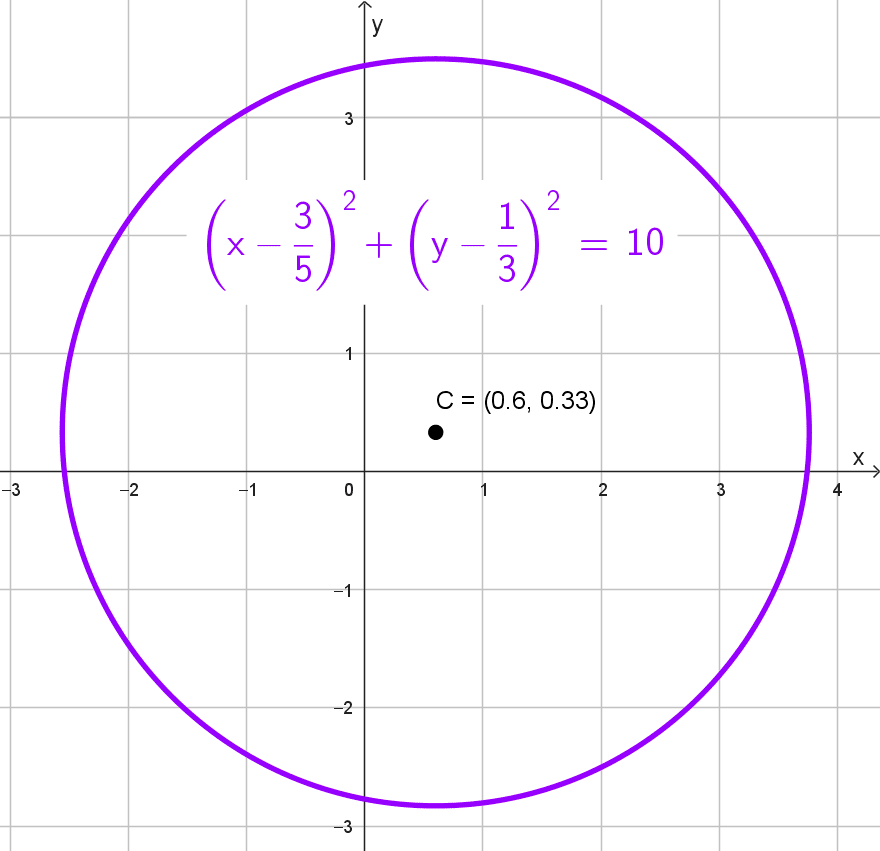
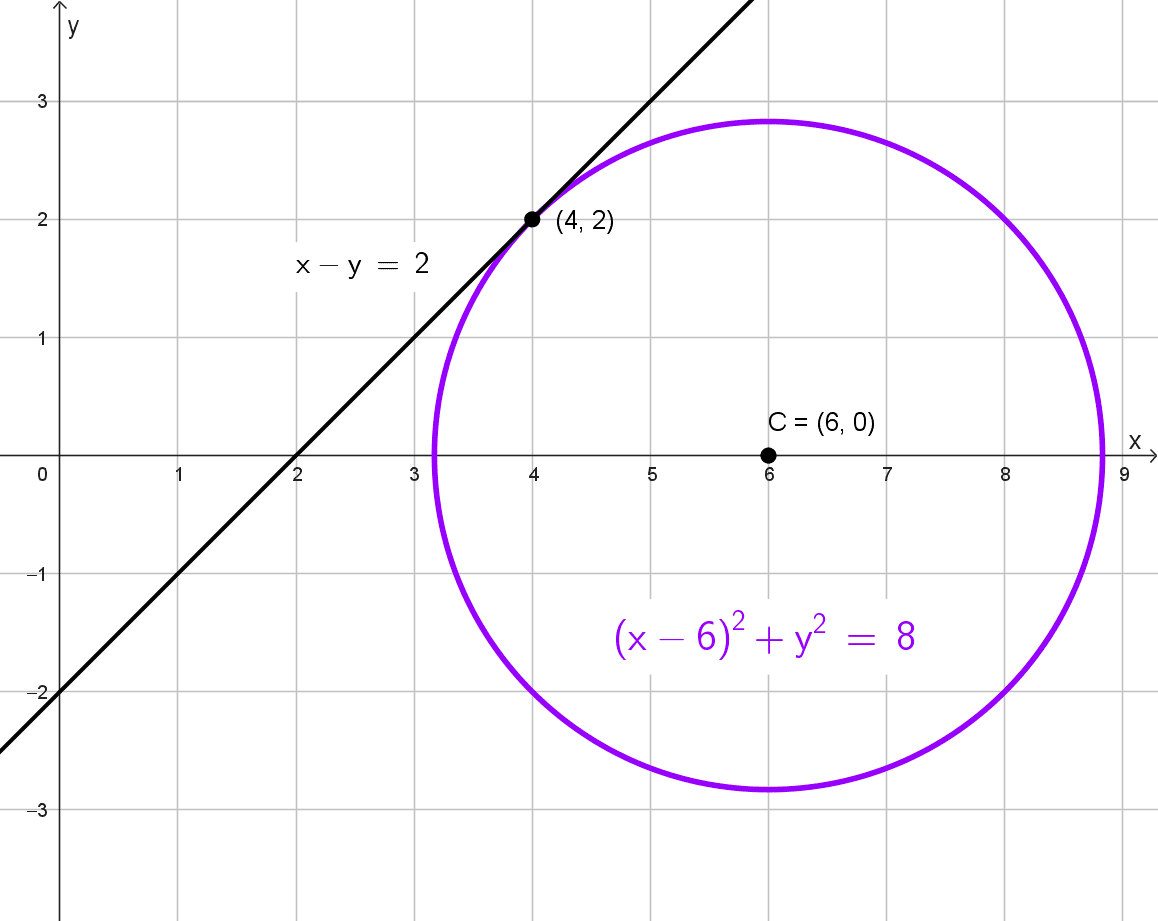
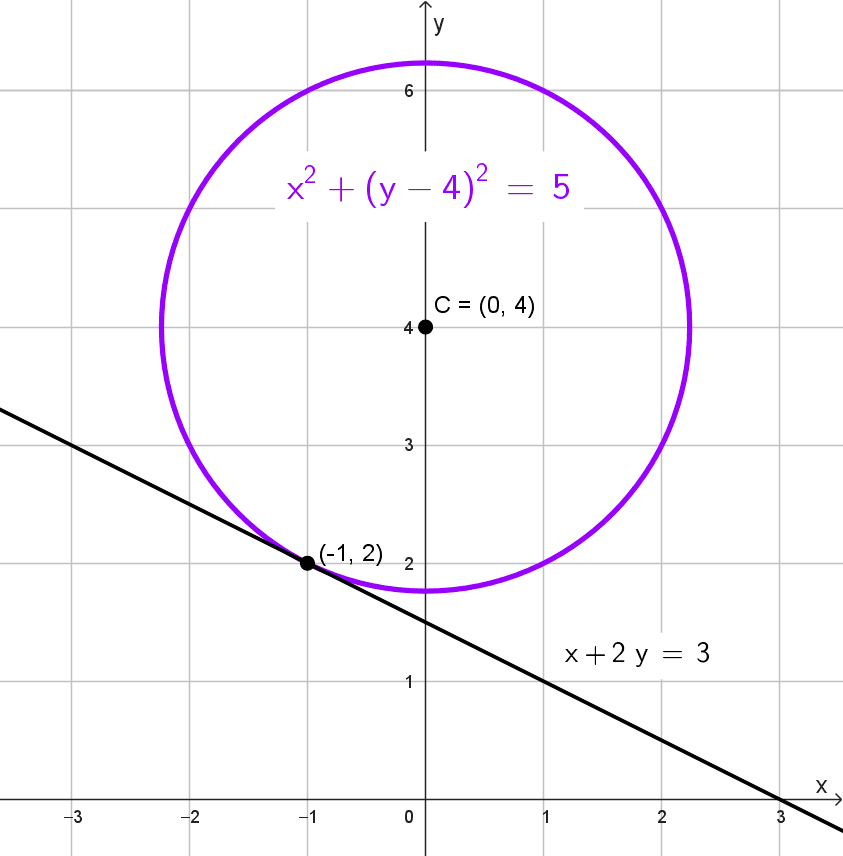
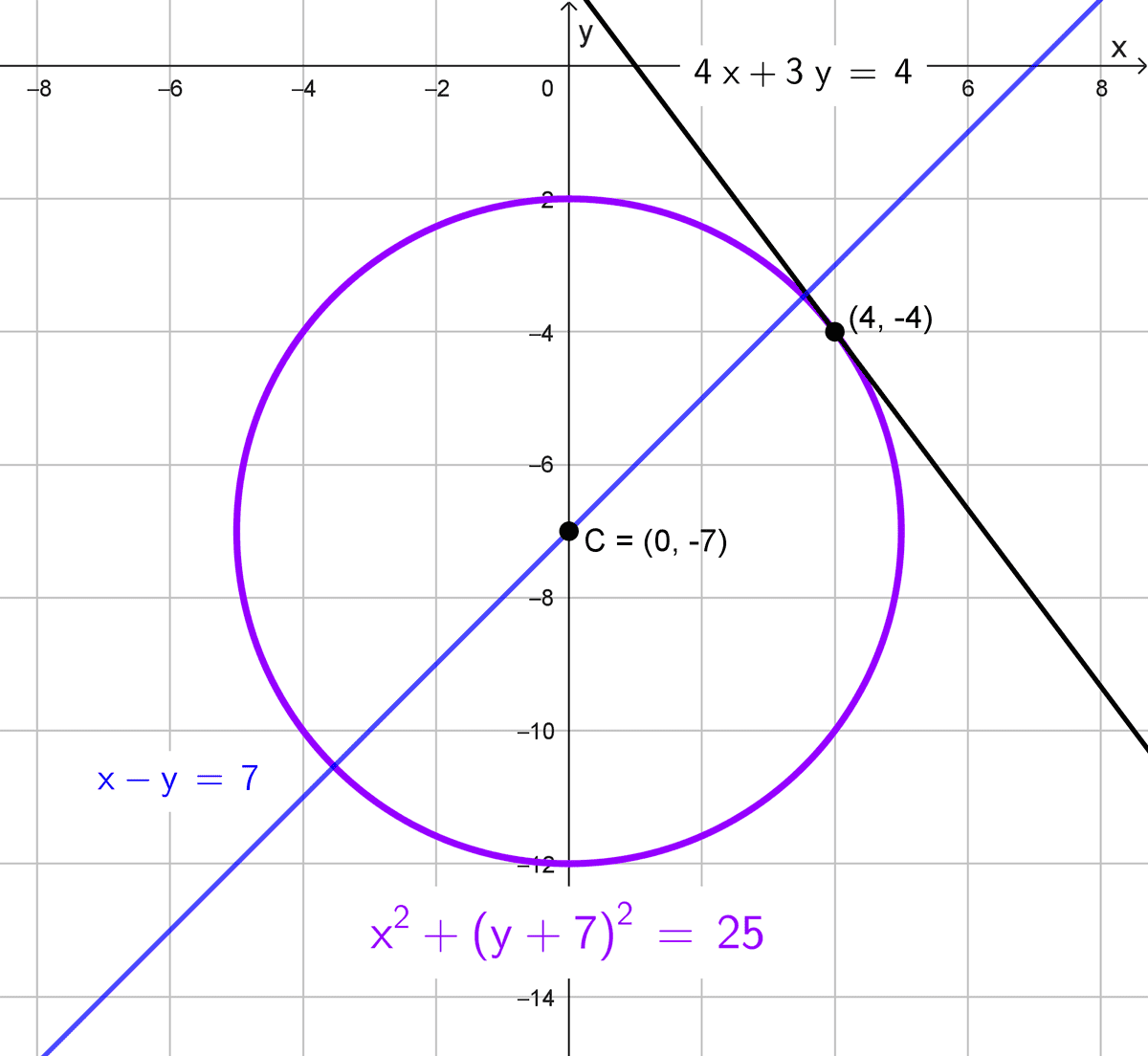
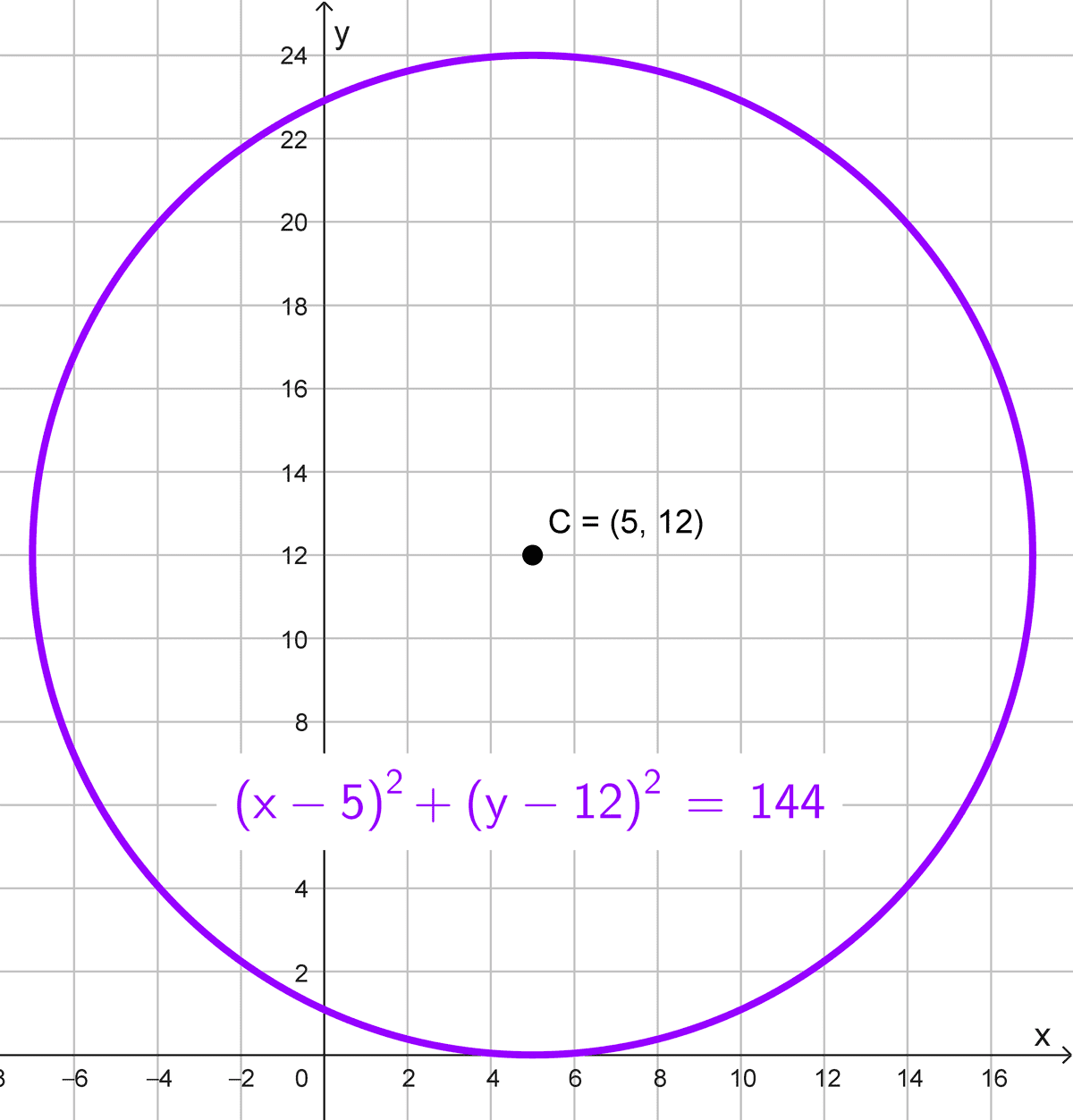
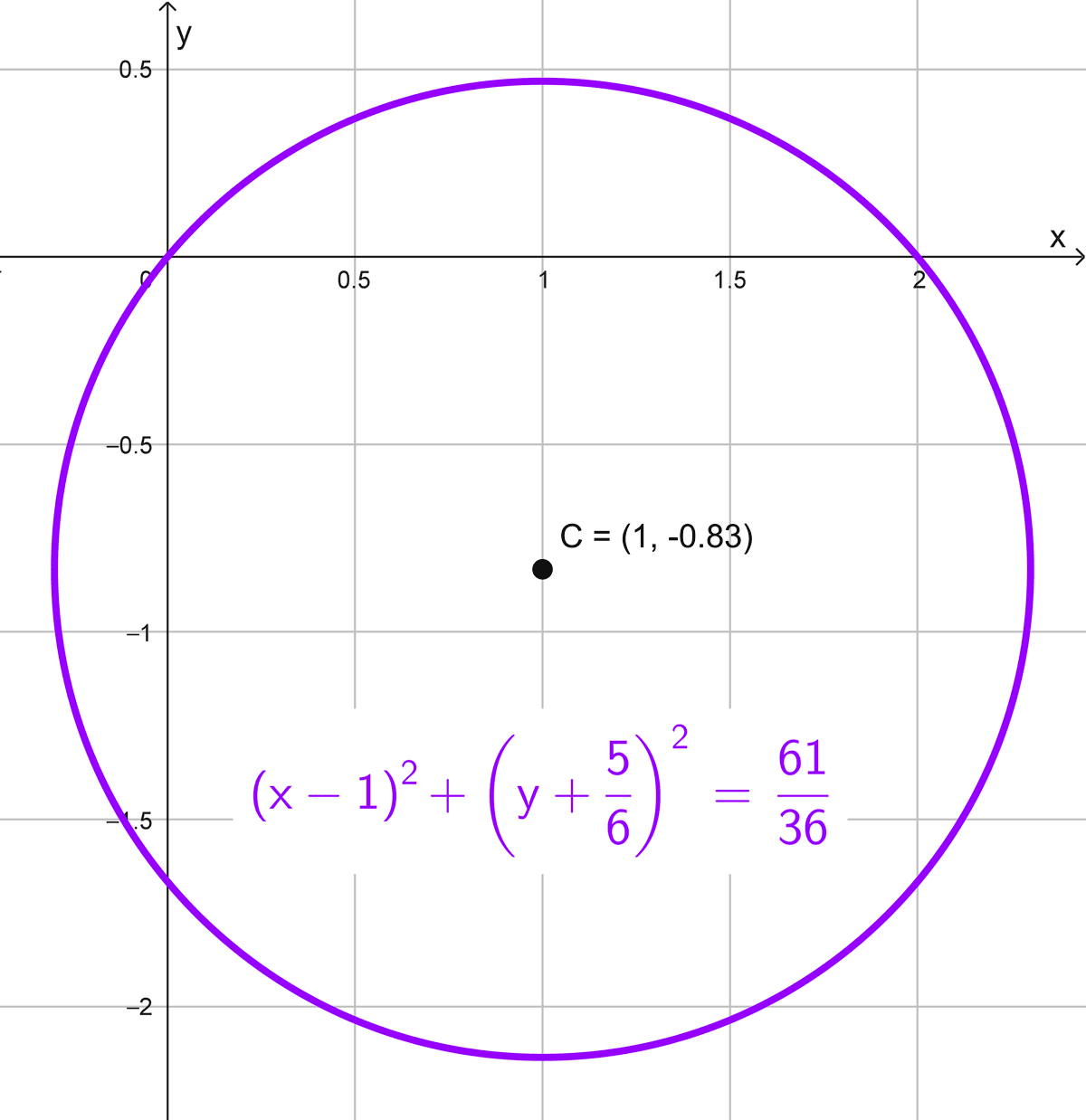
Otros artículos que pueden interesarte