Focos de una elipse

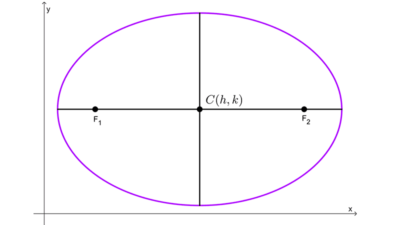
Los focos de una elipse son dos puntos fijos del plano que están sobre el eje mayor. La característica fundamental de una elipse es que la suma de las distancias desde cualquier punto de la elipse a estos focos es constante. El punto medio entre los focos es el centro de la elipse.

A continuación, veremos cómo calcular los focos de una elipse a partir de su ecuación con ejercicios resueltos paso a paso.

¿Cómo encontrar los focos?

Es posible obtener las coordenadas de los focos si se tiene la ecuación canónica de la elipse. Esta es aquella donde aparecen la suma de dos términos cuadráticos con x e y igualados a 1, es decir, de las siguientes formas:

Ecuación	Características
*\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1* *\dfrac{y^2}{a^2}+\dfrac{x^2}{b^2}=1*	El centro es el origen de coordenadas (0, 0). a es el semieje mayor. b es el semieje menor.
*\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1* *\dfrac{(y-k)^2}{a^2}+\dfrac{(x-h)^2}{b^2}=1*	El centro es el punto (h, k). a es el semieje mayor. b es el semieje menor.

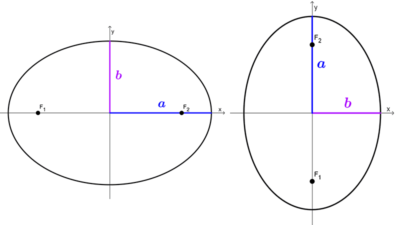
El número a² siempre es mayor que b², si son iguales se trata de una circunferencia. Si el denominador del término que tiene x es mayor que el término que tiene y, entonces la elipse es horizontal, su eje mayor es paralelo al eje x. El denominador de x es a² y el denominador de y es b².

De modo similar, si el denominador del término que tiene y es mayor que el término que tiene x, entonces la elipse es vertical (eje mayor paralelo al eje y). El denominador de y es a² y el de x es b².

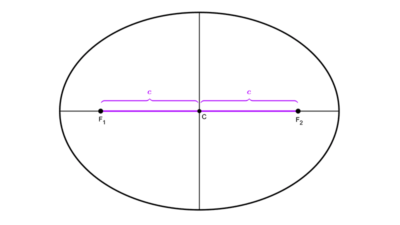
Reconocer el centro, los valores de a² y b² y saber si la elipse es horizontal o vertical es importante para calcular las coordenadas de los focos, pues lo que haremos será utilizar la propiedad c² = a² - b² → c = √(a² - b²). El valor de c es la semidistancia focal, es decir, la distancia del centro a un foco, con este dato se puede calcular la ubicación de los focos. El proceso se resume en el siguiente paso a paso.

Ejemplo 1

Calcular los focos de la elipse *\dfrac{x^2}{25}+\dfrac{y^2}{9}=1*

Solución: el denominador más grande es el de x², lo que indica que la elipse es horizontal. Además, su centro es el origen de coordenadas, el punto (0, 0).

Extraemos los valores de los denominadores: 

*a^2=25*

*b^2=9*

Hallamos la semidistancia focal:

*c=\sqrt{a^2-b^2}*

*c=\sqrt{25-9}*

*c=\sqrt{16}*

*c=4*

La distancia del centro a cada foco es de c = 4 unidades, usamos este dato para obtener las coordenadas de los focos. Debido a que es una elipse horizontal, sus focos F₁ y F₂ están en las siguientes coordenadas:

*F_1(-4,0)~~~ y ~~~F_2(4,0)*

Ejemplo 2

Encontrar los focos de la elipse con ecuación *\dfrac{y^2}{64}+\dfrac{x^2}{16}=1*

Solución: como el denominador de y² es más grande que el de x², la elipse es vertical. De la ecuación también se extrae que el centro es el origen de coordenadas. Obtenemos los cuadrados de los semiejes:

*a^2=64*

*b^2=16*

Con estos datos calculamos la semidistancia focal:

*c=\sqrt{a^2-b^2}*

*c=\sqrt{64-16}*

*c=\sqrt{48}*

*c≈6,93*

Ahora, como se trata de una elipse vertical, obtenemos los focos cambiando la coordenada y del centro por c y -c:

*F_1(0,-\sqrt{48})~~y~~F_2(0,\sqrt{48})*

Si usamos una aproximación:

*F_1(0;-6,93)~~y~~F_2(0;6,93)*

Ejemplo 3

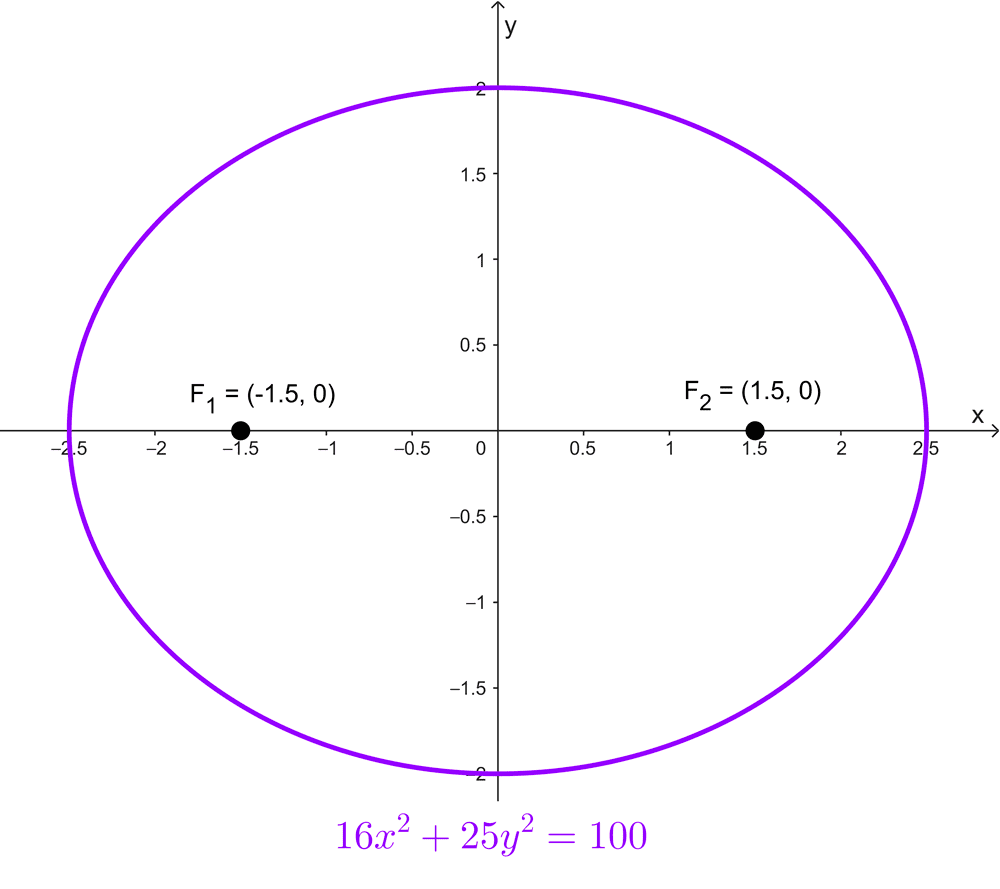
Determinar los focos de la elipse *16x^2+25y^2=100*

Solución: la ecuación no está en forma canónica, así que es necesario manipularla algebraicamente para obtener los datos necesarios. Podemos dividir numerador y denominador entre 100 para que aparezca un miembro igual a 1, luego simplificar los demás términos:

*16x^2+25y^2=100*

*\dfrac{16x^2+25y^2}{100}=\dfrac{100}{100}*

*\dfrac{16x^2}{100}+\dfrac{25y^2}{100}=1*

*\dfrac{x^2}{100/16}+\dfrac{y^2}{100/25}=1*

*\dfrac{x^2}{25/4}+\dfrac{y^2}{4}=1*

La elipse tiene centro en el origen y como 25/4 = 6,25 que es mayor que 4, el eje mayor es horizontal. Obtenemos los denominadores:

*a^2=25/4*

*b^2=4*

Ahora calculamos la semidistancia focal:

*c=\sqrt{a^2-b^2}*

*c=\sqrt{\dfrac{25}{4}-4}*

*c=\sqrt{\dfrac{9}{4}}*

*c=\dfrac{3}{2}=1,5*

Entonces, los focos de la elipse son:

*F_1(-1,5; 0)~~~ y~~~ F_2(1,5;0)*

Ejercicio 4

Hallar los focos de la elipse *\dfrac{(x-3)^2}{4}+\dfrac{(y+4)^2}{36}=1*

Solución: puede leerse en la ecuación que el centro no es el origen sino el punto (3, -4), como el denominador del término que contiene y es mayor al del que contiene x, se trata de una elipse vertical.

Obtenemos los denominadores:

*a^2=36*

*b^2=4*

Calculamos la semidistancia focal:

*c=\sqrt{a^2-b^2}*

*c=\sqrt{36-4}*

*c=\sqrt{32}*

*c≈5,66*

Para sacar las coordenadas de los focos sumamos y restamos el valor c a la ordenada (coordenada y) del centro:

*F_1(3, -4-\sqrt{32})~~~ y ~~~ F_2(3,-4+\sqrt{32})*

Usando aproximaciones:

*F_1(3; -9,66)~~~ y ~~~ F_2(3; 1,66)*

Ejercicio 5

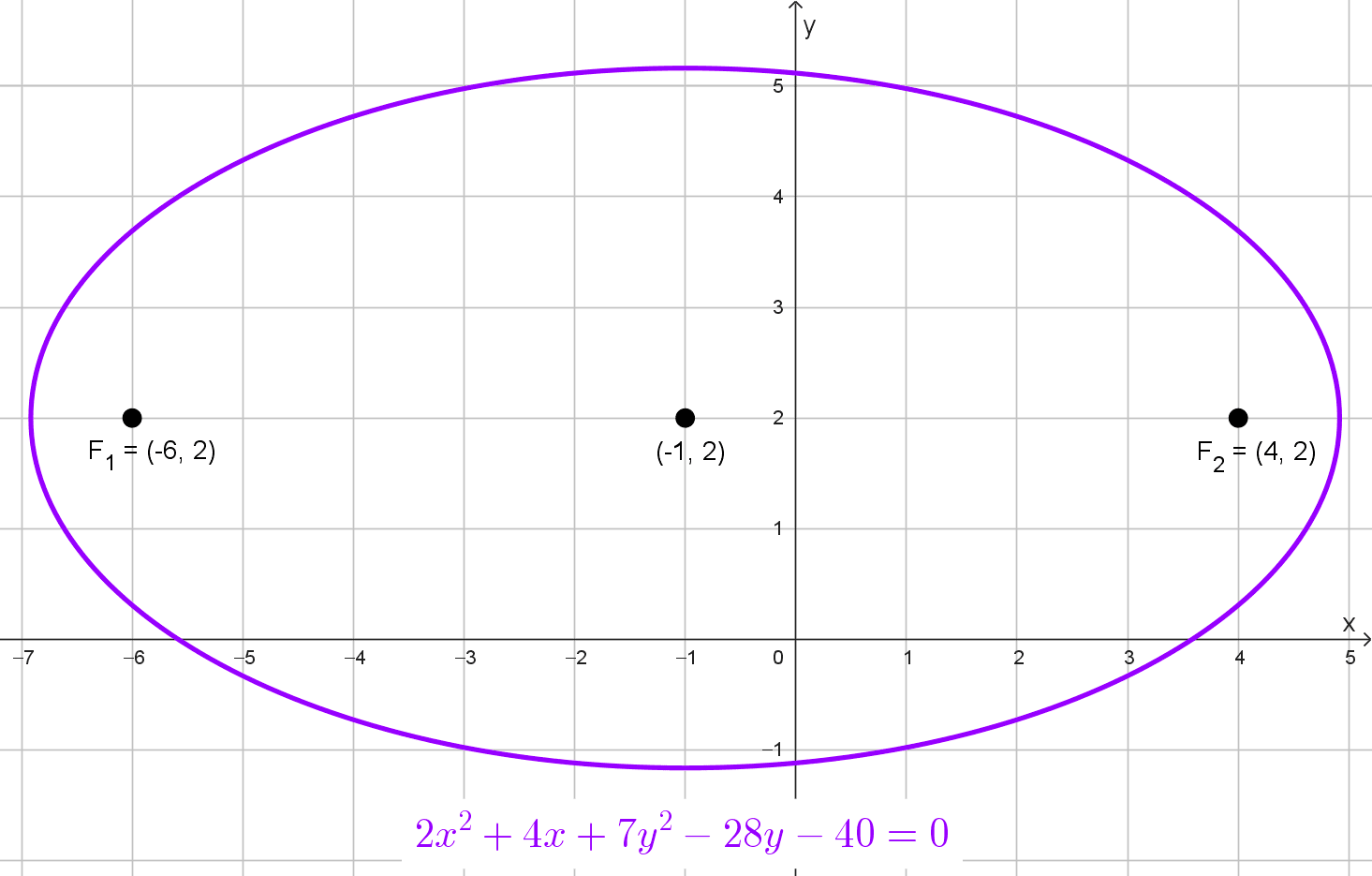
Determinar el centro de la elipse con ecuación *2x^2+4x+7y^2-28y-40=0*

Solución: la ecuación no está en forma canónica sino en forma general, así que es necesario manipularla para obtener los datos necesarios y encontrar los focos. Para hacer esto, procedemos a completar los cuadrados.

Partimos de la siguiente expresión:

*2x^2+4x+7y^2-28y-40=0*

Agrupamos los términos de de las variables y movemos el término constante al otro lado de la ecuación:

*2x^2+4x+7y^2-28y=40*

Extraemos el factor común en cada grupo:

*2(x^2+2x)+7(y^2-4y)=40*

En el término *x^2+2x,* el coeficiente de x es 2. Dividimos este coeficiente entre 2, lo elevamos al cuadrado y obtenemos 1:

*x^2+2x=(x+1)^2-1*

Sustituyendo, tenemos:

*2((x+1)^2-1)*

En el término *y^2-4y,* el coeficiente de y es -4. Dividimos este coeficiente entre 2, lo elevamos al cuadrado y obtenemos 4:

*y^2-4y=(y-2)^2-4*

Sustituyendo, tenemos:

*7((y-2)^2-4)*

Ahora reemplazamos en la ecuación original:

*2((x+1)^2-1)+7((y-2)^2-4)=40*

Distribuimos 2 y 7 en sus respectivos términos:

*2(x+1)^2-2+7(y-2)^2-28=40*

Sumamos los términos constantes en el lado izquierdo:

*2(x+1)^2+7(y-2)^2-30=40*

Luego sumamos 30 en ambos lados:

*2(x+1)^2+7(y-2)^2=70*

Dividimos toda la ecuación por 70 para obtener la forma estándar de la elipse:

*\dfrac{(x+1)^2}{35}+\dfrac{(y-2)^2}{10}=1*

Esta forma nos permite ver más claramente que el centro de la elipse está en (-1, 2) y como 35 es mayor a 10, la elipse es horizontal. Extraemos los semiejes al cuadrado:

*a^2=35*

*b^2=10*

Calculamos la semidistancia focal:

*c=\sqrt{a^2-b^2}*

*c=\sqrt{35-10}*

*c=\sqrt{25}*

*c=5*

Debido a que la elipse es horizontal, sacamos los focos sumando y restando c a la abscisa (coordenada x) del centro, así:

*F_1(-1-5, 2)~~~ y~~~F_2(-1+5,2)*

*F_1(-6, 2)~~~ y~~~F_2(4,2)*

Resumen

1. La fórmula de la semidistancia focal es *c=\sqrt{a^2-b^2}.*
2. Los focos de la elipse con centro en (h, k) están en las coordenadas F₁(h - c, k) y F₂(h + c, k) si la elipse es horizontal y en coordenadas F₁(h, k - c) y F₂(h, k + c) si la elipse es vertical.

Los siguientes videos pueden ayudarte a sacar los focos de una elipse:

Bibliografía

• Engler, A. y otros. (2020). Geometría Analítica. Universidad Nacional del Litoral.
• Fuller, G. y Tarwater, D. (1995). Geometría Analítica (7ma edición). Pearson Educación.
• Lehmann, C. (1989). Geometría Analítica. Limusa.
• Leithold. L. (1992). Álgebra y Trigonometría con Geometría Analítica. Oxford University Press.
• Mora, W., y Figueroa, G. (2009). Cónicas. Revista Digital Matemática, Educación e Internet.
• Márquez, A. y otros. (2009). Geometría Analítica. Prentice Hall.
• Raichman, S. y Totter, E. (2016). Geometría Analítica para Ciencias e Ingeniería. Universidad Nacional de Cuyo.
• Sullivan, M. (2006). Álgebra y Trigonometría. Pearson Educación.
• Swokowski, E. y Cole, J. (2009). Álgebra y Trigonometría con Geometría Analítica. Cengage Learning.