
Recta tangente a una parábola
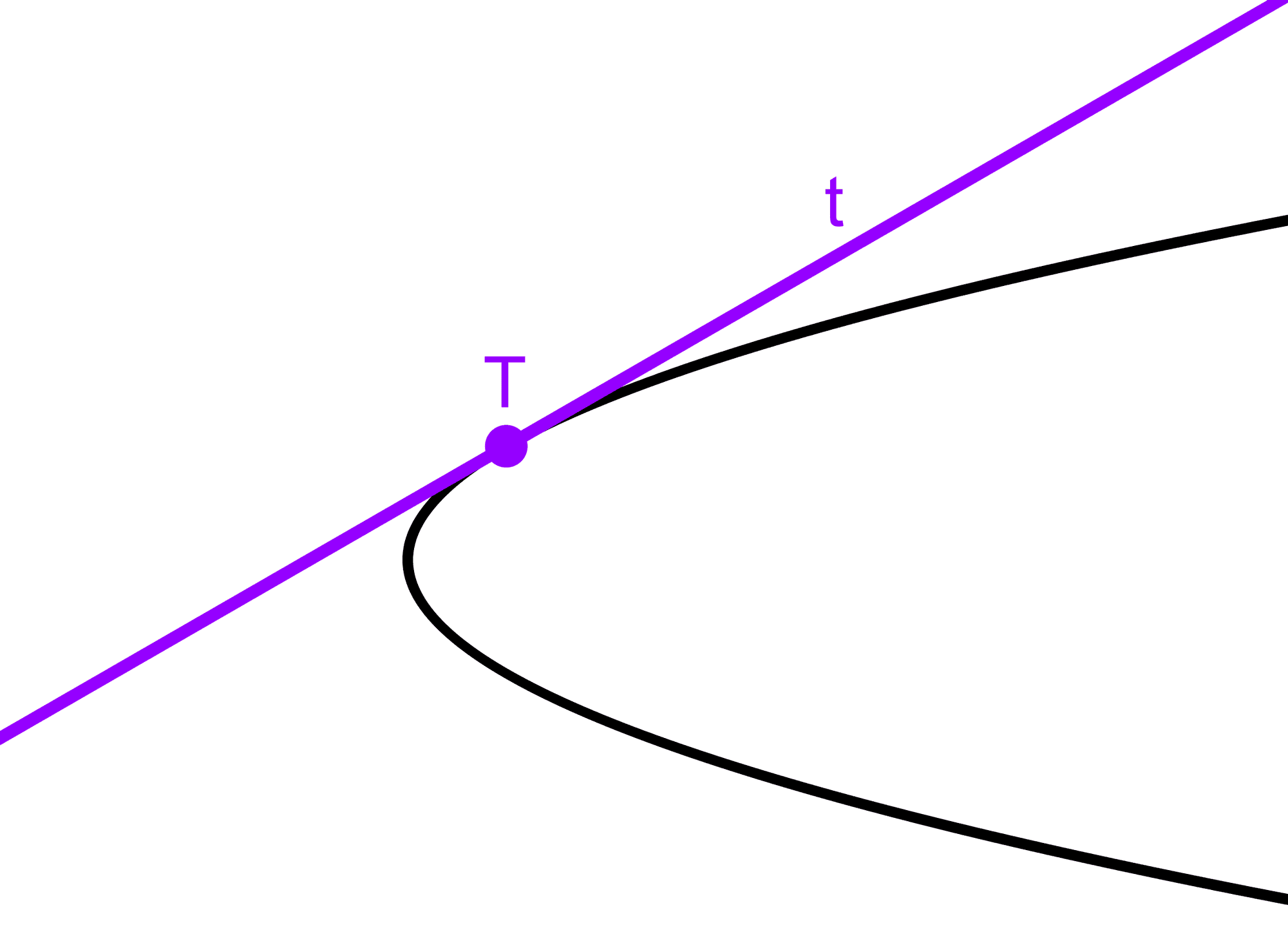
Una recta tangente a una parábola es una línea que toca la curva en un único punto, conocido como punto de tangencia. Gráficamente, todos los demás puntos de la parábola se encuentran en el mismo semiplano definido por esta recta.
Antes de trabajar con la tangente es importante conocer los elementos y ecuaciones de la parábola, puedes hacer un repaso de ellas en el artículo principal:
Índice
Tangente en un punto
Existen fórmulas que permiten hallar la tangente de manera inmediata, evitando el cálculo de derivadas. A continuación, presentamos tres de las formulaciones más útiles y comunes.
Forma canónica o simétrica
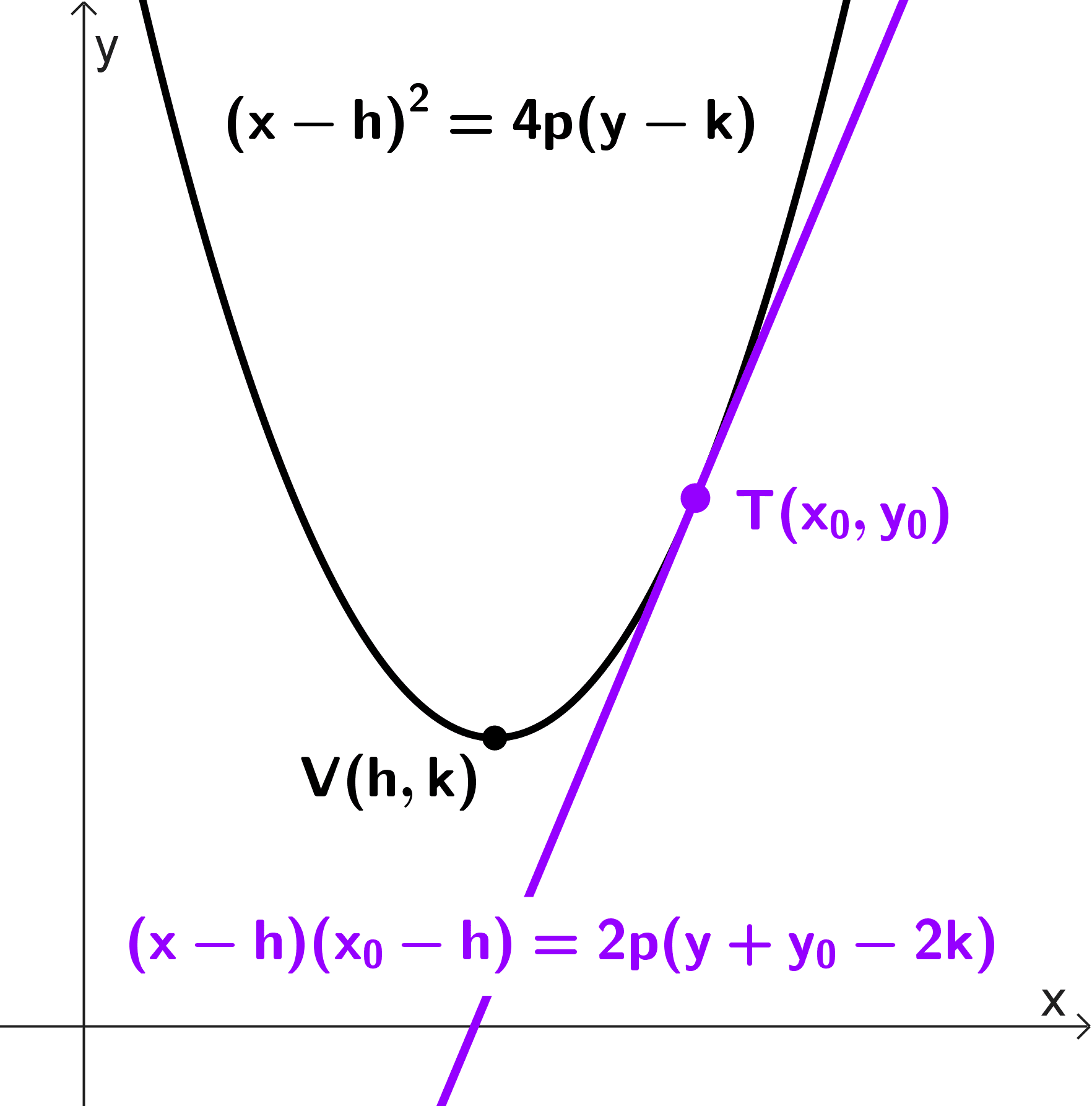
Dada la ecuación canónica de la parábola y un punto de la misma T(x0, y0), podemos encontrar la ecuación de la recta tangente en ese punto mirando en la siguiente tabla.
| Parábola | Orientación de la parábola | Ecuación de la tangente |
|---|---|---|
| y2 = 4px | Horizontal | yy0 = 2p (x + x0) |
| x2 = 4py | Vertical | xx0 = 2p (y + y0) |
| (y - k)2 = 4p (x - h) | Horizontal | (y - k) (y0 - k) = 2p (x + x0 - 2h) |
| (x - h)2 = 4p (y - k) | Vertical | (x - h) (x0 - h) = 2p (y + y0 - 2k) |
Ejemplo 1
Calcular la ecuación de la recta tangente a la parábola \(y^2=6x\) en el punto (6, 6).
Solución
Aplicamos la fórmula para una parábola horizontal con vértice en el origen. Primero, determinamos el valor del parámetro \(p\) comparando la ecuación \(y^2=6x\) con su forma canónica \(y^2=4px.\) Igualamos \(4p=6\) y despejamos \(p,\) obteniendo:
\(p=\dfrac{6}{4}=\dfrac{3}{2}\)
Conocemos ahora los valores \(x_0=6\), \(y_0=6,\) y \(p=\dfrac{3}{2}.\) Sustituimos estos valores en la fórmula \(yy_0=2p(x+x_0)\) y simplificamos:
\(y \cdot 6=2 \cdot \dfrac{3}{2} (x+6)\)
\(6y=3(x+6)\)
Para despejar \(y\) y obtener la ecuación en forma explícita, dividimos ambos miembros de la ecuación entre 3:
\(2y=x+6\)
Finalmente, dividimos ambos miembros entre 2 para obtener el resultado:
\(y=\dfrac{1}{2}x+3\)
Así, determinamos que la ecuación de la recta tangente a la parábola \(y^2=6x\) en el punto \((6, 6)\) es \(y=\dfrac{1}{2}x+3.\)
Ejemplo 2
Obtener la recta tangente a la parábola \((x-2)^2=4(y-3)\) en el punto (6, 7).
Solución
Observamos que la parábola tiene su vértice en \((h, k)=(2, 3)\) y su forma corresponde a \((x-h)^2=4p(y-k).\) Comparando con la ecuación dada, tenemos \(4p=4,\) por lo que \(p=1.\)
Aplicamos la fórmula para la tangente en un punto \((x_0, y_0)\): \((x-h)(x_0-h)=2p(y+y_0-2k).\) Sustituimos los valores conocidos: \(h=2\), \(k=3\), \(p=1\), \(x_0=6\), \(y_0=7.\) Obtenemos:
\((x-2)(6-2)=2 \cdot 1 (y+7-2 \cdot 3)\)
Simplificamos:
\((x-2)(4)=2(y+7-6)\)
\(4(x-2)=2(y+1)\)
Dividimos ambos lados entre 2:
\(2(x-2)=y+1\)
Despejamos \(y\) para hallar la ecuación explícita:
\(y=2(x-2)-1=2x-4-1=2x-5\)
Así, la ecuación de la recta tangente es \(y=2x-5.\)
Ejemplo 3
Dada la parábola \((y+2)^2=-12x,\) determinar la fórmula de la tangente en (-12, 10).
Solución
Esta parábola tiene la forma \((y-k)^2=4p(x-h),\) con vértice en \((h, k)=(0,-2)\) (ya que \(y+2=y-(-2)\)). Comparando \(4p=-12,\) obtenemos \(p=-3.\)
Aplicamos la fórmula para la tangente en \((x_0, y_0)\): \((y-k)(y_0-k)=2p(x+x_0-2h).\) Sustituimos \(h=0\), \(k=-2\), \(p=-3\), \(x_0=-12\), \(y_0=10:\)
\((y-(-2))(10-(-2))=2 \cdot (-3)(x+(-12)-2 \cdot 0)\)
Simplificamos:
\((y+2)(12)=-6(x-12)\)
Dividimos ambos lados entre 6:
\(2(y+2)=-(x-12)\)
Despejamos \(y:\)
\(2y+4=-x+12\)
\(2y=-x+8\)
\(y=-\dfrac{1}{2}x+4\)
La ecuación de la recta tangente es \(y=-\dfrac{1}{2}x+4.\)
Ejemplo 4
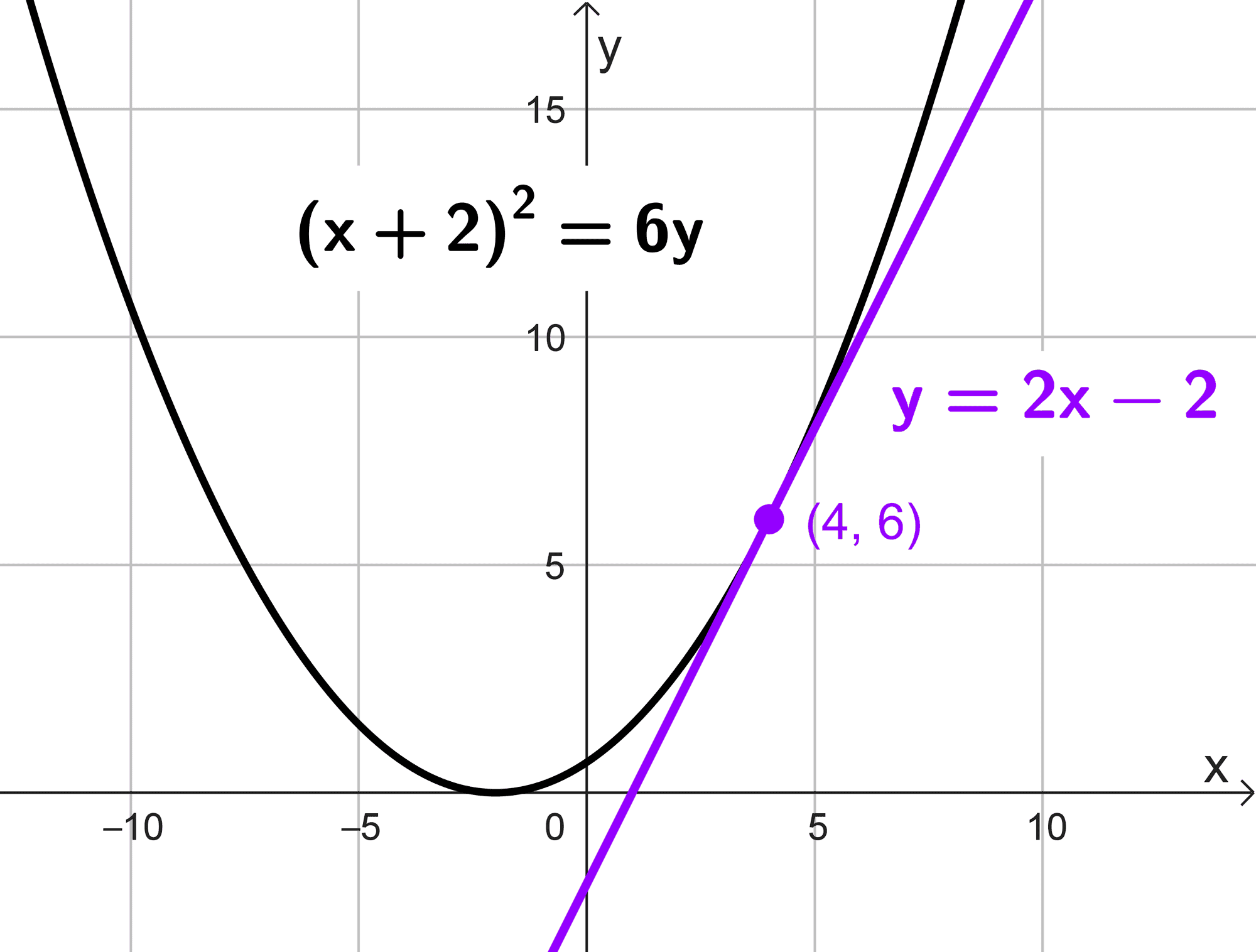
Hallar la ecuación de la recta tangente a la parábola \(x^2+4x-6y+4=0\) en el punto (4, 6).
Solución 4
Completamos el cuadrado para obtener la forma canónica:
\(x^2+4x-6y+4=0\)
\(x^2+4x+4=6y\)
\((x+2)^2=6y\)
Esta es una parábola con vértice en \((h, k)=(-2, 0)\) y \(4p=6,\) por lo que \(p=\dfrac{6}{4}=\dfrac{3}{2}.\)
Aplicamos la fórmula para la tangente en \((x_0, y_0)\): \((x-h)(x_0-h)=2p(y+y_0-2k).\) Sustituimos \(h=-2\), \(k=0\), \(p=\dfrac{3}{2}\), \(x_0=4\), \(y_0=6:\)
\((x-(-2))(4-(-2))=2 \cdot \dfrac{3}{2}(y+6-2 \cdot 0)\)
Simplificamos:
\((x+2)(6)=3(y+6)\)
Dividimos ambos lados entre 3:
\(2(x+2)=y+6\)
Despejamos \(y:\)
\(y=2(x+2)-6=2x+4-6=2x-2\)
La ecuación de la recta tangente es \(y=2x-2.\)
Demostración de la ecuación
Tenemos la parábola en su forma canónica: \(y^2=4p x\) donde \(p\) es el parámetro. Sea \((x_0, y_0)\) un punto sobre la parábola. Entonces, satisface la ecuación:
\(y_0^2=4p x_0 \quad \text{(1)}\)
Derivamos implícitamente la ecuación \(y^2=4p x\) con respecto a \(x:\)
\(\dfrac{d}{dx}(y^2)=\dfrac{d}{dx}(4p x)\)
\(2y \dfrac{dy}{dx}=4p\)
Despejamos \(\dfrac{dy}{dx}:\)
\(\dfrac{dy}{dx}=\dfrac{4p}{2y}=\dfrac{2p}{y}\)
En el punto \((x_0, y_0),\) la pendiente de la recta tangente es:
\(m=\dfrac{2p}{y_0} \quad \text{(2)}\)
La ecuación de una recta con pendiente \(m\) que pasa por \((x_0, y_0)\) es:
\(y-y_0=m (x-x_0)\)
Sustituimos \(m\) de (2):
\(y-y_0=\dfrac{2p}{y_0} (x-x_0) \quad \text{(3)}\)
Multiplicamos ambos lados de (3) por \(y_0\) (asumiendo \(y_0 \neq 0;\) el caso \(y_0=0\) se verifica por separado):
\(y_0 (y-y_0)=2p (x-x_0)\)
\(y_0 y-y_0^2=2p x-2p x_0\)
Ahora, usamos la ecuación (1): \(y_0^2=4p x_0.\) Sustituimos:
\(y_0 y-4p x_0=2p x-2p x_0\)
Reorganizamos términos:
\(y_0 y=2p x-2p x_0+4p x_0\)
\(y_0 y=2p x+2p x_0\)
\(y_0 y=2p (x+x_0) \quad \text{(4)}\)
Esta es la ecuación deseada.
Caso particular: si \(y_0=0,\) entonces de (1): \(0=4p x_0 → x_0=0.\) El punto es el vértice \((0,0).\) La pendiente de la tangente en \((0,0)\) es \(m=\dfrac{2p}{0}\) (indefinida), es decir, la tangente es vertical. La ecuación de la recta tangente en el vértice es \(x=0.\)
Las demás ecuaciones se demuestran con un argumento similar.
Forma punto pendiente
Este enfoque se alinea con la forma tradicional de la ecuación de una recta. El punto de tangencia es T(x0, y0).
| Parábola | Orientación de la parábola | Ecuación punto-pendiente de la tangente |
|---|---|---|
| y2 = 4px | Horizontal | \(y-y_0=\dfrac{2p}{y_0} (x-x_0)\) donde y0 ≠ 0 |
| x2 = 4py | Vertical | \(y-y_0=\dfrac{x_0}{2p} (x-x_0)\) |
| (y - k)2 = 4p (x - h) | Horizontal | \(y-y_0=\dfrac{2p}{y_0-k} (x-x_0)\) donde y0 ≠ k |
| (x - h)2 = 4p (y - k) | Vertical | \(y-y_0=\dfrac{x_0-h}{2p} (x-x_0)\) |
Ejemplo
Obtenga la ecuación de la tangente a la curva \(y^2-4y-4x+8=0\) en el punto (10, 8).
Solución
Si completamos los cuadrados obtenemos que la forma canónica es \((y-2)^2=4(x-1),\) lo que indica una parábola con vértice en \((h, k)=(1, 2)\) y \(4p=4,\) por lo que \(p=1.\) Aplicamos la fórmula para la tangente en un punto \((x_0, y_0)\) cuando \(y_0 \neq k:\)
\(y-y_0=\dfrac{2p}{y_0-k}(x-x_0)\)
Sustituimos los valores conocidos: \(p=1\), \(x_0=10\), \(y_0=8\), \(k=2:\)
\(y-8=\dfrac{2 \cdot 1}{8-2}(x-10)\)
Simplificamos el denominador:
\(y-8=\dfrac{2}{6}(x-10)\)
Reducimos la fracción:
\(y-8=\dfrac{1}{3}(x-10)\)
Despejamos \(y\) para obtener la ecuación explícita:
\(y=\dfrac{1}{3}(x-10)+8=\dfrac{1}{3}x-\dfrac{10}{3}+8=\dfrac{1}{3}x+\dfrac{14}{3}\)
Así, la ecuación de la recta tangente es \(y=\dfrac{1}{3}x+\dfrac{14}{3}.\)
Demostración de la ecuación
En la demostración anterior obtuvimos que la derivada de \(y^2=4p x\) respecto a x es:
\(\dfrac{dy}{dx}=\dfrac{2p}{y}\)
En el punto \((x_0, y_0),\) la pendiente de la recta tangente es:
\(m=\dfrac{2p}{y_0}\)
La ecuación de una recta con pendiente \(m\) que pasa por \((x_0, y_0)\) es:
\(y-y_0=m (x-x_0)\)
Sustituimos \(m\) con lo obtenido anteriormente:
\(y-y_0=\dfrac{2p}{y_0} (x-x_0)\)
Esta última es la ecuación que queríamos obtener.
Forma paramétrica
Esta forma permite encontrar la ecuación de la recta tangente cuando el punto de tangencia se expresa de forma paramétrica con parámetro t.
| Parábola | Orientación de la parábola | Punto de tangencia | Ecuación paramétrica de la recta tangente |
|---|---|---|---|
| y2 = 4px | Horizontal | (pt², 2pt) | ty = x + pt2 |
| x2 = 4py | Vertical | (2pt, pt²) | tx = y + pt2 |
| (y - k)2 = 4p (x - h) | Horizontal | (pt² + h, 2pt + k) | t (y - k) = (x - h) + pt2 |
| (x - h)2 = 4p (y - k) | Vertical | (2pt + h, pt² + k) | t (x - h) = (y - k) + pt2 |
Ejemplo
Determine la ecuación de la línea tangente a la parábola y2 = 12x en el punto (pt², 2pt) cuando t = 3.
Solución
La forma canónica de la parábola es \(y^2=4px,\) donde \(4p=12,\) por lo que \(p=3.\) El punto de tangencia para un valor \(t\) está dado por \((pt^2, 2pt).\) Sustituimos \(t=3\) y \(p=3:\)
\(x_0=p \cdot t^2=3 \cdot (3)^2=3 \cdot 9=27\)
\(y_0=2p \cdot t=2 \cdot 3 \cdot 3=18\)
El punto de tangencia es \((27, 18).\)
Utilizamos la fórmula paramétrica de la tangente para una parábola \(y^2=4px:\)
\(t \cdot y=x+p \cdot t^2\)
Sustituimos \(t=3\) y \(p=3:\)
\(3y=x+3 \cdot (3)^2=x+3 \cdot 9=x+27\)
Despejamos \(y\) para obtener la ecuación explícita:
\(3y=x+27\)
\(y=\dfrac{1}{3}x+9\)
Así, la ecuación de la recta tangente es \(y=\dfrac{1}{3}x+9.\)
Demostración de la ecuación
Supongamos que P (pt², 2pt) es un punto de la parábola y2 = 4px. Sustituimos estas coordenadas en la forma simétrica de la recta tangente:
\(y_0 y=2p (x+x_0)\)
\(2pt y=2p (x+pt^2)\)
\(t y=x+pt^2\)
Esta es la ecuación que queríamos obtener.
Método con cálculo diferencial
En cálculo diferencial, una de las formas más directas de encontrar la ecuación de la recta tangente a una parábola es utilizar derivadas. Este procedimiento es muy común en los primeros cursos de cálculo y se basa en el hecho de que la derivada de una función nos da la pendiente de la recta tangente en cada punto de la curva.
Supongamos que tenemos una parábola dada por la ecuación y = f(x) y un punto de tangencia (x0, y0) que pertenece a la curva. El procedimiento para hallar la recta tangente mediante derivadas es el siguiente:
- Comprobar que el punto (x0, y0) pertenece a la parábola.
- Calcular la derivada dy / dx: esta representa la pendiente de la recta tangente en cualquier punto de la curva.
- Evaluar la derivada en x0 para obtener la pendiente específica de la tangente, a la que llamamos m.
- Plantear la ecuación de la tangente con la fórmula punto-pendiente: y - y0 = m(x - x0).
Si la ecuación no está dada en forma explícita y = f(x) (como es el caso de y2 = 4px), podemos usar derivación implícita de la misma forma que hicimos en las demostraciones de las fórmulas anteriores. Esto funciona porque el teorema de la función implícita nos garantiza que, alrededor de cualquier punto que no sea el vértice, la ecuación define a y como función de x.
Ejemplo
Calcular la ecuación de la tangente a la curva y = 2x2 + 3x - 5 en el punto (2, 9).
Solución
Primero, verificamos que el punto (2, 9) pertenece a la curva. Sustituimos \(x=2\) en la ecuación:
\(y=2(2)^2+3(2)-5=2(4)+6-5=8+6-5=9\)
Obtenemos \(y=9,\) lo que confirma que el punto \((2, 9)\) está en la curva.
Ahora, calculamos la derivada de \(y\) con respecto a \(x\) para hallar la pendiente de la tangente:
\(\dfrac{dy}{dx}=\dfrac{d}{dx}(2x^2+3x-5)=4x+3\)
Evaluamos la derivada en \(x_0=2\) para obtener la pendiente \(m:\)
\(m=4(2)+3=8+3=11\)
Finalmente, planteamos la ecuación de la recta tangente usando la forma punto-pendiente:
\(y-y_0=m(x-x_0)\)
Sustituimos \(x_0=2\), \(y_0=9\), \(m=11:\)
\(y-9=11(x-2)\)
Desarrollamos y simplificamos:
\(y-9=11x-22\)
\(y=11x-22+9\)
\(y=11x-13\)
Así, la ecuación de la recta tangente es \(y=11x-13.\)
En algunos problemas más avanzados, el punto de tangencia no está dado explícitamente sino que se busca bajo cierta condición (por ejemplo, encontrar la tangente paralela a una recta dada). En esos casos también seguimos la misma lógica: calcular la pendiente con la derivada y usar la fórmula de la recta punto-pendiente.
Tangentes desde un punto exterior
Desde un punto exterior a una parábola siempre pueden trazarse dos rectas tangentes, una hacia cada lado de la curva. Para encontrarlas, podemos usar un método algebraico basado en el discriminante de una ecuación cuadrática.
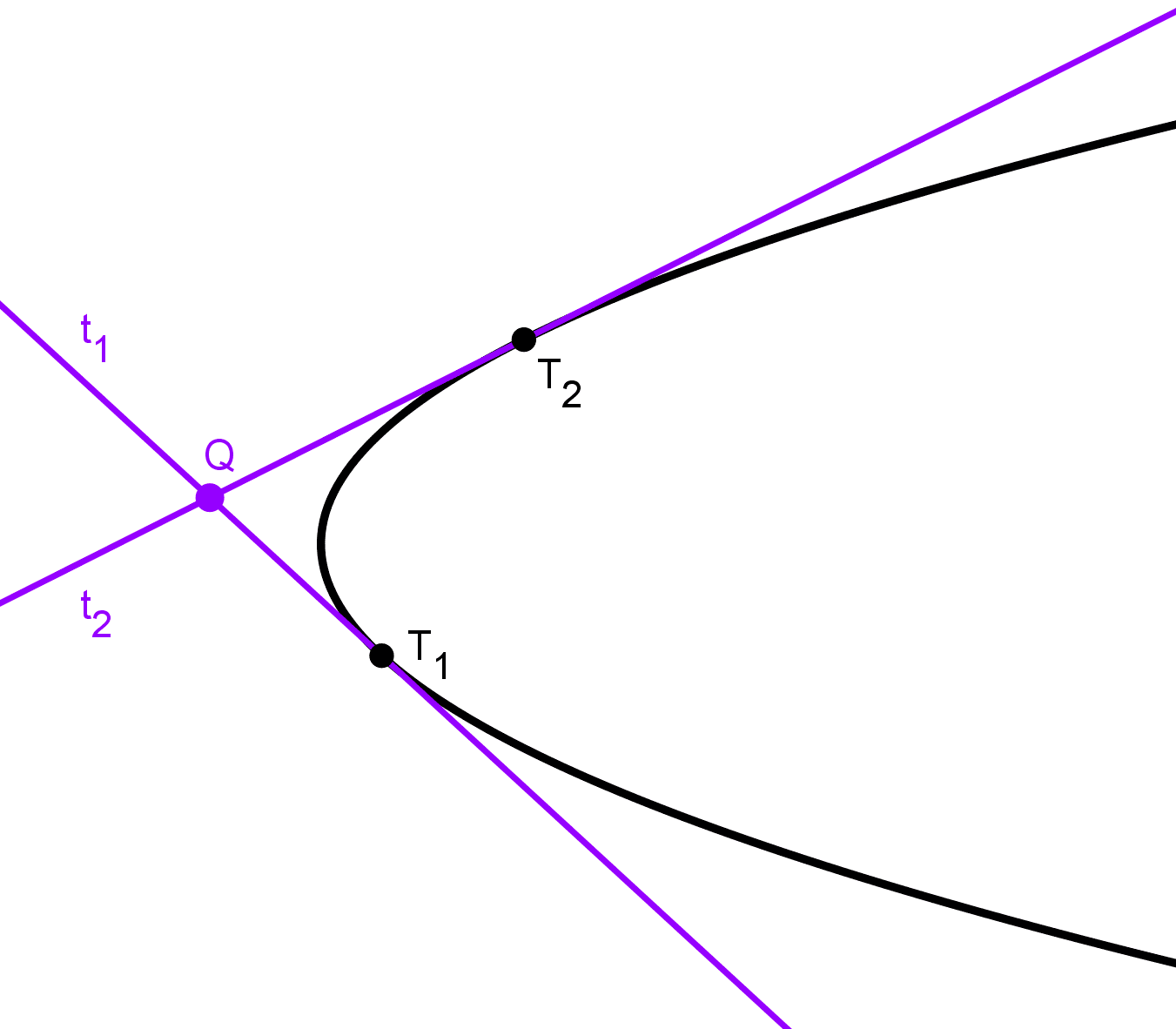
Método analítico con discriminante
Dada la ecuación de una parábola y un punto exterior Q(x1, y1), para encontrar las rectas tangentes que pasan por ese punto hacemos lo siguiente:
- Plantear la ecuación de la recta con pendiente variable que pasa por el punto exterior Q(x1, y1): y - y1 = m (x - x1).
- Sustituir esta recta en la ecuación de la parábola, de este modo obtenemos una ecuación cuadrática en x (o en y, si decidimos despejar x en la ecuación de la recta).
- Aplicar la condición de tangencia: para que la recta sea tangente, la intersección con la parábola debe reducirse a un único punto. Esto se garantiza imponiendo que el discriminante de la ecuación cuadrática sea igual a cero: B2 - 4AC = 0, donde A, B y C son los coeficientes de la cuadrática.
- Resolver la condición anterior para la pendiente m. Con esto obtendremos dos valores para m, que corresponden a las rectas tangentes que buscábamos.
- Escribir las ecuaciones de las rectas tangentes sustituyendo en la ecuación de la recta inicial: y - y1 = m (x - x1).
Ejemplo 1
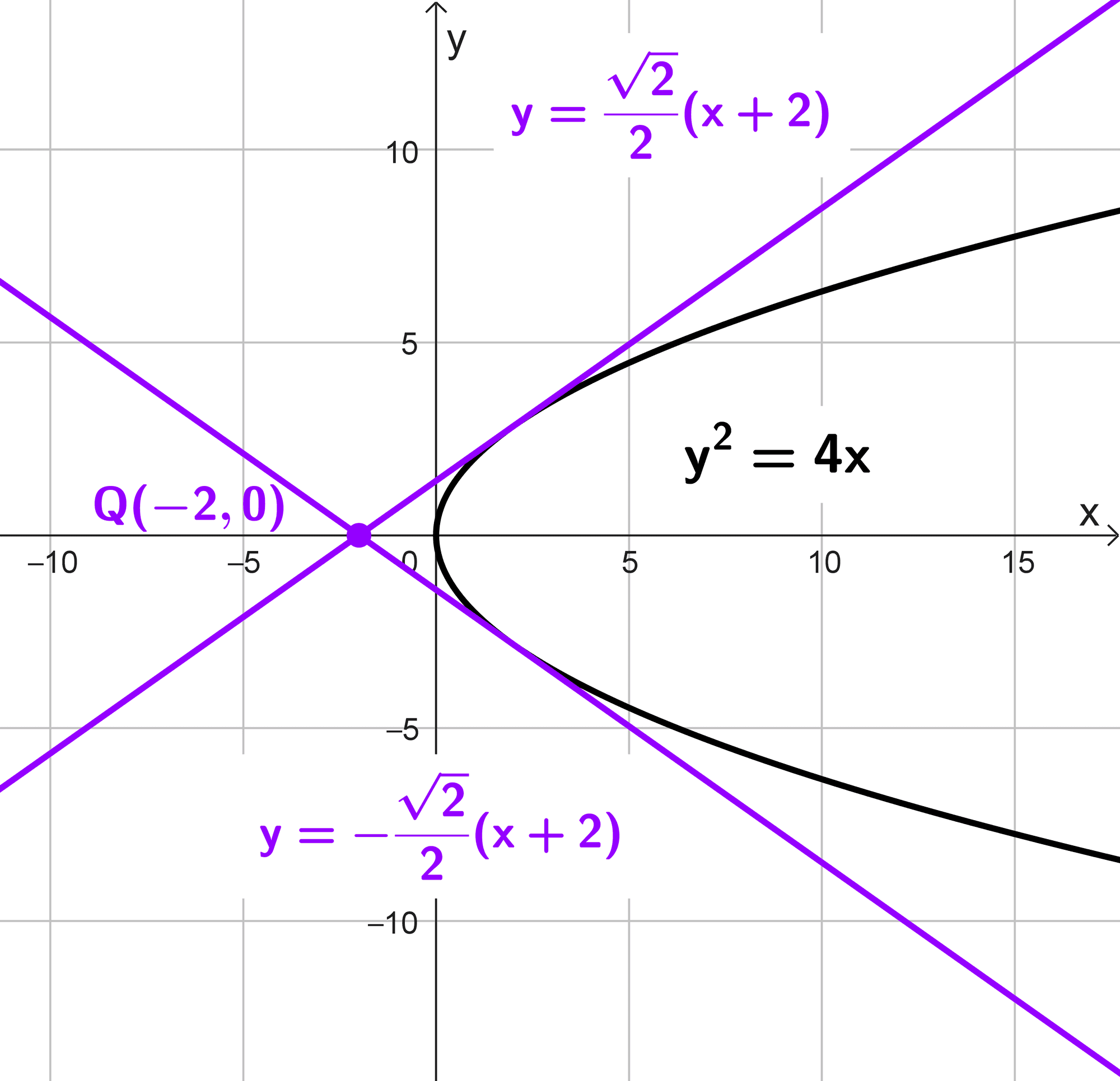
Obtener las ecuaciones de las tangentes a la parábola \(y^2=4x\) que pasan por el punto Q(-2, 0).
Solución
Comenzamos planteando la ecuación de una recta con pendiente \(m\) que pasa por el punto \(Q(-2, 0).\) Su ecuación punto-pendiente es:
\(y-0=m(x-(-2))\)
\(y=m(x+2)\)
Ahora, sustituimos esta expresión de \(y\) en la ecuación de la parábola \(y^2=4x\) para encontrar los puntos de intersección entre la recta y la parábola:
\([m(x+2)]^2=4x\)
\(m^2(x+2)^2=4x\)
\(m^2(x^2+4x+4)=4x\)
\(m^2x^2+4m^2x+4m^2-4x=0\)
\(m^2x^2+(4m^2-4)x+4m^2=0\)
Esta es una ecuación cuadrática en la variable \(x.\) Para que la recta sea tangente a la parábola, esta ecuación debe tener una única solución. Esto se garantiza cuando el discriminante de la ecuación es igual a cero. El discriminante \(\Delta\) de una ecuación de la forma \(Ax^2+Bx+C=0\) es \(B^2-4AC.\) Identificamos los coeficientes:
\(A=m^2, \quad B=(4m^2-4), \quad C=4m^2\)
Calculamos el discriminante y lo igualamos a cero:
\(\Delta=B^2-4AC=0\)
\((4m^2-4)^2-4(m^2)(4m^2)=0\)
\(16(m^2-1)^2-16m^4=0\)
\(16[(m^2-1)^2-m^4]=0\)
\((m^2-1)^2-m^4=0\)
Desarrollamos la expresión:
\((m^4-2m^2+1)-m^4=0\)
\(-2m^2+1=0\)
\(2m^2=1\)
\(m^2=\dfrac{1}{2}\)
\(m=\pm \dfrac{1}{\sqrt{2}}=\pm \dfrac{\sqrt{2}}{2}\)
Hemos obtenido dos valores para la pendiente \(m,\) lo que significa que existen dos rectas tangentes a la parábola que pasan por el punto \(Q(-2, 0).\) Finalmente, sustituimos estos valores de \(m\) en la ecuación de la recta original para hallar sus ecuaciones.
Para \(m_1=\dfrac{\sqrt{2}}{2}:\)
\(y=\dfrac{\sqrt{2}}{2}(x+2)\)
Para \(m_2=-\dfrac{\sqrt{2}}{2}:\)
\(y=-\dfrac{\sqrt{2}}{2}(x+2)\)
Por lo tanto, las ecuaciones de las tangentes a la parábola \(y^2=4x\) que pasan por el punto \(Q(-2, 0)\) son:
\(\boxed{y=\dfrac{\sqrt{2}}{2}(x+2)} \quad \text{y} \quad \boxed{y=-\dfrac{\sqrt{2}}{2}(x+2)}\)
Ejemplo 2
Calcular las ecuaciones de las rectas que pasan por Q(-3, 5) y son tangentes a \(y=-x^2-8x-13.\)
Solución
Primero, planteamos la ecuación de una recta con pendiente \(m\) que pasa por \(Q:\)
\(y-5=m(x-(-3))\)
\(y=m(x+3)+5\)
Sustituimos esta expresión de \(y\) en la ecuación de la parábola para hallar los puntos de intersección:
\(m(x+3)+5=-x^2-8x-13\)
Reorganizamos todos los términos en un solo lado de la ecuación para formar una ecuación cuadrática en \(x:\)
\(m(x+3)+5+x^2+8x+13=0\)
\(x^2+8x+mx+3m+5+13=0\)
\(x^2+(8+m)x+(3m+18)=0\)
Esta es una ecuación cuadrática de la forma \(Ax^2+Bx+C=0,\) donde:
\(A=1, \quad B=(8+m), \quad C=(3m+18)\)
Para que la recta sea tangente a la parábola, esta ecuación debe tener una única solución. Esto ocurre cuando su discriminante es igual a cero:
\(\Delta=B^2-4AC=0\)
\((8+m)^2-4(1)(3m+18)=0\)
Desarrollamos esta ecuación para resolverla y encontrar los valores de \(m:\)
\((64+16m+m^2)-4(3m+18)=0\)
\(64+16m+m^2-12m-72=0\)
\(m^2+4m-8=0\)
Resolvemos esta ecuación cuadrática en \(m\) utilizando la fórmula general:
\(m=\dfrac{-4±\sqrt{4^2-4(1)(-8)}}{2(1)}=\dfrac{-4±\sqrt{16+32}}{2}=\dfrac{-4±\sqrt{48}}{2}=\dfrac{-4±4\sqrt{3}}{2}=-2±2\sqrt{3}\)
Hemos obtenido dos valores para la pendiente \(m:\)
\(m_1=-2+2\sqrt{3}, \quad m_2=-2-2\sqrt{3}\)
Finalmente, sustituimos estos valores en la ecuación de la recta original \(y=m(x+3)+5\) para obtener las ecuaciones de las tangentes.
Para \(m_1=-2+2\sqrt{3}:\)
\(y=(-2+2\sqrt{3})(x+3)+5\)
Para \(m_2=-2-2\sqrt{3}:\)
\(y=(-2-2\sqrt{3})(x+3)+5\)
Por lo tanto, las ecuaciones de las rectas tangentes a la parábola \(y=-x^2-8x-13\) que pasan por el punto \(Q(-3, 5)\) son:
\(\boxed{y=(-2+2\sqrt{3})(x+3)+5} \quad \text{y} \quad \boxed{y=(-2-2\sqrt{3})(x+3)+5}\)
Tangente dada la pendiente
En este tipo de problemas se nos da una pendiente y debemos hallar la ecuación de la recta tangente a la parábola que tenga esa pendiente y, si es necesario, el punto de tangencia. El dato puede ser la pendiente o una recta de la cual hay que extraer la pendiente.
Fórmulas directas
Para encontrar las ecuaciones de las tangentes se hace uso de las condiciones de tangencia:
- Para que la recta y = mx + b sea tangente a la parábola y2 = 4px, debe ocurrir que b = p/m, el punto de tangencia es (p/m2, 2p/m).
- Para que la recta y = mx + b sea tangente a la parábola x2 = 4py, debe ocurrir que b = -pm2, el punto de tangencia es (2pm, pm²).
Las fórmulas se resumen en la siguiente tabla.
| Parábola | Orientación de la parábola | Punto de tangencia | Ecuación de la recta tangente |
|---|---|---|---|
| y2 = 4px | Horizontal | (p/m2, 2p/m) | y = mx + p / m |
| x2 = 4py | Vertical | (2pm, pm²) | y = mx - pm2 |
| (y - k)2 = 4p (x - h) | Horizontal | (h + p/m2, k + 2p/m) | y - k = m (x - h) + p / m |
| (x - h)2 = 4p (y - k) | Vertical | (h + 2pm, k + pm²) | y - k = m (x - h) - pm2 |
Ejemplo 1
Calcular el punto de contacto y la ecuación de la recta tangente a la parábola \((y-4)^2=-6(x+2)\) que tiene la misma dirección que la recta \(y=-3x+10.\)
Solución
Observamos en la ecuación que el vértice \((h, k)\) es \((-2, 4)\) y la parábola es horizontal. Podemos calcular \(p\) despejando: \(4p=-6,\) lo que nos da \(p=-\dfrac{6}{4}=-\dfrac{3}{2}.\)
La recta tangente que buscamos debe tener la misma dirección que la recta \(y=-3x+10.\) La dirección de una recta está determinada por su pendiente, por lo que la pendiente de la tangente será \(m=-3.\) Para hallar la ecuación, utilizamos la fórmula específica proporcionada: \(y-k=m (x-h)+\dfrac{p}{m}.\) Sustituimos los valores conocidos: \(k=4\), \(h=-2\), \(p=-\dfrac{3}{2},\) y \(m=-3.\)
\(y-4=(-3)(x-(-2))+\dfrac{-\dfrac{3}{2}}{-3}\)
Simplificamos los términos:
\(y-4=-3(x+2)+\dfrac{1}{2}\)
Ahora, expandimos y simplificamos para obtener la ecuación de la recta en su forma explícita:
\(y-4=-3x-6+\dfrac{1}{2}\)
\(y-4=-3x-\dfrac{11}{2}\)
\(y=-3x-\dfrac{11}{2}+4\)
\(y=-3x-\dfrac{3}{2}\)
Por lo tanto, la ecuación de la recta tangente es \(y=-3x-\dfrac{3}{2}.\)
Ahora, determinamos el punto de tangencia utilizando la fórmula dada: \(\left(h+\dfrac{p}{m^2}, k+\dfrac{2p}{m}\right).\) Sustituimos los valores conocidos:
\(x_t=h+\dfrac{p}{m^2}=-2+\dfrac{-3/2}{(-3)^2}=-2+\dfrac{-3/2}{9}=-2-\dfrac{3}{18}=-2-\dfrac{1}{6}=-\dfrac{12}{6}-\dfrac{1}{6}=-\dfrac{13}{6}\)
\(y_t=k+\dfrac{2p}{m}=4+\dfrac{2 \cdot (-3/2)}{-3}=4+\dfrac{-3}{-3}=4+1=5\)
Así, el punto de tangencia es \(\left(-\dfrac{13}{6}, 5\right).\)
Para verificar, podemos sustituir este punto en la ecuación de la parábola y en la de la recta tangente, confirmando que satisface ambas.
Ejemplo 2
Encuentre la ecuación de la tangente a la parábola \(x^2+4x+12y-8=0\) que es paralela a la recta \(3x+9y-11=0,\) también determine el punto de contacto.
Solución
Completando cuadrados llegamos a la ecuación de la parábola en su forma canónica:
\((x+2)^2=-12(y-1)\)
Al comparar esta ecuación con la forma canónica de una parábola vertical \((x-h)^2=4p(y-k),\) identificamos de inmediato las coordenadas del vértice \((h, k)=(-2, 1).\) También, \(4p=-12,\) por tanto \(p=-3.\)
Ahora, buscamos la ecuación de la recta tangente a esta parábola que sea paralela a la recta \(3x+9y-11=0.\) Primero, encontramos la pendiente de esta recta dada. Escribimos su ecuación en la forma pendiente-ordenada al origen (\(y=mx+b\)):
\(9y=-3x+11\)
\(y=-\dfrac{1}{3}x+\dfrac{11}{9}\)
Por lo tanto, la pendiente de la recta dada es \(m=-\dfrac{1}{3}.\) Como la tangente buscada debe ser paralela a esta recta, compartirá la misma pendiente: \(m_t=-\dfrac{1}{3}.\)
Utilizamos la fórmula específica proporcionada para la ecuación de la tangente a una parábola de la forma \((x-h)^2=4p(y-k),\) que es:
\(y-k=m (x-h)-p m^2\)
Sustituimos los valores que conocemos: \(h=-2\), \(k=1\), \(p=-3,\) y \(m=-\dfrac{1}{3}.\)
\(y-1=\left(-\dfrac{1}{3}\right) (x-(-2))-(-3) \left(-\dfrac{1}{3}\right)^2\)
Simplificamos:
\(y-1=-\dfrac{1}{3}(x+2)-\left(-\dfrac{1}{3}\right)\)
\(y-1=-\dfrac{1}{3}(x+2)+\dfrac{1}{3}\)
\(y-1=-\dfrac{1}{3}x-\dfrac{2}{3}+\dfrac{1}{3}\)
\(y-1=-\dfrac{1}{3}x-\dfrac{1}{3}\)
Finalmente, despejamos \(y\) para obtener la ecuación de la recta tangente en su forma explícita:
\(y=-\dfrac{1}{3}x-\dfrac{1}{3}+1\)
\(y=-\dfrac{1}{3}x+\dfrac{2}{3}\)
Para mayor claridad, podemos escribirla sin fracciones multiplicando toda la ecuación por 3:
\(3y=-x+2\)
\(x+3y-2=0\)
Ahora, determinamos el punto de contacto (punto de tangencia) utilizando la fórmula proporcionada: \((h+2pm, k+pm^2).\) Sustituimos los valores conocidos: \(h=-2\), \(k=1\), \(p=-3\), \(m=-\dfrac{1}{3}.\)
Calculamos la coordenada \(x_t\) del punto de tangencia:
\(x_t=h+2pm=-2+2(-3)\left(-\dfrac{1}{3}\right)\)
\(x_t=-2+2(1)\)
\(x_t=-2+2\)
\(x_t=0\)
Calculamos la coordenada \(y_t\) del punto de tangencia:
\(y_t=k+pm^2=1+(-3)\left(\dfrac{1}{9}\right)\)
\(y_t=1-\dfrac{3}{9}\)
\(y_t=\dfrac{2}{3}\)
Por lo tanto, la ecuación de la tangente es \(x+3y-2=0\) y el punto de contacto es \(\left(0, \dfrac{2}{3}\right).\)
Método usando cálculo diferencial
Cuando se conoce la pendiente m de la recta tangente que queremos hallar, podemos determinar tanto el punto de tangencia como la ecuación de la recta utilizando derivadas. Para ello, seguimos los siguientes pasos:
- Identificar la pendiente m de la recta tangente. Si el problema nos da la ecuación de una recta, debemos despejar y para reescribir la recta en la forma y = mx + b, donde podemos extraer el valor de la pendiente m.
- Calcular la derivada de la parábola para obtener la pendiente de la tangente en función de las variables.
- Igualar la derivada a la pendiente conocida: de esta manera obtenemos una relación que permite calcular una de las coordenadas del punto de tangencia.
- Hallar el punto de tangencia: con el valor de la coordenada encontrado en el paso anterior, sustituimos en la ecuación original de la parábola para calcular la coordenada faltante. Así determinamos el punto (x0, y0) donde la recta de pendiente m toca la parábola.
- Escribir la ecuación de la recta tangente: teniendo la pendiente m y el punto de tangencia (x0, y0), utilizamos la fórmula punto-pendiente para escribir la ecuación de la recta tangente: y - y0 = m (x - x0).
Ejemplo
Encontrar la ecuación de la tangente a \(y^2=4x\) paralela a la recta \(y-2x-1=0\)
Solución
Comenzamos determinando la pendiente requerida. Despejamos \(y\) en la ecuación de la recta dada: \(y=2x+1,\) de donde obtenemos que su pendiente es \(m=2.\) Como las rectas paralelas tienen la misma pendiente, la tangente que buscamos también debe tener \(m=2.\)
Ahora, para aplicar el cálculo diferencial, derivamos implícitamente la ecuación de la parábola \(y^2=4x.\) Derivamos ambos lados con respecto a \(x:\)
\(\dfrac{d}{dx}(y^2)=\dfrac{d}{dx}(4x)\)
\(2y \dfrac{dy}{dx}=4\)
Despejamos la derivada \(\dfrac{dy}{dx},\) que representa la pendiente de la tangente en cualquier punto \((x, y)\) de la parábola:
\(\dfrac{dy}{dx}=\dfrac{4}{2y}=\dfrac{2}{y}\)
Igualamos esta expresión a la pendiente \(m=2:\)
\(\dfrac{2}{y}=2\)
Resolvemos para \(y:\)
\(2=2y\)
\(y=1\)
Con este valor de \(y,\) sustituimos en la ecuación original de la parábola para hallar la coordenada \(x\) correspondiente:
\((1)^2=4x\)
\(1=4x\)
\(x=\dfrac{1}{4}\)
Así, el punto de tangencia es \(\left(\dfrac{1}{4}, 1 \right).\)
Finalmente, escribimos la ecuación de la recta tangente utilizando la forma punto-pendiente \(y-y_0=m(x-x_0),\) con \(m=2\) y el punto \(\left(\dfrac{1}{4}, 1 \right):\)
\(y-1=2 \left(x-\dfrac{1}{4} \right)\)
Simplificamos:
\(y-1=2x-\dfrac{1}{2}\)
\(y=2x-\dfrac{1}{2}+1\)
\(y=2x+\dfrac{1}{2}\)
Para expresarla en forma general, multiplicamos ambos lados por 2 para eliminar fracciones:
\(2y=4x+1\)
\(4x-2y+1=0\)
Por lo tanto, la ecuación de la tangente es \(4x-2y+1=0.\)
Métodos geométricos de construcción
Existen diversos métodos geométricos para trazar rectas tangentes a una parábola, utilizados principalmente en dibujo técnico. Estos métodos se fundamentan en las propiedades geométricas esenciales de la parábola y en su definición como un lugar geométrico.
Tangente en un punto P de la parábola
Para trazar la recta tangente en un punto específico P perteneciente a la parábola, se sigue este procedimiento:
- Desde el punto P, trace una línea perpendicular a la directriz. Esta perpendicular cortará a la directriz en un punto que denominaremos A.
- La recta tangente en P es la mediatriz del segmento AF, siendo F el foco de la parábola.
Tangentes desde un punto exterior Q
Cuando se requiere encontrar las tangentes a la parábola desde un punto exterior Q, el método es el siguiente:
- Con centro en el punto Q, trace un arco con un radio igual a la distancia QF (la distancia desde el punto exterior al foco). Este arco debe cortar la directriz en dos puntos, A y B.
- Trace las mediatrices de los segmentos AF y BF. Estas mediatrices son las dos rectas tangentes buscadas.
- Para hallar los puntos de tangencia correspondientes, trace líneas perpendiculares a la directriz que pasen por los puntos A y B. La intersección de estas rectas con la parábola determinará los puntos de tangencia.
Tangente paralela a una dirección dada
Este método se emplea para dibujar una recta tangente que tenga una dirección (y por lo tanto una pendiente) específica.
- Trace una línea que sea perpendicular a la dirección dada y que pase por el foco (F) de la parábola. Esta recta perpendicular cortará a la directriz en un punto A.
- La mediatriz del segmento AF es la recta tangente buscada, ya que es paralela a la dirección especificada.
- Para identificar el punto de tangencia T, dibuje una recta perpendicular a la directriz que pase por el punto A. La intersección de esta recta con la parábola será el punto T.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta

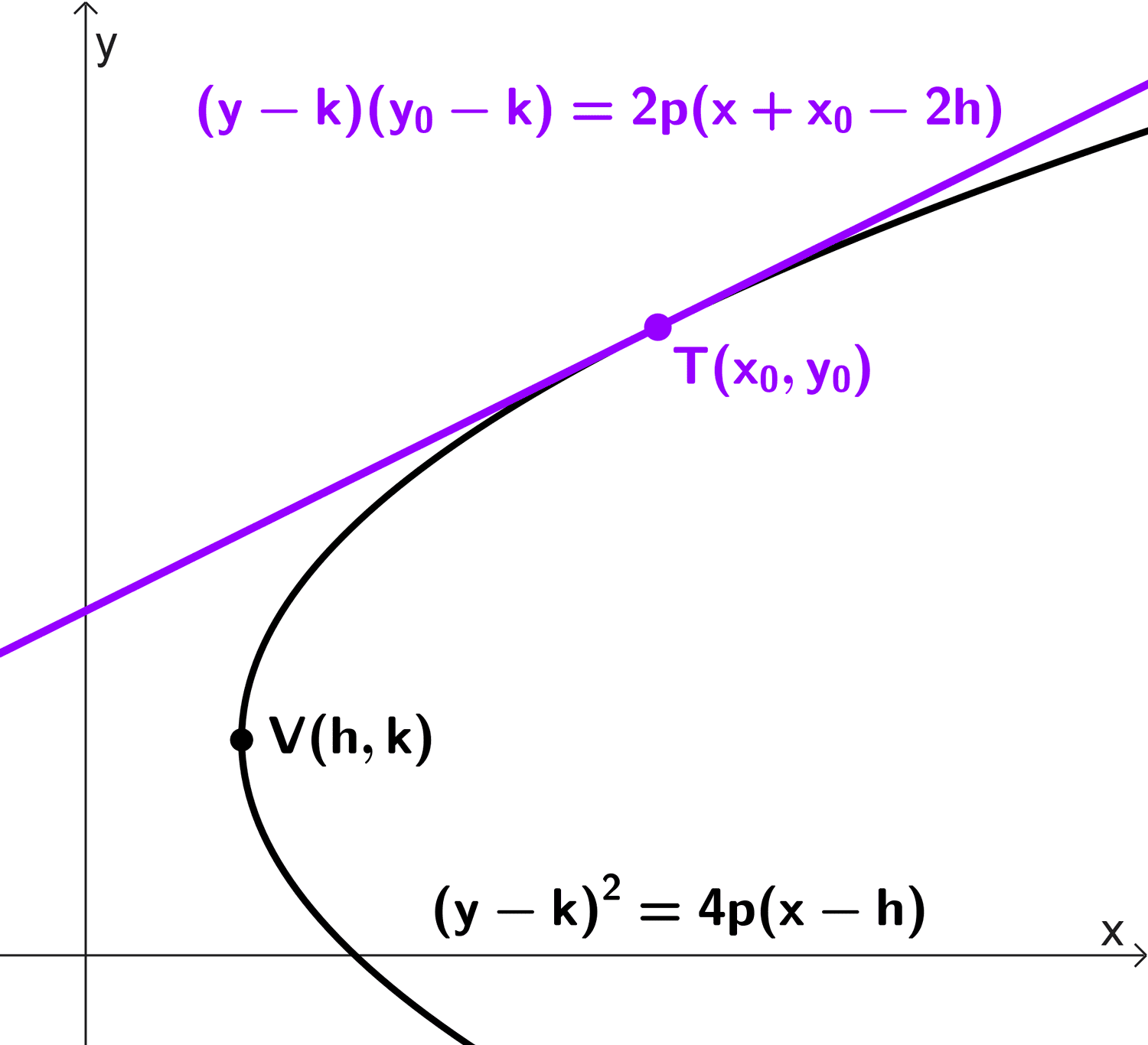
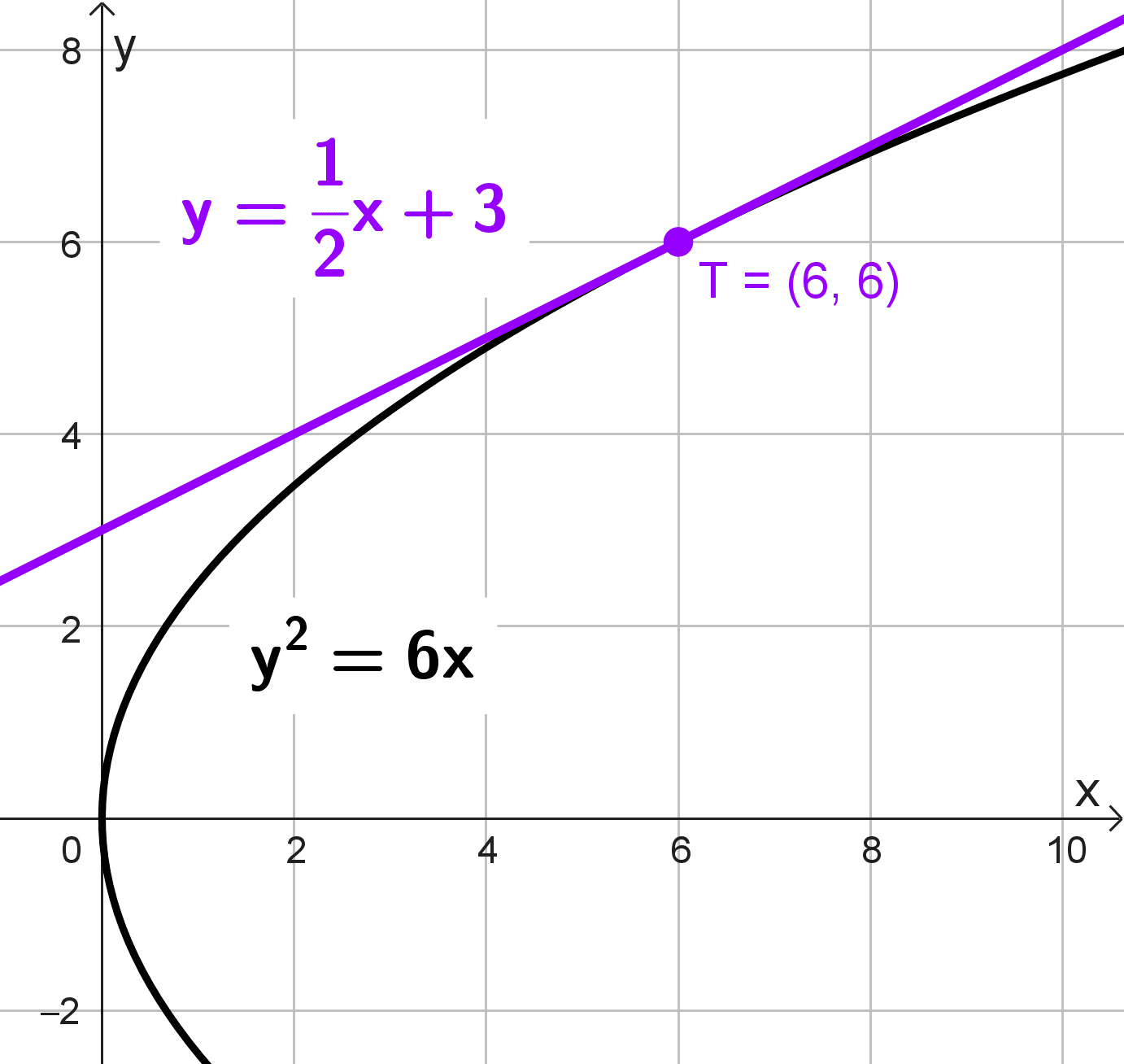
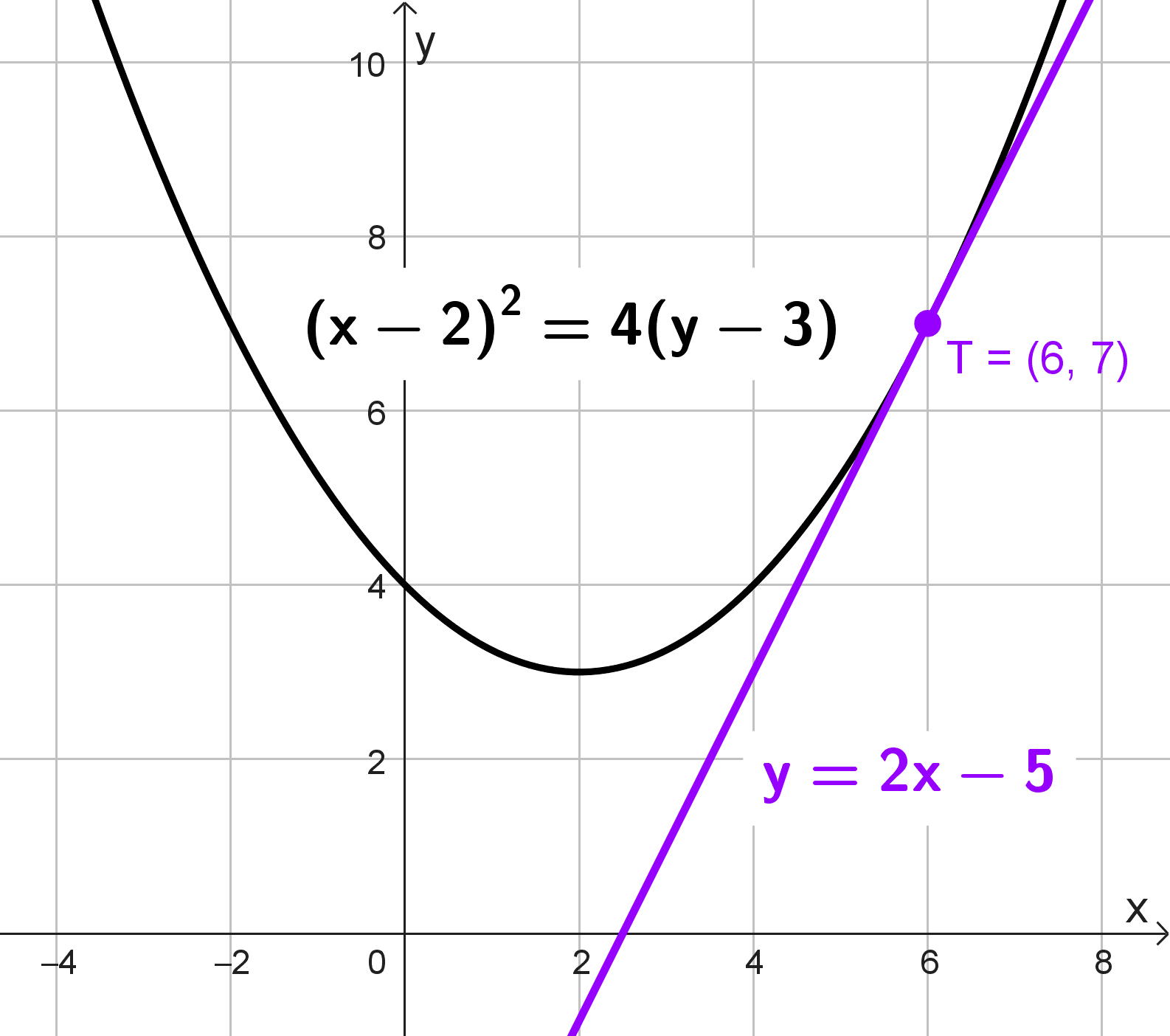
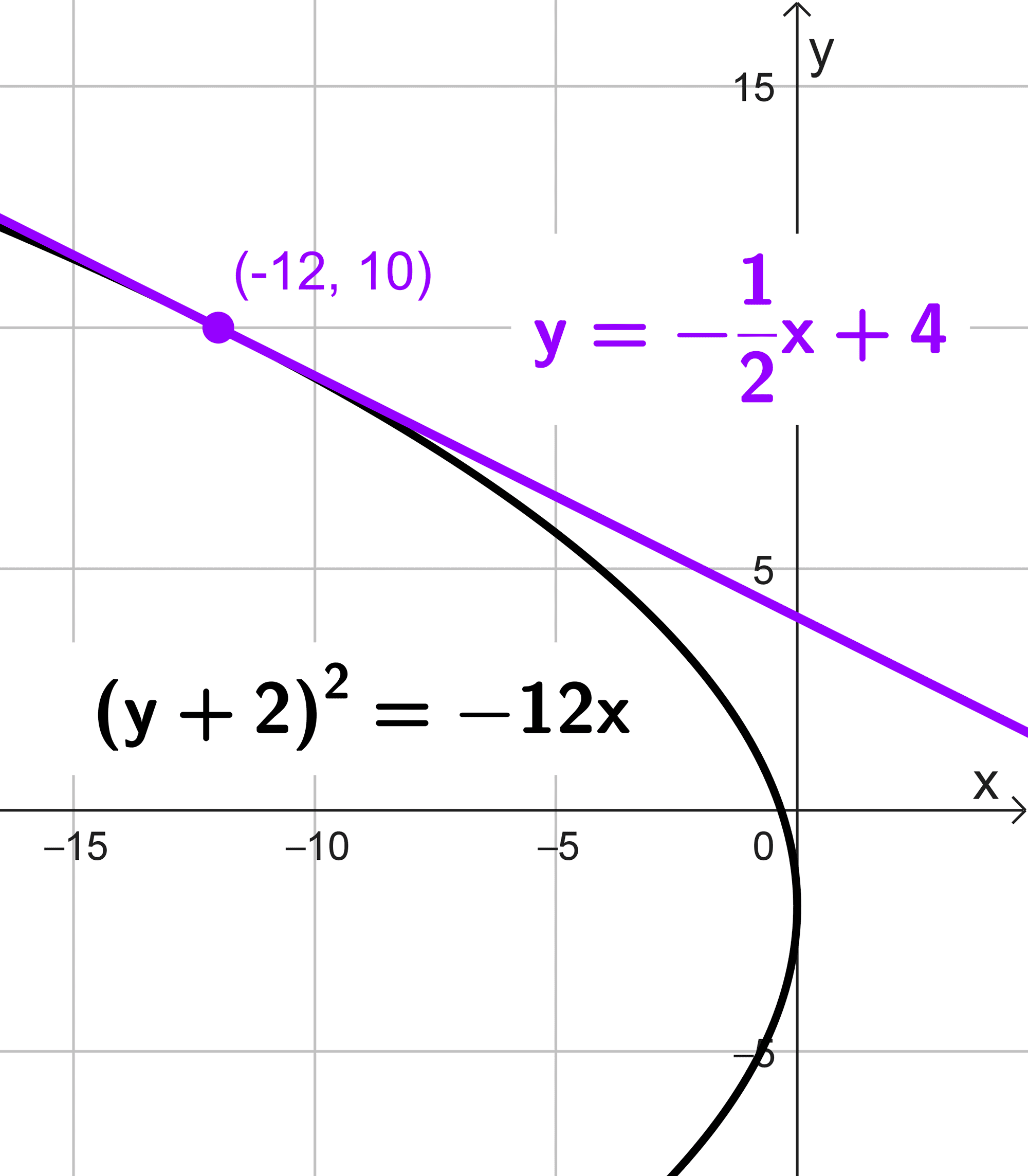
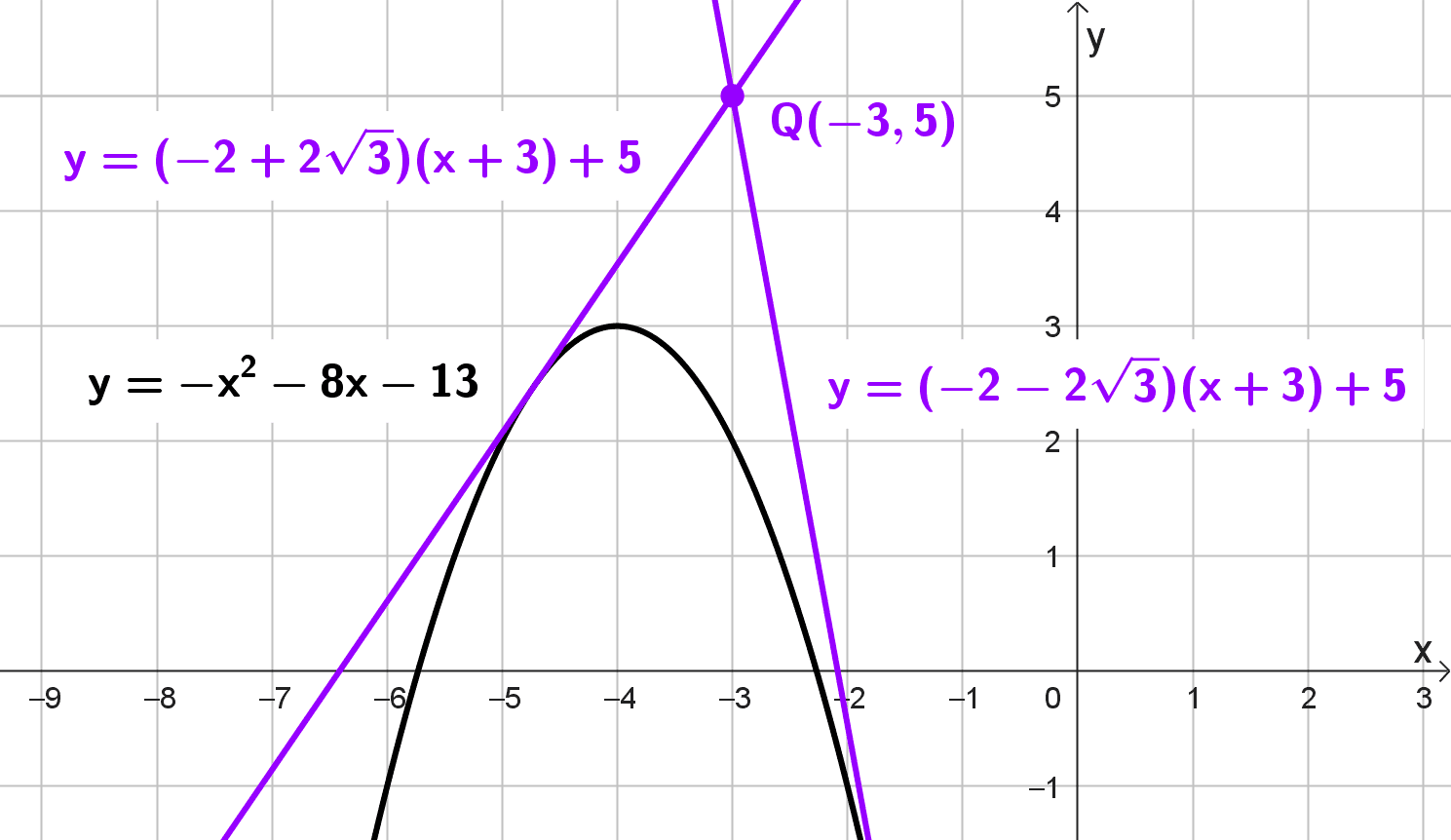
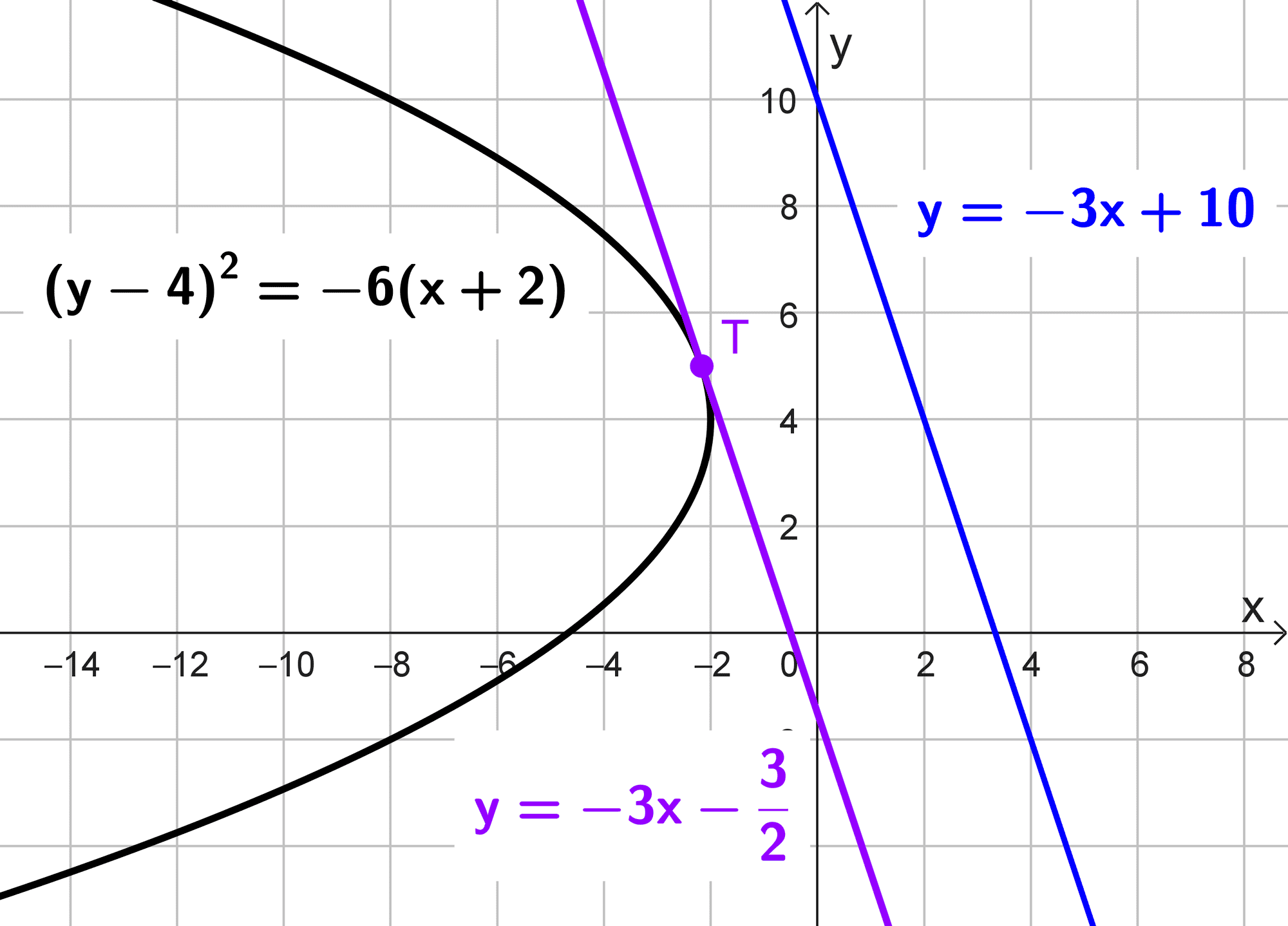
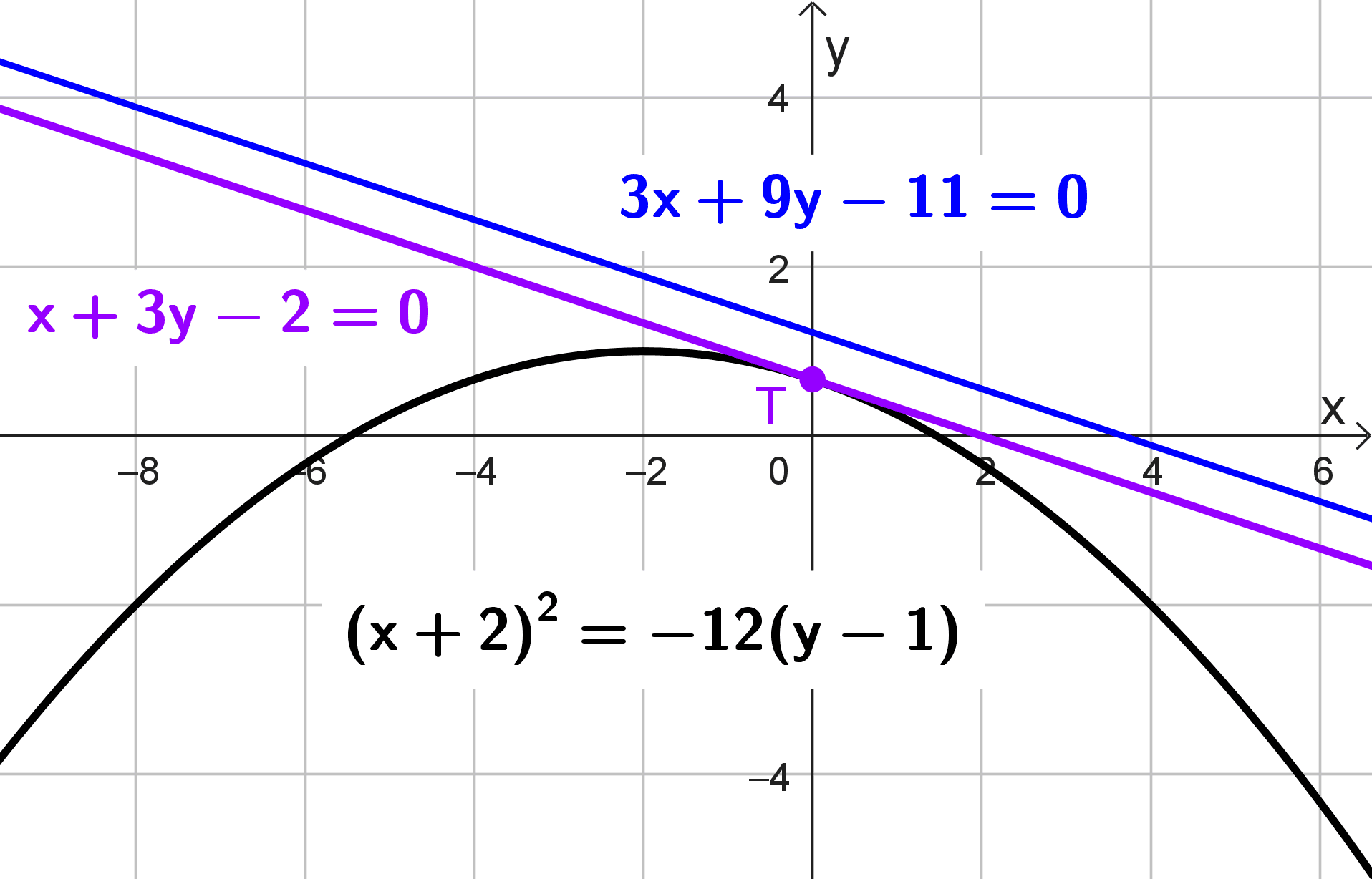




Otros artículos que pueden interesarte