Distancia focal de una parábola

La distancia focal de una parábola es la distancia que existe entre el vértice y el foco a lo largo del eje de simetría. Este valor se puede determinar a partir de la ecuación canónica de la parábola.

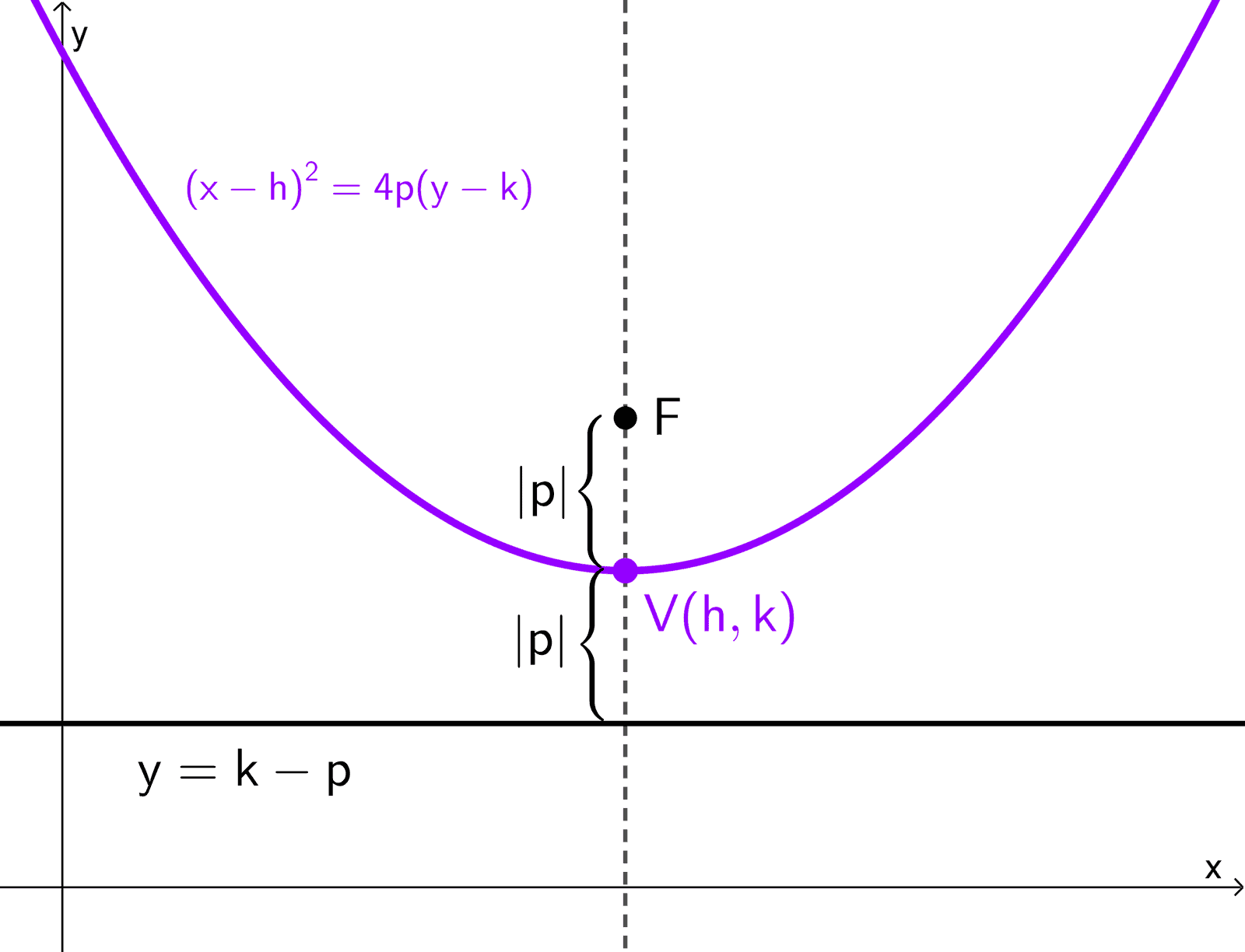
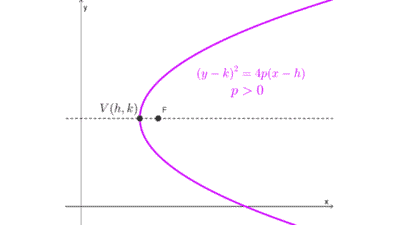
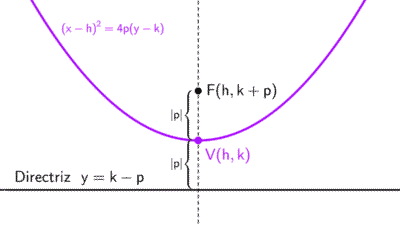
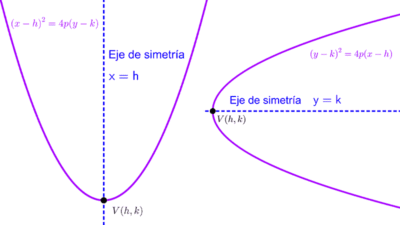
Una parábola vertical con vértice en el origen tiene por ecuación x² = 4py, mientras que una horizontal tiene como ecuación y² = 4px. En ambos casos, la distancia focal es:

d_F = |p|

Es decir, el valor absoluto del parámetro “p” de la ecuación. Si el vértice está en otro punto, la fórmula no cambia.

Distancia focal en una parábola vertical

Distancia focal en una parábola horizontal

La distancia entre el vértice y el foco afecta a la “apertura” de la parábola:

Si |p| es grande, la parábola es más ancha.
Si |p| es pequeña, la parábola es más estrecha.

Nota: aquí nos enfocamos solo en un elemento de la parábola. Para comprenderlo mejor, te recomiendo que antes revises el artículo principal sobre esta cónica, donde abordamos su teoría básica:

Ejemplos

Vimos que para determinar la distancia focal es necesario tener la ecuación canónica y calcular el valor absoluto del parámetro p. Sin embargo, si se tiene la ecuación general en las formas y = ax² + bx + c (parábolas verticales) o x = ay² + by + c (parábolas horizontales), puede obtenerse la distancia focal calculando |1 / 4a|, siendo “a” el coeficiente principal. Esto ocurre porque p = 1 / 4a.

Ecuación de la parábola	Distancia focal
x² = 4py y² = 4px	\|p\|
y = ax² + bx + c x = ay² + by + c	\|1 / 4a\|

Ejercicio

Calcular la distancia focal de las siguientes parábolas:

*y^2=-8x*
*(x+2)^2=-6(y-3)*
*(y-2)^2=4(x-1)*
*x^2=-4 (y-7)*
*y=-2x^2+3x-5*
*-3y^2-x+6y=0*

Solución 1

Ecuación: *y^2=-8x*

Se trata de una parábola horizontal con vértice en el origen. La forma estándar es *y^2=4px,* donde *4p=-8.* Al despejar p, obtenemos *p=-2.* La distancia focal se calcula como *|p|,* por lo que resulta igual a 2.

Solución 2

Ecuación: *(x+2)^2=-6 (y-3)*

Esta es una parábola vertical con vértice en (-2, 3). La forma estándar es *(x-h)^2=4p (y-k),* donde *4p=-6.* Hallamos *p=-1,5* y la distancia focal es *|p|=1,5.*

Solución 3

Ecuación: *(y-2)^2=4 (x-1)*

Corresponde a una parábola horizontal con vértice en (1, 2). Comparando con la forma *(y-k)^2=4p (x-h),* determinamos que *4p=4,* así que *p=1.* La distancia focal es *|p|=1.*

Solución 4

Ecuación: *x^2=-4 (y-7)*

Es una parábola vertical con vértice en *(0, 7).* La ecuación se ajusta a *x^2=4p (y-k),* donde *4p=-4.* Calculamos *p=-1,* y la distancia focal es *|p|=1.*

Solución 5

Ecuación: *y=-2x^2+3x-5*

Identificamos que es una parábola vertical con coeficiente principal *a=-2.* La distancia focal se calcula directamente como:

*\text{Distancia focal}=\left| \dfrac{1}{4a} \right|=\left| \dfrac{1}{4(-2)} \right|=\left|-\dfrac{1}{8} \right|=0,125*

Solución 6

Ecuación: *-3y^2-x+6y=0*

Despejamos *x* para expresarla como *x=ay^2+by+c:*

*x=-3y^2+6y*

El coeficiente principal es *a=-3.*

La distancia focal se calcula como:

*\text{Distancia focal}=\left| \dfrac{1}{4a} \right|=\left| \dfrac{1}{4(-3)} \right|=\left|-\dfrac{1}{12} \right|=\dfrac{1}{12} ≈ 0,0833*

Bibliografía consultada

Lehmann, C. (1989). Geometría Analítica. Limusa.
Sullivan, M. (2006). Álgebra y Trigonometría. Pearson Educación.
Swokowski, E. y Cole, J. (2009). Álgebra y Trigonometría con Geometría Analítica. Cengage Learning.