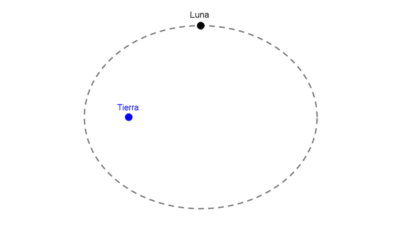
Elipses con centro en el origen y fuera del origen
En este artículo explicamos las ecuaciones de una elipse dependiendo de si el centro es el origen de coordenadas o un punto diferente (h, k).
Índice
Ecuación de la elipse con centro en el origen
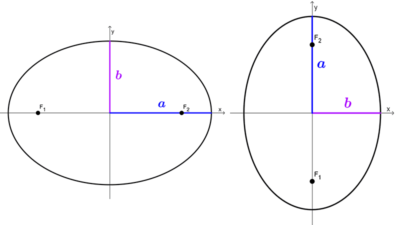
La ecuación canónica u ordinaria de una elipse centrada en el origen de coordenadas varía según si el eje mayor de la misma es horizontal o vertical:
Elipse horizontal: \(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\)
Elipse vertical: \(\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1\)
en donde:
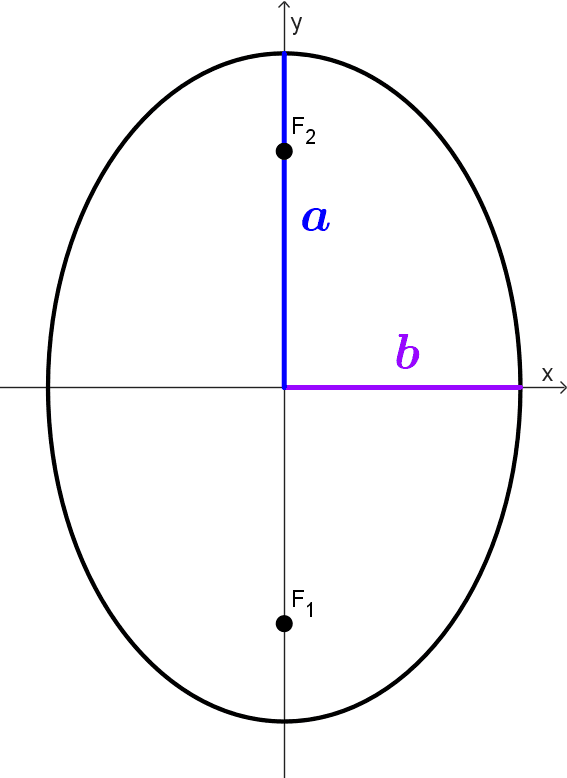
- a > b
- El eje mayor mide 2a.
- El eje menor mide 2b.
Cuando el centro es el origen, los ejes mayor y menor de la elipse están sobre los ejes cartesianos. El eje focal es el eje x si la elipse es horizontal y es el eje y si la elipse es vertical.
En la siguiente tabla se muestran los demás elementos que pueden extraerse a partir de la ecuación ordinaria:
| Ecuación | Eje mayor | Centro | Focos | Vértices |
|---|---|---|---|---|
| \(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\) | Sobre el eje x | (0, 0) | (±c, 0) donde c = √(a2 - b2) | (±a, 0) (0, ±b) |
| \(\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1\) | Sobre el eje y | (0, 0) | (0, ±c) donde c = √(a2 - b2) | (0, ±a) (±b, 0) |
La ecuación general de una elipse con centro en el origen se puede obtener reacomodando la fórmula reducida hasta que tome la siguiente forma:
Ax2 + Cy2 + F = 0
donde A ≠ C y ambos tienen el mismo signo.
Nótese que el hecho de estar centrada en (0, 0) hace que no aparezcan términos lineales (Dx y Ey) en la ecuación general.
Ejemplos
Las siguientes son ecuaciones de elipses centradas en (0, 0):
- \(\dfrac{x^2}{16}+\dfrac{y^2}{9}=1\)
- \(\dfrac{x^2}{4}+\dfrac{y^2}{25}=1\)
- \(16x^2+25y^2-100=0\)
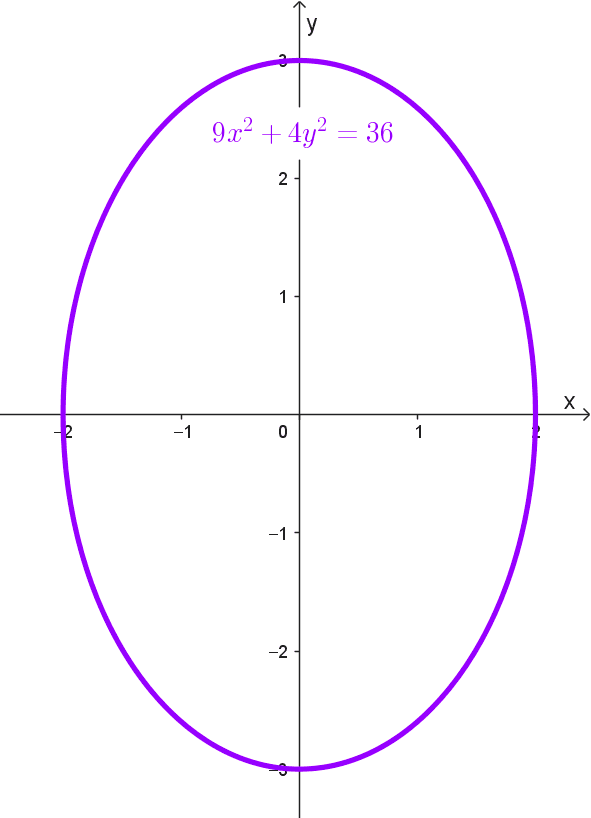
- \(9x^2+4y^2=36\)
Ecuación de la elipse con centro fuera del origen
Cuando el centro de la elipse está desplazado del origen, la ecuación canónica toma una forma ligeramente diferente a lo que se vio anteriormente. Se utilizan las letras h y k como coordenadas genéricas del centro y se reemplaza x por (x - h) e y por (y - k) en las ecuaciones.
De nuevo, las ecuaciones de una elipse con centro en (h, k) varían dependiendo de si el eje mayor es horizontal o vertical:
Elipse horizontal: \(\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1\)
Elipse vertical: \(\dfrac{(x-h)^2}{b^2}+\dfrac{(y-k)^2}{a^2}=1\)
donde:
- a > b
- El eje mayor mide 2a.
- El eje menor mide 2b.
Cuando el centro está fuera del origen, los ejes mayor y menor de la elipse son paralelos a los ejes cartesianos. El eje focal es paralelo al eje x si la elipse es horizontal y paralelo al eje y si la elipse es vertical.
¿Te está sirviendo este artículo? ¡Por favor, califícalo!
En la siguiente tabla se muestran los demás elementos que pueden obtenerse a partir de la ecuación ordinaria:
| Ecuación | Eje mayor | Centro | Focos | Vértices |
|---|---|---|---|---|
| \(\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1\) | Paralelo al eje x | (h, k) | (h ± c, k) donde c = √(a2 - b2) | (h ± a, k) (h, k ± b) |
| \(\dfrac{(x-h)^2}{b^2}+\dfrac{(y-k)^2}{a^2}=1\) | Paralelo al eje y | (h, k) | (h, k ± c) donde c = √(a2 - b2) | (h, k ± a) (h ± b, k) |
La ecuación general de una elipse con centro fuera del origen se puede obtener desarrollando los cuadrados y acomodando los términos para que tomen la siguiente forma:
Ax2 + Cy2 + Dx + Ey + F = 0
donde A ≠ C y ambos tienen el mismo signo.
A diferencia del caso anterior, cuando el centro no es el origen, en la fórmula general aparecen términos lineales (Dx o Ey, o ambos).
Ejemplos
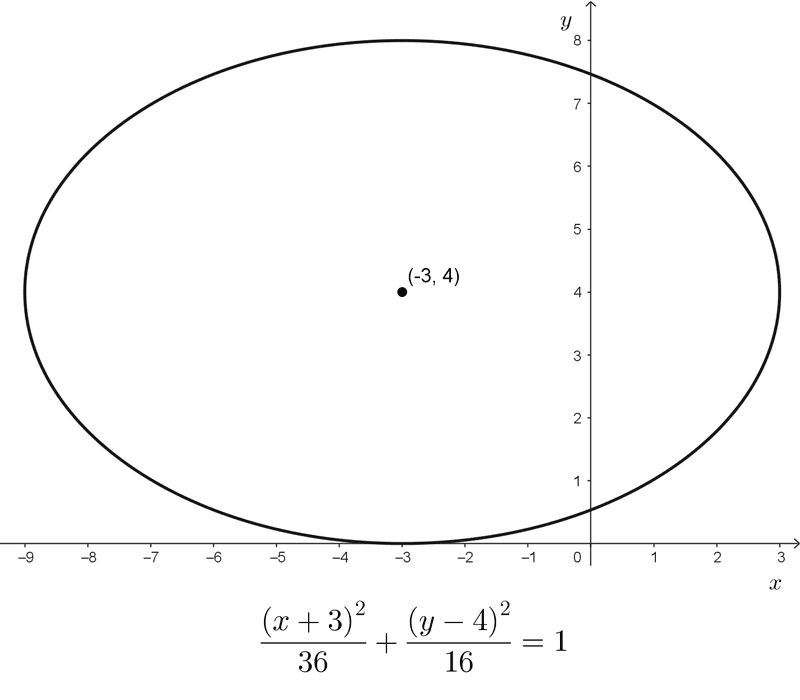
- \(\dfrac{(x+3)^2}{36}+\dfrac{(y-4)^2}{16}=1\) es una elipse con centro en (-3, 4)
- \(\dfrac{(x-1)^2}{9}+\dfrac{(y+2)^2}{25}=1\) tiene centro en (1, -2)
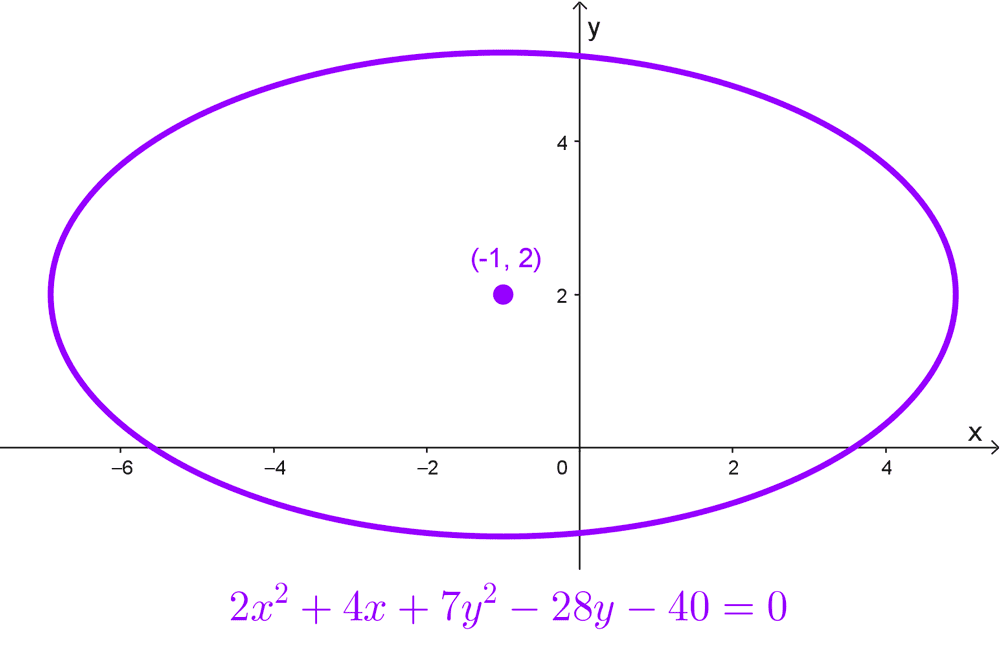
- \(2x^2+4x+7y^2-28y-40=0\) es una elipse con centro fuera del origen, se puede reescribir como \(\dfrac{(x+1)^2}{35}+\dfrac{(y-2)^2}{10}=1,\) de donde extraemos que el centro es (-1, 2).
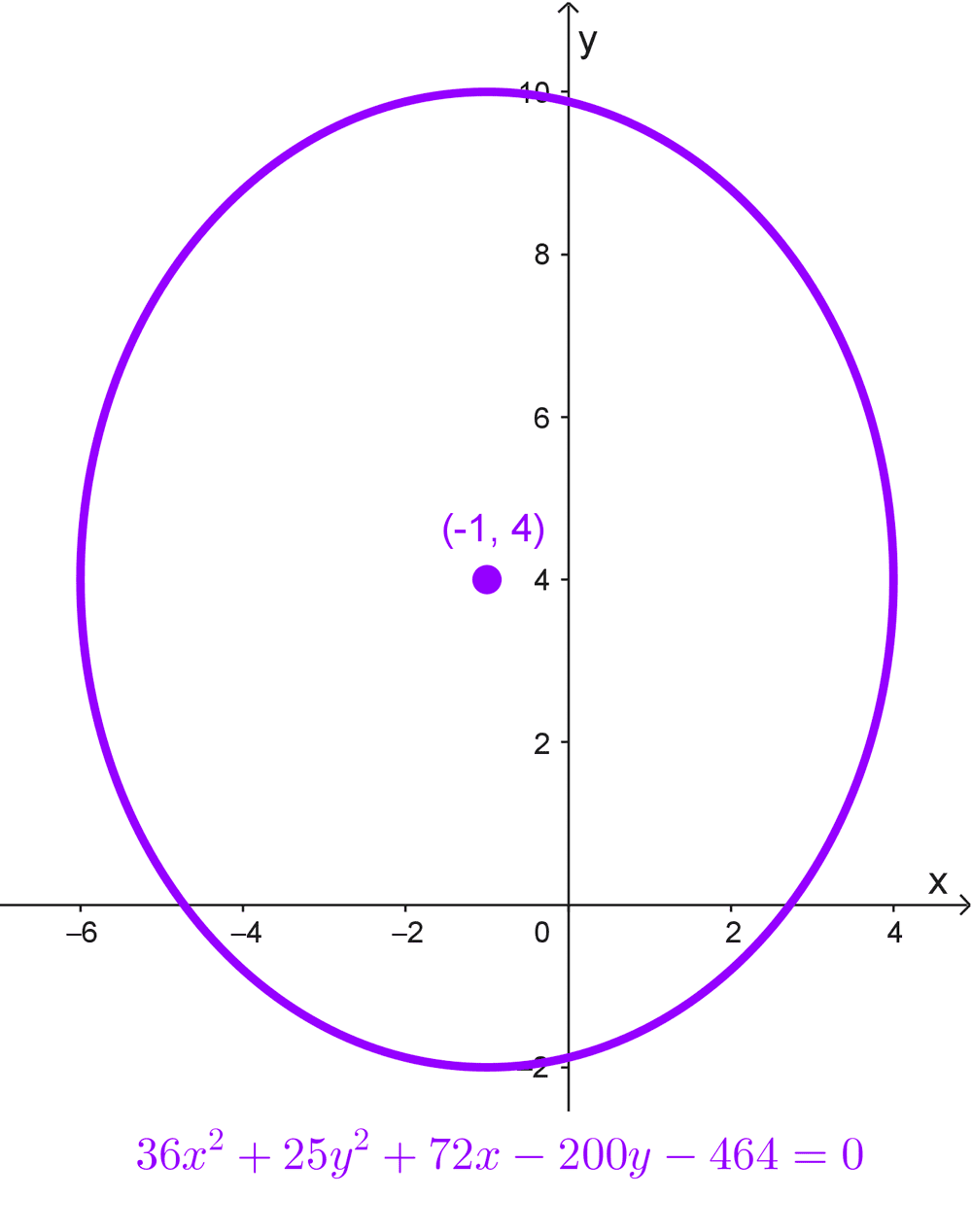
- \(36x^2+25y^2+72x-200y-464=0\) tiene centro desplazado del origen, se puede reescribir como \(\dfrac{(x+1)^2}{25}+\dfrac{(y-4)^2}{36}=1,\) de aquí se extrae que el centro es C(-1, 4).
Ejercicios resueltos
A continuación, veremos algunos ejercicios sobre armado de ecuaciones. Los ejercicios que consisten en encontrar el centro de una elipse están en el siguiente artículo:
Ejercicio 1
Determinar la ecuación de una elipse vertical centrada en el origen cuya distancia focal es 4 y el semieje menor mide 3 unidades.
Solución
Los datos del problema son:
- Distancia focal: 2c = 4
- Semieje menor: b = 3
Como el centro es el origen y la elipse es vertical, se busca una ecuación de la siguiente forma:
\(\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1\)
Sabiendo que b = 3 y c = 4/2 = 2, se puede obtener el semieje mayor mediante la relación fundamental:
\(c^2=a^2-b^2→a^2=c^2+b^2\)
Reemplazando los datos:
\(a^2=2^2+3^2\)
\(a^2=4+9\)
\(a^2=13\)
Ahora tenemos a2 = 13 y b2 = 9, estos datos los sustituimos en la ecuación:
\(\dfrac{x^2}{9}+\dfrac{y^2}{13}=1\)
Esta última es la ecuación canónica de la elipse que buscamos.
Ejercicio 2
Escriba la ecuación de la elipse horizontal con centro en (2, 1) con eje mayor igual a 25 y eje menor igual a 4.
Solución
El problema nos da la siguiente información:
- Centro: (2, 1)
- Elipse horizontal.
- Eje mayor: 2a = 25 → a = 25/2
- Eje menor: 2b = 4 → b = 2
Teniendo en cuenta todo esto, buscamos una elipse con la siguiente ecuación:
\(\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1\)
donde (h, k) es el centro de la elipse.
Reemplazando los datos obtenemos:
\(\dfrac{(x-2)^2}{(25/2)^2}+\dfrac{(y-1)^2}{(2)^2}=1\)
Simplificando:
\(\dfrac{(x-2)^2}{625/4}+\dfrac{(y-1)^2}{4}=1\)
Esta última es la ecuación que se estaba buscando.
Ejercicio 3
Encuentra la ecuación de la elipse vertical si a = 4 y b = 1 y el centro es el punto (0, 0).
Solución
Teniendo en cuenta que la elipse es vertical y el centro es el origen, se busca una ecuación así:
\(\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1\)
Reemplazando los datos conocidos y simplificando obtenemos la ecuación de la elipse:
\(\dfrac{x^2}{1^2}+\dfrac{y^2}{4^2}=1\)
\(\dfrac{x^2}{1}+\dfrac{y^2}{16}=1\)
\(x^2+\dfrac{y^2}{16}=1\)
Ejercicio 4
Encuentre la ecuación canónica de una elipse cuyo eje menor es vertical, sus focos son (1, 2) y (5, 2) y un vértice secundario está en (3, 4).
Solución
Datos del problema:
- La elipse es horizontal porque su eje menor es vertical.
- Focos: F1(1, 2) y F2(5, 2).
- Vértice secundario: Vs(3, 4).
Primero calculamos el centro de la elipse, que es el punto medio de los focos:
\(C=\left(\dfrac{1+5}{2}, \dfrac{2+2}{2} \right)=(3, 2)\)
El centro de la elipse es C(3, 2).
Ahora determinamos la distancia focal 2c, que es la distancia entre los focos:
\(2c=\sqrt{(5-1)^2+(2-2)^2}=\sqrt{4^2}=4\)
Por lo tanto, c = 2.
El vértice secundario Vs(3, 4) está alineado verticalmente con el centro C(3, 2). Esto implica que la distancia del centro al vértice secundario es b.
Calculamos b:
\(b=|y_{\text{vértice}}-y_{\text{centro}}|=|4-2|=2\)
Por lo tanto, b = 2.
La relación entre a, b y c para una elipse es:
\(c^2=a^2-b^2\)
Sustituimos c = 2 y b = 2:
\(2^2=a^2-2^2 → 4=a^2-4 → a^2=8\)
La ecuación canónica de una elipse con eje mayor horizontal es:
\(\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1\)
donde (h, k) es el centro.
Sustituimos h = 3, k = 2, a2 = 8 y b2 = 4:
\(\dfrac{(x-3)^2}{8}+\dfrac{(y-2)^2}{4}=1\)
Esta última es la ecuación canónica de la elipse.
Ejercicio 5
Determine si la ecuación \(x^2+3y^2-6x+6y=0\) representa una elipse con centro en el origen o fuera del origen.
Solución
Observando la ecuación vemos que aparecen términos lineales -6x y 6y. La existencia de términos lineales en la ecuación general nos indica que el centro de la elipse está fuera del origen de coordenadas.
Recursos adicionales
Los siguientes videos explican cómo varían las ecuaciones dependiendo del centro de la elipse.
Bibliografía consultada
- Engler, A., Müller, D., Vrancken, S. y Hecklein, M. (2020). Geometría analítica. Universidad Nacional del Litoral.
- Fuller, G. y Tarwater, D. (1995). Geometría analítica (7.ª ed.). Pearson Educación.
- Lehmann, C. (1989). Geometría analítica. Limusa.
- Leithold. L. (1992). Álgebra y trigonometría con geometría analítica. Oxford University Press.
- Márquez, A., Vázquez, F., Ruiz, H., Villegas, M. y Figueroa, M. (2009). Geometría analítica. Prentice Hall.
- Raichman, S. y Totter, E. (2016). Geometría analítica para ciencias e ingeniería. Universidad Nacional de Cuyo.
- Sullivan, M. (2006). Álgebra y trigonometría. Pearson Educación.
- Swokowski, E. y Cole, J. (2009). Álgebra y trigonometría con geometría analítica. Cengage Learning.
¿Te ha servido este contenido? ¡Califícalo!
-
hola me gusta el contenido
2 Comentarios
Deja una respuesta



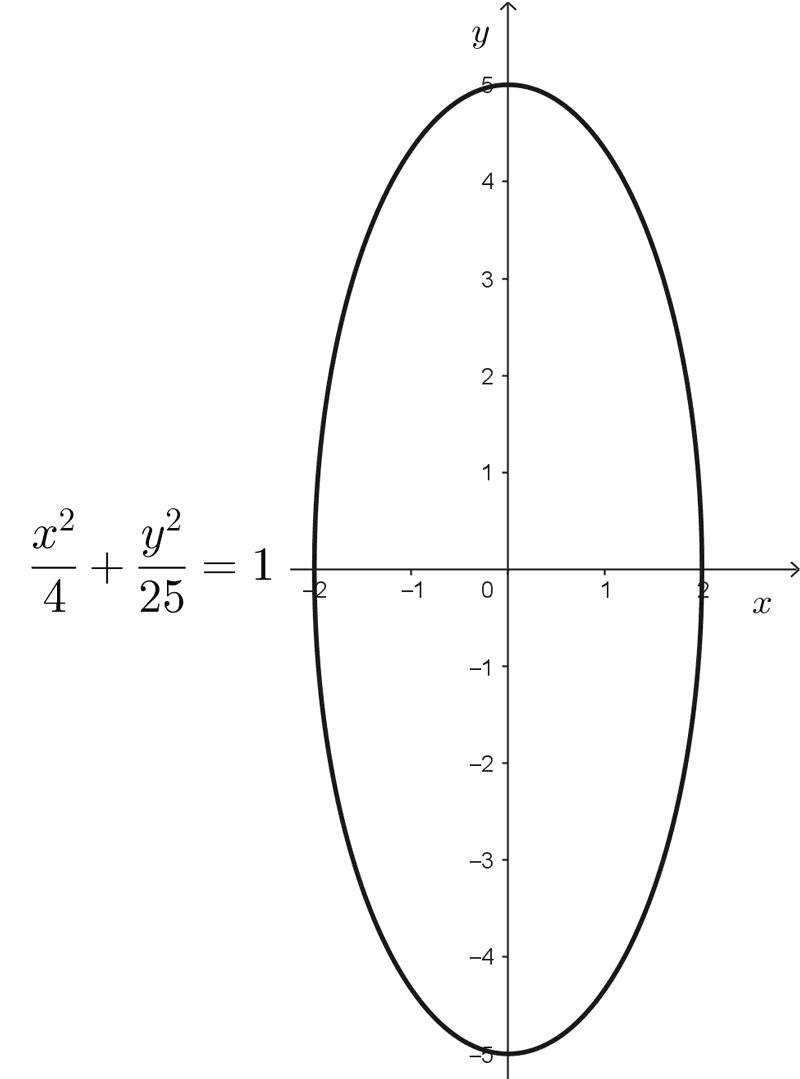



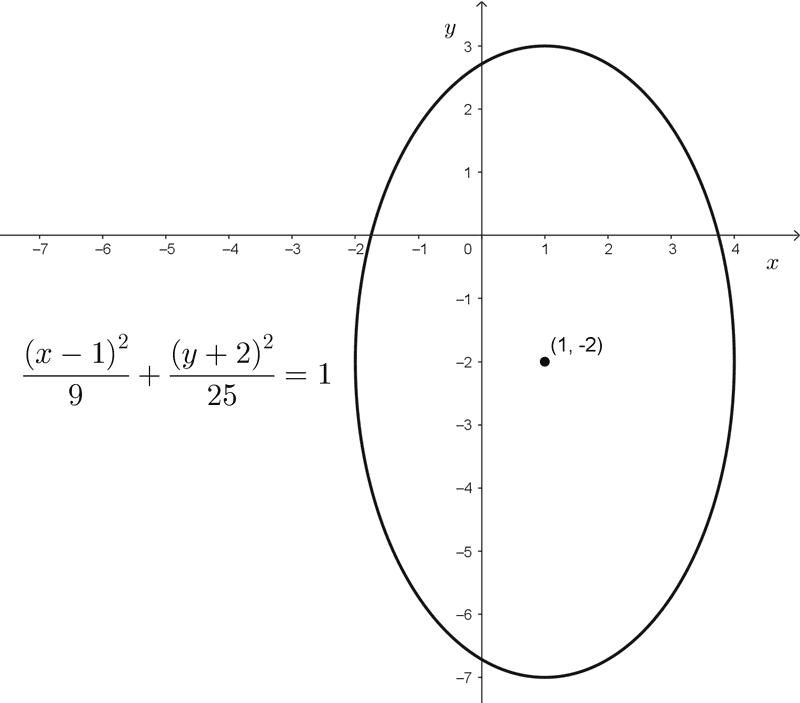


Otros artículos que pueden interesarte