Cónicas degeneradas
En geometría analítica, una cónica degenerada es aquella que no exhibe las propiedades habituales que caracterizan a las secciones cónicas. Esto ocurre cuando algunos de los coeficientes en la ecuación general se anulan, lo que provoca que la cónica adopte formas más simples.
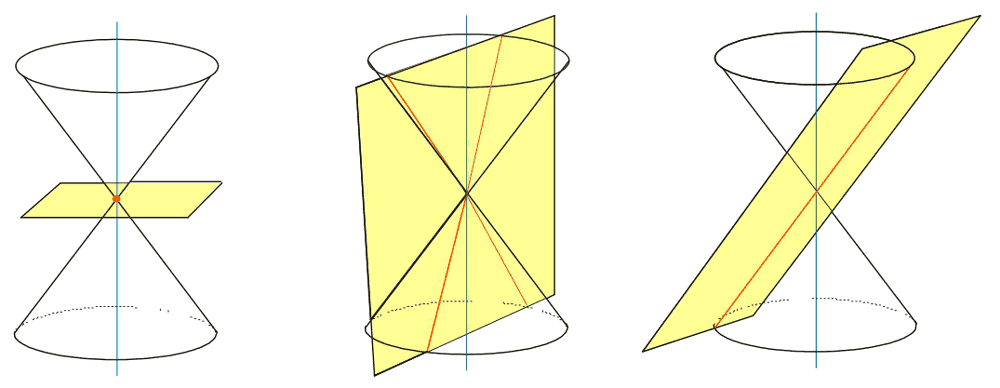
Desde una perspectiva geométrica, una cónica degenerada puede visualizarse como el resultado de la intersección de un plano con un cono circular recto de dos hojas, cuando dicho plano pasa por el vértice del cono.
Las cónicas degeneradas se clasifican en tres tipos principales:
- Punto: cuando el plano corta al vértice y no a las hojas.
- Recta (dos rectas coincidentes): cuando el plano tiene la misma inclinación que una generatriz del cono y pasa por el vértice. Como las rectas coinciden, se ven como solo una.
- Par de rectas que se cruzan: cuando el plano pasa por el vértice y corta las dos hojas del cono.
Cada una de las secciones cónicas tiene sus casos degenerados, los cuales pueden verse en la siguiente tabla:
| Cónica | Caso degenerado | Ecuación degenerada |
|---|---|---|
| Elipse | Un punto real | (x - h)² + (y - k)² = 0 La gráfica es el punto (h, k) |
| Hipérbola | Dos rectas que se cruzan formando una X. | (x - h)² / a² - (y - k)² / b² = 0 (y - k)² / a² - (x - h)² / b² = 0 La gráfica son dos rectas que se cortan en (h, k) formando una cruz. |
| Parábola | Dos rectas paralelas o coincidentes, reales o imaginarias. | (x - h)² = a (y - k)² = a Cuando a>0, se trata de rectas reales. Cuando a<0, son rectas imaginarias. Si a=0, las rectas son coincidentes. |
Índice
Ejemplos
Elipses degeneradas: las siguientes son ecuaciones de elipses que se degeneran en un único punto.
- *x^2+y^2=0*
- *(y-3)^2+(x+1)^2=0*
- *x^2+(y+6)^2=0*
- *-(x+4)^2-y^2=0*
- *(x-2)^2=-(y+4)^2*
Una ecuación del tipo *(x-h)^2+(y-k)^2=k* donde k es negativo, corresponde a una elipse imaginaria y no a un caso degenerado. Por ejemplo, la ecuación *x^2+y^2=-1* es una elipse sin puntos reales. Las siguientes son gráficas de elipses degeneradas:
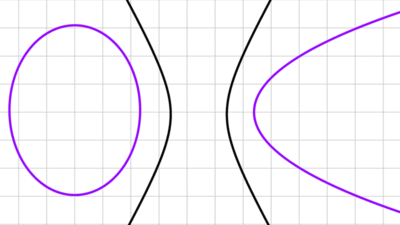
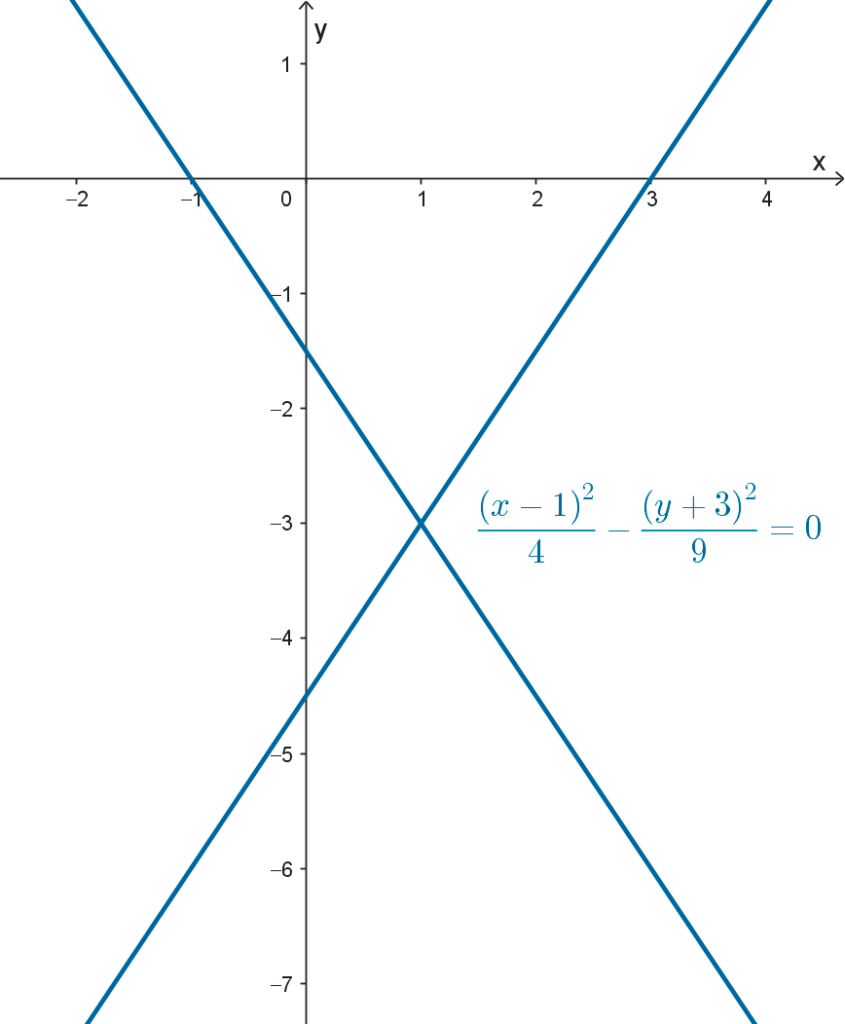
Hipérbolas degeneradas: las siguientes son ecuaciones de hipérbolas que se degeneran en dos rectas.
- *x^2-y^2=0*
- *(x+5)^2-(y+1)^2 = 0*
- *\dfrac{(x-1)^2}{4}-\dfrac{(y+3)^2}{9}=0*
- *\dfrac{(y-2)^2}{16}-\dfrac{(x+5)^2}{25}=0*
- *\dfrac{(x+3)^2}{1}=\dfrac{(y-4)^2}{2}*
Una ecuación de la forma *\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=0* representa dos rectas que se cruzan cuyas pendientes son a/b y -a/b. Las siguientes son gráficas de hipérbolas degeneradas:
Parábolas degeneradas: las siguientes son ecuaciones de parábolas que se degeneran en líneas paralelas o coincidentes. Estas pueden ser reales o imaginarias.
- *x^2=0* (rectas coincidentes)
- *y^2=-6* (rectas imaginarias)
- *(y-2)^2=3*
- *(x+1)^2=0*
- *y^2-3y=-2*
- *x^2=5*
En ecuaciones de la forma (x-h)² = a o (y-k)² = a, las rectas paralelas están separadas por una distancia |2a|. Las siguientes son gráficas de parábolas degeneradas:
Nota: a partir de la ecuación general Ax2 + Bxy + Cy2 + Dx + Ey + F = 0, si ocurre que A, B y C son cero, la fórmula se reduce a Dx + Ey + F = 0, lo cual representa una recta en el plano. Sin embargo, una ecuación del último tipo no representa una cónica, por tanto, este no es un caso de cónica degenerada. Para que una ecuación del tipo Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 represente una cónica (regular o degenerada) debe ocurrir que A, B y C no sean todos cero al mismo tiempo, es decir, al menos uno de estos coeficientes debe ser distinto de cero, cosa que no ocurre en Dx + Ey + F = 0.
¿Cómo identificar una cónica degenerada?
Existen dos métodos principales para determinar si una ecuación corresponde a una cónica degenerada: uno práctico y otro más avanzado.
La primera forma consiste en analizar la ecuación de la cónica. Si el término xy no aparece en la ecuación, es posible completar los cuadrados y determinar si la forma canónica resultante corresponde a un caso degenerado. Por otro lado, si el término xy está presente, se puede intentar factorizar la expresión o despejar una variable en términos de la otra para determinar su naturaleza.
Ejemplo 1
Determinar la naturaleza de la ecuación *2x^2+7xy+3y^2+x-7y-6=0.*
Solución: para hacer la determinación, la ecuación se trata como una ecuación cuadrática en x y se aplica la fórmula cuadrática. Así, se obtiene
*2x^2+(7y+1)x+(3y^2-7y-6)=0*
*x=\dfrac{-(7y+1)\pm\sqrt{(7y+1)^2+4\cdot2\cdot(3y^2-7y-6)}}{4}*
*x=\dfrac{-(7y+1)\pm\sqrt{49y^2+14y+1+24y^2-56y-48}}{4}*
*x=\dfrac{-(7y+1)\pm\sqrt{25y^2+70y+49}}{4}*
*x=\dfrac{-(7y+1)\pm(5y+7)}{4}*
Por tanto,
*x=\dfrac{-y+3}{2}~~~ y~~~x=-3y-2*
son las soluciones. Esto significa que la ecuación dada se puede presentar en la forma factorizada
*(2x+y-3)(x+3y+2)=0*
Si las coordenadas de un punto hacen uno de estos factores igual a cero, harán que el producto sea igual a cero, y por tanto satisfacen la ecuación original. Por ello, la gráfica consta de dos rectas cuyas ecuaciones son:
*y-2x-3=0~~~~y~~~~y-2x+4=0*
Es decir, se trata de una hipérbola degenerada.
Ejemplo 2
Probar la ecuación *y^2-4xy+4x^2-2x+y-12=0.*
Solución: despejando en la ecuación para y en términos de x, se encuentran las ecuaciones
*y-2x-3=0~~~~y~~~~y-2x+4=0*
Por consiguiente, la gráfica de la ecuación dada consta de dos rectas paralelas, siendo un caso de parábola degenerada.
La segunda forma para saber si una ecuación es de una cónica degenerada consiste en realizar un estudio de la ecuación utilizando el método de invariantes. Sabemos que la ecuación general de segundo grado que representa a cualquier cónica, ya sea regular o degenerada, tiene la forma: Ax2 + Bxy + Cy2 + Dx + Ey + F = 0.
Para identificar si la cónica es regular o degenerada podemos calcular el determinante de la matriz asociada a la ecuación cuadrática:
*δ = \begin{vmatrix} 2A & B & D \\ B & 2C & E \\ D & E & 2F \\ \end{vmatrix}*
Desarrollando se llega a la expresión:
*δ = 8ACF-2AE^2-2B^2F+2BED-2CD^2*
El valor de este determinante nos indicará si la cónica es regular o es un caso degenerado:
- Si δ ≠ 0: la cónica es regular, lo que significa que la ecuación representa una curva cerrada o abierta en el plano, como una circunferencia, elipse, parábola o hipérbola.
- Si δ = 0: la cónica es degenerada, lo que significa que la ecuación representa un punto o un par de rectas paralelas o coincidentes.
Una vez que se ha determinado que la cónica es degenerada (δ = 0), el siguiente paso es identificar el tipo de degeneración. Para ello, se utiliza el discriminante dado por:
Δ = B2 - 4AC
Este valor nos permite clasificar la cónica degenerada de la siguiente manera:
- B2 - 4AC > 0: la cónica es una hipérbola degenerada, que se manifiesta como un par de líneas reales que se intersectan.
- B2 - 4AC < 0: la cónica es una elipse degenerada que se presenta como un punto real en el plano.
- B2 - 4AC = 0: la cónica es una parábola degenerada, que se muestra como dos líneas paralelas o coincidentes, reales o imaginarias.
Resumiendo, el proceso para determinar si una ecuación del tipo Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 corresponde a una cónica degenerada es:
- Calcular el determinante *δ = \begin{vmatrix} 2A & B & D \\ B & 2C & E \\ D & E & 2F \\ \end{vmatrix}.* Si el resultado es cero, la cónica es degenerada; si es distinto de cero, la cónica es regular.
- Calcular el discriminante Δ = B2 - 4AC, si su valor es positivo, se corresponde a una hipérbola degenerada; si es negativo, corresponde a una elipse degenerada; si es cero, corresponde a una parábola degenerada.
| Determinante | Discriminante | Cónica |
|---|---|---|
| δ = 0 | B2 - 4AC > 0 | Hipérbola degenerada: par de líneas reales que se intersectan. |
| δ = 0 | B2 - 4AC < 0 | Elipse degenerada: un punto real. |
| δ = 0 | B2 - 4AC = 0 | Parábola degenerada: dos líneas paralelas o coincidentes, reales o imaginarias. |
Ejemplo 1
Analizar la ecuación *y^2+2xy+x^2-2x-2y=0*
Solución: comenzamos identificando los coeficientes que corresponden a la forma general de una cónica *Ax^2+Bxy+Cy^2+Dx+Ey+F=0.* En este caso, los coeficientes son A=1, B=2, C=1, D=-2, E=-2, y F=0.
El primer paso es calcular el determinante de la matriz asociada a la ecuación cuadrática para identificar si la cónica es regular o degenerada:
*\delta=\begin{vmatrix} 2A & B & D \\ B & 2C & E \\ D & E & 2F \end{vmatrix}=\begin{vmatrix} 2(1) & 2 & -2 \\ 2 & 2(1) & -2 \\ -2 & -2 & 2(0) \end{vmatrix}*
Desarrollamos el determinante:
*\delta=8\cdot1\cdot0-2\cdot1\cdot(-2)^2-2\cdot2^2\cdot0+2\cdot2\cdot(-2)\cdot(-2)-2\cdot1\cdot(-2)^2=0*
El resultado es δ = 0, lo que indica que la cónica es degenerada. A continuación, debemos identificar el tipo de degeneración calculando el discriminante:
*\Delta=B^2-4AC=2^2-4(1)(1)=4-4=0*
El valor del discriminante es Δ = 0, lo que clasifica a la cónica como una parábola degenerada. Esto significa que la ecuación representa dos líneas paralelas o coincidentes.
Ejemplo 2
Determinar si la ecuación *2x^2-xy-y^2+2x+y=0* representa una cónica regular o degenerada y de qué tipo.
Solución: primero, identificamos los coeficientes de la ecuación en la forma general *Ax^2+Bxy+Cy^2+Dx+Ey+F=0.* En este caso, los coeficientes son A=2, B=-1, C=-1, D=2, E=1, y F=0.
El primer paso es calcular el determinante de la matriz asociada a la ecuación cuadrática:
*\delta= \begin{vmatrix} 2A & B & D \\ B & 2C & E \\ D & E & 2F \end{vmatrix}=\begin{vmatrix} 2(2) & -1 & 2 \\ -1 & 2(-1) & 1 \\ 2 & 1 & 2(0) \end{vmatrix}*
Desarrollamos el determinante:
*\delta=8\cdot(-2)\cdot0-2\cdot2\cdot1^2-2\cdot(-1)^2\cdot0+2\cdot(-1)\cdot1\cdot2-2\cdot(-1)\cdot2^2*
Simplificando, obtenemos:
*\delta=0-4-0-4+8=0*
El resultado es δ = 0, lo que indica que la cónica es degenerada. Ahora, para clasificar el tipo de degeneración, calculamos el discriminante:
*\Delta=B^2-4AC=(-1)^2-4(2)(-1)=1+8=9*
El valor del discriminante es Δ = 9, que es mayor que cero. Esto indica que la cónica es una hipérbola degenerada, lo cual se manifiesta como un par de líneas reales que se intersectan.
Ejemplo 3
Realizar el análisis de la ecuación *25x^2 + 36y^2 + 30xy = 0*
Solución: comenzamos identificando los coeficientes que corresponden a la forma general, ellos son A=25, B=30, C=36, D=0, E=0, y F=0.
El siguiente paso es calcular el determinante de la matriz asociada a la cónica para verificar si se trata de una cónica regular o degenerada:
*\delta=\begin{vmatrix} 2A & B & D \\ B & 2C & E \\ D & E & 2F \end{vmatrix} =\begin{vmatrix} 2(25) & 30 & 0 \\ 30 & 2(36) & 0 \\ 0 & 0 & 2(0) \end{vmatrix}*
Desarrollando este determinante, obtenemos:
*\delta=(50)(72)(0)-2(25)(0)^2-2(30)^2(0)+2(30)(0)(0)-2(36)(0)^2=0*
Simplificando, el resultado es δ = 0, lo cual nos indica que la cónica es degenerada. A continuación, evaluamos el tipo de degeneración calculando el discriminante:
*\Delta=B^2-4AC=(30)^2-4(25)(36)=900-3600=-2700*
El discriminante es Δ = -2700, un valor negativo, lo cual indica que la cónica es una elipse degenerada. Este tipo de degeneración se presenta como un punto en el plano.
Recursos adicionales
El siguiente video explica cómo identificar y analizar las cónicas a partir de ecuaciones de segundo grado, aplicando rotaciones y transformaciones para simplificar las ecuaciones y determinar las características de la sección cónica resultante:
Bibliografía
- Barco, V., Caraballo, L. y Murinigo, A. (2015). Estudio de la ecuación general de segundo grado. Universidad Nacional de Rosario.
- Escobar, J. y Ávila, H. (2018). Ecuación general de segundo grado en dos y tres variables. Instituto Tecnológico Metropolitano.
- Fuller, G. y Tarwater, D. (1995). Gemetría Analítica (7ma edición). Pearson Educación.
- García Jiménez, M. (2008). La clasificación de las cónicas.
- Lehman, C. (1989). Geometría Analítica. Limusa.
- Leithold, L. (1992). Álgebra y Trigonometría con Geometría Analítica. Oxford University Press.
- Márquez, A. y otros. (2009). Geometría Analítica. Pearson.
- Reyes, G. (2013). La clasificación de las cónicas. University of Tokyo.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta

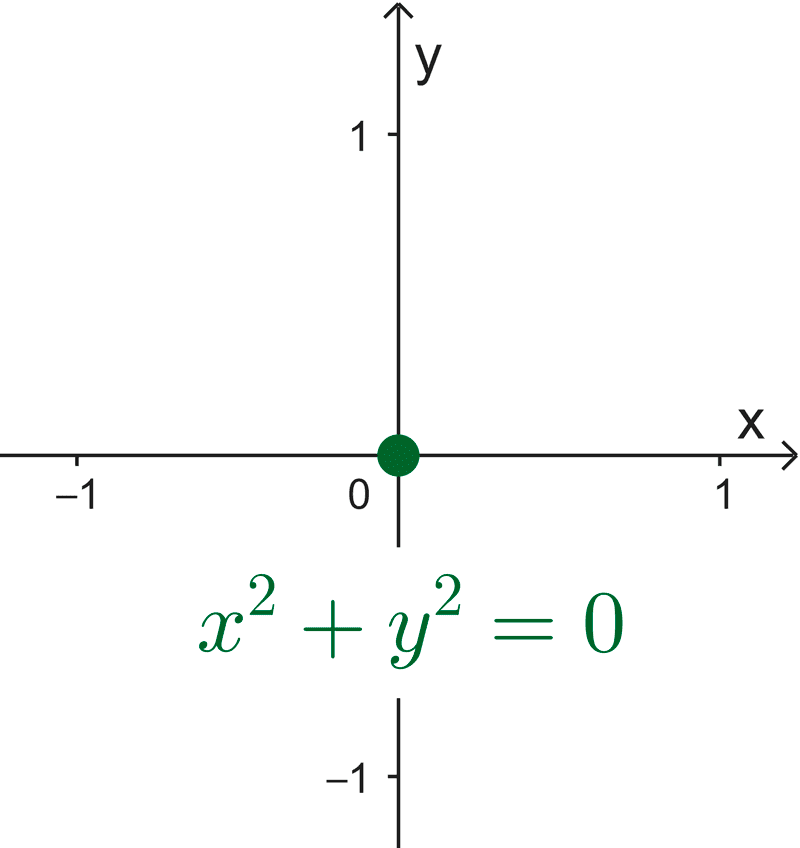
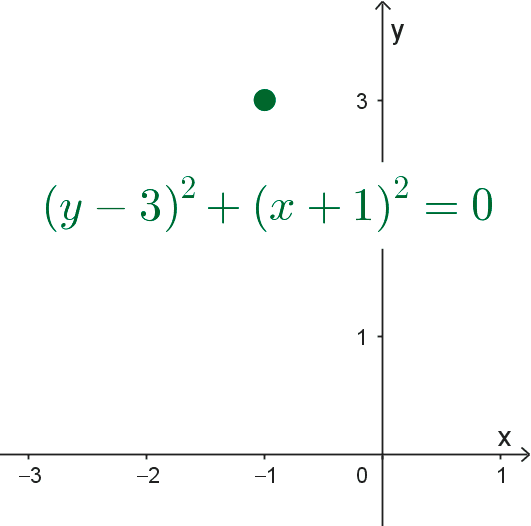
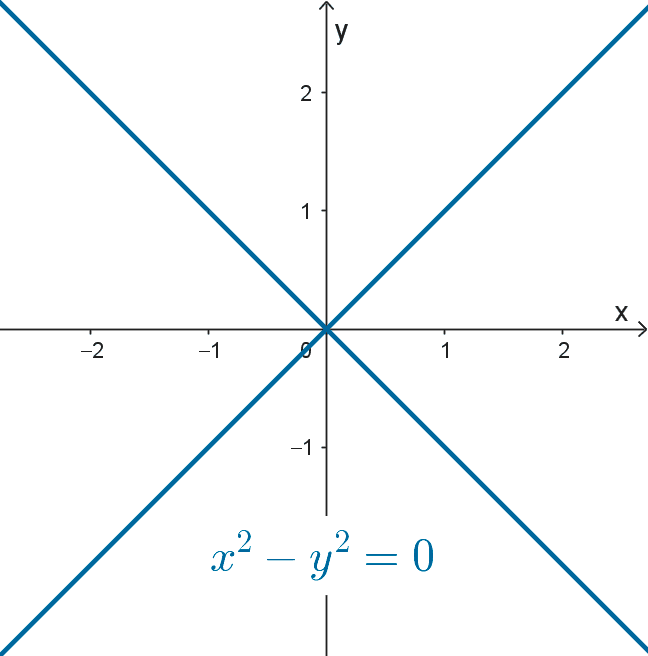
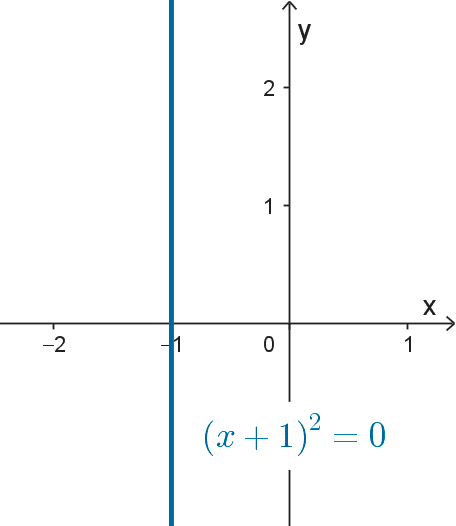
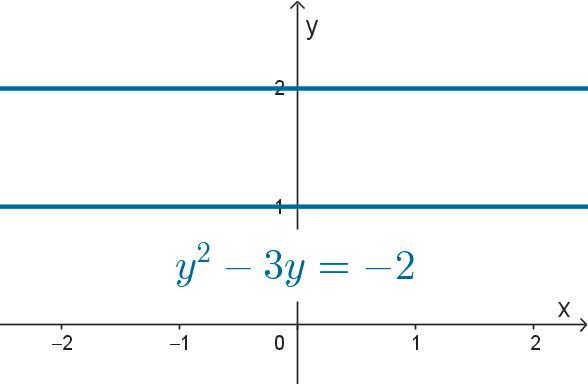
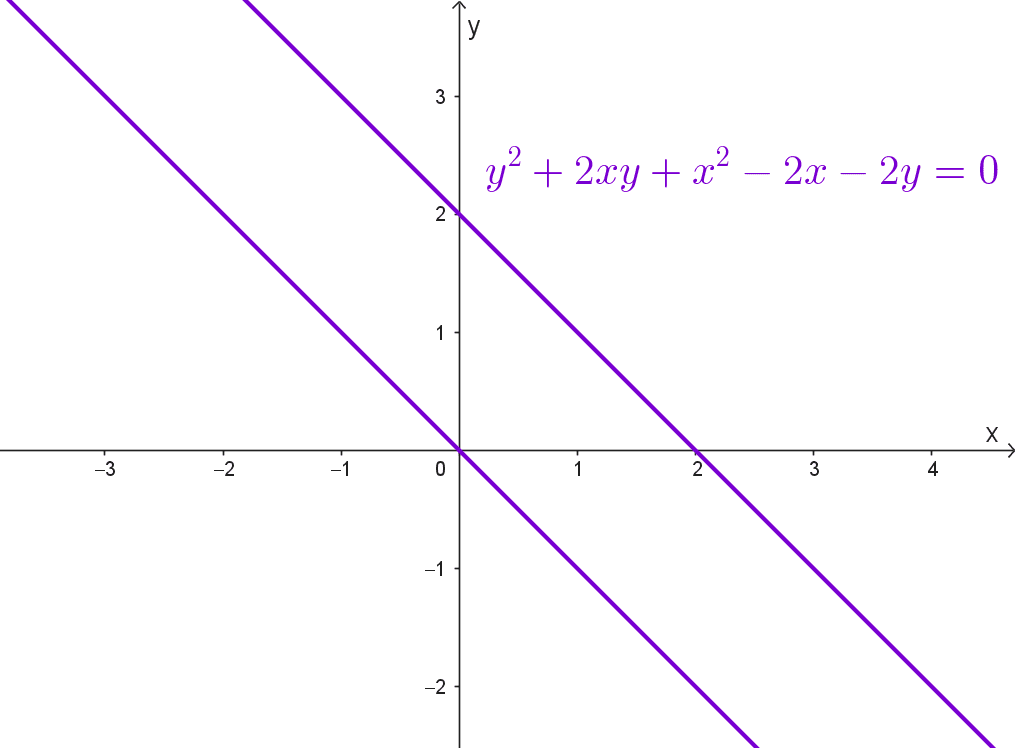

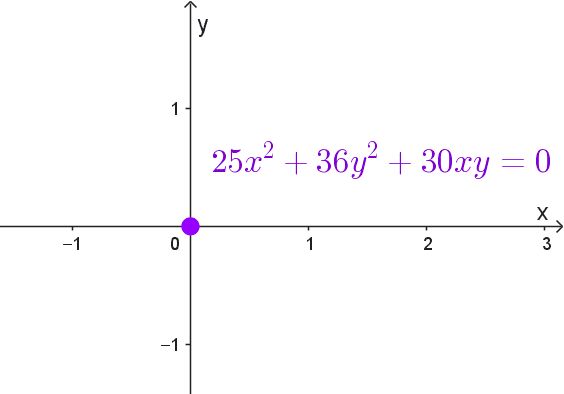

Otros artículos que pueden interesarte