
Ejercicios de hipérbola
Aquí encontrarás ejercicios de hipérbola resueltos y explicados paso a paso con gráficas para todos los niveles educativos. Si aún no conoces sus conceptos fundamentales, te recomiendo revisar primero el artículo principal donde abordamos su teoría básica:
Índice
Ejercicios generales
Los siguientes artículos tienen ejercicios resueltos sobre los elementos principales de una hipérbola:




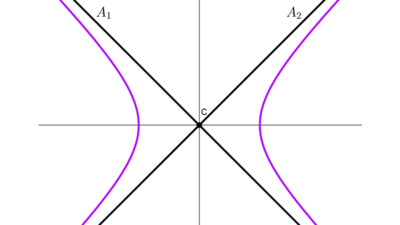
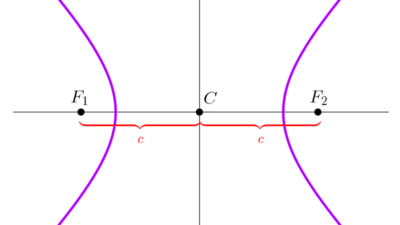
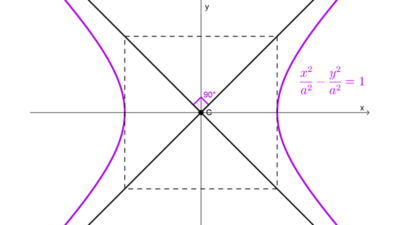
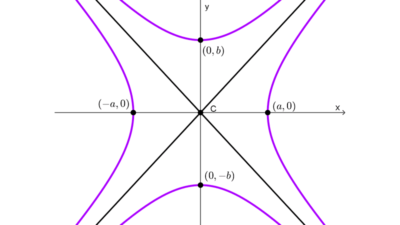
Encontrar la ecuación de una hipérbola a partir de datos
Los siguientes ejercicios consisten en obtener la ecuación canónica o general de una hipérbola teniendo alguna información de la misma, ya sean coordenadas de los focos, los vértices, las asíntotas, etc.
Centro en el origen
Ejercicio 1
Hallar la ecuación de la hipérbola que tiene su centro en el origen, un foco en (0, 2) y el eje transversal es vertical y de longitud 2.
Solución
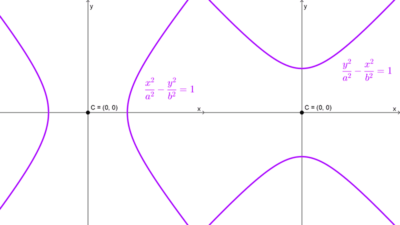
La ecuación canónica de una hipérbola con centro en el origen y eje transversal vertical es:
\(\dfrac{y^2}{a^2}-\dfrac{x^2}{b^2}=1\)
donde:
- a es la distancia desde el centro hasta cada vértice.
- c es la distancia desde el centro hasta cada foco.
- b se obtiene a partir de la relación \(c^2=a^2+b^2.\)
Dado que el eje transversal es vertical y tiene longitud 2, se tiene que \(2a=2,\) por lo que a=1.
Además, el foco está en (0, 2), lo que indica que \(c=2.\)
Ahora calculamos b^2 utilizando la relación mencionada:
\(c^2=a^2+b^2\)
\(2^2=1^2+b^2\)
\(4=1+b^2\)
\(b^2=3\)
Con esto, la ecuación de la hipérbola es:
\(\dfrac{y^2}{1^2}-\dfrac{x^2}{3}=1\)
\(\dfrac{y^2}{1}-\dfrac{x^2}{3}=1\)
\(y^2-\dfrac{x^2}{3}=1\)
Ejercicio 2
Obtener la ecuación ordinaria de la hipérbola con centro en (0, 0), foco en (3, 0) y un vértice en (1, 0).
Solución
Sabemos que la ecuación estándar de una hipérbola con centro en (0, 0) y eje focal horizontal es:
\(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\)
Se nos da que uno de los vértices es (1, 0), lo que indica que los vértices están en \((\pm a, 0).\) Esto nos da:
a=1
También sabemos que uno de los focos está en (3, 0), por lo que los focos están en \((\pm c, 0).\) Esto nos da:
\(c=3\)
En una hipérbola, la relación entre a, b y c es:
\(c^2=a^2+b^2\)
Sustituyendo los valores:
\(3^2=1^2+b^2\)
\(9=1+b^2\)
\(b^2=8\)
Sustituyendo estos valores en la ecuación de la hipérbola:
\(\dfrac{x^2}{1^2}-\dfrac{y^2}{8}=1\)
\(\dfrac{x^2}{1}-\dfrac{y^2}{8}=1\)
\(x^2-\dfrac{y^2}{8}=1\)
Por lo tanto, la ecuación ordinaria de la hipérbola es:
\(x^2-\dfrac{y^2}{8}=1\)
Ejercicio 3
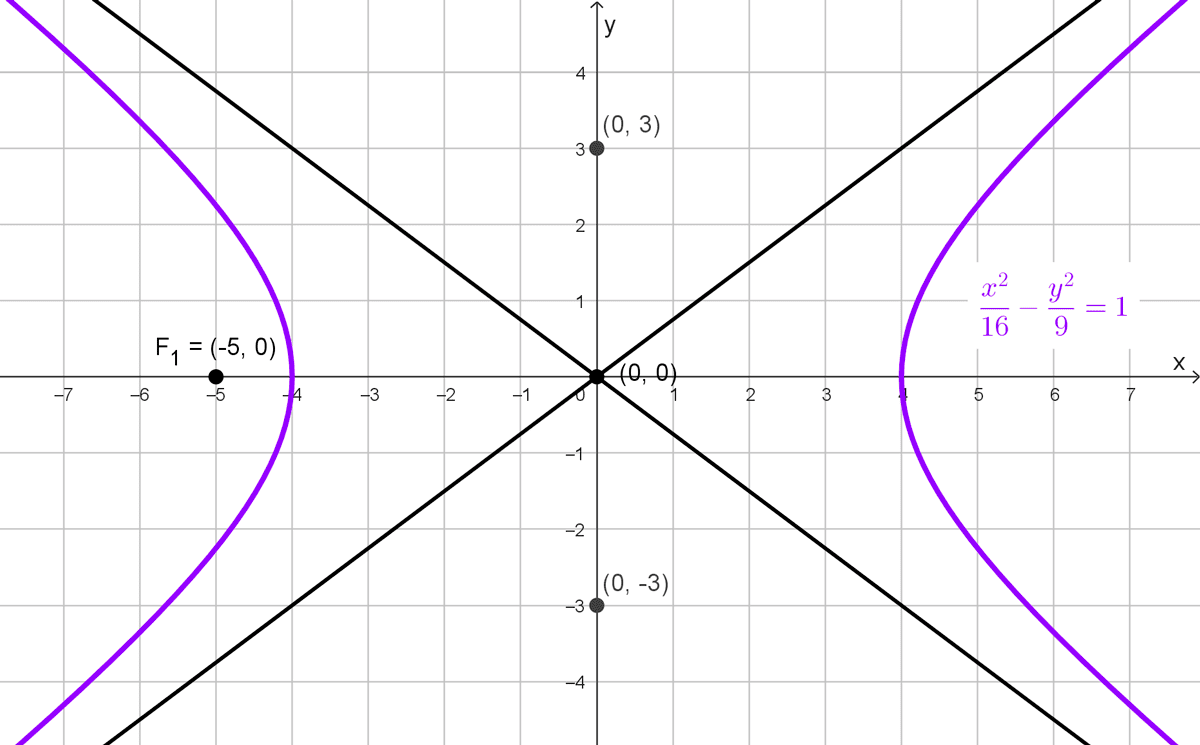
Una hipérbola tiene sus focos en (±5, 0) y un vértice en (3, 0), calcule su ecuación reducida.
Solución
Sabemos que la ecuación estándar de una hipérbola con centro en el origen (0, 0) y eje focal horizontal es:
\(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\)
En este caso, los focos están en \((\pm 5, 0),\) por lo que la distancia c de los focos al centro es:
\(c=5\)
Además, uno de los vértices está en (3, 0), lo que nos da:
\(a=3\)
Sabemos que en una hipérbola se cumple la relación entre a, b y c:
\(c^2=a^2+b^2\)
Sustituyendo los valores de c y a:
\(5^2=3^2+b^2\)
\(25=9+b^2\)
\(b^2=16\)
Ahora podemos escribir la ecuación de la hipérbola con los valores de \(a^2=9\) y \(b^2=16:\)
\(\dfrac{x^2}{3^2}-\dfrac{y^2}{4^2}=1\)
\(\dfrac{x^2}{9}-\dfrac{y^2}{16}=1\)
Ejercicio 4
Determinar la ecuación canónica de una hipérbola cuyos vértices están en (0, -6) y (0, 6) y una de las asíntotas tiene ecuación y = 2x.
Solución
Como primer paso, la ecuación canónica de la hipérbola con eje transversal en el eje y tiene la forma:
\(\dfrac{y^2}{a^2}-\dfrac{x^2}{b^2}=1\)
Donde a es la distancia desde el centro hasta los vértices y b está relacionado con la pendiente de las asíntotas. Sabemos que los vértices están en (0, -6) y (0, 6), lo que implica que la distancia entre los vértices es \(2a=12.\) Entonces, tenemos:
\(a=6\)
El siguiente paso es encontrar el valor de b. Las ecuaciones de las asíntotas para una hipérbola de esta forma son:
\(y=\pm \dfrac{a}{b}x\)
Dado que una de las asíntotas tiene ecuación \(y=2x,\) podemos igualar la pendiente \(\dfrac{a}{b}\) a 2:
\(\dfrac{a}{b}=2\)
Sustituyendo \(a=6\) en esta ecuación, obtenemos:
\(\dfrac{6}{b}=2\)
Despejando b, tenemos:
\(b=3\)
Finalmente, con a=6 y b=3, sustituimos estos valores en la ecuación canónica de la hipérbola:
\(\dfrac{y^2}{6^2}-\dfrac{x^2}{3^2}=1\)
Lo que simplifica a:
\(\dfrac{y^2}{36}-\dfrac{x^2}{9}=1\)
Ejercicio 5
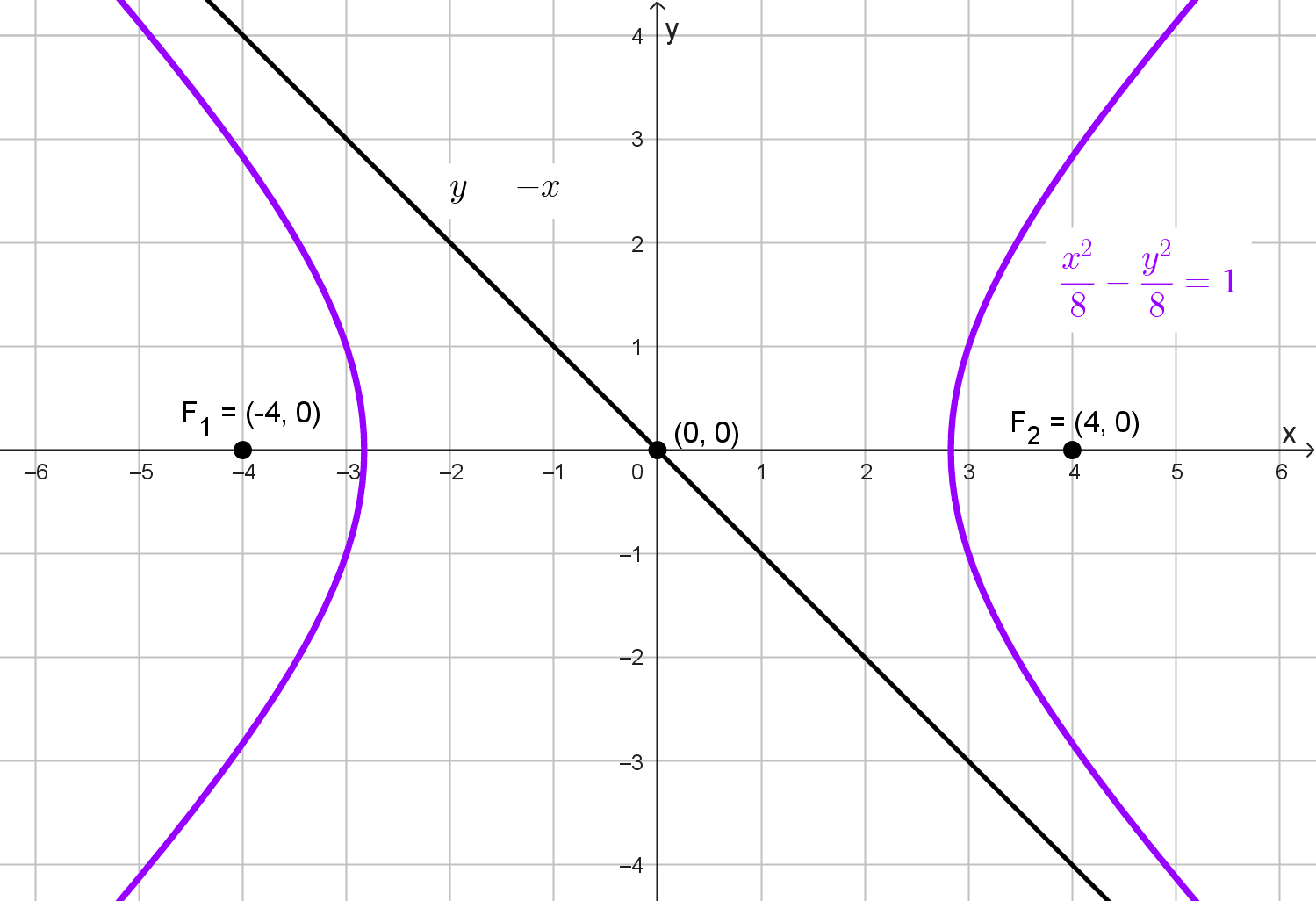
Sacar la ecuación de la hipérbola cuyos focos son (-4, 0) y (4, 0) y una asíntota es y = -x.
Solución
Los focos están en (-4, 0) y (4, 0), lo que indica que la hipérbola tiene su eje transversal sobre el eje x y su centro está en el punto medio de los focos, ubicando en (0, 0).
La ecuación canónica de la hipérbola con el eje transversal sobre el eje x y centro en el origen es:
\(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\)
Sabemos que los focos están en (-4, 0) y (4, 0), por lo que la distancia focal 2c es 8. Entonces, la distancia c es:
\(c=4\)
Y, como en una hipérbola se cumple la relación:
\(c^2=a^2+b^2\)
Sabemos que \(c=4,\) por lo que \(c^2=16.\) Esto nos da la ecuación:
\(a^2+b^2=16\)
La ecuación de las asíntotas para una hipérbola con eje transversal sobre el eje x tiene la forma:
\(y=\pm \dfrac{b}{a}x\)
Se nos dice que una de las asíntotas es \(y=-x,\) lo que implica que la pendiente de la asíntota es -1. Entonces, podemos igualar la pendiente \(\dfrac{b}{a}\) a 1:
\(\dfrac{b}{a}=1\)
Despejando b, obtenemos:
\(b=a\)
Sustituyendo b=a en la ecuación \(a^2+b^2=16,\) obtenemos:
\(a^2+a^2=16\)
\(2a^2=16\)
\(a^2=8\)
Finalmente, como b=a, también tenemos \(b^2=8.\) Con \(a^2=8\) y \(b^2=8,\) la ecuación canónica de la hipérbola es:
\(\dfrac{x^2}{8}-\dfrac{y^2}{8}=1\)
Ejercicio 6
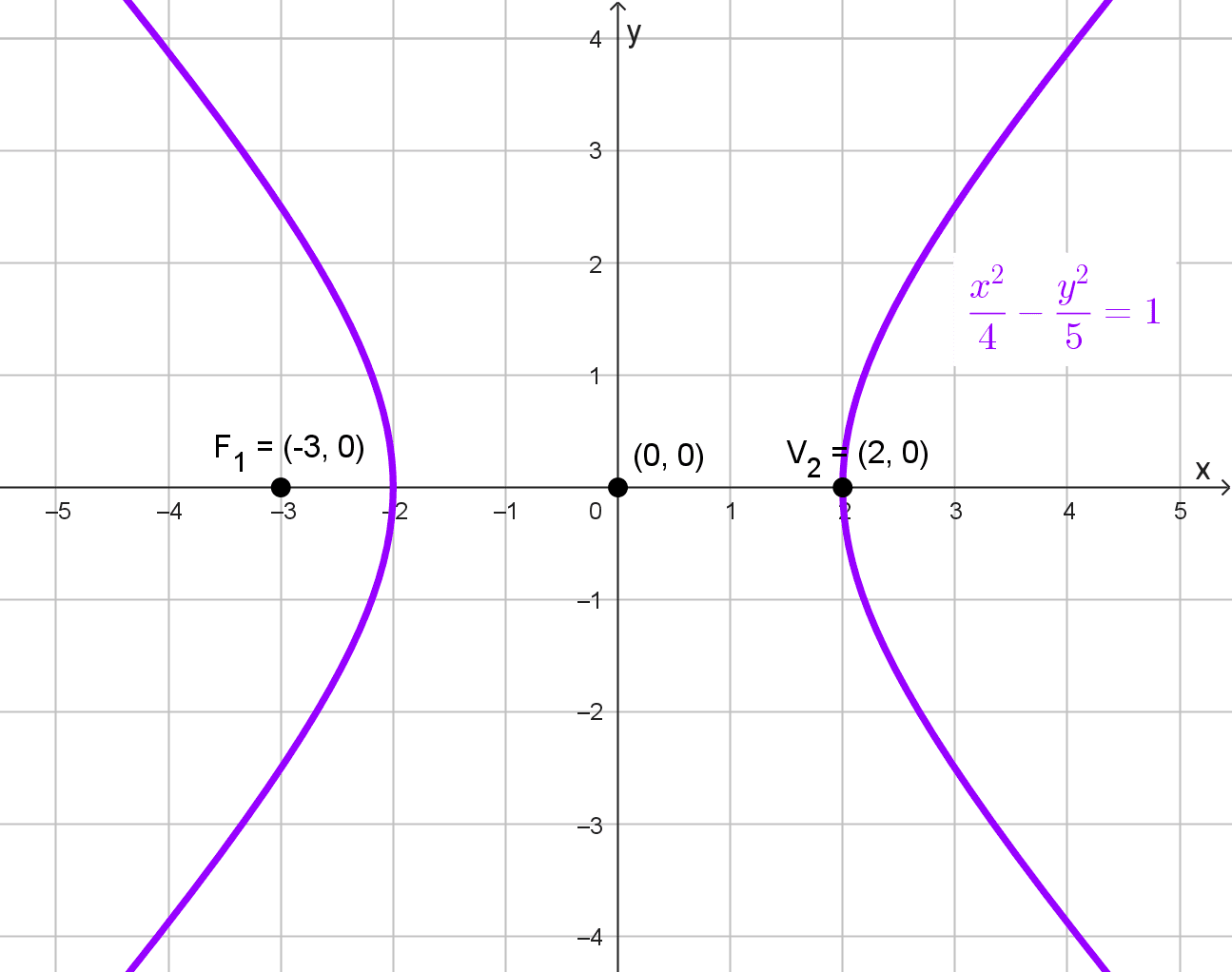
Hallar la ecuación de la hipérbola con centro el origen, foco en (-3, 0) y vértice en (2, 0).
Solución
Primero, identificamos que la hipérbola tiene su centro en el origen (0, 0) y que sus focos y vértices están sobre el eje x. Esto nos indica que la hipérbola está orientada horizontalmente, por lo que su ecuación estándar es de la forma:
\(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\)
Sabemos que el vértice está en (2, 0), por lo que la distancia a es 2. Así, a=2. También sabemos que el foco está en (-3, 0), por lo que la distancia c es 3. Así, c=3.
En una hipérbola, la relación entre a, b y c está dada por la ecuación:
\(c^2=a^2+b^2\)
Sustituyendo los valores conocidos de a y c, obtenemos:
\(3^2=2^2+b^2\)
\(9=4+b^2\)
\(b^2=9-4\)
\(b^2=5\)
Ahora que tenemos \(a^2=4\) y \(b^2=5,\) sustituimos estos valores en la ecuación estándar de la hipérbola:
\(\dfrac{x^2}{4}-\dfrac{y^2}{5}=1\)
Ejercicio 7
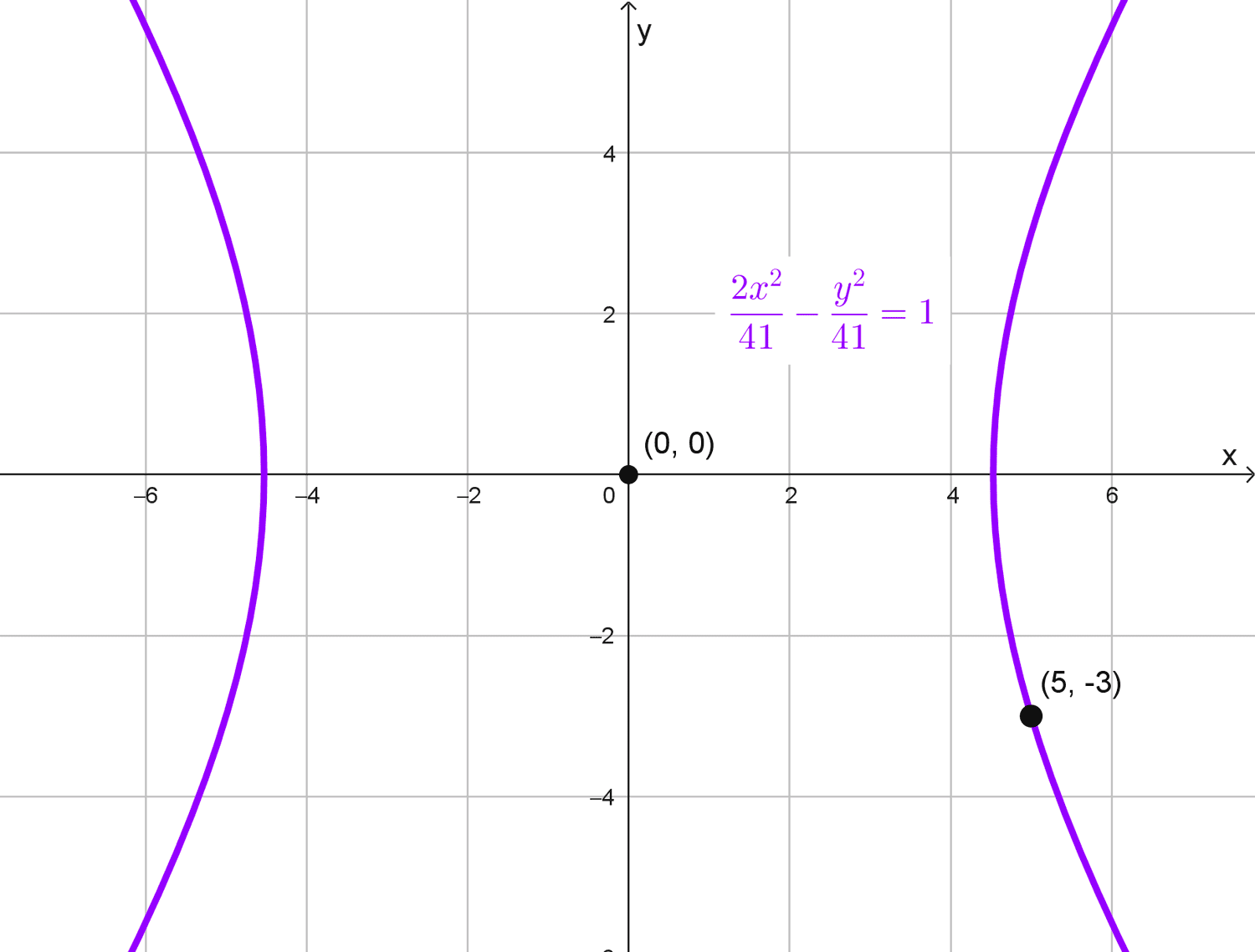
Una hipérbola horizontal con centro en el origen pasa por el punto (5, -3) y tiene excentricidad \(\sqrt{3},\) ¿cuál es su ecuación?
Solución
Comenzamos recordando que la ecuación canónica de una hipérbola con centro en el origen y eje transversal en el eje x es:
\(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\)
Además, la excentricidad e de una hipérbola se define como:
\(e=\dfrac{c}{a}\)
Donde c es la distancia del centro a cada foco, y se cumple que:
\(c^2=a^2+b^2\)
En este problema, se nos da la excentricidad \(e=\sqrt{3}\) y un punto por el que pasa la hipérbola, (5, -3). Como primer paso, usamos la excentricidad para relacionar a y c:
\(e=\dfrac{c}{a} → \sqrt{3}=\dfrac{c}{a} → c=a\sqrt{3}\)
Sustituyendo \(c=a\sqrt{3}\) en la relación \(c^2=a^2+b^2,\) obtenemos:
\((a\sqrt{3})^2=a^2+b^2 → 3a^2=a^2+b^2 → b^2=2a^2\)
Ahora, sustituimos \(b^2=2a^2\) en la ecuación canónica de la hipérbola:
\(\dfrac{x^2}{a^2}-\dfrac{y^2}{2a^2}=1\)
Como la hipérbola pasa por el punto (5, -3), sustituimos \(x=5\) y \(y=-3\) en la ecuación:
\(\dfrac{5^2}{a^2}-\dfrac{(-3)^2}{2a^2}=1 → \dfrac{25}{a^2}-\dfrac{9}{2a^2}=1\)
Para simplificar, multiplicamos toda la ecuación por \(2a^2:\)
\(2 \cdot 25-9=2a^2 → 50-9=2a^2 → 41=2a^2 → a^2=\dfrac{41}{2}\)
Con \(a^2=\dfrac{41}{2},\) podemos encontrar \(b^2:\)
\(b^2=2a^2=2 \cdot \dfrac{41}{2}=41\)
Finalmente, sustituimos \(a^2\) y \(b^2\) en la ecuación canónica de la hipérbola:
\(\dfrac{x^2}{\dfrac{41}{2}}-\dfrac{y^2}{41}=1\)
Podemos eliminar el denominador en el primer término multiplicando toda la ecuación por 2:
\(\dfrac{2x^2}{41}-\dfrac{y^2}{41}=1\)
Ejercicio 8
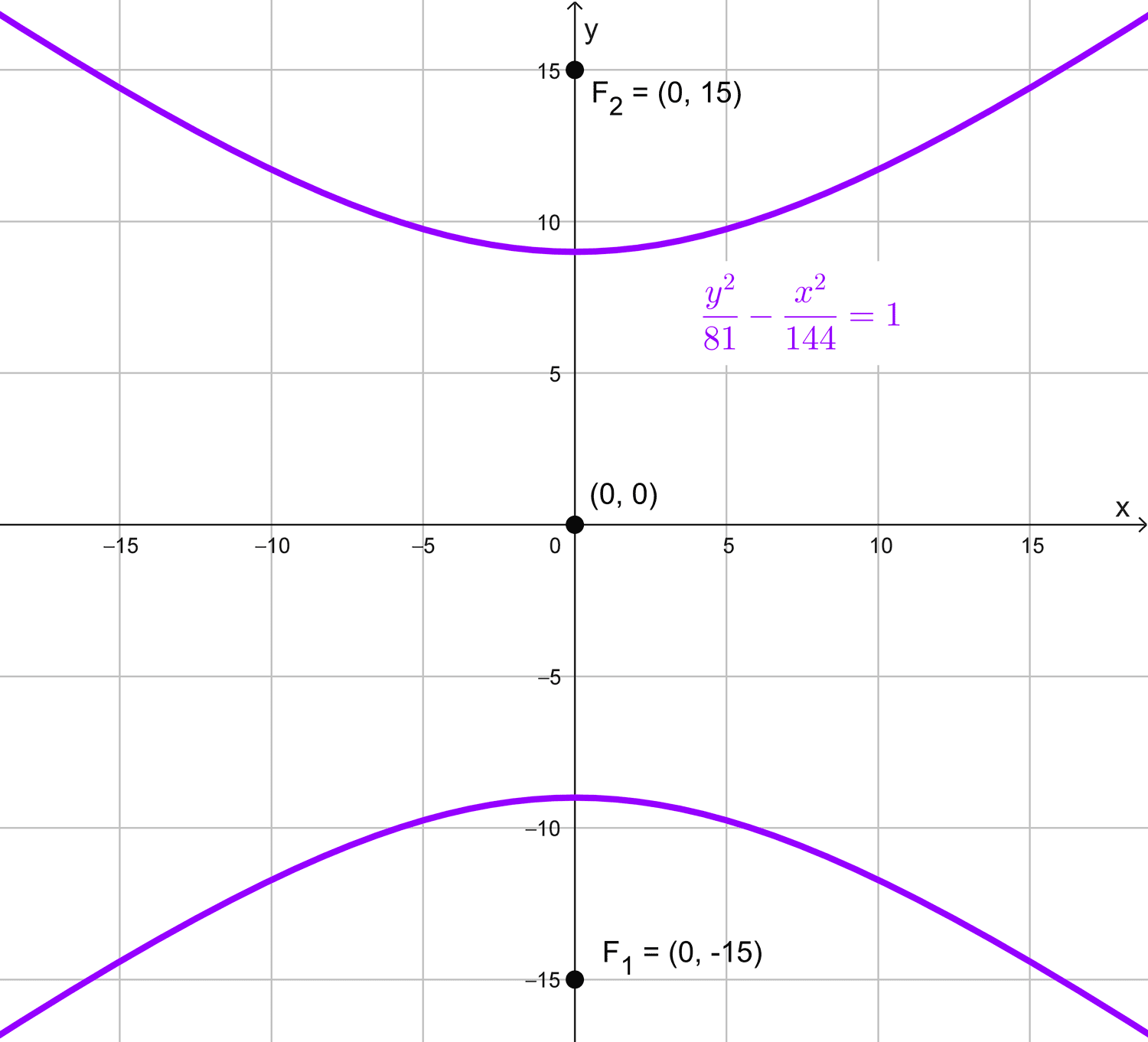
La distancia focal de una hipérbola es 30, su centro es (0, 0) y su eje transverso es vertical y mide 18, obtenga su ecuación canónica.
Solución
En una hipérbola con eje transverso vertical y centro (0, 0), la ecuación canónica es de la forma:
\(\dfrac{y^2}{a^2}-\dfrac{x^2}{b^2}=1\)
El eje transverso es vertical y mide 2a, por lo que:
\(2a=18 → a=9\)
La distancia focal es 2c, donde c es la distancia del centro a cada foco. Dado que la distancia focal es 30:
\(2c=30 → c=15\)
En una hipérbola, la relación entre a, b y c está dada por:
\(c^2=a^2+b^2\)
Sustituyendo los valores conocidos de a y c:
\(15^2=9^2+b^2 → 225=81+b^2 → b^2=225-81=144\)
Por lo tanto, b=12.
Finalmente, sustituyendo a y b en la ecuación canónica de la hipérbola, obtenemos:
\(\dfrac{y^2}{81}-\dfrac{x^2}{144}=1\)
Esta es la ecuación canónica de la hipérbola con las condiciones dadas.
Ejercicio 9
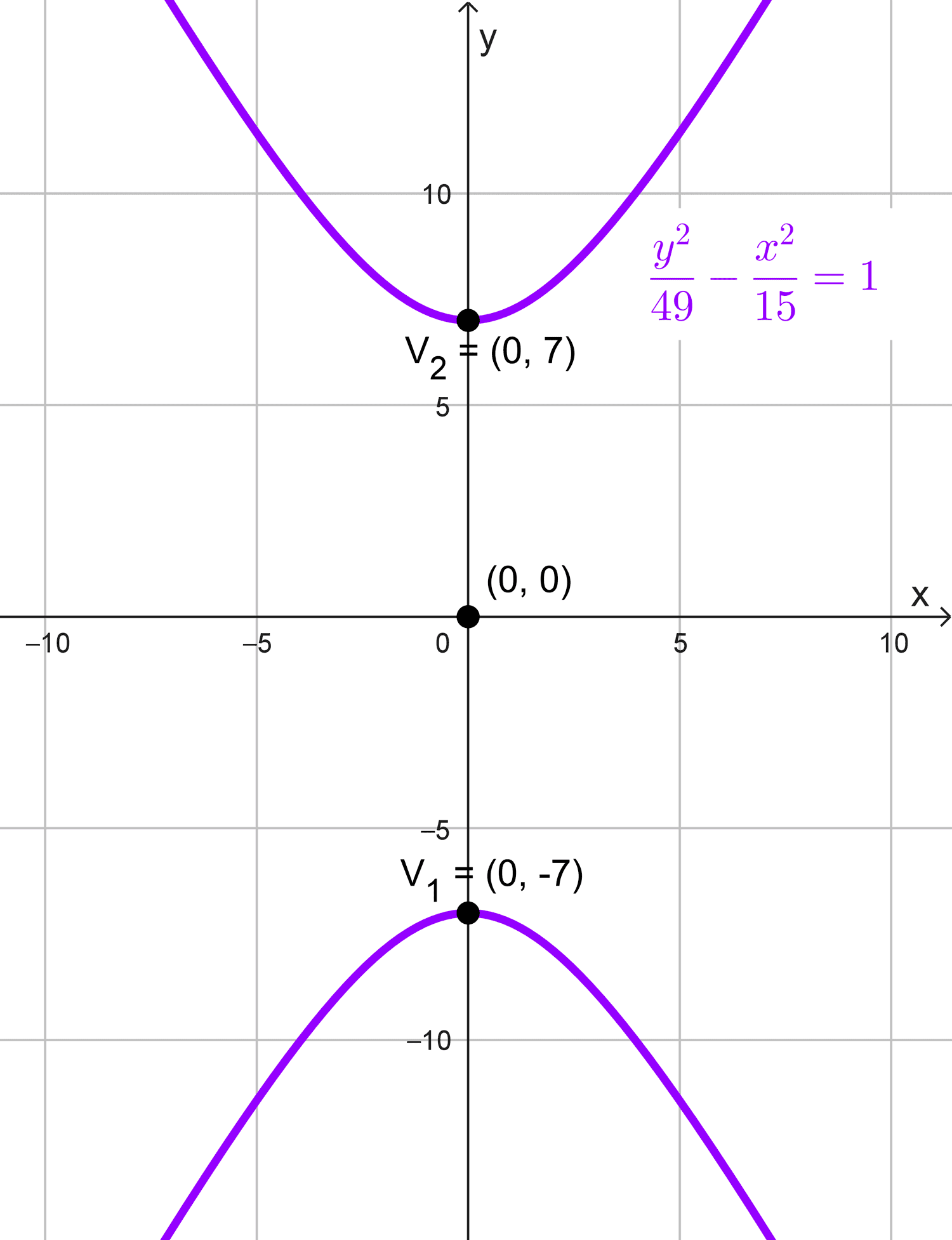
Calcular la ecuación de la hipérbola con vértices en (0, ±7) y excentricidad e = 8/7.
Solución
Como los vértices están en \((0, \pm7),\) esto indica que el eje transverso de la hipérbola es vertical y que el centro de la hipérbola está en el origen (0, 0). Además, la distancia desde el centro a cada vértice es a=7.
En una hipérbola con eje transverso vertical, la ecuación canónica es de la forma:
\(\dfrac{y^2}{a^2}-\dfrac{x^2}{b^2}=1\)
donde a es la distancia del centro a cada vértice, y b es la longitud del semieje conjugado.
La excentricidad e de una hipérbola está dada por:
\(e=\dfrac{c}{a}\)
donde c es la distancia del centro a cada foco. Sabemos que \(e=\dfrac{8}{7}\) y \(a=7,\) por lo que podemos despejar c:
\(\dfrac{8}{7}=\dfrac{c}{7} → c=8\)
En una hipérbola, la relación entre a, b y c está dada por:
\(c^2=a^2+b^2\)
Sustituyendo los valores conocidos de a y c:
\(8^2=7^2+b^2 → 64=49+b^2 → b^2=64-49=15\)
Por lo tanto, \(b=\sqrt{15}.\)
Finalmente, sustituyendo a y b en la ecuación canónica de la hipérbola, obtenemos:
\(\dfrac{y^2}{49}-\dfrac{x^2}{15}=1\)
Esta es la ecuación canónica de la hipérbola con las condiciones dadas.
Ejercicio 10
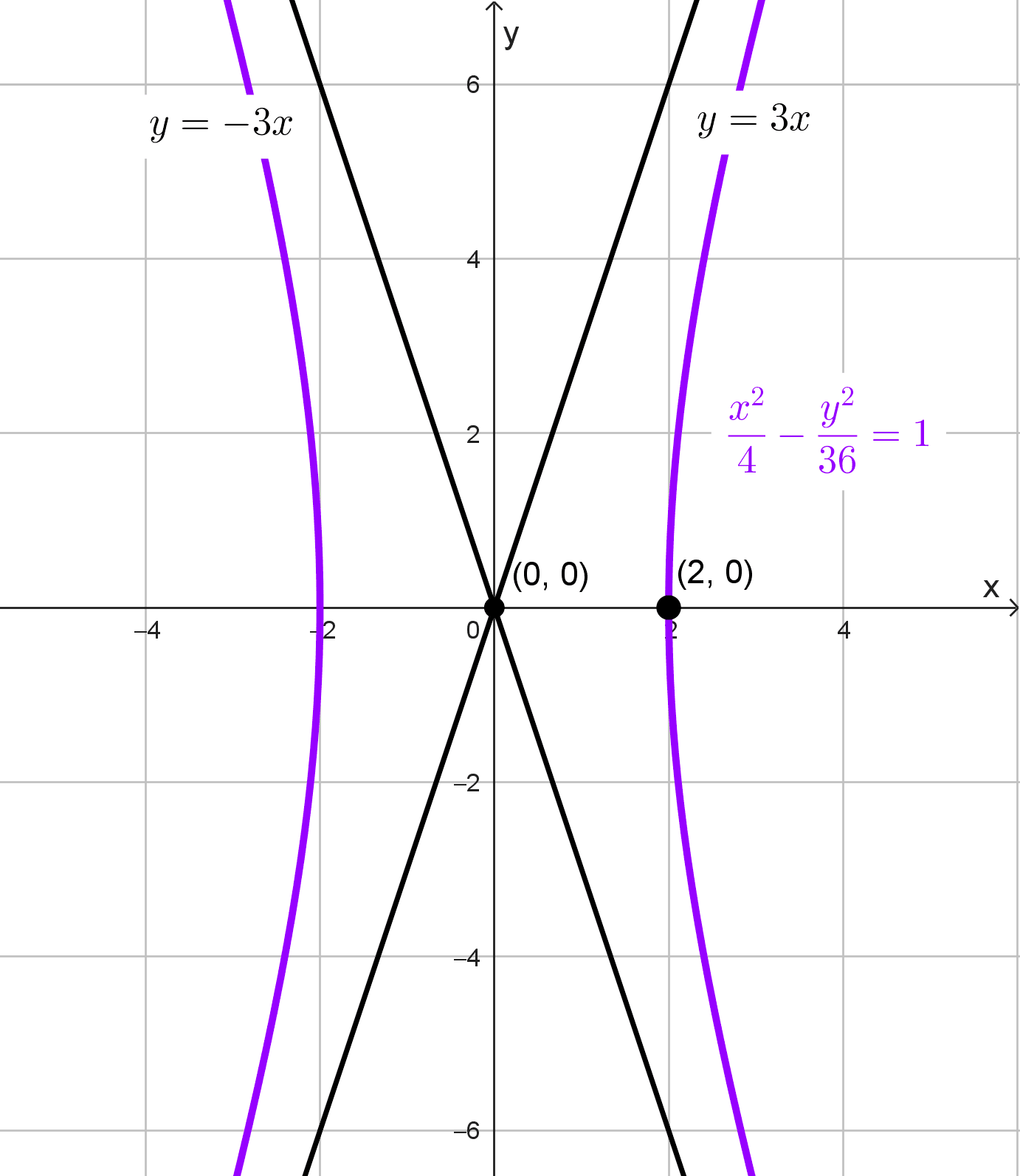
Una hipérbola pasa por el punto (2, 0) y sus asíntotas son las rectas y = ±3x, determina su ecuación.
Solución
Las asíntotas de una hipérbola nos dan información importante sobre su orientación y sus parámetros. Por la ubicación del punto de la hipérbola (sobre el eje x), deducimos que su orientación es horizontal.
En una hipérbola horizontal con centro en el origen (0, 0), las ecuaciones de las asíntotas son de la forma:
\(y=\pm\dfrac{b}{a}x\)
Comparando con las asíntotas dadas \(y=\pm3x,\) deducimos que:
\(\dfrac{b}{a}=3 → b=3a\)
Ahora, como la hipérbola pasa por el punto (2, 0), este punto debe satisfacer la ecuación de la hipérbola:
\(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\)
Sustituyendo el punto (2, 0) en la ecuación:
\(\dfrac{2^2}{a^2}-\dfrac{0^2}{b^2}=1 → \dfrac{4}{a^2}=1 → a^2=4 → a=2\)
Como \(b=3a,\) entonces:
\(b=3 \cdot 2=6 → b^2=36\)
Finalmente, sustituyendo a y b en la ecuación canónica de la hipérbola, obtenemos:
\(\dfrac{x^2}{4}-\dfrac{y^2}{36}=1\)
Esta es la ecuación canónica de la hipérbola con las condiciones dadas.
Ejercicio 11
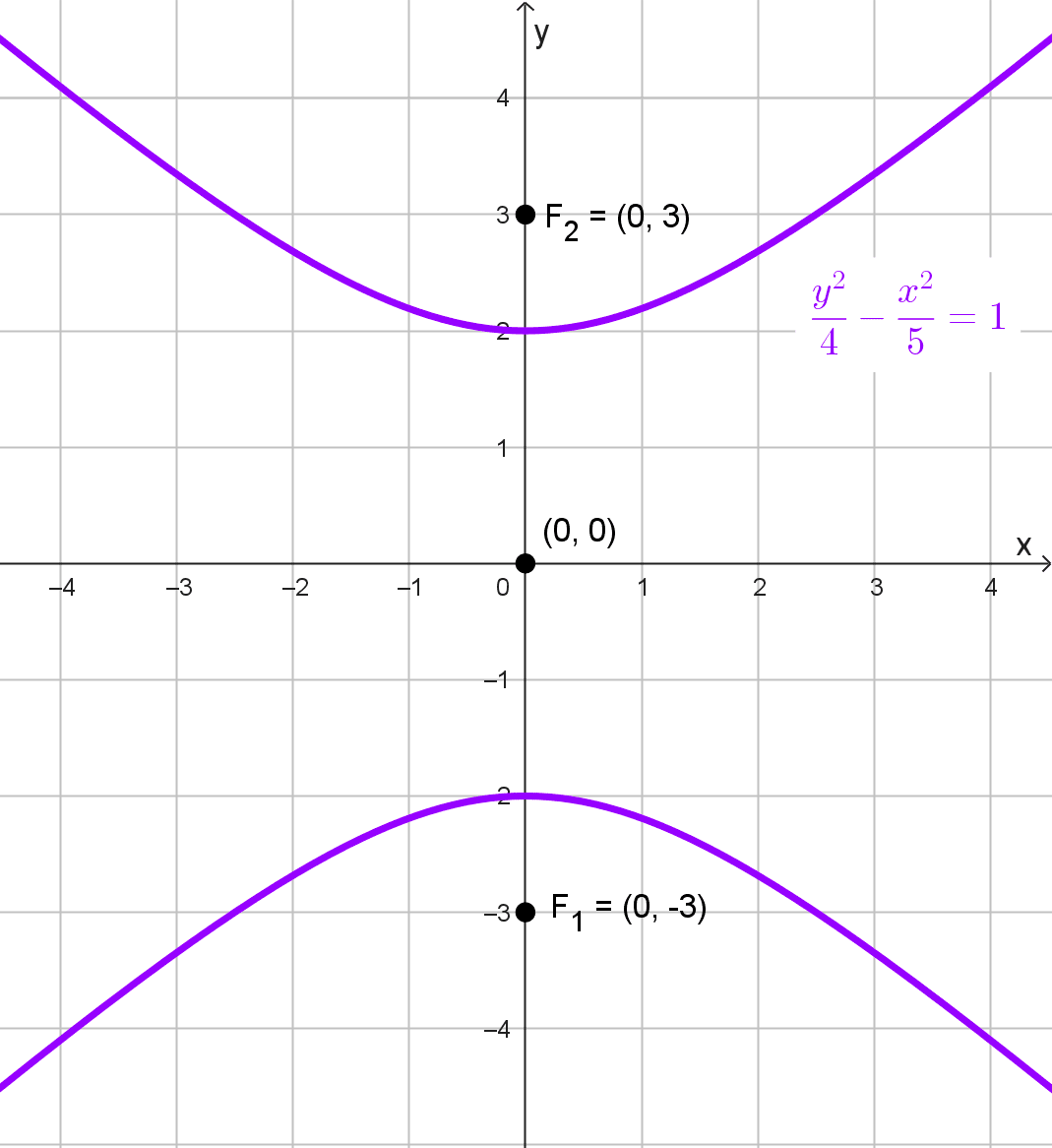
Los focos de una hipérbola se ubican en las coordenadas (0, -3) y (0, 3) y la distancia entre sus vértices es 4. Hallar su ecuación canónica.
Solución
Primero, observamos que los focos están ubicados sobre el eje y, lo que indica que la hipérbola tiene su eje transverso vertical. Por lo tanto, su ecuación canónica es de la forma:
\(\dfrac{y^2}{a^2}-\dfrac{x^2}{b^2}=1\)
Dado que los focos están en (0, -3) y (0, 3), la distancia entre ellos es \(2c=6,\) por lo que:
\(c=3\)
También sabemos que la distancia entre los vértices es 4, lo que significa que \(2a=4,\) por lo que:
\(a=2\)
En una hipérbola, la relación entre a, b y c está dada por:
\(c^2=a^2+b^2\)
Sustituyendo los valores conocidos de a y c:
\(3^2=2^2+b^2 → 9=4+b^2 → b^2=9-4=5\)
Por lo tanto, \(b=\sqrt{5}.\)
Finalmente, sustituyendo a y b en la ecuación canónica de la hipérbola, obtenemos:
\(\dfrac{y^2}{4}-\dfrac{x^2}{5}=1\)
Esta es la ecuación canónica de la hipérbola con las condiciones dadas.
Ejercicio 12
Obtenga la ecuación reducida de la hipérbola si sus intersecciones con el eje x están en ±2 y las asíntotas son y = ±x / 4
Solución
Las intersecciones con el eje x nos indican que los vértices de la hipérbola están en (\pm2, 0). Esto sugiere que la hipérbola tiene su eje transverso horizontal, ya que los vértices están sobre el eje x. Por lo tanto, su ecuación canónica es de la forma:
\(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\)
Dado que los vértices están en \((\pm2, 0),\) entonces:
\(a=2\)
Las asíntotas de una hipérbola con eje transverso horizontal son de la forma:
\(y=\pm\dfrac{b}{a}x\)
Comparando con las asíntotas dadas \(y=\pm\dfrac{x}{4},\) deducimos que:
\(\dfrac{b}{a}=\dfrac{1}{4}\)
Como \(a=2,\) sustituimos para encontrar b:
\(\dfrac{b}{2}=\dfrac{1}{4} → b=\dfrac{2}{4}=\dfrac{1}{2}\)
Por lo tanto, \(b^2=\left (\dfrac{1}{2}\right)^2=\dfrac{1}{4}.\)
Finalmente, sustituyendo a y b en la ecuación canónica de la hipérbola, obtenemos:
\(\dfrac{x^2}{4}-\dfrac{y^2}{1/4}=1\)
Esta es la ecuación reducida de la hipérbola con las condiciones dadas.
Ejercicio 13
Los extremos del eje conjugado de una hipérbola son los puntos (0, -3) y (0, 3), uno de sus focos está en (5, 0), calcule su ecuación canónica.
Solución
Los extremos del eje conjugado nos indican que \(b=3.\) Además, como los extremos del eje conjugado están sobre el eje y, esto sugiere que la hipérbola tiene su eje transverso horizontal. Por lo tanto, su ecuación canónica es de la forma:
\(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\)
Dado que uno de los focos está en (5, 0), la distancia del centro al foco es c=5.
En una hipérbola, la relación entre a, b y c está dada por:
\(c^2=a^2+b^2\)
Sustituyendo los valores conocidos de b y c:
\(5^2=a^2+3^2 → 25=a^2+9 → a^2=25-9=16 → a=4\)
Por lo tanto, \(a^2=16\) y \(b^2=9.\)
Finalmente, sustituyendo a y b en la ecuación canónica de la hipérbola, obtenemos:
\(\dfrac{x^2}{16}-\dfrac{y^2}{9}=1\)
Ejercicio 14
Encuentre la ecuación para el conjunto de puntos en un plano xy tal que la diferencia de distancias de un punto (x, y) a los puntos F(13, 0) y F’(-13,0) es k = 24.
Solución
Para resolver este ejercicio, comenzamos identificando que se trata de una hipérbola, ya que la diferencia de distancias de un punto (x, y) a dos puntos fijos (los focos) es constante. Los focos están dados en F (13, 0) y F'(-13, 0), y la diferencia de distancias es k = 24.
En una hipérbola, la diferencia de distancias de cualquier punto a los focos es igual a 2a, donde a es la distancia del centro a uno de los vértices. Por lo tanto, tenemos que:
\(2a=24 → a=12\)
El centro de la hipérbola es el punto medio entre los dos focos. Dado que los focos están en (13, 0) y (-13, 0), el centro es:
\(\left (\dfrac{13+(-13)}{2}, \dfrac{0+0}{2} \right)=(0, 0)\)
La distancia desde el centro a cada foco se denota como c, y en este caso es:
\(c=13\)
Ahora, para encontrar b, que es la distancia del centro a cada uno de los extremos del eje conjugado, utilizamos la relación fundamental de la hipérbola:
\(c^2=a^2+b^2\)
Sustituyendo los valores conocidos:
\(13^2=12^2+b^2 → 169=144+b^2 → b^2=25 → b=5\)
Finalmente, la ecuación de la hipérbola con centro en (0, 0), eje transversal horizontal (ya que los focos están sobre el eje x), y valores de a y b calculados, es:
\(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\)
Sustituyendo \(a=12\) y \(b=5,\) obtenemos:
\(\dfrac{x^2}{144}-\dfrac{y^2}{25}=1\)
Esta es la ecuación que describe el conjunto de puntos (x, y) en el plano xy cuya diferencia de distancias a los focos F (13, 0) y F'(-13, 0) es 24.
¿Te está sirviendo este artículo? ¡Por favor, califícalo!
0,0 / 5 — 0 votos
Centro fuera del origen
Ejercicio 1
Una hipérbola tiene su centro en el punto (-3, 2), uno de sus vértices es el punto (1, 2) y la longitud de su eje imaginario es 4, ¿cuál es su ecuación?
Solución
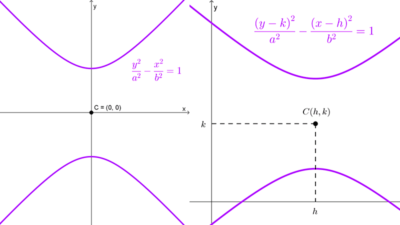
Sabemos que la ecuación estándar de una hipérbola con centro en (h, k) y eje focal horizontal es:
\(\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1\)
El centro de la hipérbola es (-3, 2), por lo que \(h=-3\) y \(k=2.\) También se nos da que uno de sus vértices es (1, 2). Como los vértices de una hipérbola con eje horizontal están a una distancia a del centro, calculamos a como la distancia entre el centro y el vértice:
\(a=|1-(-3)|=|1+3|=4\)
La longitud del eje imaginario es 2b, y nos dicen que esta medida es 4. Entonces:
\(2b=4 → b=2\)
Ahora podemos escribir la ecuación de la hipérbola sustituyendo los valores encontrados:
\(\dfrac{(x+3)^2}{4^2}-\dfrac{(y-2)^2}{2^2}=1\)
\(\dfrac{(x+3)^2}{16}-\dfrac{(y-2)^2}{4}=1\)
Por lo tanto, la ecuación de la hipérbola es:
\(\dfrac{(x+3)^2}{16}-\dfrac{(y-2)^2}{4}=1\)
Ejercicio 2
Determinar las ecuaciones de las siguientes hipérbolas, todos sus elementos y graficarlas.
- C(4, -1); foco (7, -1); vértice (6, -1).
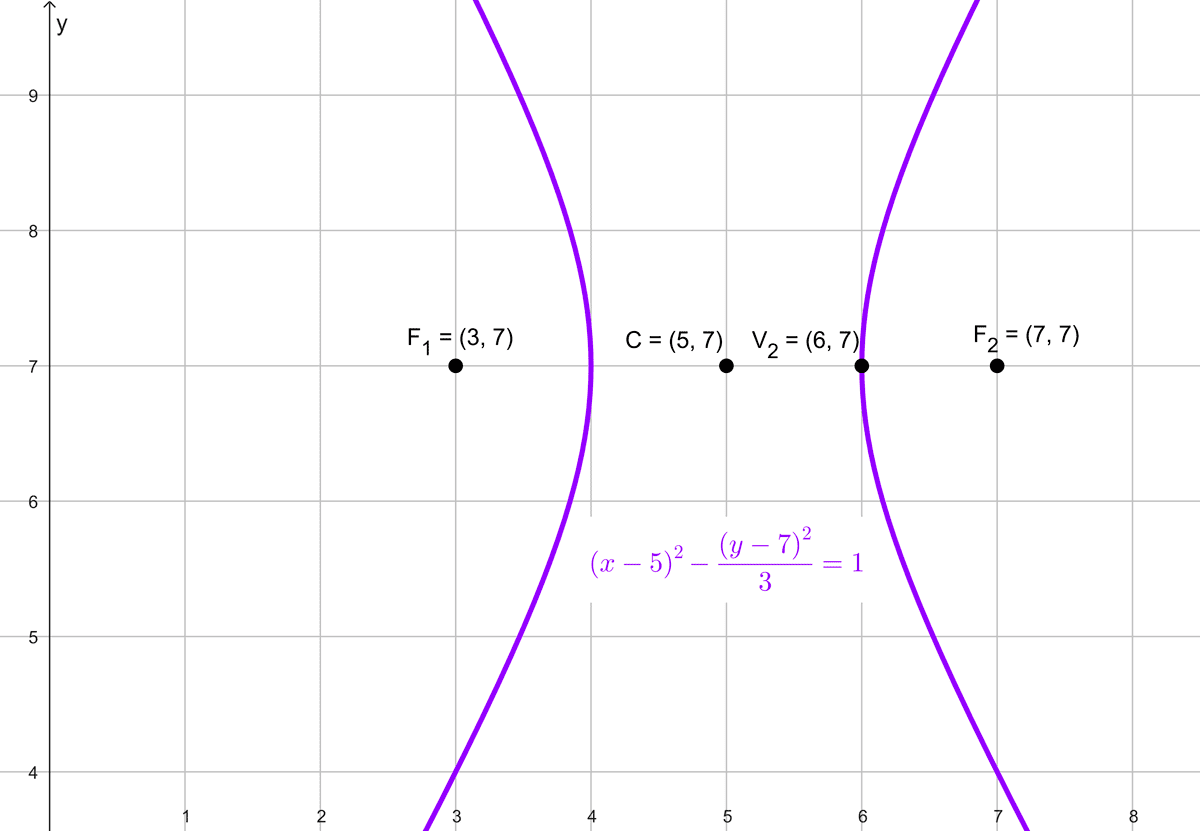
- Focos en (3, 7) y (7, 7), vértice en (6, 7).
- Vértices en (-1, -1) y (3, -1), asíntota y + 1 = (3 / 2) (x - 1)
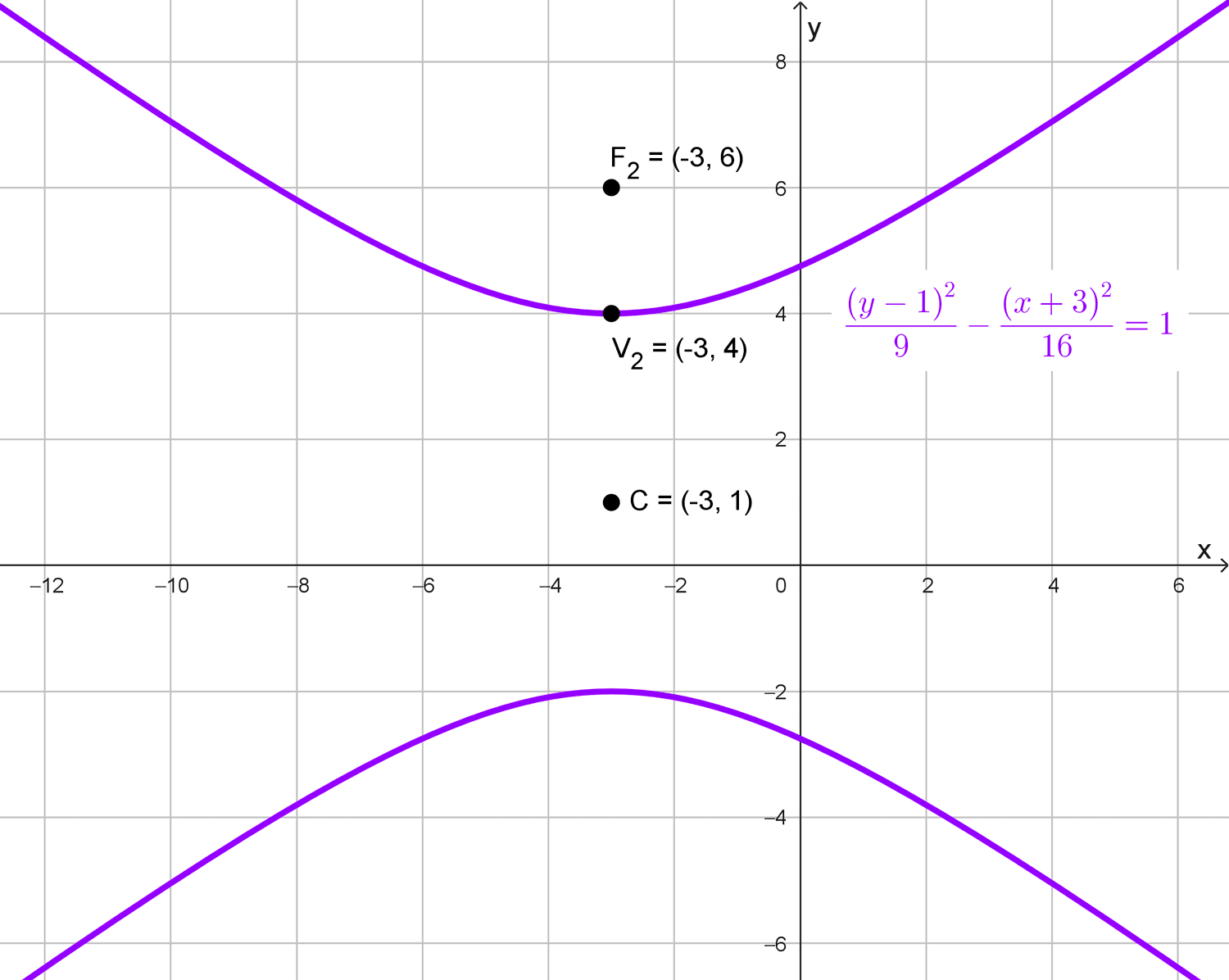
- Centro (-3, 1), foco (-3, 6), vértice (-3, 4).
- Foco (-4, 0), vértices (-4, 4) y (-4, 2)
- Focos (3, 4) y (3, -2); excentricidad igual a 2.
Solución del problema 1
Datos proporcionados:
- Centro de la hipérbola: C (4, -1)
- Foco: (7, -1)
- Vértice: (6, -1)
Observamos que tanto el centro, el foco y el vértice tienen la misma coordenada y, lo que indica que la hipérbola está orientada horizontalmente. Por lo tanto, la ecuación canónica de la hipérbola es:
\(\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1\)
donde (h, k) es el centro de la hipérbola.
El centro es C (4, -1), por lo que \(h=4\) y \(k=-1.\)
La distancia entre el centro y el vértice es a. El vértice es (6, -1), entonces:
\(a=6-4=2\)
La distancia entre el centro y el foco es c. El foco es (7, -1), entonces:
\(c=7-4=3\)
Para una hipérbola, se cumple que:
\(c^2=a^2+b^2\)
Sustituyendo los valores conocidos:
\(3^2=2^2+b^2 → 9=4+b^2 → b^2=5 → b=\sqrt{5}\)
Sustituyendo los valores de h, k, a y b en la ecuación:
\(\dfrac{(x-4)^2}{4}-\dfrac{(y+1)^2}{5}=1\)
Para una hipérbola horizontal, las ecuaciones de las asíntotas son:
\(y-k=\pm \dfrac{b}{a}(x-h)\)
Sustituyendo los valores conocidos:
\(y+1=\pm \dfrac{\sqrt{5}}{2}(x-4)\)
La excentricidad e de una hipérbola se calcula como:
\(e=\dfrac{c}{a}\)
Sustituyendo los valores conocidos:
\(e=\dfrac{3}{2}=1,5\)
El lado recto LR de una hipérbola se calcula como:
\(L_R=\dfrac{2b^2}{a}\)
Sustituyendo los valores conocidos:
\(L_R=\dfrac{2 \cdot 5}{2}=5\)
Elementos de la hipérbola:
- Centro: (4, -1)
- Focos: (7, -1) y (1, -1)
- Vértices: (6, -1) y (2, -1)
- Semieje transversal: \(a=2\)
- Semieje conjugado: \(b=\sqrt{5}\)
- Asíntotas: \(y+1=\pm \dfrac{\sqrt{5}}{2}(x-4)\)
- Excentricidad: \(e=1, 5\)
- Lado recto: \(L_R=5\)
Ecuación: \(\dfrac{(x-4)^2}{4}-\dfrac{(y+1)^2}{5}=1\)
Solución del problema 2
Datos proporcionados:
- Focos: (3, 7) y (7, 7).
- Vértice: (6, 7).
Observamos que tanto los focos como el vértice tienen la misma coordenada y = 7, lo que indica que la hipérbola está orientada horizontalmente. Por lo tanto, la ecuación reducida de la hipérbola es:
\(\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1\)
donde (h, k) es el centro de la hipérbola.
El centro de la hipérbola es el punto medio entre los focos. Dados los focos (3, 7) y (7, 7), el centro se calcula como:
\(h=\dfrac{3+7}{2}=5, \quad k=\dfrac{7+7}{2}=7\)
Por lo tanto, el centro es C (5, 7).
La distancia entre el centro y el vértice es a. El vértice es (6, 7), y el centro es (5, 7), entonces:
\(a=6-5=1\)
La distancia entre el centro y uno de los focos es c. El foco es (7, 7), y el centro es (5, 7), entonces:
\(c=7-5=2\)
Para una hipérbola, se cumple que \(c^2=a^2+b^2.\) Sustituyendo los valores conocidos:
\(2^2=1^2+b^2 → 4=1+b^2 → b^2=3 → b=\sqrt{3}\)
Sustituyendo los valores de \(h=5, k=7, a=1\) y \(b=\sqrt{3}\) en la ecuación, obtenemos:
\(\dfrac{(x-5)^2}{1}-\dfrac{(y-7)^2}{3}=1\)
Simplificando, la ecuación queda:
\((x-5)^2-\dfrac{(y-7)^2}{3}=1\)
Para una hipérbola horizontal, las ecuaciones de las asíntotas son:
\(y-k=\pm \dfrac{b}{a}(x-h)\)
Sustituyendo los valores conocidos:
\(y-7=\pm \dfrac{\sqrt{3}}{1}(x-5) → y-7=\pm \sqrt{3}(x-5)\)
La excentricidad de la hipérbola es:
\(e=\dfrac{c}{a}=\dfrac{2}{1}=2\)
El lado recto de la hipérbola es:
\(L_R=\dfrac{2b^2}{a}=\dfrac{2 \cdot 3}{1}=6\)
Elementos de la hipérbola:
- Centro: (5, 7)
- Focos: (7, 7) y (3, 7)
- Vértices: (6, 7) y (4, 7)
- Semieje transversal: \(a=1\)
- Semieje conjugado: \(b=\sqrt{3}\)
- Asíntotas: \(y-7=\pm \sqrt{3}(x-5)\)
- Excentricidad: \(e=2\)
- Lado recto: \(L_R=6\)
Ecuación: \((x-5)^2-\dfrac{(y-7)^2}{3}=1\)
Solución del problema 3
Datos proporcionados:
- Vértices: (-1, -1) y (3, -1).
- Asíntota: \(y+1=\dfrac{3}{2}(x-1).\)
Observamos que los vértices tienen la misma coordenada \(y=-1,\) lo que indica que la hipérbola está orientada horizontalmente. Por lo tanto, la ecuación canónica de la hipérbola es:
\(\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1\)
donde (h, k) es el centro de la hipérbola.
El centro de la hipérbola es el punto medio entre los vértices. Dados los vértices (-1, -1) y (3, -1), el centro se calcula como:
\(h=\dfrac{-1+3}{2}=1, \quad k=\dfrac{-1+(-1)}{2}=-1\)
Por lo tanto, el centro es C (1, -1).
La distancia entre el centro y uno de los vértices es a. El vértice es (3, -1), y el centro es (1, -1), entonces:
\(a=3-1=2\)
Para una hipérbola horizontal, las ecuaciones de las asíntotas son:
\(y-k=\pm \dfrac{b}{a}(x-h)\)
Dada la asíntota \(y+1=\dfrac{3}{2}(x-1),\) comparamos con la forma general y obtenemos:
\(\dfrac{b}{a}=\dfrac{3}{2}\)
Como ya conocemos a = 2, sustituimos para encontrar b:
\(\dfrac{b}{2}=\dfrac{3}{2} → b=3\)
Para una hipérbola, se cumple que \(c^2=a^2+b^2.\) Sustituyendo los valores conocidos:
\(c^2=2^2+3^2=4+9=13 → c=\sqrt{13}\)
Utilizaremos el valor de c para calcular las coordenadas de los focos, que se encuentran a c unidades a la izquierda y derecha del centro. Es decir, en las coordenadas \((1+\sqrt{13}, -1)\) y \((1-\sqrt{13}, -1).\)
Sustituyendo los valores de \(h=1, k=-1, a=2\) y \(b=3\) en la ecuación canónica, obtenemos:
\(\dfrac{(x-1)^2}{4}-\dfrac{(y+1)^2}{9}=1\)
Las ecuaciones de las asíntotas son:
\(y+1=\pm \dfrac{3}{2}(x-1)\)
La excentricidad de la hipérbola es:
\(e=\dfrac{c}{a}=\dfrac{\sqrt{13}}{2}\)
El lado recto de la hipérbola es:
\(L_R=\dfrac{2b^2}{a}=\dfrac{2 \cdot 9}{2}=9\)
Elementos de la hipérbola:
- Centro: (1, -1)
- Focos: \((1+\sqrt{13}, -1)\) y \((1-\sqrt{13}, -1)\)
- Vértices: (3, -1) y (-1, -1)
- Semieje transversal: \(a=2\)
- Semieje conjugado: \(b=3\)
- Asíntotas: \(y+1=\pm \dfrac{3}{2}(x-1)\)
- Excentricidad: \(e=\dfrac{\sqrt{13}}{2}\)
- Lado recto: \(L_R=9\)
Ecuación: \(\dfrac{(x-1)^2}{4}-\dfrac{(y+1)^2}{9}=1\)
Solución del problema 4
Datos proporcionados:
- Centro: (-3, 1)
- Foco: (-3, 6)
- Vértice: (-3, 4)
Observamos que el centro, el foco y el vértice tienen la misma coordenada \(x=-3,\) lo que indica que la hipérbola está orientada verticalmente. Por lo tanto, la ecuación canónica de la hipérbola es:
\(\dfrac{(y-k)^2}{a^2}-\dfrac{(x-h)^2}{b^2}=1\)
donde (h, k) es el centro de la hipérbola.
Dado el centro (-3, 1), tenemos:
\(h=-3, \quad k=1\)
La distancia entre el centro y el vértice es a. El vértice es (-3, 4), y el centro es (-3, 1), entonces:
\(a=4-1=3\)
La distancia entre el centro y el foco es c. El foco es (-3, 6), y el centro es (-3, 1), entonces:
\(c=6-1=5\)
Podemos calcular b utilizando la relación \(c^2=a^2+b^2.\) Sustituyendo los valores conocidos:
\(c^2=a^2+b^2 → 5^2=3^2+b^2 → 25=9+b^2 → b^2=16 → b=4\)
Sustituyendo los valores de \(h=-3, k=1, a=3\) y \(b=4\) en la ecuación canónica, obtenemos:
\(\dfrac{(y-1)^2}{9}-\dfrac{(x+3)^2}{16}=1\)
Para una hipérbola vertical, las ecuaciones de las asíntotas son:
\(y-k=\pm \dfrac{a}{b}(x-h)\)
Sustituyendo los valores conocidos:
\(y-1=\pm \dfrac{3}{4}(x+3)\)
La excentricidad de la hipérbola es:
\(e=\dfrac{c}{a}=\dfrac{5}{3}\)
El lado recto de la hipérbola es:
\(L_R=\dfrac{2b^2}{a}=\dfrac{2 \cdot 16}{3}=\dfrac{32}{3}\)
Elementos de la hipérbola:
- Centro: (-3, 1)
- Focos: (-3, 6) y (-3, -4)
- Vértices: (-3, 4) y (-3, -2)
- Semieje transversal: a=3
- Semieje conjugado: b=4
- Asíntotas: \(y-1=\pm \dfrac{3}{4}(x+3)\)
- Excentricidad: \(e=\dfrac{5}{3}\)
- Lado recto: \(L_R=\dfrac{32}{3}\)
Ecuación: \(\dfrac{(y-1)^2}{9}-\dfrac{(x+3)^2}{16}=1\)
Solución del problema 5
Datos proporcionados:
- Foco: (-4, 0)
- Vértices: (-4, 4) y (-4, 2)
Observamos que el foco y los vértices tienen la misma coordenada \(x=-4,\) lo que indica que la hipérbola está orientada verticalmente. Por lo tanto, la ecuación canónica de la hipérbola es:
\(\dfrac{(y-k)^2}{a^2}-\dfrac{(x-h)^2}{b^2}=1\)
donde (h, k) es el centro de la hipérbola.
El centro de la hipérbola es el punto medio entre los vértices. Dados los vértices (-4, 4) y (-4, 2), el centro se calcula como:
\(h=\dfrac{-4+(-4)}{2}=-4, \quad k=\dfrac{4+2}{2}=3\)
Por lo tanto, el centro es C (-4, 3).
La distancia entre el centro y uno de los vértices es a. El vértice es (-4, 4), y el centro es (-4, 3), entonces:
\(a=4-3=1\)
La distancia entre el centro y el foco es c. El foco es (-4, 0), y el centro es (-4, 3), entonces:
\(c=3-0=3\)
Ahora calculamos b utilizando la relación \(c^2=a^2+b^2.\) Sustituyendo los valores conocidos:
\(c^2=a^2+b^2 → 3^2=1^2+b^2 → 9=1+b^2 → b^2=8 → b=2\sqrt{2}\)
Sustituyendo los valores de \(h=-4, k=3, a=1\) y \(b=2\sqrt{2}\) en la ecuación canónica, obtenemos:
\(\dfrac{(y-3)^2}{1}-\dfrac{(x+4)^2}{8}=1\)
Para una hipérbola vertical, las ecuaciones de las asíntotas son:
\(y-k=\pm \dfrac{a}{b}(x-h)\)
Sustituyendo los valores conocidos:
\(y-3=\pm \dfrac{1}{2\sqrt{2}}(x+4)\)
\(y-3=\pm \dfrac{\sqrt{2}}{4}(x+4)\)
La excentricidad de la hipérbola es:
\(e=\dfrac{c}{a}=\dfrac{3}{1}=3\)
El lado recto de la hipérbola es:
\(L_R=\dfrac{2b^2}{a}=\dfrac{2 \cdot 8}{1}=16\)
Elementos de la hipérbola:
- Centro: (-4, 3)
- Focos: (-4, 6) y (-4, 0)
- Vértices: (-4, 4) y (-4, 2)
- Semieje transversal: \(a=1\)
- Semieje conjugado: \(b=2\sqrt{2}\)
- Asíntotas: \(y-3=\pm \dfrac{\sqrt{2}}{4}(x+4)\)
- Excentricidad: \(e=3\)
- Lado recto: \(L_R=16\)
Ecuación: \(\dfrac{(y-3)^2}{1}-\dfrac{(x+4)^2}{8}=1\)
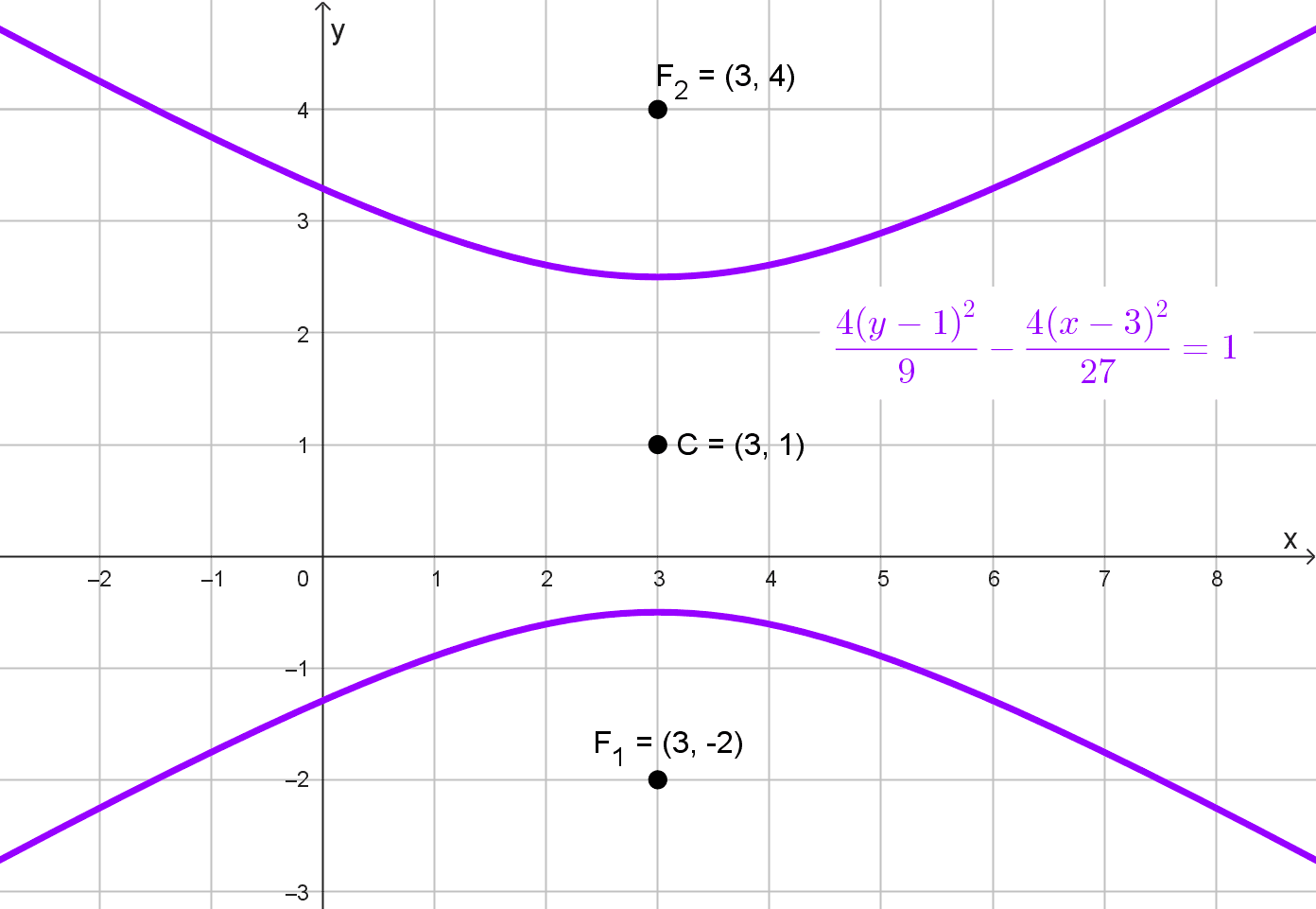
Solución del problema 6
Datos proporcionados:
- Focos: (3, 4) y (3, -2)
- Excentricidad: e = 2
Observamos que los focos tienen la misma coordenada x = 3, lo que indica que la hipérbola está orientada verticalmente. Por lo tanto, la ecuación canónica de la hipérbola es:
\(\dfrac{(y-k)^2}{a^2}-\dfrac{(x-h)^2}{b^2}=1\)
donde (h, k) es el centro de la hipérbola.
El centro de la hipérbola es el punto medio entre los focos. Dados los focos (3, 4) y (3, -2), el centro se calcula como:
\(h=\dfrac{3+3}{2}=3, \quad k=\dfrac{4+(-2)}{2}=1\)
Por lo tanto, el centro es C (3, 1).
La distancia entre el centro y uno de los focos es c. El foco es (3, 4), y el centro es (3, 1), entonces:
\(c=4-1=3\)
Dada la excentricidad e = 2, tenemos:
\(e=\dfrac{c}{a} → 2=\dfrac{3}{a} → a=\dfrac{3}{2}\)
Calculamos b utilizando la relación \(c^2=a^2+b^2.\) Sustituyendo los valores conocidos:
\(c^2=a^2+b^2 → 3^2=\left (\dfrac{3}{2}\right)^2+b^2 → 9=\dfrac{9}{4}+b^2 → b^2=9-\dfrac{9}{4}=\dfrac{27}{4} → b=\dfrac{3\sqrt{3}}{2}\)
Sustituyendo los valores de \(h=3, k=1, a=\dfrac{3}{2}\) y \(b=\dfrac{3\sqrt{3}}{2}\) en la ecuación canónica, obtenemos:
\(\dfrac{(y-1)^2}{\left (\dfrac{3}{2}\right)^2}-\dfrac{(x-3)^2}{\left (\dfrac{3\sqrt{3}}{2}\right)^2}=1\)
Simplificando:
\(\dfrac{(y-1)^2}{\dfrac{9}{4}}-\dfrac{(x-3)^2}{\dfrac{27}{4}}=1\)
Multiplicando ambos lados por 4 para eliminar los denominadores:
\(\dfrac{4 (y-1)^2}{9}-\dfrac{4 (x-3)^2}{27}=1\)
Para una hipérbola vertical, las ecuaciones de las asíntotas son:
\(y-k=\pm \dfrac{a}{b}(x-h)\)
Sustituyendo los valores conocidos:
\(y-1=\pm \dfrac{\dfrac{3}{2}}{\dfrac{3\sqrt{3}}{2}}(x-3) → y-1=\pm \dfrac{1}{\sqrt{3}}(x-3)\)
\(y-1=\pm \dfrac{\sqrt{3}}{3}(x-3)\)
El lado recto de la hipérbola es:
\(L_R=\dfrac{2b^2}{a}=\dfrac{2 \cdot \dfrac{27}{4}}{\dfrac{3}{2}}=\dfrac{\dfrac{54}{4}}{\dfrac{3}{2}}=\dfrac{54}{4} \cdot \dfrac{2}{3}=\dfrac{108}{12}=9\)
Elementos de la hipérbola:
- Centro: (3, 1)
- Focos: (3, 4) y (3, -2)
- Vértices: \((3; 1+a)=(3; 2,5)\) y \((3; 1-a)=(3; -0,5)\)
- Semieje transversal: \(a=\dfrac{3}{2}\)
- Semieje conjugado: \(b=\dfrac{3\sqrt{3}}{2}\)
- Asíntotas: \(y-1=\pm \dfrac{\sqrt{3}}{3}(x-3)\)
- Excentricidad: \(e=2\)
- Lado recto: \(L_R=9\)
Ecuación: \(\dfrac{4 (y-1)^2}{9}-\dfrac{4 (x-3)^2}{27}=1\)
Ejercicio 3
Escribe las ecuaciones de las hipérbolas que se muestran en los siguientes gráficos.
Soluciones
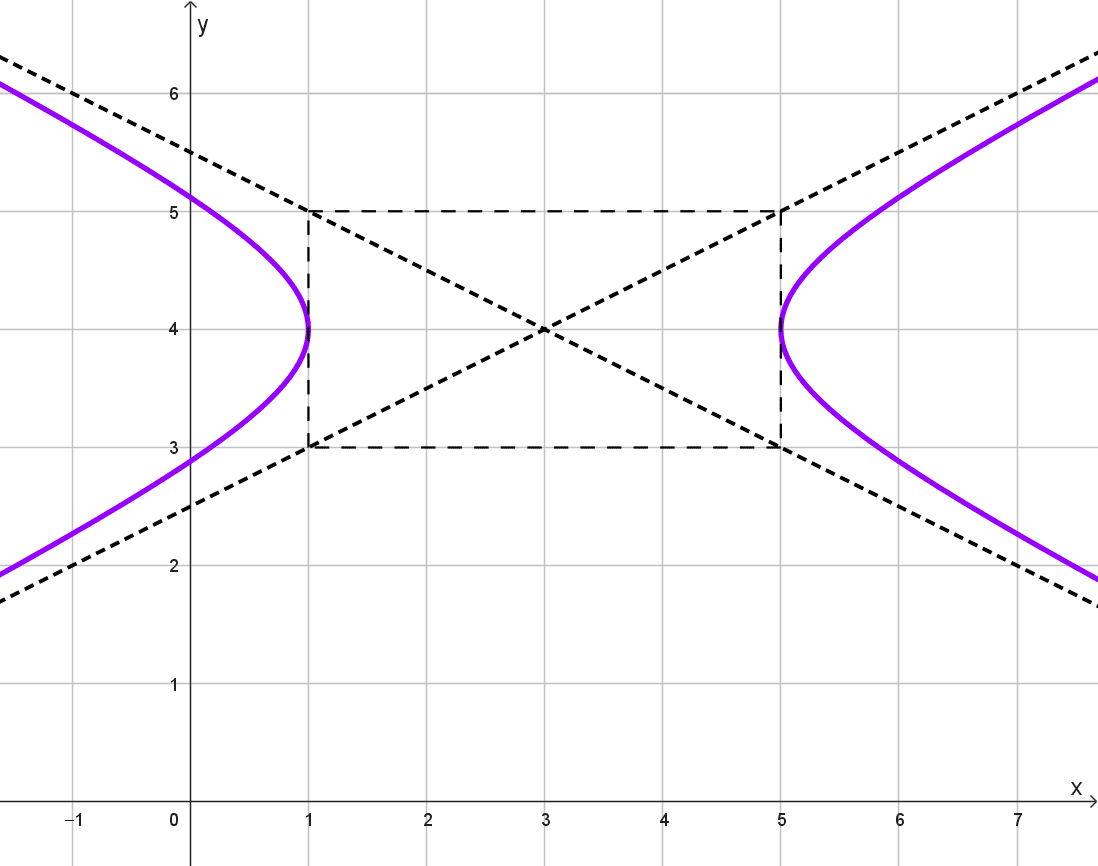
Hipérbola A
Identificamos que la orientación es horizontal y las asíntotas se intersectan en (3, 4), por tanto ese punto es el centro. Teniendo en cuenta esto, la ecuación es:
\(\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1\)
\(\dfrac{(x-3)^2}{a^2}-\dfrac{(y-4)^2}{b^2}=1\)
El rectángulo auxiliar tiene 2 unidades de alto (longitud del eje conjugado) y 4 unidades de ancho (longitud del eje transversal). Por tanto \(2b=2→b=1\) y \(2a=4→a=2.\) Reemplazando estos datos obtenemos la ecuación:
\(\dfrac{(x-3)^2}{2^2}-\dfrac{(y-4)^2}{1^2}=1\)
\(\dfrac{(x-3)^2}{4}-\dfrac{(y-4)^2}{1}=1\)
\(\dfrac{(x-3)^2}{4}-(y-4)^2=1\)
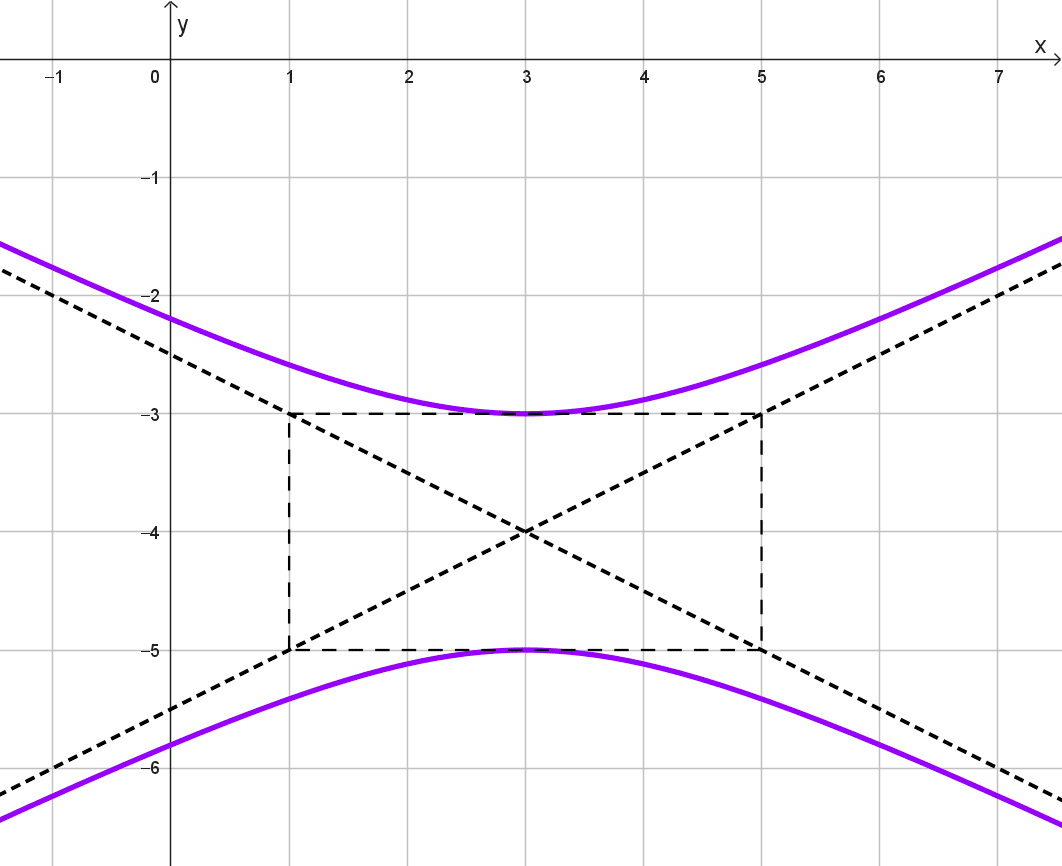
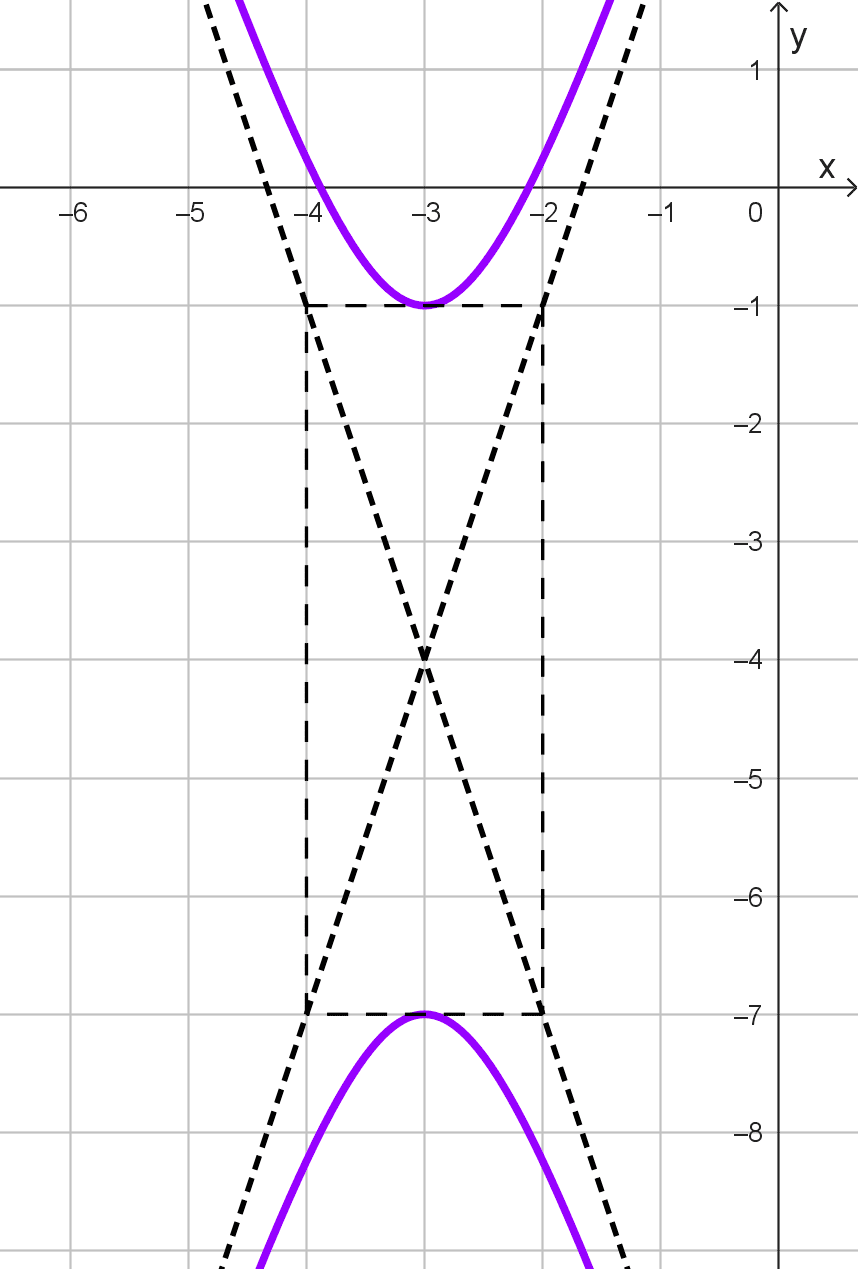
Hipérbola B
Identificamos que la orientación es vertical y las asíntotas se intersectan en (3, -4), por tanto ese punto es el centro. Teniendo en cuenta esto, la ecuación es:
\(\dfrac{(y-k)^2}{a^2}-\dfrac{(x-h)^2}{b^2}=1\)
\(\dfrac{(y-(-4))^2}{a^2}-\dfrac{(x-3)^2}{b^2}=1\)
\(\dfrac{(y+4)^2}{a^2}-\dfrac{(x-3)^2}{b^2}=1\)
El rectángulo auxiliar tiene 2 unidades de alto (longitud del eje transversal) y 4 unidades de ancho (longitud del eje conjugado). Por tanto \(2a=2→a=1\) y \(2b=4→b=2.\) Reemplazando estos datos obtenemos la ecuación:
\(\dfrac{(y+4)^2}{1^2}-\dfrac{(x-3)^2}{2^2}=1\)
\(\dfrac{(y+4)^2}{1}-\dfrac{(x-3)^2}{4}=1\)
\((y+4)^2-\dfrac{(x-3)^2}{4}=1\)
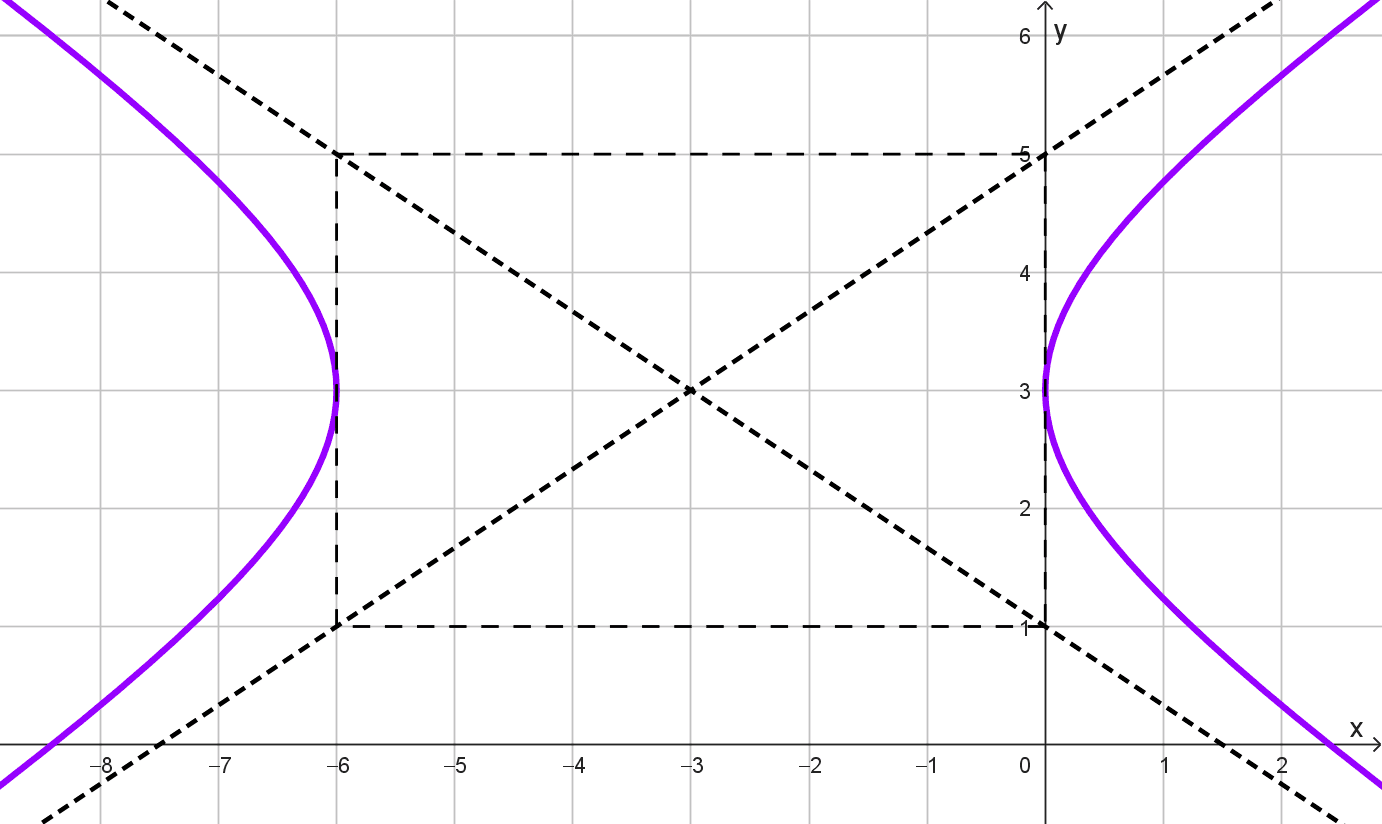
Hipérbola C
Reconocemos que la orientación es horizontal y las asíntotas se intersectan en (-3, 3), por tanto ese punto es el centro. Teniendo en cuenta esto, la ecuación es:
\(\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1\)
\(\dfrac{(x+3)^2}{a^2}-\dfrac{(y-3)^2}{b^2}=1\)
El rectángulo auxiliar tiene 4 unidades de alto (longitud del eje conjugado) y 6 unidades de ancho (longitud del eje transversal). Por tanto \(2b=4→b=2\) y \(2a=6→a=3.\) Reemplazando estos datos obtenemos la ecuación:
\(\dfrac{(x+3)^2}{3^2}-\dfrac{(y-3)^2}{2^2}=1\)
\(\dfrac{(x+3)^2}{9}-\dfrac{(y-3)^2}{4}=1\)
Hipérbola D
Identificamos que la orientación es vertical y las asíntotas se intersectan en (-3, -4), por tanto ese punto es el centro. Teniendo en cuenta esto, la ecuación es:
\(\dfrac{(y-k)^2}{a^2}-\dfrac{(x-h)^2}{b^2}=1\)
\(\dfrac{(y+4)^2}{a^2}-\dfrac{(x+3)^2}{b^2}=1\)
El rectángulo auxiliar tiene 6 unidades de alto (longitud del eje transversal) y 2 unidades de ancho (longitud del eje conjugado). Por tanto \(2a=6→a=3\) y \(2b=2→b=1.\) Reemplazando estos datos obtenemos la ecuación:
\(\dfrac{(y+4)^2}{3^2}-\dfrac{(x+3)^2}{1^2}=1\)
\(\dfrac{(y+4)^2}{9}-\dfrac{(x+3)^2}{1}=1\)
\(\dfrac{(y+4)^2}{9}-(x+3)^2=1\)
Determinar los elementos de una hipérbola a partir de su ecuación
Consigna: dadas las siguientes ecuaciones de hipérbolas, hallar las coordenadas de su centro, vértices y focos, las longitudes de los ejes transverso y conjugado, la excentricidad, lado recto y las ecuaciones de las asíntotas.
- \(\dfrac{x^2}{25}-\dfrac{y^2}{9}=1\)
- \(\dfrac{y^2}{16}-\dfrac{x^2}{4}=1\)
- \(\dfrac{(x-2)^2}{4}-\dfrac{(y+3)^2}{9}=1\)
- \(\dfrac{(y+3)^2}{10}-\dfrac{(x-2)^2}{20}=1\)
- \(y^2-\dfrac{x^2}{5}=1\)
- \(4x^2-y^2=16\)
- \(y^2-x^2=25\)
- \(2x^2-y^2+4x+4y-4=0\)
- \(2y^2-x^2+2x+8y+3=0\)
- \(25x^2-9y^2+100x-54y+10=0\)
Soluciones
Ecuación 1
Ecuación: \(\dfrac{x^2}{25}-\dfrac{y^2}{9}=1\)
Esta ecuación corresponde a una hipérbola centrada en el origen ya que sigue la forma estándar:
\(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\)
En este caso, \(a^2=25\) y \(b^2=9,\) por lo que \(a=5\) y \(b=3.\) La orientación es horizontal porque el término positivo contiene a la variable x.
Los vértices se encuentran a una distancia a del centro a lo largo del eje transverso (que en este caso está sobre el eje x). Por lo tanto, las coordenadas de los vértices son \((\pm a, 0),\) es decir, (5, 0) y (-5, 0).
Para encontrar los focos, necesitamos calcular la distancia focal c, que se obtiene mediante la relación \(c^2=a^2+b^2.\) Sustituyendo los valores conocidos:
\(c^2=25+9=34 \quad → \quad c=\sqrt{34}\)
Los focos están ubicados en \((\pm c, 0),\) es decir, \((\sqrt{34}, 0)\) y \((-\sqrt{34}, 0).\)
La excentricidad se calcula como \(e=\dfrac{c}{a}.\) Sustituyendo los valores:
\(e=\dfrac{\sqrt{34}}{5}\)
El lado recto (o ancho focal) de una hipérbola se calcula como \(\dfrac{2b^2}{a}.\) Sustituyendo los valores:
\(L_R=\dfrac{2 \cdot 9}{5}=\dfrac{18}{5}=3,6\)
Las asíntotas de una hipérbola son rectas que pasan por el centro y tienen pendientes \(\pm \dfrac{b}{a}.\) Por lo tanto, las ecuaciones de las asíntotas son:
\(y=\pm \dfrac{3}{5}x\)
En resumen:
- Centro: (0, 0)
- Vértices: (5, 0) y (-5, 0)
- Focos: \((\sqrt{34}, 0)\) y \((-\sqrt{34}, 0)\)
- Longitud del eje transverso: \(2a=10\)
- Longitud del eje conjugado: \(2b=6\)
- Excentricidad: \(e=\dfrac{\sqrt{34}}{5}\)
- Lado recto: \(L_R=3,6\)
- Asíntotas: \(y=\pm \dfrac{3}{5}x\)
Ecuación 2
Ecuación: \(\dfrac{y^2}{16}-\dfrac{x^2}{4}=1\)
Esta ecuación corresponde a una hipérbola centrada en el origen, pero en este caso, la orientación es vertical porque el término positivo contiene a la variable y. La forma estándar es:
\(\dfrac{y^2}{a^2}-\dfrac{x^2}{b^2}=1\)
De la ecuación dada, identificamos que \(a^2=16\) y \(b^2=4,\) por lo que \(a=4\) y \(b=2.\)
Como primer paso, determinamos las coordenadas del centro. Dado que la hipérbola está centrada en el origen, el centro es (0, 0).
Los vértices de una hipérbola vertical se encuentran a una distancia a del centro a lo largo del eje transverso (que en este caso está sobre el eje y). Por lo tanto, las coordenadas de los vértices son \((0, \pm a),\) es decir, (0, 4) y (0, -4).
Para encontrar los focos, necesitamos calcular c, que se obtiene mediante la relación \(c^2=a^2+b^2.\) Sustituyendo los valores conocidos:
\(c^2=16+4=20 \quad \rightarrow \quad c=\sqrt{20}=2\sqrt{5}\)
Los focos están ubicados en \((0, \pm c),\) es decir, \((0, 2\sqrt{5})\) y \((0, -2\sqrt{5}).\)
La excentricidad se calcula como:
\(e=\dfrac{c}{a}=\dfrac{2\sqrt{5}}{4}=\dfrac{\sqrt{5}}{2}\)
El lado recto de la hipérbola se calcula como:
\(L_R=\dfrac{2b^2}{a}=\dfrac{2 \cdot 4}{4}=\dfrac{8}{4}=2\)
Las asíntotas de una hipérbola son rectas que pasan por el centro y tienen pendientes \(\pm \dfrac{a}{b}.\) Por lo tanto, las ecuaciones de las asíntotas son:
\(y=\pm \dfrac{4}{2}x=\pm 2x\)
Elementos:
- Centro: (0, 0)
- Vértices: (0, 4) y (0, -4)
- Focos: \((0, 2\sqrt{5})\) y \((0, -2\sqrt{5})\)
- Longitud del eje transverso: \(2a=8\)
- Longitud del eje conjugado: \(2b=4\)
- Excentricidad: \(e=\dfrac{\sqrt{5}}{2}\)
- Lado recto: \(L_R=2\)
- Asíntotas: \(y=\pm 2x\)
Ecuación 3
Ecuación: \(\dfrac{(x-2)^2}{4}-\dfrac{(y+3)^2}{9}=1\)
Esta ecuación corresponde a una hipérbola centrada fuera del origen. La orientación es horizontal porque el término positivo contiene a la variable x. La forma estándar de una hipérbola horizontal es:
\(\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1\)
De la ecuación dada, identificamos que \(a^2=4\) y \(b^2=9,\) por lo que \(a=2\) y \(b=3.\)
Como primer paso, determinamos las coordenadas del centro. Dado que la hipérbola está centrada en (h, k), el centro es (2, -3).
Los vértices de una hipérbola horizontal se encuentran a una distancia a del centro a lo largo del eje transverso (que en este caso es paralelo al eje x). Por lo tanto, las coordenadas de los vértices son \((h \pm a, k),\) es decir, \((2+2, -3)=(4, -3)\) y \((2-2, -3)=(0, -3).\)
Para encontrar los focos, necesitamos calcular c, que se obtiene mediante la relación \(c^2=a^2+b^2.\) Sustituyendo los valores conocidos:
\(c^2=4+9=13 \quad \rightarrow \quad c=\sqrt{13}\)
Los focos están ubicados a c unidades del centro sobre el eje transverso, es decir, en \((h \pm c, k):\) \((2+\sqrt{13}, -3)\) y \((2-\sqrt{13}, -3).\)
La excentricidad se calcula como:
\(e=\dfrac{c}{a}=\dfrac{\sqrt{13}}{2}\)
El lado recto se calcula como:
\(L_R=\dfrac{2b^2}{a}=\dfrac{2 \cdot 9}{2}=\dfrac{18}{2}=9\)
Las asíntotas de una hipérbola son rectas que pasan por el centro y tienen pendientes \(\pm \dfrac{b}{a}.\) Por lo tanto, las ecuaciones de las asíntotas son:
\(y-k=\pm \dfrac{b}{a}(x-h) \quad \rightarrow \quad y+3=\pm \dfrac{3}{2}(x-2)\)
Simplificando, las ecuaciones de las asíntotas quedan:
\(y=\dfrac{3}{2}x-6\) y \(y=-\dfrac{3}{2}x\)
Elementos:
- Centro: (2, -3)
- Vértices: (4, -3) y (0, -3)
- Focos: \((2+\sqrt{13}, -3)\) y \((2-\sqrt{13}, -3)\)
- Longitud del eje transverso: \(2a=4\)
- Longitud del eje conjugado: \(2b=6\)
- Excentricidad: \(e=\dfrac{\sqrt{13}}{2}\)
- Lado recto: \(L_R=9\)
- Asíntotas: \(y=\dfrac{3}{2}x-6\) y \(y=-\dfrac{3}{2}x\)
Ecuación 4
Ecuación: \(\dfrac{(y+3)^2}{10}-\dfrac{(x-2)^2}{20}=1\)
Esta ecuación corresponde a una hipérbola centrada fuera del origen. La orientación es vertical porque el término positivo contiene a la variable y. La forma estándar de una hipérbola vertical es:
\(\dfrac{(y-k)^2}{a^2}-\dfrac{(x-h)^2}{b^2}=1\)
De la ecuación dada, identificamos que \(a^2=10\) y \(b^2=20,\) por lo que \(a=\sqrt{10}\) y \(b=\sqrt{20}=2\sqrt{5}.\)
Como primer paso, determinamos las coordenadas del centro. Dado que la hipérbola está centrada en (h, k), el centro es (2, -3).
Los vértices de una hipérbola vertical se encuentran a una distancia a del centro a lo largo del eje transverso. Por lo tanto, las coordenadas de los vértices son \((h, k \pm a),\) es decir, \((2, -3+\sqrt{10})\) y \((2, -3-\sqrt{10}).\)
Para encontrar los focos, necesitamos calcular la distancia focal c, que se obtiene mediante la relación \(c^2=a^2+b^2.\) Sustituyendo los valores conocidos:
\(c^2=10+20=30 \quad \rightarrow \quad c=\sqrt{30}\)
Los focos están ubicados en \((h, k \pm c),\) es decir, \((2, -3+\sqrt{30})\) y \((2, -3-\sqrt{30}).\)
La excentricidad se calcula como:
\(e=\dfrac{c}{a}=\dfrac{\sqrt{30}}{\sqrt{10}}=\sqrt{3}\)
El lado recto de la hipérbola se calcula como:
\(L_R=\dfrac{2b^2}{a}=\dfrac{2 \cdot 20}{\sqrt{10}}=\dfrac{40}{\sqrt{10}}=4\sqrt{10}\)
Las asíntotas de una hipérbola son rectas que pasan por el centro y tienen pendientes \(\pm \dfrac{a}{b}.\) Por lo tanto, las ecuaciones de las asíntotas son:
\(y-k=\pm \dfrac{a}{b}(x-h) \quad \rightarrow \quad y+3=\pm \dfrac{\sqrt{10}}{2\sqrt{5}}(x-2)\)
Elementos:
- Centro: (2, -3)
- Vértices: \((2, -3+\sqrt{10})\) y \((2, -3-\sqrt{10})\)
- Focos: \((2, -3+\sqrt{30})\) y \((2, -3-\sqrt{30})\)
- Longitud del eje transverso: \(2a=2\sqrt{10}\)
- Longitud del eje conjugado: \(2b=4\sqrt{5}\)
- Excentricidad: \(e=\sqrt{3}\)
- Lado recto: \(L_R=4\sqrt{10}\)
- Asíntotas: \(y+3=\pm \dfrac{\sqrt{10}}{2\sqrt{5}}(x-2)\)
Ecuación 5
Ecuación: \(y^2-\dfrac{x^2}{5}=1\)
Esta ecuación corresponde a una hipérbola centrada en el origen, ya que no hay términos h o k que desplacen el centro. Además, la orientación es vertical porque el término positivo contiene a la variable y. Identificamos que \(a^2=1\) y \(b^2=5,\) por lo que \(a=\sqrt{1}=1\) y \(b=\sqrt{5}.\)
Los vértices de una hipérbola vertical se encuentran a una distancia a del centro a lo largo del eje transverso. Por lo tanto, las coordenadas de los vértices son \((h, k \pm a),\) es decir, \((0, 0+1)=(0, 1)\) y \((0, 0-1)=(0, -1).\)
Para encontrar los focos, necesitamos calcular la distancia focal c, que se obtiene mediante la relación \(c^2=a^2+b^2.\) Sustituyendo los valores conocidos:
\(c^2=1+5=6 \quad \rightarrow \quad c=\sqrt{6}\)
Los focos están ubicados en \((h, k \pm c),\) es decir, \((0, 0+\sqrt{6})=(0, \sqrt{6})\) y \((0, 0-\sqrt{6})=(0, -\sqrt{6}).\)
La excentricidad se calcula como:
\(e=\dfrac{c}{a}=\dfrac{\sqrt{6}}{1}=\sqrt{6}\)
El lado recto de la hipérbola se calcula como:
\(L_R=\dfrac{2b^2}{a}=\dfrac{2 \cdot 5}{1}=10\)
Las asíntotas de una hipérbola son rectas que pasan por el centro y tienen pendientes \pm \dfrac{a}{b}. Por lo tanto, las ecuaciones de las asíntotas son:
\(y-k=\pm \dfrac{a}{b}(x-h) \quad \rightarrow \quad y=\pm \dfrac{1}{\sqrt{5}}x\)
Elementos:
- Centro: (0, 0)
- Vértices: (0, 1) y (0, -1)
- Focos: \((0, \sqrt{6})\) y \((0, -\sqrt{6})\)
- Longitud del eje transverso: \(2a=2 \cdot 1=2\)
- Longitud del eje conjugado: \(2b=2 \cdot \sqrt{5}=2\sqrt{5}\)
- Excentricidad: \(e=\sqrt{6}\)
- Lado recto: \(L_R=10\)
- Asíntotas: \(y=\pm \dfrac{1}{\sqrt{5}}x\)
Ecuación 6
Ecuación: \(4x^2-y^2=16\)
Dividiendo ambos miembros entre 16, obtenemos la ecuación canónica:
\(\dfrac{x^2}{4}-\dfrac{y^2}{16}=1\)
Esta ecuación corresponde a una hipérbola centrada en el origen. Además, la orientación es horizontal porque el término positivo contiene a la variable x. Identificamos que \(a^2=4\) y \(b^2=16,\) por lo que \(a=\sqrt{4}=2 y b=\sqrt{16}=4.\)
Los vértices de una hipérbola horizontal se encuentran a una distancia a del centro a lo largo del eje transverso. Por lo tanto, las coordenadas de los vértices son \((h \pm a, k),\) es decir, \((0+2, 0)=(2, 0)\) y \((0-2, 0)=(-2, 0).\)
Para encontrar los focos, necesitamos calcular la distancia focal c, que se obtiene mediante la relación \(c^2=a^2+b^2.\) Sustituyendo los valores conocidos:
\(c^2=4+16=20 \quad \rightarrow \quad c=\sqrt{20}=2\sqrt{5}\)
Los focos están ubicados en \((h \pm c, k),\) es decir, \((0+2\sqrt{5}, 0)=(2\sqrt{5}, 0)\) y \((0-2\sqrt{5}, 0)=(-2\sqrt{5}, 0).\)
La excentricidad se calcula como:
\(e=\dfrac{c}{a}=\dfrac{2\sqrt{5}}{2}=\sqrt{5}\)
El lado recto de la hipérbola se calcula como:
\(L_R=\dfrac{2b^2}{a}=\dfrac{2 \cdot 16}{2}=16\)
Las asíntotas de una hipérbola son rectas que pasan por el centro y tienen pendientes \(\pm \dfrac{b}{a}.\) Por lo tanto, las ecuaciones de las asíntotas son:
\(y-k=\pm \dfrac{b}{a}(x-h) \quad \rightarrow \quad y=\pm \dfrac{4}{2}x \quad \rightarrow \quad y=\pm 2x\)
Elementos:
- Centro: (0, 0)
- Vértices: (2, 0) y (-2, 0)
- Focos: \((2\sqrt{5}, 0)\) y \((-2\sqrt{5}, 0)\)
- Longitud del eje transverso: \(2a=2 \cdot 2=4\)
- Longitud del eje conjugado: \(2b=2 \cdot 4=8\)
- Excentricidad: \(e=\sqrt{5}\)
- Lado recto: \(L_R=16\)
- Asíntotas: \(y=\pm 2x\)
Ecuación 7
Ecuación: \(y^2-x^2=25\)
Dividiendo ambos miembros entre 25 obtenemos la forma reducida:
\(\dfrac{y^2}{25}-\dfrac{x^2}{25}=1\)
La ecuación dada corresponde a una hipérbola centrada en el origen. La orientación es vertical porque el término positivo contiene a la variable y. Se identifica que \(a^2=25\) y \(b^2=25,\) por lo que \(a=5\) y \(b=5.\)
Los vértices de una hipérbola vertical se encuentran a una distancia a del centro a lo largo del eje transverso. Por lo tanto, las coordenadas de los vértices son \((0, \pm 5),\) es decir, (0, 5) y (0, -5).
Para encontrar los focos, calculamos la distancia focal c, usando la relación \(c^2=a^2+b^2:\)
\(c^2=25+25=50 \quad → \quad c=\sqrt{50}=5\sqrt{2}\)
Los focos están ubicados en \((0, \pm c),\) es decir, \((0, 5\sqrt{2})\) y \((0, -5\sqrt{2}).\)
La excentricidad se calcula como:
\(e=\dfrac{c}{a}=\dfrac{5\sqrt{2}}{5}=\sqrt{2}\)
El lado recto de la hipérbola se calcula con la fórmula:
\(L_R=\dfrac{2b^2}{a}=\dfrac{2 \cdot 25}{5}=\dfrac{50}{5}=10\)
Las asíntotas de una hipérbola son rectas que pasan por el centro y tienen pendientes \(\pm \dfrac{a}{b}.\) Dado que \(a=b=5,\) la pendiente es \(\pm 1.\) Así, las ecuaciones de las asíntotas son:
\(y=\pm x\)
Elementos:
- Centro: (0, 0)
- Vértices: (0, 5) y (0, -5)
- Focos: \((0, 5\sqrt{2})\) y \((0, -5\sqrt{2})\)
- Longitud del eje transverso: \(2a=10\)
- Longitud del eje conjugado: \(2b=10\)
- Excentricidad: \(e=\sqrt{2}\)
- Lado recto: \(L_R=10\)
- Asíntotas: \(y=\pm x\)
Ecuación 8
Ecuación: \(2x^2-y^2+4x+4y-4=0\)
Si completamos los cuadrados (véase los ejercicios de pasar de la forma general a la canónica) obtenemos la expresión:
\((x+1)^2-\dfrac{(y-2)^2}{2}=1\)
La ecuación representa una hipérbola con centro fuera del origen. Como el término positivo corresponde a la variable x, se trata de una hipérbola de orientación horizontal. La forma estándar de una hipérbola horizontal es:
\(\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1\)
Comparando con la ecuación dada se observa que el denominador del primer término es \(a^2\) y el del segundo es \(b^2.\) En este caso, como el primer término no tiene denominador, se asume que \(a^2=1,\) por lo que \(a=1.\) Además, \(b^2=2,\) lo que implica que \(b=\sqrt{2}.\)
Para determinar el centro, identificamos los valores de h y k a partir de los términos cuadráticos. Dado que \((x+1)^2=(x-(-1))^2\) y \((y-2)^2\) ya está expresado en la forma estándar, el centro se encuentra en (-1, 2).
Los vértices de una hipérbola horizontal están ubicados a una distancia a del centro en dirección paralela al eje x. Por lo tanto, los vértices son \((-1 \pm 1, 2),\) lo que da las coordenadas (0, 2) y (-2, 2).
Ahora calculamos la distancia focal c utilizando la relación:
\(c^2=a^2+b^2\)
\(c^2=1+2=3 \quad → \quad c=\sqrt{3}\)
Los focos están ubicados a una distancia c del centro a lo largo del eje focal, es decir \((-1 \pm \sqrt{3}, 2),\) lo que nos da los puntos \((-1+\sqrt{3}, 2)\) y \((-1-\sqrt{3}, 2).\)
La excentricidad se obtiene como:
\(e=\dfrac{c}{a}=\dfrac{\sqrt{3}}{1}=\sqrt{3}\)
El lado recto se calcula con la fórmula:
\(L_R=\dfrac{2b^2}{a}=\dfrac{2 \cdot 2}{1}=4\)
Las asíntotas de una hipérbola pasan por el centro y tienen pendiente \(\pm \dfrac{b}{a}.\) Como \(b=\sqrt{2}\) y \(a=1,\) la pendiente es \(\pm \sqrt{2}.\) Entonces, las ecuaciones de las asíntotas son:
\(y-2=\pm \sqrt{2} (x+1)\)
Resumen de elementos:
- Centro: (-1, 2)
- Vértices: (0, 2) y (-2, 2)
- Focos: \((-1+\sqrt{3}, 2)\) y \((-1-\sqrt{3}, 2)\)
- Longitud del eje transverso: \(2a=2\)
- Longitud del eje conjugado: \(2b=2\sqrt{2}\)
- Excentricidad: \(e=\sqrt{3}\)
- Lado recto: \(L_R=4\)
- Asíntotas: \(y-2=\pm \sqrt{2} (x+1)\)
Ecuación 9
Ecuación: \(2y^2-x^2+2x+8y+3=0\)
Completando los cuadrados se obtiene:
\(\dfrac{(y+2)^2}{2}-\dfrac{(x-1)^2}{4}=1\)
La ecuación dada corresponde a una hipérbola cuyo centro no está en el origen. Como el término positivo es el que contiene la variable y, la hipérbola tiene una orientación vertical. La forma estándar de una hipérbola vertical es:
\(\dfrac{(y-k)^2}{a^2}-\dfrac{(x-h)^2}{b^2}=1\)
Comparando con la ecuación proporcionada se identifican los valores \(a^2=2\) y \(b^2=4,\) por lo que \(a=\sqrt{2}\) y \(b=2.\)
Para hallar el centro, observamos que los valores de h y k se obtienen de los términos cuadráticos. Como \((y+2)^2=(y-(-2))^2\) y \((x-1)^2\) ya está en la forma estándar, el centro es (1, -2).
Los vértices de una hipérbola vertical se ubican a una distancia a del centro a lo largo del eje transversal. Por lo tanto, los vértices están en \((1, -2 \pm \sqrt{2}),\) lo que da los puntos \((1, -2+\sqrt{2})\) y \((1, -2-\sqrt{2}).\)
Ahora calculamos la distancia focal c utilizando la relación \(c^2=a^2+b^2:\)
\(c^2=2+4=6 \quad → \quad c=\sqrt{6}\)
Los focos están a una distancia c del centro en la dirección vertical, por lo que sus coordenadas son \((1, -2 \pm \sqrt{6}),\) lo que nos da los puntos \((1, -2+\sqrt{6})\) y \((1, -2-\sqrt{6}).\)
La excentricidad se obtiene como:
\(e=\dfrac{c}{a}=\dfrac{\sqrt{6}}{\sqrt{2}}=\sqrt{3}\)
El lado recto se calcula con la fórmula:
\(L_R=\dfrac{2b^2}{a}=\dfrac{2 \cdot 4}{\sqrt{2}}=\dfrac{8}{\sqrt{2}}=4\sqrt{2}\)
Las asíntotas de una hipérbola pasan por el centro y tienen pendiente \(\pm \dfrac{a}{b}.\) Como el centro es \((1, -2), a=\sqrt{2}\) y \(b=2,\) la pendiente es \(\pm \dfrac{\sqrt{2}}{2}.\) Entonces, las ecuaciones de las asíntotas son:
\(y+2=\pm \dfrac{\sqrt{2}}{2} (x-1)\)
Elementos:
- Centro: (1, -2)
- Vértices: \((1, -2+\sqrt{2})\) y \((1, -2-\sqrt{2})\)
- Focos: \((1, -2+\sqrt{6})\) y \((1, -2-\sqrt{6})\)
- Longitud del eje transverso: \(2a=2\sqrt{2}\)
- Longitud del eje conjugado: \(2b=4\)
- Excentricidad: \(e=\sqrt{3}\)
- Lado recto: \(L_R=4\sqrt{2}\)
- Asíntotas: \(y+2=\pm \dfrac{\sqrt{2}}{2} (x-1)\)
Ecuación 10
Ecuación: \(25x^2-9y^2+100x-54y+10=0\)
Completando los cuadrados obtenemos la forma canónica de la hipérbola:
\(\dfrac{(x+2)^2}{9/25}-(y+3)^2=1\)
La ecuación representa una hipérbola cuyo centro no está en el origen. Como el término positivo está asociado a la variable x, la hipérbola tiene una orientación horizontal. La forma estándar de una hipérbola con eje transverso horizontal es:
\(\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1\)
Comparando con la ecuación proporcionada se identifica que \(a^2=\dfrac{9}{25},\) por lo que \(a=\dfrac{3}{5},\) y que \(b^2=1,\) lo que implica que \(b=1.\)
Para hallar el centro, observamos que los valores de h y k se obtienen de los términos cuadráticos. Como \((x+2)^2=(x-(-2))^2\) y \((y+3)^2=(y-(-3))^2,\) el centro se encuentra en (-2, -3).
Los vértices de una hipérbola horizontal se ubican a una distancia a del centro en la dirección del eje x. Por lo tanto, los vértices están en \((-2 \pm \dfrac{3}{5}, -3),\) lo que da las coordenadas \(\left (-2+\dfrac{3}{5}, -3\right)\) y \(\left (-2-\dfrac{3}{5}, -3\right),\) que simplificadas son:
\(\left (-\dfrac{7}{5}, -3\right)\) y \(\left (-\dfrac{13}{5}, -3\right)\)
Ahora calculamos la distancia focal c con la relación:
\(c^2=a^2+b^2\)
\(c^2=\dfrac{9}{25}+1=\dfrac{9}{25}+\dfrac{25}{25}=\dfrac{34}{25} \quad → \quad c=\dfrac{\sqrt{34}}{5}\)
Los focos se encuentran a una distancia c del centro en la dirección del eje x, es decir \((-2 \pm \dfrac{\sqrt{34}}{5}, -3),\) lo que nos da los puntos:
\(\left (-2+\dfrac{\sqrt{34}}{5}, -3\right) y \left (-2-\dfrac{\sqrt{34}}{5}, -3\right)\)
La excentricidad se obtiene como:
\(e=\dfrac{c}{a}=\dfrac{\dfrac{\sqrt{34}}{5}}{\dfrac{3}{5}}=\dfrac{\sqrt{34}}{3}\)
El lado recto se calcula con la fórmula:
\(L_R=\dfrac{2b^2}{a}=\dfrac{2 \cdot 1}{\dfrac{3}{5}}=\dfrac{2}{\dfrac{3}{5}}=\dfrac{10}{3}\)
Las asíntotas de una hipérbola pasan por el centro y tienen pendiente \(\pm \dfrac{b}{a}.\) Como \(b=1\) y \(a=\dfrac{3}{5},\) la pendiente es:
\(\pm \dfrac{1}{\dfrac{3}{5}}=\pm \dfrac{5}{3}\)
Por lo que las ecuaciones de las asíntotas son:
\(y+3=\pm \dfrac{5}{3} (x+2)\)
Resumen de elementos:
- Centro: (-2, -3)
- Vértices: \(\left (-\dfrac{7}{5}, -3\right)\) y \(\left (-\dfrac{13}{5}, -3\right)\)
- Focos: \(\left (-2+\dfrac{\sqrt{34}}{5}, -3\right)\) y \(\left (-2-\dfrac{\sqrt{34}}{5}, -3\right)\)
- Longitud del eje transverso: \(2a=\dfrac{6}{5}\)
- Longitud del eje conjugado: \(2b=2\)
- Excentricidad: \(e=\dfrac{\sqrt{34}}{3}\)
- Lado recto: \(L_R=\dfrac{10}{3}\)
- Asíntotas: \(y+3=\pm \dfrac{5}{3} (x+2)\)
Pasar de la ecuación general a la canónica
Consigna: convertir las siguientes ecuaciones de hipérbolas a su forma canónica.
- \(4x^2-y^2=16\)
- \(2x^2-y^2+4x+4y-4=0\)
- \(2y^2-x^2+2x+8y+3=0\)
- \(25x^2-9y^2+100x-54y+10=0\)
Soluciones
Ecuación 1
Ecuación: \(4x^2-y^2=16\)
Como primer paso, dividimos ambos miembros de la ecuación por 16 para que el lado derecho se convierta en 1. De esta forma se obtiene
\(\dfrac{4x^2}{16}-\dfrac{y^2}{16}=1\)
lo que se simplifica a
\(\dfrac{x^2}{4}-\dfrac{y^2}{16}=1\)
Con ello se llega a la forma canónica deseada.
Ecuación 2
Ecuación: \(2x^2-y^2+4x+4y-4=0\)
Comenzamos agrupando los términos según la variable: se agrupan los términos en x y en y, de modo que se puede escribir como
\(2 (x^2+2x)-\bigl (y^2-4y\bigr)-4=0\)
Como siguiente paso, completamos el cuadrado en cada grupo. Para \(x^2+2x\) sumamos y restamos 1 recordando que \((x+1)^2=x^2+2x+1,\) obteniéndose
\(x^2+2x=(x+1)^2-1\)
De manera similar, para \(y^2-4y\) sumamos y restamos 4 ya que \((y-2)^2=y^2-4y+4,\) de donde
\(y^2-4y=(y-2)^2-4\)
Reemplazando en la ecuación se tiene:
\(2\bigl[(x+1)^2-1\bigr]-\Bigl[(y-2)^2-4\Bigr]-4=0\)
Al desarrollar y simplificar los términos constantes se obtiene
\(2 (x+1)^2-(y-2)^2-2=0\)
Luego, sumamos 2 a ambos lados y dividimos la ecuación resultante por 2, obteniendo:
\((x+1)^2-\dfrac{(y-2)^2}{2}=1\)
Así se alcanza la forma canónica.
Ecuación 3
Ecuación: \(2y^2-x^2+2x+8y+3=0\)
Primero se reagrupan los términos según la variable, separando los términos en x y en y. Se escribe como:
\(2 (y^2+4y)-\bigl (x^2-2x\bigr)+3=0\)
Se completa el cuadrado en cada grupo. Para \(y^2+4y\) se suma y resta 4 ya que \((y+2)^2=y^2+4y+4;\) es decir:
\(y^2+4y=(y+2)^2-4\)
Para \(x^2-2x\) se suma y resta 1 (pues \((x-1)^2=x^2-2x+1\)), de modo que:
\(x^2-2x=(x-1)^2-1\)
Al sustituir en la ecuación se obtiene:
\(2\Bigl[(y+2)^2-4\Bigr]-\Bigl[(x-1)^2-1\Bigr]+3=0\)
Desarrollando se llega a:
\(2 (y+2)^2-8-(x-1)^2+1+3=0\)
La suma de los términos constantes \(-8+1+3\) es igual a \(-4,\) por lo que la ecuación queda:
\(2 (y+2)^2-(x-1)^2-4=0\)
A continuación, se suma 4 a ambos lados y se divide la ecuación por 4 para dejar el 1 en el lado derecho:
\(\dfrac{2 (y+2)^2}{4}-\dfrac{(x-1)^2}{4}=1\)
lo que se simplifica a:
\(\dfrac{(y+2)^2}{2}-\dfrac{(x-1)^2}{4}=1\)
Ecuación 4
Ecuación: \(25x^2-9y^2+100x-54y+10=0\)
El primer paso consiste en agrupar los términos en x y y. Se agrupa de la siguiente forma:
\(25x^2+100x-9y^2-54y+10=0\)
En el caso de los términos en x se factoriza 25 y y para los términos en y se factoriza -9, resultando:
\(25 (x^2+4x)-9 (y^2+6y)+10=0\)
A continuación, se completa el cuadrado en cada grupo. Para \(x^2+4x\) se añade y sustrae 4 porque \((x+2)^2=x^2+4x+4,\) es decir:
\(x^2+4x=(x+2)^2-4\)
Para \(y^2+6y\) se añade y sustrae 9, pues \((y+3)^2=y^2+6y+9;\) por lo tanto:
\(y^2+6y=(y+3)^2-9\)
Sustituyendo estas expresiones en la ecuación original se tiene:
\(25\Bigl[(x+2)^2-4\Bigr]-9\Bigl[(y+3)^2-9\Bigr]+10=0\)
Al desarrollar se obtiene:
\(25 (x+2)^2-100-9 (y+3)^2+81+10=0\)
Sumamos los términos constantes, por lo que la ecuación se transforma en:
\(25 (x+2)^2-9 (y+3)^2-9=0\)
A continuación, sumamos 9 a ambos lados para aislar los términos cuadrados:
\(25 (x+2)^2-9 (y+3)^2=9\)
Finalmente, dividimos toda la ecuación por 9 para dejar el 1 en el lado derecho:
\(\dfrac{25 (x+2)^2}{9}-\dfrac{9 (y+3)^2}{9}=1\)
lo que se simplifica a
\(\dfrac{25(x+2)^2}{9}-(y+3)^2=1\)
Recordando que esta expresión es equivalente a
\(\dfrac{(x+2)^2}{9/25}-(y+3)^2=1\)
Pasar de la ecuación canónica a la general
Consigna: convertir las siguientes ecuaciones a su forma general.
- \(\dfrac{x^2}{25}-\dfrac{y^2}{9}=1\)
- \(\dfrac{(x-2)^2}{4}-\dfrac{(y+3)^2}{9}=1\)
- \(\dfrac{(y+3)^2}{10}-\dfrac{(x-2)^2}{20}=1\)
Soluciones
Ecuación 1
Ecuación: \(\dfrac{x^2}{25}-\dfrac{y^2}{9}=1\)
Multiplicamos ambos miembros por 225 (mínimo común múltiplo de 25 y 9) para eliminar los denominadores, lo que nos lleva a:
\(225\cdot\dfrac{x^2}{25}-225\cdot\dfrac{y^2}{9}=225\)
Simplificando:
\(9x^2-25y^2=225\)
Restando 225 a ambos lados se obtiene la forma general:
\(9x^2-25y^2-225=0\)
Ecuación 2
Ecuación: \(\dfrac{(x-2)^2}{4}-\dfrac{(y+3)^2}{9}=1\)
Como primer paso se desarrollan los cuadrados: \((x-2)^2=x^2-4x+4\) y \((y+3)^2=y^2+6y+9.\) Con esto, la ecuación se reescribe como:
\(\dfrac{x^2-4x+4}{4}-\dfrac{y^2+6y+9}{9}=1\)
Multiplicamos ambos miembros por 36 (mínimo común múltiplo de 4 y 9) para despejar los denominadores, obteniendo:
\(9 (x^2-4x+4)-4 (y^2+6y+9)=36\)
Al desarrollar se tiene
\(9x^2-36x+36-4y^2-24y-36=36\)
donde los términos constantes 36-36 se cancelan, dejando
\(9x^2-36x-4y^2-24y=36\)
Finalmente, al restar 36 a ambos lados se llega a
\(9x^2-36x-4y^2-24y-36=0\)
Ecuación 3
Ecuación: \(\dfrac{(y+3)^2}{10}-\dfrac{(x-2)^2}{20}=1\)
Como primer paso, multiplicamos ambos lados por 20 (el mínimo común múltiplo de 10 y 20) para eliminar los denominadores, obteniendo:
\(2 (y+3)^2-(x-2)^2=20\)
A continuación, desarrollamos los cuadrados: \((y+3)^2=y^2+6y+9\) y \((x-2)^2=x^2-4x+4.\) Sustituyendo estas expresiones, la ecuación se transforma en:
\(2\bigl (y^2+6y+9\bigr)-\bigl (x^2-4x+4\bigr)=20\)
Al distribuir los términos se tiene:
\(2y^2+12y+18-x^2+4x-4=20\)
Observamos que \(18-4=14;\) por ello, la ecuación queda:
\(-x^2+2y^2+4x+12y+14=20\)
Restamos 20 a ambos lados para obtener la forma general igualada a cero:
\(-x^2+2y^2+4x+12y-6=0\)
Como es habitual tener el coeficiente del término x^2 positivo, multiplicamos toda la ecuación por -1 y obtenemos finalmente:
\(x^2-2y^2-4x-12y+6=0\)
Problemas de la vida real
Los siguientes son ejercicios de aplicación de la hipérbola en la vida cotidiana y las ciencias.
Ejercicio 1
Una torre de enfriamiento es una estructura hiperbólica. Suponga que el diámetro de su base es de 100 metros y su diámetro más pequeño es de 48 metros que se encuentra a 84 metros de la base. Si la torre mide 120 metros de altura, calcule su diámetro en la parte más alta.
Solución
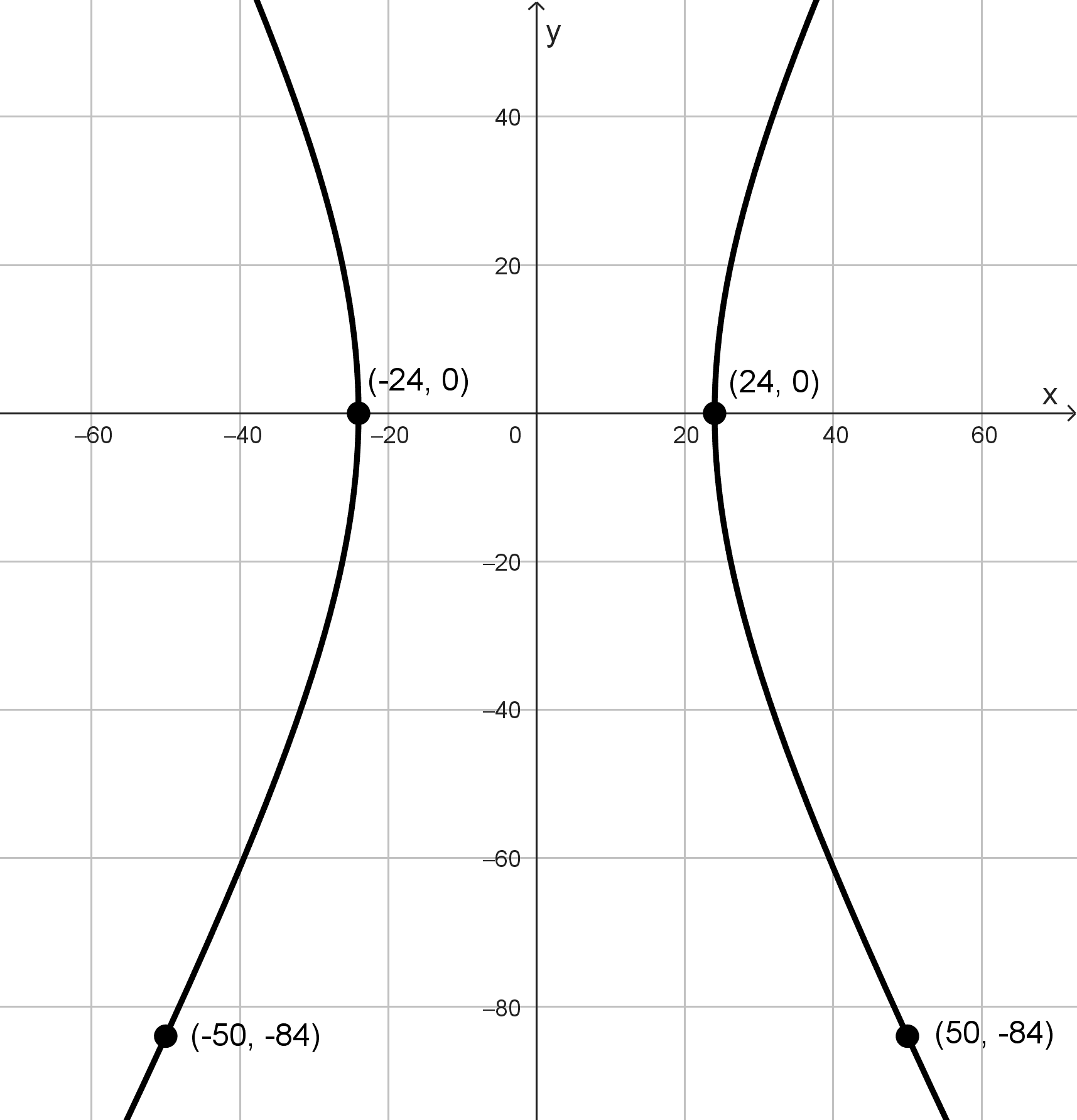
Ubicamos una hipérbola de forma conveniente en el plano cartesiano. Haremos que el diámetro más pequeño esté sobre el eje x, de modo que los vértices de la hipérbola son los puntos (24, 0) y (-24, 0), la distancia entre ellos es de 48 unidades.
La base tiene 100 metros de diámetro y se encuentra a 84 unidades del diámetro más pequeño, es decir, la hipérbola pasa por los puntos (-50, -84) y (50, -84).
Lo que nos pide el problema es el diámetro de la parte más alta. Sabiendo que la torre tiene 120 metros de altura, buscamos calcular el diámetro cuando \(y=120-84=36.\)
En base a la información que tenemos, podemos armar la ecuación de la hipérbola y hallar el x correspondiente a \(y=36.\) La ecuación tendrá la siguiente forma:
\(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\)
Conocemos los vértices, la distancia entre ellos es \(2a=48,\) entonces \(a=24.\) Para calcular b utilizamos el hecho de que la hipérbola pasa por el punto (-50, -84):
\(\dfrac{(-50)^2}{24^2}-\dfrac{(-84)^2}{b^2}=1\)
\(\dfrac{625}{144}-\dfrac{7056}{b^2}=1\)
\(-\dfrac{7056}{b^2}=1-\dfrac{625}{144}\)
\(-\dfrac{7056}{b^2}=-\dfrac{481}{144}\)
\(b^2=\dfrac{7056\cdot 144}{481}\)
\(b^2=\dfrac{1016064}{481}\)
Teniendo los valores de \(a^2\) y \(b^2,\) los reemplazamos en la ecuación canónica:
\(\dfrac{x^2}{576}-\dfrac{481 y^2}{1016064}=1\)
Si \(y=36,\) entonces:
\(\dfrac{x^2}{576}-\dfrac{481\cdot 36^2}{1016064}=1\)
\(\dfrac{x^2}{576}=1+\dfrac{623376}{1016064}\)
\(x^2=576\cdot \left(1+\dfrac{623376}{1016064}\right)\)
\(x=\sqrt{576\cdot \left(1+\dfrac{623376}{1016064}\right)}\)
\(x≈30,49\)
Entonces, como \(x≈30,49\) es la mitad del diámetro buscado, multiplicamos por dos para obtener el valor final: \(2\cdot 30,49=60,97\)
En conclusión, el diámetro de la parte más alta es de 60,97 metros.
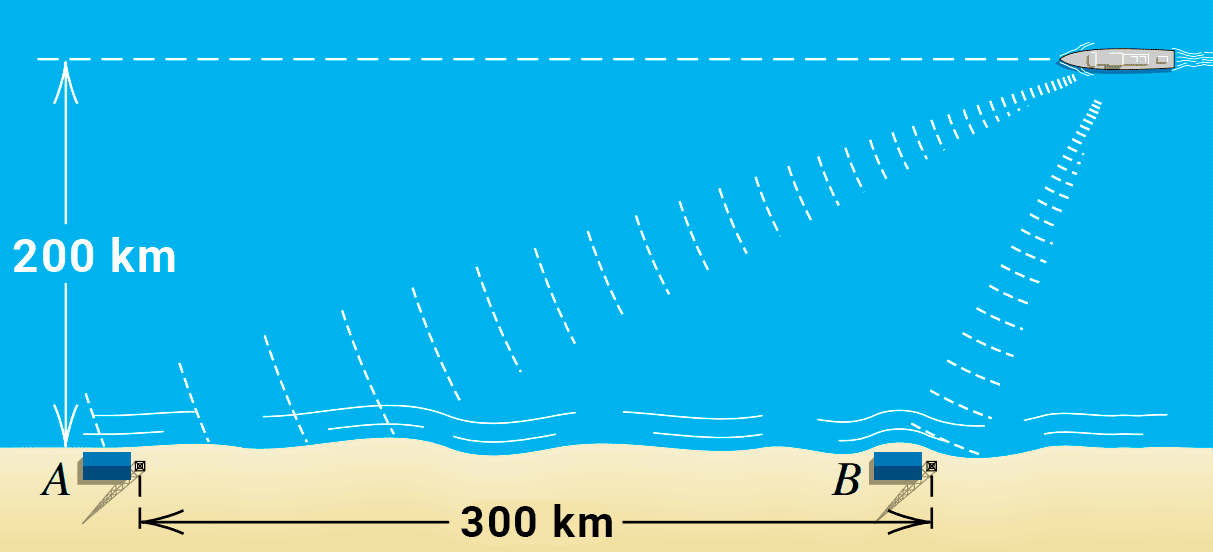
Ejercicio 2
Un barco está siguiendo un curso que está a 200 km de una costa recta y paralelo a ésta. El barco transmite una señal de auxilio que es recibida por dos estaciones de guardacostas A y B, situadas a 300 km una de la otra, como se ve en la figura. Al medir la diferencia entre los tiempos de recepción de señal, se determina que el barco está 250 km más cerca de B que de A. ¿Dónde está el barco?
Solución
Modelamos esta situación de forma conveniente en un plano cartesiano: ubicamos a las estaciones sobre el eje x en las coordenadas A(-150, 0) y B(150, 0), de modo que las separa una distancia de 300 unidades. El barco se mueve sobre la recta y = 100.
El problema nos dice que el barco está 250 km más cerca de B que de A, dicho de otro modo, la distancia del barco hasta A supera en 250 km a la distancia del barco hasta B. Simbolizamos al barco con el punto P, entonces:
\(d(A,P)=250+d(B,P)\)
Reordenando:
\(d(A,P)-d(B,P)=250\)
Viendo esto nos damos cuenta que el barco se encuentra sobre una hipérbola cuya constante es \(2a=250.\) Entonces \(a=125\) y \(a^2=15625.\)
Los focos son las estaciones A y B, la distancia entre ellas es la distancia focal \(2c=300,\) entonces \(c=150.\) Sabiendo que en una hipérbola se cumple la relación \(c^2=a^2+b^2,\) reemplazamos los datos conocidos:
\(150^2=125^2+b^2→b^2=6875\)
Conociendo a y b podemos armar la ecuación de la hipérbola:
\(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\)
\(\dfrac{x^2}{15625}-\dfrac{y^2}{6875}=1\)
Ahora bien, sabemos que el barco se mueve sobre la recta \(y=200,\) sustituyendo en la ecuación:
\(\dfrac{x^2}{15625}-\dfrac{200^2}{6875}=1\)
\(\dfrac{x^2}{15625}=1+\dfrac{40000}{6875}\)
\(\dfrac{x^2}{15625}=\dfrac{75}{11}\)
\(x^2=15625\cdot \dfrac{75}{11}\)
\(x=\sqrt{\dfrac{15625\cdot 75}{11}}\)
\(x=125\cdot \dfrac{\sqrt{75}}{\sqrt{11}}\)
\(x=125\cdot \dfrac{5\sqrt{3}}{\sqrt{11}}\)
\(x=625\dfrac{\sqrt{3}}{\sqrt{11}}≈326,4\)
Entonces, basado en este sistema de referencia, el barco se encuentra en las coordenadas \(\left(625\dfrac{\sqrt{3}}{\sqrt{11}}, 200\right).\)
Podemos calcular las distancias desde las estaciones hasta el barco, usando la aproximación \(x=326,4.\) Así:
Distancia del barco hasta A: \(\sqrt{(326,4+150)^2+(200-0)^2}=516,68 km\)
Distancia del barco hasta B: \(\sqrt{(326,4-150)^2+(200-0)^2}=266,68 km\)
Como se esperaba, la diferencia de distancias es de 250 km.
Conclusión: en el sistema de referencia, el barco se encuentra en las coordenadas \(\left(625\dfrac{\sqrt{3}}{\sqrt{11}}, 200\right),\) a 516,68 km de la estación A y a 266,68 km de la estación B.
Ejercicio 3
Dos estaciones de Loran están a 200 kilómetros una de la otra, a lo largo de una costa recta. Un barco registra una diferencia de tiempo de 0,00038 segundos entre las señales Loran.
- Establezca un sistema de coordenadas rectangulares apropiado para determinar a qué parte de la costa llegará el barco si siguiera la hipérbola correspondiente a esta diferencia de tiempo.
- Si el barco está a 50 km de la costa al momento de obtener la diferencia de tiempo, ¿cuál es la ubicación aproximada del barco?
Solución
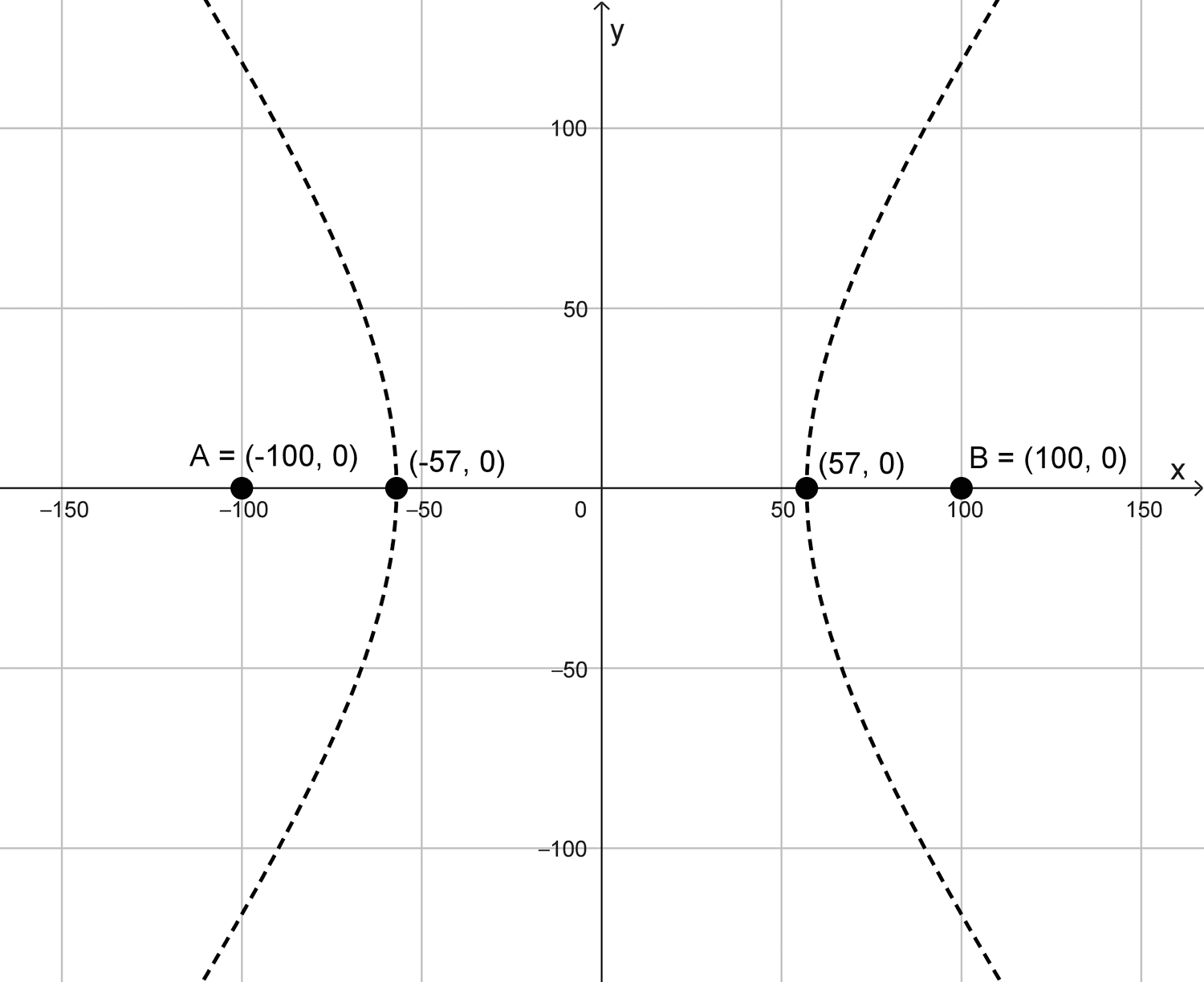
a) Llamaremos A y B a las estaciones de Loran y las colocaremos sobre el eje x, una en coordenada (-100, 0) y otra en la (100, 0), de este modo quedan separadas por 200 unidades.
Se registra una diferencia de tiempo de \(Δt=0,00038 s\) y las señales viajan a la velocidad de la luz, que es de aproximadamente 300000 km/s. Entonces, convertimos la diferencia de tiempo en una diferencia de distancias multiplicando ambos valores:
\(Δd = 0,00038 s \cdot 300000 km/s = 114 km\)
Esta diferencia de 114 km corresponde a la constante 2a de la hipérbola. Es decir, \(a=57→a^2=3249.\) La distancia entre los focos (las estaciones) es de 200 unidades, por tanto: \(2c=200→c=100.\) Utilizando la relación \(c^2=a^2+b^2\) obtenemos \(b^2:\)
\(100^2=57^2+b^2→b^2=6751\)
Con estos datos podemos armar la ecuación de la hipérbola sobre la cual se mueve el barco:
\(\dfrac{x^2}{3249}-\dfrac{y^2}{6751}=1\)
La costa es la recta \(y=0,\) por tanto, sustituyendo en la ecuación:
\(\dfrac{x^2}{3249}-\dfrac{0}{6751}=1\)
\(\dfrac{x^2}{3249}=1\)
\(x^2=3249\)
\(x=\pm 57\)
Entonces, el barco llegará a la costa en las coordenadas (57, 0) o (-57, 0) bajo este sistema de referencia. Es decir, llegará a 57 km hacia el este o el oeste del punto medio entre las estaciones de Loran. Si el barco está más cerca de B (como en el gráfico), llegará a la costa en el punto (57, 0); si está más cerca de A, lo hará en el punto (-57, 0).
b) Si el barco está a 50 km de la costa, esto corresponde al punto (x, 50) de la hipérbola. Hallaremos el valor de x correspondiente sustituyendo y = 50 en la ecuación:
\(\dfrac{x^2}{3249}-\dfrac{y^2}{6751}=1\)
\(\dfrac{x^2}{3249}-\dfrac{50^2}{6751}=1\)
\(\dfrac{x^2}{3249}=1+\dfrac{2500}{6751}\)
\(x^2=3249\left(1+\dfrac{2500}{6751}\right)\)
\(x≈\pm 66,72\)
Entonces, la ubicación aproximada del barco es \((\pm 66,72; 50)\) en el sistema de referencia. Que se tome el signo positivo dependerá de si el barco está más cerca de la estación A o de la estación B.
Ejercicios avanzados
Los ejercicios anteriores son de hipérbolas horizontales y verticales, los siguientes artículos contienen un tipo de problema más general donde los ejes de la hipérbola pueden estar inclinados con respecto a los ejes coordenados, resultando en una hipérbola rotada:
Bibliografía
- Engler, A., Müller, D., Vrancken, S. y Hecklein, M. (2020). Geometría analítica. Universidad Nacional del Litoral.
- Fuller, G. y Tarwater, D. (1995). Geometría analítica (7.ª ed.). Pearson Educación.
- Lehmann, C. (1989). Geometría analítica. Limusa.
- Leithold. L. (1992). Álgebra y trigonometría con geometría analítica. Oxford University Press.
- Márquez, A., Vázquez, F., Ruiz, H., Villegas, M. y Figueroa, M. (2009). Geometría analítica. Prentice Hall.
- Raichman, S. y Totter, E. (2016). Geometría analítica para ciencias e ingeniería. Universidad Nacional de Cuyo.
- Sullivan, M. (2006). Álgebra y trigonometría. Pearson Educación.
- Swokowski, E. y Cole, J. (2009). Álgebra y trigonometría con geometría analítica. Cengage Learning.
¿Te ha servido este contenido? ¡Califícalo!
0,0 / 5 — 0 votos
CÓMO CITAR ESTE ARTÍCULO
Machado, D. (2025, 28 de marzo). Ejercicios de hipérbola. Exponty. https://exponty.com/ejercicios-hiperbola
Subir





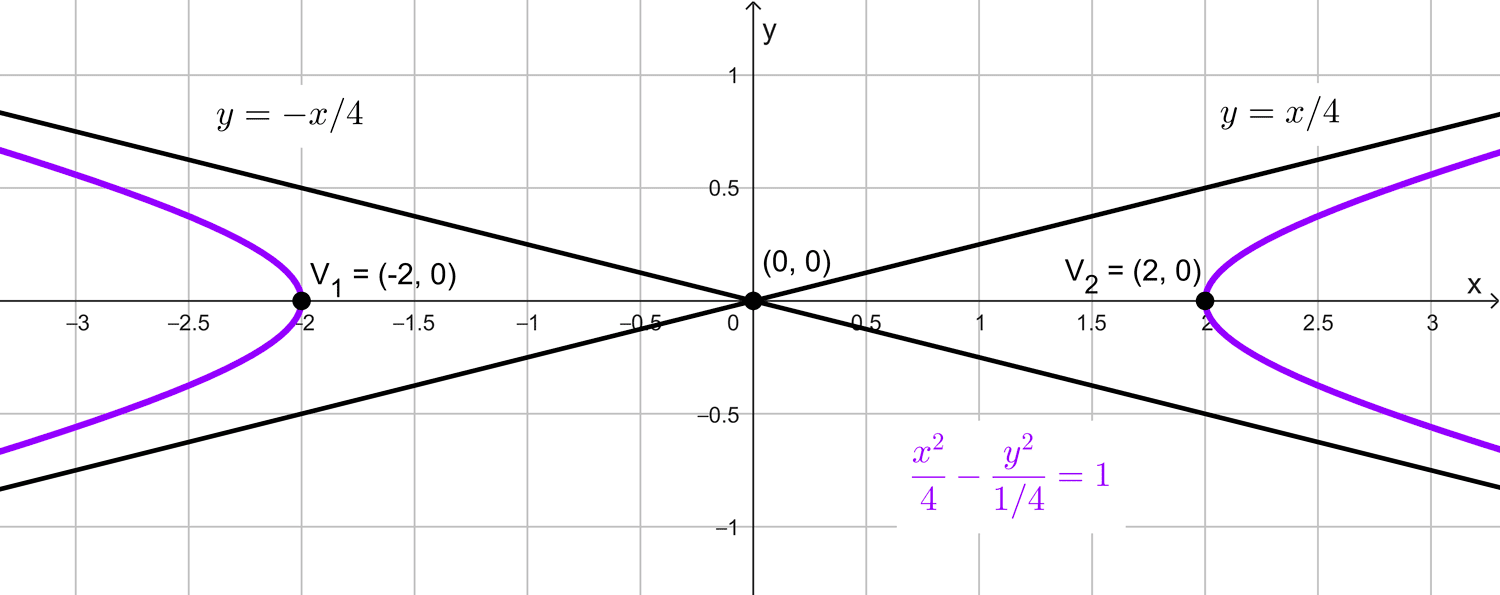
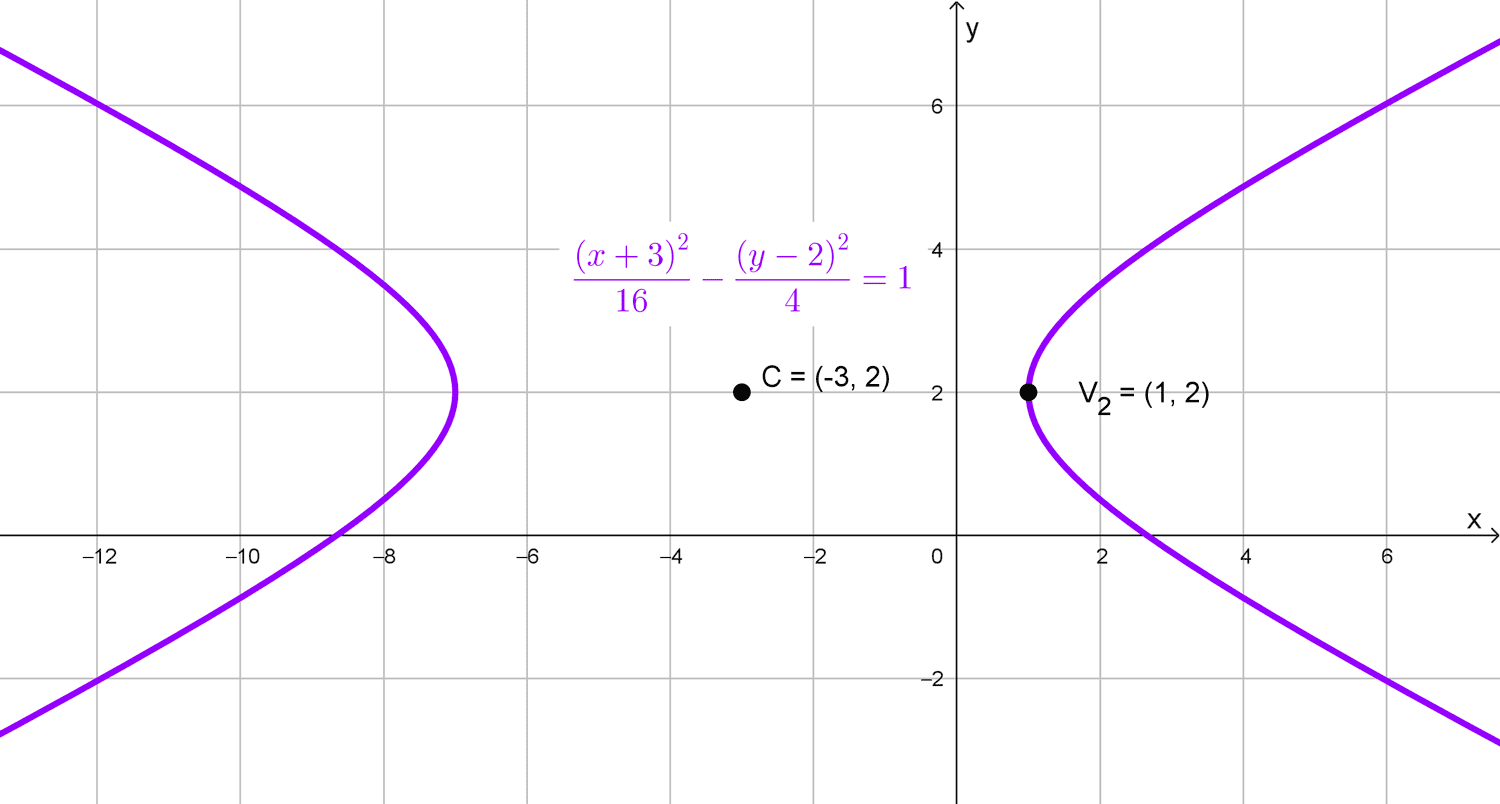
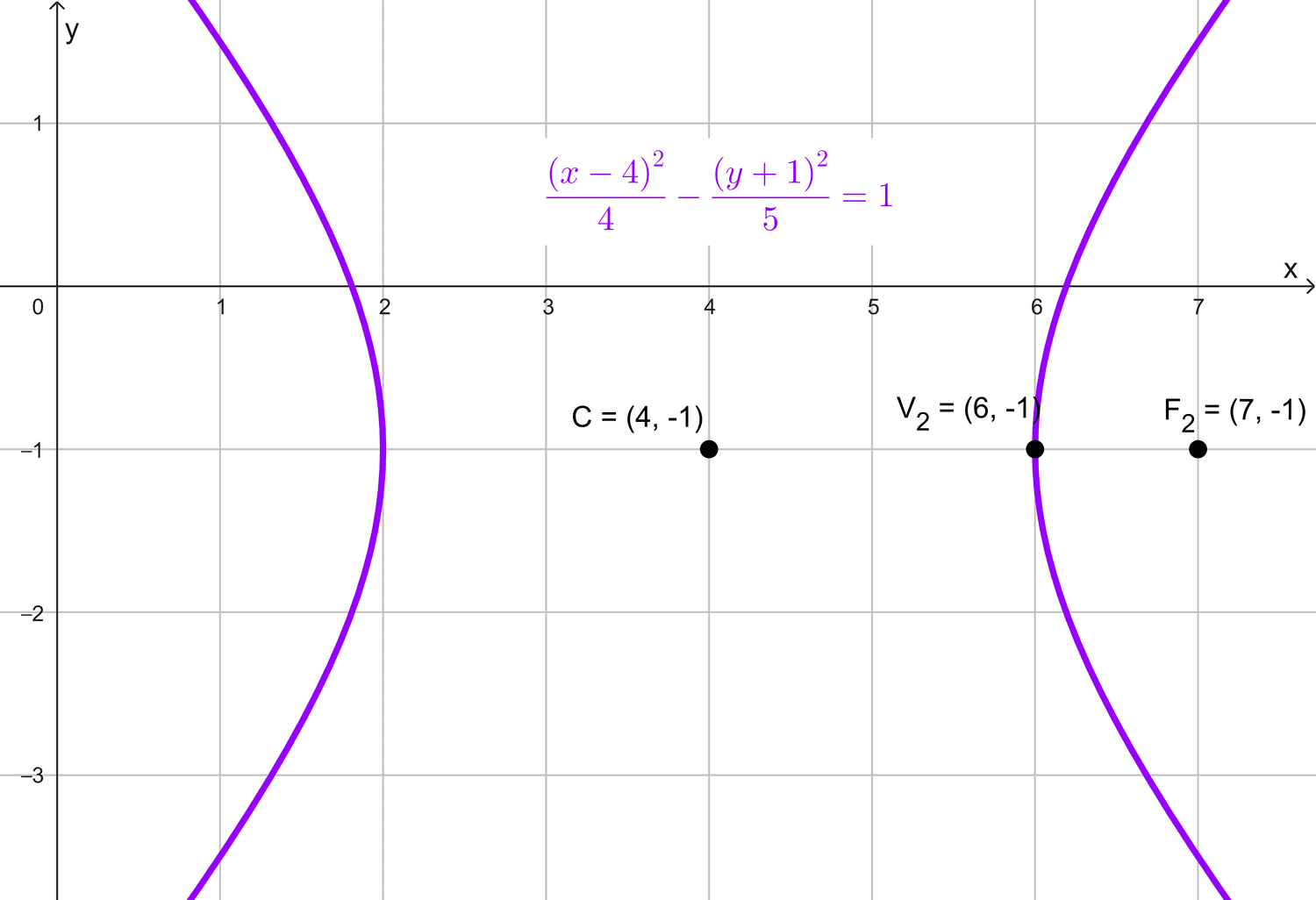

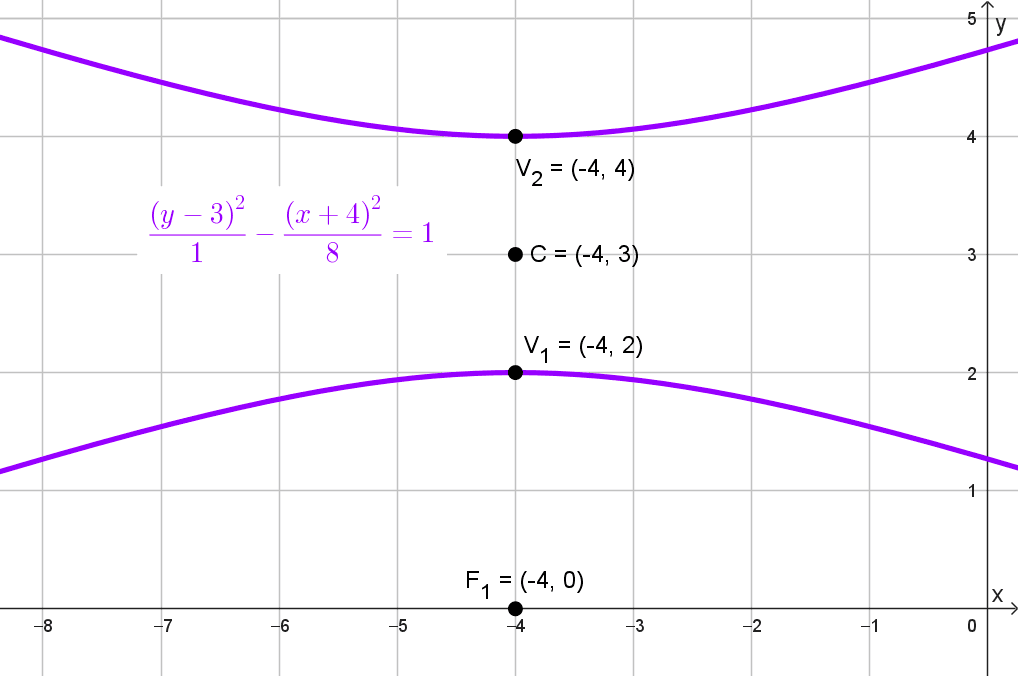


Deja una respuesta