
Vértice de una parábola
El vértice de una parábola es el punto donde la parábola corta a su eje de simetría, también es el punto más cercano al foco y la directriz. El vértice se denota con las coordenadas (h, k) y puede ser el origen de coordenadas u otro punto del plano.
Si se trata de una parábola vertical, el vértice es el punto máximo o mínimo, dependiendo de si las ramas abren hacia abajo (forma de ∩) o hacia arriba (forma de U), respectivamente. En una parábola horizontal, el vértice es el punto de la parábola con abscisa más alta o más baja, dependiendo de si las ramas abren hacia la izquierda (forma de ⊃) o hacia la derecha (forma de ⊂), respectivamente.
A continuación, veremos cómo hallar el vértice dependiendo de la orientación de la parábola con ejemplos paso a paso.
Aclaración: este artículo aborda un tema particular de la parábola. Si aún no tienes claros los conceptos básicos de esta cónica, te invito a revisar primero el artículo principal donde la tratamos en profundidad:
Índice
Vértice de una parábola vertical
Existen varias formas de hallar el vértice dependiendo de la ecuación que tengamos.
Con la ecuación canónica
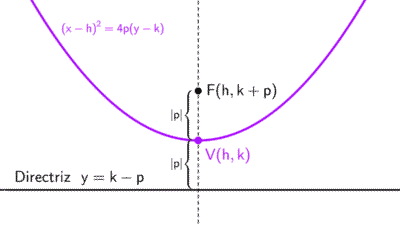
La ecuación canónica de una parábola vertical con vértice en (h, k) es:
\((x-h)^2=4p(y-k)\)
donde |p| es la distancia entre el foco y el vértice. Otra forma de escribirla es como:
\(y=a(x-h)^2+k ~~\text{donde}~~ a=\dfrac{1}{4p}\)
Estas se conocen como la "forma vértice", ya que las coordenadas del mismo pueden leerse en la ecuación.
Ejemplos
- En la ecuación \((x-2)^2=4 (y-3),\) podemos identificar directamente los valores de h y k que definen las coordenadas del vértice. Aquí, h es el valor que se resta de x dentro del paréntesis elevado al cuadrado, por lo que h=2. De manera similar, k es el valor que se resta de y dentro del otro paréntesis, lo que nos da k=3. Por lo tanto, las coordenadas del vértice son (2, 3).
- En el caso de \((x+2)^2=6y,\) la ecuación puede reescribirse como \((x-(-2))^2=6 (y-0).\) Identificamos que h = -2 (debido al signo positivo dentro del paréntesis) y k = 0, ya que no hay término constante restado en y. Así, el vértice se ubica en (-2, 0).
- Examinemos la ecuación \((x+1)^2=7 (y+2).\) Al compararla con la forma canónica, notamos que podemos expresarla como \((x-(-1))^2=7 (y-(-2)).\) Esto nos permite determinar que el valor de h es -1 y el valor de k es -2. Por tanto, el vértice de esta parábola se localiza en el punto (-1, -2).
- Con la ecuación \((x+3)^2=8 (y-4),\) procedemos a identificar que h = -3, pues es el número que restado a x da como resultado (x+3). Por otro lado, k = 4, ya que es el número que se resta directamente de y. Por consiguiente, las coordenadas del vértice de esta parábola son (-3, 4).
Si el vértice es el origen de coordenadas (0, 0), la ecuación se simplifica a \(x^2=4py.\) Por ejemplo, las siguientes parábolas tienen su vértice en el origen:
- \(x=2y^2\)
- \(x=-5y^2\)
- \(x=\dfrac{1}{4}y^2\)
Con la ecuación general
La ecuación de una parábola vertical puede presentarse en la forma:
y = ax2 + bx + c
donde a, b y c son números reales. Como las parábolas verticales son funciones cuadráticas, otra forma habitual es:
f(x) = ax2 + bx + c
El vértice en estos casos tiene coordenadas (h, k) que se obtienen con las siguientes fórmulas:
\(h=\dfrac{-b}{2a}\)
\(k=f(h)=-\dfrac{b^2-4ac}{4a}\)
No es necesario memorizar la segunda fórmula ya que, sustituyendo x por h en la ecuación de la parábola, se puede obtener el valor de k.
Ejemplo 1
Hallar el vértice de la parábola con ecuación: \(y=x^2+4x+3\)
Solución
Primero identificamos los coeficientes a y b:
- Coeficiente a: es el número que multiplica a \(x^2.\) En este caso, \(a=1.\)
- Coeficiente b: es el número que multiplica a \(x.\) Aquí, \(b=4.\)
Ahora calculamos la abscisa del vértice (h) utilizando la fórmula:
\(h=\dfrac{-b}{2a}\)
Sustituyendo los valores:
\(h=\dfrac{-4}{2 (1)}=\dfrac{-4}{2}=-2\)
Ahora determinamos la ordenada del vértice (k), para ello sustituimos \(h=-2\) en la ecuación original:
\(k=(-2)^2+4 (-2)+3=4-8+3=-1\)
En conclusión, el vértice de la parábola es (-2, -1).
Ejemplo 2
Encontrar el vértice de la parábola con ecuación: \(y=2x^2-8x+5\)
Solución
Comenzamos identificando los coeficientes de la ecuación cuadrática. En este caso, los coeficientes son \(a=2\) y \(b=-8.\)
Calculamos la abscisa del vértice (h) usando la fórmula conocida:
\(h=\dfrac{-b}{2a}\)
Sustituyendo los valores de \(a\) y \(b:\)
\(h=\dfrac{-(-8)}{2 \cdot 2}=\dfrac{8}{4}=2\)
Ahora, para sacar la ordenada del vértice (k), reemplazamos \(h=2\) en la ecuación original:
\(k=2(2)^2-8(2)+5=2(4)-16+5=8-16+5=-3\)
Finalmente, concluimos que el vértice de la parábola es el punto (2, -3).
Ejemplo 3
Determinar el vértice de la parábola \(y=3x^2-12\)
Solución
Primero, observamos los coeficientes de la ecuación cuadrática. Aquí, \(a=3\) y, como no hay término lineal, \(b=0.\)
Calculamos la coordenada x del vértice (h) con la fórmula estándar:
\(h=\dfrac{-b}{2a}=\dfrac{-0}{2 \cdot 3}=0\)
Luego, encontramos la coordenada y del vértice (k) evaluando \(h=0\) en la ecuación original:
\(k=3(0)^2-12=0-12=-12\)
Por lo tanto, el vértice de esta parábola se encuentra en el punto (0, -12). En este caso, como b = 0, el vértice coincide con el punto donde la parábola intersecta al eje y.
Ejemplo 4
Encontrar las coordenadas del vértice de \(y=-x^2+6x-9\)
Solución
La ecuación cuadrática está en la forma \(y=ax^2+bx+c.\) En este caso:
- \(a=-1\) (coeficiente de \(x^2\))
- \(b=6\) (coeficiente de \(x\))
- \(c=-9\) (término independiente)
Para calcular la abscisa del vértice usamos la fórmula:
\(h=\dfrac{-b}{2a}=\dfrac{-6}{2 \cdot (-1)}=\dfrac{-6}{-2}=3\)
Ahora determinamos la ordenada del vértice reemplazando \(h=3\) en la ecuación original:
\(k=-(3)^2+6(3)-9=-9+18-9=0\)
Por tanto, el vértice de la parábola \(y=-x^2+6x-9\) está en el punto \((3, 0).\)
Si factorizamos la ecuación, obtenemos \(y=-(x^2-6x+9)=-(x-3)^2,\) lo cual confirma que el vértice está en \((3, 0).\) Esta forma muestra directamente que la parábola tiene su máximo en ese punto, ya que el coeficiente de \(x^2\) es negativo.
Ejemplo 5
Calcular las coordenadas del vértice de la parábola \(x^2+2x+8y+9=0\)
Solución
Para encontrar el vértice de la parábola definida por la ecuación, primero necesitamos despejar \(y\) para expresarla en una forma más manejable.
Comenzamos aislando el término con \(y:\)
\(8y=-x^2-2x-9\)
Ahora, dividimos ambos lados de la ecuación entre 8 para despejar \(y:\)
\(y=-\dfrac{1}{8}x^2-\dfrac{2}{8}x-\dfrac{9}{8}\)
Simplificamos los coeficientes:
\(y=-\dfrac{1}{8}x^2-\dfrac{1}{4}x-\dfrac{9}{8}\)
Con la ecuación ahora en la forma \(y=ax^2+bx+c,\) identificamos los coeficientes:
\(a=-\dfrac{1}{8}\)
\(b=-\dfrac{1}{4}\)
Para encontrar la abscisa del vértice (h), aplicamos la fórmula:
\(h=\dfrac{-b}{2a}=\dfrac{-\left(-\dfrac{1}{4}\right)}{2 \left(-\dfrac{1}{8}\right)}=\dfrac{\dfrac{1}{4}}{-\dfrac{1}{4}}=-1\)
Ahora calculamos la ordenada del vértice (k) sustituyendo \(h=-1\) en la ecuación despejada:
\(k=-\dfrac{1}{8}(-1)^2-\dfrac{1}{4}(-1)-\dfrac{9}{8}=-\dfrac{1}{8}+\dfrac{1}{4}-\dfrac{9}{8}\)
Para operar correctamente, expresamos todas las fracciones con denominador común (8):
\(k=-\dfrac{1}{8}+\dfrac{2}{8}-\dfrac{9}{8}=\left(-1+2-9\right)/8=\dfrac{-8}{8}=-1\)
Por lo tanto, el vértice de la parábola está en el punto \((-1, -1).\)
Ejemplo 6
Obtener el vértice de la parábola que tiene por ecuación \(x^2+12x+3y+39=0\)
Solución
Primero despejamos \(y\) para expresar la ecuación en la forma estándar \(y=ax^2+bx+c,\) lo que nos permitirá aplicar directamente las fórmulas del vértice.
Comenzamos despejando el término con \(y:\)
\(3y=-x^2-12x-39\)
Ahora dividimos toda la ecuación entre 3:
\(y=-\dfrac{1}{3}x^2-4x-13\)
Con la ecuación ya en su forma estándar, identificamos los coeficientes necesarios para calcular el vértice:
\(a=-\dfrac{1}{3}\) (coeficiente de \(x^2\))
\(b=-4\) (coeficiente de \(x\))
Calculamos primero la coordenada x del vértice usando la fórmula correspondiente:
\(h=\dfrac{-b}{2a}=\dfrac{-(-4)}{2 \times (-1/3)}=\dfrac{4}{-2/3}=4 \times (-3/2)=-6\)
Ahora determinamos la coordenada y del vértice sustituyendo \(h=-6\) en la ecuación despejada:
\(k=-\dfrac{1}{3}(-6)^2-4(-6)-13=-\dfrac{1}{3}(36)+24-13=-12+24-13=-1\)
Por lo tanto, el vértice de la parábola se encuentra en el punto \((-6, -1).\)
Completando cuadrados
Otra forma de obtener el vértice teniendo la ecuación y = ax2 + bx + c es completando los cuadrados hasta llegar a la forma canónica donde las coordenadas pueden extraerse fácilmente. De hecho, las fórmulas del vértice surgen de realizar este proceso.
Partiremos de la ecuación \(y=ax^2+bx+c\)
Primero, aislamos los términos que contienen \(x:\)
\(y=ax^2+bx+c\)
\(y-c=ax^2+bx\)
Sacamos \(a\) como factor común de los términos \(ax^2+bx:\)
\(y-c=a\left(x^2+\dfrac{b}{a}x\right)\)
Para completar el cuadrado en \(x^2+\dfrac{b}{a}x,\) seguimos estos pasos:
Tomamos el coeficiente de \(x,\) que es \(\dfrac{b}{a},\) lo dividimos entre 2 y lo elevamos al cuadrado:
\(\left(\dfrac{\dfrac{b}{a}}{2}\right)^2=\left(\dfrac{b}{2a}\right)^2=\dfrac{b^2}{4a^2}\)
Sumamos y restamos este término dentro del paréntesis para no alterar la ecuación:
\(y-c=a\left(x^2+\dfrac{b}{a}x+\dfrac{b^2}{4a^2}-\dfrac{b^2}{4a^2}\right)\)
Esto se puede reescribir como:
\(y-c=a\left(\left(x+\dfrac{b}{2a}\right)^2-\dfrac{b^2}{4a^2}\right)\)
Distribuimos \(a\) en los términos dentro del paréntesis:
\(y-c=a\left(x+\dfrac{b}{2a}\right)^2-\dfrac{b^2}{4a}\)
Luego, pasamos el término constante \(\left (-\dfrac{b^2}{4a}\right)\) al lado izquierdo:
\(y-c+\dfrac{b^2}{4a}=a\left(x+\dfrac{b}{2a}\right)^2\)
Simplificamos el lado izquierdo:
\(y=a\left(x+\dfrac{b}{2a}\right)^2+c-\dfrac{b^2}{4a}\)
Podemos escribir esto como:
\(\left(x-\left(-\dfrac{b}{2a}\right)\right)^2=\dfrac{1}{a}\left(y-\left(c-\dfrac{b^2}{4a}\right)\right)\)
La forma canónica de una parábola vertical es:
\((x-h)^2=4p(y-k)\)
Aquí podemos extraer que:
\(h=-\dfrac{b}{2a}\)
\(k=c-\dfrac{b^2}{4a}=-\dfrac{b^2-4ac}{4a}\)
\(4p=\dfrac{1}{a}\)
Como se quería demostrar.
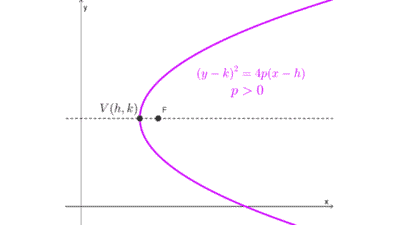
Vértice de una parábola horizontal
La ecuación canónica de una parábola horizontal con vértice en (h, k) es:
\((y-k)^2=4p(x-h)\)
donde |p| es la distancia entre el foco y el vértice. Otra forma de escribirla es como:
\(x=a(y-k)^2+h ~~\text{donde}~~ a=\dfrac{1}{4p}\)
Al igual que antes, en estas formas las coordenadas del vértice pueden leerse en la ecuación. Si el vértice es el origen de coordenadas (0, 0), la ecuación se simplifica: \(y^2=4px.\)
Ejemplos
- La ecuación \(y^2=-9 (x+1)\) puede expresarse como \((y-0)^2=-9 (x-(-1)),\) donde identificamos que \(h=-1\) y \(k=0\) (porque no hay término constante restado en \(y\) ). Por lo tanto, las coordenadas del vértice son \((-1, 0).\)
- Con la ecuación \((y-2)^2=4 (x-1)\) al compararla con la estructura \((y-k)^2=4p (x-h),\) reconocemos que \(h=1\) (el valor que acompaña a \(x\) dentro del paréntesis) y \(k=2\) (el término restado de \(y\)). Esto nos indica que el vértice está ubicado en \((1, 2).\)
- La ecuación \((y+3)^2=-8 (x+2)\) puede reescribirse como \((y-(-3))^2=-8 (x-(-2)),\) lo que nos permite identificar directamente que \(h=-2\) y \(k=-3.\) De esta forma, el vértice de la parábola se sitúa en el punto \((-2, -3).\)
Al igual que antes, la ecuación canónica de la parábola puede desarrollarse y reescribirse en forma general despejando la x:
\(x=ay^2+by+c\)
En esta forma, las coordenadas del vértice también pueden obtenerse con fórmulas:
\(h=-\dfrac{b^2-4ac}{4a}\)
\(k=\dfrac{-b}{2a}\)
A diferencia de la parábola vertical, aquí primero conviene obtener el valor de k y luego sustituirlo en la ecuación para obtener el valor de h.
Ejemplo 1
Obtener el vértice de la parábola horizontal \(x=4y^2+3y-6\)
Solución
Primero, identificamos los coeficientes de la ecuación cuadrática en términos de \(y.\) La ecuación tiene la forma general \(x=ay^2+by+c,\) donde:
- \(a=4\)
- \(b=3\)
- \(c=-6\)
Ahora, calculamos \(k,\) que es la coordenada \(y\) del vértice, usando la fórmula:
\(k=\dfrac{-b}{2a}\)
Sustituyendo los valores de \(a\) y \(b:\)
\(k=\dfrac{-3}{2 \times 4}=\dfrac{-3}{8}\)
Ahora, sustituimos \(k\) en la ecuación original para encontrar \(h,\) que es la coordenada \(x\) del vértice.
\(h=4\left(-\dfrac{3}{8}\right)^2+3\left(-\dfrac{3}{8}\right)-6\)
\(h=\dfrac{9}{16}-\dfrac{9}{8}-6\)
\(h=\dfrac{9}{16}-\dfrac{18}{16}-\dfrac{96}{16}=\dfrac{9-18-96}{16}=\dfrac{-105}{16}\)
Finalmente, el vértice de la parábola es el punto \(\left(-\dfrac{105}{16},-\dfrac{3}{8} \right),\) aproximadamente \((-6,56;~ -0,38)\)
Ejemplo 2
Calcular las coordenadas del vértice de la parábola \(x=-5y^2+7y+1\)
Solución
La ecuación dada es una parábola horizontal de la forma \(x=ay^2+by+c,\) donde:
- \(a=-5\)
- \(b=7\)
- \(c=1\)
Calculamos \(k\) (coordenada \(y\) del vértice):
\(k=\dfrac{-b}{2a}=\dfrac{-7}{2(-5)}=\dfrac{7}{10}\)
Sustituimos \(k\) en la ecuación para hallar \(h\) (coordenada \(x\) del vértice):
\(h=-5\left(\dfrac{7}{10}\right)^2+7\left(\dfrac{7}{10}\right)+1\)
Simplificamos:
\(h=-5 \left(\dfrac{49}{100}\right)+\dfrac{49}{10}+1=-\dfrac{245}{100}+\dfrac{490}{100}+\dfrac{100}{100}\)
Sumamos las fracciones:
\(h=\dfrac{-245+490+100}{100}=\dfrac{345}{100}=\dfrac{69}{20}\)
En conclusión, el vértice de la parábola es el punto \(\left (\dfrac{69}{20},~ \dfrac{7}{10} \right),\) que en notación decimal es \((3,45;~ 0,7).\)
Ejemplo 3
Encontrar el vértice de \(x=-3y^2-2y-3\)
Solución
La ecuación tiene la forma general \(x=ay^2+by+c,\) donde:
- \(a=-3\)
- \(b=-2\)
- \(c=-3\)
Calculamos \(k\) (coordenada \(y\) del vértice) utilizando la fórmula:
\(k=\dfrac{-b}{2a}=\dfrac{-(-2)}{2(-3)}=\dfrac{2}{-6}=-\dfrac{1}{3}\)
Sustituimos \(k\) en la ecuación para hallar \(h\) (coordenada \(x\) del vértice):
\(h=-3\left(-\dfrac{1}{3}\right)^2-2\left(-\dfrac{1}{3}\right)-3\)
\(h=-3\left(\dfrac{1}{9}\right)+\dfrac{2}{3}-3=-\dfrac{3}{9}+\dfrac{2}{3}-3\)
\(h=-\dfrac{1}{3}+\dfrac{2}{3}-3=\left(-\dfrac{1}{3}+\dfrac{2}{3}\right)-3=\dfrac{1}{3}-3\)
\(h=\dfrac{1}{3}-\dfrac{9}{3}=-\dfrac{8}{3}\)
El vértice de la parábola es el punto \(\left (-\dfrac{8}{3},~ -\dfrac{1}{3} \right),\) aproximadamente \((-2,67;~-0,33).\)
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta












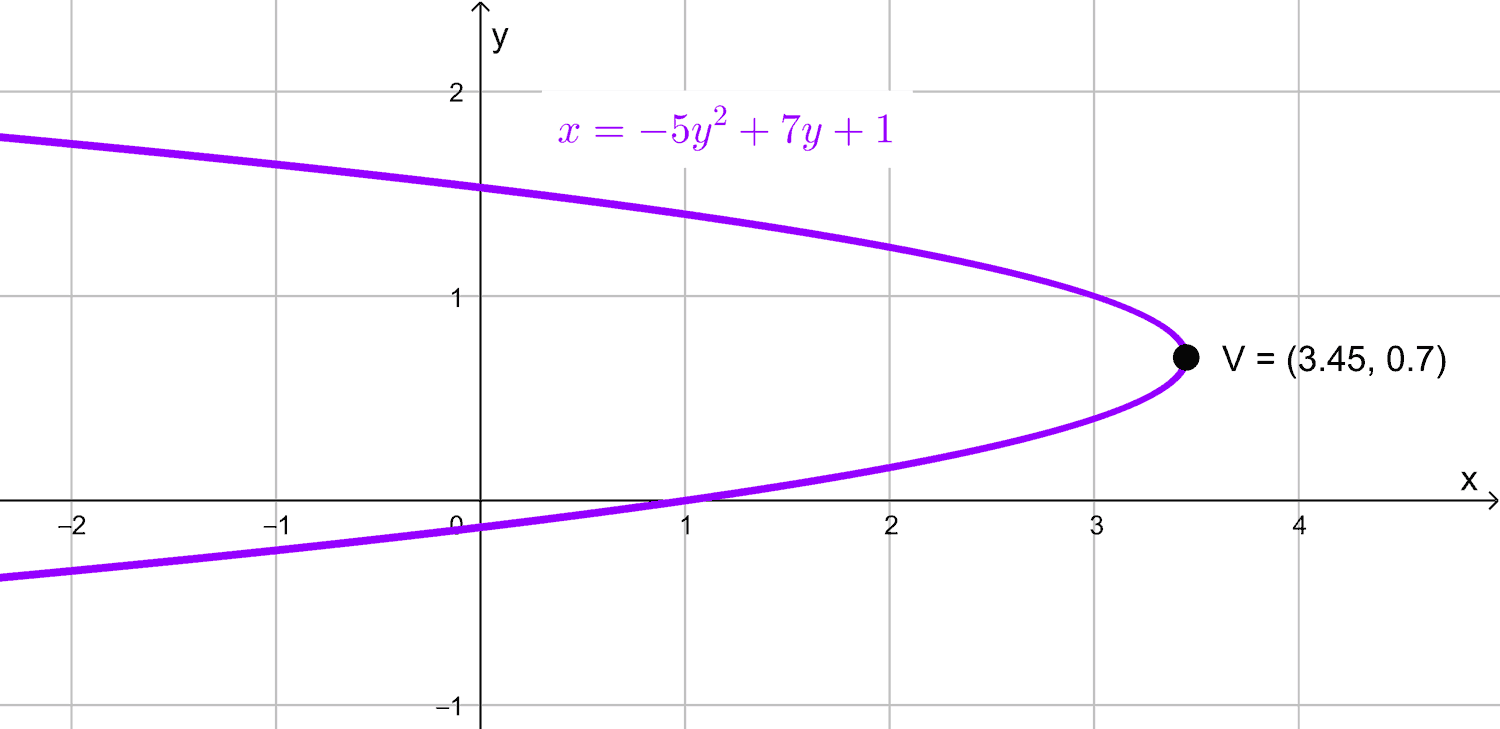



Otros artículos que pueden interesarte