Ecuación general de las cónicas

En este artículo explicamos qué es la ecuación general de una cónica, sus elementos y ejemplos de cómo determinar el tipo de cónica teniendo la fórmula general.

Ecuación general de una cónica

Toda ecuación de segundo grado de la forma anterior representa una sección cónica regular o una cónica degenerada (un punto o un par de rectas). Si se trata de una cónica, el análisis de los coeficientes permite determinar su tipo. Dependiendo de los valores y relaciones entre A, B, y C, podemos identificar si la cónica es una elipse, una parábola, una hipérbola.

En algunos casos, el coeficiente B puede ser igual a cero, lo que significa que en la ecuación no aparece el término mixto Bxy, con lo que se transforma en Ax² + Cy² + Dx + Ey + F = 0. Esto ocurre en cónicas cuyos ejes son paralelos a los ejes x e y, lo que simplifica su análisis y representación gráfica. Si B es distinto de cero, los ejes de la cónica presentan una rotación con respecto a los ejes coordenados.

Discriminante de la ecuación general

El discriminante es una expresión matemática que permite determinar el tipo de cónica representada por una ecuación general de segundo grado. Dada una ecuación general Ax² + Bxy + Cy² + Dx + Ey + F = 0, el discriminante, denotado como Δ, se expresa de la siguiente manera:

Δ = B² - 4AC

Cuando la fórmula general representa una cónica no degenerada, el signo del discriminante nos permite identificar el tipo de cónica que describe:

• Si Δ > 0: la ecuación corresponde a una hipérbola.
• Si Δ = 0: la ecuación describe una parábola.
• Si Δ < 0: la ecuación representa una elipse o una circunferencia.

Es decir, cuando el discriminante es positivo, la ecuación representa una hipérbola. Si es cero, se trata de una parábola. Y si es negativo, la ecuación corresponde a una elipse o una circunferencia.

Cónica	Discriminante
Hipérbola	B2 - 4AC > 0
Parábola	B2 - 4AC = 0
Elipse	B2 - 4AC < 0

Ejemplo

Analizar el discriminante de las siguientes ecuaciones para determinar a qué tipo de cónica corresponden:

1. *3x^2+4xy+5y^2-6x+8y+1=0*
2. *2x^2-6xy+3y^2+7x-2y-10=0*
3. *10xy+5x^2+5y^2-x+4y=0*
4. *16y^2+8xy+x^2-9x+y+12=0*
5. *7x^2+12xy+5y^2+4x-3y-9=0*

Soluciones

1) Consideremos la ecuación general de la cónica *3x^2+4xy+5y^2-6x+8y+1=0*. Para esta ecuación, identificamos los coeficientes A=3, B=4, y C=5. Calculamos el discriminante como:

*B^2-4AC=4^2-4\cdot3\cdot5=16-60=-44*

Dado que el discriminante es negativo, podemos concluir que esta ecuación representa una elipse.

2) Analicemos la ecuación *2x^2-6xy+3y^2+7x-2y-10=0.* Aquí, los valores de los coeficientes son A=2, B=-6, y C=3. Al calcular el discriminante obtenemos:

*B^2-4AC=(-6)^2-4\cdot2\cdot3=36-24=12*

Como el discriminante es positivo, deducimos que esta ecuación corresponde a una hipérbola.

3) En la ecuación *10xy+5x^2+5y^2-x+4y=0* identificamos los coeficientes: A=5, B=10, y C=5. Calculamos el discriminante: 

*B^2-4AC=10^2-4\cdot5\cdot5=100-100=0*

Dado que el discriminante es cero, concluimos que la ecuación corresponde a una parábola.

4) Analicemos la siguiente ecuación de cónica: *16y^2+8xy+x^2-9x+y+12=0.* En este caso, los coeficientes son A=1, B=8, y C=16. Calculamos el discriminante como:

*B^2-4AC=8^2-4\cdot1\cdot16=64-64=0*

Debido a que el discriminante es igual a cero, la ecuación representa una parábola.

5) Examinando la ecuación *7x^2+12xy+5y^2+4x-3y-9=0,* los coeficientes son A=7, B=12, y C=5. Al calcular el discriminante, obtenemos:

*B^2-4AC=12^2-4\cdot7\cdot5=144-140=4*

Como el discriminante es mayor que cero, concluimos que la ecuación representa una hipérbola.

Cuando en la ecuación general de las cónicas no aparece el término Bxy, es decir, cuando B = 0, la ecuación toma la forma simplificada Ax² + Cy² + Dx + Ey + F = 0. En este caso, si la expresión representa una cónica, no es necesario calcular el discriminante para determinar el tipo, sino que basta con analizar los signos de los coeficientes A y C:

• Si A y C tienen el mismo signo (es decir, ambos son positivos o ambos son negativos), la ecuación representa una elipse o una circunferencia (en el caso particular donde A=C).
• Si A y C tienen signos opuestos (uno positivo y el otro negativo), la ecuación describe una hipérbola.
• Si uno de los coeficientes es cero (A=0 o C=0), la ecuación representa una parábola.

Cónica	Coeficientes
Elipse	A y C tienen el mismo signo: A ⋅ C > 0
Hipérbola	A y C tienen signos opuestos: A ⋅ C < 0
Parábola	A es cero o C es cero, el producto A ⋅ C = 0

Ejemplo

Analizar las siguientes ecuaciones y determinar a qué tipo de cónica corresponden:

1. *3x^2-7y^2+2x+5y+1=0*
2. *4x^2+9y^2-8x+6y-12=0*
3. *x^2-6x+4y-5=0*

Soluciones

1) Consideremos la ecuación *3x^2-7y^2+2x+5y+1=0.* Aquí, los valores de los coeficientes son A=3 y C=-7. Notamos que A y C tienen signos opuestos, lo que nos permite determinar que esta ecuación corresponde a una hipérbola.

2) En la ecuación *4x^2+9y^2-8x+6y-12=0* observamos que A=4 y C=9. Como ambos coeficientes son positivos, podemos concluir que la ecuación representa una elipse.

3) Analizando la ecuación *x^2-6x+4y-5=0,* los coeficientes son A=1 y C=0. Dado que C=0, podemos identificar que esta es la ecuación de una parábola.

Cómo llegar a una ecuación canónica a partir de la general

Hasta este punto, hemos aprendido a identificar el tipo de cónica representada por una ecuación general utilizando el discriminante. Sin embargo, también nos interesa conocer los elementos característicos de la cónica como su centro, vértices, focos, ejes principales, excentricidad y la longitud de los semiejes.

Cuando el término Bxy no está presente en la ecuación, el proceso para encontrar estos elementos es relativamente sencillo y se puede realizar mediante la técnica de completar el cuadrado. No obstante, cuando el término Bxy aparece, el procedimiento se complica, requiriendo un paso adicional para eliminar el término mixto mediante una rotación de ejes antes de completar los cuadrados y así llegar a la forma canónica.

El objetivo siempre es conseguir llegar de una forma general a una forma estándar sencilla de graficar:

Cónica	Ecuación	Detalles
Circunferencia	*(x-h)^2+(y-k)^2=r^2*	El centro es (h, k). El radio es r.
Elipse horizontal	*\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1*	El centro es (h, k). a es la longitud del semieje mayor. b es la longitud del semieje menor.
Elipse vertical	*\dfrac{(y-k)^2}{a^2}+\dfrac{(x-h)^2}{b^2}=1*	El centro es (h, k). a es la longitud del semieje mayor. b es la longitud del semieje menor.
Parábola (hacia derecha o izquierda)	*(y-k)^2=±4p(x-h)*	(h, k) es el vértice. p es la distancia entre el foco y el vértice.
Parábola (hacia arriba o abajo)	*(x-h)^2=±4p(y-k)*	(h, k) es el vértice. p es la distancia entre el foco y el vértice.
Hipérbola (con ramas hacia los lados)	*\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1*	El centro es (h, k). a es la longitud del semieje transversal. b es la longitud del semieje conjugado.
Hipérbola (con ramas hacia arriba y abajo)	*\dfrac{(y-k)^2}{a^2}-\dfrac{(x-h)^2}{b^2}=1*	El centro es (h, k). a es la longitud del semieje transversal. b es la longitud del semieje conjugado.

Cuando B = 0

Ejemplo 1

Convertir la siguiente ecuación a su forma canónica: *36x^2 + 25y^2 + 72x - 200y - 464 = 0*

Solución: para transformar la ecuación, seguiremos el siguiente proceso:

Primero, agrupamos los términos de x e y, luego movemos el término constante al otro lado de la ecuación:

*36x^2+72x+25y^2-200y=464*

A continuación, sacamos el factor común en cada grupo de términos cuadráticos:

*36(x^2+2x)+25(y^2-8y)=464*

Para completar el cuadrado en los términos de x y y, sumaremos y restaremos los valores necesarios dentro de cada paréntesis.

Para x: tomamos el término lineal *2x.* Completamos el cuadrado sumando *\left(\dfrac{2}{2}\right)^2=1:*

*x^2+2x=(x+1)^2-1*

Multiplicamos por 36:

*36[(x+1)^2-1]=36(x+1)^2-36*

Para y: tomamos el término lineal *-8y.* Completamos el cuadrado sumando *\left(\dfrac{-8}{2}\right)^2=16:*

*y^2-8y=(y-4)^2-16*

Multiplicamos por 25:

*25[(y-4)^2-16]=25(y-4)^2-400*

Sustituyendo los resultados obtenidos en la ecuación inicial:

*36(x+1)^2-36+25(y-4)^2-400=464*

Simplificamos los términos constantes:

*36(x+1)^2+25(y-4)^2-436=464*

Sumamos 436 a ambos lados:

*36(x+1)^2+25(y-4)^2=900*

Dividimos toda la ecuación entre 900 para obtener la forma estándar:

*\dfrac{36(x+1)^2}{900}+\dfrac{25(y-4)^2}{900}=1*

Simplificamos los coeficientes:

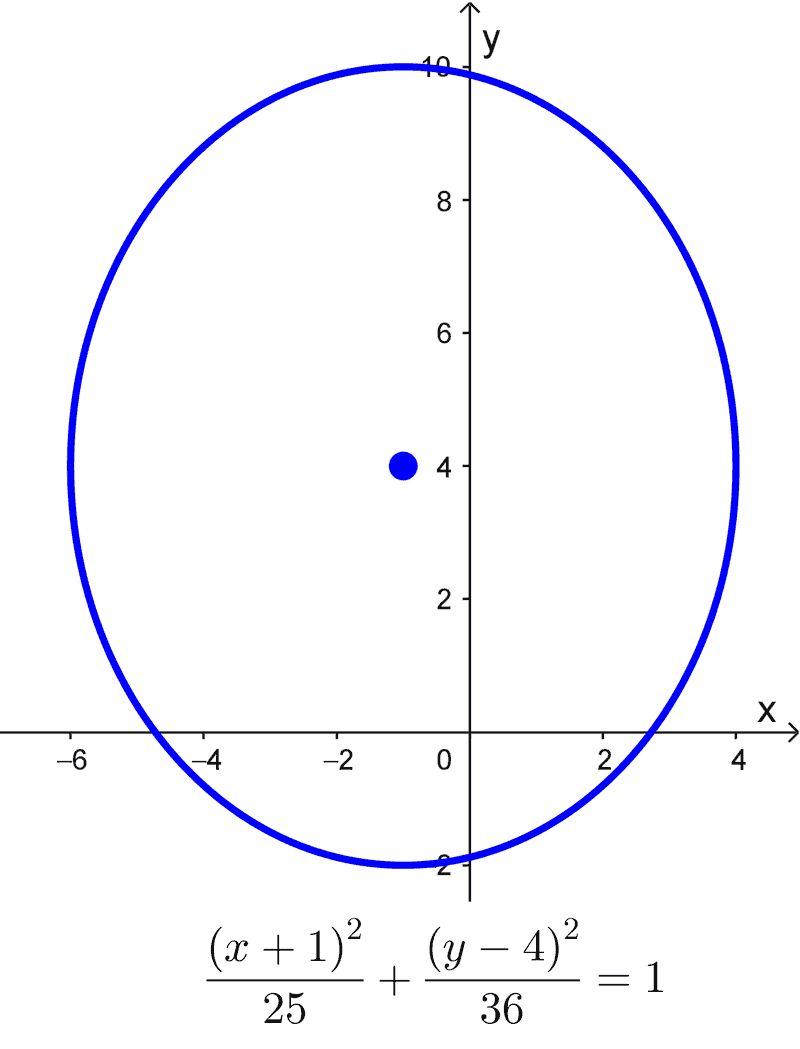
*\dfrac{(x+1)^2}{25}+\dfrac{(y-4)^2}{36}=1*

Esto muestra que la ecuación representa una elipse con centro en (-1, 4), semieje mayor de longitud 6 y semieje menor de longitud 5.

Ejemplo 2

Llevar la ecuación *-25x^2+4y^2-150x-8y-321=0* a su forma canónica.

Solución: seguiremos un proceso similar al anterior:

Primero, agrupamos los términos de x e y, y movemos el término constante al otro lado de la ecuación:

*-25x^2-150x+4y^2-8y=321*

A continuación, sacamos el factor común en cada grupo de términos cuadráticos:

*-25(x^2+6x)+4(y^2-2y)=321*

Para completar el cuadrado en los términos de x y y, sumaremos y restaremos los valores necesarios dentro de cada paréntesis.

Para x: tomamos el término lineal 6x. Completamos el cuadrado sumando *\left(\dfrac{6}{2}\right)^2=9:*

*x^2+6x=(x+3)^2-9*

Multiplicamos por -25:

*-25[(x+3)^2-9]=-25(x+3)^2+225*

Para y: tomamos el término lineal -2y. Completamos el cuadrado sumando *\left(\dfrac{-2}{2}\right)^2=1:*

*y^2-2y=(y-1)^2-1*

Multiplicamos por 4:

*4[(y-1)^2-1]=4(y-1)^2-4*

Sustituyendo los resultados obtenidos en la ecuación inicial:

*-25(x+3)^2+225+4(y-1)^2-4=321*

Simplificamos los términos constantes:

*-25(x+3)^2+4(y-1)^2+221=321*

Restamos 221 a ambos lados:

*-25(x+3)^2+4(y-1)^2=100*

Dividimos toda la ecuación entre 100 para obtener la forma estándar:

*\dfrac{4(y-1)^2}{100}-\dfrac{25(x+3)^2}{100}=1*

Simplificamos los coeficientes:

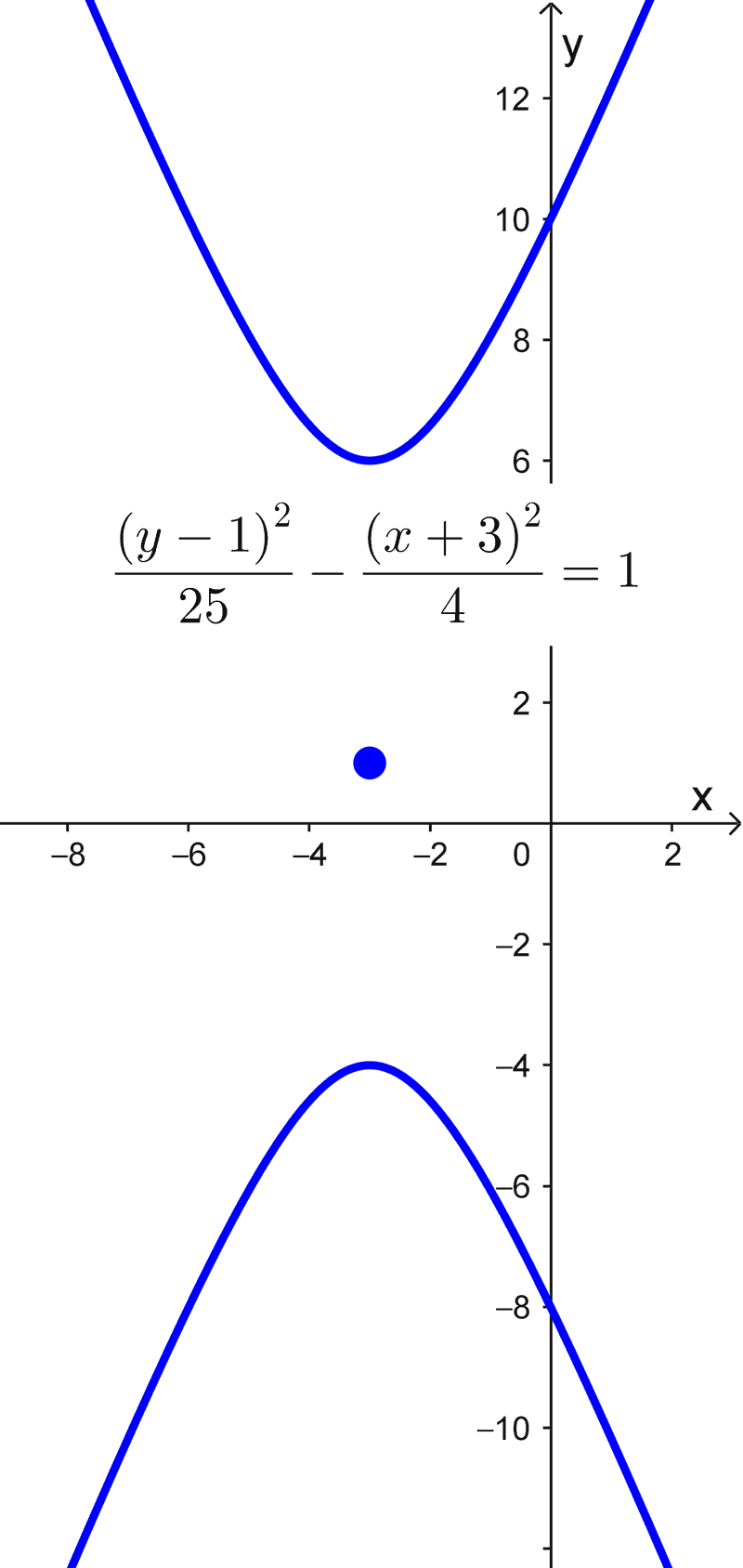
*\dfrac{(y-1)^2}{25}-\dfrac{(x+3)^2}{4}=1*

Esto muestra que la ecuación representa una hipérbola con centro en (-3, 1), donde el término positivo indica la dirección de la apertura vertical, teniendo los semiejes de longitud 5 en el eje y y 2 en el eje x.

Ejemplo 3

Encontrar la fórma canónica de la ecuación *x^2-4x-12y-8=0*

Solución: procederemos de la siguiente manera:

Primero, agrupamos los términos con x y llevamos los términos de y y la constante al otro lado de la ecuación:

*x^2-4x=12y+8*

Ahora, completamos el cuadrado en los términos de x. Tomamos el término lineal -4x y completamos el cuadrado sumando y restando *\left(\dfrac{-4}{2}\right)^2=4:*

*x^2-4x=(x-2)^2-4*

Sustituyendo este resultado en la ecuación original, obtenemos:

*(x-2)^2-4=12y+8*

Sumamos 4 a ambos lados de la ecuación para aislar el término cuadrático:

*(x-2)^2=12y+12*

Simplificamos el lado derecho sacando factor común 12:

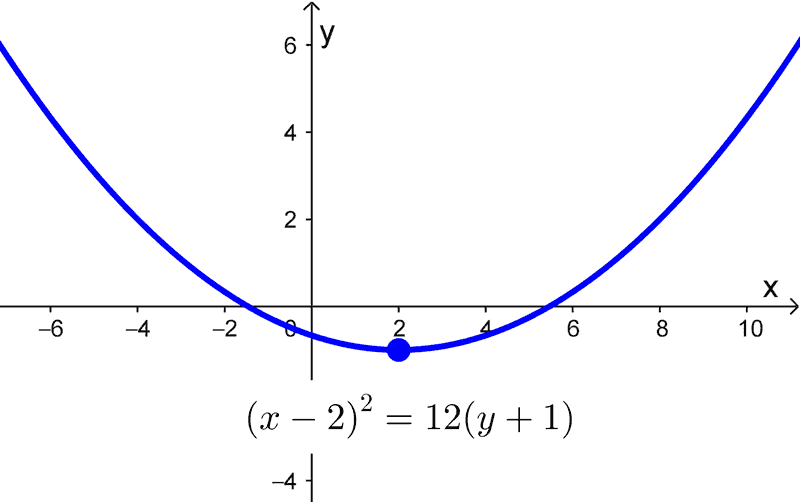
*(x-2)^2=12(y+1)*

Esta ecuación representa una parábola con vértice en (2, -1), que abre hacia arriba debido al término cuadrático en x y el término lineal en y.

Cuando B ≠ 0

Cuando el término Bxy está presente en la ecuación general de una cónica, es necesario realizar una rotación de ejes para eliminarlo y simplificar la ecuación. Esta rotación nos permite obtener una nueva ecuación en términos de variables transformadas, x' e y', que estará alineada con los nuevos ejes.

La nueva ecuación, después de la rotación, tendrá la forma:

A'x'² + C'y'² + D'x' + E'y' + F' = 0

Para llevar a cabo esta rotación, definimos las coordenadas x e y en función de las coordenadas nuevas x’ e y’, utilizando las siguientes fórmulas de transformación:

*x=x' \cos\alpha-y'\sin\alpha*

*y=x' \sin\alpha+y'\cos\alpha*

El ángulo de rotación α se elige de tal manera que elimine el término mixto. Este ángulo se puede calcular utilizando la fórmula basada en la tangente doble:

*\tan(2α)=\dfrac{B}{A-C}*

Una vez que se conoce tan(2α), se pueden utilizar las siguientes identidades trigonométricas para calcular los valores de cos(α) y sin(α):

*\cos(2\alpha)=\dfrac{1}{\sqrt{\tan^2(2\alpha)+1}}*

*\sin\alpha=\sqrt{\dfrac{1-\cos(2\alpha)}{2}}*

*\cos\alpha=\sqrt{\dfrac{1+\cos(2\alpha)}{2}}*

Es importante tomar cos(2α) con el mismo signo de tan(2α). Una consideración especial ocurre cuando A = C, en este caso el ángulo de rotación es de 45°.

Después de aplicar esta rotación, el término mixto desaparece de la ecuación, y podemos proceder a completar los cuadrados en la nueva ecuación para obtener la forma canónica de la cónica. 

Ejemplo 1

Realice una rotación para eliminar el término xy de la ecuación *3x^2+3xy-y^2=9*

Solución: comenzamos identificando los coeficientes relevantes: A=3, B=3, y C=-1. La primera etapa es calcular el ángulo de rotación α que nos permitirá eliminar el término mixto. Utilizamos la fórmula para la tangente doble del ángulo:

*\tan(2\alpha)=\dfrac{B}{A-C}=\dfrac{3}{3-(-1)}=\dfrac{3}{4}*

Con este resultado, ahora calculamos *\cos(2\alpha):*

*\cos(2\alpha)=\dfrac{1}{\sqrt{\tan^2(2\alpha)+1}}=\dfrac{1}{\sqrt{\left(\dfrac{3}{4}\right)^2+1}}=\dfrac{1}{\sqrt{\dfrac{9}{16}+1}}=\dfrac{1}{\sqrt{\dfrac{25}{16}}}=\dfrac{4}{5}*

Una vez que tenemos este valor, calculamos los valores de *\sin\alpha* y *\cos\alpha* usando las identidades trigonométricas:

*\sin\alpha=\sqrt{\dfrac{1-\cos(2\alpha)}{2}}=\sqrt{\dfrac{1-\dfrac{4}{5}}{2}}=\sqrt{\dfrac{\dfrac{1}{5}}{2}}=\sqrt{\dfrac{1}{10}}=\dfrac{1}{\sqrt{10}}*

*\cos\alpha=\sqrt{\dfrac{1+\cos(2\alpha)}{2}}=\sqrt{\dfrac{1+\dfrac{4}{5}}{2}}=\sqrt{\dfrac{\dfrac{9}{5}}{2}}=\sqrt{\dfrac{9}{10}}=\dfrac{3}{\sqrt{10}}*

Ahora aplicamos la rotación de ejes utilizando las fórmulas de transformación de coordenadas:

*x=x'\cos\alpha-y'\sin\alpha=x'\left(\dfrac{3}{\sqrt{10}}\right)-y'\left(\dfrac{1}{\sqrt{10}}\right)=\dfrac{3x'-y'}{\sqrt{10}}*

*y=x'\sin\alpha+y'\cos\alpha=x'\left(\dfrac{1}{\sqrt{10}}\right)+y'\left(\dfrac{3}{\sqrt{10}}\right)=\dfrac{x'+3y'}{\sqrt{10}}*

Sustituyendo estas expresiones en la ecuación original *3x^2+3xy-y^2=9,* desarrollamos y simplificamos las operaciones. Primero, reemplazamos x y y en la ecuación de la cónica:

*3\left(\dfrac{3x'-y'}{\sqrt{10}}\right)^2+3\left(\dfrac{3x'-y'}{\sqrt{10}}\right)\left(\dfrac{x'+3y'}{\sqrt{10}}\right)-\left(\dfrac{x'+3y'}{\sqrt{10}}\right)^2=9*

Al expandir y simplificar los términos cuadráticos y mixtos, se reorganizan los coeficientes para obtener la forma simplificada:

*7x'^2-3y'^2=18*

La ecuación resultante corresponde a una hipérbola, ya que presenta términos cuadrados con signos opuestos. Para llevarla a su forma canónica en los nuevos ejes, dividimos toda la ecuación por 18:

*\dfrac{7x'^2}{18}-\dfrac{3y'^2}{18}=1*

Simplificando, obtenemos:

*\dfrac{x'^2}{\dfrac{18}{7}}-\dfrac{y'^2}{6}=1*

La forma canónica de la hipérbola en los nuevos ejes es entonces:

*\dfrac{x'^2}{\dfrac{18}{7}}-\dfrac{y'^2}{6}=1*

Lo cual indica que los ejes de la hipérbola están alineados con los ejes transformados x' e y', con semiejes *\sqrt{\dfrac{18}{7}}* y *\sqrt{6},* respectivamente.

Ejemplo 2

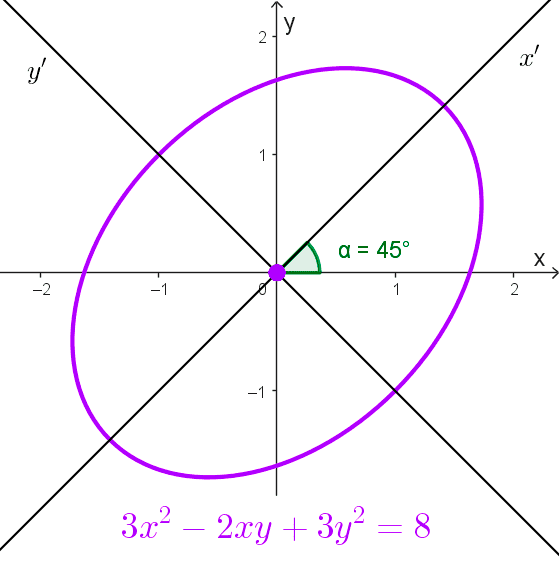
Mediante una rotación de ejes eliminar el término xy, e identificar la naturaleza de la curva de ecuación: *3x^2-2xy+3y^2=8*

Solución

Al comparar con la ecuación general se determina que A=3, B=-2 y C=3, como A = C, entonces el ángulo de rotación es de 45°; por tanto, las ecuaciones son:

*x=x'\cos45^\circ-y'\sin45^\circ=\dfrac{1}{\sqrt{2}}x'-\dfrac{1}{\sqrt{2}}y'=\dfrac{x'-y'}{\sqrt{2}}*

*y=x'\sin45^\circ+y'\cos45^\circ=\dfrac{1}{\sqrt{2}}x'+\dfrac{1}{\sqrt{2}}y'=\dfrac{x'+y'}{\sqrt{2}}*

Se sustituyen en la ecuación *3x^2-2xy+3y^2=8:*

*3\left(\dfrac{x'-y'}{\sqrt{2}}\right)^2-2\left(\dfrac{x'-y'}{\sqrt{2}}\right)\left(\dfrac{x'+y'}{\sqrt{2}}\right)+3\left(\dfrac{x'+y'}{\sqrt{2}}\right)^2=8*

Ahora, al desarrollar y simplificar, se encuentra la ecuación de la curva sin término en xy:

*3\left(\dfrac{x'^2}{2}-2\dfrac{x'y'}{2}+\dfrac{y'^2}{2}\right)-2\left(\dfrac{x'^2}{2}-\dfrac{y'^2}{2}\right)+3\left(\dfrac{x'^2}{2}+2\dfrac{x'y'}{2}+\dfrac{y'^2}{2}\right)=8*

*3\left(\dfrac{x'^2}{2}-\dfrac{2x'y'}{2}+\dfrac{y'^2}{2}\right)-2\left(\dfrac{x'^2}{2}-\dfrac{y'^2}{2}\right)+3\left(\dfrac{x'^2}{2}+\dfrac{2x'y'}{2}+\dfrac{y'^2}{2}\right)=8*

*\dfrac{3x'^2}{2}-3x'y'+\dfrac{3y'^2}{2}-x'^2+y'^2+\dfrac{3x'^2}{2}+3x'y'+\dfrac{3y'^2}{2}=8*

*\dfrac{6x'^2}{2}+\dfrac{6y'^2}{2}-x'^2+y'^2=8*

*2x'^2+4y'^2=8*

Finalmente, la ecuación es:

*x'^2+2y'^2=4*

Esta representa una elipse. Para llevarla a su forma canónica, dividimos toda la ecuación por 4:

*\dfrac{x'^2}{4}+\dfrac{2y'^2}{4}=1*

Simplificamos:

*\dfrac{x'^2}{4}+\dfrac{y'^2}{2}=1*

Vemos entonces que la elipse tiene semiejes *a=2* y *b=\sqrt{2}.*

Puntos clave

• La fórmula general de una cónica es Ax² + Bxy + Cy² + Dx + Ey + F = 0.
• El discriminante de la ecuación general es Δ = B² - 4AC.
• Si la ecuación representa una cónica no degenerada, un discriminante positivo indica que se trata de una hipérbola; si es cero, se trata de una parábola; si es negativo, se trata de una elipse.
• A partir de la ecuación general se puede logar una forma canónica y conocer los elementos característicos de la cónica como su centro, vértices, focos, ejes principales, excentricidad y la longitud de los semiejes.
• Cuando el término Bxy no está presente en la ecuación, el proceso para encontrar estos elementos se puede realizar completando cuadrados. Cuando el término Bxy aparece, se debe realizar primero una rotación de ejes antes de completar los cuadrados.

Recursos adicionales

El siguiente video trata sobre la ecuación general de segundo grado en dos variables y cómo identificar las diferentes cónicas (circunferencia, elipse, parábola e hipérbola) a partir de dicha ecuación.

Con el siguiente recurso de GeoGebra podrás modificar los coeficientes de la ecuación general de segundo grado y observar cómo cambia la gráfica en tiempo real, además podrás ver el valor del discriminante:

Lecturas recomendadas:

• Fuller, G. y Tarwater, D. (1995). Gemetría Analítica (7ma edición). Pearson Educación.
• Lehman, C. (1989). Geometría Analítica. Limusa.
• Leithold, L. (1992). Álgebra y Trigonometría con Geometría Analítica. Oxford University Press.
• Márquez, A. y otros. (2009). Geometría Analítica. Pearson.