Lado recto de una cónica
En este artículo explicamos qué es y cómo calcular el lado recto de una sección cónica con ejemplos paso a paso.
Índice
¿Qué es el lado recto?
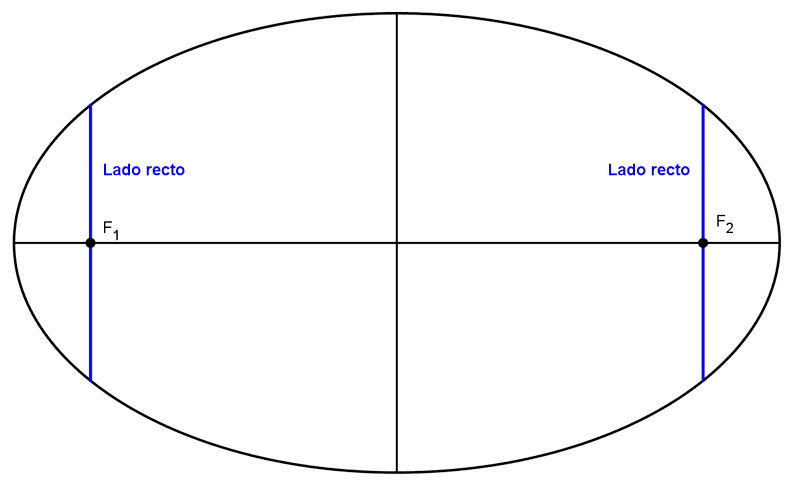
El lado recto de una cónica es un segmento que une dos puntos de la misma, es perpendicular al eje principal y pasa por uno de sus focos. Este concepto, también denominado latus rectum, anchura focal o cuerda focal, se aplica en el caso de las parábolas, elipses y las hipérbolas.
Elipse
El lado recto de una elipse es un segmento que une dos puntos de la misma, es perpendicular al eje mayor y pasa por un foco. Una elipse tiene dos lados rectos, uno por cada foco, y sus longitudes pueden obtenerse con la siguiente fórmula:
*L=\dfrac{2b^2}{a}*
donde a es la longitud del semieje mayor y b la longitud del semieje menor.
Ejemplos
A continuación, veremos algunos ejercicios resueltos del cálculo del lado recto de elipses.
Ejemplo 1
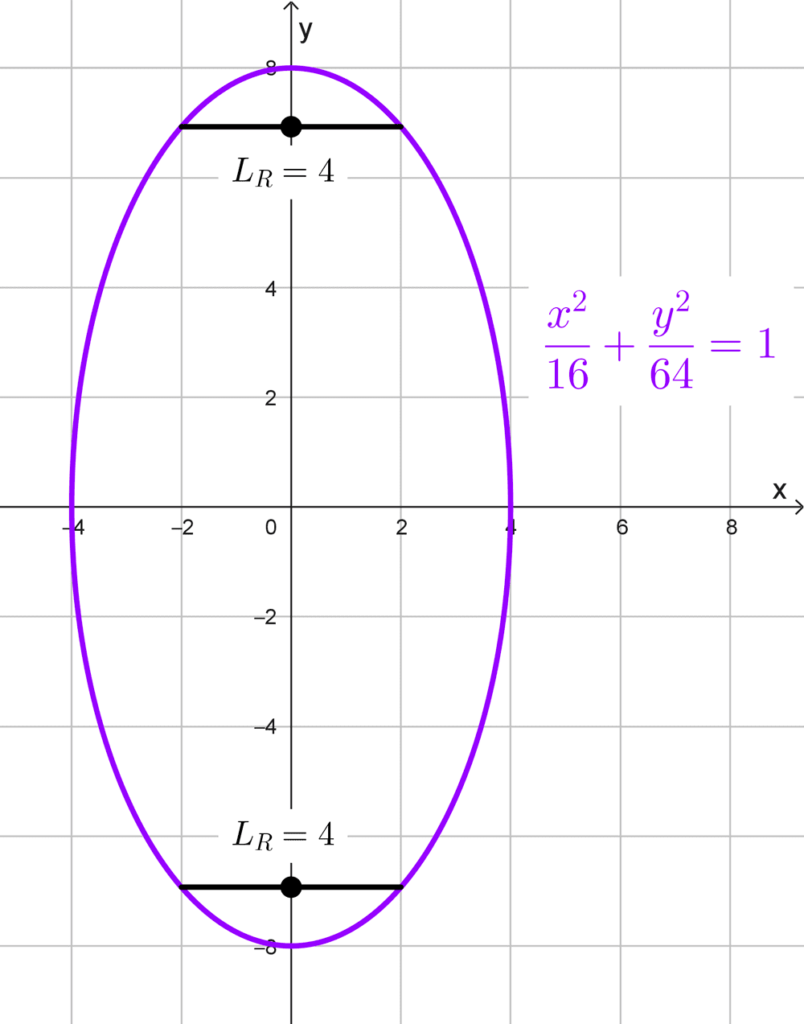
Obtener el lado recto de la elipse *\dfrac{x^2}{16}+\dfrac{y^2}{64}=1*
Solución: la ecuación está en forma canónica así que podemos extraer los datos que necesitamos:
*a^2=64 → a=\sqrt{64}=8*
*b^2=16*
Para determinar la longitud del lado recto, reemplazamos los datos en la fórmula:
*L_R=\dfrac{2b^2}{a}*
*=\dfrac{2\cdot 16}{8}*
*=\dfrac{32}{8}*
*=4*
Para poder graficar el lado recto primero se debe conocer la ubicación de los focos, puedes aprender cómo hacerlo en este artículo:
Ejemplo 2
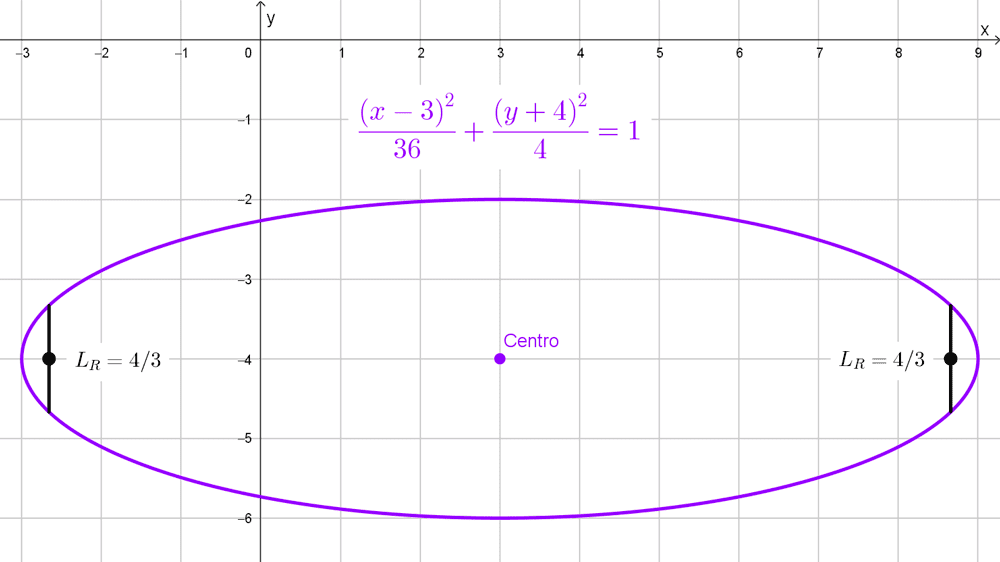
Calcular la longitud del lado recto de la elipse con ecuación *\dfrac{(x-3)^2}{36}+\dfrac{(y+4)^2}{4}=1*
Solución: de la ecuación podemos leer que la elipse no está centrada en el origen como en el caso anterior, sin embargo, este hecho no afecta la longitud del lado recto. Extraemos los datos necesarios:
*a^2=36→a=\sqrt{36}=6*
*b^2=4*
Con estos valores sacamos el lado recto:
*L_R=\dfrac{2b^2}{a}*
*=\dfrac{2\cdot 4}{6}*
*=\dfrac{8}{6}*
*=\dfrac{4}{3}*
*=1,33…*
Ejemplo 3
Hallar el valor del lado recto de la elipse *2x^2+4x+7y^2-28y-40=0*
Solución: en este caso, tenemos la ecuación general y no la canónica, por tanto no podemos extraer directamente los datos necesarios. Si realizamos el proceso de completar los cuadrados, llegaremos a la siguiente ecuación:
*\dfrac{(x+1)^2}{35}+\dfrac{(y-2)^2}{10}=1*
Con la ecuación en esta forma sí podemos sacar los datos necesarios:
*a^2=35 → a=\sqrt{35}*
*b^2=10*
Entonces:
*L_R=\dfrac{2b^2}{a}*
*=\dfrac{2\cdot 10}{\sqrt{35}}*
*=\dfrac{20}{\sqrt{35}}*
*≈3,38*
Demostración
Vamos a demostrar que el lado recto de una elipse tiene longitud *L_R=\dfrac{2b^2}{a}.*
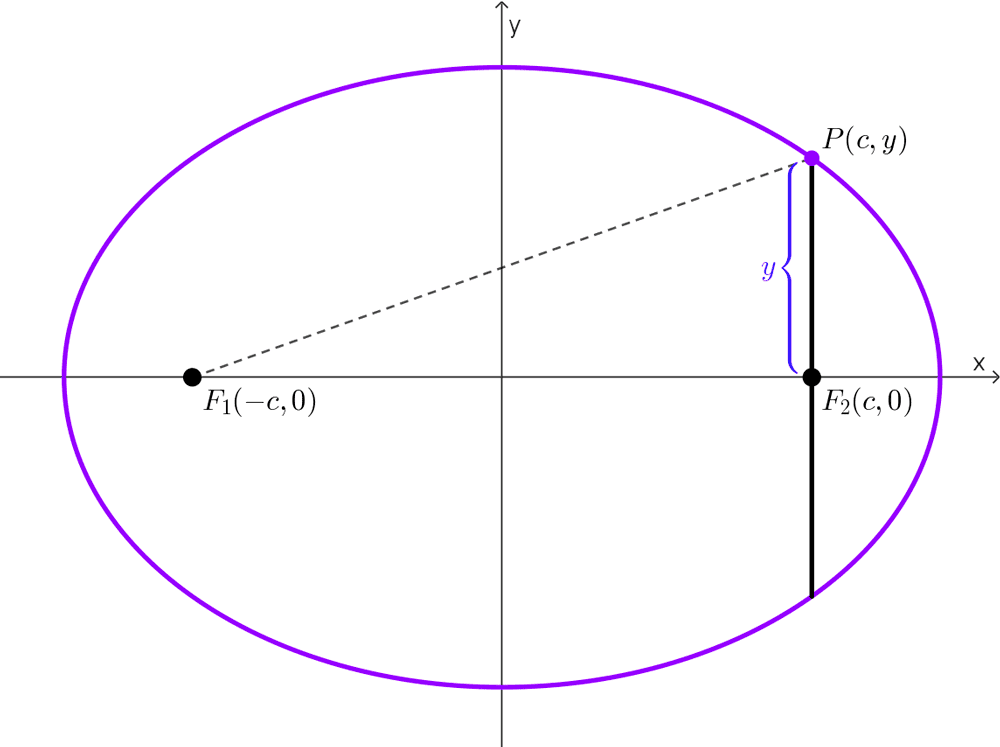
Comenzamos con una elipse ubicada de forma conveniente en el plano cartesiano como se muestra en el gráfico. Consideremos uno de los extremos del lado recto, por ejemplo, P (c, y).
Por definición de elipse, debe cumplirse que:
*d(F_1, P)+d(F_2,P)=2a*
*\sqrt{(c-(-c))^2+(y-0)^2}+\sqrt{(c-c)^2+y^2}=2a*
*\sqrt{(2c)^2+y^2}+\sqrt{y^2}=2a*
Si consideramos y > 0, entonces:
*\sqrt{(2c)^2+y^2}+y=2a*
*\sqrt{4c^2+y^2}=2a-y*
*(\sqrt{4c^2+y^2})^2=(2a-y)^2*
*4c^2+y^2=4a^2-4ay+y^2*
*4c^2+\cancel{y^2}=4a^2-4ay+\cancel{y^2}*
*4ay=4a^2-4c^2*
*4ay=4(a^2-c^2)*
*y=\dfrac{a^2-c^2}{a}*
Debido a que *a^2-c^2=b^2,* se concluye que:
*y=\dfrac{b^2}{a}*
Como la ordenada del punto P corresponde a la mitad del lado recto, se tiene que la longitud del lado recto es:
*L_R=2\dfrac{b^2}{a}*
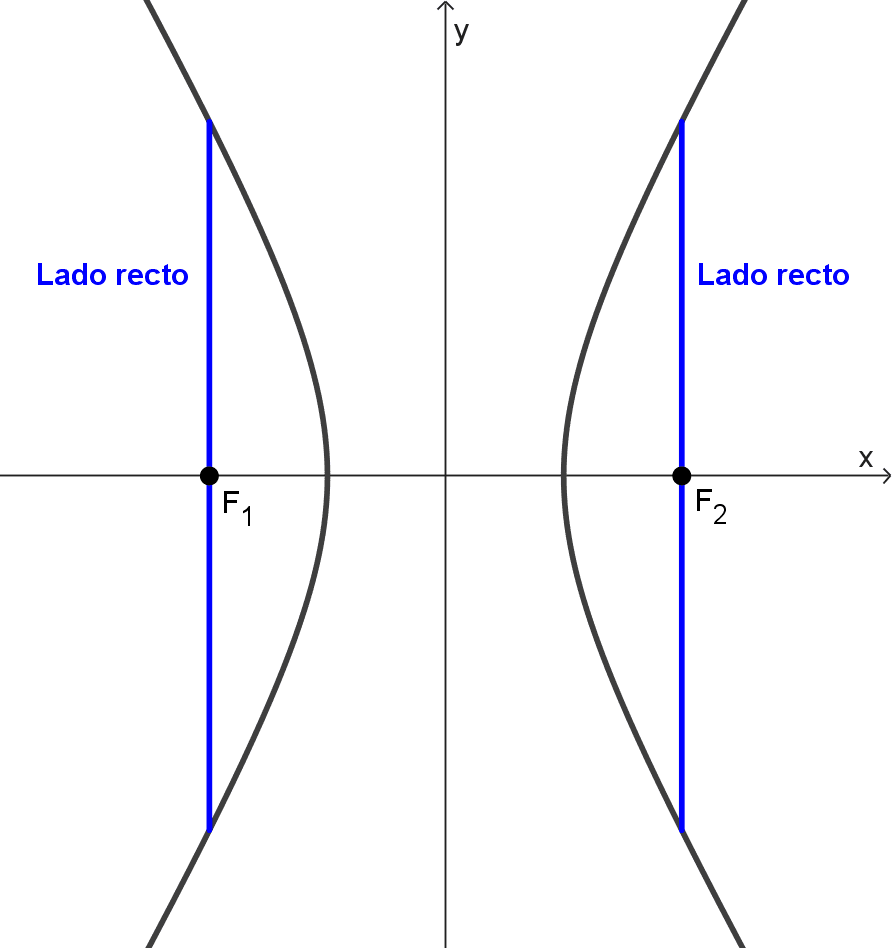
Hipérbola
El lado recto de una hipérbola es un segmento perpendicular al eje principal y pasa por uno de los focos. Si a es la longitud del semieje transversal y b la del semieje conjugado, la longitud del lado recto se calcula como:
*L=\dfrac{2b^2}{a}*
donde a es la longitud del semieje transversal y b la longitud del semieje conjugado.
Ejemplos
Calcular el lado recto de las siguientes hipérbolas:
- *\dfrac{(x-3)^2}{4}-(y+2)^2=1*
- *\dfrac{(y-1)^2}{9}-\dfrac{(x+5)^2}{16}=1*
- *\dfrac{x^2}{7}-\dfrac{(y-4)^2}{8}=1*
Soluciones
1) En *\dfrac{(x-3)^2}{4}-(y+2)^2=1* identificamos *a^2=4→a=\sqrt{4}=2* y *b^2=1* porque el término positivo contiene a la variable x.
Calculamos el lado recto:
*L=\dfrac{2b^2}{a}=\dfrac{2\cdot 1}{2}=\dfrac{2}{2}=1*
2) En *\dfrac{(y-1)^2}{9}-\dfrac{(x+5)^2}{16}=1* identificamos que *a^2=9\rightarrow a=\sqrt{9}=3* y *b^2=16* porque el término positivo contiene a la variable y.
Calculamos el lado recto:
*L=\dfrac{2b^2}{a}=\dfrac{2\cdot 16}{3}=\dfrac{32}{3}*
3) En *\dfrac{x^2}{7}-\dfrac{(y-4)^2}{8}=1* identificamos que *a^2=7\rightarrow a=\sqrt{7}* y *b^2=8* porque el término positivo contiene a la variable x.
Calculamos el lado recto:
*L=\dfrac{2b^2}{a}=\dfrac{2\cdot 8}{\sqrt{7}}=\dfrac{16}{\sqrt{7}}=\dfrac{16\sqrt{7}}{7}*
Parábola
El lado recto de una parábola es un segmento perpendicular al eje focal que pasa por su foco. Si |p| es la distancia focal (del vértice al foco), la longitud del lado recto es cuatro veces la distancia focal, es decir:
*L=|4p|*
Ejemplos
Determinar el lado recto de las siguientes parábolas:
- *3y+4=(x-2)^2-5*
- *x+5=-2(y-1)^2+3*
- *y=-\dfrac{1}{2}(x+3)^2+4*
Soluciones
1) Buscamos una ecuación de la forma *(x-h)^2=4p(y-k)* para obtener directamente el valor del lado recto L = |4p|. Reescribimos la ecuación dada:
*3y+4=(x-2)^2-5*
*(x-2)^2=3y+4+5*
*(x-2)^2=3y+9*
*(x-2)^2=3(y+3)*
De aquí podemos extraemos vemos que *4p=3,* por lo que el lado recto es *|3| = 3:*
*L=3*
2) Buscamos una ecuación de la forma *(y-k)^2=4p(x-h).* Reescribiendo:
*x+5=-2(y-1)^2+3*
*-2(y-1)^2=x+5-3*
*-2(y-1)^2=x+2*
*(y-1)^2=-\dfrac{1}{2}(x+2)*
De aquí vemos que *4p=-\dfrac{1}{2}* , por lo que el lado recto es:
*L=\left|-\dfrac{1}{2}\right|=\dfrac{1}{2}*
3) Buscamos una ecuación de la forma *(x-h)^2=4p(y-k).* Acomodando:
*y=-\dfrac{1}{2}(x+3)^2+4*
*(x+3)^2=-2(y-4)*
De aquí vemos que *4p=-2,* por lo que el lado recto es:
*L=|-2|=2*
Resumen de fórmulas
| Sección cónica | Lado recto |
|---|---|
| Elipse | L = 2b² / a² |
| Hipérbola | L = 2b² / a² |
| Parábola | L = |4p| |
Bibliografía
- Có, P. (2018). Álgebra y Geometría Analítica: Secciones cónicas. Universidad Nacional de Rosario.
- Fuller, G. y Tarwater, D. (1995). Geometría Analítica (7ma edición). Pearson Educación.
- Lehmann, C. (1989). Geometría Analítica. Limusa.
- Mora, W., y Figueroa, G. (2009). Cónicas, cálculo superior. Revista Digital Matemática, Educación e Internet.
- Márquez, A. y otros. (2009). Geometría Analítica. Prentice Hall.
- Sullivan, M. (2006). Álgebra y Trigonometría. Pearson Educación.
- Swokowski, E. y Cole, J. (2009). Álgebra y Trigonometría con Geometría Analítica. Cengage Learning.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta



Otros artículos que pueden interesarte