Ejercicios de elipse
En este artículo veremos ejercicios de la elipse en matemáticas resueltos paso a paso para todos los niveles educativos. Si todavía no conoces su significado y conceptos fundamentales, te invito a revisar primero el artículo principal donde abordamos su definición, fórmulas, partes, características y otros aspectos:
Índice
Ejercicios generales
Los siguientes artículos ofrecen ejercicios resueltos sobre los principales elementos de la elipse:


Encontrar la ecuación de una elipse a partir de datos
Los siguientes ejercicios consisten en encontrar la ecuación canónica o general de una elipse partiendo de datos, ya sean los focos y un punto, puntos por los que pasa la curva, longitudes de semiejes, etc.
Ecuación de una elipse a partir los focos y un punto
Recordemos que una elipse es un conjunto de puntos cuya suma de distancias a dos puntos fijos llamados focos es una constante igual a la longitud del eje mayor, 2a. En los siguientes ejemplos veremos cómo hallar la ecuación conociendo los focos y un punto de la elipse.
Ejercicio 1
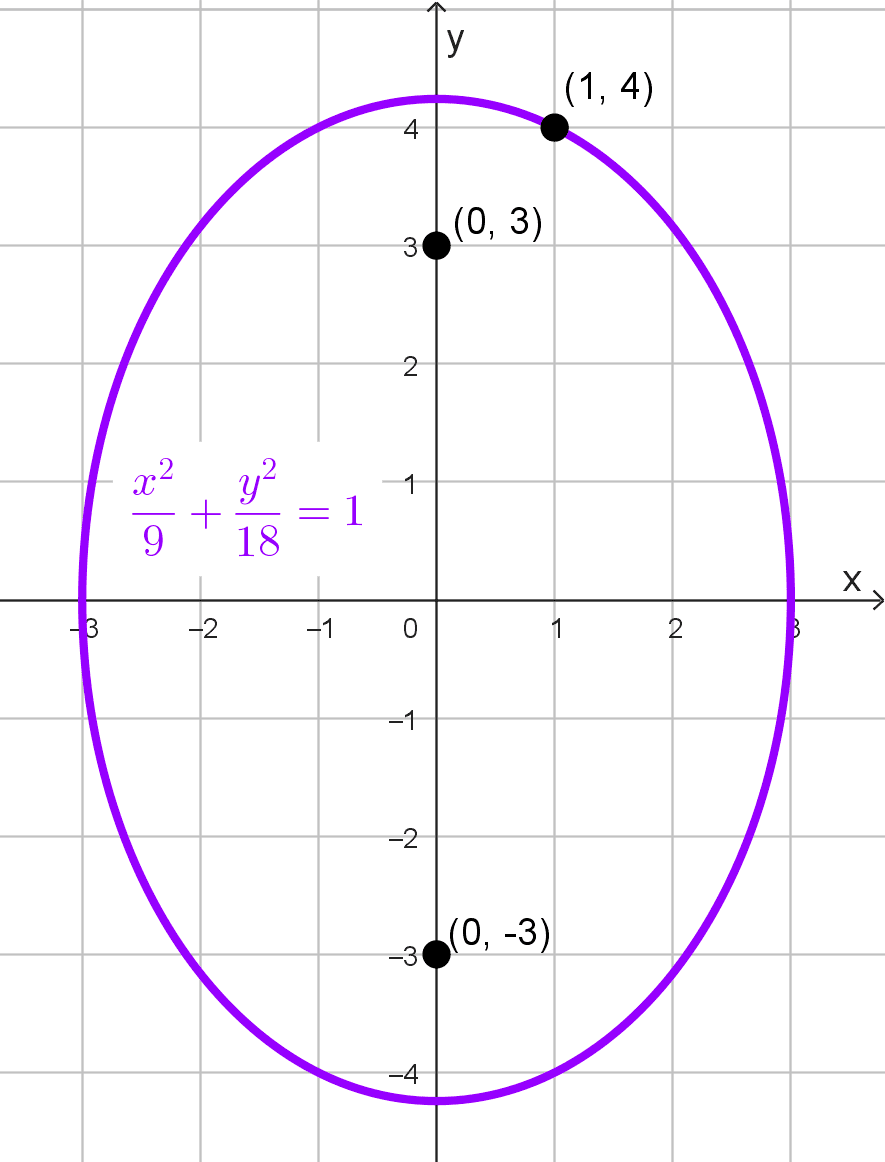
Hallar la ecuación de la elipse con focos en F1(0, -3) y F2(0, 3) y pasa por el punto P(1, 4).
Solución
Comenzamos utilizando la definición de la elipse:
\(d(F_1,P)+d(F_2,P)=2a\)
Calculamos las distancias, utilizando la fórmula de distancia entre dos puntos.
Distancia de \(F_1(0,-3)\) a \(P(1,4):\)
\(d(F_1,P)=\sqrt{(1-0)^2+(4-(-3))^2}=\sqrt{1^2+(4+3)^2}=\sqrt{1+49}=\sqrt{50}=5\sqrt{2}\)
Distancia de \(F_2(0,3)\) a \(P(1,4):\)
\(d(F_2,P)=\sqrt{(1-0)^2+(4-3)^2}=\sqrt{1^2+1^2}=\sqrt{1+1}=\sqrt{2}\)
Ahora encontramos 2a:
\(2a=d(F_1,P)+d(F_2,P)=5\sqrt{2}+\sqrt{2}=6\sqrt{2}\)
Por lo tanto:
\(a=\dfrac{6\sqrt{2}}{2}=3\sqrt{2}\)
El centro de la elipse es el punto medio entre los focos:
\(\text{Centro}=\left(0,\dfrac{-3+3}{2}\right)=(0,0)\)
Dado que los focos están sobre el eje y, la elipse es vertical. Su ecuación canónica tiene la siguiente forma:
\(\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1\)
La distancia focal 2c es igual a la distancia entre los focos:
\(2c=6→c=3\)
Usamos la relación característica de la elipse:
\(c^2=a^2-b^2 → b^2=a^2-c^2\)
Sabemos que \(a=3\sqrt{2},\) por lo que:
\(a^2=(3\sqrt{2})^2=9\cdot2=18\)
Sustituimos \(a^2\) y \(c^2:\)
\(b^2=a^2-c^2=18-9=9\)
Sustituimos \(a^2=18\) y \(b^2=9\) en la ecuación reducida:
\(\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1\)
\(\dfrac{x^2}{9}+\dfrac{y^2}{18}=1\)
Ejercicio 2
Hallar la ecuación de la elipse cuyos focos son F1(-2, 0) y F2(2, 0) y pasa por el punto P(3, 1).
Solución
Comenzamos utilizando la definición de elipse:
\(d(F_1, P)+d(F_2,P)=2a\)
Ahora necesitamos calcular las distancias del primer miembro, utilizaremos la fórmula de distancia entre dos puntos:
Distancia de F1(-2, 0) a P(3, 1):
\(d(F_1, P)=\sqrt{(3-(-2))^2+(1-0)^2}=\sqrt{(3+2)^2+1^2}=\sqrt{25+1}=\sqrt{26}\)
Distancia de F2(2, 0) a P(3, 1):
\(d(F_2, P)=\sqrt{(3-2)^2+(1-0)^2}=\sqrt{1^2+1^2}=\sqrt{2}\)
Ahora encontraremos el valor de 2a:
\(2a=d(F_1, P)+d(F_2,P)=\sqrt{26}+\sqrt{2}\)
Este es uno de los datos que necesitamos para obtener la ecuación. Ahora hallamos el centro de la elipse como el punto medio entre los focos, en este caso es el origen (0, 0). Los focos se encuentran sobre el eje x, lo que resulta en una elipse horizontal. Es decir, la ecuación tendrá la siguiente forma:
\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\)
Utilizaremos la distancia focal c para hallar el valor de b. La distancia entre los focos es de 4 unidades, esto quiere decir que:
\(2c=4→c=2\)
Ahora usamos una propiedad de la elipse:
\(c^2=a^2-b^2→b^2=a^2-c^2\)
Sabemos que \(2a=\sqrt{26}+\sqrt{2},\) entonces \(a=\dfrac{\sqrt{26}+\sqrt{2}}{2}.\)
Calculamos \(b^2:\)
\(b^2=a^2-c^2\)
\(=\left(\dfrac{\sqrt{26}+\sqrt{2}}{2}\right)^2-(2)^2\)
\(=\dfrac{(\sqrt{26}+\sqrt{2})^2}{4}-4\)
Con estos datos podemos armar la ecuación canónica:
\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\)
\(\dfrac{x^2}{\dfrac{(\sqrt{26}+\sqrt{2})^2}{4}}+\dfrac{y^2}{\dfrac{(\sqrt{26}+\sqrt{2})^2}{4}-4}=1\)
Ejercicio 3
Hallar la ecuación de la elipse con focos en (2, 3) y (2, 7) y pasa por el punto (4, 5).
Solución
Aplicamos la definición de la elipse:
\(d(F_1,P)+d(F_2,P)=2a\)
Calculamos las distancias entre los focos y el punto dado, usando la fórmula de distancia entre dos puntos.
Distancia de F1(2, 3) a P(4, 5):
\(d(F_1,P)=\sqrt{(4-2)^2+(5-3)^2}=\sqrt{2^2+2^2}=\sqrt{4+4}=\sqrt{8}=2\sqrt{2}\)
Distancia de F2(2, 7) a P(4, 5):
\(d(F_2,P)=\sqrt{(4-2)^2+(5-7)^2}=\sqrt{2^2+(-2)^2}=\sqrt{4+4}=\sqrt{8}=2\sqrt{2}\)
Calculamos 2a:
\(2a=d(F_1,P)+d(F_2,P)=2\sqrt{2}+2\sqrt{2}=4\sqrt{2}\)
Por lo tanto:
\(a=\dfrac{4\sqrt{2}}{2}=2\sqrt{2}\)
Determinamos el centro de la elipse, que es el punto medio entre los focos:
\(\text{Centro}=\left(\dfrac{2+2}{2},\dfrac{3+7}{2}\right)=(2,5)\)
Identificamos la orientación de la elipse. Como los focos están alineados verticalmente (x = 2 es constante), la elipse es vertical. Su ecuación es:
\(\dfrac{(x-h)^2}{b^2}+\dfrac{(y-k)^2}{a^2}=1\)
donde el centro es \((h, k)=(2, 5).\)
Determinamos c y calculamos \(b^2\). La distancia focal 2c es igual a la distancia entre los focos:
\(2c=7-3=4 → c=2\)
Usamos la relación fundamental de la elipse:
\(c^2=a^2-b^2 → b^2=a^2-c^2\)
Calculamos \(a^2\) y \(c^2:\)
\(a^2=(2\sqrt{2})^2=4\cdot2=8\)
\(c^2=2^2=4\)
Sustituimos:
\(b^2=a^2-c^2=8-4=4\)
Ahora escribimos la ecuación de la elipse. Sustituimos \(h=2, k=5, a^2=8,~ y~ b^2=4\) en la ecuación canónica:
\(\dfrac{(x-2)^2}{4}+\dfrac{(y-5)^2}{8}=1\)
Esta última es la ecuación de la elipse obtenida mediante los focos y un punto de la curva.
Ecuación de una elipse a partir de sus semiejes
Queremos encontrar la ecuación de la elipse cuando se conocen los focos y la longitud de algún semieje, o solo las longitudes de los semiejes y el centro.
Ejercicio 1
Determinar la ecuación de la elipse con focos en (2, -1) y (2, -5) cuyo eje mayor tiene longitud 10.
Solución
Solución: podemos encontrar el centro como el punto medio de los focos:
\(\text{Centro}=\left(\dfrac{2+2}{2},\dfrac{-1+(-5)}{2}\right)=(2, -3)\)
La elipse tiene eje mayor vertical (x = 2 es constante en los focos), por tanto buscamos una ecuación de la forma:
\(\dfrac{(x-h)^2}{b^2}+\dfrac{(y-k)^2}{a^2}=1\)
donde (h, k) = (2, -3).
El eje mayor tiene longitud 10, es decir, 2a=10, de aquí se obtiene que \(a=5\) y \(a^2=25.\) La distancia entre los focos es \(2c=6→c=3→c^2=9\)
Obtenemos \(b^2\) por la propiedad fundamental de la elipse:
\(b^2=a^2-c^2\)
\(b^2=25-9\)
\(b^2=16\)
Ya tenemos los datos para obtener la ecuación canónica:
\(\dfrac{(x-h)^2}{b^2}+\dfrac{(y-k)^2}{a^2}=1\)
\(\dfrac{(x-2)^2}{16}+\dfrac{(y+3)^2}{25}=1\)
Ejercicio 2
Hallar la ecuación de la elipse sabiendo que sus vértices principales son (-2, 4) y (4, 4) y uno de sus focos está en (3, 4).
Solución
Solución: podemos encontrar el centro como el punto medio de los vértices principales:
\(\text{Centro}=\left(\dfrac{-2+4}{2},\dfrac{4+4}{2}\right)=(1,4)\)
La elipse tiene eje mayor horizontal (los vértices principales varían en la coordenada x), por lo que buscamos una ecuación de la forma:
\(\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1\)
donde \((h,k)=(1,4).\)
La distancia entre los vértices principales es igual a la longitud del eje mayor, 2a:
\(2a=\sqrt{(4-(-2))^2+(4-4)^2}=6→ a=3→ a^2=9\)
La distancia de un foco al centro es c, y uno de los focos está en (3, 4), Calculamos c:
\(c=\sqrt{(3-(-1))^2+(4-4)^2}=4→ c=2→ c^2=4\)
Usamos la relación fundamental de la elipse para encontrar b^2:
\(b^2=a^2-c^2\)
\(b^2=9-4=5\)
Finalmente, sustituimos los valores de \(h, k, a^2,\) y \(b^2\) en la ecuación canónica de la elipse:
\(\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1\)
\(\dfrac{(x-1)^2}{9}+\dfrac{(y-4)^2}{5}=1\)
Ecuación de una elipse que pasa por cuatro puntos
Para encontrar la ecuación podemos sustituir los puntos dados en la ecuación general y así obtener un sistema de ecuaciones con cuatro incógnitas, la solución del sistema determina los coeficientes de la ecuación.
Ejercicio 1
Encontrar la ecuación de una elipse que pasa por cuatro puntos (0, -1), (2, 0), (4, -1) y (2, -2).
Solución
Sustituimos los puntos en la ecuación general de la elipse tomando A = 1; es decir, se sustituye en x2 + Cy2 + Dx + Ey + F = 0.
Punto (0, -1)
\((0)^2+(-1)C+(0)D+(-1)E+F=0→C-E+F=0\)
Punto (2, 0)
\((2)^2+(0)^2C+(2)D+(0)E+F=0→2D+F=-4\)
Punto (4, -1)
\((4)^2+(-1)^2C+(4)D+(-1)E+F=0→C+4D-E+F=-16\)
Punto (2, -2)
\((2)^2+(-2)^2C+(2)D+(-2)E+F=0→4C+2D-2E+F=-4\)
Entonces se obtiene un sistema de cuatro ecuaciones con cuatro incógnitas:
\(\begin{cases}C-E+F=0 \\2D+F=-4 \\C+4D-E+F=-16 \\4C+2D-2E+F=-4 \end{cases}\)
Resolviendo el sistema se obtiene que:
\(C=4, D=-4, E=8~ y~ F=4\)
Estos valores se sustituyen en la ecuación general de la elipse:
\(x^2+Cy^2+Dx+Ey+F=0\)
Y se obtiene finalmente la ecuación de la elipse:
\(x^2+4y^2-4x+8y+4=0\)
Ejercicio 2
Determina la ecuación de la elipse que pasa por los puntos \((0, 3), (2, 0), (1, 3\sqrt{3}/2)\) y \((1/2, 3\sqrt{15}/4).\)
Solución
Se sustituyen los puntos en la ecuación general de la elipse tomando A = 1:
Punto (0, 3)
\((0)^2+(3)^2C+(0)D+(3)E+F=0→9C+3E+F=0\)
Punto (2,0)
\((2)^2+(0)^2+(2)D+(0)E+F=0→2D+F=-4\)
Punto \((1, 3\sqrt{3}/2)\)
\((1)^2+\left(\dfrac{3\sqrt{3}}{2}\right)C+(1)D+\left(\dfrac{3\sqrt{3}}{2}\right)E+F=0→27C+4D+6\sqrt{3}E+4F=-4\)
Punto \((1/2, 3\sqrt{15}/4)\)
\(\left(\dfrac{1}{2}\right)^2+\left(\dfrac{3\sqrt{15}}{4}\right)^2C+\left(\dfrac{1}{2}\right)D+\left(\dfrac{3\sqrt{15}}{4}\right)E+F=0→135C+8D+12\sqrt{15}E+16F=-4\)
Se obtiene un sistema de cuatro ecuaciones con cuatro incógnitas, cuyos resultados son:
\(C=\dfrac{4}{9}, D=0, E=0, F=-4\)
Estos valores se sustituyen en la ecuación general de la elipse:
\(x^2+Cy^2+Dx+Ey+F=0\)
\(x^2+\dfrac{4}{9}y^2-4=0\)
Finalmente, el resultado es la ecuación de la elipse:
\(9x^2+4y^2-36=0\)
Ecuación de una elipse a partir de su gráfica
Ejercicio: identificar los elementos y escribir las ecuaciones de las elipses cuyos gráficos son los siguientes:
Mostrar soluciones
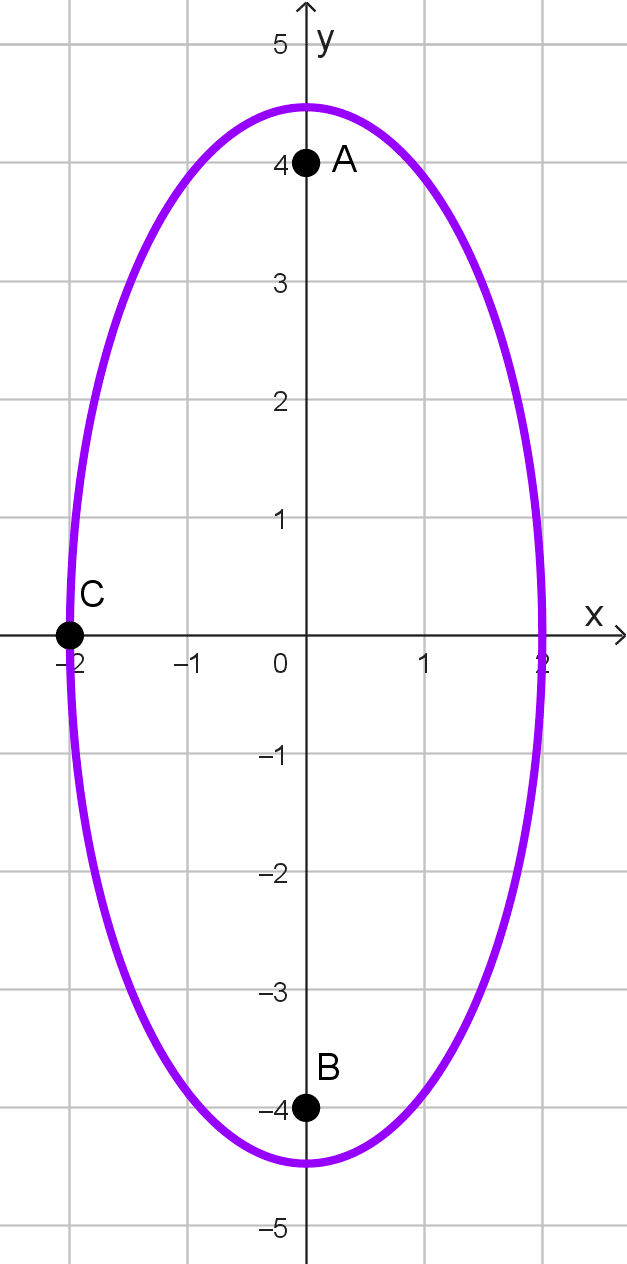
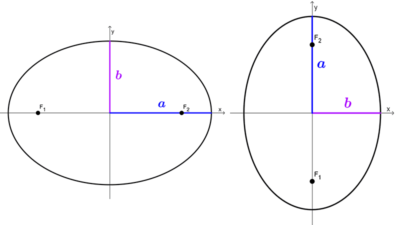
Elipse A
A partir del gráfico se extrae que:
- La elipse es vertical, pues sus focos están sobre el eje y en las coordenadas (0, -4) y (0, 4).
- Los ejes de la elipse están sobre los ejes cartesianos.
- El centro es el origen de coordenadas.
- Un vértice secundario está en (-2, 0), lo que significa que el semieje menor es b = 2.
- La distancia entre los focos (distancia focal) es 2c = 8, entonces c = 4.
Con esta información podemos obtener el valor del cuadrado del semieje mayor utilizando la relación fundamental:
\(c^2=a^2-b^2→a^2=c^2+b^2\)
\(a^2=(4)^2+(2)^2=16+4=20\)
Con estos datos ya podemos armar la ecuación, la cual tendrá la forma:
\(\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1\)
por tener centro en el origen y eje mayor vertical. Reemplazando los datos obtenemos finalmente la ecuación de la elipse:
\(\dfrac{x^2}{4}+\dfrac{y^2}{20}=1\)
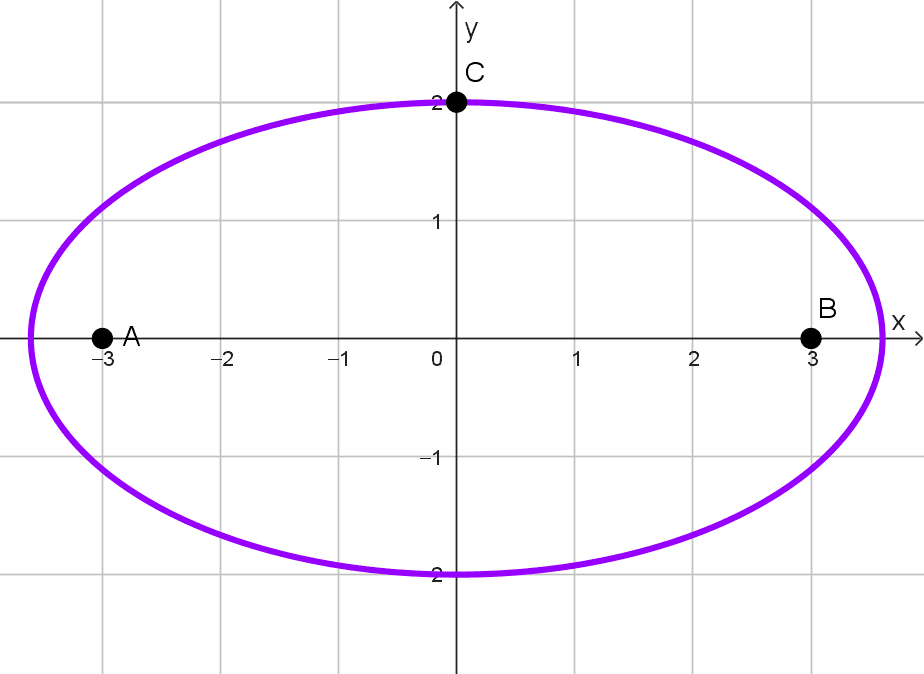
Elipse B
A partir del gráfico se extrae que:
- La elipse es horizontal, pues sus focos están sobre el eje x en las coordenadas (-3, 0) y (3, 0).
- Los ejes de la elipse están sobre los ejes cartesianos.
- El centro es el origen de coordenadas.
- Un vértice secundario está en (0, 2), lo que significa que el semieje menor es b = 2.
- La distancia entre los focos (distancia focal) es 2c = 6, entonces c = 3.
Utilizando la relación fundamental:
\(a^2=c^2+b^2=3^2+2^2=9+4=13\)
Con estos datos armamos la ecuación:
\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\)
\(\dfrac{x^2}{13}+\dfrac{y^2}{4}=1\)
¿Te está sirviendo este artículo? ¡Por favor, califícalo!
3,3 / 5 — 3 votos
Combinaciones de los casos anteriores
A partir de los siguientes datos encontrar la ecuación de la elipse, todos sus elementos y graficarla.
- Centro en el origen, foco en el punto (0, 3) y semieje mayor igual a 5.
- Eje mayor sobre el eje y, tiene un vértice principal en (0, 5), un vértice secundario en (3, 0) y tiene centro en el origen de coordenadas.
- Sus vértices principales son los puntos (1, -6) y (9, -6) y la longitud de cada lado recto es 9/2.
- Los focos son los puntos (3, 8) y (3, 2), la longitud de su eje menor es 8.
- Los focos de la elipse son (2, 4) y (2, 10) y uno de sus vértices es (2, 12).
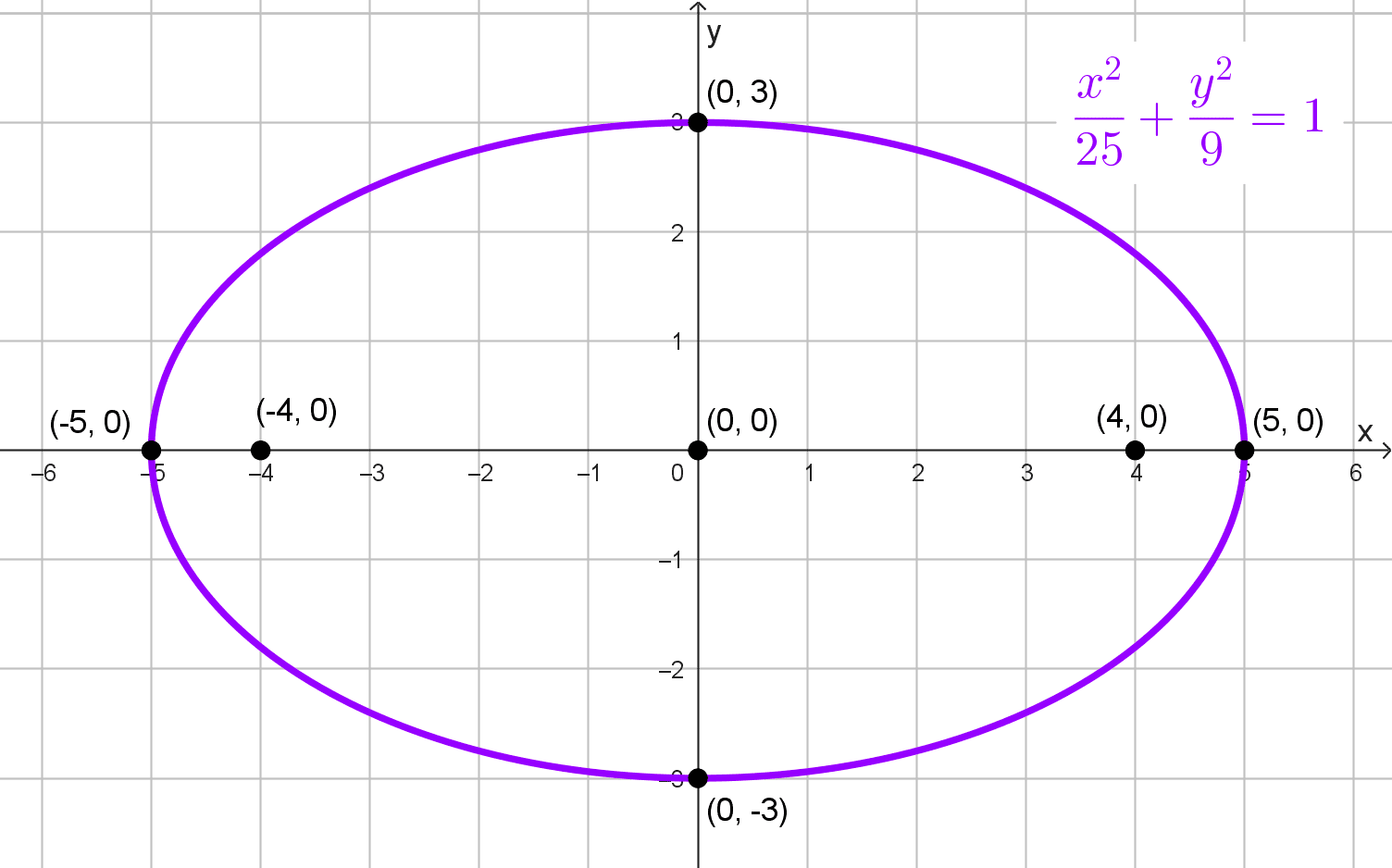
- Los vértices son (-5, 0) y (5, 0) y el valor de b es 3.
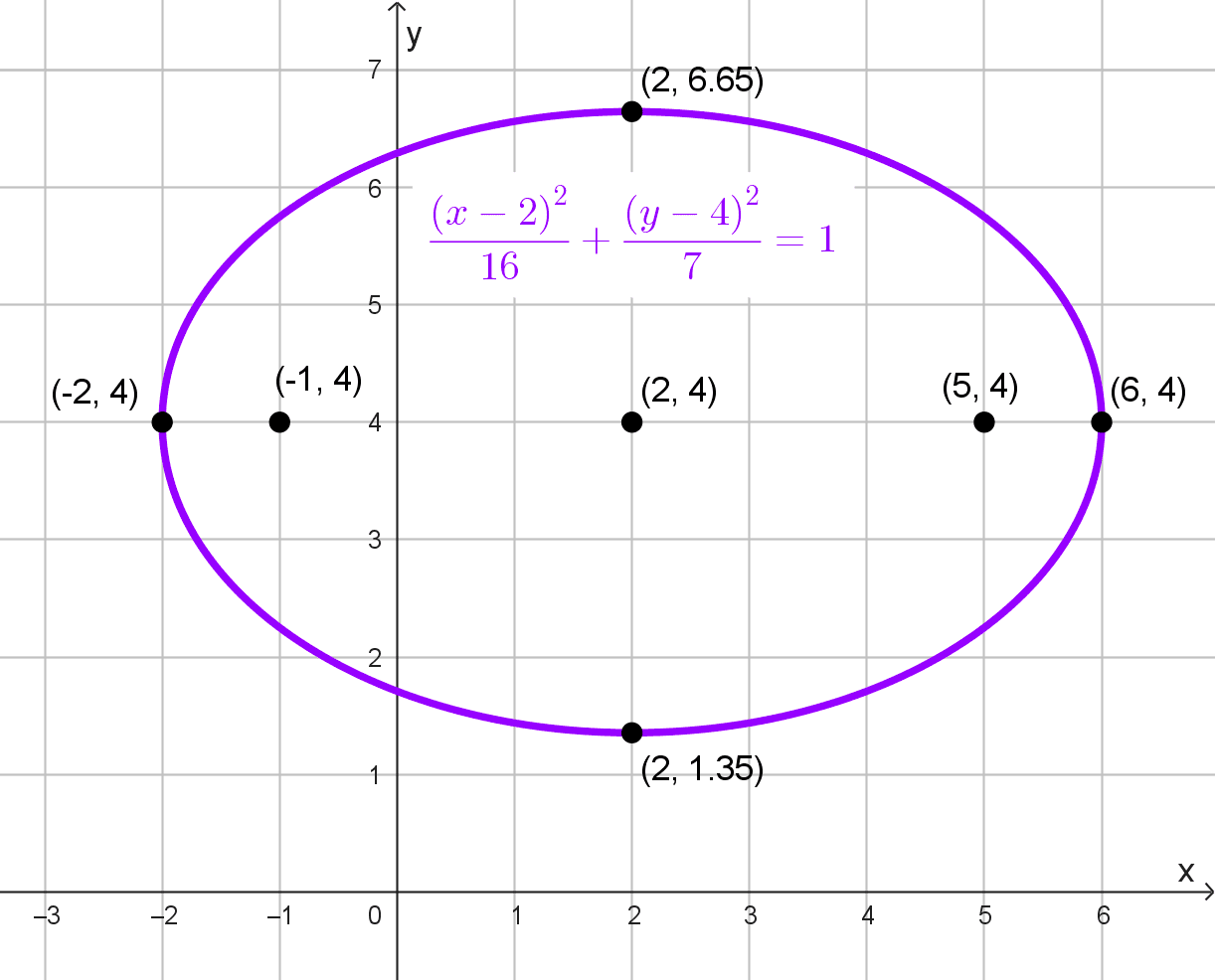
- Sus vértices son V(6, 4) y V’(-2, 4) y sus focos son los puntos F(5, 4) y F’(-1, 4)
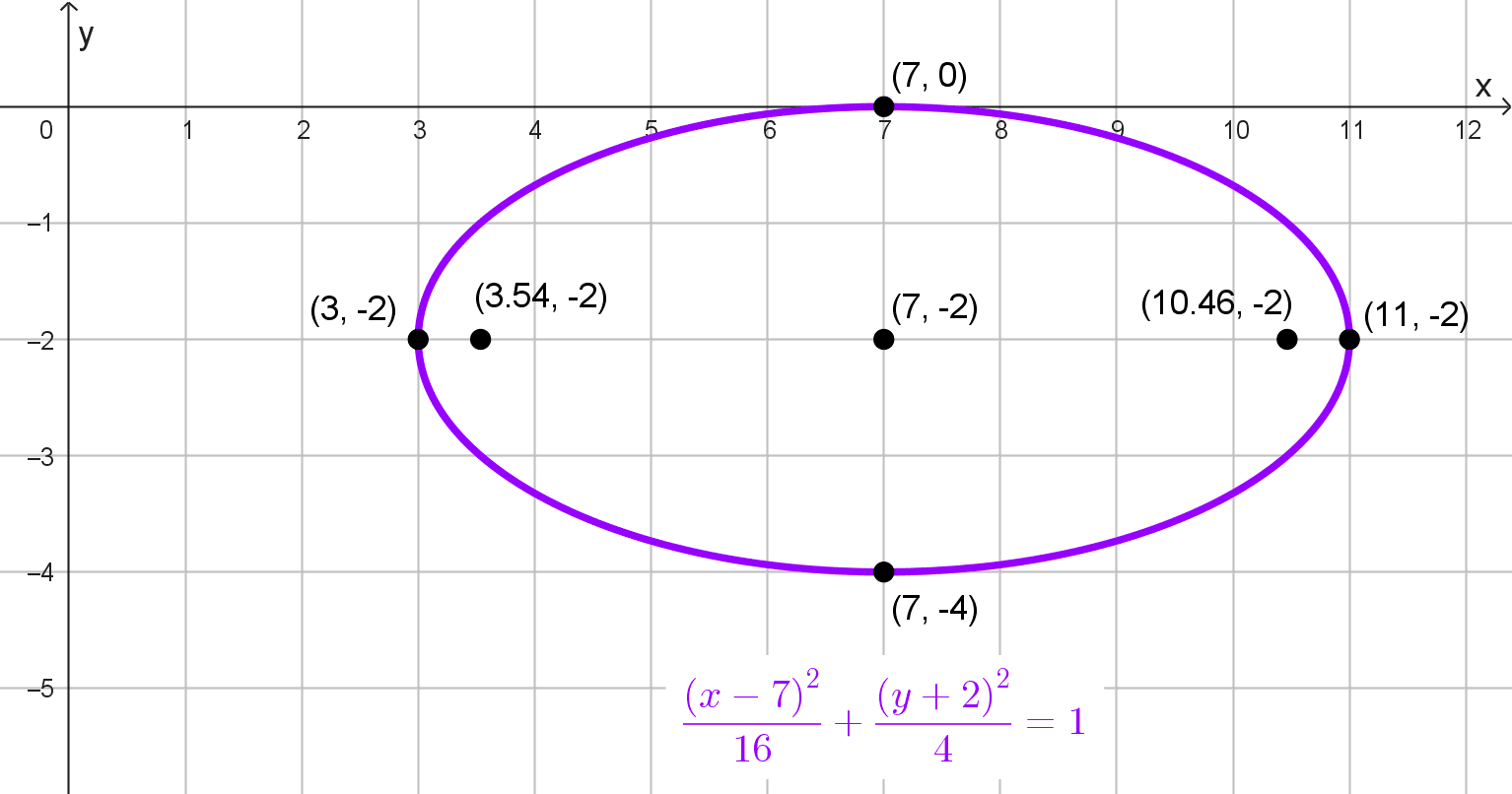
- Centro C(7, -2), eje mayor = 8, eje menor = 4 y eje focal paralelo al eje x.
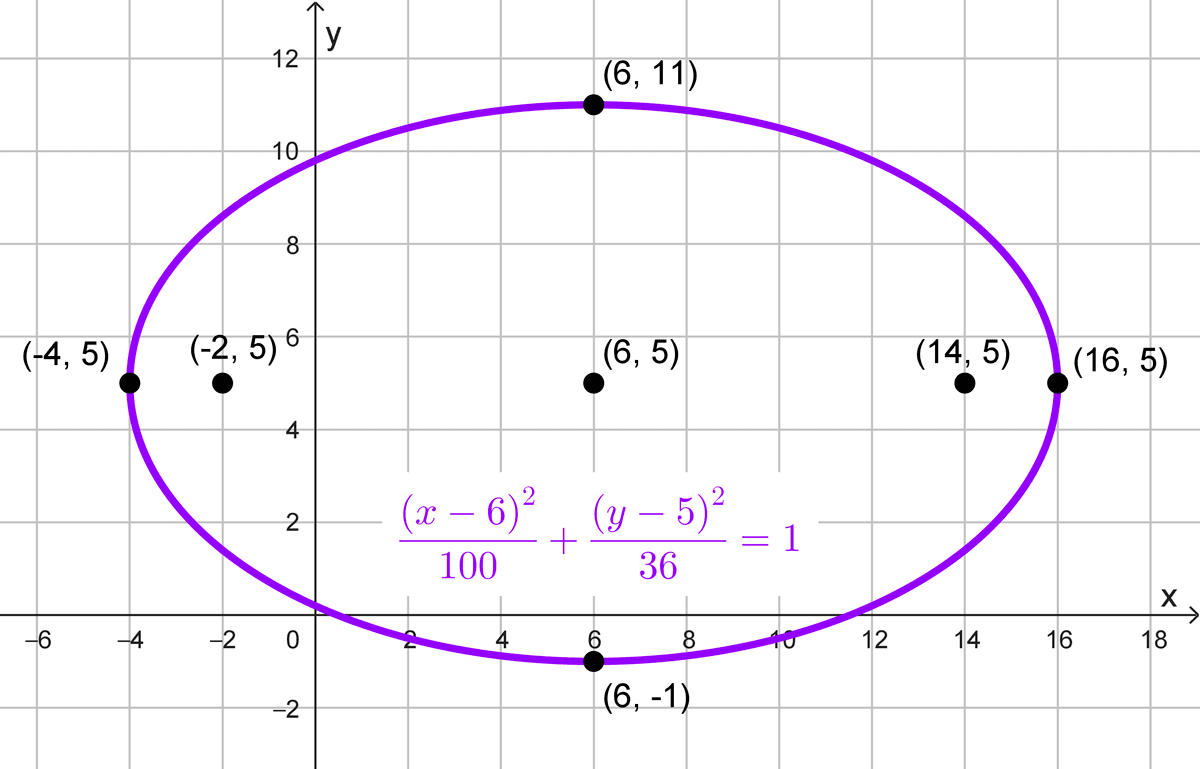
- Vértices principales en (-4, 5) y (16, 5) y su excentricidad es 4/5.
- Su excentricidad es igual a 2/3 y las coordenadas de sus focos son los puntos (0, 0) y (0, -4).
Soluciones
Solución del ejercicio 1
Datos del problema:
- Centro: (0, 0)
- Foco: (0, 3)
- Semieje mayor: a = 5
Como el centro y el foco están sobre el eje x, la elipse es horizontal, lo que significa que tendrá una ecuación de la forma:
\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\)
Conocemos un semieje, obtendremos el otro mediante la relación fundamental. Primero necesitamos la semidistancia focal c, la cual es la distancia entre el centro y el foco, en este caso c = 3.
Ahora aplicamos la relación fundamental
\(c^2=a^2-b^2→b^2=a^2-c^2\)
Así:
\(b^2=5^2-3^2=25-9=16\)
Conociendo estos datos podemos armar la ecuación canónica de la elipse:
\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\)
\(\dfrac{x^2}{25}+\dfrac{y^2}{16}=1\)
Conociendo las medidas a, b y c se pueden obtener los demás elementos de la elipse.
Elementos de la elipse:
- Focos: (0, 3) y (0, -3)
- Centro: (0, 0)
- Semiejes: a = 5, b = 4
- Distancia focal: 2c = 6
- Vértices principales: (5, 0) y (-5, 0)
- Vértices secundarios: (0, 4) y (0, -4)
- Lado recto: \(L_R=\dfrac{2b^2}{a}=\dfrac{2\cdot 16}{5}=6,4\)
- Excentricidad: \(e=\dfrac{c}{a}=\dfrac{3}{5}=0,6\)
Solución del ejercicio 2
Datos iniciales:
- Centro: (0, 0)
- Vértice principal: (0, 5)
- Vértice secundario: (3, 0)
- Eje mayor sobre el eje y.
El eje mayor está sobre el eje y, por lo que la ecuación canónica de la elipse será:
\(\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1\)
donde a es el semieje mayor y b el semieje menor.
El vértice principal (0,5) nos indica que la longitud del semieje mayor es a = 5.
El vértice secundario (3,0) nos indica que la longitud del semieje menor es b = 3.
Usamos la relación fundamental para las elipses:
\(c^2=a^2-b^2\)
Sustituyendo los valores:
\(c^2=5^2-3^2=25-9=16\)
Por lo tanto:
\(c=\sqrt{16}=4\)
Con \(a^2=25\) y \(b^2=9,\) la ecuación canónica de la elipse será:
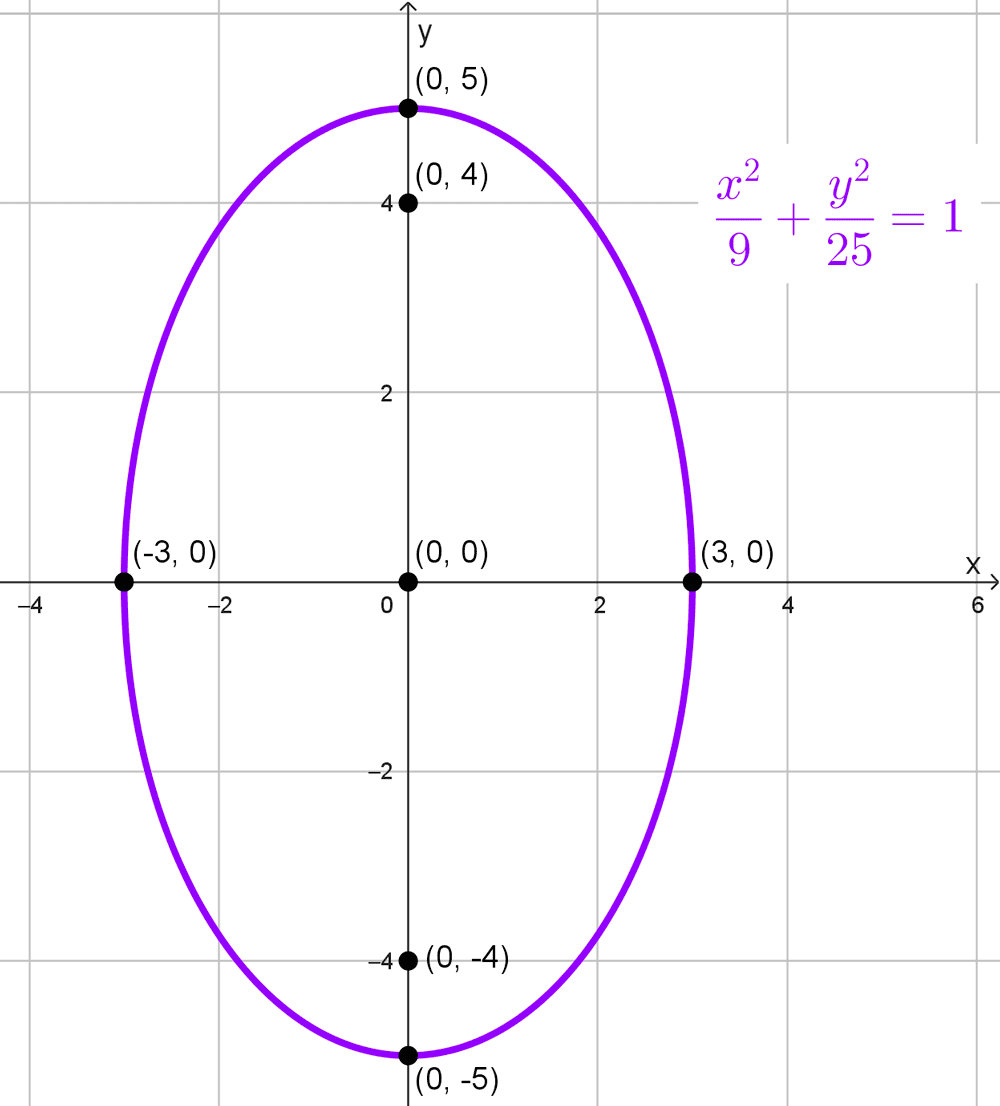
\(\dfrac{x^2}{9}+\dfrac{y^2}{25}=1\)
Elementos de la elipse:
- Centro: (0, 0)
- Focos: (0, 4) y (0, -4), ya que c = 4 y están sobre el eje y.
- Semiejes: a = 5, b = 3
- Vértices principales: (0, 5) y (0, -5)
- Vértices secundarios: (3, 0) y (-3, 0)
- Distancia focal: 2c = 8
- Lado recto: \(L_R=\dfrac{2b^2}{a}=\dfrac{2\cdot9}{5}=\dfrac{18}{5}=3,6\)
- Excentricidad: \(e=\dfrac{c}{a}=\dfrac{4}{5}=0,8 \)
Solución del ejercicio 3
Datos iniciales:
- Vértices principales: (1, -6) y (9, -6)
- Longitud del lado recto: 9/2
La elipse tiene sus vértices principales alineados horizontalmente, ya que comparten la misma coordenada y.
El centro es el punto medio entre los vértices principales:
\(\text{Centro}=\left(\dfrac{1+9}{2},-6\right)=(5,-6)\)
El eje mayor es paralelo al eje x, por lo que la ecuación canónica de la elipse será:
\(\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1\)
donde (h, k) es el centro, a es el semieje mayor y b es el semieje menor.
La distancia entre el centro y cualquiera de los vértices principales es la longitud del semieje mayor a:
\(a=9-5=4\)
Por lo tanto:
\(a^2=4^2=16\)
La fórmula del lado recto de la elipse es:
\(L_R=\dfrac{2b^2}{a}\)
Sustituyendo los valores conocidos:
\(\dfrac{2b^2}{4}=\dfrac{9}{2}→ b^2=\dfrac{9}{2}\cdot 2=9\)
Por lo tanto:
\(b=3\)
Usamos la relación fundamental de las elipses:
\(c^2=a^2-b^2\)
Sustituyendo los valores:
\(c^2=16-9=7→ c=\sqrt{7}\)
Con \(a^2=16, b^2=9\) y el centro en (5, -6), la ecuación de la elipse es:
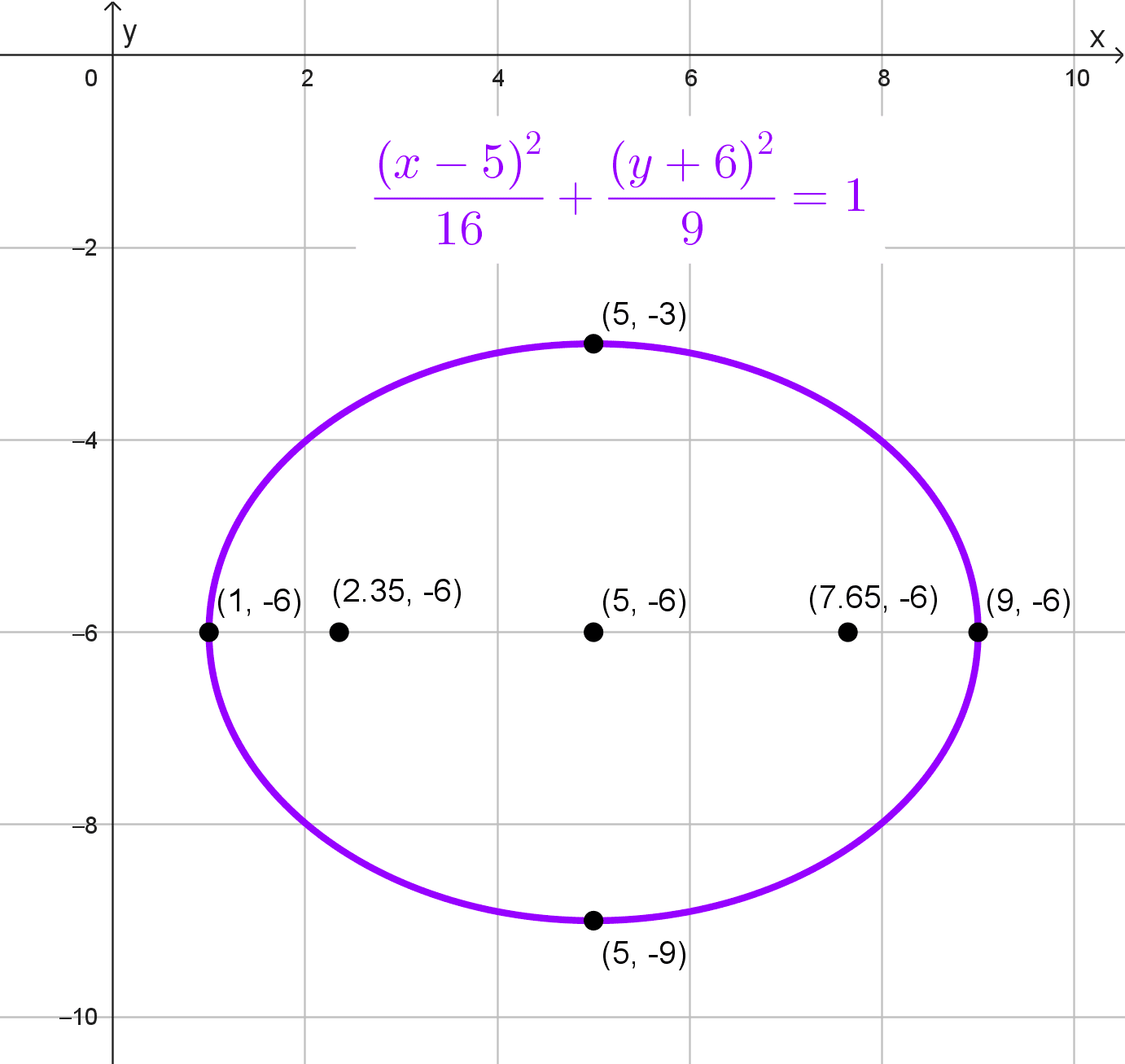
\(\dfrac{(x-5)^2}{16}+\dfrac{(y+6)^2}{9}=1\)
Elementos de la elipse
- Centro: (5, -6)
- Focos: están a una distancia \(c=\sqrt{7}\) a la izquierda y derecha del centro, es decir:
\((5-\sqrt{7},-6)\) y \((5+\sqrt{7},-6)\) - Semiejes: a = 4, b = 3
- Vértices principales: (1, -6) y (9, -6)
- Vértices secundarios: están a una distancia b = 3 arriba y abajo del centro, es decir:
\((5, -6+3)=(5, -3)\) y \((5, -6-3)=(5, -9)\) - Distancia focal: \(2c=2\sqrt{7}\)
- Lado recto: \(L_R=9/2\)
- Excentricidad: \(e=\dfrac{c}{a}=\dfrac{\sqrt{7}}{4}≈0,66\)
Solución del ejercicio 4
Datos iniciales:
- Focos: (3, 8) y (3, 2)
- Longitud del eje menor: b = 8
El centro de la elipse es el punto medio entre los focos:
\(\text{Centro}=\left(\dfrac{3+3}{2},\dfrac{8+2}{2}\right)=(3,5)\)
Los focos tienen la misma coordenada x, por lo que la elipse está orientada verticalmente. La ecuación canónica de la elipse será:
\(\dfrac{(x-h)^2}{b^2}+\dfrac{(y-k)^2}{a^2}=1\)
donde (h, k) es el centro, a es el semieje mayor y b el semieje menor.
La distancia entre los focos es 2c, así que:
\(2c=8-2=6→c=3\)
La relación entre a, b, y c en una elipse es:
\(c^2=a^2-b^2→a^2=c^2+b^2\)
La longitud del eje menor es 2b = 8, por lo que:
\(b=\dfrac{8}{2}=4→b^2=16\)
Sustituyendo los valores de \(c^2\) y \(b^2:\)
\(a^2=3^2+4^2=9+16=25→a=5\)
Sustituyendo los valores de \(a^2, b^2,\) y el centro \((h, k)=(3, 5):\)
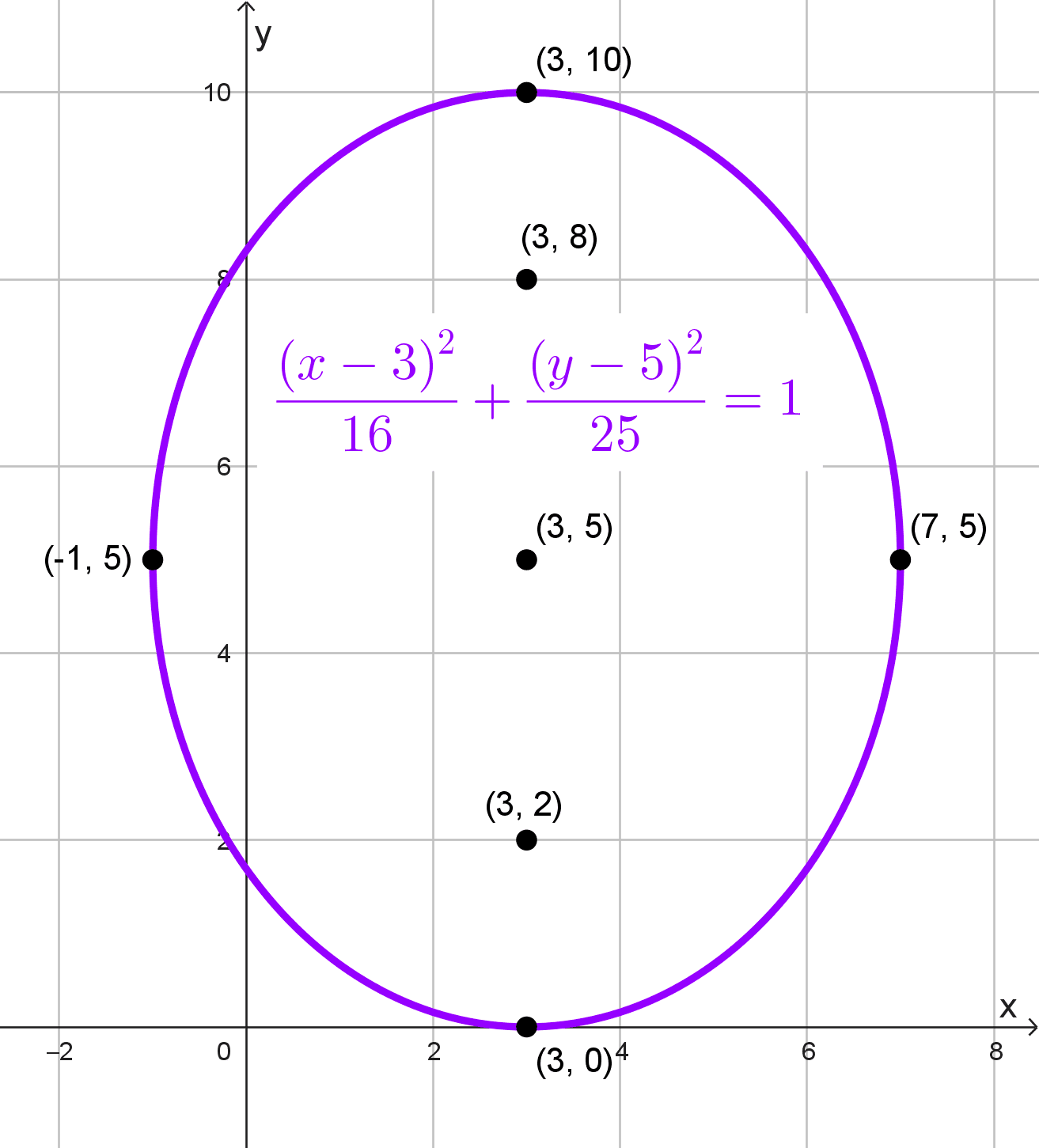
\(\dfrac{(x-3)^2}{16}+\dfrac{(y-5)^2}{25}=1\)
Elementos de la elipse
- Centro: (3, 5)
- Focos: están a una distancia c = 3 arriba y abajo del centro: \((3, 5+3)=(3, 8)\) y \((3, 5-3)=(3,2).\)
- Semiejes: a = 5, b = 4
- Vértices principales: están a una distancia a = 5 arriba y abajo del centro: \((3,5+5)=(3,10)\) y \((3,5-5)=(3,0).\)
- Vértices secundarios: están a una distancia b = 4 a la izquierda y derecha del centro: \((3+4,5)=(7,5)\) y \((3-4,5)=(-1,5).\)
- Distancia focal: \(2c=2·3=6\)
- Lado recto: \(L_R=\dfrac{2b^2}{a}=\dfrac{2·16}{5}=\dfrac{32}{5}=6,4\)
- Excentricidad: \(e=\dfrac{c}{a}=\dfrac{3}{5}=0,6 \)
Solución del ejercicio 5
Datos iniciales:
- Focos: (2, 4) y (2, 10)
- Un vértice: (2, 12)
El centro de la elipse es el punto medio entre los focos:
\(\text{Centro}=\left(\dfrac{2+2}{2},\dfrac{4+10}{2}\right)=(2,7)\)
Los focos tienen la misma coordenada x, por lo que la elipse está orientada verticalmente.
La ecuación canónica de la elipse será:
\(\dfrac{(x-h)^2}{b^2}+\dfrac{(y-k)^2}{a^2}=1\)
donde (h, k) es el centro, a es el semieje mayor y b el semieje menor.
Primero determinaremos la longitud del semieje mayor. Como el vértice (2, 12) está a una distancia a del centro (2, 7):
\(a=12-7=5→a^2=5^2=25\)
La distancia entre los focos es 2c, así que:
\(2c=10-4=6→c=3→c^2=3^2=9\)
La relación entre a, b, y c en una elipse es:
\(c^2=a^2-b^2→b^2=a^2-c^2\)
Sustituyendo los valores:
\(b^2=25-9=16→b=4\)
Sustituyendo los valores de \(a^2=25, b^2=16,\) y el centro \((h, k)=(2, 7):\)
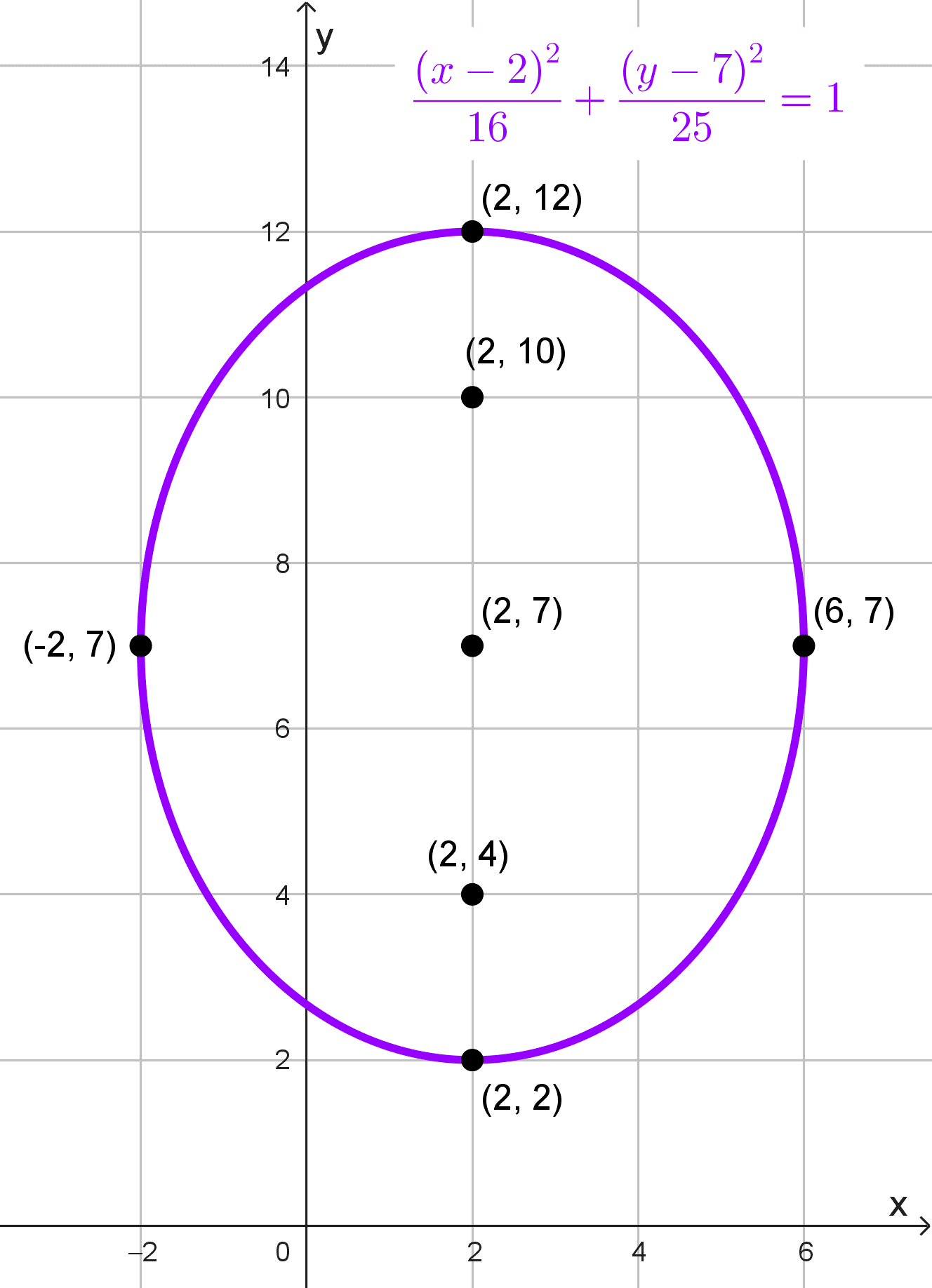
\(\dfrac{(x-2)^2}{16}+\dfrac{(y-7)^2}{25}=1\)
Elementos de la elipse
- Centro: (2, 7)
- Focos: están a una distancia c = 3 arriba y abajo del centro: \((2,7+3)=(2,10)\) y \((2,7-3)=(2,4)\)
- Semiejes: a = 5, b = 4
- Vértices principales: están a una distancia a = 5 arriba y abajo del centro: \((2,7+5)=(2,12)\) y \((2,7-5)=(2,2)\)
- Vértices secundarios: están a una distancia b = 4 a la izquierda y derecha del centro: \((2+4,7)=(6,7)\) y \((2-4,7)=(-2,7) \)
- Distancia focal: \(2c=2·3=6 \)
- Lado recto: \(L_R=\dfrac{2b^2}{a}=\dfrac{2·16}{5}=\dfrac{32}{5}=6,4 \)
- Excentricidad: \(e=\dfrac{c}{a}=\dfrac{3}{5}=0,6 \)
Solución del ejercicio 6
Datos del problema:
- Vértices: (-5, 0) y (5, 0)
- Semieje menor: b = 3
El centro de la elipse es el punto medio entre los vértices:
\(\text{Centro}=\left(\dfrac{-5+5}{2},\dfrac{0+0}{2}\right)=(0,0)\)
Los vértices tienen la misma coordenada y, por lo que la elipse está orientada horizontalmente. La ecuación canónica de la elipse será:
\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\)
donde a es el semieje mayor y b el semieje menor.
La distancia entre el centro y uno de los vértices es a:
\(a=5→a^2=5^2=25\)
La relación entre a, b, y c en una elipse es:
\(c^2=a^2-b^2\)
Sustituyendo los valores:
\(c^2=25-3^2=25-9=16→c=\sqrt{16}=4\)
Sustituyendo los valores de \(a^2=25, b^2=9\) en la ecuación canónica:
\(\dfrac{x^2}{25}+\dfrac{y^2}{9}=1\)
Elementos de la elipse
- Centro: (0, 0)
- Focos: están a una distancia c = 4 a la izquierda y derecha del centro: (-4, 0) y (4, 0)
- Semiejes: a = 5, b = 3
- Vértices principales: (-5, 0) y (5, 0)
- Vértices secundarios: están a una distancia b=3 arriba y abajo del centro: (0, 3) y (0, -3)
- Distancia focal: \(2c=2·4=8\)
- Lado recto: \(L_R=\dfrac{2b^2}{a}=\dfrac{2·9}{5}=\dfrac{18}{5}=3,6\)
- Excentricidad: \(e=\dfrac{c}{a}=\dfrac{4}{5}=0,8\)
Solución del ejercicio 7
Datos iniciales:
- Vértices principales: V(6, 4) y V'(-2, 4)
- Focos: F(5, 4) y F'(-1, 4)
El centro de la elipse es el punto medio entre los vértices principales, también podría calcularse como el punto medio entre los focos:
\(\text{Centro}=\left(\dfrac{6+(-2)}{2}, \dfrac{4+4}{2}\right) = (2, 4)\)
Los vértices y los focos tienen la misma coordenada y, por lo que la elipse está orientada horizontalmente. La ecuación canónica de la elipse será:
\(\dfrac{(x-h)^2}{a^2} + \dfrac{(y-k)^2}{b^2} = 1\)
donde (h, k) es el centro, a el semieje mayor, y b el semieje menor.
La distancia entre el centro y uno de los vértices principales es a:
\(a = 6 - 2 = 4 → a^2 = 4^2 = 16\)
La distancia entre el centro y uno de los focos es c:
\(c = 5 - 2 = 3 → c^2 = 3^2 = 9\)
La relación entre a, b, y c en una elipse es:
\(c^2 = a^2 - b^2 → b^2 = a^2 - c^2\)
Sustituyendo los valores:
\(b^2 = 16 - 9 = 7 → b = \sqrt{7}\)
Sustituyendo los valores de \(a^2 = 16, b^2 = 7,\) y el centro \((h, k) = (2, 4),\) obtenemos la ecuación de la elipse:
\(\dfrac{(x-2)^2}{16}+\dfrac{(y-4)^2}{7}=1\)
Elementos de la elipse
- Centro: (2, 4)
- Focos: F(5, 4) y F'(-1, 4)
- Semiejes: \(a=4, b=\sqrt{7}\)
- Vértices principales: V(6, 4) y V'(-2, 4)
- Vértices secundarios: están a una distancia \(b=\sqrt{7}\) arriba y abajo del centro: \((2, 4+\sqrt{7})\) y \((2, 4-\sqrt{7}).\)
- Distancia focal: \(2c = 2 · 3 = 6\)
- Lado recto: \(L_R = \dfrac{2b^2}{a} = \dfrac{2 · 7}{4} = \dfrac{14}{4} = 3,5\)
- Excentricidad: \(e = \dfrac{c}{a} = \dfrac{3}{4} = 0,75\)
Solución del ejercicio 8
Datos iniciales:
- Centro: C(7, -2)
- Eje mayor: 2a = 8
- Eje menor: 2b = 4
- El eje focal es paralelo al eje x, lo que indica que la elipse está orientada horizontalmente.
El eje mayor tiene longitud 8, por lo que el semieje mayor es:
\(a=\dfrac{8}{2}=4\)
El eje menor tiene longitud 4, por lo que el semieje menor es:
\(b=\dfrac{4}{2}=2\)
La relación entre a, b, y c en una elipse es:
\(c^2=a^2-b^2\)
Sustituyendo los valores:
\(c^2=4^2-2^2=16-4=12 → c=\sqrt{12}=2\sqrt{3}\)
Dado que la elipse tiene el eje mayor paralelo al eje x y el centro está en C(7, -2), la ecuación canónica de la elipse será:
\(\dfrac{(x-7)^2}{4^2}+\dfrac{(y+2)^2}{2^2}=1\)
Lo que se simplifica a:
\(\dfrac{(x-7)^2}{16}+\dfrac{(y+2)^2}{4}=1\)
Elementos de la elipse
- Centro: (7, -2)
- Focos: están a una distancia \(c=2\sqrt{3}\) a la izquierda y derecha del centro: \((7+2\sqrt{3},-2)\) y \((7-2\sqrt{3},-2)\)
- Semiejes: a = 4, b = 2
- Vértices principales: \((7+4,-2)=(11,-2)\) y \((7-4,-2)=(3,-2)\)
- Vértices secundarios: están a una distancia b = 2 arriba y abajo del centro: \((7,-2+2)=(7, 0)\) y \((7,-2-2)=(7,-4)\)
- Distancia focal: \(2c=2 \cdot 2\sqrt{3}=4\sqrt{3}\)
- Lado recto: \(L_R=\dfrac{2b^2}{a}=\dfrac{2 \cdot 4}{4}=2\)
- Excentricidad: \(e=\dfrac{c}{a}=\dfrac{2\sqrt{3}}{4}=\dfrac{\sqrt{3}}{2} \approx 0,866\)
Solución del ejercicio 9
Datos iniciales:
- Vértices principales: (-4, 5) y (16, 5)
- Excentricidad: e = 4/5
El centro de la elipse es el punto medio entre los vértices principales:
\(\text{Centro}=\left(\dfrac{-4+16}{2}, \dfrac{5+5}{2}\right)=(6, 5)\)
Los vértices comparten la misma coordenada y, por lo que la elipse está orientada horizontalmente. La ecuación canónica de la elipse será:
\(\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1\)
donde (h, k) es el centro, a es el semieje mayor, y b el semieje menor.
La distancia entre el centro y uno de los vértices principales es a:
\(a=16-6=10 → a^2=10^2=100\)
Sabemos que la excentricidad e está relacionada con a y c mediante la fórmula:
\(e=\dfrac{c}{a}\)
Sustituyendo \(e=\dfrac{4}{5}\) y \(a=10:\)
\(\dfrac{4}{5}=\dfrac{c}{10} → c=\dfrac{4}{5} \cdot 10=8\)
La relación entre a, b, y c en una elipse es:
\(c^2=a^2-b^2 → b^2=a^2-c^2\)
Sustituyendo los valores:
\(b^2=100-8^2=100-64=36 → b=6\)
Sustituyendo los valores de \(a^2=100, b^2=36,\) y el centro \((h, k)=(6, 5),\) obtenemos la ecuación de la elipse:
\(\dfrac{(x-6)^2}{100}+\dfrac{(y-5)^2}{36}=1\)
Elementos de la elipse
- Centro: (6, 5)
- Focos: están a una distancia c = 8 a la izquierda y derecha del centro: \((6+8, 5)=(14, 5)\) y \((6-8, 5)=(-2, 5)\)
- Semiejes: a = 10, b = 6
- Vértices principales: (-4, 5) y (16, 5)
- Vértices secundarios: están a una distancia b = 6 arriba y abajo del centro: \((6, 5+6)=(6, 11)\) y \((6, 5-6)=(6,-1)\)
- Distancia focal: \(2c=2 \cdot 8=16\)
- Lado recto: \(L_R=\dfrac{2b^2}{a}=\dfrac{2 \cdot 36}{10}=\dfrac{72}{10}=7,2\)
- Excentricidad: \(e=4/5=0,8\)
Solución del ejercicio 10
Datos iniciales:
- Excentricidad: e = 2/3
- Focos: (0, 0) y (0,-4)
El centro de la elipse es el punto medio entre los focos:
\(\text{Centro}=\left(\dfrac{0+0}{2}, \dfrac{0+(-4)}{2}\right)=(0,-2)\)
Como los focos comparten la misma coordenada x, la elipse tiene su eje mayor paralelo al eje y. La ecuación canónica de la elipse será:
\(\dfrac{(x-h)^2}{b^2}+\dfrac{(y-k)^2}{a^2}=1\)
donde \((h, k)=(0,-2)\) es el centro, a es el semieje mayor, y b es el semieje menor.
La distancia entre el centro y cualquiera de los focos es c:
\(c=|-2-0|=2\)
Sabemos que la excentricidad e está relacionada con a y c:
\(e=\dfrac{c}{a}\)
Sustituyendo \(e=\dfrac{2}{3}\) y \(c=2:\)
\(\dfrac{2}{3}=\dfrac{2}{a} → a=3\)
Por lo tanto:
\(a^2=3^2=9\)
La relación entre a, b, y c en una elipse es:
\(c^2=a^2-b^2 → b^2=a^2-c^2\)
Sustituyendo los valores:
\(b^2=9-2^2=9-4=5\)
Sustituyendo los valores de \(a^2=9, b^2=5,\) y el centro \((h, k)=(0, -2),\) obtenemos la ecuación de la elipse:
\(\dfrac{x^2}{5}+\dfrac{(y+2)^2}{9}=1\)
Elementos de la elipse
- Centro: (0, -2)
- Focos: (0, 0) y (0,-4)
- Semiejes: \(a=3, b=\sqrt{5} \approx 2,24\)
- Vértices principales: están a una distancia a = 3 arriba y abajo del centro: \((0,-2+3)=(0, 1)\) y \((0,-2-3)=(0, -5)\)
- Vértices secundarios: están a una distancia \(b=\sqrt{5}\) a la izquierda y derecha del centro: \((0+\sqrt{5},-2) \approx (2,24,-2)\) y \((0-\sqrt{5},-2) \approx (-2,24,-2)\)
- Distancia focal: \(2c=2 \cdot 2=4\)
- Lado recto: \(L_R=\dfrac{2b^2}{a}=\dfrac{2 \cdot 5}{3}=\dfrac{10}{3} \approx 3,33\)
- Excentricidad: \(e=\dfrac{c}{a}=\dfrac{2}{3} \approx 0,67\)
Determinar los elementos de una elipse a partir de su ecuación
Los siguientes ejercicios consisten en hallar los elementos de una elipse a partir de su ecuación canónica o su ecuación general.
Conocer las cantidades a (semieje mayor), b (semieje menor) y c (semidistancia focal) es fundamental para resolver este tipo de ejercicios, ya que todos los elementos pueden obtenerse con esos valores:
| Ecuación | Eje mayor | Centro | Focos | Vértices |
|---|---|---|---|---|
| \(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\) | Sobre el eje x | (0, 0) | (±c, 0) | (±a, 0) (0, ±b) |
| \(\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1\) | Sobre el eje y | (0, 0) | (0, ±c) | (0, ±a) (±b, 0) |
| \(\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1\) | Paralelo al eje x | (h, k) | (h ± c, k) | (h ± a, k) (h, k ± b) |
| \(\dfrac{(x-h)^2}{b^2}+\dfrac{(y-k)^2}{a^2}=1\) | Paralelo al eje y | (h, k) | (h, k ± c) | (h, k ± a) (h ± b, k) |
La semidistancia focal se calcula como \(c=\sqrt{a^2-b^2}.\) Si no se tiene la ecuación en forma canónica, es necesario manipularla algebraicamente para conseguirlo.
El lado recto y la excentricidad se calculan de la misma forma para cualquier elipse:
Lado recto: \(L_R=\dfrac{2b^2}{a}\)
Excentricidad: \(e=\dfrac{c}{a}~~\) o \(~~e=\dfrac{\sqrt{a^2-b^2}}{a}\)
Ejercicio: determinar los elementos de las siguientes elipses: centro, focos, semiejes, vértices principales y secundarios, lados rectos y excentricidad. Luego graficar.
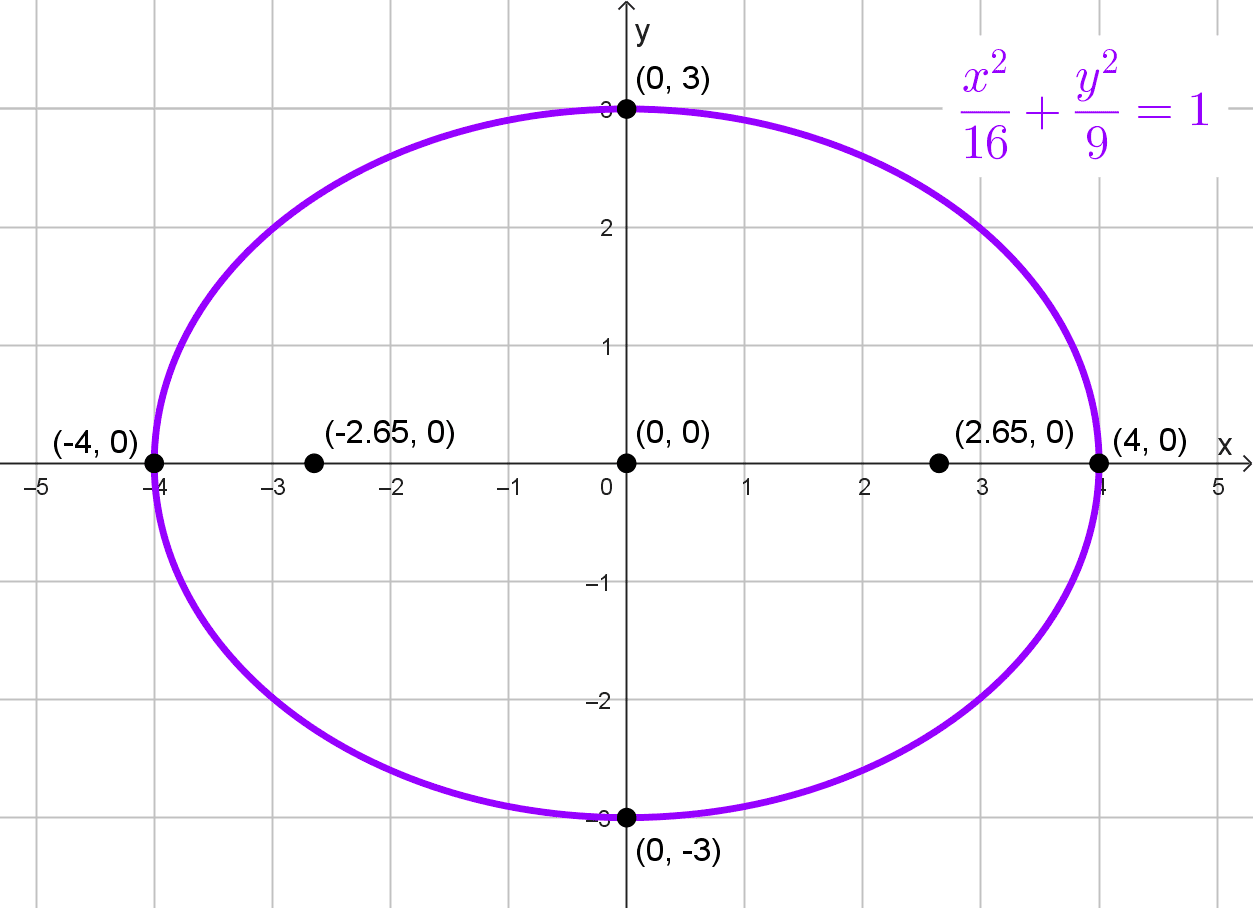
- \(\dfrac{x^2}{16}+\dfrac{y^2}{9}=1\)
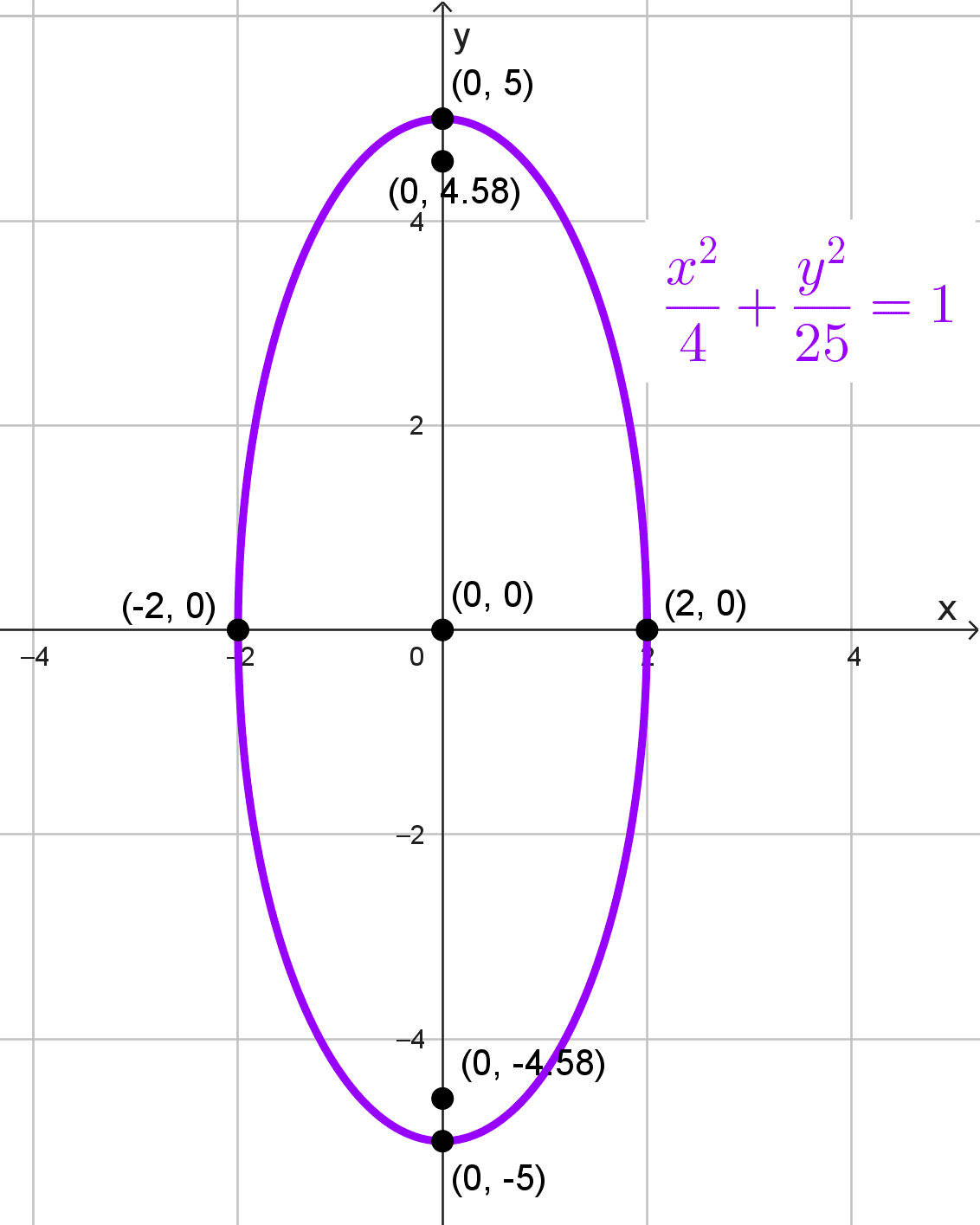
- \(\dfrac{x^2}{4}+\dfrac{y^2}{25}=1\)
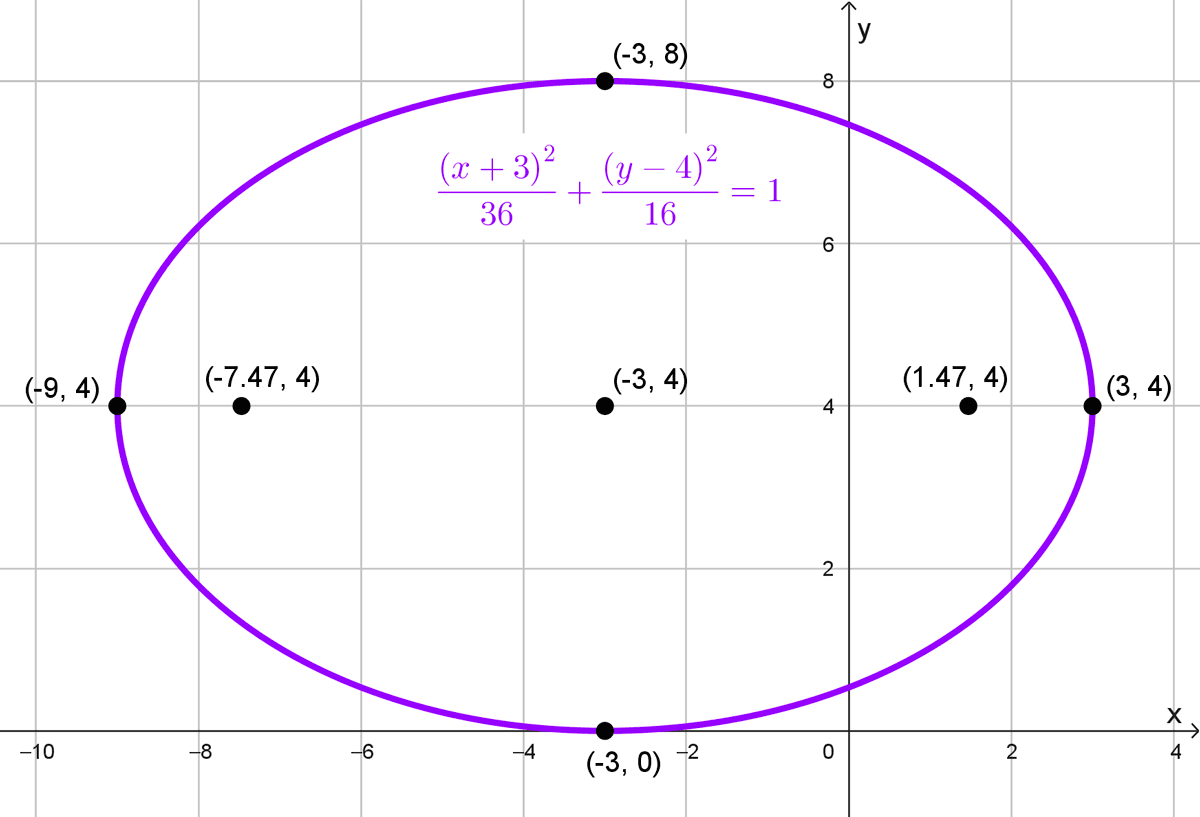
- \(\dfrac{(x+3)^2}{36}+\dfrac{(y-4)^2}{16}=1\)
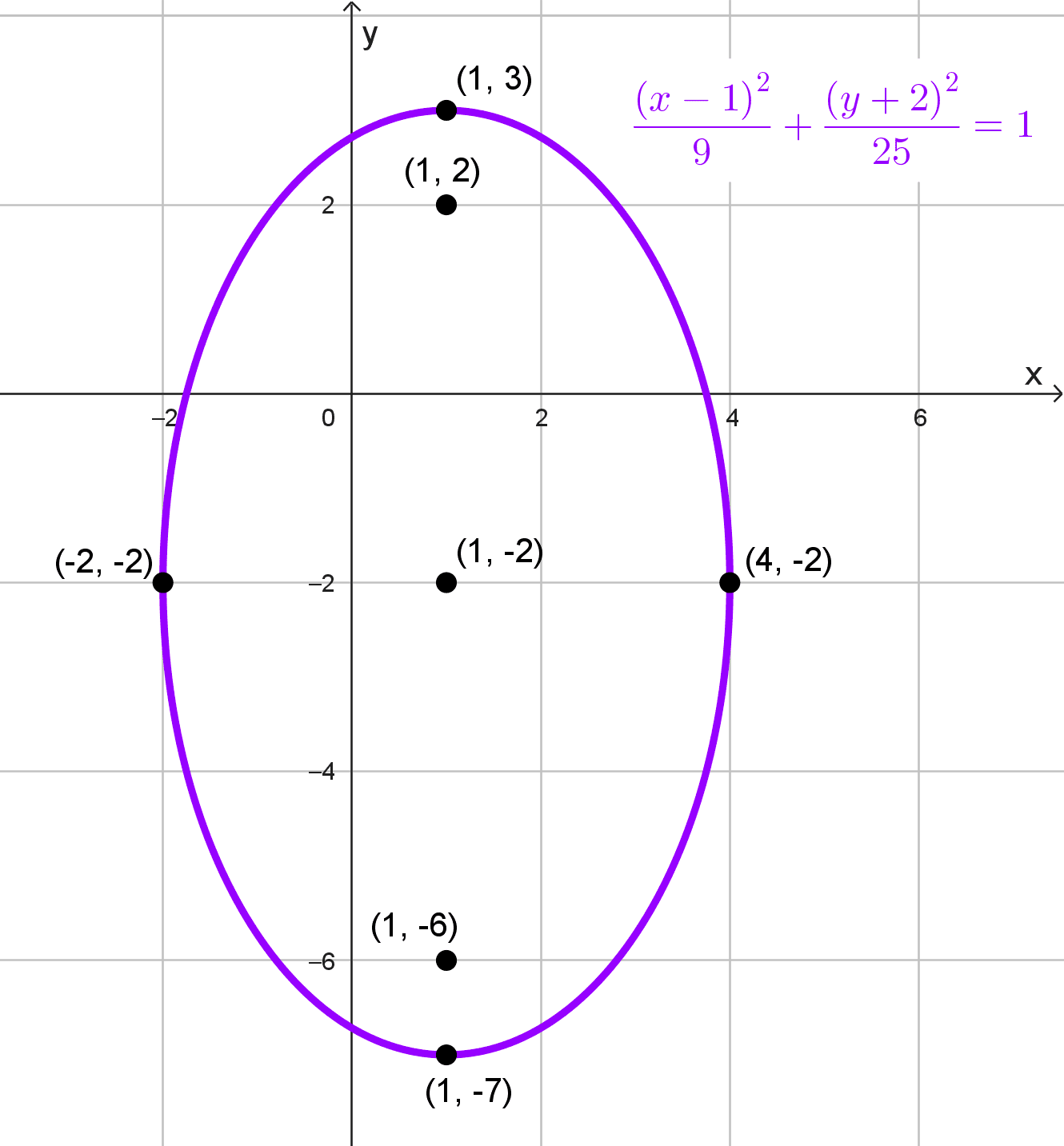
- \(\dfrac{(x-1)^2}{9}+\dfrac{(y+2)^2}{25}=1\)
- \(\dfrac{(x-1)^2}{36}+\dfrac{(y-\frac{5}{2})^2}{49}=1\)
- \(\dfrac{x^2}{25}+\dfrac{(y+5)^2}{16}=1\)
- \(3x^2+4y^2=12\)
- \(25x^2+16y^2=400\)
- \(4x^2+9y^2-16x-32=0\)
- \(16x^2+9y^2-64x-54y+1=0\)
- \(8x^2+25y^2-48x+50y+47=0\)
- \(36x^2+25y^2+72x-200y-464=0\)
Soluciones
Solución del ejercicio 1
Ecuación: \(\dfrac{x^2}{16}+\dfrac{y^2}{9}=1\)
Comenzamos identificando que el centro es el origen de coordenadas (0, 0) y la elipse es horizontal (el denominador más grande lo tiene x2), ya que la ecuación está en forma canónica y así lo indica.
Las longitudes de los semiejes pueden obtenerse desde los denominadores de las variables, el más grande corresponde al cuadrado del semieje mayor y el más pequeño al cuadrado del semieje menor:
\(a^2=16→a=\sqrt{16}=4\)
\(b^2=9→b=\sqrt{9}=3\)
Usando la relación fundamental en la elipse, calculamos la semidistancia focal, la cual nos permitirá obtener los focos:
\(c=\sqrt{a^2-b^2}=\sqrt{16-9}=\sqrt{7}\)
Como la elipse es horizontal, los focos se encuentran a una distancia \(c=\sqrt{7}\) a la izquierda y derecha del centro: \((-\sqrt{7}, 0)\) y \((\sqrt{7}, 0).\)
Los vértices principales se encuentran a una distancia a = 4 del centro, a la izquierda y la derecha: (-4, 0) y (4, 0). Los vértice secundarios están a una distancia b = 3 arriba y abajo del centro: (0, 3) y (0, -3)
Finalmente, calculamos el lado recto y la excentricidad:
\(L_R=\dfrac{2b^2}{a}=\dfrac{2\cdot 9}{4}=4,5\)
\(e=\dfrac{c}{a}=\dfrac{\sqrt{7}}{4}≈0,66\)
Elementos de la elipse:
- Focos: \((-\sqrt{7}, 0)\) y \((\sqrt{7}, 0)\)
- Centro: (0, 0)
- Semiejes: a = 4, b = 3
- Distancia focal: \(2c = 2\sqrt{7}\)
- Vértices principales: (-4, 0) y (4, 0)
- Vértices secundarios: (0, 3) y (0, -3)
- Lado recto: \(L_R=4,5\)
- Excentricidad: \(e≈0,66\)
Solución del ejercicio 2
Ecuación: \(\dfrac{x^2}{4}+\dfrac{y^2}{25}=1\)
La ecuación está en forma canónica y podemos leer que el centro es (0, 0). La elipse es vertical, porque el denominador mayor está bajo \(y^2.\)
Obtenemos las longitudes de los semiejes:
\(a^2=25 → a=\sqrt{25}=5\)
\(b^2=4 → b=\sqrt{4}=2\)
La semidistancia focal se calcula mediante la relación fundamental en la elipse:
\(c=\sqrt{a^2-b^2}=\sqrt{25-4}=\sqrt{21}\)
Dado que la elipse es vertical, los focos se encuentran a una distancia \(c=\sqrt{21}\) arriba y abajo del centro: \((0,-\sqrt{21})\) y \((0, \sqrt{21}).\)
Los vértices principales están a una distancia a = 5 arriba y abajo del centro: (0, -5) y (0, 5). Los vértices secundarios se encuentran a una distancia b = 2 a la izquierda y derecha del centro: (-2, 0) y (2, 0)
El lado recto de la elipse se calcula como:
\(L_R=\dfrac{2b^2}{a}=\dfrac{2 \cdot 4}{5}=\dfrac{8}{5}=1,6\)
La excentricidad se obtiene mediante la fórmula:
\(e=\dfrac{c}{a}=\dfrac{\sqrt{21}}{5}≈0,92\)
Elementos de la elipse:
- Focos: \((0,-\sqrt{21})\) y \((0, \sqrt{21})\)
- Centro: (0, 0)
- Semiejes: a = 5, b = 2
- Distancia focal: \(2c=2\sqrt{21}\)
- Vértices principales: (0, -5) y (0, 5)
- Vértices secundarios: (-2, 0) y (2, 0)
- Lado recto: \(L_R=1,6\)
- Excentricidad: \(e≈0,92\)
Solución del ejercicio 3
Ecuación: \(\dfrac{(x+3)^2}{36}+\dfrac{(y-4)^2}{16}=1\)
El centro de la elipse es (-3, 4), y la elipse es horizontal, porque el denominador mayor está bajo \((x+3)^2.\)
Longitudes de los semiejes:
\(a^2=36 → a=\sqrt{36}=6\)
\(b^2=16 → b=\sqrt{16}=4\)
Cálculo de la semidistancia focal:
\(c=\sqrt{a^2-b^2}=\sqrt{36-16}=\sqrt{20}=2\sqrt{5}\)
Los focos están a una distancia \(c=2\sqrt{5}\) a la izquierda y derecha del centro: \((-3-2\sqrt{5}, 4)\) y \((-3+2\sqrt{5}, 4).\)
Vértices principales: \((-3-6, 4)=(-9, 4)\) y \((-3+6, 4)=(3, 4)\)
Vértices secundarios: \((-3, 4-4)=(-3, 0)\) y \((-3, 4+4)=(-3, 8)\)
Lado recto: \(L_R=\dfrac{2b^2}{a}=\dfrac{2 \cdot 16}{6}=\dfrac{32}{6}≈5,33\)
Excentricidad: \(e=\dfrac{c}{a}=\dfrac{2\sqrt{5}}{6}=\dfrac{\sqrt{5}}{3}≈0,75\)
Elementos de la elipse:
- Focos: \((-3-2\sqrt{5}, 4)\) y \((-3+2\sqrt{5}, 4)\)
- Centro: (-3, 4)
- Semiejes: a=6, b=4
- Distancia focal: \(2c=4\sqrt{5}\)
- Vértices principales: (-9, 4) y (3, 4)
- Vértices secundarios: (-3, 0) y (-3, 8)
- Lado recto: \(L_R≈5,33\)
- Excentricidad: \(e≈0,75\)
Solución del ejercicio 4
Ecuación: \(\dfrac{(x-1)^2}{9}+\dfrac{(y+2)^2}{25}=1\)
El centro de la elipse es (1, -2), y la elipse es vertical, porque el denominador mayor está bajo \((y+2)^2.\)
Longitudes de los semiejes
\(a^2=25 → a=\sqrt{25}=5\)
\(b^2=9 → b=\sqrt{9}=3\)
Cálculo de la semidistancia focal:
\(c=\sqrt{a^2-b^2}=\sqrt{25-9}=\sqrt{16}=4\)
Los focos están a una distancia c = 4 arriba y abajo del centro: \((1, -2-4)=(1, -6)\) y \((1, -2+4)=(1, 2)\)
Vértices principales: \((1,-2-5)=(1,-7)\) y \((1,-2+5)=(1, 3)\)
Vértices secundarios: \((1-3,-2)=(-2,-2)\) y \((1+3,-2)=(4,-2)\)
Lado recto: \(L_R=\dfrac{2b^2}{a}=\dfrac{2 \cdot 9}{5}=\dfrac{18}{5}=3,6\)
Excentricidad: \(e=\dfrac{c}{a}=\dfrac{4}{5}=0,8\)
Elementos de la elipse:
- Focos: (1, -6) y (1, 2)
- Centro: (1, -2)
- Semiejes: a = 5, b = 3
- Distancia focal: 2c=8
- Vértices principales: (1, -7) y (1, 3)
- Vértices secundarios: (-2, -2) y (4, -2)
- Lado recto: \(L_R=3,6\)
- Excentricidad: \(e=0,8\)
Solución del ejercicio 5
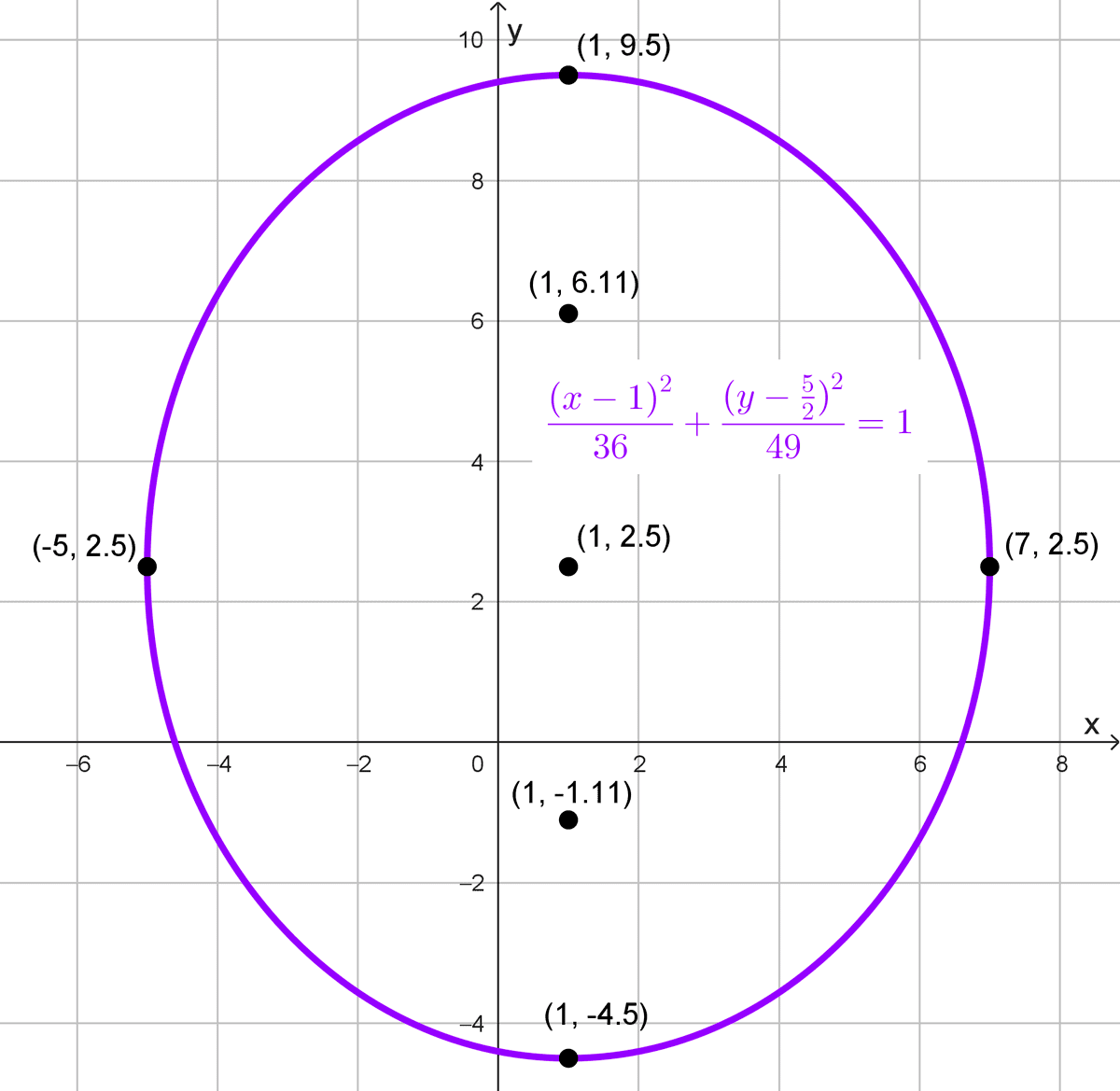
Ecuación: \(\dfrac{(x-1)^2}{36}+\dfrac{(y-\frac{5}{2})^2}{49}=1\)
El centro de la elipse es (1, 5/2), y la elipse es vertical, porque el denominador mayor está bajo \(\left(y-\dfrac{5}{2}\right)^2.\)
Longitudes de los semiejes:
\(a^2=49 → a=\sqrt{49}=7\)
\(b^2=36 → b=\sqrt{36}=6\)
Cálculo de la semidistancia focal:
\(c=\sqrt{a^2-b^2}=\sqrt{49-36}=\sqrt{13}\)
Los focos están a una distancia \(c=\sqrt{13}\) arriba y abajo del centro:
\(\left(1, \dfrac{5}{2}-\sqrt{13}\right) y \left(1, \dfrac{5}{2}+\sqrt{13}\right)\)
Vértices principales:
\(\left(1, \dfrac{5}{2}-7\right)=\left(1,-\dfrac{9}{2}\right)\)
\(\left(1, \dfrac{5}{2}+7\right)=\left(1, \dfrac{19}{2}\right)\)
Vértices secundarios:
\(\left(1-6, \dfrac{5}{2}\right)=\left(-5, \dfrac{5}{2}\right)\)
\(\left(1+6, \dfrac{5}{2}\right)=\left(7, \frac{5}{2}\right)\)
Lado recto:
\(L_R=\dfrac{2b^2}{a}=\dfrac{2 \cdot 36}{7}=\dfrac{72}{7}≈10,29\)
Excentricidad:
\(e=\dfrac{c}{a}=\dfrac{\sqrt{13}}{7}≈0,51\)
Elementos de la elipse:
- Focos: \(\left(1, \dfrac{5}{2}-\sqrt{13}\right)\) y \(\left(1, \dfrac{5}{2}+\sqrt{13}\right)\)
- Centro: \((1, 5/2)\)
- Semiejes: a = 7, b = 6
- Distancia focal: \(2c=2\sqrt{13}\)
- Vértices principales: \(\left(1,-\dfrac{9}{2}\right)\) y \(\left(1, \dfrac{19}{2}\right)\)
- Vértices secundarios: \(\left(-5, \dfrac{5}{2}\right)\) y \(\left(7, \dfrac{5}{2}\right)\)
- Lado recto: \(L_R≈10,29\)
- Excentricidad: \(e≈0,51\)
Solución del ejercicio 6
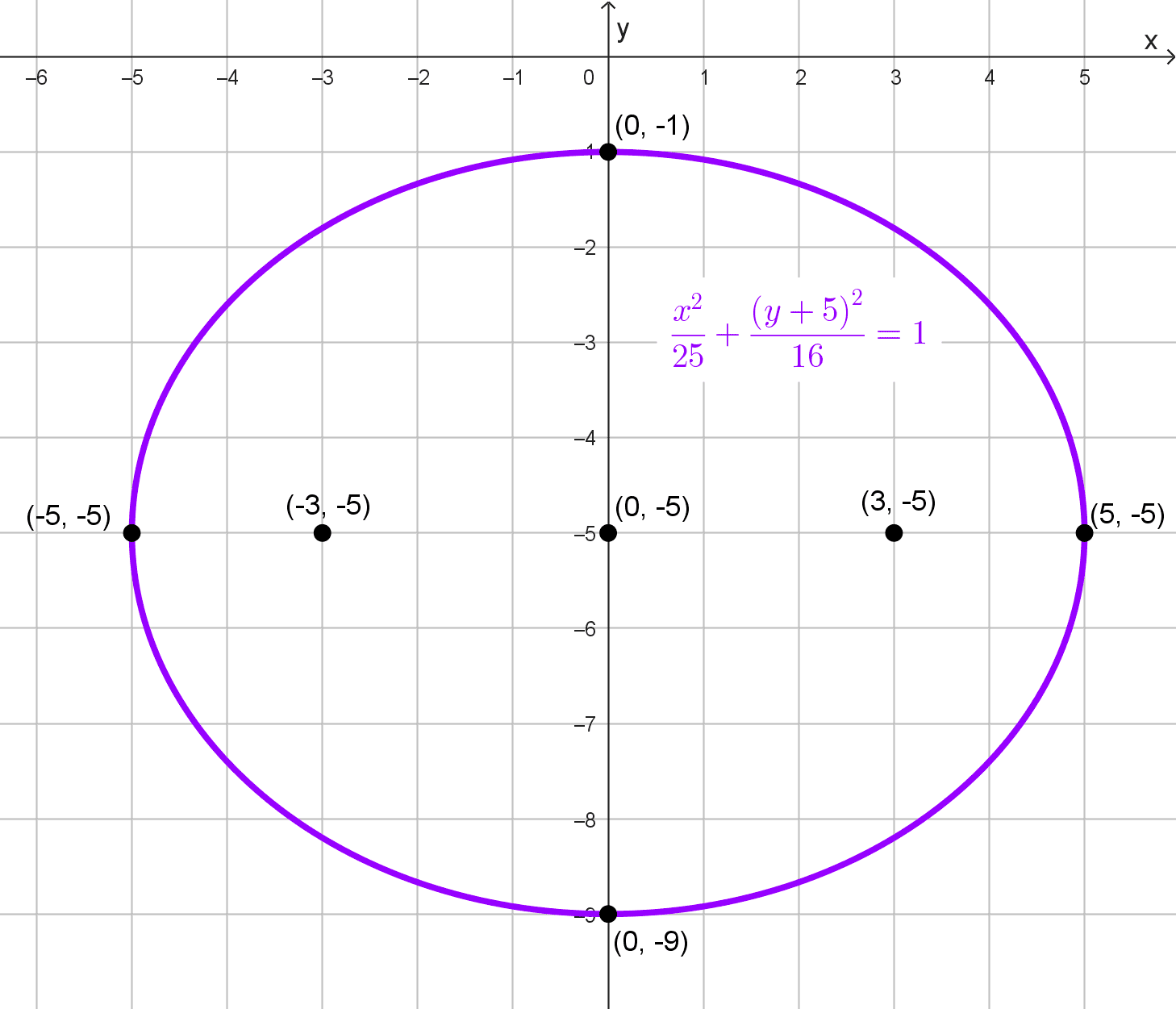
Ecuación: \(\dfrac{x^2}{25}+\dfrac{(y+5)^2}{16}=1\)
El centro de la elipse es (0, -5), y la elipse es horizontal, porque el denominador mayor está bajo \(x^2.\)
Longitudes de los semiejes
\(a^2=25 → a=\sqrt{25}=5\)
\(b^2=16 → b=\sqrt{16}=4\)
Cálculo de la semidistancia focal:
\(c=\sqrt{a^2-b^2}=\sqrt{25-16}=\sqrt{9}=3\)
Los focos están a una distancia c = 3 a la izquierda y derecha del centro: (-3, -5) y (3, -5)
Vértices principales: (-5, -5) y (5, -5)
Vértices secundarios: \((0, -5-4)=(0, -9)\) y \((0, -5+4)=(0, -1)\)
Lado recto: \(L_R=\dfrac{2b^2}{a}=\dfrac{2 \cdot 16}{5}=\dfrac{32}{5}=6,4\)
Excentricidad: \(e=\dfrac{c}{a}=\dfrac{3}{5}=0,6\)
Elementos de la elipse:
- Focos: (-3, -5) y (3, -5)
- Centro: (0, -5)
- Semiejes: a = 5, b = 4
- Distancia focal: 2c=6
- Vértices principales: (-5, -5) y (5, -5)
- Vértices secundarios: (0, -9) y (0, -1)
- Lado recto: \(L_R=6,4\)
- Excentricidad: e=0,6
Solución del ejercicio 7
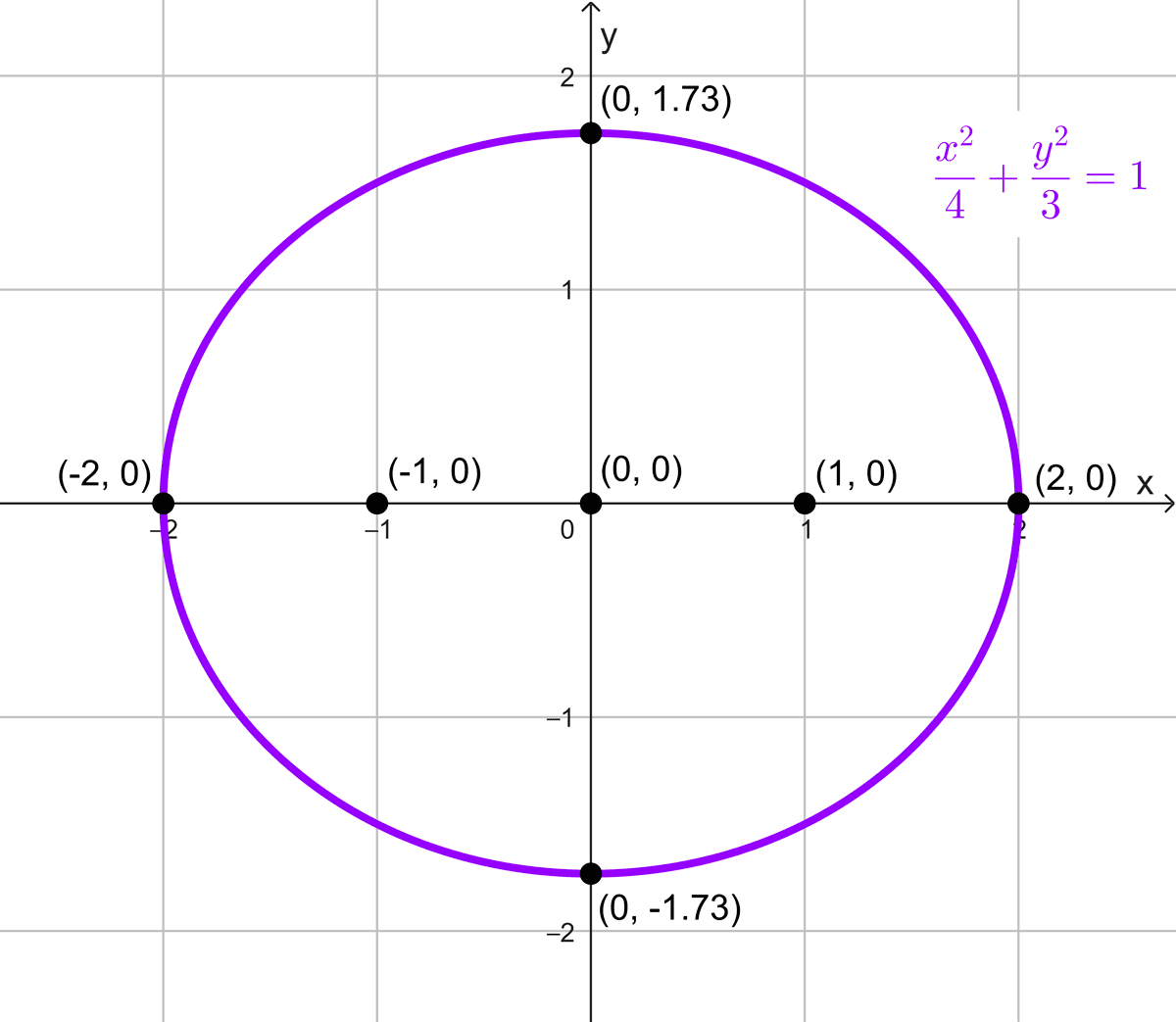
Ecuación: \(3x^2+4y^2=12\)
Esta ecuación no está en la forma canónica, sin embargo podemos manipularla algebraicamente para que lo esté (véase los ejercicios de cómo pasar de la ecuación general a la canónica más abajo). Realizando esto, se obtiene una expresión equivalente:
\(\dfrac{x^2}{4}+\dfrac{y^2}{3}=1\)
El centro de la elipse es (0, 0), y la elipse es horizontal, porque el denominador mayor está bajo \(x^2.\)
Longitudes de los semiejes
\(a^2=4 → a=\sqrt{4}=2\)
\(b^2=3 → b=\sqrt{3}\)
Cálculo de la semidistancia focal
\(c=\sqrt{a^2-b^2}=\sqrt{4-3}=\sqrt{1}=1\)
Los focos están a una distancia c = 1 a la izquierda y derecha del centro: (-1, 0) y (1, 0)
Vértices principales: (-2, 0) y (2, 0)
Vértices secundarios: \((0,-\sqrt{3})\) y \((0, \sqrt{3})\)
Lado recto: \(L_R=\dfrac{2b^2}{a}=\dfrac{2 \cdot 3}{2}=3\)
Excentricidad: \(e=\dfrac{c}{a}=\dfrac{1}{2}=0,5\)
Elementos de la elipse:
- Focos: (-1, 0) y (1, 0)
- Centro: (0, 0)
- Semiejes: \(a=2, b=\sqrt{3}\)
- Distancia focal: 2c=2
- Vértices principales: (-2, 0) y (2, 0)
- Vértices secundarios: \((0,-\sqrt{3})\) y \((0, \sqrt{3})\)
- Lado recto: \(L_R=3\)
- Excentricidad: \(e=0,5\)
Solución del ejercicio 8
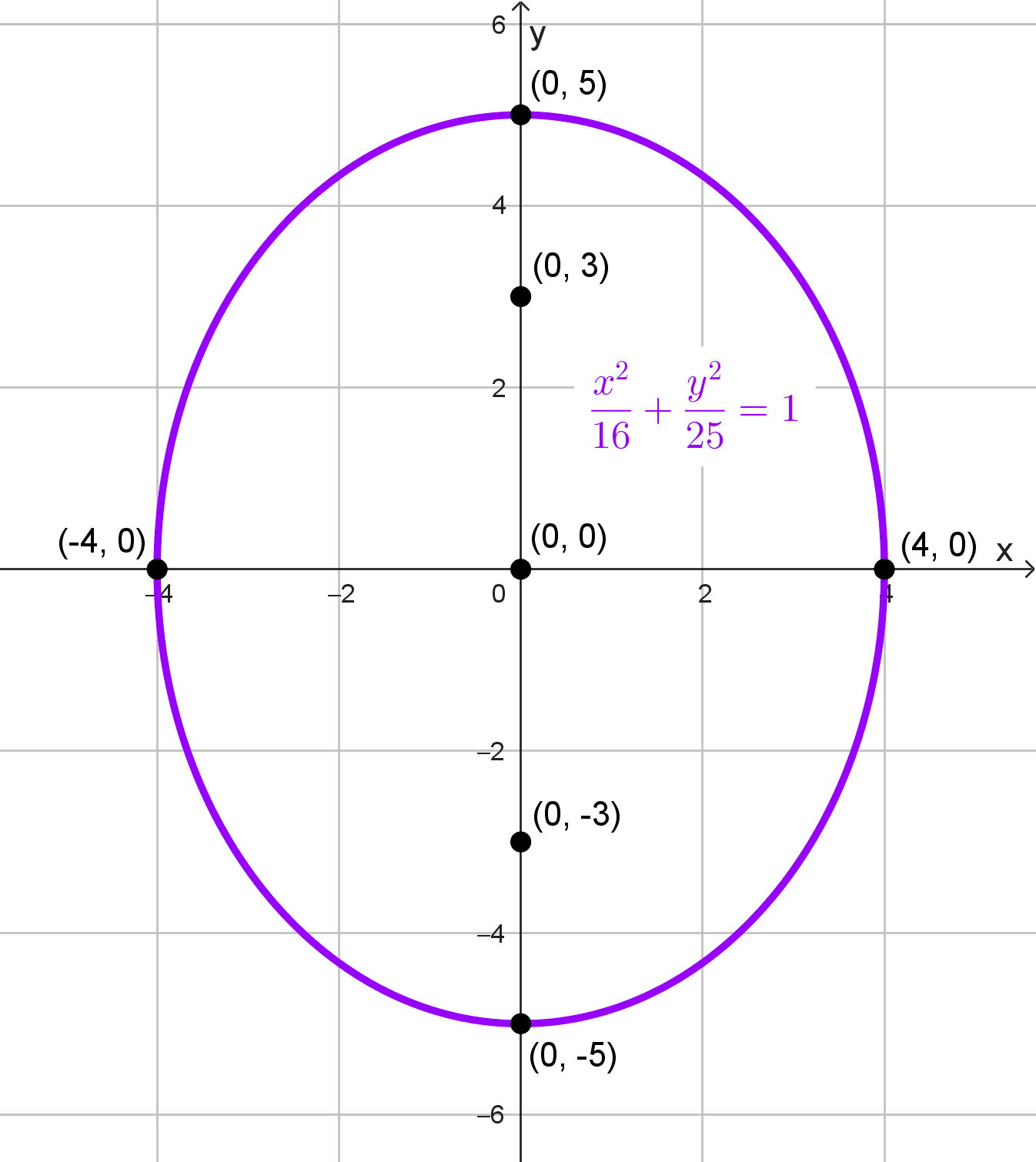
Ecuación: \(25x^2+16y^2=400\)
Reacomodando se obtiene la forma canónica:
\(\dfrac{x^2}{16}+\dfrac{y^2}{25}=1\)
El centro de la elipse es (0, 0), y la elipse es vertical, porque el denominador mayor está bajo \(y^2.\)
Longitudes de los semiejes:
\(a^2=25 → a=\sqrt{25}=5\)
\(b^2=16 → b=\sqrt{16}=4\)
Cálculo de la semidistancia focal:
\(c=\sqrt{a^2-b^2}=\sqrt{25-16}=\sqrt{9}=3\)
Los focos están a una distancia c = 3 arriba y abajo del centro: (0, -3) y (0, 3)
Vértices principales: (0, -5) y (0, 5)
Vértices secundarios: (-4, 0) y (4, 0)
Lado recto: \(L_R=\dfrac{2b^2}{a}=\dfrac{2 \cdot 16}{5}=\dfrac{32}{5}=6,4\)
Excentricidad: \(e=\dfrac{c}{a}=\dfrac{3}{5}=0,6\)
Elementos de la elipse:
- Focos: (0, -3) y (0, 3)
- Centro: (0, 0)
- Semiejes: a = 5, b = 4
- Distancia focal: 2c=6
- Vértices principales: (0, -5) y (0, 5)
- Vértices secundarios: (-4, 0) y (4, 0)
- Lado recto: \(L_R=6,4\)
- Excentricidad: e=0,6
Solución del ejercicio 9
Ecuación: \(4x^2+9y^2-16x-32=0\)
Completando los cuadrados se obtiene la forma reducida (véase los ejercicios de cómo pasar de la ecuación general a la canónica):
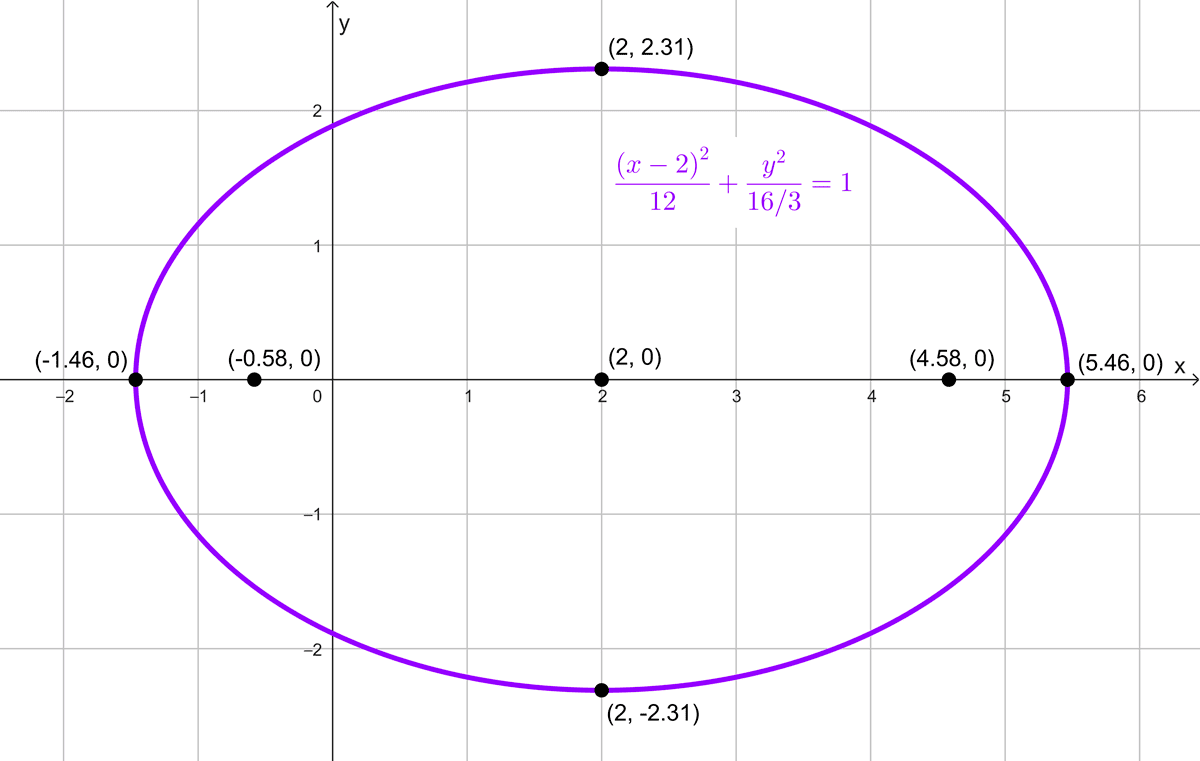
\(\dfrac{(x-2)^2}{12}+\dfrac{y^2}{16/3}=1\)
El centro de la elipse es (2, 0), y la elipse es horizontal, porque el denominador mayor está bajo \((x-2)^2.\)
Longitudes de los semiejes
\(a^2=12 → a=\sqrt{12}=2\sqrt{3}\)
\(b^2=\dfrac{16}{3} → b=\sqrt{\dfrac{16}{3}}=\dfrac{4}{\sqrt{3}}=\dfrac{4\sqrt{3}}{3}\)
Cálculo de la semidistancia focal:
\(c=\sqrt{a^2-b^2}=\sqrt{12-\dfrac{16}{3}}=\sqrt{\dfrac{36}{3}-\dfrac{16}{3}}=\sqrt{\dfrac{20}{3}}=\dfrac{\sqrt{60}}{3}=\dfrac{2\sqrt{15}}{3}\)
Los focos están a una distancia \(c=\dfrac{2\sqrt{15}}{3}\) a la izquierda y derecha del centro:
\(\left(2-\dfrac{2\sqrt{15}}{3}, 0\right)\) y \(\left(2+\dfrac{2\sqrt{15}}{3}, 0\right)\)
Vértices principales:
\((2-2\sqrt{3}, 0)\)
\((2+2\sqrt{3}, 0)\)
Vértices secundarios:
\(\left(2,-\dfrac{4\sqrt{3}}{3}\right)\)
\(\left(2, \dfrac{4\sqrt{3}}{3}\right)\)
Lado recto:
\(L_R=\dfrac{2b^2}{a}=\dfrac{2 \cdot \dfrac{16}{3}}{2\sqrt{3}}=\dfrac{\dfrac{32}{3}}{2\sqrt{3}}=\dfrac{16}{3\sqrt{3}}=\dfrac{16\sqrt{3}}{9}\)
Excentricidad:
\(e=\dfrac{c}{a}=\dfrac{\dfrac{2\sqrt{15}}{3}}{2\sqrt{3}}=\dfrac{\sqrt{15}}{3\sqrt{3}}=\dfrac{\sqrt{5}}{3}≈0,75\)
Elementos de la elipse:
- Focos: \(\left(2-\dfrac{2\sqrt{15}}{3}, 0\right)\) y \(\left(2+\dfrac{2\sqrt{15}}{3}, 0\right)\)
- Centro: (2, 0)
- Semiejes: \(a=2\sqrt{3}, b=\dfrac{4\sqrt{3}}{3}\)
- Distancia focal: \(2c=\dfrac{4\sqrt{15}}{3}\)
- Vértices principales: \((2-2\sqrt{3}, 0)\) y \((2+2\sqrt{3}, 0)\)
- Vértices secundarios: \(\left(2,-\dfrac{4\sqrt{3}}{3}\right)\) y \(\left(2, \dfrac{4\sqrt{3}}{3}\right)\)
- Lado recto: \(L_R=\dfrac{16\sqrt{3}}{9}\)
- Excentricidad: \(e≈0,75\)
Solución del ejercicio 10
Ecuación: \(16x^2+9y^2-64x-54y+1=0\)
Completando los cuadrados y reacomodando la expresión, se obtiene la forma canónica:
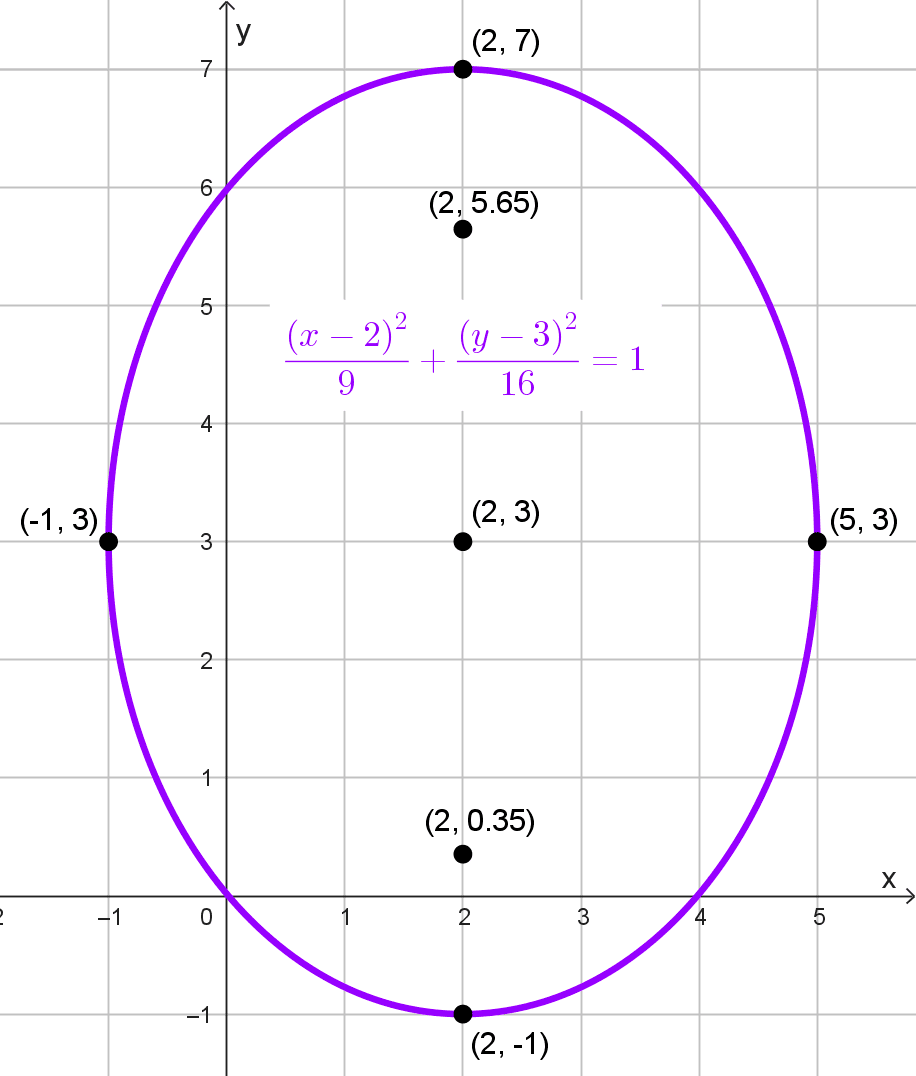
\(\dfrac{(x-2)^2}{9}+\dfrac{(y-3)^2}{16}=1\)
El centro de la elipse es (2, 3), y la elipse es vertical, porque el denominador mayor está bajo \((y-3)^2.\)
Longitudes de los semiejes
\(a^2=16 → a=\sqrt{16}=4\)
\(b^2=9 → b=\sqrt{9}=3\)
Cálculo de la semidistancia focal:
\(c=\sqrt{a^2-b^2}=\sqrt{16-9}=\sqrt{7}\)
Los focos están a una distancia \(c=\sqrt{7}\) arriba y abajo del centro:
\((2, 3-\sqrt{7})\) y \((2, 3+\sqrt{7})\)
Vértices principales:
\((2, 3-4)=(2, -1)\)
\((2, 3+4)=(2, 7)\)
Vértices secundarios:
\((2-3, 3)=(-1, 3)\)
\((2+3, 3)=(5, 3)\)
Lado recto: \(L_R=\dfrac{2b^2}{a}=\dfrac{2 \cdot 9}{4}=\dfrac{18}{4}=4,5\)
Excentricidad: \(e=\dfrac{c}{a}=\dfrac{\sqrt{7}}{4} ≈ 0,66\)
Elementos de la elipse:
- Focos: \((2, 3-\sqrt{7})\) y \((2, 3+\sqrt{7})\)
- Centro: (2, 3)
- Semiejes: a = 4, b = 3
- Distancia focal: \(2c=2\sqrt{7}\)
- Vértices principales: (2, -1) y (2, 7)
- Vértices secundarios: (-1, 3) y (5, 3)
- Lado recto: \(L_R=4,5\)
- Excentricidad: \(e ≈ 0,66\)
Solución del ejercicio 11
Ecuación: \(8x^2+25y^2-48x+50y+47=0\)
Completando los cuadrados se obtiene la forma canónica:
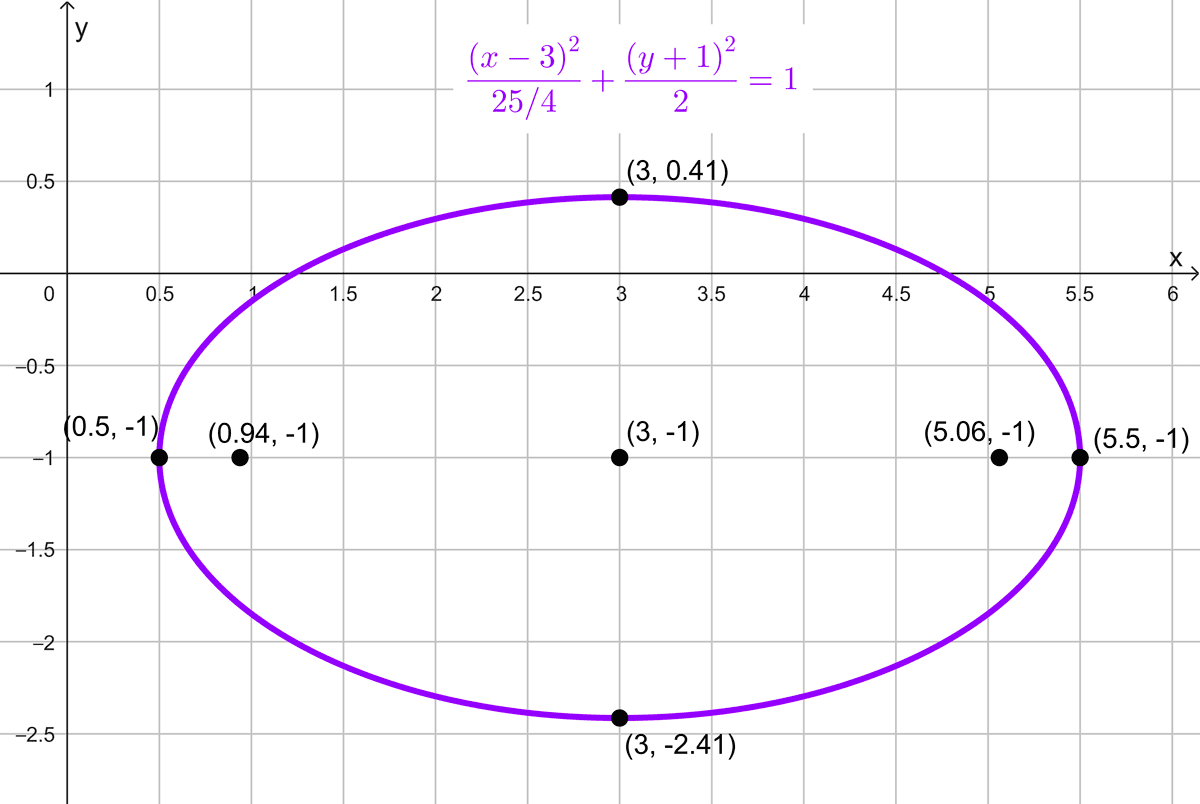
\(\dfrac{(x-3)^2}{25/4}+\dfrac{(y+1)^2}{2}=1\)
El centro de la elipse es (3, -1). Dado que el denominador mayor está bajo \((x-3)^2,\) la elipse es horizontal.
Para calcular los semiejes principales y secundarios:
\(a=\sqrt{\dfrac{25}{4}}=\dfrac{5}{2}=2,5\)
\(b=\sqrt{2}\)
La semidistancia focal se calcula con:
\(c=\sqrt{a^2-b^2}=\sqrt{\dfrac{25}{4}-2}=\sqrt{\dfrac{25}{4}-\dfrac{8}{4}}=\sqrt{\dfrac{17}{4}}=\dfrac{\sqrt{17}}{2}\)
Los focos están ubicados a una distancia \(c=\dfrac{\sqrt{17}}{2}\) a la derecha e izquierda del centro, ya que la elipse es horizontal:
\(\left(3-\dfrac{\sqrt{17}}{2}, -1\right)\) y \(\left(3+\dfrac{\sqrt{17}}{2}, -1\right)\)
Vértices principales:
\((3-2,5; -1)=(0,5; -1)\)
\((3+2,5; -1)=(5,5; -1)\)
Vértices secundarios:
\((3, -1-\sqrt{2})\)
\((3, -1+\sqrt{2})\)
La longitud del lado recto está dada por:
\(L_R=\dfrac{2b^2}{a}=\dfrac{2 \cdot 2}{2,5}=\dfrac{4}{2,5}=1,6\)
La excentricidad se calcula como:
\(e=\dfrac{c}{a}=\dfrac{\dfrac{\sqrt{17}}{2}}{2,5}=\dfrac{\sqrt{17}}{5}≈0,82\)
Elementos de la elipse:
- Centro: (3, -1)
- Focos: \(\left(3-\dfrac{\sqrt{17}}{2}, -1\right)\) y \(\left(3+\dfrac{\sqrt{17}}{2}, -1\right)\)
- Semiejes: \(a=2,5, b=\sqrt{2}\)
- Distancia focal: \(2c=\sqrt{17}\)
- Vértices principales: \((0,5; -1)\) y \((5,5; -1)\)
- Vértices secundarios: \((3, -1-\sqrt{2})\) y \((3, -1+\sqrt{2})\)
- Lado recto: \(L_R=1,6\)
- Excentricidad: \(e≈0,82\)
Solución del ejercicio 12
Ecuación: \(36x^2+25y^2+72x-200y-464=0\)
Luego de completar los cuadrados se obtiene la expresión:
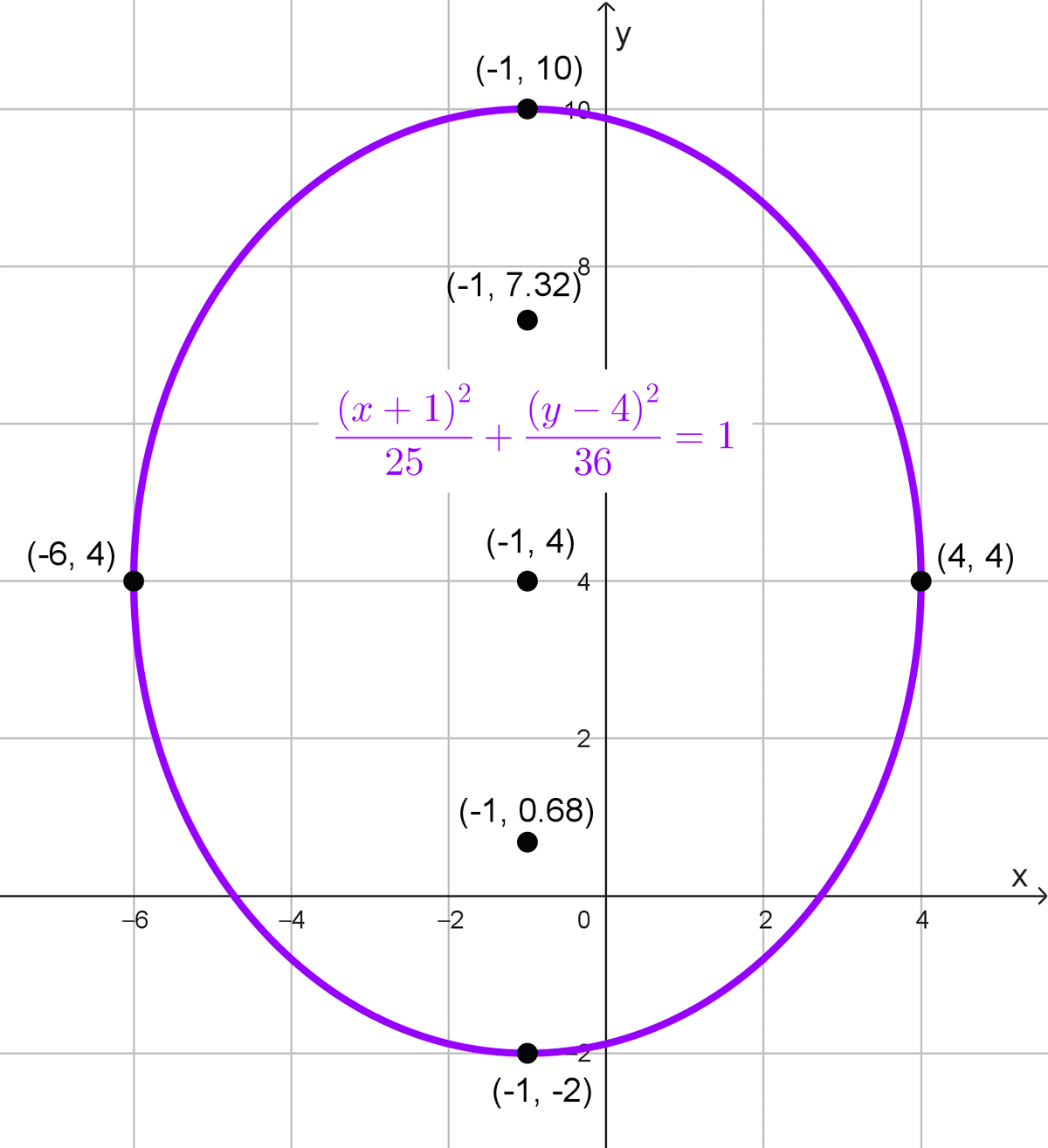
\(\dfrac{(x+1)^2}{25}+\dfrac{(y-4)^2}{36}=1\)
El centro de la elipse es (-1, 4). Dado que el denominador mayor está bajo \((y-4)^2,\) la elipse es vertical.
Para calcular los semiejes principales y secundarios:
\(a=\sqrt{36}=6\)
\(b=\sqrt{25}=5\)
La semidistancia focal se calcula con:
\(c=\sqrt{a^2-b^2}=\sqrt{36-25}=\sqrt{11}\)
Los focos están ubicados a una distancia \(c=\sqrt{11}\) arriba y abajo del centro, ya que la elipse es vertical:
\((-1, 4-\sqrt{11})\) y \((-1, 4+\sqrt{11})\)
Vértices principales:
\((-1, 4-6)=(-1, -2)\)
\((-1, 4+6)=(-1, 10)\)
Vértices secundarios:
\((-1-5, 4)=(-6, 4)\)
\((-1+5, 4)=(4, 4)\)
La longitud del lado recto está dada por:
\(L_R=\dfrac{2b^2}{a}=\dfrac{2 \cdot 25}{6}=\dfrac{50}{6}≈8,33\)
La excentricidad se calcula como:
\(e=\dfrac{c}{a}=\dfrac{\sqrt{11}}{6}≈0,55\)
Elementos de la elipse:
- Centro: (-1, 4)
- Focos: \((-1, 4-\sqrt{11})\) y \((-1, 4+\sqrt{11})\)
- Semiejes: a = 6, b = 5
- Distancia focal: \(2c=2\sqrt{11}\)
- Vértices principales: (-1, -2) y (-1, 10)
- Vértices secundarios: (-6, 4) y (4, 4)
- Lado recto: \(L_R≈8,33\)
- Excentricidad: \(e≈0,55\)
Pasar de la ecuación general a la canónica
Tener la ecuación canónica de una elipse es necesario para poder extraer sus elementos con facilidad. Cuando tenemos la fórmula general, podemos completar los cuadrados y acomodar la expresión para que tome la forma reducida.
Ejercicio: pasar las siguientes ecuaciones de elipses a su forma canónica.
- \(3x^2+4y^2=12\)
- \(25x^2+16y^2=400\)
- \(4x^2+9y^2-16x-32=0\)
- \(16x^2+9y^2-64x-54y+1=0\)
- \(8x^2+25y^2-48x+50y+47=0\)
- \(36x^2+25y^2+72x-200y-464=0\)
- \(2x^2+4x+7y^2-28y-40=0\)
Soluciones
Solución del ejercicio 1
Ecuación: \(3x^2+4y^2=12\)
Observamos que es una ecuación de segundo grado con términos cuadráticos en x y y, y no aparecen términos lineales, esto indica que la ecuación corresponde a una elipse con centro en el origen.
En la forma canónica de la elipse, el lado derecho de la ecuación debe ser igual a 1. Dividimos toda la ecuación entre 12:
\(\dfrac{3x^2}{12}+\dfrac{4y^2}{12}=\dfrac{12}{12}\)
Simplificando cada término:
\(\dfrac{x^2}{4}+\dfrac{y^2}{3}=1\)
La ecuación ahora está en la forma reducida.
Solución del ejercicio 2
Ecuación: \(25x^2+16y^2=400\)
Primero, identificamos que se trata de una ecuación de segundo grado con términos cuadráticos en x y y, sin términos lineales. Esto nos indica que corresponde a una elipse con centro en el origen.
Para expresar la ecuación en su forma canónica, debemos asegurarnos de que el lado derecho sea igual a 1. Para ello, dividimos todos los términos de la ecuación entre 400:
\(\dfrac{25x^2}{400}+\dfrac{16y^2}{400}=\dfrac{400}{400}\)
Simplificamos cada término:
\(\dfrac{x^2}{16}+\dfrac{y^2}{25}=1\)
Solución del ejercicio 3
Ecuación: \(4x^2+9y^2-16x-32=0\)
Primero, observamos que la ecuación tiene términos cuadráticos en x y y, pero únicamente hay un término lineal en x. Esto indica que la curva es una elipse cuyo centro no se encuentra en el origen.
Reorganizamos los términos para separar los que dependen de x y y:
\(4x^2-16x+9y^2=32\)
El término lineal en x nos indica que debemos completar el cuadrado. Extraemos el factor común 4 de los términos en x:
\(4(x^2-4x)+9y^2=32\)
Ahora, para completar el cuadrado dentro del corchete que contiene x, tomamos el coeficiente de x, que es-4, lo dividimos entre 2 y luego lo elevamos al cuadrado. Esto nos da:
\(\left(\dfrac{-4}{2}\right)^2=(-2)^2=4\)
Añadimos y restamos 4 dentro del corchete:
\(4[(x^2-4x+4)-4]+9y^2=32\)
Simplificamos dentro del paréntesis:
\(4[(x-2)^2-4]+9y^2=32\)
Distribuimos el 4:
\(4(x-2)^2-16+9y^2=32\)
Llevamos el -16 al lado derecho de la ecuación:
\(4(x-2)^2+9y^2=48\)
Dividimos toda la ecuación entre 48 para que el lado derecho sea 1:
\(\dfrac{4(x-2)^2}{48}+\dfrac{9y^2}{48}=\dfrac{48}{48}\)
Simplificamos cada término:
\(\dfrac{(x-2)^2}{12}+\dfrac{y^2}{16/3}=1\)
Y así obtenemos la ecuación de la elipse en su forma canónica. No fue necesario completar el cuadrado porque no hay un término lineal asociado a esta variable.
Solución del ejercicio 4
Ecuación: \(16x^2+9y^2-64x-54y+1=0\)
La ecuación incluye términos cuadráticos en x y y, así como términos lineales en ambas variables. Esto indica que se trata de una elipse cuyo centro no se encuentra en el origen.
Agrupamos los términos que dependen de x y y, y llevamos el término constante al lado derecho:
\(16x^2-64x+9y^2-54y=-1\)
Extraemos el factor común de los términos cuadráticos en x y y:
\(16[x^2-4x]+9[y^2-6y]=-1\)
Completamos el cuadrado para x y y:
Para x, tomamos el coeficiente de x, que es -4, lo dividimos entre 2 y lo elevamos al cuadrado:
\(\left(\dfrac{-4}{2}\right)^2=(-2)^2=4\)
Añadimos y restamos 4 dentro del corchete:
\(16[(x^2-4x+4)-4]=16[(x-2)^2-4]\)
Para y, tomamos el coeficiente de y, que es -6, lo dividimos entre 2 y lo elevamos al cuadrado:
\(\left(\dfrac{-6}{2}\right)^2=(-3)^2=9\)
Añadimos y restamos 9 dentro del corchete:
\(9[(y^2-6y+9)-9]=9[(y-3)^2-9]\)
Sustituyendo estas expresiones en la ecuación:
\(16[(x-2)^2-4]+9[(y-3)^2-9]=-1\)
Distribuimos los factores 16 y 9:
\(16(x-2)^2-64+9(y-3)^2-81=-1\)
Sumamos 64 y 81 al lado derecho:
\(16(x-2)^2+9(y-3)^2=144\)
Dividimos toda la ecuación entre 144 para que el lado derecho sea igual a 1:
\(\dfrac{16(x-2)^2}{144}+\dfrac{9(y-3)^2}{144}=\dfrac{144}{144}\)
Simplificamos los coeficientes:
\(\dfrac{(x-2)^2}{9}+\dfrac{(y-3)^2}{16}=1\)
Solución del ejercicio 5
Ecuación: \(8x^2+25y^2-48x+50y+47=0\)
La ecuación contiene términos cuadráticos en x y y, así como términos lineales en ambas variables. Esto indica que se trata de una elipse cuyo centro no está en el origen.
Agrupamos los términos que dependen de x y y, y llevamos el término constante al lado derecho:
\(8x^2-48x+25y^2+50y=-47\)
Extraemos el factor común de los términos cuadráticos en x y y:
\(8[x^2-6x]+25[y^2+2y]=-47\)
Para x, tomamos el coeficiente de x, que es -6, lo dividimos entre 2 y lo elevamos al cuadrado:
\(\left(\dfrac{-6}{2}\right)^2=(-3)^2=9\)
Añadimos y restamos 9 dentro del corchete:
\(8[(x^2-6x+9)-9]=8[(x-3)^2-9]\)
Para y, tomamos el coeficiente de y, que es 2, lo dividimos entre 2 y lo elevamos al cuadrado:
\(\left(\dfrac{2}{2}\right)^2=1^2=1\)
Añadimos y restamos 1 dentro del corchete:
\(25[(y^2+2y+1)-1]=25[(y+1)^2-1]\)
Sustituyendo estas expresiones en la ecuación:
\(8[(x-3)^2-9]+25[(y+1)^2-1]=-47\)
Distribuimos los factores 8 y 25:
\(8(x-3)^2-72+25(y+1)^2-25=-47\)
Sumamos 72 y 25 al lado derecho:
\(8(x-3)^2+25(y+1)^2=50\)
Dividimos toda la ecuación entre 50 para que el lado derecho sea igual a 1:
\(\dfrac{8(x-3)^2}{50}+\dfrac{25(y+1)^2}{50}=\dfrac{50}{50}\)
Simplificamos los coeficientes:
\(\dfrac{(x-3)^2}{50/8}+\dfrac{(y+1)^2}{2}=1\)
\(\dfrac{(x-3)^2}{25/4}+\dfrac{(y+1)^2}{2}=1\)
Solución del ejercicio 6
Ecuación: \(36x^2+25y^2+72x-200y-464=0\)
Agrupamos los términos que dependen de x y y, y llevamos el término constante al lado derecho:
\(36x^2+72x+25y^2-200y=464\)
Extraemos el factor común de los términos cuadráticos en x y y:
\(36[x^2+2x]+25[y^2-8y]=464\)
Para x, tomamos el coeficiente de x, que es 2, lo dividimos entre 2 y lo elevamos al cuadrado:
\(\left(\dfrac{2}{2}\right)^2=1^2=1\)
Añadimos y restamos 1 dentro del corchete:
\(36[(x^2+2x+1)-1]=36[(x+1)^2-1]\)
Para y, tomamos el coeficiente de y, que es-8, lo dividimos entre 2 y lo elevamos al cuadrado:
\(\left(\dfrac{-8}{2}\right)^2=(-4)^2=16\)
Añadimos y restamos 16 dentro del corchete:
\(25[(y^2-8y+16)-16]=25[(y-4)^2-16]\)
Sustituyendo estas expresiones en la ecuación:
\(36[(x+1)^2-1]+25[(y-4)^2-16]=464\)
Distribuimos 36 y 25 y simplificamos:
\(36(x+1)^2-36+25(y-4)^2-400=464\)
Sumamos 36 y 400 al lado derecho:
\(36(x+1)^2+25(y-4)^2=900\)
Dividimos toda la ecuación entre 900 para que el lado derecho sea igual a 1:
\(\dfrac{36(x+1)^2}{900}+\dfrac{25(y-4)^2}{900}=\dfrac{900}{900}\)
Simplificamos los coeficientes:
\(\dfrac{(x+1)^2}{25}+\dfrac{(y-4)^2}{36}=1\)
Solución del ejercicio 7
Ecuación: \(2x^2+4x+7y^2-28y-40=0\)
Agrupamos los términos que dependen de x y y, y llevamos el término constante al lado derecho:
\(2x^2+4x+7y^2-28y=40\)
Extraemos el factor común de los términos cuadráticos en x y y:
\(2[x^2+2x]+7[y^2-4y]=40\)
Para x, tomamos el coeficiente de x, que es 2, lo dividimos entre 2 y lo elevamos al cuadrado:
\(\left(\dfrac{2}{2}\right)^2=1^2=1\)
Añadimos y restamos 1 dentro del corchete:
\(2[(x^2+2x+1)-1]=2[(x+1)^2-1]\)
Para y, tomamos el coeficiente de y, que es-4, lo dividimos entre 2 y lo elevamos al cuadrado:
\(\left(\dfrac{-4}{2}\right)^2=(-2)^2=4\)
Añadimos y restamos 4 dentro del corchete:
\(7[(y^2-4y+4)-4]=7[(y-2)^2-4]\)
Sustituyendo estas expresiones en la ecuación:
\(2[(x+1)^2-1]+7[(y-2)^2-4]=40\)
Distribuimos 2 y 7 y simplificamos:
\(2(x+1)^2-2+7(y-2)^2-28=40\)
Sumamos 2 y 28 al lado derecho:
\(2(x+1)^2+7(y-2)^2=70\)
Dividimos toda la ecuación entre 70 para que el lado derecho sea igual a 1:
\(\dfrac{2(x+1)^2}{70}+\dfrac{7(y-2)^2}{70}=\dfrac{70}{70}\)
Simplificamos los coeficientes:
\(\dfrac{(x+1)^2}{35}+\dfrac{(y-2)^2}{10}=1\)
Pasar de la ecuación canónica a la general
Se puede llegar a la fórmula general a partir de la ecuación ordinaria desarrollando todos los exponentes y acomodando la expresión para que tome la forma Ax2 + Cy2 + Dx + Ey + F = 0.
Ejercicio: encontrar la ecuación general de las siguientes elipses.
- \(\dfrac{x^2}{16}+\dfrac{y^2}{9}=1\)
- \(\dfrac{x^2}{4}+\dfrac{y^2}{25}=1 \)
- \(\dfrac{(x+3)^2}{36}+\dfrac{(y-4)^2}{16}=1\)
- \(\dfrac{(x-1)^2}{9}+\dfrac{(y+2)^2}{25}=1\)
- \(\dfrac{(x-1)^2}{36}+\dfrac{(y-\frac{5}{2})^2}{49}=1\)
- \(\dfrac{x^2}{25}+\dfrac{(y+5)^2}{16}=1\)
Soluciones
Solución del ejercicio 1
Ecuación 1
\(\dfrac{x^2}{16}+\dfrac{y^2}{9}=1\)
Primero eliminamos los denominadores, para conseguirlo multiplicamos toda la ecuación por el producto entre los denominadores, que es \(16\cdot 9=144\)
\(144 \cdot \left(\dfrac{x^2}{16}\right)+144 \cdot \left(\dfrac{y^2}{9}\right)=144 \cdot 1\)
Distribuimos el 144 y realizamos las divisiones:
\(\dfrac{144x^2}{16}+\dfrac{144y^2}{9}=144\)
Simplificando cada término:
\(9x^2+16y^2=144\)
Reorganizamos los términos de modo que queden igualados a 0, si es necesario:
\(9x^2+16y^2-144=0\)
Esta es la forma general de la elipse.
Solución del ejercicio 2
Ecuación 2
\(\dfrac{x^2}{4}+\dfrac{y^2}{25}=1\)
Para eliminar los denominadores, multiplicamos toda la ecuación por el producto de los denominadores, que en este caso es \(4 \cdot 25=100.\)
\(100 \cdot \left(\dfrac{x^2}{4}\right)+100 \cdot \left(\dfrac{y^2}{25}\right)=100 \cdot 1\)
Distribuimos el 100 en cada término y realizamos las divisiones:
\(\dfrac{100x^2}{4}+\dfrac{100y^2}{25}=100\)
\(25x^2+4y^2=100\)
Reorganizamos los términos para que queden igualados a 0:
\(25x^2+4y^2-100=0\)
Solución del ejercicio 3
Ecuación 3
\(\dfrac{(x+3)^2}{36}+\dfrac{(y-4)^2}{16}=1\)
Multiplicamos toda la ecuación por el producto de los denominadores, que es \(36 \cdot 16=576.\)
\(576 \cdot \left(\dfrac{(x+3)^2}{36}\right)+576 \cdot \left(\dfrac{(y-4)^2}{16}\right)=576 \cdot 1\)
Distribuimos el 576 y realizamos las divisiones:
\(\dfrac{576(x+3)^2}{36}+\dfrac{576(y-4)^2}{16}=576\)
\(16(x+3)^2+36(y-4)^2=576\)
Expandimos cada binomio:
\(16(x^2+6x+9)+36(y^2-8y+16)=576\)
\(16x^2+96x+144+36y^2-288y+576=576\)
Simplificamos y reorganizamos los términos:
\(16x^2+36y^2+96x-288y+144+576-576=0\)
\(16x^2+36y^2+96x-288y+144=0\)
Esta última es la ecuación general.
Solución del ejercicio 4
Ecuación 4
\(\dfrac{(x-1)^2}{9}+\dfrac{(y+2)^2}{25}=1\)
Multiplicamos toda la ecuación por el producto de los denominadores, que es \(9 \cdot 25=225.\)
\(225 \cdot \left(\dfrac{(x-1)^2}{9}\right)+225 \cdot \left(\dfrac{(y+2)^2}{25}\right)=225 \cdot 1\)
Distribuimos el 225 y realizamos las divisiones:
\(\dfrac{225(x-1)^2}{9}+\dfrac{225(y+2)^2}{25}=225\)
\(25(x-1)^2+9(y+2)^2=225\)
Expandimos cada binomio:
\(25\big(x^2-2x+1\big)+9\big(y^2+4y+4\big)=225\)
\(25x^2-50x+25+9y^2+36y+36=225\)
Simplificamos y reorganizamos los términos:
\(25x^2+9y^2-50x+36y+25+36-225=0\)
\(25x^2+9y^2-50x+36y-164=0\)
Solución del ejercicio 5
\(\dfrac{(x-1)^2}{36}+\dfrac{(y-\frac{5}{2})^2}{49}=1\)
Multiplicamos toda la ecuación por el producto de los denominadores, que es \(36 \cdot 49=1764.\)
\(1764 \cdot \left(\dfrac{(x-1)^2}{36}\right)+1764 \cdot \left(\dfrac{\left(y-\frac{5}{2}\right)^2}{49}\right)=1764 \cdot 1\)
Distribuimos el 1764 y realizamos las divisiones:
\(\dfrac{1764(x-1)^2}{36}+\dfrac{1764\left(y-\dfrac{5}{2}\right)^2}{49}=1764\)
\(49(x-1)^2+36\left(y-\dfrac{5}{2}\right)^2=1764\)
Expandimos cada binomio:
\(49(x^2-2x+1)+36\left(y^2-5y+\dfrac{25}{4}\right)=1764\)
\(49x^2-98x+49+36y^2-180y+225=1764\)
Simplificamos y reorganizamos los términos:
\(49x^2+36y^2-98x-180y+49+225-1764=0\)
\(49x^2+36y^2-98x-180y-1490=0\)
Solución del ejercicio 6
\(\dfrac{x^2}{25}+\dfrac{(y+5)^2}{16}=1\)
Multiplicamos toda la ecuación por el producto de los denominadores, que es \(25 \cdot 16=400.\)
\(400 \cdot \left(\dfrac{x^2}{25}\right)+400 \cdot \left(\dfrac{(y+5)^2}{16}\right)=400 \cdot 1\)
Distribuimos el 400 y realizamos las divisiones:
\(\dfrac{400x^2}{25}+\dfrac{400(y+5)^2}{16}=400\)
\(16x^2+25(y+5)^2=400\)
Expandimos el binomio:
\(16x^2+25(y^2+10y+25)=400\)
\(16x^2+25y^2+250y+625=400\)
Simplificamos y reorganizamos los términos:
\(16x^2+25y^2+250y+625-400=0\)
\(16x^2+25y^2+250y+225=0\)
Problemas de la vida real
Los siguientes ejercicios son aplicaciones de la elipse en la vida real. La Primera Ley de Kepler nos dice que los planetas se mueven alrededor del Sol en órbitas elípticas con el Sol en uno de sus focos, por ello es común ver problemas relacionados con las órbitas de cuerpos celestes.
Ejercicio 1
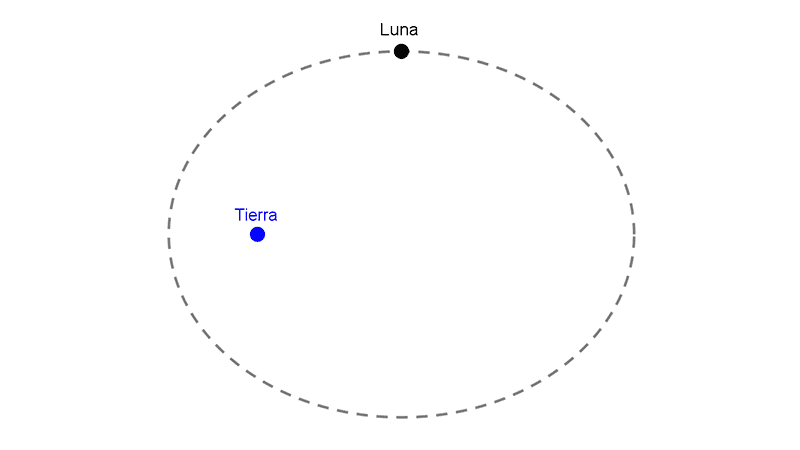
La órbita de la Luna es una trayectoria elíptica y la Tierra es uno de los focos de esa elipse. La distancia del centro de la Tierra al centro de la Luna varía desde un mínimo de 356 000 km hasta un máximo de 406 000 km. Calcular la excentricidad de la órbita lunar y las longitudes de los ejes mayor y menor.
Solución
Datos iniciales
- Distancia mínima (perigeo): dmin = 356000 km.
- Distancia máxima (apogeo): dmax = 406000 km.
Sabemos que en una elipse:
- El eje mayor (2a) es la distancia total entre los dos extremos de la elipse.
- La distancia focal (2c) es la separación entre los dos focos.
- La excentricidad (e) se define como \(e=\dfrac{c}{a},\) donde c es la distancia focal y a es el semieje mayor.
El eje mayor de la elipse es la distancia total entre el perigeo y el apogeo. Esto equivale a:
\(2a=d_{\text{min}}+d_{\text{max}}\)
Sustituyendo los valores:
\(2a=356000+406000=762000 km\)
Por lo tanto, el semieje mayor es:
\(a=\dfrac{2a}{2}=\dfrac{762000}{2}=381000 \, \text{km}\)
La distancia focal (c) se puede determinar con la fórmula:
\(c=a-d_{\text{min}}\)
Sustituyendo los valores:
\(c=381000-356000=25000 \, \text{km}\)
La excentricidad se calcula como:
\(e=\dfrac{c}{a}\)
Sustituyendo los valores:
\(e=\dfrac{25000}{381000}≈0,0656\)
El semieje menor se calcula usando la relación entre los ejes de una elipse:
\(b=\sqrt{a^2-c^2}\)
Sustituyendo los valores:
\(b=\sqrt{(381000)^2-(25000)^2}\)
\(b=\sqrt{145161000000-625000000}=\sqrt{144536000000}≈380173 \ \text{km}\)
Resultados finales
- Longitud del eje menor: \(2b ≈ 760346~ km.\)
- Excentricidad: \(e ≈ 0,0656.\)
- Longitud del eje mayor: \(2a = 762000~ km.\)
Ejercicio 2
Determinar la longitud del semieje menor de la órbita de Mercurio, si su excentricidad es de 0,206 y su semieje mayor mide 0,387 unidades astronómicas (UA).
Solución
El semieje mayor es a = 0, 387 y la excentricidad es \(e=\dfrac{c}{a}=0,206:\)
\(\dfrac{c}{0, 387}=0,206→c=0,079722\)
Al sustituir en \(b=\sqrt{a^2-c^2}=\sqrt{(0,387)^2-(0,079722)^2}=0,3787 UA.\)
Por lo tanto, la longitud del semieje mayor es de 0,3787 UA.
Ejercicio 3
La órbita de Saturno alrededor del Sol es una elipse con el Sol en uno de sus focos. La distancia más pequeña a la que pasa Saturno del Sol se llama perihelio y es de aproximadamente 8,29 UA y la distancia más grande se llama aphelio con aproximadamente 10.03 UA. Obtenga una ecuación para la órbita de Saturno.
Solución
Datos iniciales
- Perihelio: dmin = 8,29 UA.
- Afelio: dmax = 10,03 UA.
En el sistema de coordenadas centrado en el centro de la elipse, la ecuación estándar de la elipse es:
\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\)
donde:
- a es el semieje mayor.
- b es el semieje menor.
- La distancia focal (c) está relacionada con el semieje mayor por \(c=\sqrt{a^2-b^2}.\)
El Sol está en uno de los focos, a una distancia c del centro.
El eje mayor (2a) es la distancia total entre el perihelio y el afelio:
\(2a=d_{\text{min}}+d_{\text{max}}\)
Sustituyendo los valores:
\(2a=8,29+10,03=18,32 ~\text{UA}\)
Por lo tanto, el semieje mayor es:
\(a=\dfrac{2a}{2}=\dfrac{18,32}{2}=9,16 \ \text{UA}\)
La distancia focal (c) se calcula como:
\(c=a-d_{\text{min}}\)
Sustituyendo los valores:
\(c=9,16-8,29=0,87 \ \text{UA}\)
El semieje menor (b) está relacionado con a y c por la fórmula:
\(b=\sqrt{a^2-c^2}\)
Sustituyendo los valores:
\(b=\sqrt{(9,16)^2-(0,87)^2}\)
\(b=\sqrt{83,9056-0,7569}=\sqrt{83,1487}≈9,12 \ \text{UA}\)
Con el semieje mayor a = 9,16 y el semieje menor b ≈ 9,12, la ecuación de la elipse centrada en el origen (0, 0) con el eje mayor en el eje x es:
\(\dfrac{x^2}{9,16^2}+\dfrac{y^2}{9,12^2}=1\)
Simplificando los denominadores:
\(\dfrac{x^2}{83,9056}+\dfrac{y^2}{83,1744}=1\)
Por lo tanto, la ecuación es aproximadamente:
\(\dfrac{x^2}{83,91}+\dfrac{y^2}{83,17}=1\)
Esta ecuación describe la órbita de Saturno alrededor del Sol en unidades astronómicas (UA).
El Sol se encuentra en uno de los focos de la elipse, a una distancia de c = 0,87 UA del centro.
Ejercicio 4
La puerta de entrada de un teatro tendrá forma de semielipse, de 20 metros de ancho en su base y 6 metros de altura en el centro. Obtenga una ecuación para la elipse. ¿Qué altura tiene la entrada a una distancia de 4 metros del centro?
Solución
Datos iniciales
- Ancho de la base: 2a = 20m, por lo que a = 10 m.
- Altura máxima en el centro: b = 6 m (semieje vertical, ya que se trata de una semielipse).
El teatro tiene una puerta con forma de semielipse con el eje mayor horizontal (x) y el eje menor vertical (y). La ecuación de la elipse completa sería:
\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\)
Como la puerta es una semielipse superior, solo consideraremos la parte positiva de y.
Sustituyendo los valores de a = 10 y b = 6:
\(\dfrac{x^2}{10^2}+\dfrac{y^2}{6^2}=1\)
\(\dfrac{x^2}{100}+\dfrac{y^2}{36}=1\)
Esta es la ecuación de la elipse completa. Para la puerta, tomamos únicamente:
\(y=\sqrt{36 \left(1-\dfrac{x^2}{100}\right)}\)
Calculamos la altura a 4 metros del centro sustituyendo x = 4 en la ecuación:
\(y=\sqrt{36 \left(1-\dfrac{4^2}{100}\right)}\)
\(y=\sqrt{30,24}≈5,5 m\)
Resultados finales
- Ecuación de la puerta del teatro (semielipse): \(y=\sqrt{36 \left(1-\dfrac{x^2}{100}\right)}\)
- Altura a 4 metros del centro: \(y ≈ 5,5~ m.\)
Ejercicios avanzados
Hasta ahora se han visto ejercicios de elipses horizontales y verticales, los siguientes artículos contienen un tipo de problema más general donde los ejes de la elipse pueden estar inclinados con respecto a los ejes coordenados, resultando en una elipse rotada:
Bibliografía
Los ejercicios de este artículo están inspirados en los problemas de elipse de los siguientes libros:
- Engler, A., Müller, D., Vrancken, S. y Hecklein, M. (2020). Geometría analítica. Universidad Nacional del Litoral.
- Fuller, G. y Tarwater, D. (1995). Geometría analítica (7.ª ed.). Pearson Educación.
- Lehmann, C. (1989). Geometría analítica. Limusa.
- Leithold. L. (1992). Álgebra y trigonometría con geometría analítica. Oxford University Press.
- Márquez, A., Vázquez, F., Ruiz, H., Villegas, M. y Figueroa, M. (2009). Geometría analítica. Prentice Hall.
- Raichman, S. y Totter, E. (2016). Geometría analítica para ciencias e ingeniería. Universidad Nacional de Cuyo.
- Sullivan, M. (2006). Álgebra y trigonometría. Pearson Educación.
- Swokowski, E. y Cole, J. (2009). Álgebra y trigonometría con geometría analítica. Cengage Learning.
¿Te ha servido este contenido? ¡Califícalo!
3,3 / 5 — 3 votos
CÓMO CITAR ESTE ARTÍCULO
Machado, D. (2024, 6 de diciembre). Ejercicios de elipse. Exponty. https://exponty.com/ejercicios-elipse
-
es de gran ayuda esta información y muy grato y sencillo su comprensión y estudio
2 Comentarios
Deja una respuesta


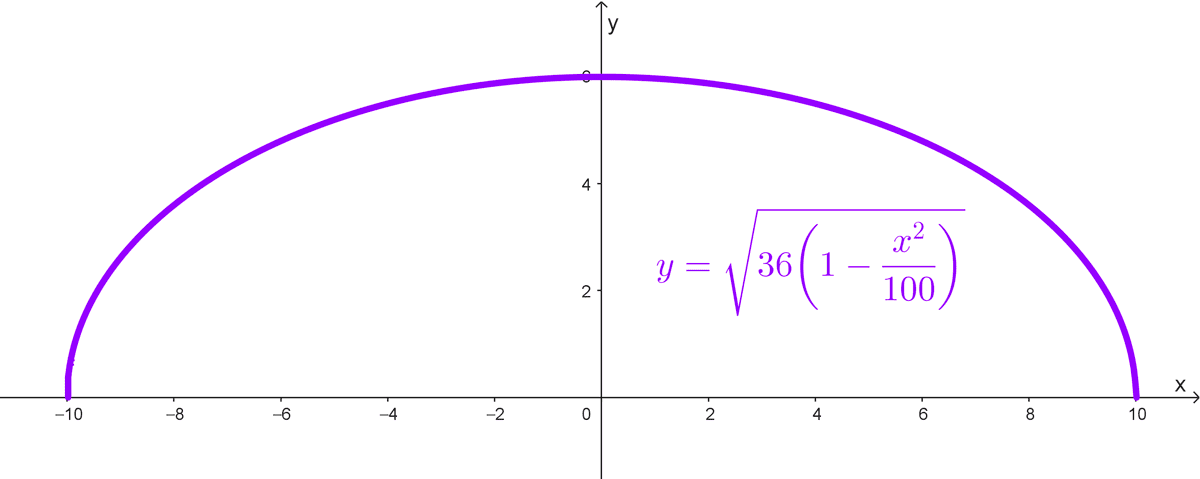

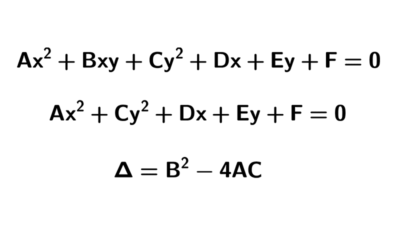
Otros artículos que pueden interesarte