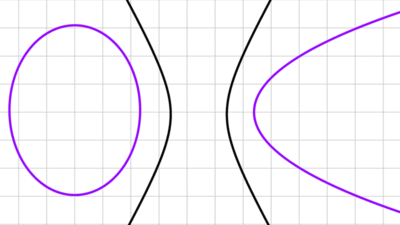
Propiedades de las secciones cónicas

Daniel Machado · Actualizado el 14/09/2024

En este artículo explicamos las propiedades fundamentales de las secciones cónicas. Analizaremos las definiciones, ecuaciones, propiedades geométricas y reflexivas, entre otras cosas.

Índice

Lugares geométricos

Las secciones cónicas (circunferencia, elipse, hipérbola y parábola) se pueden definir cada una como un lugar geométrico en el plano, es decir, como un conjunto de puntos que cumplen una determinada condición o conjunto de condiciones.

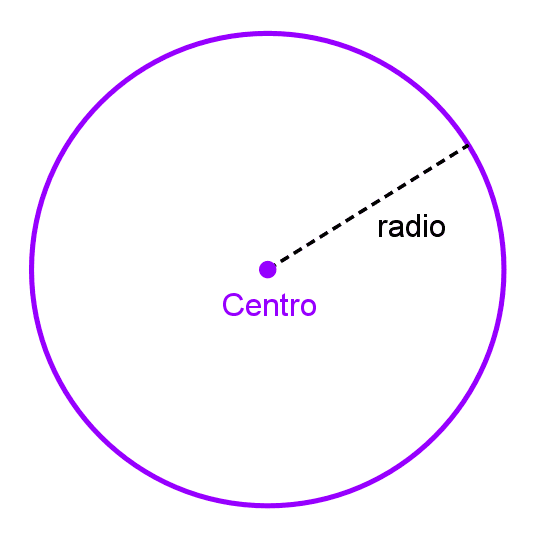
Circunferencia: es el conjunto de todos los puntos en un plano que están a una distancia fija (radio) de un punto dado (centro).
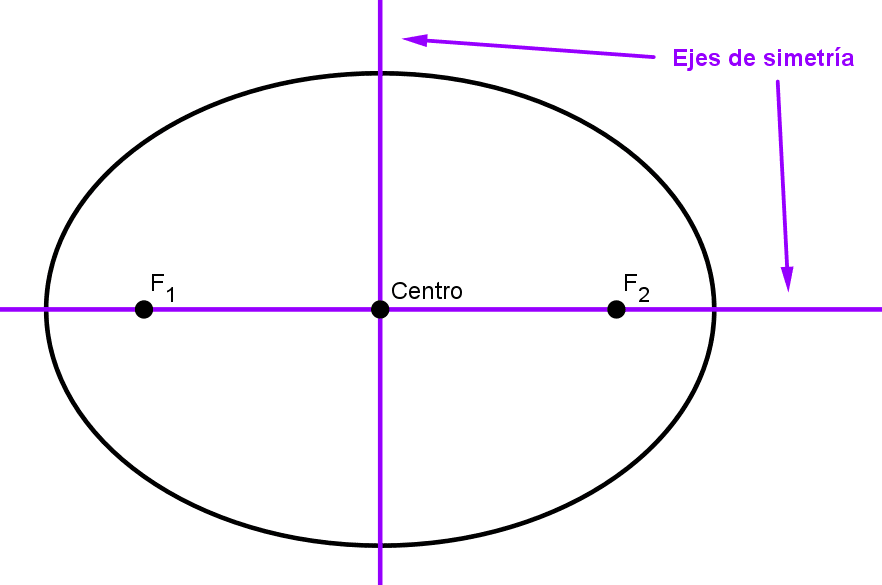
Elipse: es el conjunto de todos los puntos cuya suma de distancias a dos puntos fijos (focos) es constante.
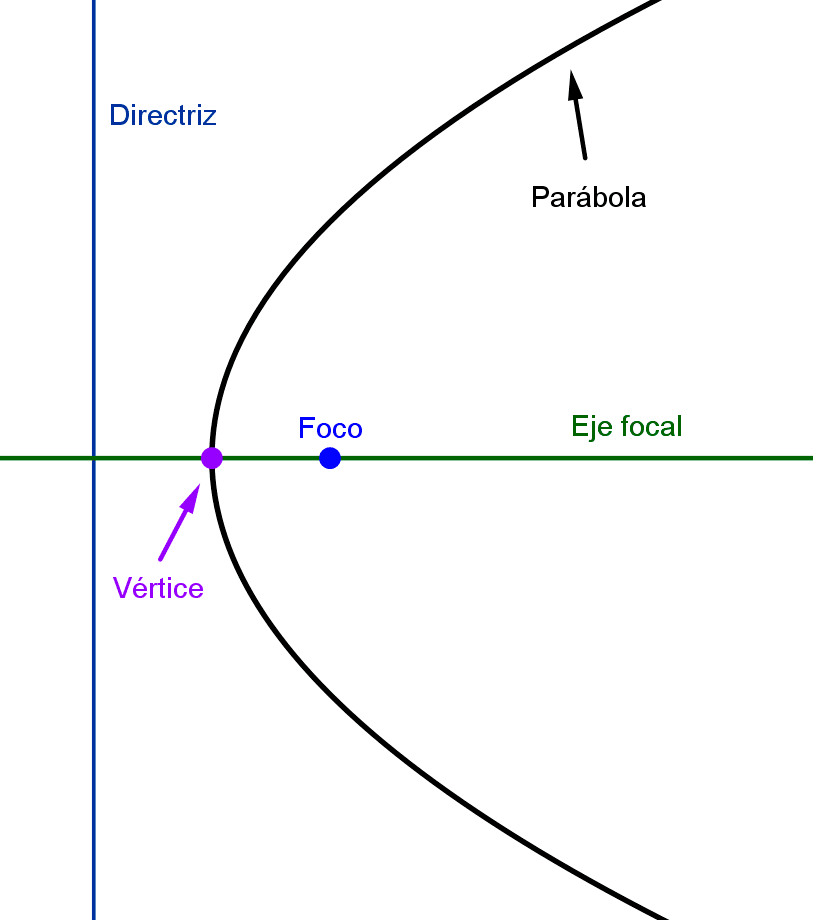
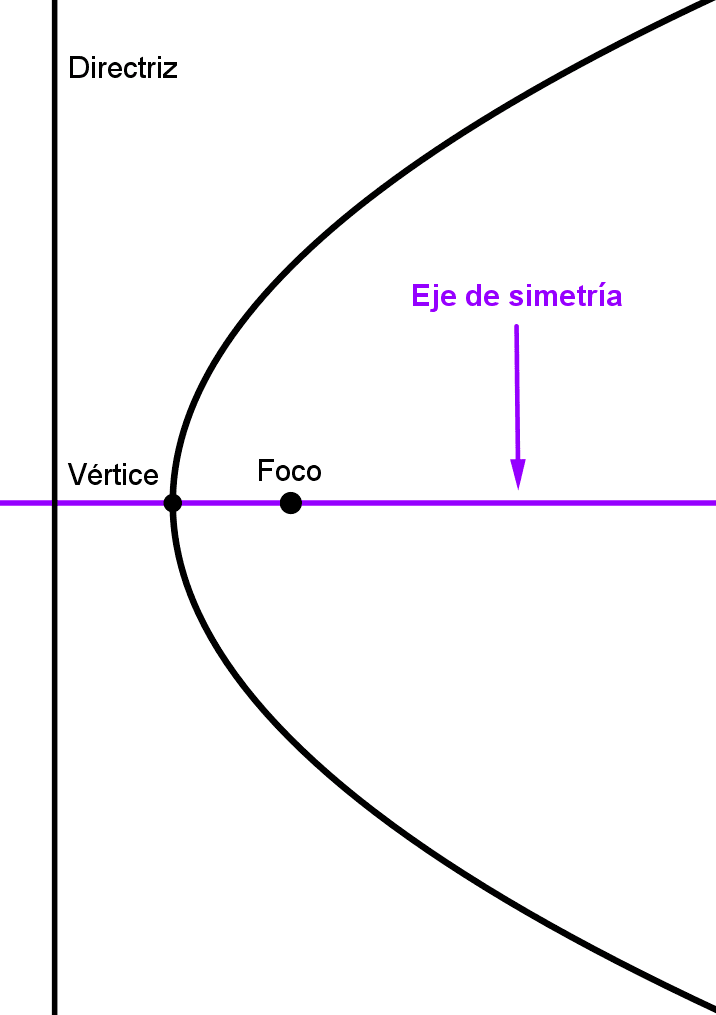
Parábola: es el conjunto de todos los puntos que equidistan de un punto fijo (foco) y una recta fija (directriz).
Hipérbola: es el conjunto de todos los puntos cuya diferencia de distancias a dos puntos fijos (focos) es constante.

Gráfica de una circunferencia — Circunferencia

Ecuaciones

Cuando introducimos un sistema de coordenadas en el plano, podemos encontrar ecuaciones para cada sección cónica.

Cónica	Ecuación	Detalles
Circunferencia	(x-h)^2+(y-k)^2=r^2	El centro es (h, k). El radio es r.
Elipse horizontal	\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1	El centro es (h, k). a es la longitud del semieje mayor. b es la longitud del semieje menor.
Elipse vertical	\dfrac{(y-k)^2}{a^2}+\dfrac{(x-h)^2}{b^2}=1	El centro es (h, k). a es la longitud del semieje mayor. b es la longitud del semieje menor.
Parábola horizontal (hacia derecha o izquierda)	(y-k)^2=4p(x-h)	(h, k) es el vértice. \|p\| es la distancia entre el foco y el vértice.
Parábola vertical (hacia arriba o abajo)	(x-h)^2=4p(y-k)	(h, k) es el vértice. \|p\| es la distancia entre el foco y el vértice.
Hipérbola horizontal (con ramas hacia los lados)	\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1	El centro es (h, k). a es la longitud del semieje transversal. b es la longitud del semieje conjugado.
Hipérbola vertical (con ramas hacia arriba y abajo)	\dfrac{(y-k)^2}{a^2}-\dfrac{(x-h)^2}{b^2}=1	El centro es (h, k). a es la longitud del semieje transversal. b es la longitud del semieje conjugado.

Simetrías

Las secciones cónicas poseen propiedades de simetría que se refieren a la capacidad de estas figuras de reflejarse de manera idéntica a través de ciertas líneas o puntos específicos.

La circunferencia es completamente simétrica respecto a cualquier línea que pase por su centro. En otras palabras, al dividir la circunferencia a través de su centro con cualquier línea recta, las dos mitades serán siempre idénticas.
La elipse, que incluye a la circunferencia como caso especial, tiene dos ejes de simetría que son las rectas que contienen al eje mayor y al eje menor. Cada recta divide la elipse en dos partes iguales.
La parábola posee simetría con respecto a una única línea llamada eje de simetría (o eje focal), que pasa por su vértice y es perpendicular a su directriz. Esta línea divide a la parábola en dos partes congruentes.
La hipérbola tiene dos ejes de simetría que son las rectas que contienen al eje transversal y el eje conjugado. El eje transversal es la línea que une los dos vértices de la hipérbola, mientras que el eje conjugado es perpendicular al eje transversal, pasa por el centro y no intersecta a la hipérbola.

Propiedades reflexivas

Las secciones cónicas poseen propiedades reflexivas únicas que las hacen especialmente útiles en aplicaciones prácticas en la vida real. Estas refieren a la forma en que las cónicas reflejan ondas, como la luz o el sonido, cuando pasan o salen de sus focos.

Elipse: cualquier rayo que parte de uno de sus focos se refleja hacia el otro foco. Esta característica es crucial en la construcción de dispositivos ópticos, como los reflectores de sonido y telescopios, así como en aplicaciones médicas con ultrasonidos.
Parábola: cualquier rayo paralelo a su eje de simetría se refleja hacia su foco, del mismo modo, cualquier rayo que salga de su foco será dirigido en dirección paralela al eje de simetría. Esta propiedad es la base de diseño para antenas parabólicas, telescopios reflectores y faros de automóviles.
Hipérbola: cualquier rayo que parta de un foco y se refleje en una de las ramas se dirigirá al otro foco. Esta propiedad es útil en sistemas de navegación y comunicación.

Otras propiedades

Todas las cónicas tienen un parámetro llamado excentricidad que mide la desviación de la cónica con respecto a una circunferencia; se representa por la letra e. En el caso de la circunferencia, la excentricidad es cero. La elipse tiene una excentricidad que varía entre 0 y 1 (0 ≤ e < 1). La parábola tiene una excentricidad exactamente igual a 1. La hipérbola tiene una excentricidad mayor que uno, es decir, e > 1.
Por cinco puntos no alineados pasa una única cónica (como una elipse, parábola o hipérbola) que los contiene. Si al menos tres de los puntos están alineados, se obtiene una cónica degenerada.

Bibliografía

Alegría, P. (s.f.). Las cónicas y sus aplicaciones.
Có, P. (2018). Álgebra y Geometría Analítica: Secciones cónicas. Universidad Nacional de Rosario.
Engler, A. y otros. (2020). Geometría Analítica. Universidad Nacional del Litoral.
Lehmann, C. (1989). Geometría Analítica. Limusa.
Mora, W., y Figueroa, G. (2009). Cónicas, cálculo superior. Revista Digital Matemática, Educación e Internet.
Muñoz González, A. (2015). Curvas cónicas desde su origen hasta sus aplicaciones en la actualidad. Universidad de Valladolid.
Pérez Gutiérrez, I. (2012). Estudio de las aplicaciones de las cónicas mediado por la modelación desde una visión analítica. Universidad Nacional de Colombia.
Sullivan, M. (2006). Álgebra y Trigonometría. Pearson Educación.
Swokowski, E. y Cole, J. (2009). Álgebra y Trigonometría con Geometría Analítica. Cengage Learning.