Hipérbola equilátera

En este artículo explicamos qué es la hipérbola equilátera (también llamada rectangular o cuadrada), sus ecuaciones y características con ejemplos y gráficos. Además, resolvemos algunos ejercicios paso a paso.

¿Qué es una hipérbola equilátera?

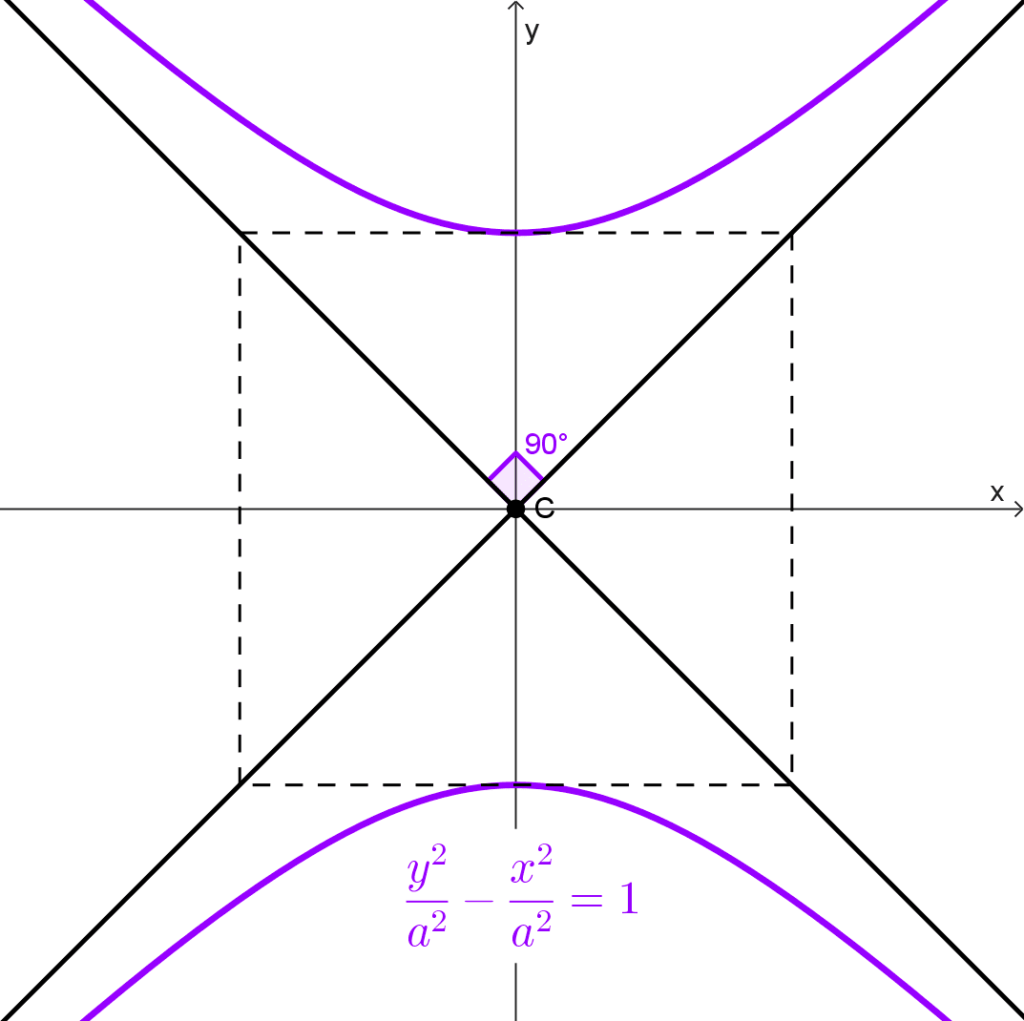
Se llama hipérbola equilátera o rectangular a aquella cuyos semiejes transversal y conjugado tienen la misma longitud, es decir, a = b. Sus asíntotas tienen pendientes ±1, causando que sean perpendiculares entre sí, pues forman un ángulo de 90°.

Ecuaciones

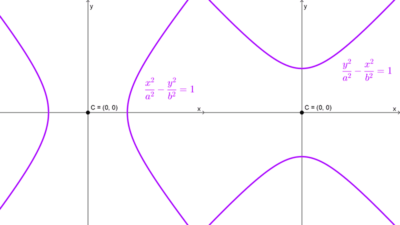
Las fórmulas de las hipérbolas rectangulares tienen una forma más simple que las demás. Partimos primero de la ecuación de la hipérbola horizontal:

*\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1*

Como *a=b,* resulta que *a^2=b^2,* reemplazamos:

*\dfrac{x^2}{a^2}-\dfrac{y^2}{a^2}=1*

Multiplicando ambos miembros por *a^2* y simplificando:

*a^2\dfrac{x^2}{a^2}-a^2\dfrac{y^2}{a^2}=a^2*

*x^2-y^2=a^2*

Del mismo modo, si partimos de la ecuación reducida de la hipérbola vertical llegamos a:

*y^2-x^2=a^2*

Entonces, las ecuaciones para cada caso son:

• Hipérbola equilátera horizontal: *x^2-y^2=a^2*
• Hipérbola equilátera vertical: *y^2-x^2=a^2*

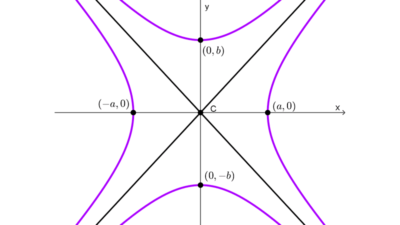
Las asíntotas en ambos casos con *y=x* e *y=-x.* Los elementos de las hipérbolas se resumen en la siguiente tabla:

Ecuación canónica	Orientación	Centro	Focos	Vértices	Asíntotas
*x^2-y^2=a^2*	Horizontal	(0, 0)	(±c, 0) c = a ⋅ √2	(±a, 0)	y = ±x
*y^2-x^2=a^2*	Vertical	(0, 0)	(0, ±c) c = a ⋅ √2	(0, ±a)	y = ±x

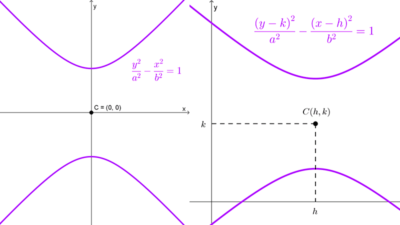
Se suele trabajar con hipérbolas equiláteras centradas en el origen, aunque la definición también es válida si el centro está fuera del origen en un punto (h, k), en tal caso las ecuaciones son:

• Hipérbola equilátera horizontal: *(x-h)^2-(y-k)^2=a^2*
• Hipérbola equilátera vertical: *(y-k)^2-(x-h)^2=a^2*

Ejemplos

Los siguientes son ejemplos de hipérbolas rectangulares:

1. *x^2-y^2=4* tiene orientación horizontal y sus semiejes son *a=b=\sqrt{4}=2.*
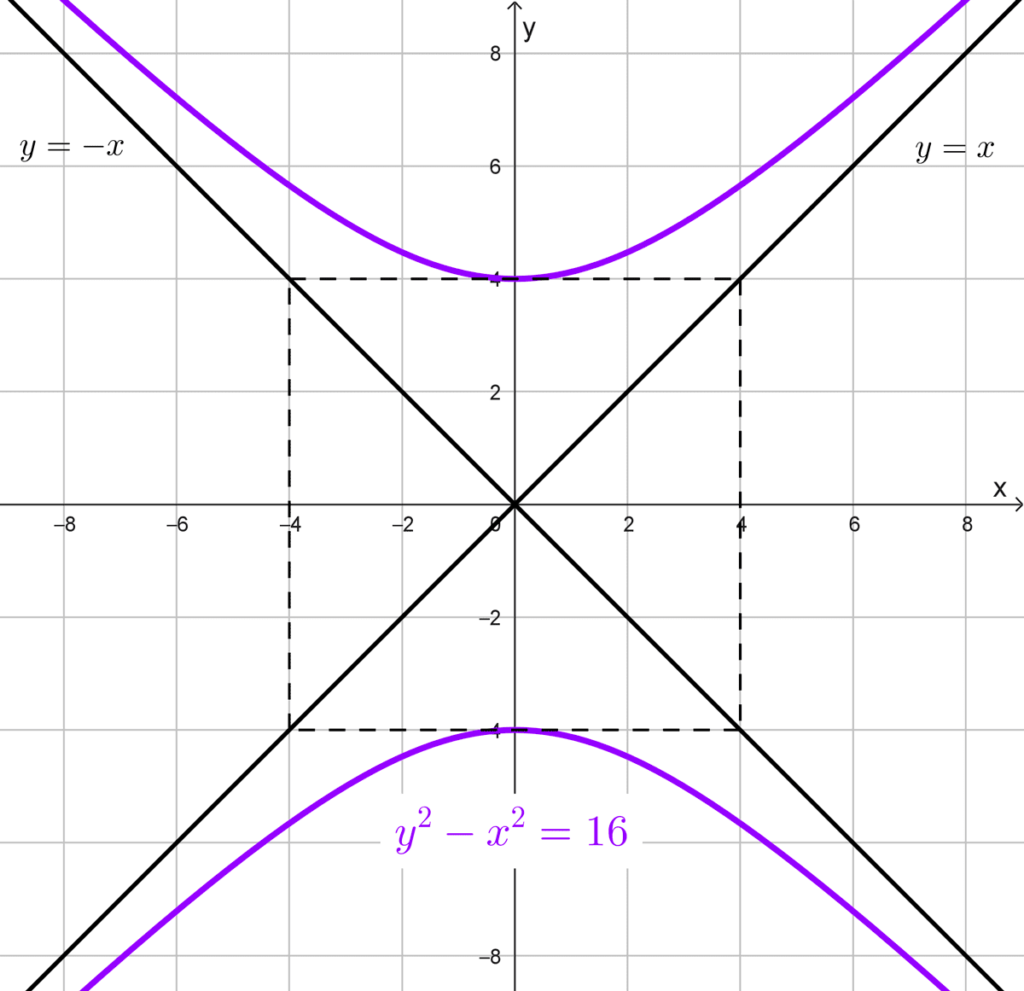
2. *y^2-x^2=16* es vertical y *a=b=\sqrt{16}=4.*
3. *y^2-x^2=2* es vertical y *a=b=\sqrt{2}.*
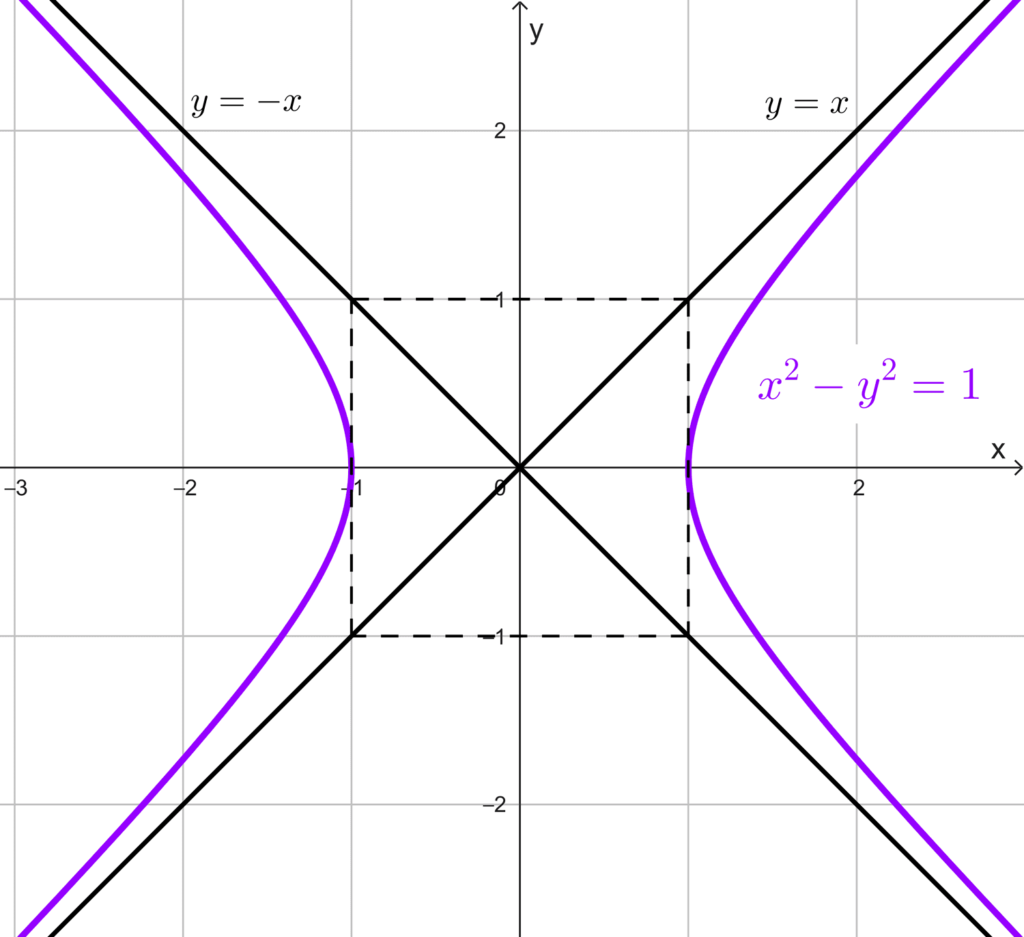
4. *x^2-y^2=1* es horizontal y sus semiejes son *a=b=1.* Esta también es llamada hipérbola unitaria.

Una forma de identificar una hipérbola equilátera es verificar las longitudes de sus semiejes. Si son iguales, la hipérbola es equilátera; si no, es no equilátera. Por ejemplo, la hipérbola *\dfrac{x^2}{4}-\dfrac{y^2}{9}=1* no es equilátera porque a = 2 y b = 3, por tanto a ≠ b. Otra forma es verificar si las asíntotas forman un ángulo de 90°, en tal caso podemos asegurar que sus semiejes tienen la misma longitud. 

Características

Las siguientes son propiedades de las hipérbolas equiláteras:

• La excentricidad de una hipérbola equilátera es raíz cuadrada de 2: *e=\sqrt{2}.* Esto se demuestra aplicando la fórmula: *e=\sqrt{1+\dfrac{b^2}{a^2}}=\sqrt{1+1}=\sqrt{2}.*
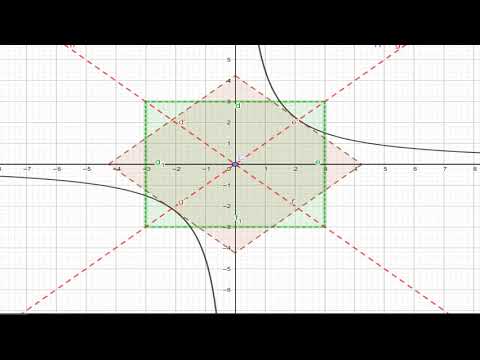
• Las asíntotas tienen pendientes +1 y -1, por tanto son perpendiculares entre sí (forman un ángulo de 90°). Por este ángulo recto es que un nombre alternativo es hipérbola rectangular. El rectángulo auxiliar que sirve para trazar la gráfica es un cuadrado.
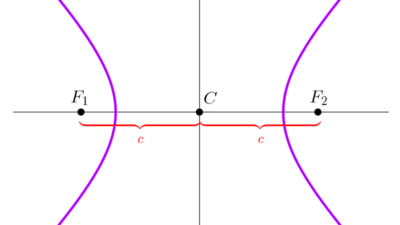
• La semidistancia focal en una hipérbola equilátera es *c=\sqrt{2}a* y la distancia focal es *2c=2\sqrt{2}a.* De nuevo, aplicando la fórmula: *c=\sqrt{a^2+b^2}=\sqrt{2a^2}=\sqrt{2}\sqrt{a^2}=\sqrt{2}a* porque a > 0.

Hipérbola equilátera referida a sus asíntotas

Hemos visto que las asíntotas de una hipérbola equilátera son *y=x* e *y=-x.* Nos interesa aplicar una rotación de ejes para que las asíntotas coincidan con los ejes cartesianos. De ese modo, la ecuación de la hipérbola se simplificará.

Si partimos de la ecuación ordinaria de la hipérbola equilátera vertical *y^2-x^2=a^2* y hacemos una rotación de ejes de 45°, obtendremos la siguiente ecuación:

*xy=\dfrac{a^2}{2}*

A la cantidad *\dfrac{a^2}{2}* se la simboliza como k:

*xy=k*

Despejando y:

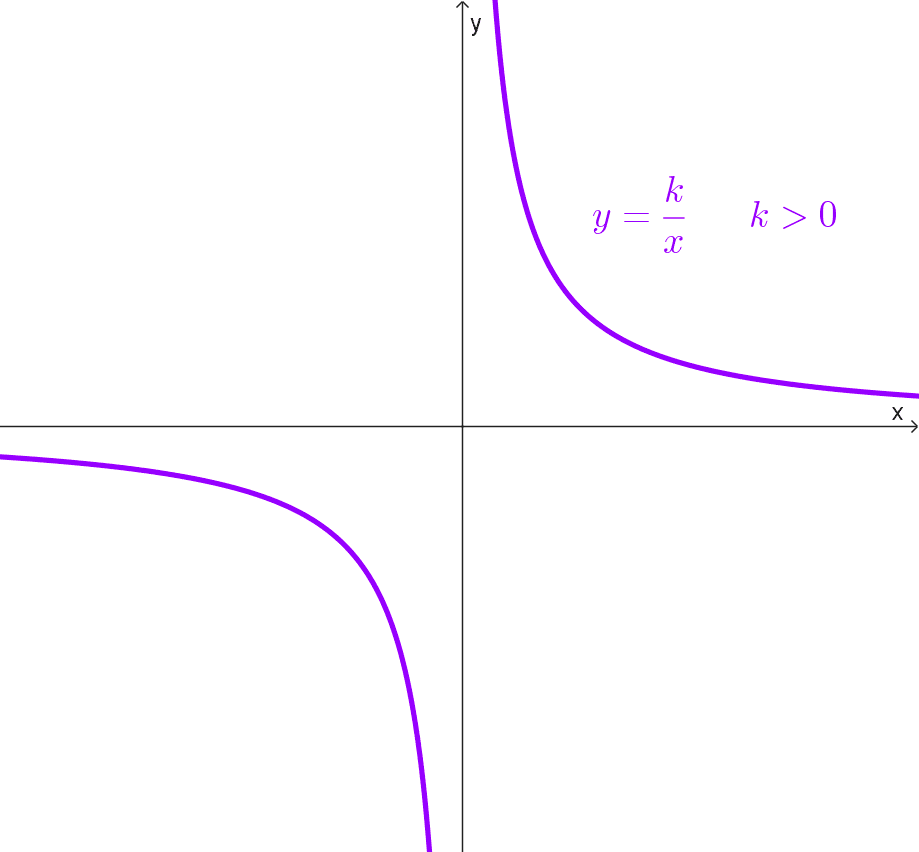
*y=\dfrac{k}{x}*

Esta es llamada la ecuación de la hipérbola equilátera referida a sus asíntotas, ya que éstas son los ejes cartesianos. El número k puede ser positivo o negativo, si partimos de la ecuación *x^2-y^2=a^2* y aplicamos una rotación de 45°, llegaremos a un k negativo. 

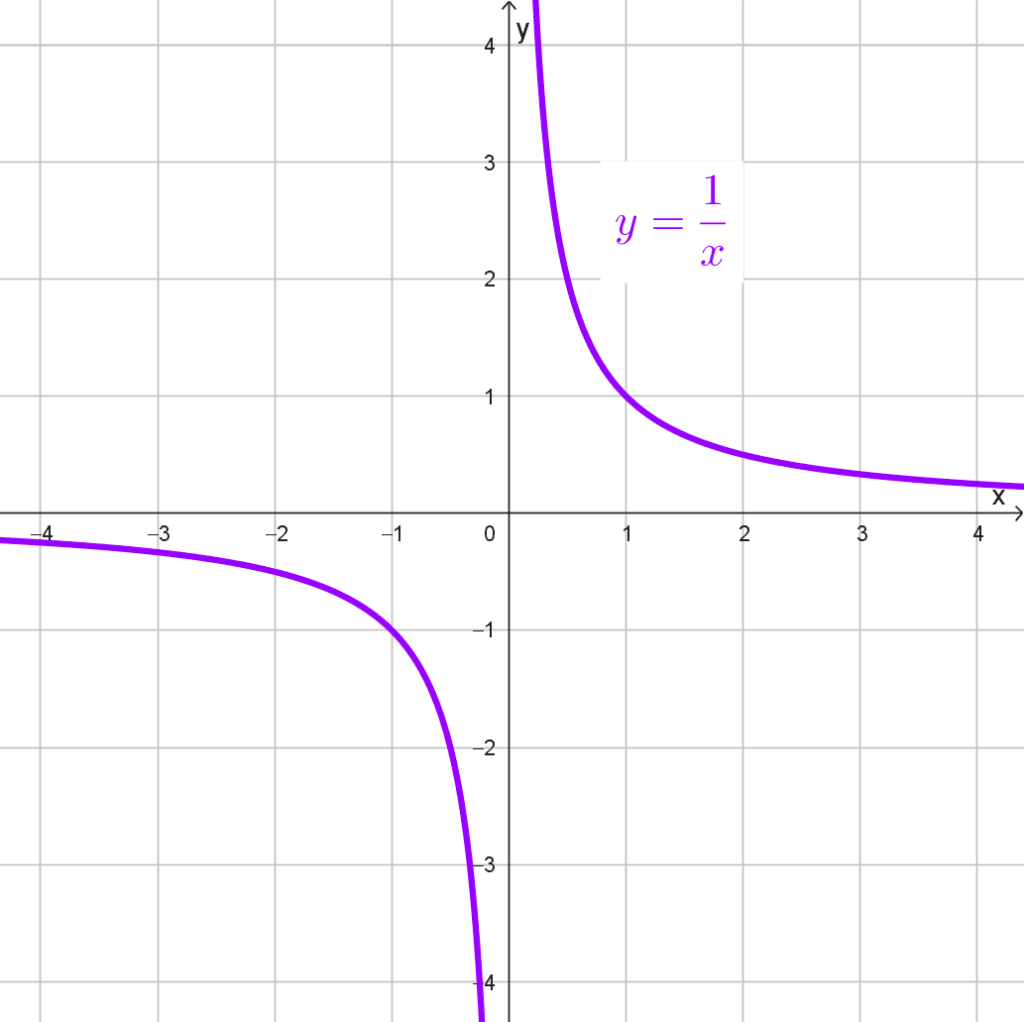
Recordemos que no todas las hipérbolas son funciones, sin embargo, la ecuación y = k/x es también una función matemática conocida como la función de proporcionalidad inversa. 

Ejemplos

1. *xy=1*
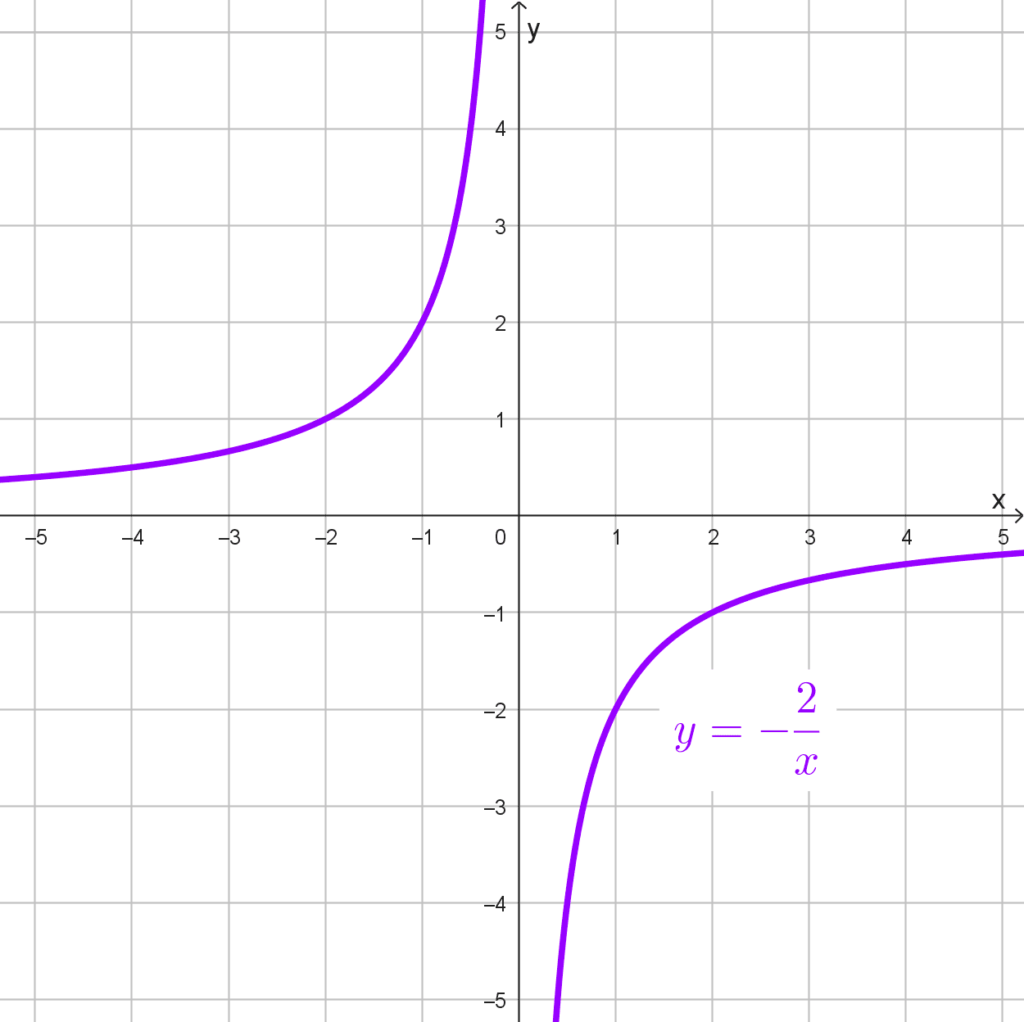
2. *y=-\dfrac{2}{x}*
3. *y=\dfrac{3}{4x}*
4. *y=-\dfrac{5}{x}*

Demostración de la ecuación

Aplicaremos la rotación de 45° a la ecuación original *y^2-x^2=a^2* para obtener su forma transformada. Comenzamos utilizando las fórmulas de transformación:

*x=x'\cos\theta-y'\sin\theta, \quad y=x'\sin\theta+y'\cos\theta*

Con *\theta=45^\circ,* tenemos *\cos 45^\circ=\sin 45^\circ=\dfrac{\sqrt{2}}{2}.* 

Sustituyendo:

*x=\dfrac{\sqrt{2}}{2}(x'-y')~~~~~ y=\dfrac{\sqrt{2}}{2}(x'+y')*

Sustituyendo x e y en *y^2-x^2=a^2:*

*\left(\dfrac{\sqrt{2}}{2}(x'+y')\right)^2-\left(\dfrac{\sqrt{2}}{2}(x'-y')\right)^2=a^2*

Expandimos los términos:

*\dfrac{2}{4} \left((x')^2+2x'y'+(y')^2\right)-\dfrac{2}{4} \left((x')^2-2x'y'+(y')^2\right)=a^2*

*\dfrac{1}{2} \left((x')^2+2x'y'+(y')^2\right)-\dfrac{1}{2} \left((x')^2-2x'y'+(y')^2\right)=a^2*

Distribuimos y agrupamos términos:

*\dfrac{1}{2}\left((x')^2+2x'y'+(y')^2-(x')^2+2x'y'-(y')^2\right)=a^2*

*\dfrac{1}{2} \left(4x'y'\right)=a^2*

Simplificando:

*2x'y'=a^2*

*x'y'=\dfrac{a^2}{2}*

Ejercicios resueltos

Ejercicio 1

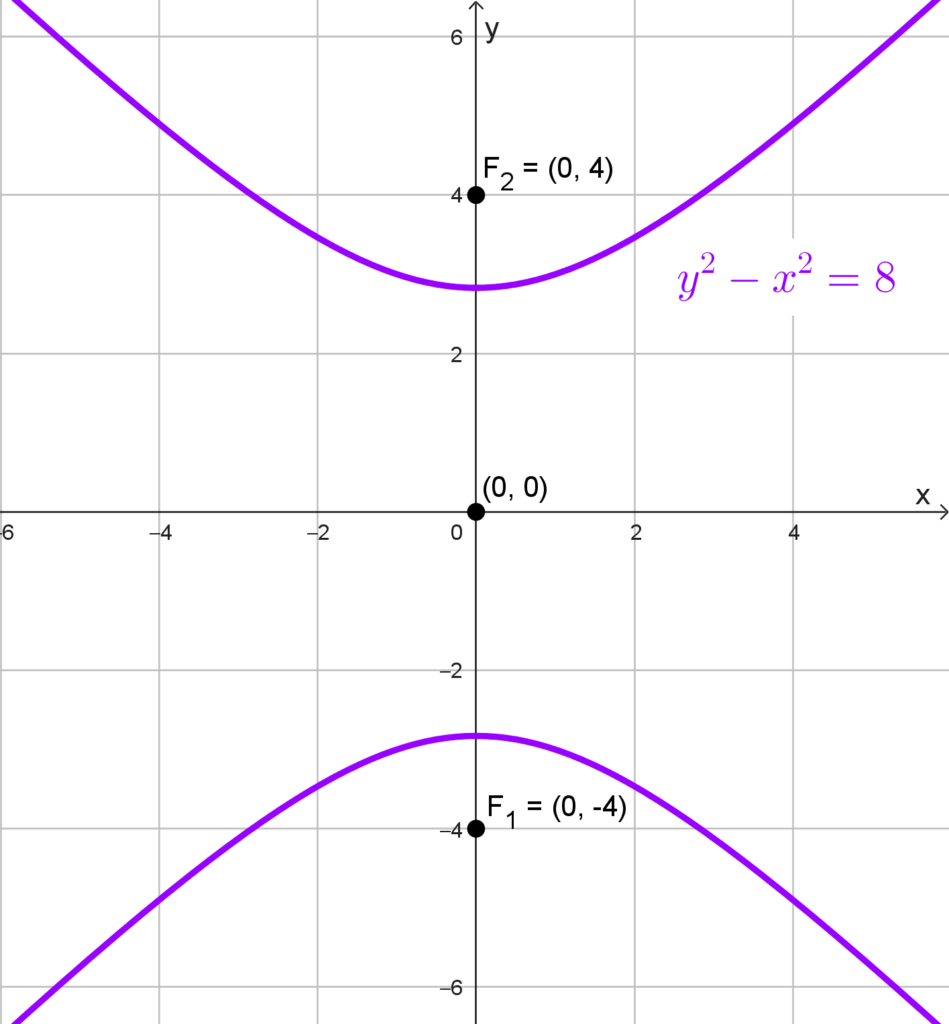
Dados los focos F₁(0, -4) y F₂(0, 4) de una hipérbola equilátera, obtener su ecuación.

Solución

Primero, identificamos que la distancia entre los focos es  2c=8 , por lo que  c=4 . 

En una hipérbola equilátera, se cumple la relación *c=\sqrt{2}a.* Despejando a:

*a=\dfrac{c}{\sqrt{2}}=\dfrac{4}{\sqrt{2}}=2\sqrt{2}*

Dado que la hipérbola es vertical porque sus focos están sobre el eje y, su ecuación tiene la forma *y^2-x^2=a^2.*

Sustituimos *a^2=(2\sqrt{2})^2=8:*

*y^2-x^2=8*

Por tanto, la ecuación de la hipérbola es:

*\boxed{y^2-x^2=8}*

Ejercicio 2

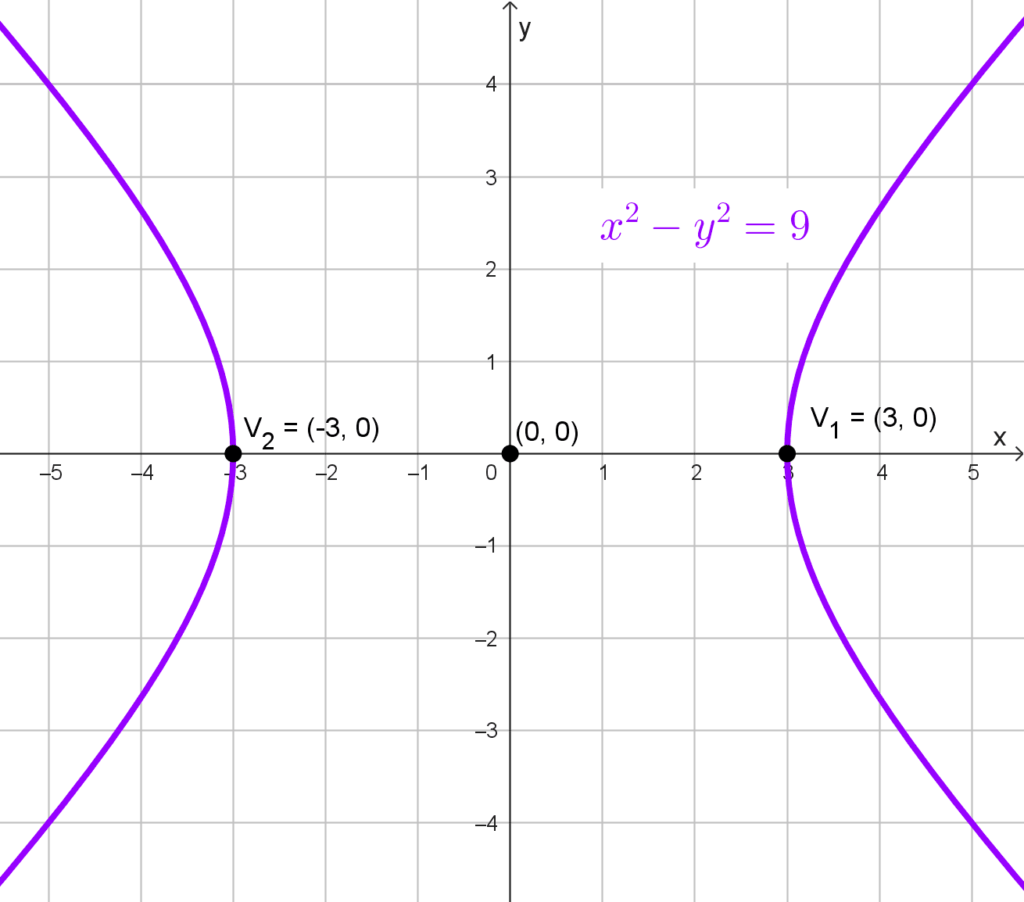
Una hipérbola equilátera tiene como vértices los puntos V₁(3, 0) y V₂(-3, 0). Encuentra su ecuación.

Solución

La distancia entre los vértices es  2a=6, por lo que  a=3. Como la hipérbola es horizontal, su ecuación es:

*x^2-y^2=a^2*

Sustituimos *a^2=3^2=9:*

*x^2-y^2=9*

La ecuación de la hipérbola es:

*\boxed{x^2-y^2=9}*

Ejercicio 3

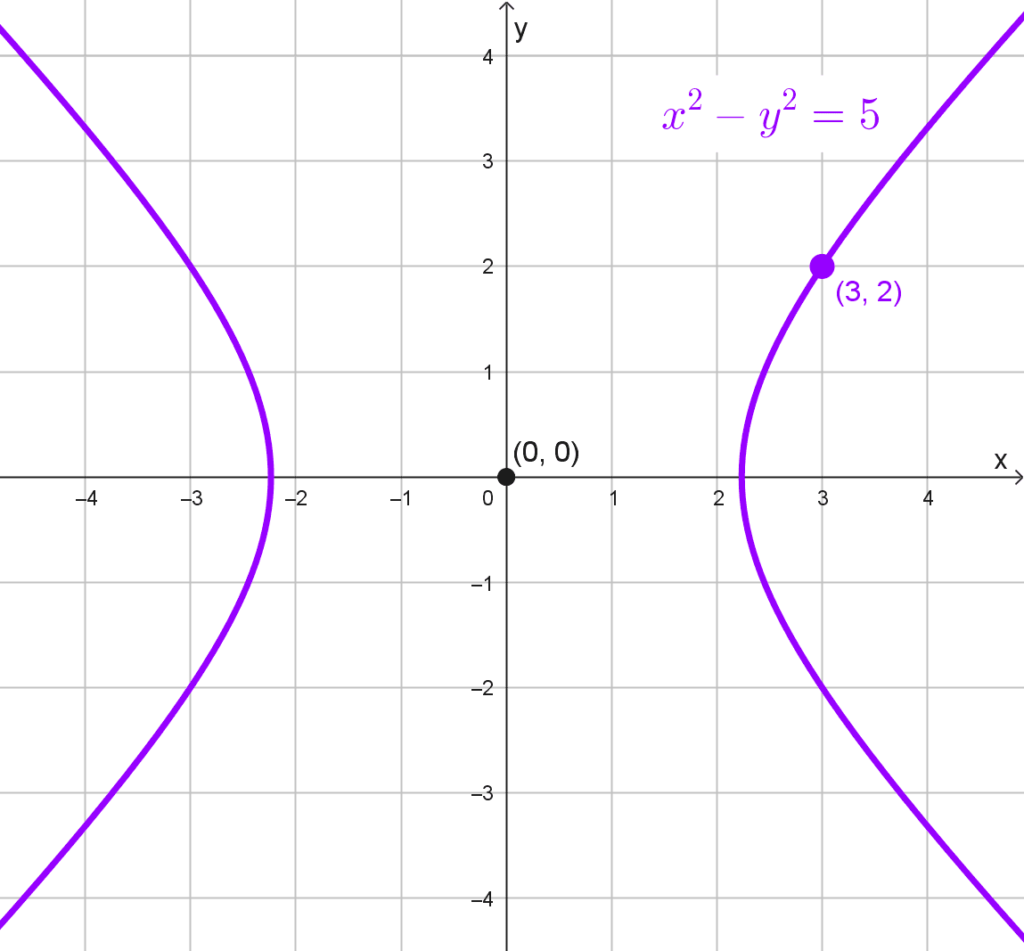
Determinar la ecuación de la hipérbola equilátera horizontal que pasa por el punto (3, 2).

Solución

La ecuación de una hipérbola equilátera horizontal es: *x^2-y^2=a^2.*

Sustituimos las coordenadas del punto dado (x, y) = (3, 2):

*3^2-2^2=a^2*

Resolviendo:

*9-4=a^2 → a^2=5.*

Por lo tanto, la ecuación de la hipérbola es:

*\boxed{x^2-y^2=5}*

Ejercicio 4

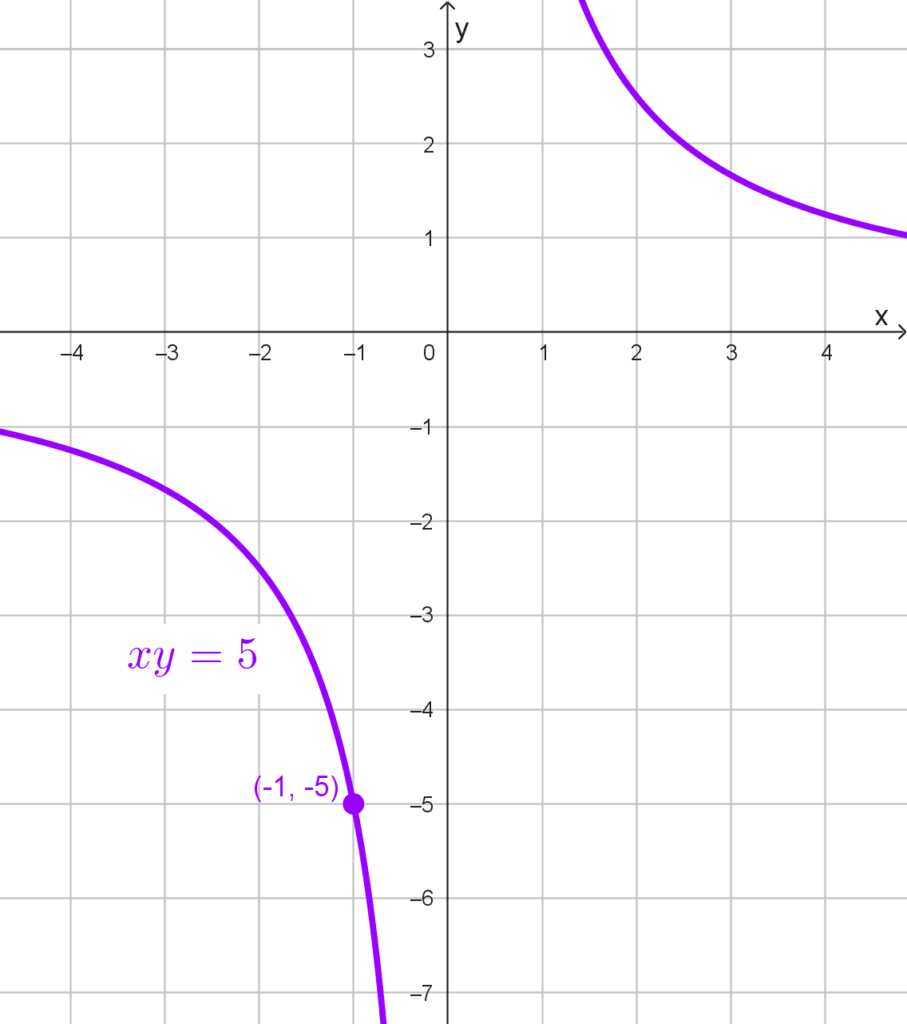
Hallar la ecuación de la hipérbola equilátera que pasa por el punto (-1, -5) y tiene por asíntotas a los ejes coordenados.

Solución

Cuando las asíntotas son los ejes coordenados, la ecuación de la hipérbola es: xy=k.

Sustituimos las coordenadas del punto dado (x, y) = (-1, -5) para encontrar k:

*(-1)(-5)=k → k=5*

Por lo tanto, la ecuación de la hipérbola es:

*\boxed{xy=5}*

Recursos adicionales

El siguiente video contiene más información acerca del tiema:

Bibliografía consultada

Para crear este artículo se han consultado las siguientes fuentes:

• Lehmann, C. (1989). Geometría Analítica. Limusa.
• Sullivan, M. (2006). Álgebra y Trigonometría. Pearson Educación. 
• Swokowski, E. y Cole, J. (2009). Álgebra y Trigonometría con Geometría Analítica. Cengage Learning.