
Hipérbola: qué es, elementos, ecuaciones y ejemplos
Una hipérbola es una curva abierta que consta de dos ramas que se alejan indefinidamente. Se define como el lugar geométrico de todos los puntos en un plano tales que la diferencia de las distancias a dos puntos fijos, llamados focos, es constante en valor absoluto.
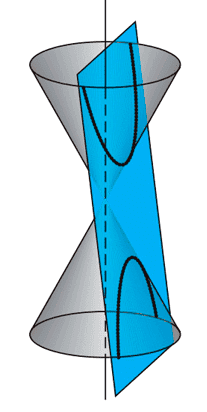
Desde la perspectiva de las secciones cónicas, una hipérbola se obtiene al intersectar un cono doble con un plano que corta ambas hojas del cono sin pasar por el vértice. La forma de la curva dependerá del ángulo de inclinación del plano con respecto al eje del cono.
A continuación, explicaremos más aspectos sobre la hipérbola en matemáticas: sus elementos, ecuaciones, ejemplos, propiedades y aplicaciones, entre otras cosas.
Índice
Elementos
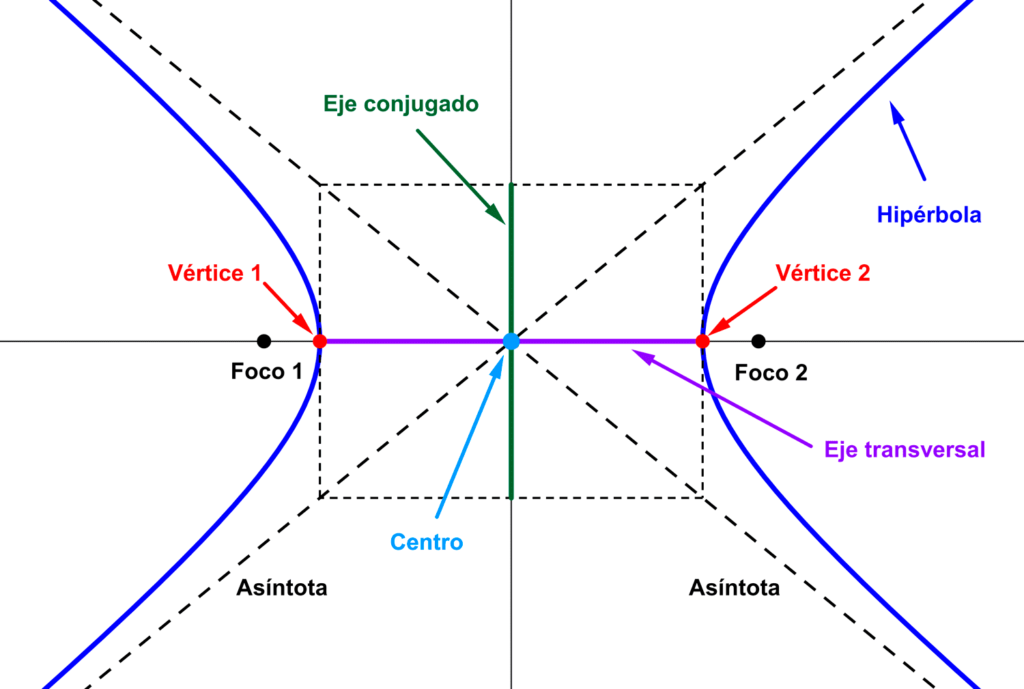
Las partes principales de una hipérbola son las siguientes:
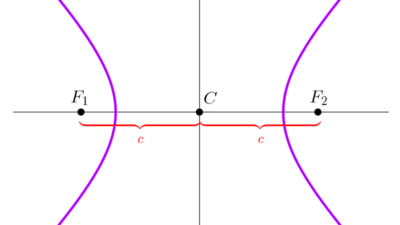
- Focos: son puntos fijos del plano. La recta sobre la que se ubican se llama eje focal, principal o real.
- Centro: es el punto medio entre los dos focos. La recta perpendicular al eje focal que pasa por el centro se llama eje imaginario.
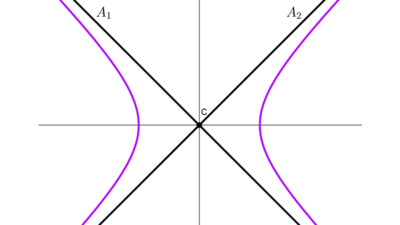
- Vértices: son dos puntos de intersección de la hipérbola con su eje principal.
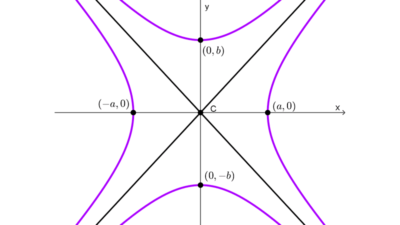
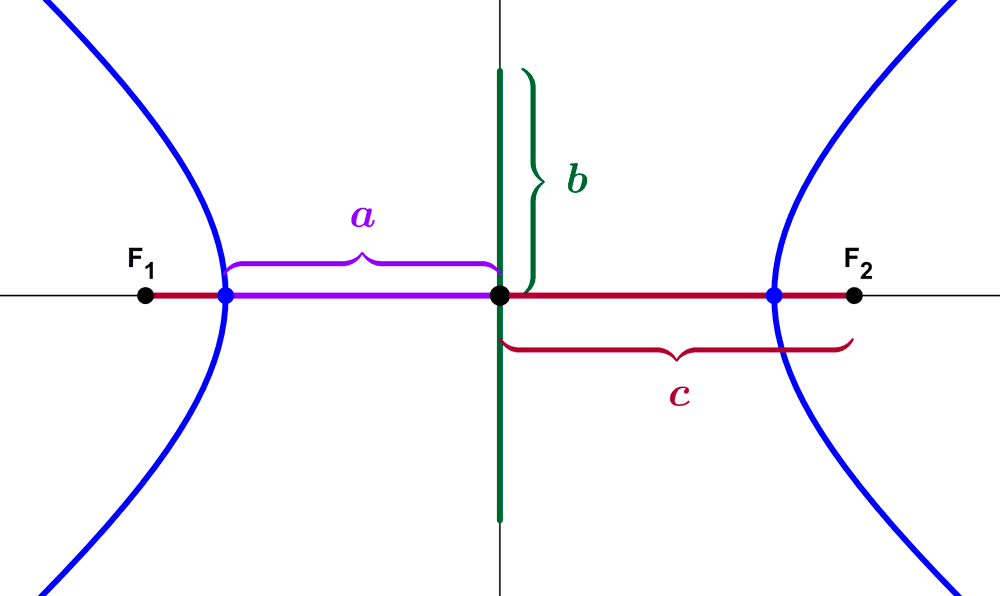
- Eje transversal: es el segmento que une los vértices de la hipérbola pasando por el centro. La longitud de este eje se simboliza 2a, donde a es la distancia del centro a un vértice. A la mitad de este eje se le llama semieje transversal y su longitud es a.
- Eje conjugado: es el segmento perpendicular al eje transversal que pasa por el centro, su longitud es 2b. A la mitad de este eje se le llama semieje conjugado y su longitud es b.
- Distancia focal: es la distancia entre los focos, se simboliza como 2c, donde c es la distancia del centro a un foco. Este valor está relacionado con los semiejes mediante la relación fundamental c2 = a2 + b2. La distancia focal siempre es mayor que la distancia entre los vértices (2c > 2a, c > a).
- Asíntotas: son líneas rectas a las cuales las ramas de la hipérbola se aproximan a medida que se extienden hacia el infinito pero nunca las cortan. Las ecuaciones de las asíntotas se obtienen de la ecuación de la hipérbola.
- Excentricidad: es la razón entre la distancia del centro a un foco (c) y la distancia del cenro a un vértice: e = c / a. En toda hipérbola, la excentricidad es mayor a uno (e > 1).
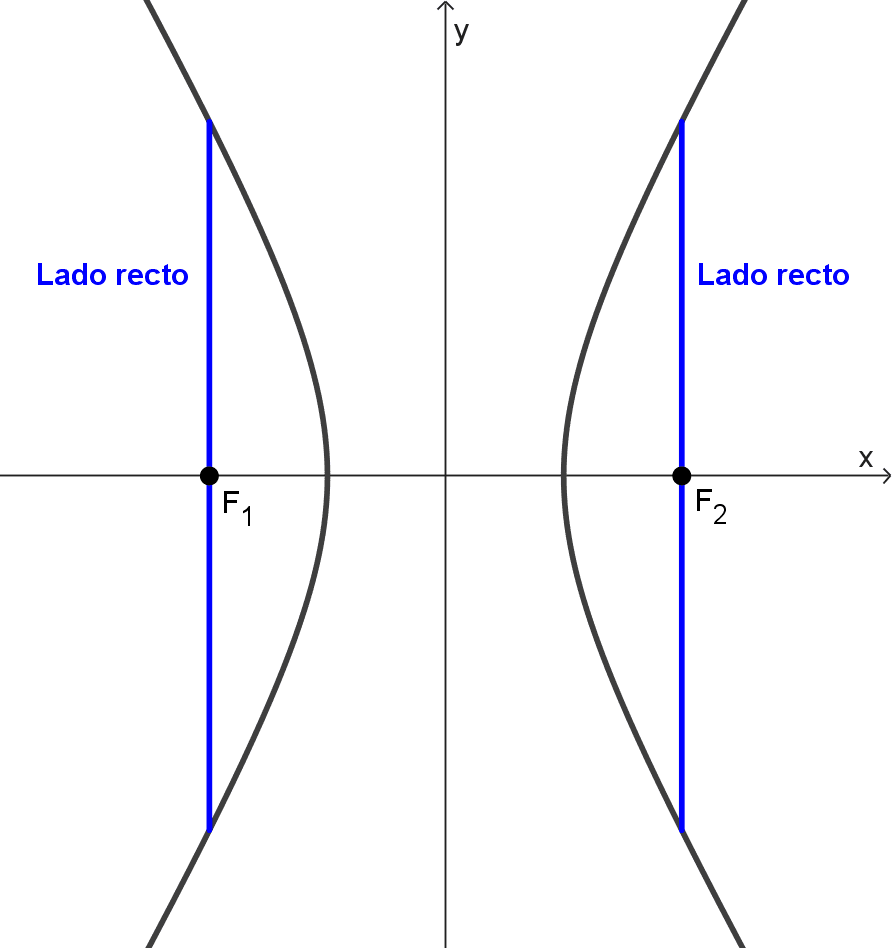
- Lado recto: es un segmento que une dos puntos de la hipérbola, es perpendicular al eje transverso y pasa por un foco. Toda hipérbola tiene dos lados rectos cuyas longitudes son LR = 2b2 / a.
Ecuación canónica
La ecuación canónica u ordinaria de la hipérbola en coordenadas cartesianas se presenta en formas diferentes dependiendo de la orientación del eje transversal (horizontal o vertical) y de las coordenadas del centro (en el origen u otro punto).
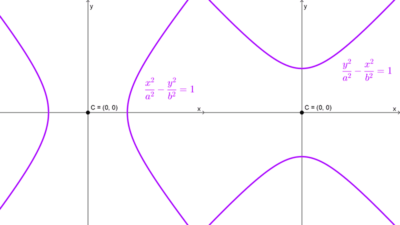
1) Si el centro es el origen de coordenadas (0, 0), las ecuaciones son:
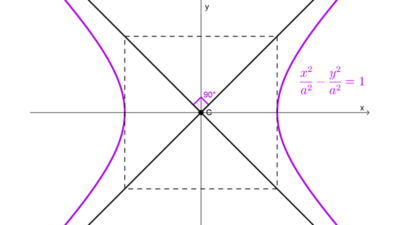
- Hipérbola horizontal: *\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1*
- Hipérbola vertical: *\dfrac{y^2}{a^2}-\dfrac{x^2}{b^2}=1*
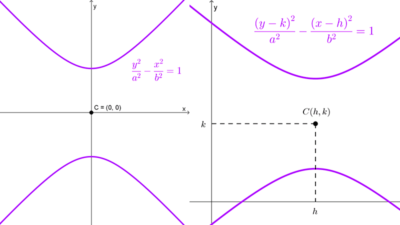
2) Si el centro es un punto (h, k) del plano cartesiano, las ecuaciones son:
- Hipérbola horizontal: *\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1*
- Hipérbola vertical: *\dfrac{(y-k)^2}{a^2}-\dfrac{(x-h)^2}{b^2}=1*
En los cuatro casos, a es la longitud del semieje transversal y b es la longitud del semieje conjugado. A diferencia de la elipse, en la hipérbola el parámetro b puede ser mayor que a, y esto afecta la "apertura" de las ramas. Las demostraciones de las fórmulas se harán más adelante en este artículo.
Ejemplos
Algunos ejemplos de hipérbolas son:
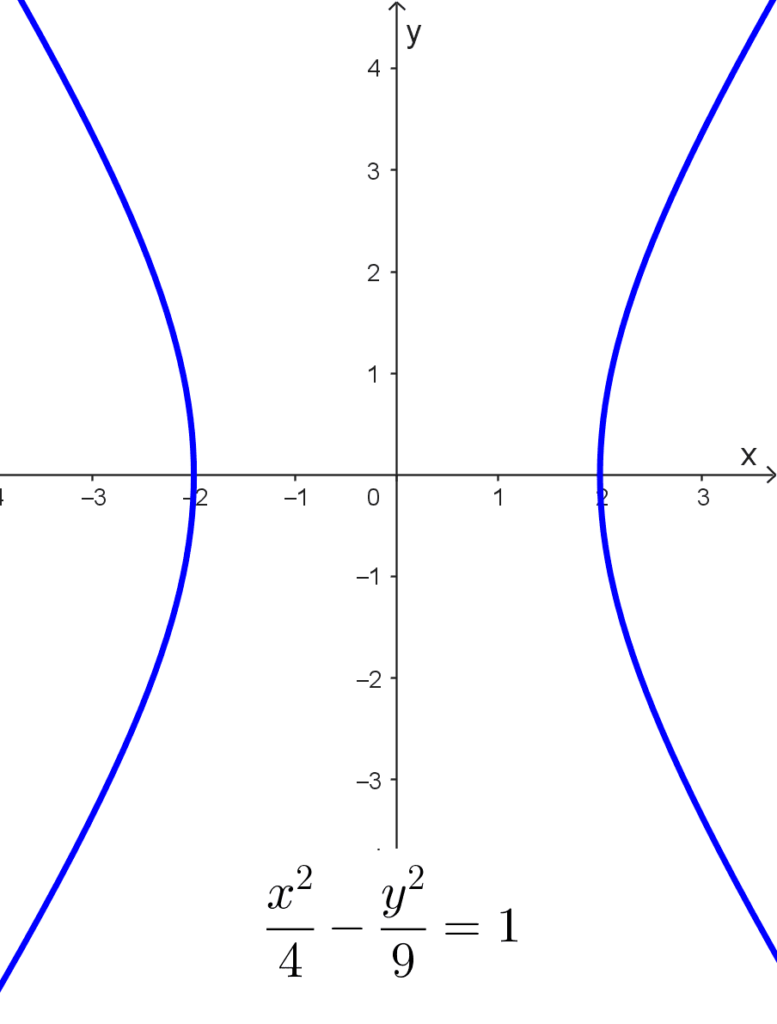
- *\dfrac{x^2}{4}-\dfrac{y^2}{9}=1* es una hipérbola horizontal centrada en el origen de coordenadas cuyas ramas abren hacia los lados. El semieje transversal es *a=\sqrt{4}=2* y el conjugado es *b=\sqrt{9}=3.*
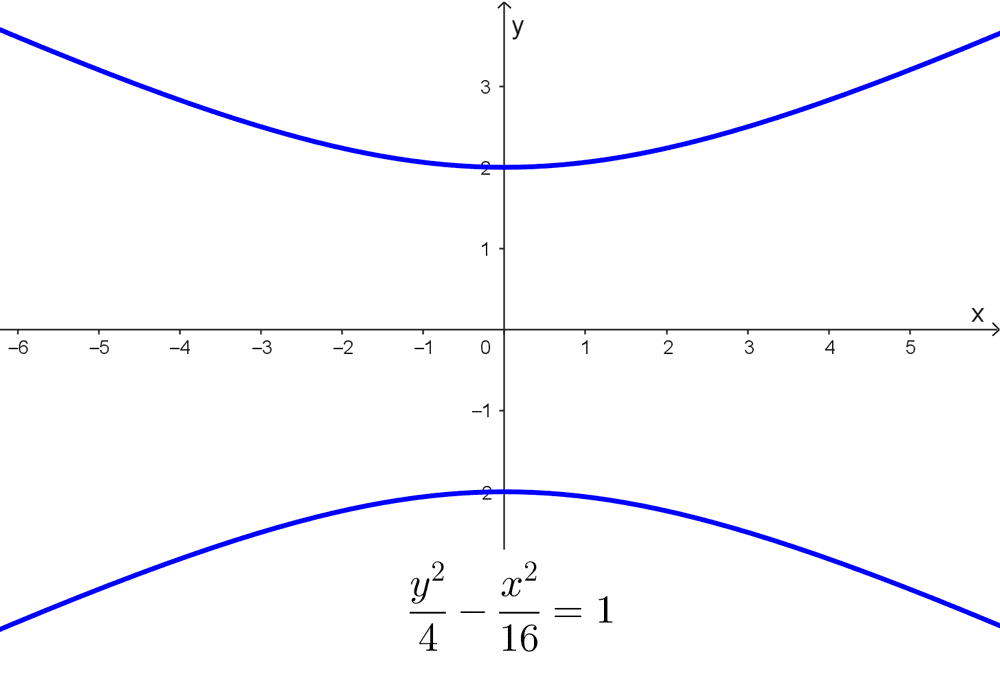
- *\dfrac{y^2}{4}-\dfrac{x^2}{16}=1* es una hipérbola con eje transverso vertical y centro en (0, 0) cuyas ramas abren hacia arriba y abajo. El semieje transverso es *a=\sqrt{4}=2* y el semieje conjugado es *b=\sqrt{16}=4.*
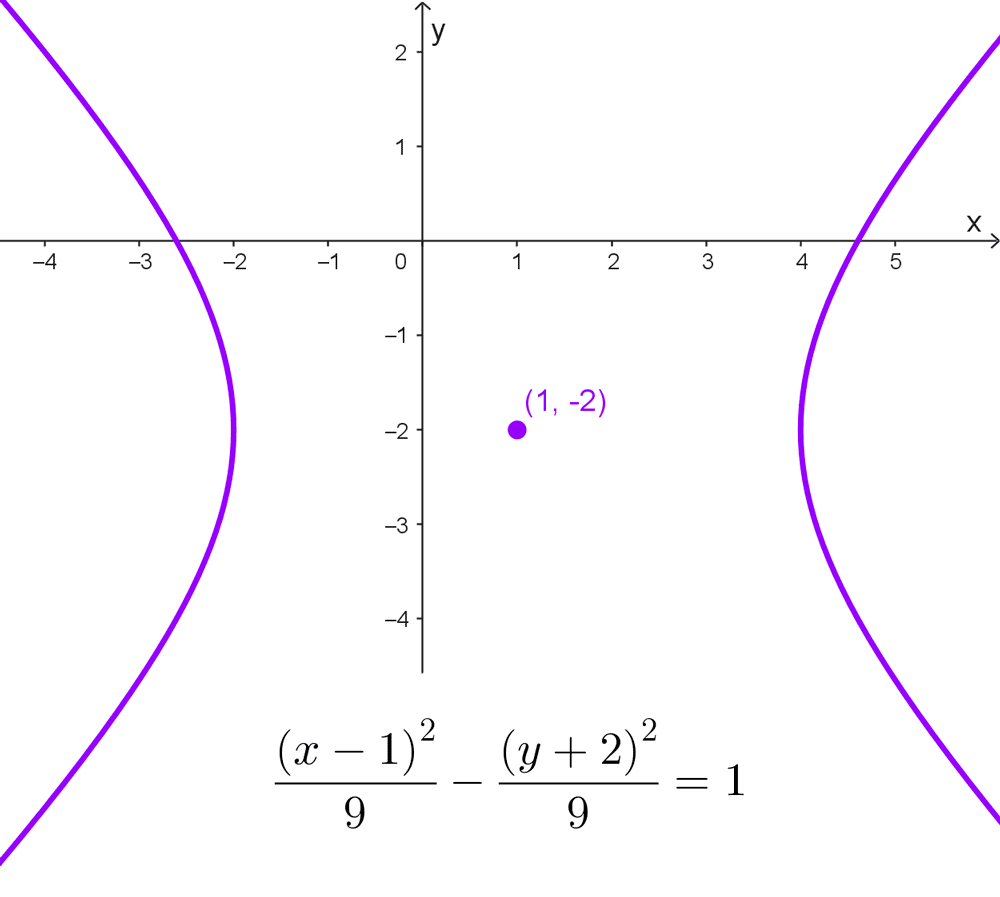
- *\dfrac{(x-1)^2}{9}-\dfrac{(y+2)^2}{9}=1* es una hipérbola con eje transversal horizontal y centro en (1, -2). Como las longitudes de los semiejes son iguales *(a=b=\sqrt{9}=3),* se llama hipérbola equilátera.
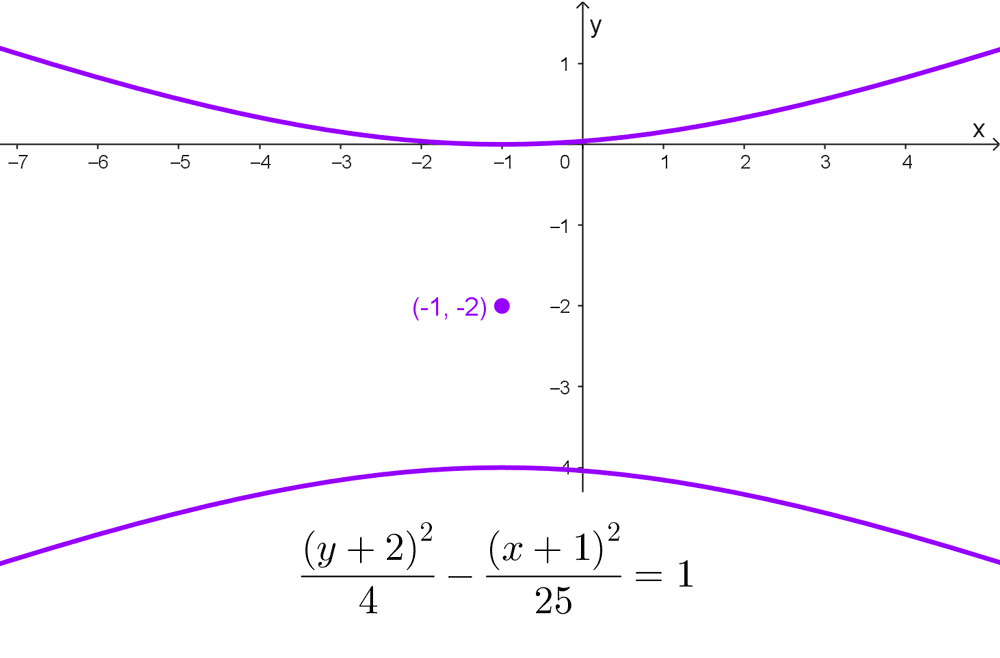
- *\dfrac{(y+2)^2}{4}-\dfrac{(x+1)^2}{25}=1* es una hipérbola vertical con centrada en (-1, 2), su semiejes son *a=\sqrt{4}=2* y *b=\sqrt{25}=5.*
Para determinar la orientación del eje transversal de una hipérbola, se debe observar el término positivo de la ecuación. Si el término positivo es el que contiene x, el eje transversal es horizontal. Si el término positivo es el que contiene y, el eje transversal es vertical.
Los elementos de una hipérbola (focos, centro, vértices, ejes, asíntotas, excentricidad y lado recto) pueden obtenerse a partir de su ecuación canónica. Puedes ver cómo hacerlo en el artículo de ejercicios de hipérbola:
Ecuación general
La ecuación general de la hipérbola es Ax2 + Cy2 + Dx + Ey + F = 0 donde A y C tienen distintos signos (A ⋅ C < 0) y los ejes de la hipérbola son paralelos a los ejes cartesianos. Si la hipérbola tiene una rotación de ejes, se introduce un término mixto en la ecuación, resultando en Ax2 + Bxy + Cy2 + Dx + Ey + F = 0, donde se debe cumplir que B2 - 4AC > 0.
Ejemplos de hipérbolas en su forma general:
- *9x^2-4y^2-36=0*
- *-4x^2+25y^2-8x+100y-4=0*
- *9x^2-4y^2-54x+117=0*
- *5x^2-2y^2-10x+8y-13=0*
- *-7x^2+12y^2+28x+72y-4=0*
Propiedades
Las hipérbolas tienen una serie de características importantes:
- Relación fundamental: la distancia del centro a cada foco (c), del centro a cada vértice (a) y la longitud del eje semieje conjugado (b) están relacionados por la fórmula c2 = a2 + b2.
- Simetría: la hipérbola es una curva simétrica respecto a dos rectas perpendiculares que pasan por su centro: el eje focal y el eje imaginario, los cuales contienen al eje transversal y al eje conjugado, respectivamente. El eje focal pasa por los vértices y focos, mientras que el eje imaginario es perpendicular y también atraviesa el centro.
- Asíntotas: son rectas a las que la hipérbola se aproxima pero nunca toca. Se extienden desde el centro y delimitan la región por la que se despliega la curva.
- Excentricidad: es una medida de cuán "abierta" o "estrecha" es la hipérbola. Su valor es siempre mayor que 1. A mayor excentricidad, las ramas se abren más ampliamente; a menor (pero aún mayor a 1), son más cerradas.
- Propiedad reflectiva: como en las elipses, cualquier rayo que pasa por un foco se refleja hacia el otro. Esta propiedad es clave en aplicaciones de óptica y acústica.
Aplicaciones
La hipérbola tiene usos en la vida real y en ciencias que aprovechan sus propiedades geométricas:
- Uso en navegación: en sistemas como LORAN, las hipérbolas se utilizan para determinar la posición de un objeto en movimiento, como un barco. El receptor mide la diferencia de tiempo entre señales emitidas por dos transmisores, lo que equivale a una diferencia de distancia. Esta diferencia sitúa al barco sobre una hipérbola cuyos focos son las posiciones de los transmisores.
- Acústica y óptica: las propiedades reflectivas de las hipérbolas se aprovechan en el diseño de antenas y espejos. Toda onda que pasa por un foco se refleja hacia el otro, lo que permite enfocar sonido o luz con gran precisión. Esto es útil en telescopios, sistemas acústicos y comunicaciones.
- Astronomía: las trayectorias de algunos cometas y sondas espaciales que escapan del campo gravitacional de un planeta siguen órbitas hiperbólicas. Estas trayectorias abiertas se modelan con precisión mediante ecuaciones de hipérbolas.
- Localización mediante señales: sistemas de rastreo por radio y variantes del GPS usan diferencias de tiempo o distancia entre señales para determinar la posición de un objeto. Estas diferencias definen hipérbolas con focos en los transmisores, sobre las cuales se encuentra el receptor.
- Diseño de radiadores en ingeniería térmica: algunos sistemas de disipación térmica, especialmente en el espacio, utilizan superficies hiperbólicas para maximizar la eficiencia en la emisión de calor por radiación.
- Análisis de señales en telecomunicaciones: en técnicas como TDOA (Time Difference of Arrival), las hipérbolas permiten calcular la posición de un emisor a partir de las diferencias en los tiempos de llegada de una señal a distintas antenas receptoras.
- Arquitectura: en auditorios y teatros, se pueden emplear superficies hiperbólicas para reflejar el sonido desde una fuente a un punto específico, mejorando la acústica sin necesidad de amplificación electrónica.
Resumen de ecuaciones
Las fórmulas y ecuaciones más importantes vistas hasta ahora se resumen en la siguiente tabla. Recuerde que *c=\sqrt{a^2+b^2}.*
| Ecuación canónica | Eje transversal | Centro | Focos | Vértices | Asíntotas |
|---|---|---|---|---|---|
| *\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1* | Sobre el eje x | (0, 0) | (±c, 0) | (±a, 0) | y = ± (b / a) x |
| *\dfrac{y^2}{a^2}-\dfrac{x^2}{b^2}=1* | Sobre el eje y | (0, 0) | (0, ±c) | (0, ±a) | y = ± (a / b) x |
| *\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1* | Paralelo al eje x | (h, k) | (h ± c, k) | (h ± a, k) | y - k = ± (b / a) (x - h) |
| *\dfrac{(y-k)^2}{a^2}-\dfrac{(x-h)^2}{b^2}=1* | Paralelo al eje y | (h, k) | (h, k ± c) | (h, k ± a) | y - k = ± (a / b) (x - h) |
Demostraciones de las ecuaciones
Aquí se presentan las demostraciones de las fórmulas de la hipérbola.
Demostración de la ecuación canónica
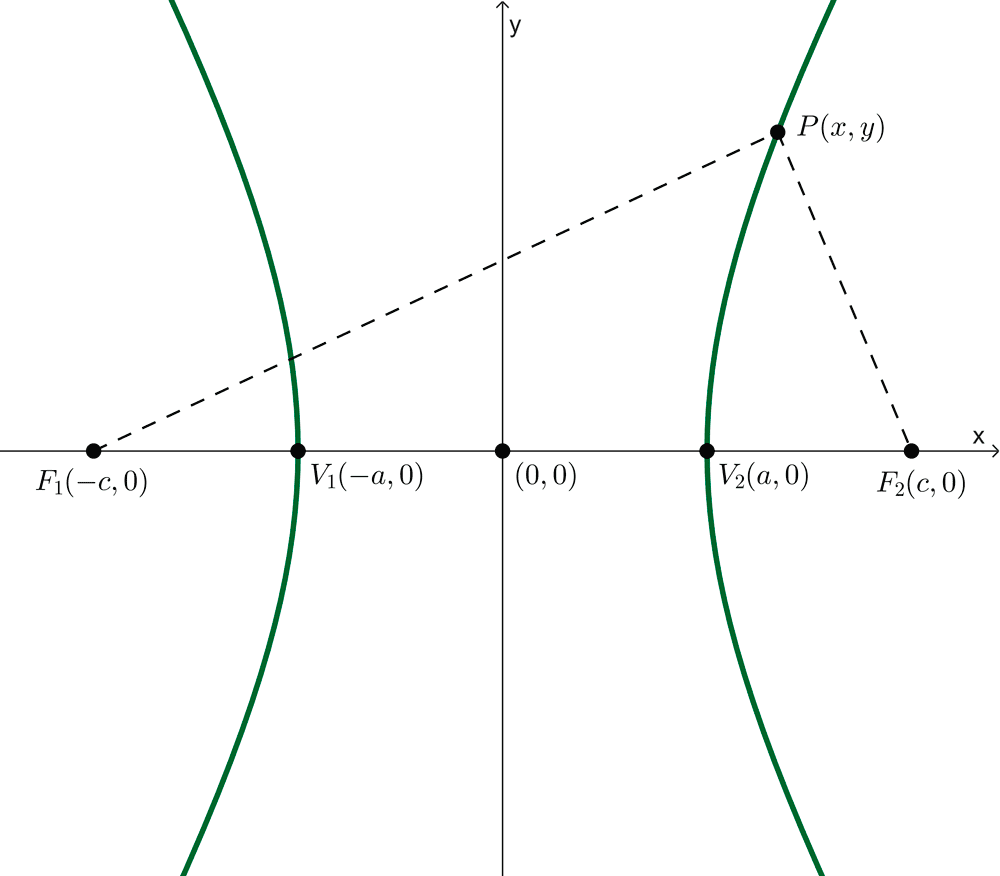
Para deducir la ecuación de la hipérbola de manera simplificada, consideraremos un caso particular donde el eje transversal está alineado con el eje x y el centro de la hipérbola está en el origen (0,0). El proceso es similar al realizado con la elipse.
En este caso, tomamos un punto genérico P(x, y) en la hipérbola. Los vértices de la hipérbola se encuentran en las coordenadas V1(-a, 0) y V2(a, 0), mientras que los focos están ubicados en F1(-c, 0) y F2(c, 0).
La definición de la hipérbola establece que la diferencia absoluta de las distancias de cualquier punto P(x, y) en la hipérbola a los dos focos F1 y F2 es igual a una constante:
*|d(P,F_2)-d(P,F_1)|=k*
Para determinar cuál es la constante, consideremos el punto V1(-a, 0), que es uno de los vértices de la hipérbola.
La distancia desde V1(-a, 0) hasta el foco F1(-c, 0) es: *d(V_1,F_1)=|-a+c|=c-a*
La distancia desde V1(-a, 0) hasta el foco F2(c, 0) es: *d(V_1,F_2)=|-a-c|=a+c*
Aplicando la definición de la hipérbola, la diferencia absoluta de estas distancias es:
*|d(V_1,F_2)-d(V_1,F_1)|=|(a+c)-(c-a)|=|a+c-c+a|=|2a|=2a*
Por lo tanto, la constante de la que habla la definición es 2a (la longitud del eje transversal). Reemplazando en la definición general:
*|d(P,F_2)-d(P,F_1)|=2a*
Quitando las barras de valor absoluto, la diferencia de las distancias desde P hasta los focos es igual a ±2a.
*d(F_1,P)-d(F_2,P)=±2a*
Usamos la fórmula de la distancia:
*\sqrt{(x+c)^2+y^2}-\sqrt{(x-c)^2+y^2}=±2a*
Aislamos a los radicales:
*\sqrt{(x+c)^2+y^2}=±2a+\sqrt{(x-c)^2+y^2}*
Elevamos ambos lados al cuadrado.
*(x+c)^2+y^2=4a^2± 4a\sqrt{(x-c)^2+y^2}+(x-c)^2+y^2*
Eliminamos paréntesis y simplificamos:
*x^2+2cx+c^2+y^2=4a^2± 4a\sqrt{(x-c)^2+y^2}+x^2-2cx+c^2+y^2*
Simplificamos aislando un radical:
*4cx-4a^2=\pm 4a\sqrt{(x-c)^2+y^2}*
Dividimos ambos lados entre cuatro:
*cx-a^2=\pm a\sqrt{(x-c)^2+y^2}*
Elevamos ambos miembros al cuadrado:
*(cx-a^2)^2=a^2[(x-c)^2+y^2]*
Simplificamos:
*c^2x^2-2ca^2x+a^4=a^2(x^2-2cx+c^2+y^2)*
Eliminamos paréntesis y simplificamos:
*c^2x^2+a^4=a^2x^2+a^2c^2+a^2y^2*
Reordenamos los términos:
*(c^2-a^2)x^2-a^2y^2=a^2c^2-a^4*
Factorizamos *a^2* en el lado derecho.
*(c^2-a^2)x^2-a^2y^2=a^2(c^2-a^2)*
La condición que se debe cumplir en toda hipérbola es que la distancia focal siempre es mayor a la longitud entre los vértices:
*2a<2c*
*a<c*
Puesto que *a<c,* también se tiene *a^2<c^2,* por lo que *c^2-a^2>0.* Hacemos *b^2=c^2-a^2, b>0.* Entonces, la ecuación se escribe:
*b^2x^2-a^2y^2=a^2b^2*
Dividiendo ambos miembros entre *a^2b^2:*
*\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1*
Que es la ecuación canónica de la hipérbola con centro en (0, 0), focos en (-c, 0) y (c, 0) y vértices en (-a, 0) y (a, 0). El eje transversal está sobre el eje x.
Para el caso de un eje transverso sobre el eje y, la deducción llevará a que el término negativo contiene a x. Cuando el centro sea (h, k), utilizamos las fórmulas de transformación de coordenadas reemplazando x por x-h e y por y-k.
Demostración de la ecuación general
Para llegar a la ecuación general de una hipérbola partiremos de su forma canónica con centro en (h, k).
Empezamos con la forma canónica para eje horizontal:
*\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1*
Multiplicamos ambos lados de la ecuación por *a^2b^2* para eliminar los denominadores:
*b^2(x-h)^2-a^2(y-k)^2=a^2b^2*
Expandiendo y reagrupando los términos:
*b^2(x^2-2hx+h^2)-a^2(y^2-2ky+k^2)=a^2b^2*
*b^2x^2-2b^2hx+b^2h^2-a^2y^2+2a^2ky-a^2k^2=a^2b^2*
Reordenamos:
*b^2x^2-a^2y^2-2b^2hx+2a^2ky+(b^2h^2-a^2k^2-a^2b^2)=0*
Esta corresponde a la ecuación general de segundo grado:
*Ax^2+Cy^2+Dx+Ey+F=0*
donde:
- *A=b^2*
- *C=-a^2*
- *D=-2b^2h*
- *E=2a^2k*
- *F=b^2h^2-a^2k^2-a^2b^2*
Para la forma canónica con eje transverso vertical ocurrirá que:
- *A=-b^2*
- *C=a^2*
- *D=2b^2h*
- *E=-2a^2k*
- *F=a^2k^2-b^2h^2-a^2b^2*
Para que una ecuación general de segundo grado de la forma *Ax^2+Cy^2+Dx+Ey+F=0* represente una hipérbola, los coeficientes A y C deben cumplir la condición:
AC < 0
Esto significa que los términos cuadráticos deben ser diferentes de cero y tener diferentes signos.
Recursos adicionales
En el siguiente video verás cómo utilizar GeoGebra para dibujar una hipérbola. Esta es una herramienta matemática dinámica que facilita la visualización y manipulación de figuras geométricas.
En el siguiente video se explica cómo dibujar una hipérbola utilizando herramientas de dibujo técnico, como el compás y la regla. Este método tradicional es esencial para aquellos que están interesados en la precisión y la técnica manual en la representación de figuras geométricas.
Relación de las hipérbolas con las funciones racionales
Las hipérbolas surgen como las gráficas de funciones homográficas, las cuales tienen la forma general:
*f(x)=\dfrac{ax+b}{cx+d}* donde *ad-bc≠0.*
Cuando graficamos estas funciones, obtenemos hipérbolas en las cuales el eje transversal está rotado 45°, y las asíntotas son paralelas a los ejes cartesianos.
Consideremos la función homográfica más simple: *y=\dfrac{k}{x},* conocida como función recíproca o función de proporcionalidad inversa. Esta tiene una gráfica que es una hipérbola con centro en el origen. Las asíntotas de esta hipérbola son las líneas x=0 e y=0, que corresponden a los ejes coordenados.
Es importante señalar que no todas las hipérbolas vistas hasta ahora son funciones. Una función, por definición, asigna a cada valor de x un único valor de y. En cambio, las gráficas de ecuaciones como *\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1* no cumplen con esta propiedad porque para un valor dado de x, puede haber dos posibles valores de y.
Lecturas recomendadas:
- Lehman, C. (1989). Geometría Analítica. Limusa.
- Sullivan, M. (2006). Álgebra y Trigonometría. Pearson Educación.
- Swokowski, E. y Cole, J. (2009). Álgebra y Trigonometría con Geometría Analítica. Cengage Learning.
Otros contenidos sobre hipérbolas





Última actualización del contenido: 07/05/2025
-
Excelente contenido! me acabo de encontrar con tu página, y como ingeniero, docente de geometría y estudiante de matemáticas debo decirte que es un trabaja simplemente hermosos, maravilloso, es genial la forma en la que has abordado cada tema. saludos desde Venezuela!.
-
Excelente contenido.
4 Comentarios
Deja una respuesta





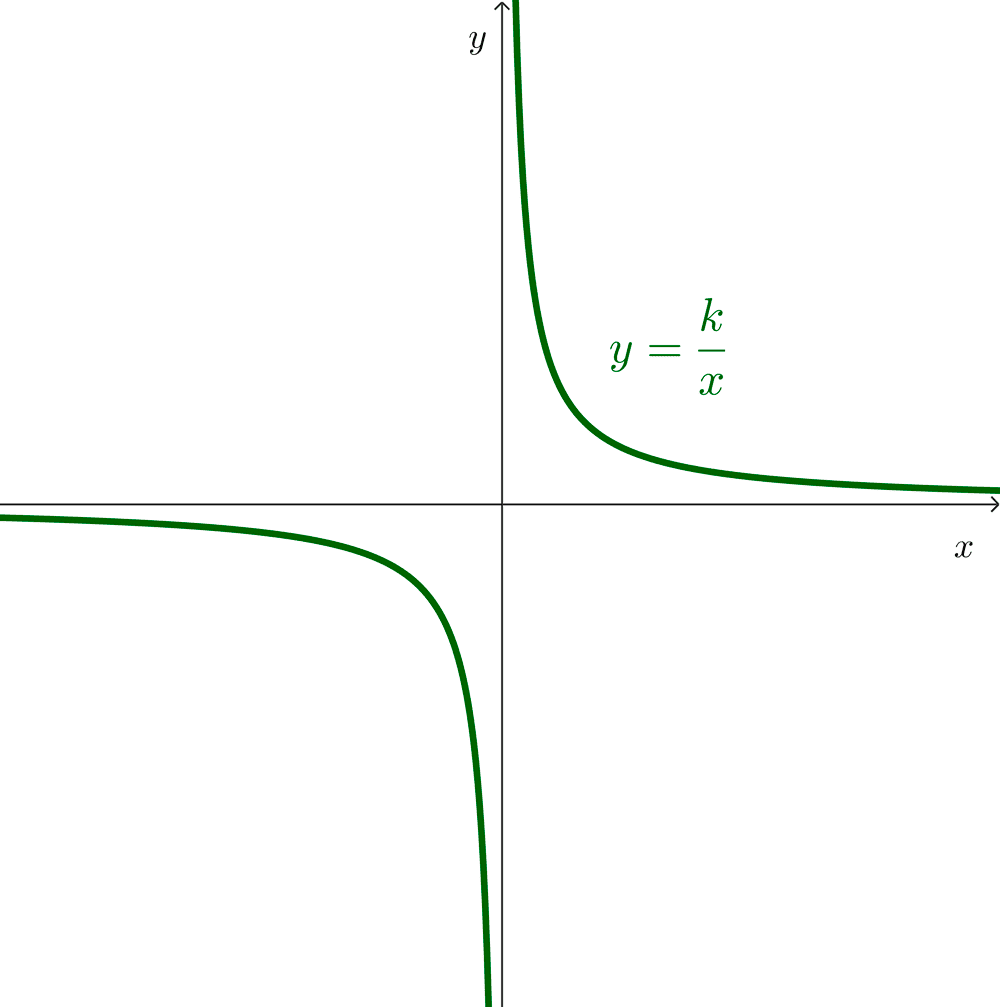
Otros artículos que pueden interesarte