Hipérbolas horizontales y verticales

En este artículo explicamos las hipérbolas horizontales y verticales junto con sus ecuaciones, gráficos, ejemplos y elementos.

Hipérbola horizontal

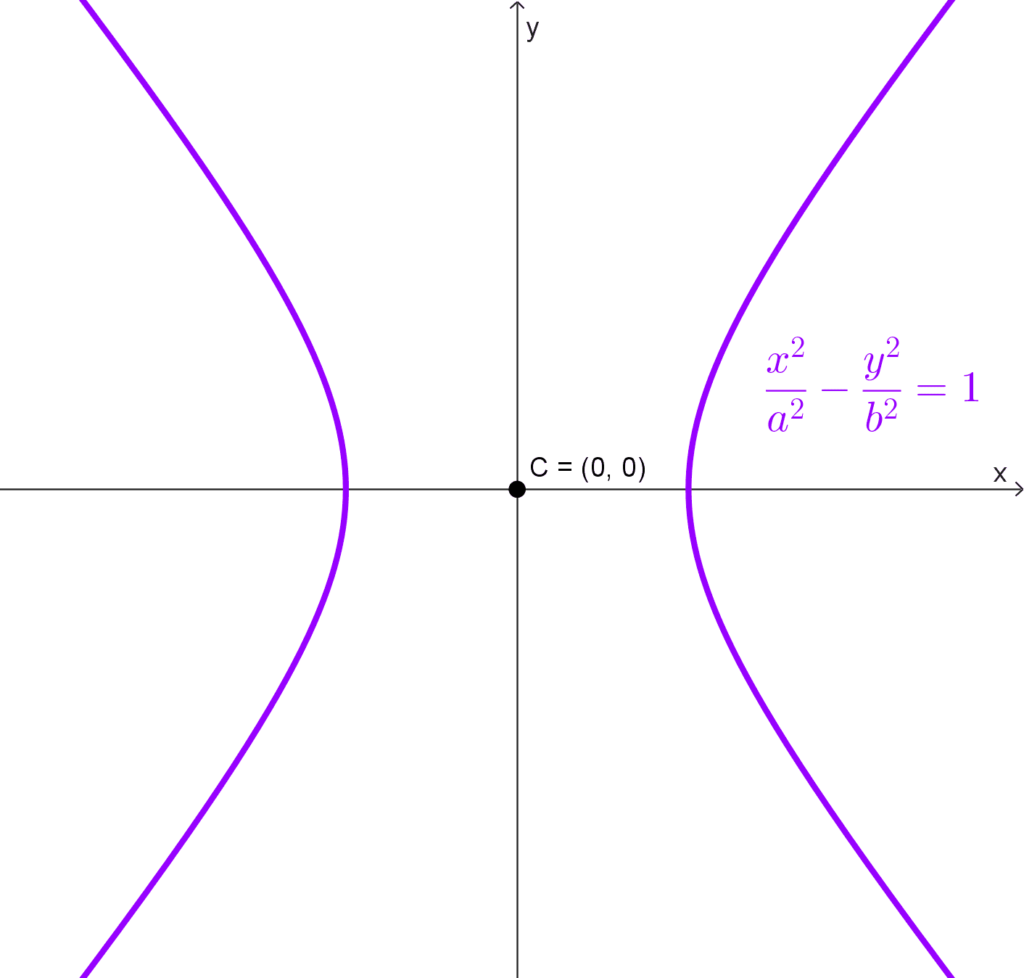
Una hipérbola horizontal es aquella cuyo eje focal (que contiene al eje transversal) es paralelo al eje x o es idéntico al mismo. Las ramas de la hipérbola se abren hacia la izquierda y la derecha. 

La ecuación canónica varía dependiendo de si el centro está en el origen de coordenadas o fuera del origen:

Centro en (0, 0): *\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1*

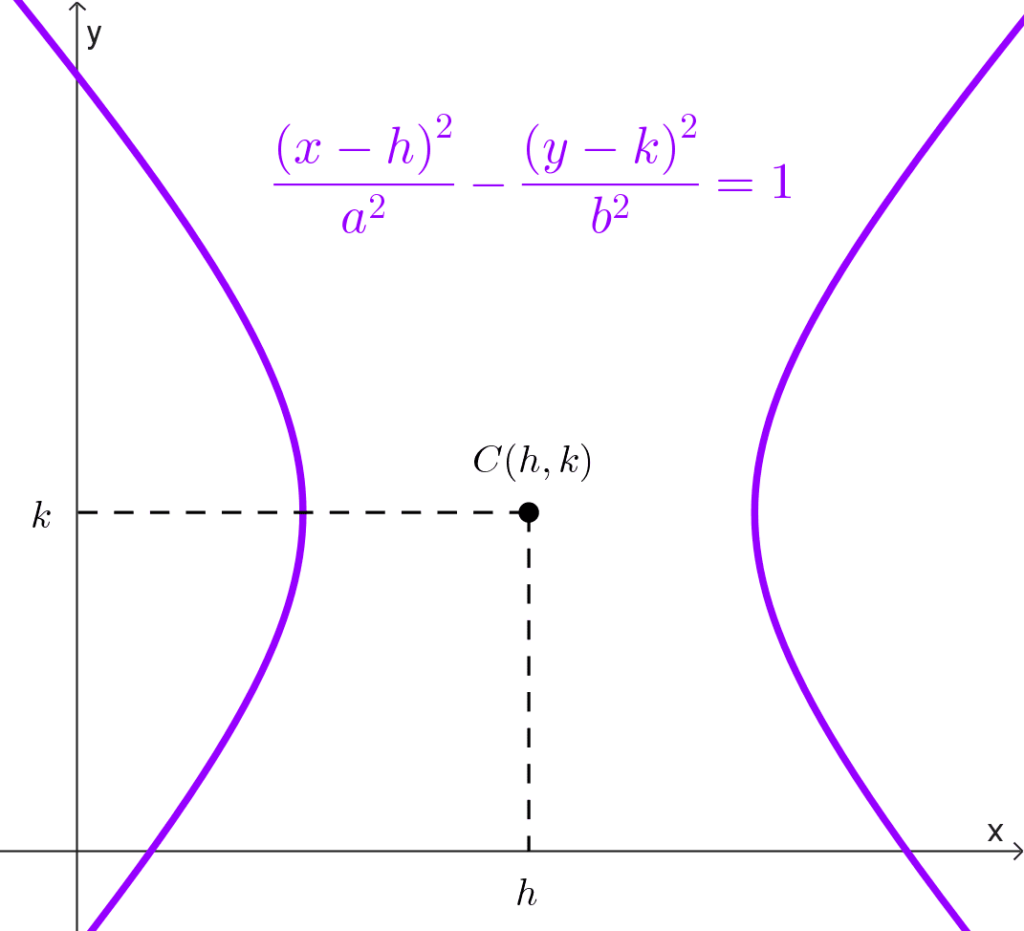
Centro en (h, k): *\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1*

donde:

• La longitud del semieje transversal es a.
• La longitud del semieje conjugado es b.

Nótese que en una hipérbola horizontal el término positivo en el primer miembro de la ecuación contiene a la variable x, mientras que el término negativo contiene a la variable y. Si el centro es el origen, el eje focal coincide con el eje x; si el centro es otro punto, el eje focal es paralelo al eje x. 

Los elementos de la hipérbola horizontal se pueden extraer de la ecuación ordinaria:

Ecuación	Centro	Focos	Vértices	Extremos del eje conjugado	Asíntotas
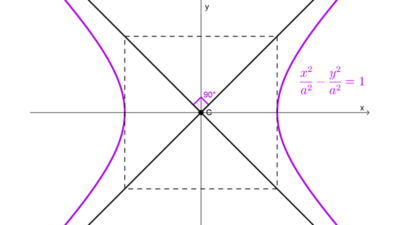
*\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1*	(0, 0)	(±c, 0) *c=\sqrt{a^2+b^2}*	(±a, 0)	(0, ±b)	*y=±\dfrac{b}{a}~x*
*\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1*	(h, k)	(h ± c, k) *c=\sqrt{a^2+b^2}*	(h ± a, k)	(h, k ± b)	*y-k=±\dfrac{b}{a}~(x-h)*

Ejemplos

1. *\dfrac{x^2}{4}-\dfrac{y^2}{9}=1* tiene eje transversal sobre el eje x, centro en el origen y sus semiejes son a = √4 = 2 y b = √9 = 3.
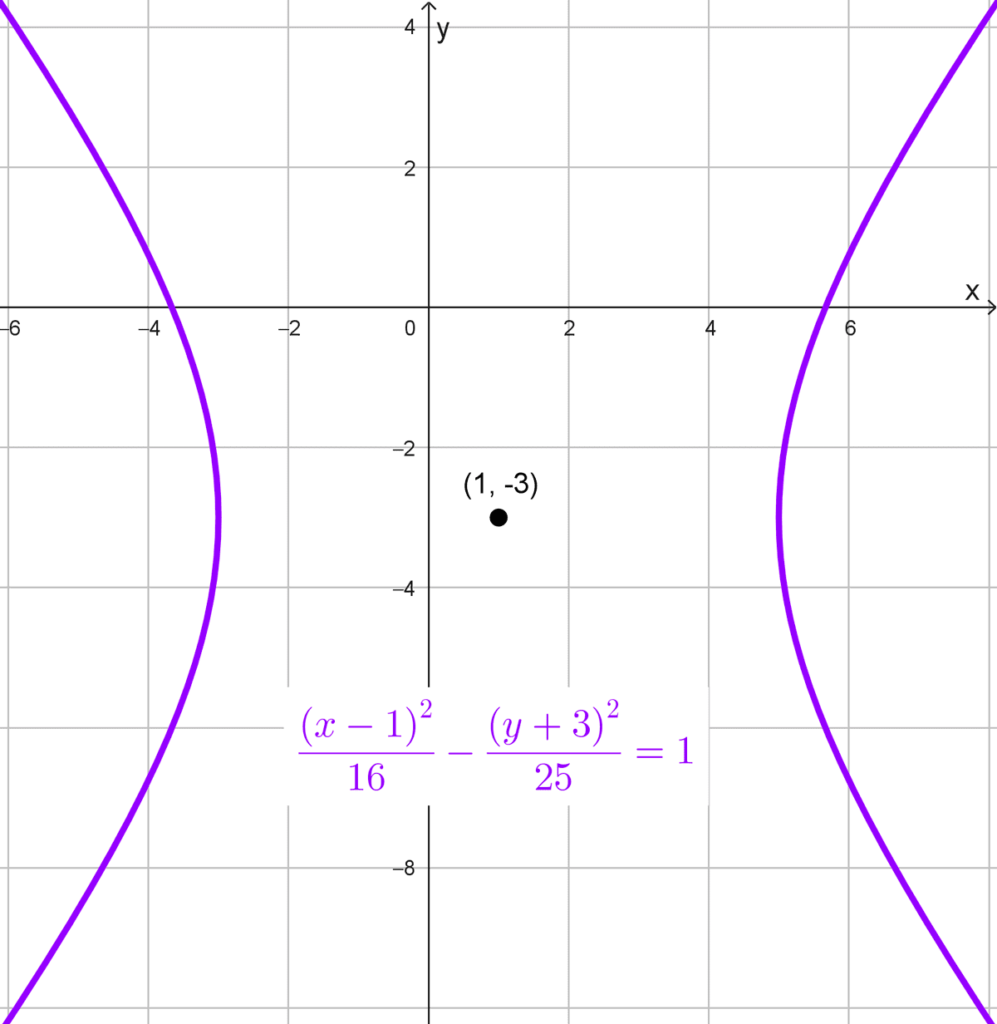
2. *\dfrac{(x-1)^2}{16}-\dfrac{(y+3)^2}{25}=1* está centrada en (1, -3), las longitudes de los semiejes son a = √16 = 4, b = √25 = 5.
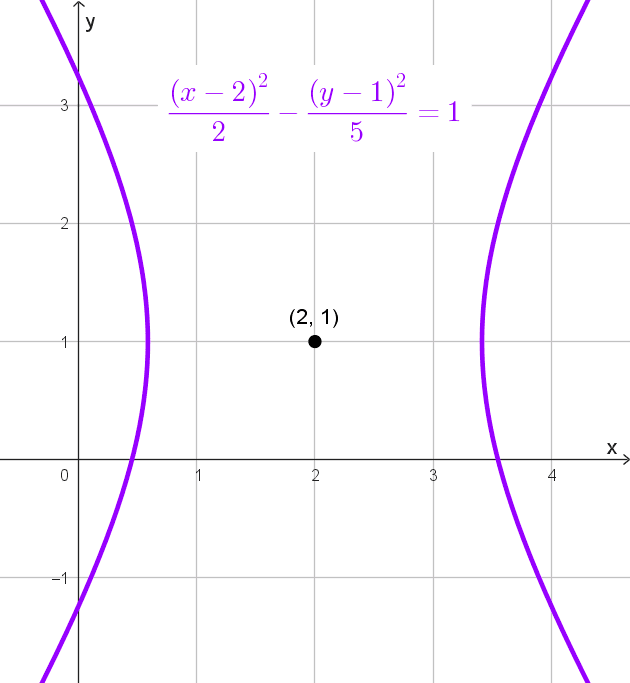
3. *\dfrac{(x-2)^2}{2}-\dfrac{(y-1)^2}{5}=1* es una hipérbola horizontal con centro en (2, 1), a = √2 y b = √5.
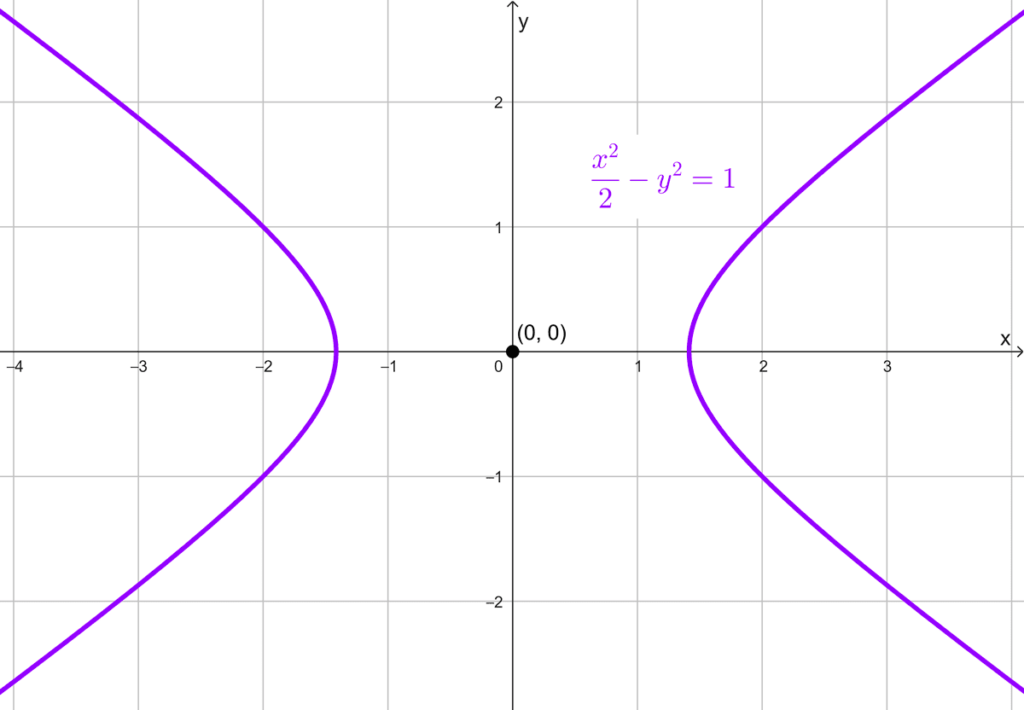
4. *x^2-2y^2-2=0* es la ecuación general de una hipérbola horizontal, se puede reescribir como *\dfrac{x^2}{2}-y^2=1* donde se extrae que el centro es (0, 0), a = √2 y b = 1.

Hipérbola vertical

Una hipérbola vertical es aquella cuyo eje focal (que contiene al eje transverso) es paralelo al eje y o es idéntico al mismo. Las ramas de la hipérbola se abren hacia arriba y hacia abajo.

De la misma forma que antes, la ecuación canónica cambia dependiendo de si la hipérbola está centrada en el origen o su centro se encuentra desplazado:

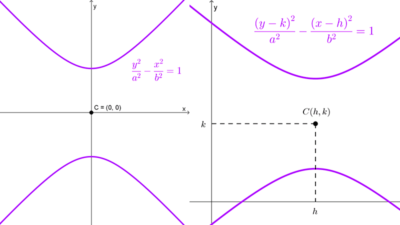
Centro en (0, 0): *\dfrac{y^2}{a^2}-\dfrac{x^2}{b^2}=1*

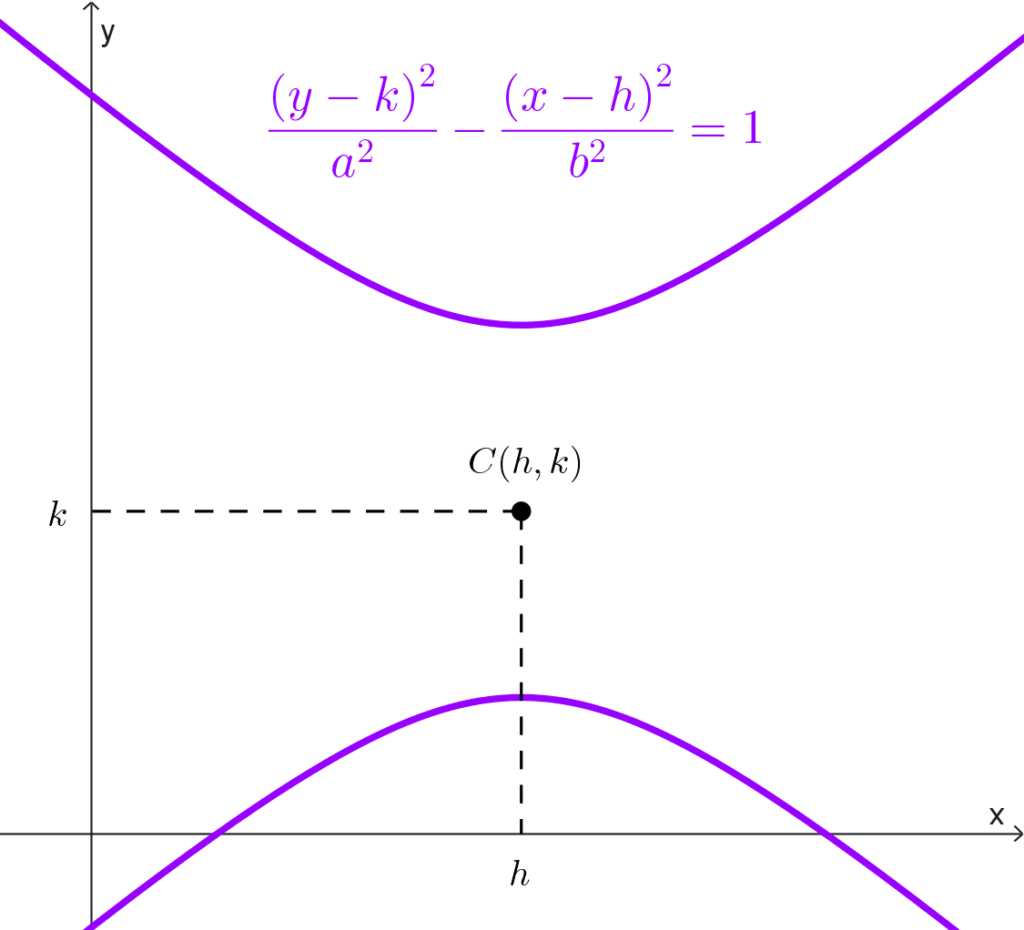
Centro en (h, k): *\dfrac{(y-k)^2}{a^2}-\dfrac{(x-h)^2}{b^2}=1*

donde:

• La longitud del semieje transversal es a.
• La longitud del semieje conjugado es b.

A diferencia de la orientación horizontal, en una hipérbola vertical el término positivo en el primer miembro de la ecuación contiene a la variable y, mientras que el término negativo contiene a la variable x. Cuando el centro es el origen, el eje focal es el eje y, mientras que el eje focal es paralelo al eje y si el centro es otro punto.

De modo análogo al anterior, los elementos de la hipérbola vertical se pueden obtener desde la ecuación ordinaria:

Ecuación	Centro	Focos	Vértices	Extremos del eje conjugado	Asíntotas
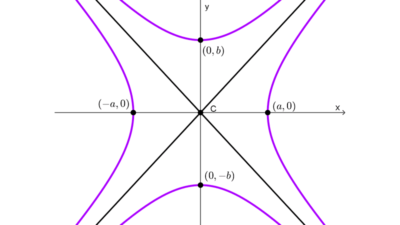
*\dfrac{y^2}{a^2}-\dfrac{x^2}{b^2}=1*	(0, 0)	(0, ±c) *c=\sqrt{a^2+b^2}*	(0, ±a)	(±b, 0)	*y=±\dfrac{a}{b}~x*
*\dfrac{(y-k)^2}{a^2}-\dfrac{(x-h)^2}{b^2}=1*	(h, k)	(h, k ± c) *c=\sqrt{a^2+b^2}*	(h, k ± a)	(h ± b, k)	*y-k=±\dfrac{a}{b}~(x-h)*

Ejemplos

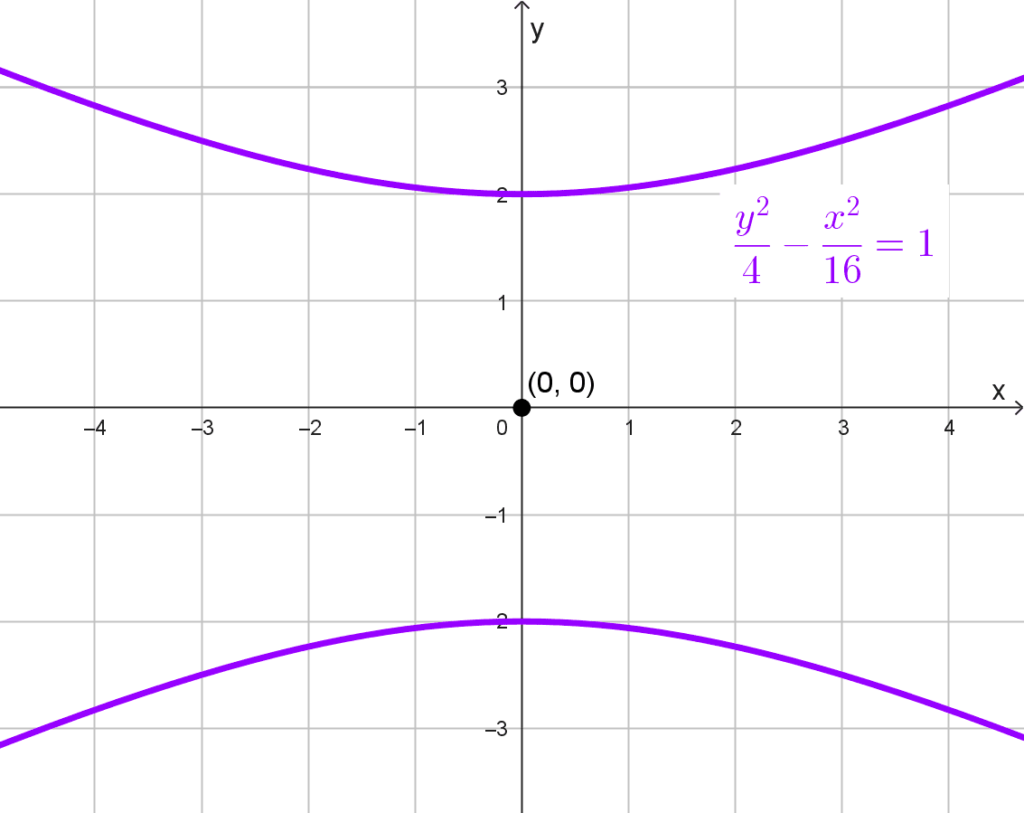
1. *\dfrac{y^2}{4}-\dfrac{x^2}{16}=1* tiene centro en (0, 0) y semiejes a = √4 =2, b = √16 = 4.
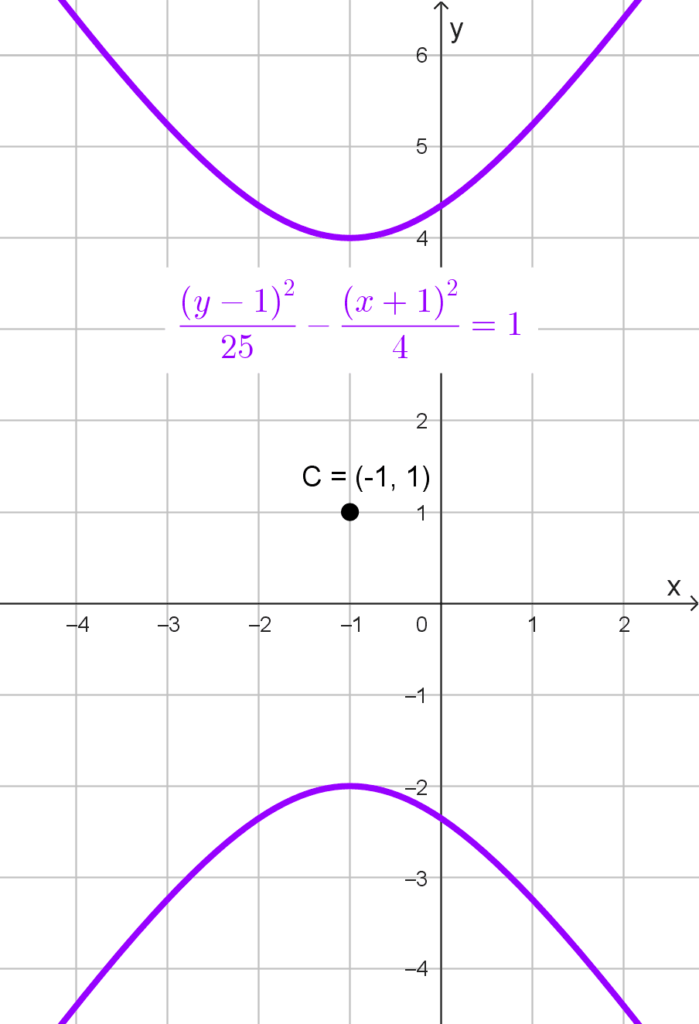
2. *\dfrac{(y-1)^2}{25}-\dfrac{(x+1)^2}{4}=1* tiene centro en (-1, 1), a = √25 = 5 y b = √4 = 2.
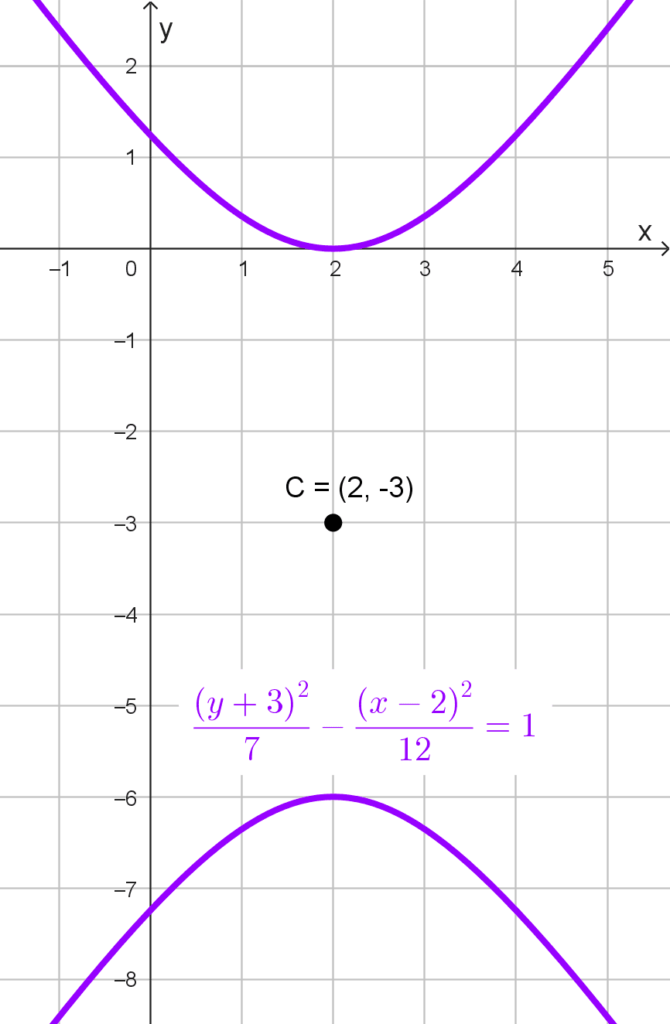
3. *-7x^2+12y^2+28x+72y-4=0* es la ecuación general de una hipérbola vertical, se puede reescribir como *\dfrac{(y+3)^2}{7}-\dfrac{(x-2)^2}{12}=1,* donde obtenemos que el centro es C(2, -3), a = √7 y b = √12.

Cómo saber si una hipérbola es horizontal o vertical

Para identificar la orientación de una hipérbola podemos valernos de su ecuación canónica. Como dijimos antes, el término positivo nos indica el eje cartesiano al cuál es paralelo el eje focal de la cónica:

• Si el término positivo en el primer miembro de la ecuación canónica contiene a la variable x, entonces se trata de una hipérbola horizontal, sus eje focal y transversal son paralelos al eje x.
• Si el término positivo en el primer miembro de la ecuación canónica contiene a la variable y, entonces se trata de una hipérbola vertical, sus eje focal y transversal son paralelos al eje y.

Cuando no se cuenta con la fórmula canónica sino la general, es necesario completar los cuadrados y reacomodar la expresión para que alcance su forma ordinaria. Nótese que para determinar la orientación no se sigue el mismo proceso que en la elipse, en donde se miraba al denominador mayor, en la hipérbola no es necesario que el semieje transversal sea mayor al semieje conjugado. 

Los otros elementos de las hipérbolas son iguales para cualquiera y no dependen de si es horizontal o vertical:

• Excentricidad: *e=\dfrac{c}{a}*
• Lado recto: *L_R=\dfrac{2b^2}{a}*
• Distancia focal: *c=\sqrt{a^2+b^2}*

Ejercicios resueltos

Determinar si las siguientes hipérbolas son horizontales o verticales.

1. *\dfrac{y^2}{10}-\dfrac{x^2}{20}=1*
2. *\dfrac{x^2}{3}-\dfrac{y^2}{5}=1*
3. *\dfrac{(y-1)^2}{10}-\dfrac{x^2}{5}=1*
4. *x^2-y^2-2x-4y-12=0*
5. *9x^2-4y^2-54x+117=0*

Soluciones

1. La ecuación está en forma canónica y el término positivo contiene a y², por tanto, la hipérbola es vertical.
2. La ecuación está en forma canónica. El término positivo contiene x², lo que significa que el eje focal de la hipérbola es horizontal, por tanto esta hipérbola es horizontal.
3. El término positivo incluye a la variable y en *(y-1)^2,* por lo que el eje transversal es vertical. En consecuencia, esta hipérbola es vertical.
4. En este caso, la ecuación no está en forma canónica, así que debemos completarla para determinar la orientación. Una vez hecho, obtenemos *\dfrac{(x-1)^2}{9}-\dfrac{(y+2)^2}{9}=1,* en donde vemos que el término positivo contiene *(x-1)^2,* lo que indica que el eje focal es horizontal. Por lo tanto, esta hipérbola es horizontal.
5. Luego de completar los cuadrados obtenemos la expresión *\dfrac{y^2}{9}-\dfrac{(x-3)^2}{4}=1,* el término positivo está asociado a la variable y, por tanto la hipérbola es vertical.

Bibliografía consultada

Para la elaboración de este contenido, se han consultado las siguientes obras.

• Engler, A. y otros. (2020). Geometría Analítica. Universidad Nacional del Litoral.
• Lehmann, C. (1989). Geometría Analítica. Limusa.
• Leithold. L. (1992). Álgebra y Trigonometría con Geometría Analítica. Oxford University Press.
• Sullivan, M. (2006). Álgebra y Trigonometría. Pearson Educación. 
• Swokowski, E. y Cole, J. (2009). Álgebra y Trigonometría con Geometría Analítica. Cengage Learning.