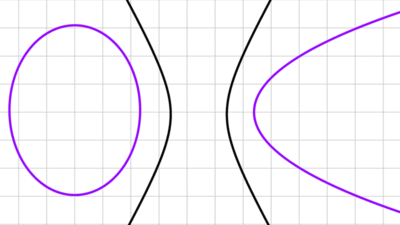
Historia de las secciones cónicas

A lo largo de la historia, el estudio de las secciones cónicas ha evolucionado de ser un desafío geométrico a convertirse en un campo fundamental dentro de las matemáticas, con aplicaciones que abarcan desde la astronomía y la física hasta la geometría moderna y la ingeniería. 

En este artículo, exploraremos la línea del tiempo del desarrollo de las cónicas, desde sus primeros descubrimientos hasta su consolidación en la matemática moderna.

Antigua Grecia

La historia de las secciones cónicas comienza en la Antigüedad Clásica, en el siglo IV a.C., con Menecmo, un discípulo de Eudoxo, quien es reconocido como el primer matemático en estudiar sistemáticamente las secciones cónicas. 

Menecmo investigó estas curvas geométricas al intentar resolver el famoso problema de la duplicación del cubo, también conocido como el problema de Delos. Su enfoque consistía en considerar las intersecciones de un cono con distintos planos, dando origen a las formas que hoy conocemos como la elipse, la parábola y la hipérbola. Aunque su trabajo no ha sobrevivido, se sabe que él utilizó propiedades geométricas y proporciones para caracterizar estas curvas, sentando las bases de su estudio matemático.

Arquímedes realizó contribuciones significativas al estudio de las cónicas en el siglo III a.C. Su trabajo se centró principalmente en la medición de áreas y volúmenes, abordando problemas que involucraban las propiedades geométricas de estas curvas. En su obra "La cuadratura de la parábola", Arquímedes logró cuadrar un segmento de parábola, es decir, determinó el área comprendida entre una parábola y una línea recta. Además, en su tratado "Sobre Conoides y Esferoides", calculó el área de una elipse y estudió los sólidos de revolución generados a partir de secciones cónicas. 

Euclides, alrededor del siglo III a.C., aunque las obras que se conservan no se enfocan directamente en las cónicas, influyó significativamente en el desarrollo posterior a través de su obra "Elementos". En esta obra, Euclides presentó fundamentos de geometría que más tarde serían esenciales para los matemáticos que estudiaron las propiedades de las cónicas. 

Fue Apolonio de Perga, otro matemático griego del mismo siglo, quien realizó la mayor contribución en este campo. Conocido como "El Gran Geómetra", Apolonio sistematizó y expandió el estudio de las secciones cónicas en su obra "Conics", una serie de ocho libros en los que definió de manera rigurosa las tres formas principales: la elipse, la parábola y la hipérbola. 

Apolonio introdujo un enfoque más abstracto y general al tratar las cónicas como secciones de un cono con diferentes inclinaciones de los planos de corte, además de desarrollar una teoría matemática que describía sus propiedades de manera más profunda y detallada, influenciando así siglos de estudio matemático.

Apolonio descubrió propiedades de las cónicas que resultaron ser de gran utilidad práctica. Entre estas, destacan las propiedades de reflexión, que establecen cómo los rayos de luz o sonido se comportan al incidir sobre superficies cónicas. Si se construye un espejo con la forma de una elipse girando alrededor de su eje, cualquier luz emitida desde uno de sus focos se reflejará y concentrará exactamente en el otro foco. De manera similar, si un espejo con forma parabólica recibe luz procedente de una fuente lejana, cuyos rayos llegan paralelos al eje del espejo, estos rayos reflejados se concentrarán en su foco.

Estas propiedades de reflexión continúan teniendo relevancia en numerosas aplicaciones científicas y tecnológicas actuales, como en telescopios, antenas parabólicas, y hornos solares, entre otras.

Edad Media

Con la caída del Imperio Romano y la llegada de la Edad Media, el conocimiento matemático europeo decayó, pero las obras de los antiguos griegos, incluidas las de Apolonio, fueron preservadas y traducidas al árabe durante el Renacimiento Islámico, hacia los siglos IX y XI. Matemáticos árabes como Al-Khwarizmi y Omar Khayyam desempeñaron un papel crucial en la conservación y ampliación de estos estudios. 

Khayyam, por ejemplo, utilizó las cónicas para desarrollar métodos geométricos que resolvían ecuaciones cúbicas, marcando una aplicación importante de estas curvas en problemas algebraicos. Gracias a las traducciones y a la expansión del conocimiento islámico, estos trabajos regresaron a Europa a través de la Escuela de Traductores de Toledo, en los siglos XII y XIII, donde matemáticos como Fibonacci comenzaron a estudiarlos nuevamente en el contexto de la matemática europea.

Renacimiento y Edad Moderna

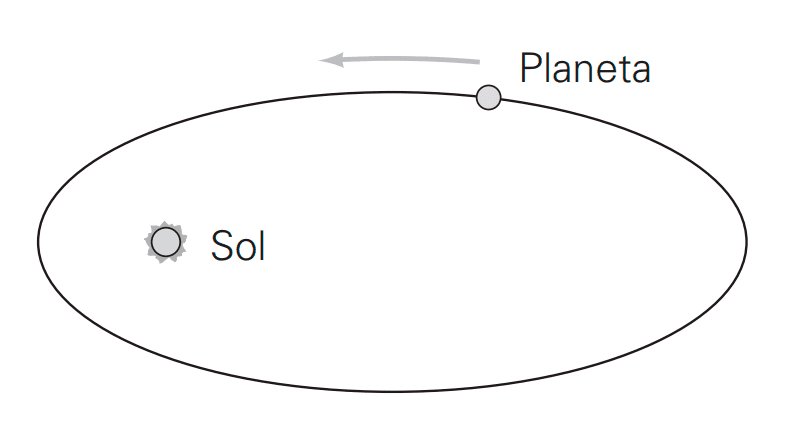
Durante el Renacimiento, en los siglos XV al XVII, las ideas matemáticas de la antigüedad clásica experimentaron un renacimiento significativo. Johannes Kepler, hacia el siglo XVII, utilizó las cónicas de manera fundamental para la astronomía. En su obra "Astronomia nova", Kepler demostró que las órbitas de los planetas alrededor del Sol no eran círculos, como se pensaba hasta entonces, sino elipses. Además, fue el primero en utilizar el término "focos" para describir los puntos especiales relacionados con las elipses.

Paralelamente, Girard Desargues y Blaise Pascal hicieron contribuciones significativas al desarrollar una teoría de las cónicas desde la perspectiva de una forma temprana de geometría proyectiva. Pascal, en particular, formuló el conocido "Teorema del hexágono místico", del cual derivan muchas propiedades fundamentales de las cónicas.

René Descartes y Pierre de Fermat revolucionaron el estudio de las cónicas al aplicar los principios de la geometría analítica, transformando problemas geométricos complejos en ecuaciones algebraicas manejables. Esta nueva aproximación permitió que matemáticos como John Wallis, en su tratado de 1655 "Tractatus de sectionibus conicis", definieran las cónicas de manera más precisa como ecuaciones de segundo grado. 

Posteriormente, Jan de Witt, en su obra "Elementa Curvarum Linearum", construyó sobre los métodos de Kepler, Fermat y Descartes, combinando la construcción geométrica con la notación algebraica, y fue uno de los primeros en introducir el término "directriz", estableciendo así las bases para el desarrollo moderno de este campo.

En el siglo XVII, el estudio de las cónicas alcanzó una nueva dimensión con matemáticos como Isaac Newton, quien aplicó estos conceptos al campo de la mecánica celeste. En su obra Philosophiæ Naturalis Principia Mathematica, Newton utilizó las propiedades de las cónicas para describir las trayectorias de los cuerpos celestes, estableciendo las bases de la gravitación universal. Este desarrollo fue fundamental para explicar cómo los planetas se mueven en el espacio, proporcionando una sólida justificación matemática para el modelo heliocéntrico de Kepler.

En el siglo XVIII, matemáticos como Leonhard Euler y Pierre-Simon Laplace aplicaron métodos analíticos y algebraicos al estudio de las cónicas en diversos contextos matemáticos y físicos. Euler, en particular, hizo importantes contribuciones a la teoría algebraica de las cónicas, desarrollando métodos analíticos para describir y comprender sus propiedades. Por otro lado, Laplace utilizó las cónicas, especialmente las elipses, en su trabajo sobre mecánica celeste para analizar las órbitas planetarias y otros fenómenos relacionados con la gravitación, integrándolas en sus estudios más amplios sobre física matemática.