Traslación de secciones cónicas
En este artículo explicamos qué es la traslación de secciones cónicas y como realizarla con ejercicios resueltos paso a paso.
Índice
¿Qué es la traslación?
En geometría analítica, una traslación de ejes implica mover el origen de coordenadas a un nuevo punto sin cambiar la orientación de los ejes, es decir, seguirán siendo paralelos a los originales.
En las secciones cónicas una traslación conveniente resulta útil para eliminar los términos lineales de la ecuación general. Muchas veces se combina también con una rotación de ejes para eliminar términos mixtos (los que contienen el producto de las variables).
Fórmulas de traslación
Consideremos un punto genérico P(x, y) ubicado en el plano. Al aplicar una traslación, el nuevo origen será el punto (h, k) y las coordenadas de P cambiarán, siendo ahora P(x’, y’).
Podemos relacionar las coordenadas originales (x, y) con las nuevas (x', y') a través de las siguientes fórmulas:
x' = x - h
y' = y - k
Ejercicios resueltos
A continuación veremos algunos ejercicios de traslación de cónicas resueltos paso a paso.
Traslación de una elipse
Aplicar una traslación para eliminar los términos lineales de la ecuación *9x^2 + 4y^2 - 36x + 24y + 36 = 0*
Solución: como los coeficientes de los términos cuadráticos tienen el mismo signo, deducimos que la ecuación representa una elipse. Debemos remover los términos -36x y 24y, para ello necesitamos determinar un nuevo origen de coordenadas que coincidirá con el centro de la cónica.
Comenzamos realizando la sustitución de x por x'+h e y por y'+k en la ecuación, entonces:
*9x^2+4y^2-36x+24y+36=0*
*9(x'+h)^2+4(y'+k)^2-36(x'+h)+24(y'+k)+36=0*
Expandiendo cada término cuadrado:
*9(x'^2+2hx'+h^2)+4(y'^2+2ky'+k^2)-36(x'+h)+24(y'+k)+36=0*
Multiplicamos los coeficientes correspondientes:
*9x'^2+18hx'+9h^2+4y'^2+8ky'+4k^2-36x'-36h+24y'+24k+36=0*
Agrupamos los términos por x', y' y los términos constantes:
*9x'^2+4y'^2+(18h-36)x'+(8k+24)y'+(9h^2+4k^2-36h+24k+36)=0*
Ahora necesitamos que los coeficientes de x' y y' sean iguales a cero, es decir:
*18h-36=0*
*8k+24=0*
Resolviendo el sistema determinamos que:
*h=2* y *k=-3*
Estos valores los sustituimos en la ecuación:
*9x'^2+4y'^2+(9(2)^2+4(-3)^2-36(2)+24(-3)+36)=0*
Desarrollando:
*9x'^2+4y'^2-36=0*
Nótese que esta ecuación no tiene términos lineales. Podemos acomodarla para encontrar la forma canónica:
*9x’^2+4y'^2=36*
*\dfrac{x’^2}{4}+\dfrac{y’^2}{9}=1*
La cual es una elipse vertical centrada en el nuevo origen, que es el punto (2, -3), con semieje mayor igual a 3 y semieje menor igual a 2.
Traslación de una hipérbola
Aplicar una traslación para eliminar los términos lineales de la ecuación *25x^2-9y^2-50x-90y-425=0.*
Solución: analizando los coeficientes cuadráticos determinamos que la ecuación representa a una hipérbola, pues tienen distintos signos. Debemos remover los términos -50x y -90y, para ello necesitamos determinar un nuevo origen de coordenadas que coincidirá con el centro de la hipérbola.
Comenzamos realizando la sustitución de x por x'+h e y por y'+k en la ecuación, entonces:
*25x^2-9y^2-50x-90y-425=0*
*25(x'+h)^2-9(y'+k)^2-50(x'+h)-90(y'+k)-425=0*
Expandiendo cada término cuadrado:
*25(x'^2+2hx'+h^2)-9(y'^2+2ky'+k^2)-50(x'+h)-90(y'+k)-425=0*
Multiplicamos los coeficientes correspondientes:
*25x'^2+50hx'+25h^2-9y'^2-18ky'-9k^2-50x'-50h-90y'-90k-425=0*
Agrupamos los términos por x', y' y los términos constantes:
*25x'^2-9y'^2+(50h-50)x'+(-18k-90)y'+(25h^2-9k^2-50h-90k-425)=0*
Ahora necesitamos que los coeficientes de x' y y' sean iguales a cero, es decir:
*50h-50=0*
*-18k-90=0*
Resolviendo, determinamos que:
*h=1* y *k=-5*
Sustituimos estos valores en la ecuación:
*25x'^2-9y'^2+(25(1)^2-9(-5)^2-50(1)-90(-5)-425)=0*
Desarrollando:
*25x'^2-9y'^2+(25-225-50+450-425)=0*
*25x'^2-9y'^2+-225=0*
Finalmente, podemos acomodarla para obtener la forma canónica:
*25x'^2-9y'^2=225*
Dividimos entre 225:
*\dfrac{x'^2}{9}-\dfrac{y'^2}{25}=1*
Esta es la ecuación de la hipérbola centrada en el nuevo origen, que es el punto (1, -5), con semieje transversal igual a 3 y semieje conjugado igual a 5.
Traslación de una parábola
Realizar una traslación para simplificar la ecuación de la parábola *y^2-4x-6y+1=0*
Solución: identificamos que la ecuación representa una parábola porque solo hay un término cuadrático, en este caso y2. En las parábolas siempre aparece un término lineal que no puede eliminarse, por lo que aplicar las ecuaciones de traslación no conducirá a nada. En su lugar, podemos completar los cuadrados primero y luego usar ecuaciones de traslación para definir un nuevo origen que coincidirá con el vértice.
Comenzamos reorganizando la ecuación:
*y^2-6y-4x+1=0*
*y^2-6y=4x-1*
Completamos el cuadrado para la parte de y. Para ello tomamos el coeficiente de y, que es -6, lo dividimos entre 2 y lo elevamos al cuadrado:
*\dfrac{-6}{2}^2=9*
Ahora añadimos y restamos 9 en el lado izquierdo para no alterar la expresión:
*y^2-6y+9-9=4x-1*
*(y-3)^2-9=4x-1*
Simplificando:
*(y-3)^2=4x-1+9*
*(y-3)^2=4x+8*
*(y-3)^2=4(x+2)*
Hemos llegado a la forma canónica de la parábola. Para simplificar esta ecuación, trasladamos las coordenadas a un nuevo sistema con un nuevo origen (h, k), el cual podemos encontrar así:
*x’=x-h=x+2 → h=-2*
*y’=y-k=y-3 → k=3*
Sustituyendo en la ecuación:
*(y-3)^2=4(x+2)*
*y’^2=4x’*
Esta es la ecuación de una parábola con vértice en el nuevo origen (-2, 3), parámetro p=1 y que abre hacia la derecha.
Traslación combinada con rotación
Muchas veces se tiene una ecuación general con términos mixtos (que incluyen un término xy) y también con términos lineales (que incluyen a x o y). En estos casos, para simplificar la ecuación es necesario realizar una rotación y una traslación.
El orden en que se realizan estas transformaciones cambia según el tipo de cónica del que se trate:
- Si la ecuación representa una elipse o hipérbola, realizar primero una traslación y luego una rotación.
- Si la ecuación representa una parábola, realizar primero una rotación y luego una traslación.
Ejemplo 1
Realice una transformación de coordenadas para eliminar el término mixto y los términos lineales en la siguiente ecuación: *73x^2-72xy+52y^2+100x-200y+100=0*
Solución: analizando el discriminante determinamos que la ecuación representa una elipse. La aparición del término xy indica que la misma está rotada con respecto a los ejes x e y. Como se trata de una elipse, realizamos primero una traslación y posteriormente una rotación.
Traslación:
La ecuación original es:
*73x^2-72xy+52y^2+100x-200y+100=0*
Reemplazamos x por x'+h y y por y'+k:
*73(x'+h)^2-72(x'+h)(y'+k)+52(y'+k)^2+100(x'+h)-200(y'+k)+100=0*
Desarrollamos los términos cuadráticos:
*73(x'^2+2x'h+h^2)-72(x'y'+x'k+hy'+hk)+52(y'^2+2y'k+k^2)+100x'+100h-200y'-200k+100=0*
Aplicamos propiedad distributiva:
*73x'^2+146x'h+73h^2-72x'y'-72x'k-72hy'-72hk+52y'^2+104y'k+52k^2+100x'+100h-200y'-200k+100=0*
Reagrupamos los términos en x', y', y los términos constantes:
*73x'^2-72x'y'+52y'^2+(146h-72k+100)x'+(-72h+104k-200)y'+(73h^2-72hk+52k^2+100h-200k+100)=0*
Para anular los términos lineales en x' e y', los coeficientes de estos términos deben ser cero, es decir que se deben cumplir simultáneamente estas ecuaciones:
*146h-72k+100=0* (ecuación 1)
*-72h+104k-200=0* (ecuación 2)
Resolvemos este sistema de ecuaciones:
De la ecuación 1:
*146h=72k-100 *
*h=\dfrac{72k-100}{146} *
Sustituimos en la ecuación 2:
*-72\left(\dfrac{72k-100}{146}\right)+104k-200=0*
*\dfrac{-5184k+7200}{146}+104k-200=0*
*-5184k+7200+15184k-29200=0*
*10000k=22000*
*k=\dfrac{22000}{10000}=\dfrac{11}{5}=2,2*
Sustituimos k en la ecuación para h:
*h=\dfrac{72(11/5)-100}{146}*
*h=\dfrac{58,4}{146}=0,4*
Por lo tanto, los valores de h y k que anulan los términos lineales en x' e y' son:
*h=0.4*
*k=2.2*
Sustituyendo en la ecuación:
*73x'^2-72x'y'+52y'^2+0x'+0y'-100=0*
*73x'^2-72x'y'+52y'^2-100=0*
La traslación a un nuevo sistema de coordenadas x’y’ con centro (0,4 ; 2,2) ha permitido eliminar los términos lineales de la ecuación general, sin embargo, todavía es necesario eliminar el término mixto x’y’, para ello realizaremos una rotación.
Rotación:
Primero identificamos que los coeficientes en la ecuación *73x'^2-72x'y'+52y'^2-100=0* son *A’=73, B’=-72* y *C’=52.* Para encontrar el ángulo de rotación adecuado usamos la fórmula:
*\tan 2\theta=\dfrac{B’}{A’-C’}=\dfrac{-72}{73-52}=\dfrac{-24}{7}*
con ello calculamos:
*\cos 2\theta=\dfrac{-7}{25}*
por tanto:
*\sin \theta=\sqrt{\dfrac{1-\cos 2\theta}{2}}=\dfrac{4}{5}*
*\cos \theta=\sqrt{\dfrac{1+\cos 2\theta}{2}}=\dfrac{3}{5}*
Las fórmulas de rotación son:
*x’=x’’\cosθ-y’’\sinθ*
*y’=x’’\sinθ+y’’\cosθ*
Sustituyendo los valores que encontramos, llegamos a:
*x’=\dfrac{3x’’-4y’’}{5} \quad \text{y} \quad y’=\dfrac{4x’’+3y’’}{5}*
Al sustituir para x’ e y’ en la ecuación dada y simplificar, se obtiene:
*25x''^2+100y''^2-100=0*
Reordenando:
*25x''^2+100y''^2=100*
Dividimos entre 100:
*\dfrac{x''^2}{4}+\dfrac{y''^2}{1}=1*
Llegamos a la ecuación de una elipse en su forma estándar. El centro es el origen de coordenadas que ahora es (0,4 ; 2,2). El semieje mayor tiene longitud 2 y el menor 1. De cualquiera de las expresiones trigonométricas extraemos el ángulo de rotación de los ejes x’’y’’ con respecto a los anteriores x’y’:
*\cos \theta=\dfrac{3}{5}→\theta=\arccos(3/5)≈53,13°*
Para ver más en detalle de dónde surgen las fórmulas para el ángulo adecuado visita el siguiente artículo:
Ejemplo 2
Lleve la siguiente ecuación a su forma más simple: *3x^2+2\sqrt{3}xy+y^2-2x-2\sqrt{3}y-2=0*
Solución: a través del discriminante determinamos que la ecuación representa una parábola, esto significa que primero será necesario realizar una rotación de ejes y luego una traslación.
Primero rotamos los ejes de modo que se eliminen los términos mixtos. Así, se obtiene:
*\tan 2\theta=\dfrac{B}{A-C}=\dfrac{2\sqrt{3}}{3-1}=\sqrt{3}*
Por consiguiente, 2θ=60°, θ=30° y las fórmulas de rotación son:
*x=\dfrac{\sqrt{3}x'}{2}-\dfrac{y'}{2}, \quad y=\dfrac{x'}{2}+\dfrac{\sqrt{3}y'}{2}*
Sustituyendo para x y y en la ecuación dada, se obtiene:
*3\left(\dfrac{\sqrt{3}x'}{2}-\dfrac{y'}{2}\right)^2+2\sqrt{3}\left(\dfrac{\sqrt{3}x'}{2}-\dfrac{y'}{2}\right)\left(\dfrac{x'}{2}+\dfrac{\sqrt{3}y'}{2}\right)+\left(\dfrac{x'}{2}+\dfrac{\sqrt{3}y'}{2}\right)^2-2\left(\dfrac{\sqrt{3}x'}{2}-\dfrac{y'}{2}\right)-2\sqrt{3}\left(\dfrac{x'}{2}+\dfrac{\sqrt{3}y'}{2}\right)-2=0*
Ahora se sacan los coeficientes de cada variable que surge de esta ecuación. Se ignoraron los términos x'y' que suman cero y se encuentra:
*\left(\dfrac{9}{4}+\dfrac{6}{4}+\dfrac{1}{4}\right)x'^2+\left(\dfrac{3}{4}-\dfrac{6}{4}+\dfrac{3}{4}\right)y'^2+(-\sqrt{3}-\sqrt{3})x'+(1-3)y'-2=0*
Resolviendo:
*4x'^2-2\sqrt{3}x'-2y'-2=0*
Al dividir entre 2 y completar el cuadrado en los términos x', se obtiene:
*2\left(x'-\dfrac{\sqrt{3}}{2}\right)^2+y'+1=y'+1+\dfrac{3}{8}*
*2\left(x'-\dfrac{\sqrt{3}}{4}\right)^2=y'+\dfrac{11}{8}*
Se han eliminado los términos mixtos, ahora es necesario realizar una traslación, observando la ecuación determinamos que una traslación que mueva el origen al punto *(\sqrt{3}/4, -11/8)* produce una ecuación final
*2x’’^2=y’’*

Puntos clave
- Una traslación puede servir para eliminar los términos lineales de la ecuación general de una cónica.
- Las fórmulas de traslación dependen del nuevo origen de coordenadas (h, k) y son las siguientes:
x' = x - h, y' = y - k - Si también se desean eliminar términos mixtos, es necesario combinar una rotación con una traslación. En las elipses e hipérbolas se realiza primero la traslación y luego la rotación, en parábolas se realiza primero la rotación y luego la traslación.
Recursos adicionales
En los siguientes videos se explica cómo realizar las rotaciones de cónicas:
Lecturas recomendadas:
- Fuller, G. y Tarwater, D. (1995). Geometría Analítica (7ma edición). Pearson Educación.
- Lehmann, C. (1989). Geometría Analítica. Limusa.
- Leithold. L. (1992). Álgebra y Trigonometría con Geometría Analítica. Oxford University Press.
- Márquez, A. y otros. (2009). Geometría Analítica. Prentice Hall.
- Sullivan, M. (2006). Álgebra y Trigonometría. Pearson Educación.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta





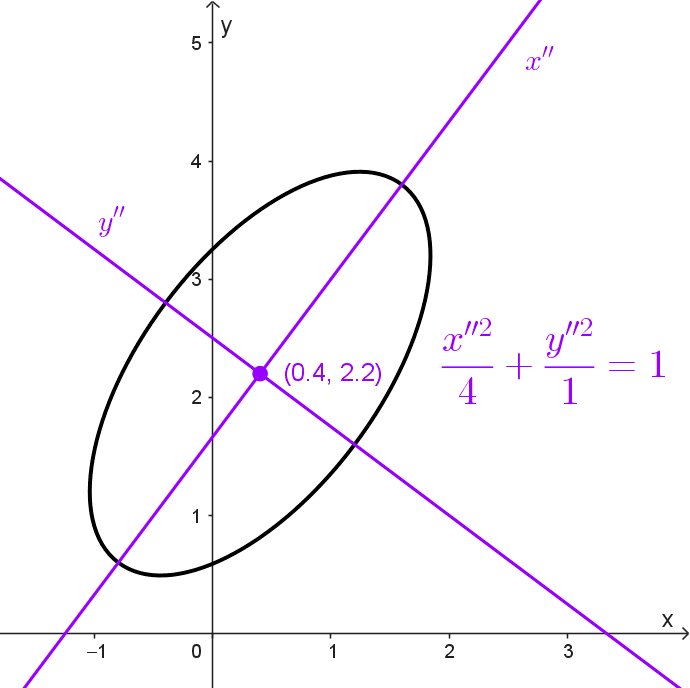


Otros artículos que pueden interesarte