Ecuaciones paramétricas de las cónicas
En este artículo explicamos las ecuaciones paramétricas de cada sección cónica con ejemplos y gráficos de cada una.
Índice
Parametrización
Sabemos que se puede expresar cualquier cónica mediante una ecuación de segundo grado con dos variables x e y. Sin embargo, existe otra manera de describir estas curvas utilizando una tercera variable y haciendo que x e y dependan de ella. De este modo, para describir una cónica se utilizarán dos ecuaciones que nos darán el valor de x y de y para cada valor de la tercera variable, la cual llamamos parámetro. Este parámetro existe en un intervalo determinado de valores.
Supongamos que *x=f(t)* y *y=g(t),* donde f y g son dos funciones cuyo dominio es cualquier intervalo I. La colección de puntos definida por *(x,y)=(f(t), g(t))* se llama curva plana. Las ecuaciones *x=f(t), y=g(t),* donde t está en I, se llaman ecuaciones paramétricas de la curva. La variable t se denomina parámetro.
Las ecuaciones paramétricas resultan útiles para describir el movimiento a lo largo de una curva. Supongamos que una curva está definida por las ecuaciones paramétricas x = f(t), y = g(t), con a ≤ t ≤ b. A medida que t varía dentro del intervalo desde t = a hacia t = b, los valores sucesivos de t dan lugar a un movimiento dirigido a lo largo de la curva, es decir, siguen la curva en cierta dirección mediante la sucesión de puntos (x, y) correspondiente.
Para expresar una cónica en forma paramétrica necesitamos un par de ecuaciones, una para x y otra para y, donde ambas dependan de un parámetro t, y un intervalo en el cual varía este parámetro. No existe una única forma de parametrizar una curva, a continuación se mostrará las que son consideradas más sencillas.
Circunferencia
La ecuación paramétrica de una circunferencia con centro en (h, k) y radio r es:
*\begin{cases} x=h+r \cos(t) \\ y=k+r \sin(t) \end{cases},~\text{donde}~0≤ t ≤2π*
Si el centro está en el origen, es decir, en el punto (0, 0), entonces la ecuación se reduce a:
*\begin{cases} x=r \cos(t) \\ y=r \sin(t) \end{cases},~\text{donde}~0≤ t ≤2π*
Ejemplos
- *x=\cos(t),~ y=\sin(t),~ 0≤t≤2π* es la parametrización de una circunferencia de radio 1 y centro en el origen, también llamada circunferencia unitaria.
- *\begin{cases} x=2\cos(t)-1 \\ y=2+2\sin(t) \end{cases},~\text{donde}~0≤ t ≤2π* es una circunferencia con centro en (-1, 2) y radio r = 2.
- *x=3\cos t, y=3+3\sin t, 0≤t≤2π* es una circunferencia con centro en (0, 3) y radio 3.
Tomemos el primer ejemplo: x = cos(t), y = sin(t), 0 ≤ t ≤ 2π. Es importante señalar que t es un ángulo (pues es el argumento de una función trigonométrica) y está medido en radianes. Podría usarse el símbolo θ en lugar de t para evidenciar esto, pero no es necesario.
Cuando t = 0 estamos en el inicio del intervalo [0, 2π], aquí, si reemplazamos el valor t obtenemos:
*x=\cos(0)=1*
*y=\sin(0)=0*
Entonces, el primer punto de la curva es (1, 0).
Si avanzamos hasta t = π/2 (90° en el sistema sexagesimal), tenemos que:
*x=\cos(π/2)=\cos(90°)=0*
*y=\sin(π/2)=\sin(90°)=1*
Entonces, otro punto de la curva es (0, 1).
Cuando t = π (180° en el sistema sexagesimal), se obtiene:
*x=\cos(π)=\cos(180°)=-1*
*y=\sin(π)=\sin(180°)=0*
Así, otro punto de la curva es (-1, 0).
Repitiendo para t = 3π/2 (270° en el sistema sexagesimal):
*x=\cos(3π/2)=\cos(270°)=0*
*y=\sin(3π/2)=\sin(270°)=-1*
Otro punto de la curva es (0, -1).
Finalmente, cuando t = 2π (360° en el sistema sexagesimal), nos encontramos en el final del intervalo de valores en el que se mueve t:
*x=\cos(2π)=\cos(360°)=1*
*y=\sin(2π)=\sin(360°)=0*
Aquí volvemos a obtener el punto de inicio: (1, 0). Esto ocurre porque la circunferencia es una curva cerrada, igual que la elipse.
Existen valores intermedios que si los consideramos dibujarán la circunferencia completa, para la explicación solo hemos usado los puntos que están sobre los ejes cartesianos. Podemos notar en el gráfico que, a medida que t avanza desde 0 hasta 2π, el punto (x, y) se mueve en sentido contrario a las agujas del reloj.
Si deseamos volver a la ecuación cartesiana es necesario eliminar el parámetro t. Esto se puede conseguir acomodando las ecuaciones, elevando al cuadrado ambos miembros y luego sumando las ecuaciones. Así:
Acomodamos las ecuaciones:
*x-h=r \cos(t)*
*y-k=r \sin(t)*
Elevamos al cuadrado:
*(x-h)^2=r^2 \cos^2(t)*
*(y-k)^2=r^2 \sin^2(t)*
Sumamos ambas ecuaciones:
*(x-h)^2+(y-k)^2=r^2 \cos^2(t)+r^2 \sin^2(t)*
*(x-h)^2+(y-k)^2=r^2 (\cos^2(t)+\sin^2(t))*
Si aplicamos la identidad pitagórica, nos queda que *\cos^2(t)+\sin^2(t)=1,* entonces:
*(x-h)^2+(y-k)^2=r^2*
Esta última es la ecuación canónica de la circunferencia con centro en (h, k) y radio r.
Elipse
La ecuación paramétrica de una elipse con centro en (h, k), eje focal horizontal (paralelo al eje x) con semieje mayor a y semieje menor b es:
*\begin{cases} x=h+a\cos(t) \\ y=k+b\sin(t) \end{cases}~\text{donde}~0≤ t ≤2π*
Si la elipse tiene eje focal vertical (paralelo al eje y) entonces los valores a y b intercambian lugares, así:
*\begin{cases} x=h+b\cos(t) \\ y=k+a\sin(t) \end{cases}~\text{donde}~0≤ t ≤2π*
Ejemplos
- *\begin{cases} x=2\cos(t)-1 \\ y=\sin(t)-2 \end{cases},~0≤ t ≤2π* es la parametrización de una elipse con centro en (-1, -2), semieje mayor a=2 y semieje menor b=1, la elipse tiene orientación horizontal pues el eje focal es paralelo al eje x.
- *\begin{cases} x=2+2\cos(t) \\ y=1+3\sin(t) \end{cases},~0≤ t ≤2π* es una elipse con centro en (2, 1), semieje mayor a=3 y menor b=2, tiene orientación vertical puesto que su eje focal es paralelo al eje y.
Hipérbola
La ecuación paramétrica de una hipérbola orientada horizontalmente con centro en (h, k) y semiejes a y b es:
*\begin{cases} x=h+a \sec(t) \\ y=k+b\tan(t) \end{cases}*
donde t está en el intervalo [0, 2π] exceptuando los valores π/2 y 3π/2, en los cuales no existen la secante ni la tangente.
Si la hipérbola está orientada verticalmente, su ecuación paramétrica es:
*\begin{cases} x=h+b \tan(t) \\ y=k+a\sec(t) \end{cases}*
donde t está en el mismo intervalo de la ecuación anterior.
Ejemplos
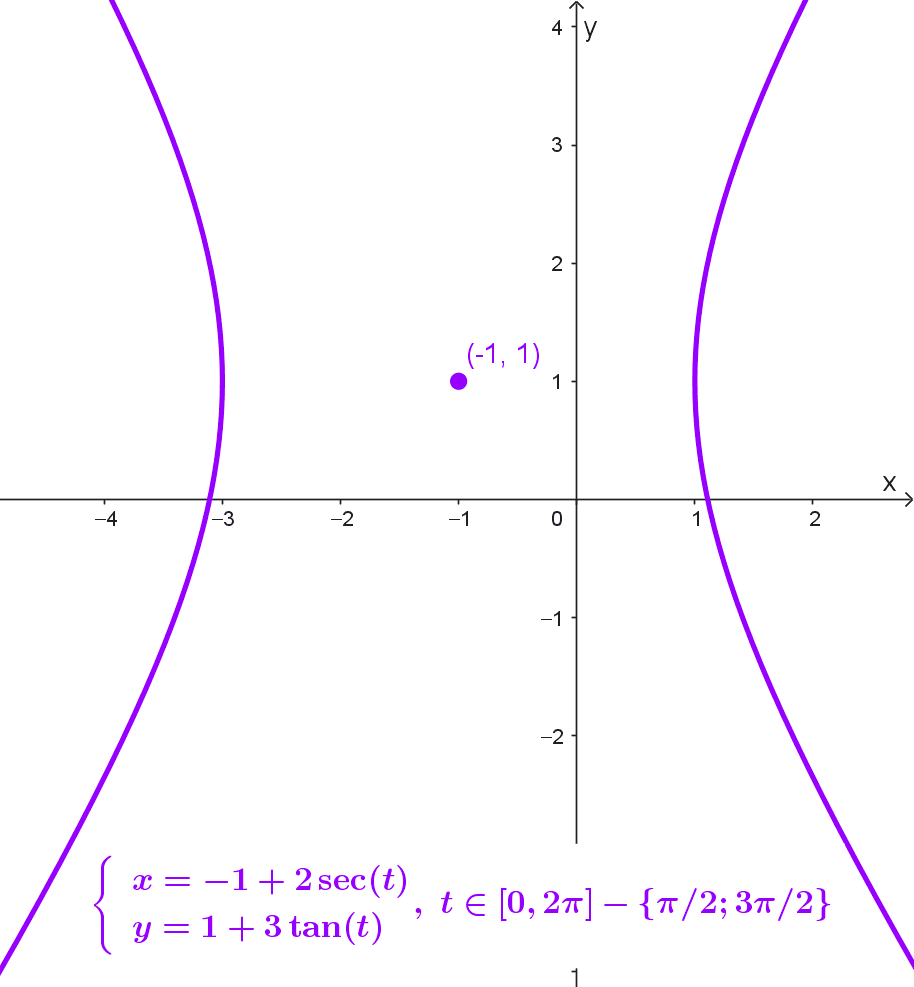
- *\begin{cases} x=-1+2 \sec(t) \\ y=1+3\tan(t) \end{cases}, ~t∈[0, 2π]-\{π/2; 3π/2\}* es una hipérbola horizontal con centro en (-1, 1), semieje transversal igual a 2 y semieje conjugado igual a 3.
- *\begin{cases} x=4+3 \tan(t) \\ y=-1+2\sec(t) \end{cases}, ~t∈[0, 2π]-\{π/2; 3π/2\}* es una hipérbola vertical con centro en (4, -1), semieje transversal igual a 2 y semieje conjugado igual a 3.
Parábola
Recordemos que las ecuaciones canónicas de una parábola con centro en (h, k) son:
- Si el eje focal es horizontal: *(y-k)^2=4p(x-h)*
- Si el eje focal es vertical: *(x-h)^2=4p(y-k)*
Reacomodando estas expresiones se pueden obtener las ecuaciones paramétricas correspondientes.
La ecuación paramétrica de una parábola orientada horizontalmente (eje focal paralelo al eje x) y vértice en (h, k) es:
*\begin{cases} x=h+pt^2 \\ y=k+2pt \end{cases},* donde t es cualquier número real, *-∞< t <+∞*
Si la parábola está orientada verticalmente (eje focal paralelo al eje y), la ecuación es:
*\begin{cases} x=h+2pt \\ y=k+pt^2 \end{cases}, -∞< t <+∞*
Ejemplos
- *\begin{cases} x=-2+0,5 t^2 \\ y=1+t \end{cases},~ t∈\mathbb{R}* es una parábola horizontal con vértice en (-2, 1) y p = 0,5 que abre hacia la izquierda.
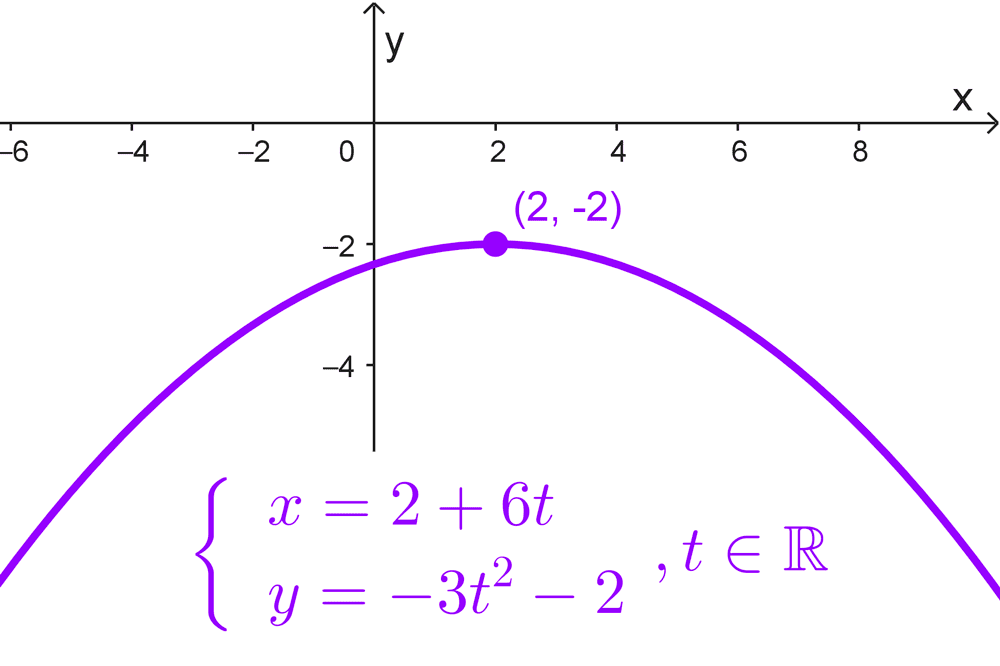
- *\begin{cases} x=2+6t \\ y=-3t^2-2 \end{cases}~, t∈\mathbb{R}* es una parábola vertical con vértice en (2, -2) y p = -3 que abre hacia abajo.
La forma de determinar hacia dónde abre la parábola es observar el signo del parámetro p en la ecuación.
Resumen de ecuaciones
Circunferencia
| Centro | Ecuación cartesiana | Ecuación paramétrica |
|---|---|---|
| Circunferencia con centro en el origen (0, 0) | x² + y² = r² | x = r cos(t) y = r sin(t) 0 ≤ t ≤ 2π |
| Circunferencia con centro en el punto (h, k) | (x - h)² + (y - k)² = r² | x = h + r cos(t) y = k + r sin(t) 0 ≤ t ≤ 2π |
Elipse
| Orientación | Ecuación cartesiana | Ecuación paramétrica |
|---|---|---|
| Elipse horizontal (eje focal paralelo al eje x) | (x - h)² / a² + (y - k)² / b² = 1 | x = h + a cos(t) y = k + b sin(t) 0 ≤ t ≤ 2π |
| Elipse vertical (eje focal paralelo al eje y) | (x - h)² / b² + (y - k)² / a² = 1 | x = h + b cos(t) y = k + a sin(t) 0 ≤ t ≤ 2π |
Hipérbola
| Orientación | Ecuación cartesiana | Ecuación paramétrica |
|---|---|---|
| Hipérbola horizontal (eje transversal paralelo al eje x) | (x - h)² / a² - (y - k)² / b² = 1 | x = h + a sec(t) y = k + b tan(t) t ∈ [0, 2π] - {π/2; 3π/2} |
| Hipérbola vertical (eje transversal paralelo al eje y) | (y - k)² / a² - (x - h)² / b² = 1 | x = h + b sec(t) y = k + a tan(t) t ∈ [0, 2π] - {π/2; 3π/2} |
Parábola
| Orientación | Ecuación cartesiana | Ecuación paramétrica |
|---|---|---|
| Parábola horizontal (eje focal paralelo al eje x) | (y - k)² = 4p(x - h) | x = h + pt² y = k + 2pt t ∈ ℝ |
| Parábola vertical (eje focal paralelo al eje y) | (x - h)² = 4p(y - k) | x = h + 2pt y = k + 2pt t ∈ ℝ |
Lecturas recomendadas:
- Fuller, G. y Tarwater, D. (1995). Geometría Analítica (7ma edición). Pearson Educación.
- Lehmann, C. (1989). Geometría Analítica. Limusa.
- Sullivan, M. (2006). Álgebra y Trigonometría. Pearson Educación.
- Swokowski, E. y Cole, J. (2009). Álgebra y Trigonometría con Geometría Analítica. Cengage Learning.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta

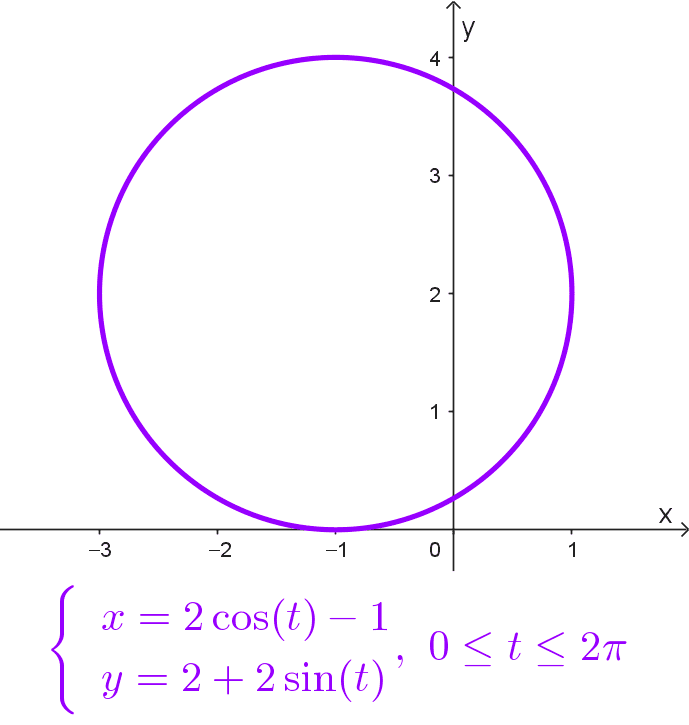


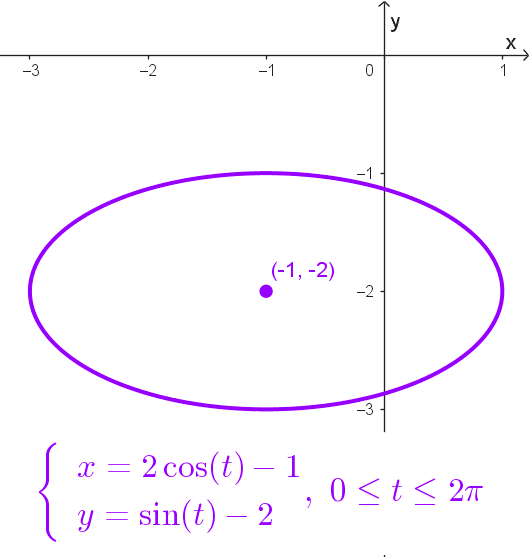


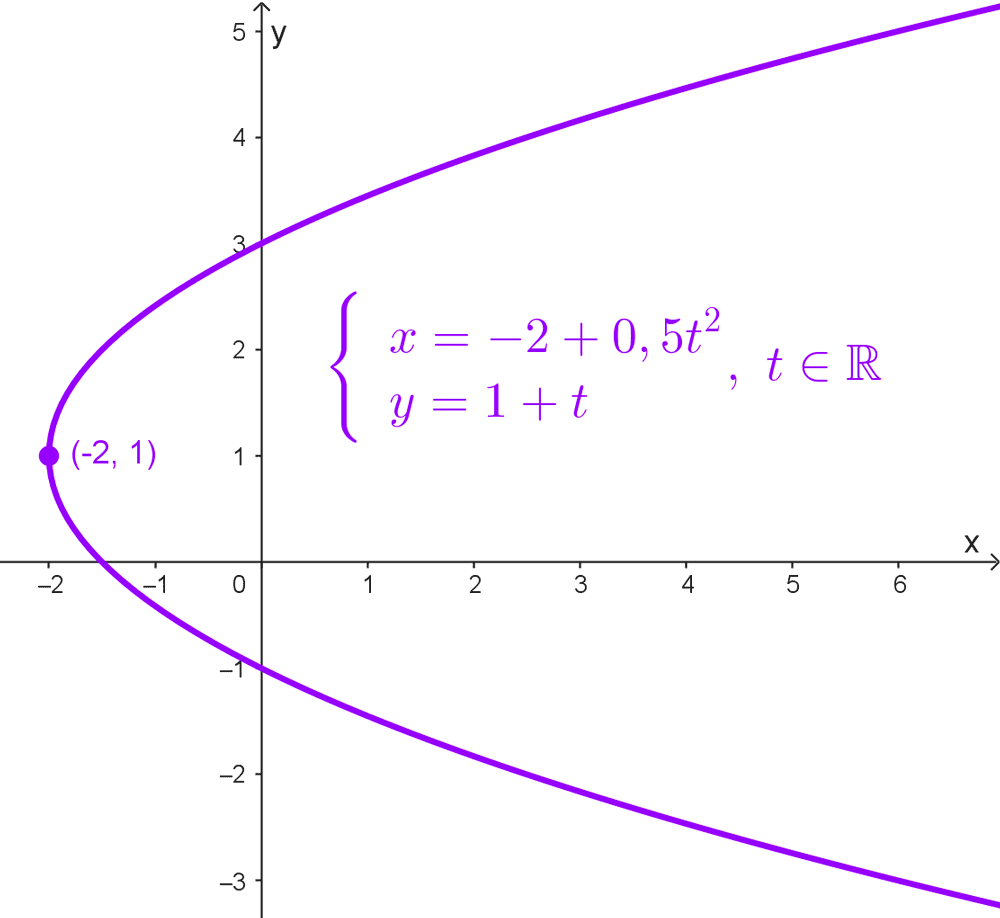
Otros artículos que pueden interesarte