
Foco de una parábola
El foco de una parábola es un punto fijo que está sobre el eje de simetría y alrededor del cual se "envuelve" la curva. Este punto aparece en la definición de parábola, ya que esta cónica es el conjunto de todos los puntos que están a igual distancia del foco y de una recta fija llamada directriz.
El vértice se encuentra a la misma distancia del foco que de la directriz, esta distancia es |p|, siendo "p" el parámetro que aparece en la ecuación canónica. Usamos esta información para encontrar las coordenadas del foco:
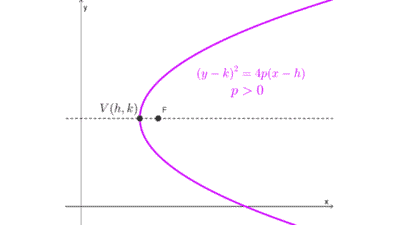
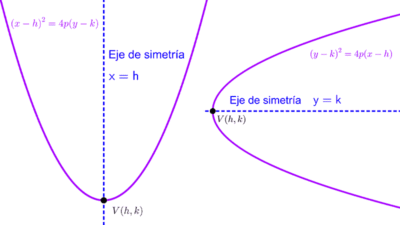
- En una parábola horizontal con vértice (h, k) y ecuación (y - k)2 = 4p (x - h), el foco está en las coordenadas (h + p, k).
- En una parábola vertical con vértice en (h, k) y ecuación (x - h)2 = 4p (y - k), el foco está ubicado en (h, k + p).
Si el vértice está en el origen de coordenadas, el foco se encuentra en (p, 0) para parábolas horizontales y (0, p) para parábolas verticales.
Nota: aquí nos enfocamos solo en un elemento de la parábola. Para comprenderlo mejor, te recomiendo que antes revises el artículo principal sobre esta cónica, donde abordamos su teoría básica:
Cómo hallar el foco
Vimos antes que para obtener el foco es necesario conocer el valor del parámetro p con su signo, las fórmulas se resumen en la siguiente tabla.
| Ecuación de la parábola | Vértice | Orientación | Foco |
|---|---|---|---|
| y2 = 4px | (0, 0) | Horizontal | (p, 0) |
| x2 = 4py | (0, 0) | Vertical | (0, p) |
| (y - k)2 = 4p (x - h) | (h, k) | Horizontal | (h + p, k) |
| (x - h)2 = 4p (y - k) | (h, k) | Vertical | (h, k + p) |
Si se tiene la ecuación general es necesario completar los cuadrados hasta llegar a la forma canónica y así obtener el valor del parámetro.
Ejemplos
Calcular las coordenadas del foco de las siguientes parábolas:
- y2 = 8x
- x2 = -2y
- (x + 2)2 = 6(y - 3)
- (y - 2)2 = 4(x - 1)
- x2 - 8x + 10y + 66 = 0
- y2 + 6x - 8y + 4 = 0
Solución 1
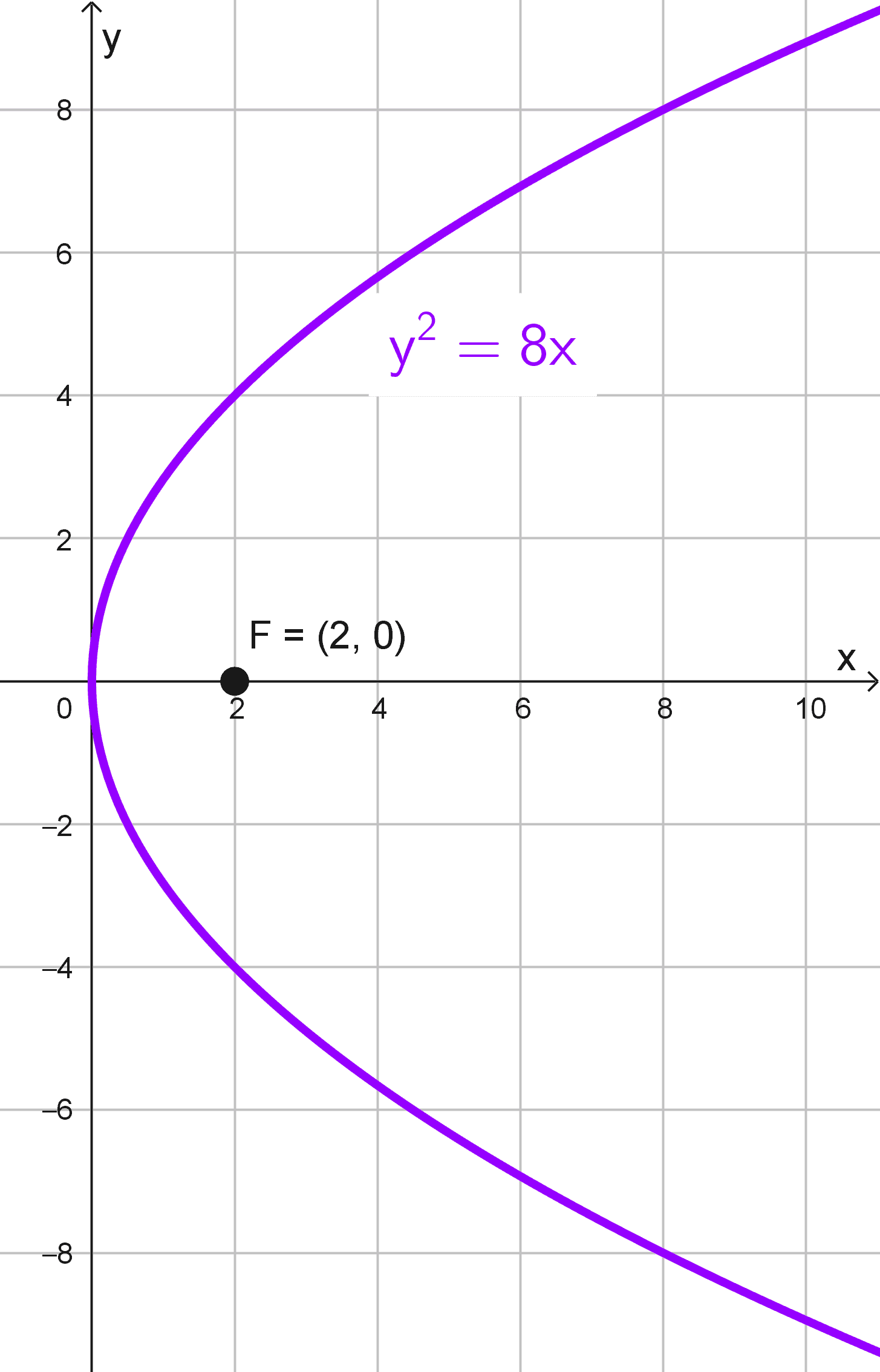
Ecuación dada: \(y^2=8x\)
Como primer paso, identificamos que la parábola es horizontal y tiene su vértice en el origen (0, 0). La forma estándar de una parábola horizontal es \(y^2=4px.\) Al comparar con la ecuación dada, \(4p=8,\) hallamos que \(p=2.\) Dado que el foco de una parábola horizontal con vértice en el origen está en (p, 0), determinamos que las coordenadas del foco son (2, 0).
Solución 2
Ecuación dada: \(x^2=-2y\)
Se trata de una parábola vertical con vértice en (0, 0). La forma estándar es \(x^2=4py.\) Igualando \(4p=-2,\) calculamos \(p=-0,5.\) Para una parábola vertical con vértice en el origen, el foco se ubica en \((0, p).\) Por lo tanto, encontramos que el foco está en \((0; -0,5).\)
Solución 3
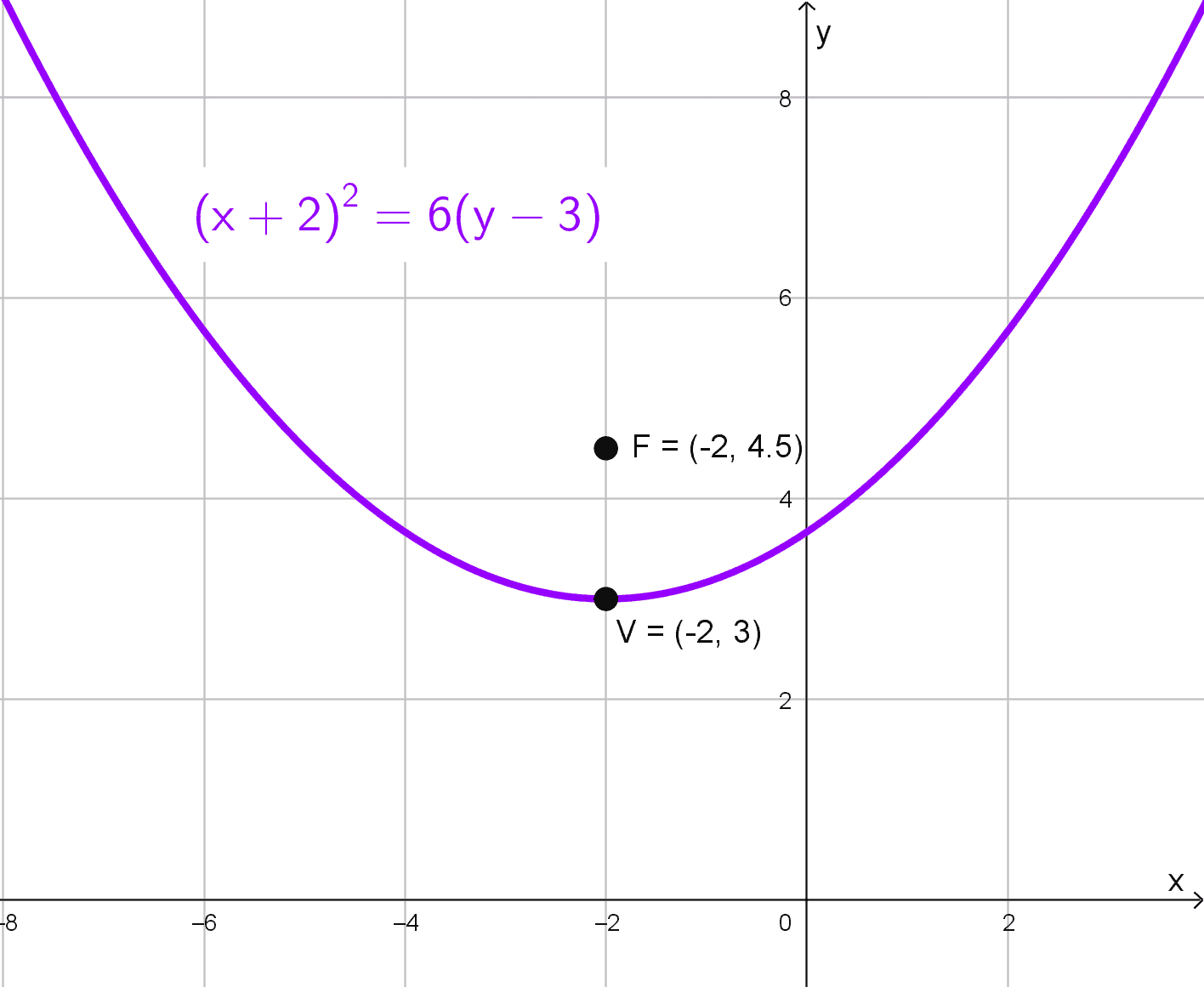
Ecuación dada: \((x+2)^2=6 (y-3)\)
Esta es una parábola vertical con vértice en (-2, 3). La forma estándar es \((x-h)^2=4p (y-k).\) Comparando, \(4p=6,\) de donde sacamos \(p=1,5.\) Como el foco de una parábola vertical está en \((h, k+p),\) determinamos que las coordenadas del foco son \((-2; 3+1,5)=(-2; 4,5).\)
Solución 4
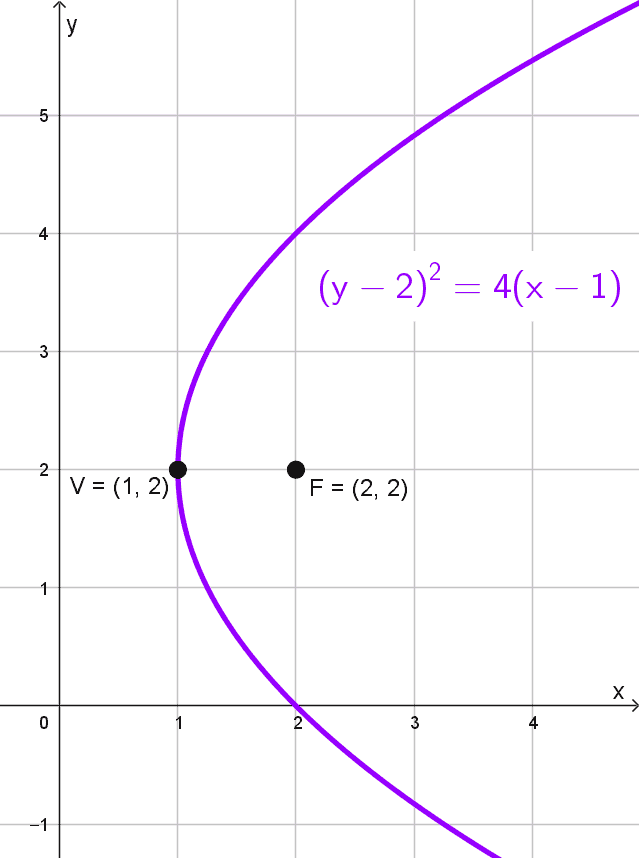
Ecuación dada: \((y-2)^2=4 (x-1)\)
Identificamos una parábola horizontal con vértice en (1, 2). La forma estándar es \((y-k)^2=4p (x-h).\) En este caso, \(4p=4,\) por lo que \(p=1.\) Para una parábola horizontal, el foco se encuentra en \((h+p, k).\) Hallamos así que el foco está en \((1+1, 2)=(2, 2).\)
Solución 5
Ecuación dada: \(x^2-8x+10y+66=0\)
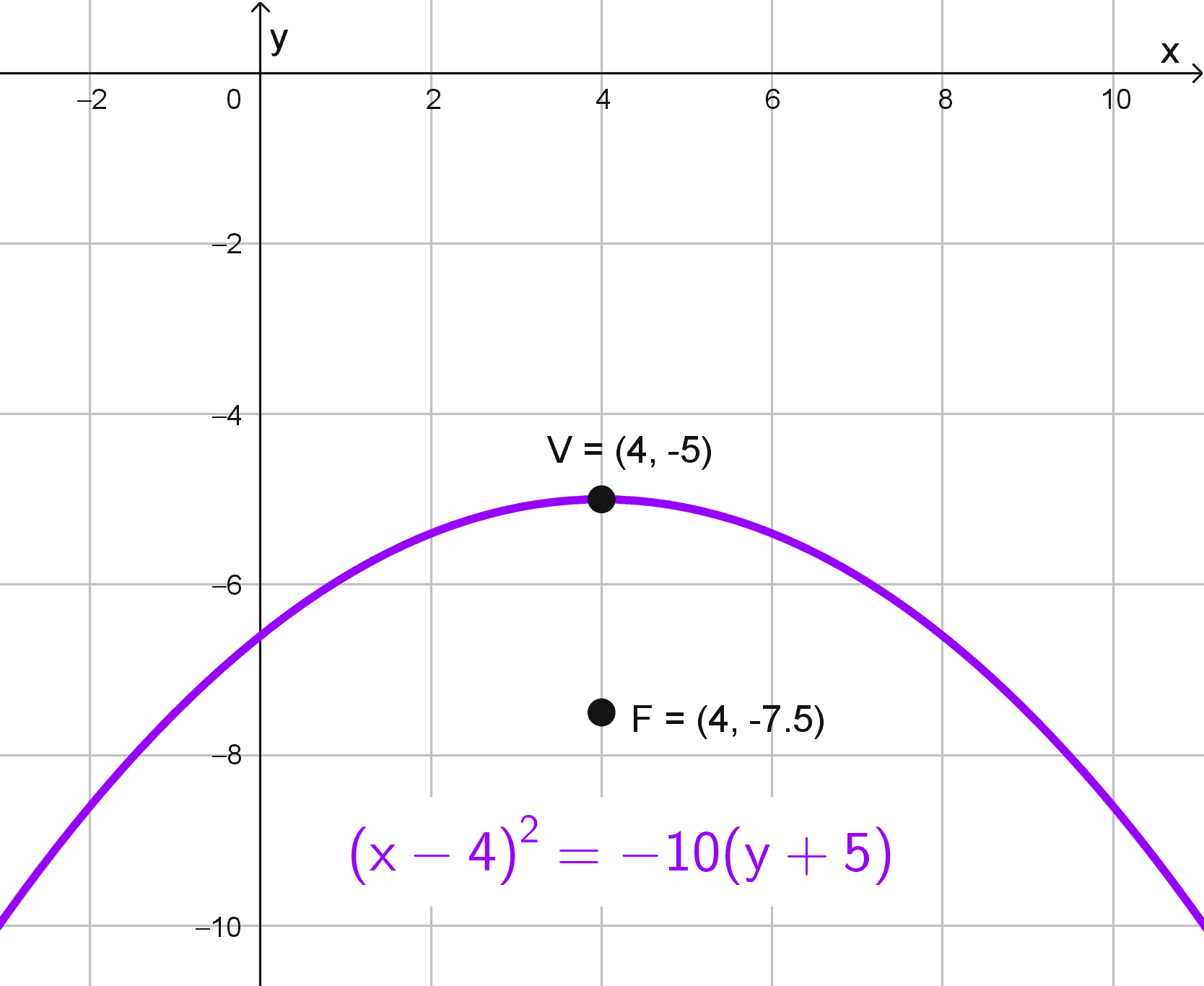
La ecuación está en forma general, pero completando los cuadrados obtenemos la forma canónica: \((x-4)^2=-10 (y+5).\)
Esta parábola es vertical con vértice en (4, -5). La ecuación estándar es \((x-h)^2=4p (y-k).\) Al comparar, \(4p=-10,\) obteniendo \(p=-2,5.\) Sabemos que el foco de una parábola vertical está en \((h, k+p).\) Por lo tanto, calculamos que el foco se ubica en \((4; -5-2,5)=(4; -7,5).\)
Solución 6
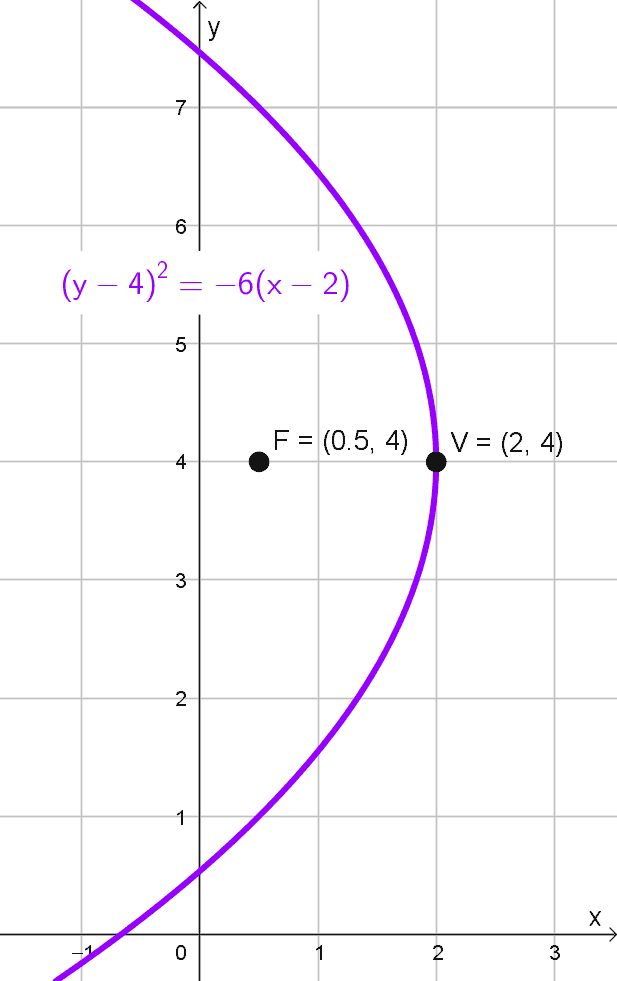
Ecuación dada: \(y^2+6x-8y+4=0\)
Nuevamente, completamos los cuadrados para sacar la forma reducida: \((y-4)^2=-6 (x-2).\)
Identificamos una parábola horizontal con vértice en (2, 4), cuya forma estándar es \((y-k)^2=4p (x-h).\) Al comparar, \(4p=-6,\) de donde hallamos \(p=-1,5.\) Como el foco de una parábola horizontal está en \((h+p, k),\) sustituimos los valores y determinamos que las coordenadas del foco son \((2-1,5~;~ 4)=(0,5~; ~4).\)
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta






Otros artículos que pueden interesarte