
Ejercicios de parábola
En este artículo veremos ejercicios de parábola en matemáticas resueltos paso a paso para todos los niveles educativos. Si aún no conoces sus conceptos fundamentales, te recomiendo revisar primero el artículo principal donde abordamos su teoría básica:
Índice
Ejercicios generales
Los siguientes artículos ofrecen ejercicios resueltos sobre los principales elementos de la parábola:

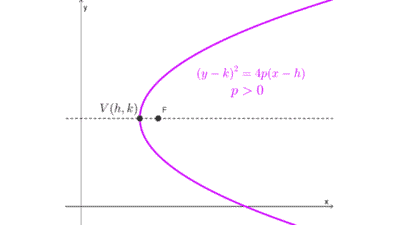

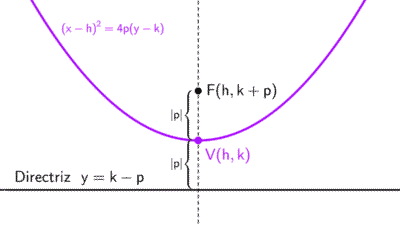
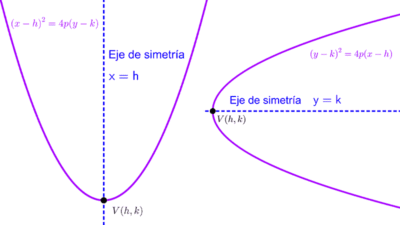




Obtener la ecuación de una parábola a partir de datos
Los siguientes ejercicios consisten en encontrar la ecuación reducida o general de una parábola a partir de cierta información de la misma.
Vértice en el origen
Encuentra las ecuaciones de las parábolas con los datos dados:
- Vértice en el origen y foco en el punto (-5, 0).
- V(0, 0) y F(0, 6).
- Vértice en (0, 0) y foco en (2, 0).
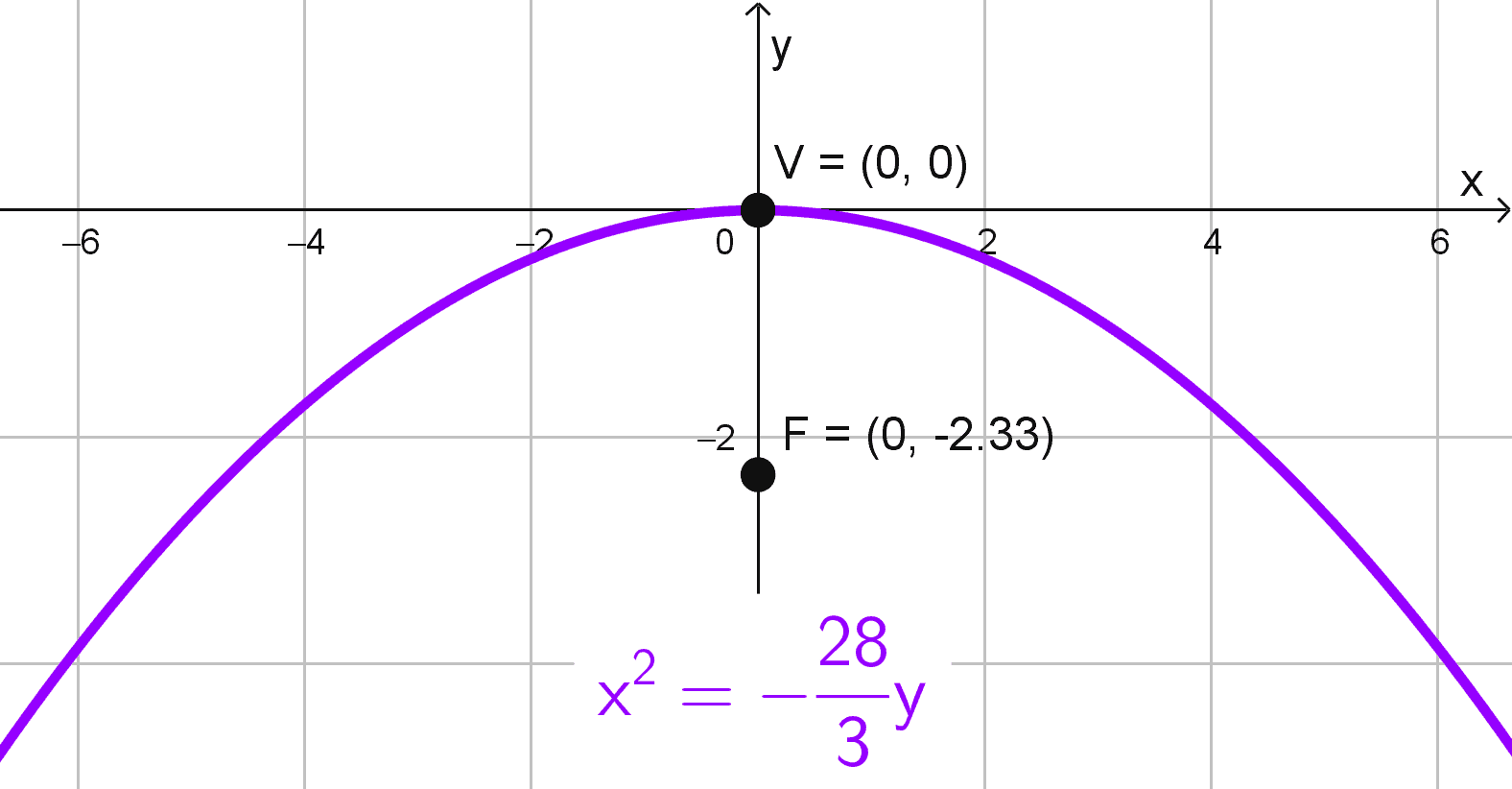
- Vértice en el origen de coordenadas y foco en (0, -7/3).
- Foco en (0, -1), directriz la recta y = 1.
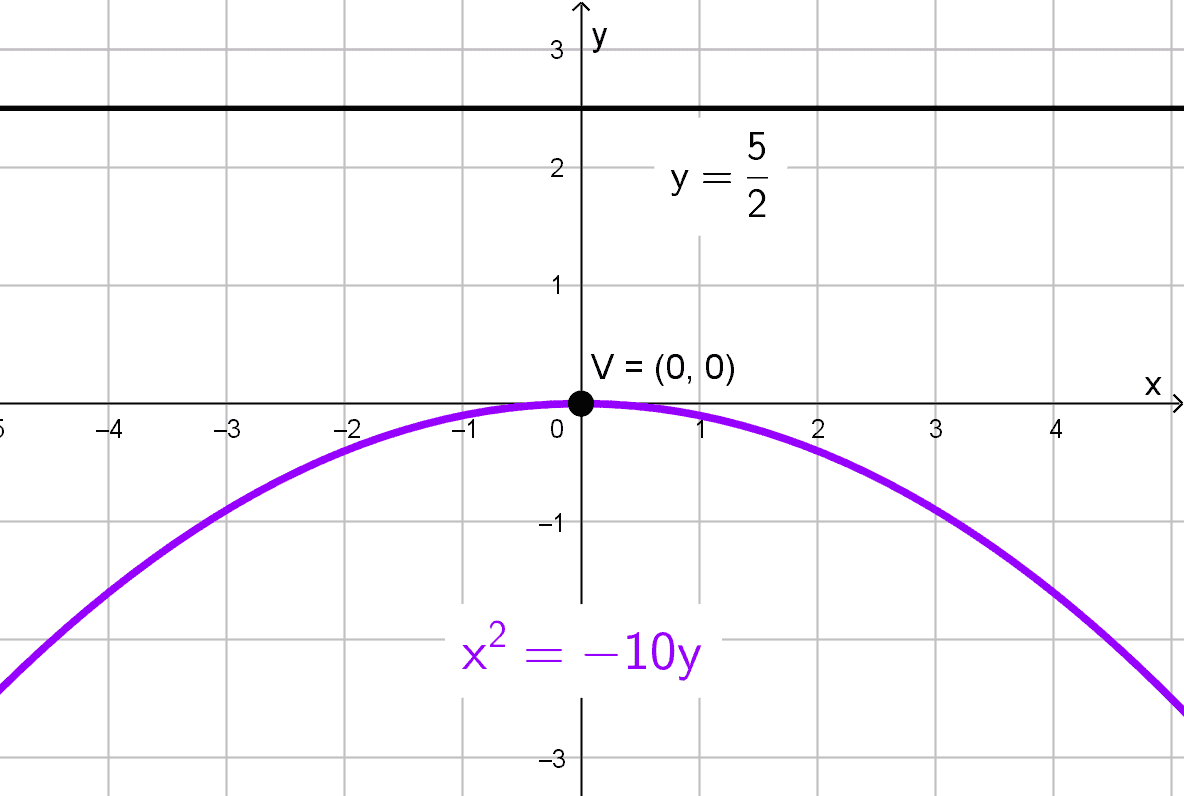
- Vértice en (0, 0) y la directriz es la recta 2y - 5 = 0.
- Foco en (4/3, 0) y directriz es la recta 3x + 4 = 0.
- Vértice en el origen, su eje coincide con el eje X y pasa por el punto (-2, 6).
Soluciones
Solución 1
Sabemos que el vértice está en el origen (0, 0) y el foco en (-5, 0). Ambos puntos están sobre el eje x así que la parábola abre horizontalmente, su ecuación tiene la forma \(y^2=4px.\) Dado que el foco está en (-5, 0), determinamos que el valor del parámetro \(p\) es \(-5,\) pues el foco en una parábola horizontal está en (p, 0).
Sustituyendo en la ecuación, obtenemos:
\(y^2=4(-5)x → y^2=-20x\)
Solución 2
El vértice está en (0, 0) y el foco en (0, 6). Como los puntos están sobre el eje y, la parábola abre verticalmente, su ecuación sigue la forma \(x^2=4py.\) Dado que el foco está en (0, 6), hallamos que el parámetro \(p=6,\) ya que el foco en una parábola vertical está en \((0, p)\).
Reemplazando en la ecuación, calculamos:
\(x^2=4(6)y → x^2=24y\)
Solución 3
Teniendo el vértice en (0, 0) y el foco en (2, 0), reconocemos que la parábola abre horizontalmente. Su ecuación canónica es \(y^2=4px.\) Como el foco está en (2, 0), determinamos que \(p=2.\)
Sustituyendo, encontramos:
\(y^2=4(2)x → y^2=8x\)
Solución 4
El vértice está en (0, 0) y el foco en (0, -7/3). Al abrir verticalmente, la ecuación de la parábola es \(x^2=4py.\) Dado que el foco está en \((0, -7/3),\) sacamos que \(p=-\dfrac{7}{3},\) pues el foco en una parábola vertical está en \((0, p)\).
Reemplazando, obtenemos:
\(x^2=4\left(-\dfrac{7}{3}\right)y → x^2=-\dfrac{28}{3}y\)
Solución 5
Dado que el foco está en (0, -1) y la directriz es la recta \(y=1,\) observamos que ambos están alineados verticalmente. Esto indica que la parábola abre verticalmente.
El vértice es el punto medio entre el foco y la directriz, que en este caso es el origen (0, 0). La distancia |p| se determina como la distancia del vértice al foco, es decir, \(|p|=1.\) Como el foco está por debajo del vértice, el parámetro p tendrá valor negativo, así que \(p=-1.\)
La ecuación canónica de una parábola vertical con vértice en el origen es:
\(x^2=4py\)
Sustituyendo \(p=-1,\) obtenemos:
\(x^2=-4y\)
Solución 6
El vértice está en (0, 0) y la directriz es la recta \(2y-5=0,\) que puede reescribirse como \(y=\dfrac{5}{2}.\) Como la directriz es horizontal, la parábola abre verticalmente. Sabemos que la directriz tiene ecuación \(y=-p,\) por lo tanto, \(p=-5/2.\)
La ecuación canónica de la parábola es:
\(x^2=4py\)
Sustituyendo \(p=-\dfrac{5}{2},\) hallamos:
\(x^2=4\left(-\dfrac{5}{2}\right)y → x^2=-10y\)
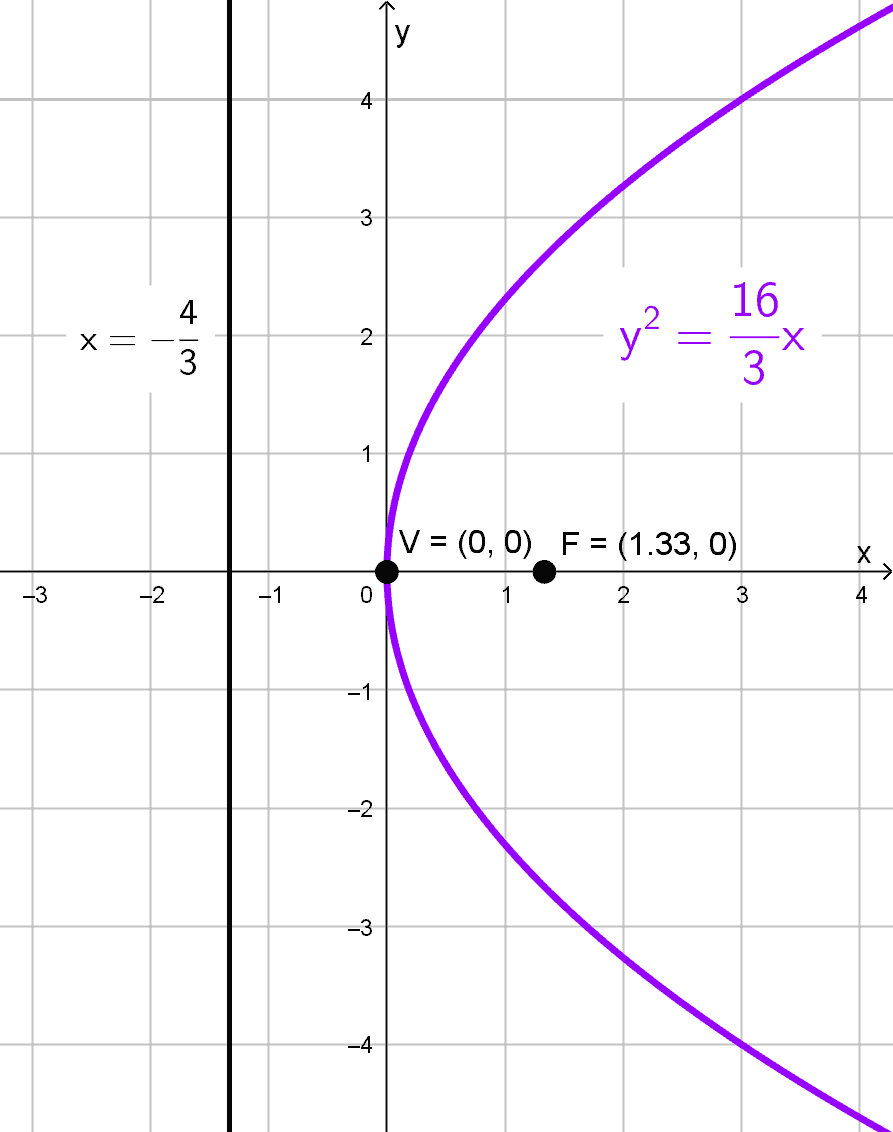
Solución 7
El foco está en \(\left (\dfrac{4}{3}, 0\right)\) y la directriz es la recta \(3x+4=0,\) que equivale a \(x=-\dfrac{4}{3}.\) Como la directriz es vertical, la parábola abre horizontalmente.
El vértice es el punto medio entre el foco y la directriz, que en este caso es el origen (0, 0). La distancia \(|p|\) es la distancia del vértice al foco (o del vértice a la directriz), es decir, \(|p|=\dfrac{4}{3}.\) Como el foco está a la derecha del vértice, el parámetro \(p\) será positivo, así que \(p=\dfrac{4}{3}.\)
La ecuación canónica de una parábola horizontal con vértice en el origen es:
\(y^2=4px\)
Sustituyendo \(p=\dfrac{4}{3},\) obtenemos:
\(y^2=4\left(\dfrac{4}{3}\right)x → y^2=\dfrac{16}{3}x\)
Solución 8
El vértice está en el origen (0, 0), su eje coincide con el eje X (lo que indica que la parábola abre horizontalmente) y pasa por el punto (-2, 6).
La ecuación canónica de una parábola horizontal con vértice en el origen es:
\(y^2=4px\)
Sustituyendo el punto \((-2, 6)\) en la ecuación para hallar \(p:\)
\(6^2=4p(-2) → 36=-8p → p=-\dfrac{9}{2}\)
Finalmente, la ecuación de la parábola es:
\(y^2=4\left(-\dfrac{9}{2}\right)x → y^2=-18x\)
Vértice fuera del origen
Determinar la ecuación de la parábola dados los siguientes datos:
- Vértice en (3, 1) y foco en (3, -1).
- V(-4, 3) y F(-1, 3).
- Vértice (3, 2) y foco (5, 2).
- V(-3, -2) y F(-3, 1/3).
- Directriz y - 1 = 0 y foco (4, -3).
- F(7, 3) y directriz y + 2 = 0
- Vértice en (1, -3) y directriz y + 5 = 0
- Vértice en (-3, 5), el lado recto mide 24 unidades y su eje es paralelo al eje Y (dos soluciones).
Soluciones
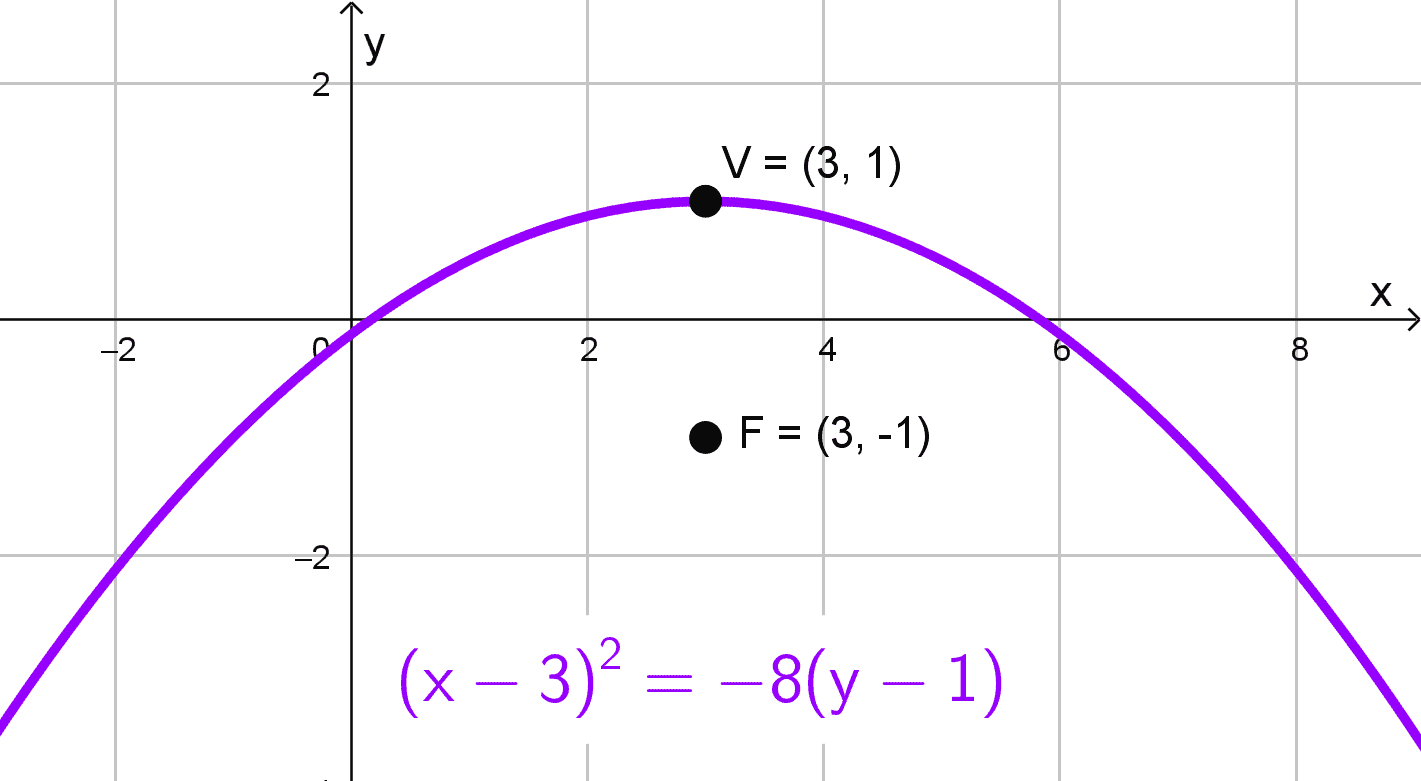
Solución 1
Como primer paso, identificamos las coordenadas del vértice V (3, 1) y del foco F (3, -1). Observamos que ambos puntos comparten la misma abscisa, lo que indica que el eje de la parábola es vertical. Calculamos el parámetro \(p\) como la diferencia entre las ordenadas del foco y el vértice:
\(p=-1-1=-2\)
Dado que \(p\) es negativo, la parábola abre hacia abajo. También nos damos cuenta de esto viendo que el foco está por debajo del vértice. Utilizando la forma canónica de una parábola con eje vertical:
\((x-h)^2=4p (y-k)\)
donde \((h, k)\) es el vértice, sustituimos los valores:
\((x-3)^2=4 (-2)(y-1)\)
Simplificando, obtenemos la ecuación:
\((x-3)^2=-8 (y-1)\)
Solución 2
En este caso, el vértice está en \(V (-4, 3)\) y el foco en \(F (-1, 3).\) Ambos puntos tienen la misma ordenada, por lo que el eje de la parábola es horizontal. Hallamos el parámetro \(p\) como la diferencia entre las abscisas del foco y el vértice:
\(p=-1-(-4)=3\)
Como \(p\) es positivo, la parábola abre hacia la derecha. La forma canónica para una parábola con eje horizontal es:
\((y-k)^2=4p (x-h)\)
Sustituyendo los valores conocidos:
\((y-3)^2=4 (3)(x-(-4))\)
Simplificando, llegamos a:
\((y-3)^2=12 (x+4)\)
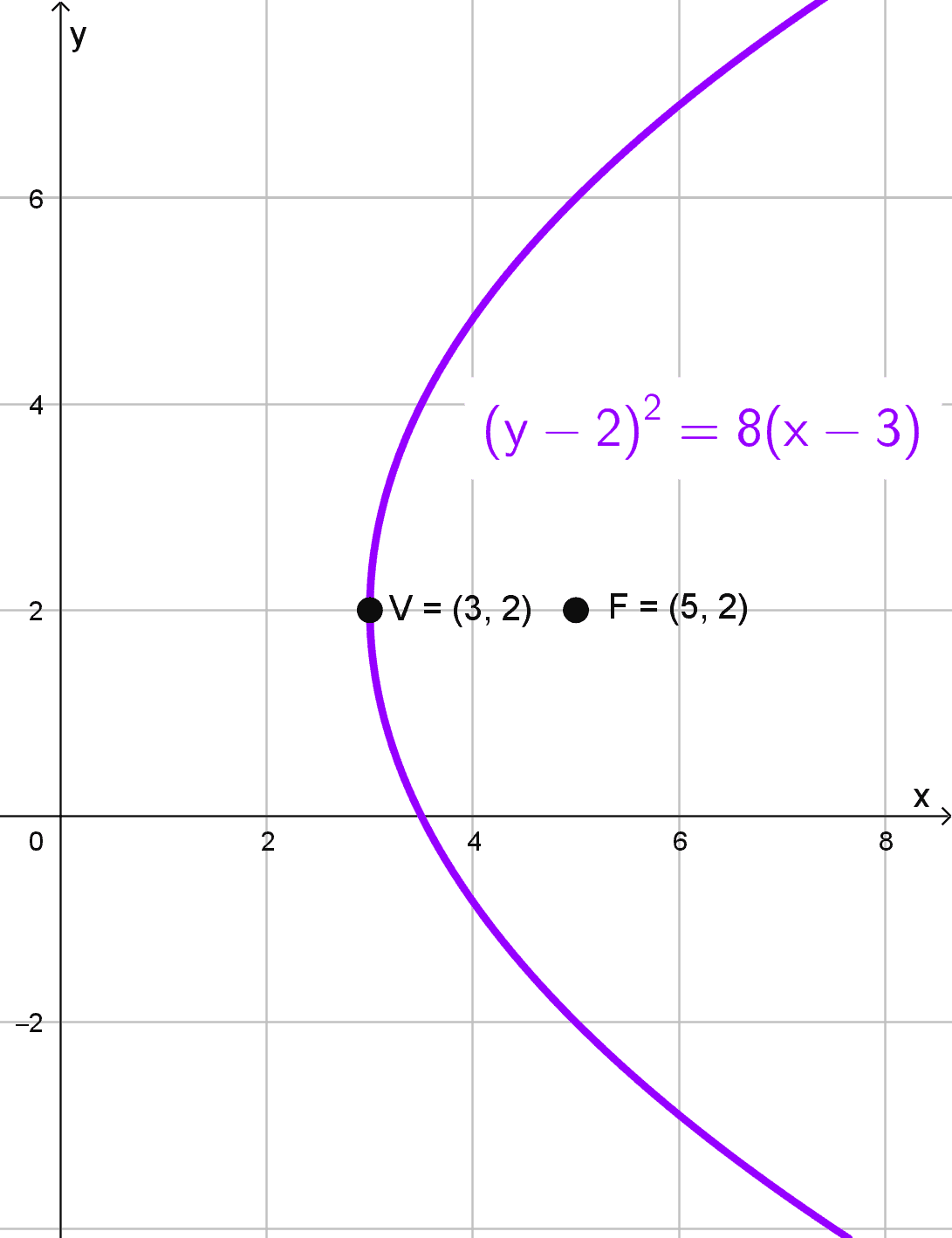
Solución 3
Partimos del vértice \(V (3, 2)\) y el foco \(F (5, 2).\) Notamos que ambos puntos tienen la misma ordenada, lo que significa que el eje de la parábola es horizontal. Determinamos \(p\) como la resta entre las abscisas del foco y el vértice:
\(p=5-3=2\)
Dado que \(p\) es positivo, la parábola abre hacia la derecha. Aplicamos la ecuación canónica para parábolas con eje horizontal:
\((y-k)^2=4p (x-h)\)
Reemplazando los valores:
\((y-2)^2=4 (2)(x-3)\)
Finalmente, la ecuación resulta:
\((y-2)^2=8 (x-3)\)
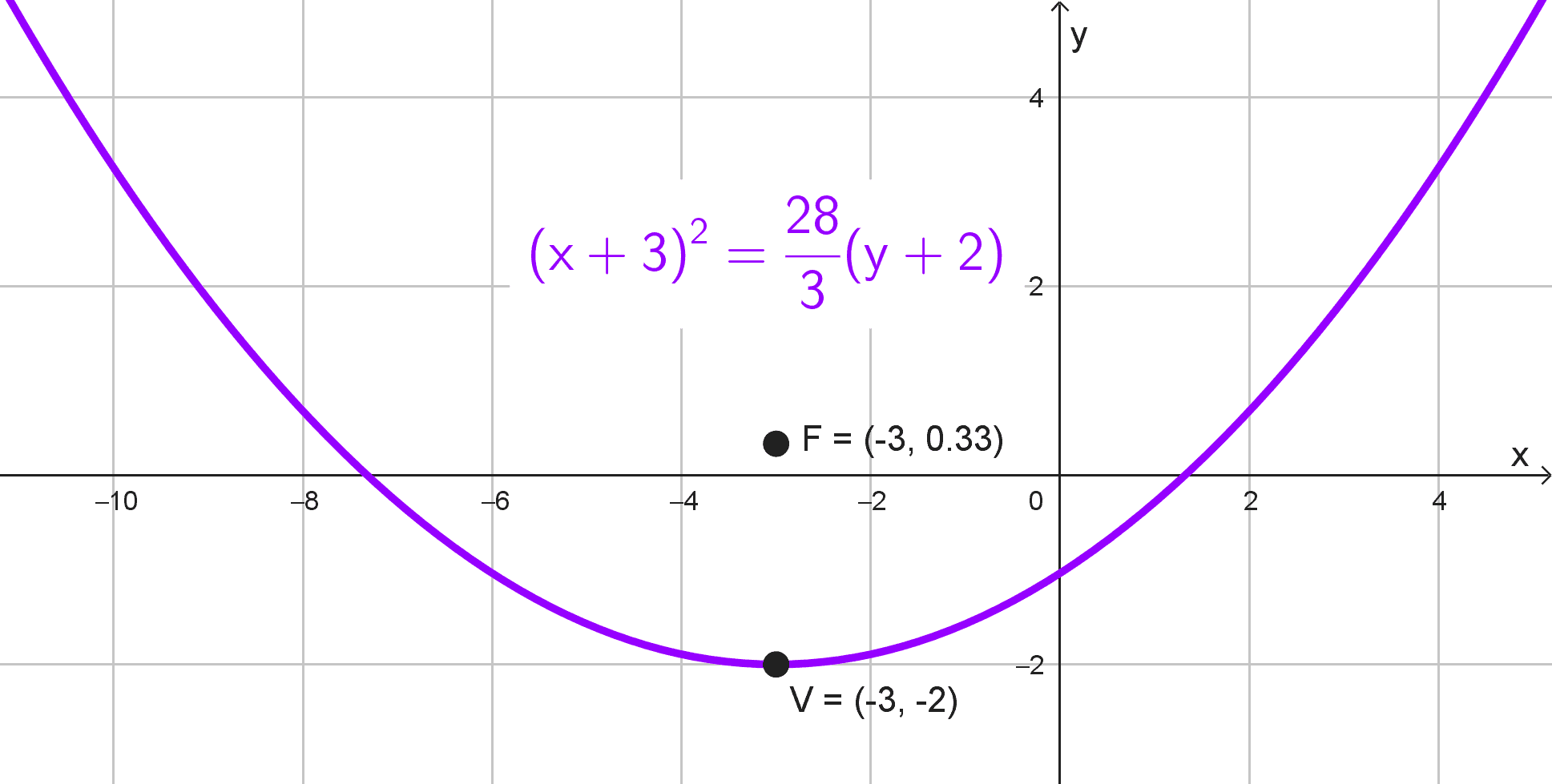
Solución 4
Tenemos el vértice en \(V (-3, -2)\) y el foco en \(F (-3, 1/3).\) Ambos puntos comparten la misma abscisa, lo que indica un eje vertical. Calculamos \(p\) como la diferencia entre las ordenadas del foco y el vértice:
\(p=\dfrac{1}{3}-(-2)=\dfrac{1}{3}+2=\dfrac{7}{3}\)
Como \(p\) es positivo, la parábola abre hacia arriba. Usamos la forma canónica para parábolas con eje vertical:
\((x-h)^2=4p (y-k)\)
Sustituyendo los valores conocidos:
\((x-(-3))^2=4\left (\dfrac{7}{3}\right)(y-(-2))\)
Simplificando, obtenemos:
\((x+3)^2=\dfrac{28}{3}(y+2)\)
Solución 5
Primero, identificamos la directriz \(y-1=0\) (es decir, \(y=1\)) y el foco \(F (4, -3).\) Como la directriz es horizontal, el eje de la parábola es vertical. Hallamos el vértice V como el punto medio entre el foco y la proyección del foco sobre la directriz.
La distancia vertical entre el foco \((4, -3)\) y la directriz \(y=1\) es:
\(\text{Distancia}=|-3-1 |=4\)
Por lo tanto, el vértice está a mitad de camino:
\(V \left(4, \dfrac{1+(-3)}{2}\right)=V (4, -1)\)
Calculamos |p| como la distancia desde el vértice al foco:
\(|p|=|-3-(-1)|=2\)
Como el foco está por debajo del vértice, la parábola abrirá hacia abajo, por tanto tendrá parámetro negativo \(p=-2.\)
Usando la forma canónica de una parábola con eje vertical:
\((x-h)^2=4p (y-k)\)
Sustituyendo \(V (4, -1)\) y \(p=-2:\)
\((x-4)^2=4 (-2)(y-(-1))\)
Simplificando, obtenemos:
\((x-4)^2=-8 (y+1)\)
Solución 6
Tenemos el foco \(F (7, 3)\) y la directriz \(y+2=0\) (es decir, \(y=-2\) ). Como la directriz es horizontal, el eje de la parábola es vertical.
Calculamos el vértice como el punto medio entre el foco y su proyección sobre la directriz:
\(V\left(7, \dfrac{3+(-2)}{2}\right)=V (7; 0,5)\)
Determinamos \(|p|\) como la distancia desde el vértice al foco:
\(|p|=|3-0,5|=2,5\)
Como el foco está por encima del vértice, p tendrá signo positivo: \(p=2,5.\)
Aplicamos la ecuación canónica para parábolas con eje vertical:
\((x-h)^2=4p (y-k)\)
Sustituyendo \(V (7; 0,5)\) y \(p=2,5:\)
\((x-7)^2=4 (2,5)(y-0,5)\)
Simplificando, la ecuación queda:
\((x-7)^2=10 (y-0,5)\)
Solución 7
El vértice está en \(V (1, -3)\) y la directriz es \(y+5=0\) (\(y=-5\)). Como la directriz es horizontal, el eje de la parábola es vertical.
Calculamos \(|p|\) como la distancia del vértice a la directriz:
\(|p|=|-3-(-5)|=2\)
Como el foco debe estar en el lado opuesto de la directriz respecto al vértice, y el vértice está en \(y=-3\) (por encima de la directriz \(y=-5\) ), la parábola abre hacia arriba. Por lo tanto, \(p=2.\)
Usamos la forma canónica para parábolas con eje vertical:
\((x-h)^2=4p (y-k)\)
Sustituyendo \(V (1, -3)\) y \(p=2:\)
\((x-1)^2=4 (2)(y-(-3))\)
Simplificando, obtenemos:
\((x-1)^2=8 (y+3)\)
Solución 8
El vértice está en \(V (-3, 5),\) el lado recto mide \(24\) unidades y el eje es paralelo al eje \(Y\) (eje vertical). Sabemos que la longitud del lado recto es \(|4p|,\) entonces:
\(|4p|=24 → |p|=6\)
Esto da dos posibilidades:
1) Si \(p=6\) (la parábola abre hacia arriba):
\((x+3)^2=4 (6)(y-5) → (x+3)^2=24 (y-5)\)
2) Si \(p=-6\) (la parábola abre hacia abajo):
\((x+3)^2=4 (-6)(y-5) → (x+3)^2=-24 (y-5)\)
Por lo tanto, las dos ecuaciones posibles son:
\((x+3)^2=24 (y-5)~~~ y~~~ (x+3)^2=-24 (y-5)\)
Parábola que pasa por tres puntos
Escribir la ecuación general de la parábola con las siguientes características:
- Eje de simetría paralelo al eje X y pasa por los puntos P(-1, 1), Q(-1, -1) y R(-5, 0).
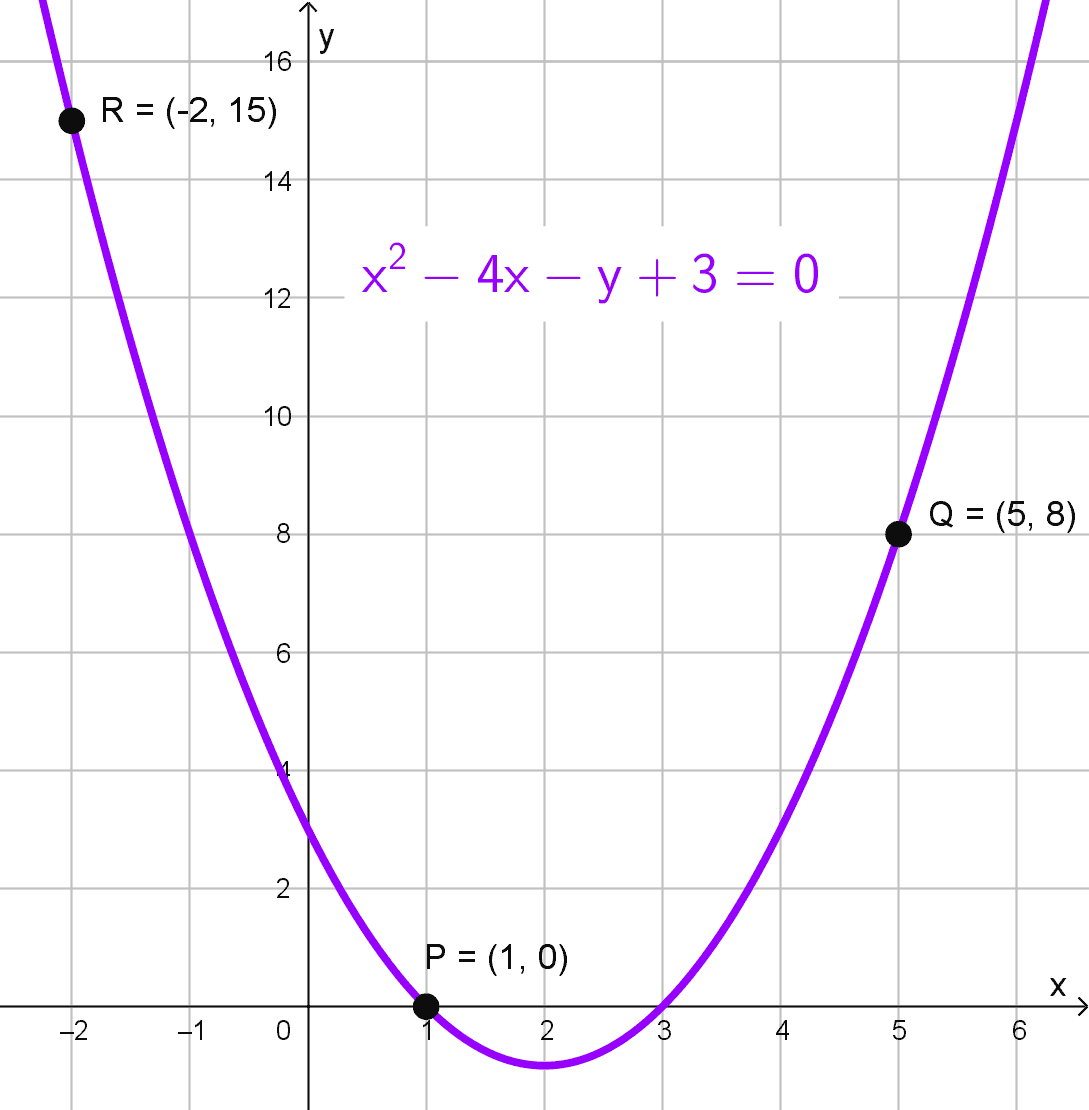
- Eje focal paralelo al eje Y y pasa por los puntos P(1, 0), Q(5, 8) y R(-2, 15).
Soluciones
Solución 1
Como primer paso, consideramos que la parábola tiene su eje de simetría paralelo al eje X, por lo que su ecuación general es de la forma:
\(y^2+Dx+Ey+F=0\)
Sustituimos los puntos dados en esta ecuación para formar un sistema de ecuaciones. Comenzamos con el punto \(P (-1, 1):\)
\((1)^2+D (-1)+E (1)+F=0\)
\(1-D+E+F=0 \quad \text{(1)}\)
Ahora, usamos el punto \(Q (-1, -1):\)
\((-1)^2+D (-1)+E (-1)+F=0\)
\(1-D-E+F=0 \quad \text{(2)}\)
Finalmente, sustituimos el punto \(R (-5, 0):\)
\((0)^2+D (-5)+E (0)+F=0\)
\(-5D+F=0 \quad \text{(3)}\)
Restamos la ecuación (2) de la ecuación (1) para eliminar D y F:
\((1-D+E+F)-(1-D-E+F)=0\)
\(2E=0\)
\(E=0\)
Sustituyendo \(E=0\) en la ecuación (1), obtenemos:
\(1-D+0+F=0\)
\(-D+F=-1 \quad \text{(4)}\)
De la ecuación (3), despejamos F:
\(F=5D\)
Reemplazamos F en la ecuación (4):
\(-D+5D=-1\)
\(4D=-1\)
\(D=-\dfrac{1}{4}\)
Con \(D=-\dfrac{1}{4},\) hallamos \(F:\)
\(F=5\left (-\dfrac{1}{4}\right)=-\dfrac{5}{4}\)
Finalmente, la ecuación general de la parábola es:
\(y^2-\dfrac{1}{4}x-\dfrac{5}{4}=0\)
Multiplicando por 4 para eliminar denominadores:
\(4y^2-x-5=0\)
Solución 2
Ahora la parábola tiene su eje focal paralelo al eje Y, por lo que su ecuación general es de la forma:
\(x^2+Dx+Ey+F=0\)
Sustituimos los puntos dados para formar un sistema de ecuaciones. Comenzamos con el punto \(P (1, 0):\)
\((1)^2+D (1)+E (0)+F=0\)
\(1+D+F=0 \quad \text{(1)}\)
Ahora, usamos el punto \(Q (5, 8):\)
\((5)^2+D (5)+E (8)+F=0\)
\(25+5D+8E+F=0 \quad \text{(2)}\)
\(mente, sustituimos el punto \)R (-2, 15):*
\( (-2)^2+D (-2)+E (15)+F=0\)
\(4-2D+15E+F=0 \quad \text{(3)}\)
De la ecuación (1), despejamos \(F:\)
\(F=-1-D\)
Sustituimos \(F=-1-D\) en las ecuaciones (2) y (3):
Para la ecuación (2):
\(25+5D+8E-1-D=0\)
\(24+4D+8E=0\)
Simplificando:
\(6+D+2E=0 \quad \text{(4)}\)
Para la ecuación (3):
\(4-2D+15E-1-D=0\)
\(3-3D+15E=0\)
Simplificando:
\(1-D+5E=0 \quad \text{(5)}\)
Resolvemos el sistema formado por (4) y (5). Despejamos \(D\) de (5):
\(D=1+5E\)
Sustituimos \(D=1+5E\) en la ecuación (4):
\(6+(1+5E)+2E=0\)
\(7+7E=0\)
\(E=-1\)
Ahora, hallamos \(D:\)
\(D=1+5 (-1)=-4\)
\(mente, calculamos \)F:*
\(F=-1-(-4)=3\)
La ecuación general de la parábola es:
\(x^2-4x-y+3=0\)
¿Te está sirviendo este artículo? ¡Por favor, califícalo!
0,0 / 5 — 0 votos
Ecuación a partir de la gráfica
Obtener la ecuación de las parábolas mostradas en los siguientes gráficos:
Soluciones
Solución A
Observamos que la parábola está abierta hacia la derecha, por lo que su ecuación tiene la forma estándar:
\((y-k)^2=4p(x-h)\)
donde \((h, k)\) es el vértice. En este caso, el vértice está en \((0, 1),\) así que sustituimos \(h=0\) y \(k=1:\)
\((y-1)^2=4p x\)
Ahora, utilizamos el punto \((1, 2)\) por el que pasa la parábola para hallar \(p.\) Sustituyendo \(x=1\) e \(y=2:\)
\((2-1)^2=4p(1) → 1=4p → p=\dfrac{1}{4}\)
Finalmente, reemplazamos \(p\) en la ecuación:
\((y-1)^2=4 \left( \dfrac{1}{4} \right) x → (y-1)^2=x\)
Solución B
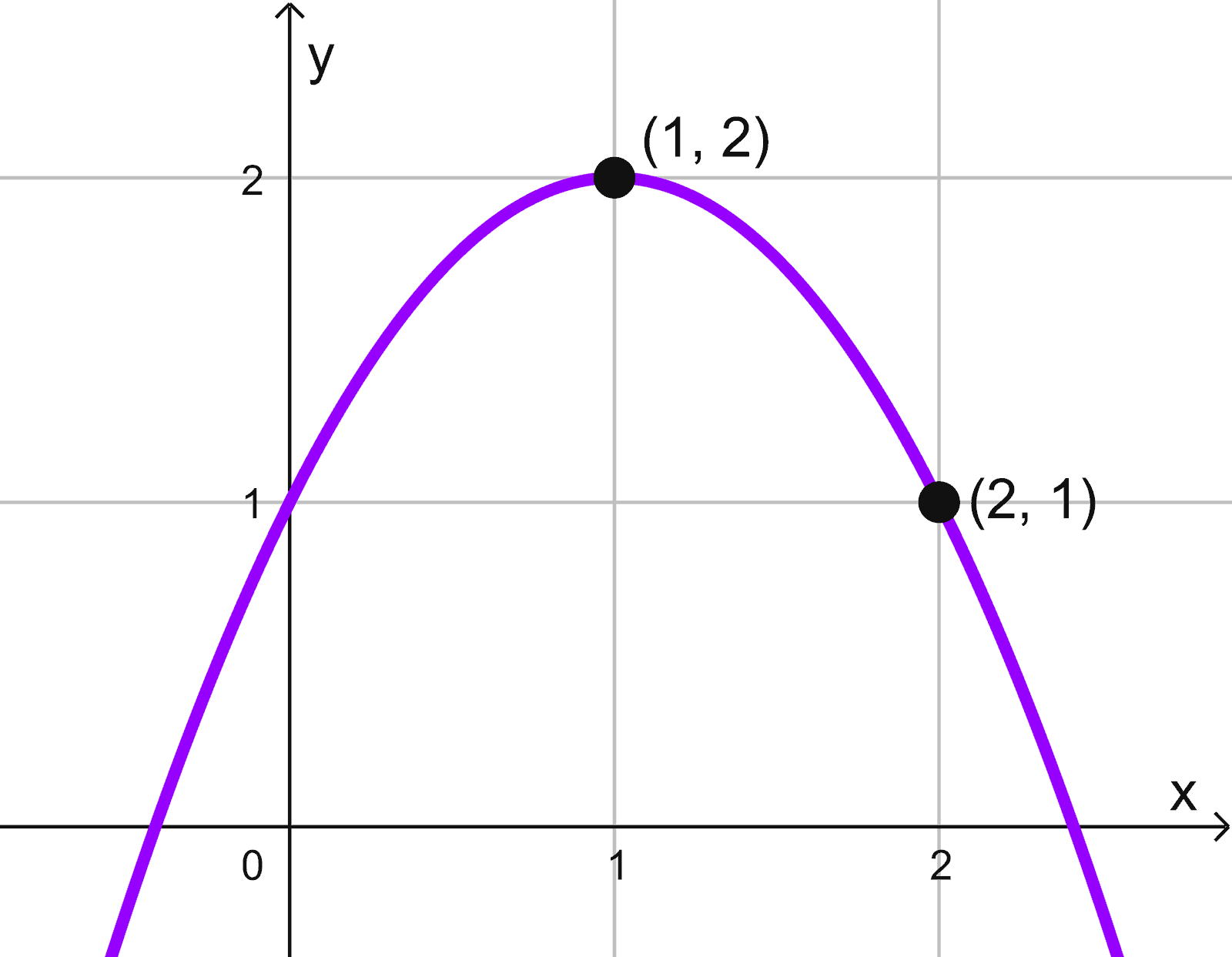
Reconocemos que la parábola está abierta hacia abajo con vértice en (1, 2). Su ecuación estándar es:
\((x-h)^2=4p(y-k)\)
Sustituyendo el vértice \((h, k)=(1, 2):\)
\((x-1)^2=4p(y-2)\)
Para encontrar \(p,\) usamos el punto \((2, 1):\)
\((2-1)^2=4p(1-2) → 1=-4p → p=-\dfrac{1}{4}\)
Reemplazando \(p\) en la ecuación, obtenemos:
\((x-1)^2=4 \left(-\dfrac{1}{4} \right)(y-2) → (x-1)^2=-(y-2)\)
Solución C
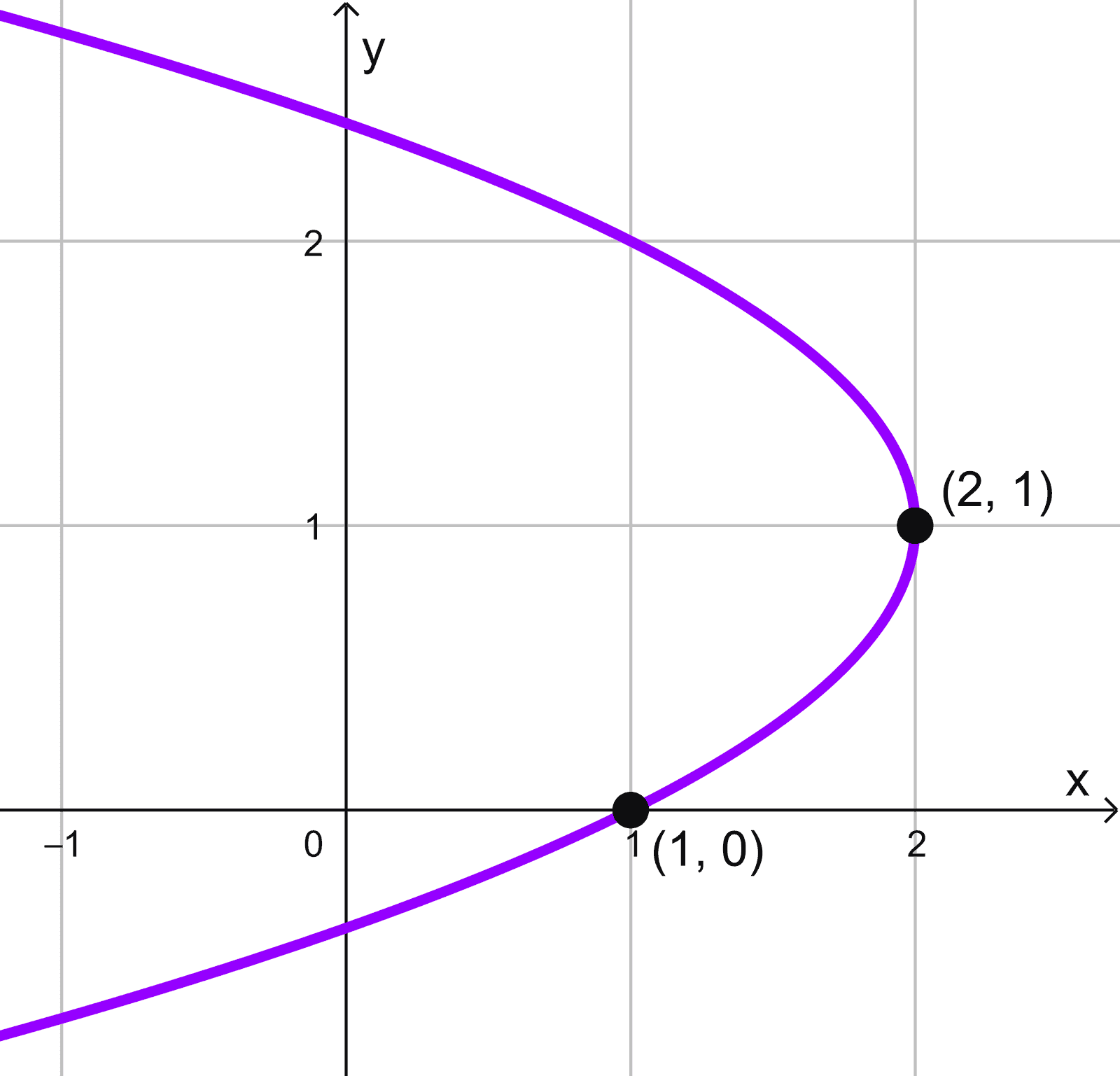
Identificamos que la parábola abre hacia la izquierda y tiene vértice en (2, 1). Su forma canónica es:
\((y-k)^2=4p(x-h)\)
Al sustituir el vértice \((h, k)=(2, 1):\)
\((y-1)^2=4p(x-2)\)
Calculamos \(p\) usando el punto \((1, 0):\)
\((0-1)^2=4p(1-2) → 1=-4p → p=-\dfrac{1}{4}\)
La ecuación final queda:
\((y-1)^2=4 \left( -\dfrac{1}{4} \right)(x-2) → (y-1)^2=-(x-2)\)
Solución D
Vemos que la parábola está abierta hacia arriba con vértice en (0, -1). Su forma estándar es:
\((x-h)^2=4p(y-k)\)
Sustituyendo \((h, k)=(0, -1):\)
\(x^2=4p(y+1)\)
Hallamos \(p\) mediante el punto \((2, 0):\)
\(2^2=4p(0+1) → 4=4p → p=1\)
La ecuación resultante es:
\(x^2=4(1)(y+1) → x^2=4(y+1)\)
Hallar los elementos de una parábola a partir de su ecuación
Dadas las siguientes ecuaciones de parábolas: obtener el foco, vértice, ecuación de la directriz, longitud del lado recto, ecuación del eje de simetría y graficarla.
- \(x^2=4y\)
- \(y^2=8x\)
- \(y^2=-16x\)
- \(x^2=-4y\)
- \((y-2)^2=8(x+1)\)
- \((x+4)^2=16(y+2)\)
- \((x-3)^2=-(y+1)\)
- \((y+1)^2=-4(x-2)\)
- \(4x^2-12x-16y+41=0\)
- \(16y^2+8y-24x+49=0\)
- \(x^2+2x=-4y+19\)
- \(8y+56=-y^2-20x\)
En estos artículos puedes ver cómo encontrar cada elemento individualmente:







Soluciones
Solución 1
Para la ecuación \(x^2=4y,\) identificamos que corresponde a una parábola vertical, porque la variable x está elevada al cuadrado. Reconocemos que el vértice está en el origen \((0, 0).\) Comparando con la forma estándar \(x^2=4py,\) determinamos que \(4p=4,\) de donde \(p=1.\) Como p es positivo, la parábola abre hacia arriba.
Calculamos el foco en \((0, p)=(0, 1).\) La directriz es la recta horizontal \(y=-p,\) es decir, \(y=-1.\) La longitud del lado recto es \(|4p|=4.\) El eje de simetría coincide con el eje \(y,\) cuya ecuación es \(x=0.\)
En conclusión:
- Vértice: \((0, 0)\)
- Foco: \((0, 1)\)
- Directriz: \(y=-1\)
- Lado recto: \(L_R=4\)
- Eje de simetría: \(x=0\)
Solución 2
La ecuación \(y^2=8x\) representa una parábola horizontal con vértice en \((0, 0),\) esto porque la variable y está elevada al cuadrado. Al compararla con la forma estándar \(y^2=4px,\) hallamos que \(4p=8,\) por lo que \(p=2.\) Como \(p>0,\) la parábola abre hacia la derecha.
El foco se ubica en \((p, 0)=(2, 0).\) La directriz es la recta vertical \(x=-p,\) es decir, \(x=-2.\) La longitud del lado recto es \(|4p|=8.\) El eje de simetría es el eje \(x,\) con ecuación \(y=0.\)
En conclusión:
- Vértice: \((0, 0)\)
- Foco: \((2, 0)\)
- Directriz: \(x=-2\)
- Lado recto: \(L_R=8\)
- Eje de simetría: \(y=0\)
Solución 3
En la ecuación \(y^2=-16x,\) reconocemos una parábola horizontal que abre hacia la izquierda, porque su parámetro es negativo. Comparando con \(y^2=4px,\) obtenemos \(4p=-16,\) lo que implica \(p=-4.\)
El foco está en \((p, 0)=(-4, 0).\) La directriz es la recta \(x=-p,\) es decir, \(x=4.\) La longitud del lado recto es \(|4p|=16.\) El eje de simetría sigue siendo \(y=0.\)
Conclusión:
- Vértice: \((0, 0)\)
- Foco: \((-4, 0)\)
- Directriz: \(x=4\)
- Lado recto: \(L_R=16\)
- Eje de simetría: \(y=0\)
Solución 4
La ecuación \(x^2=-4y\) describe una parábola vertical con vértice en el origen. Al compararla con \(x^2=4py,\) sacamos que \(4p=-4,\) entonces \(p=-1.\) Como \(p<0,\) la parábola abre hacia abajo.
El foco se encuentra en \((0, p)=(0, -1).\) La directriz es \(y=-p,\) es decir, \(y=1.\) La longitud del lado recto es \(|4p|=4.\) El eje de simetría es \(x=0.\)
Elementos:
- Vértice: \((0, 0)\)
- Foco: \((0, -1)\)
- Directriz: \(y=1\)
- Lado recto: \(L_R=4\)
- Eje de simetría: \(x=0\)
Solución 5
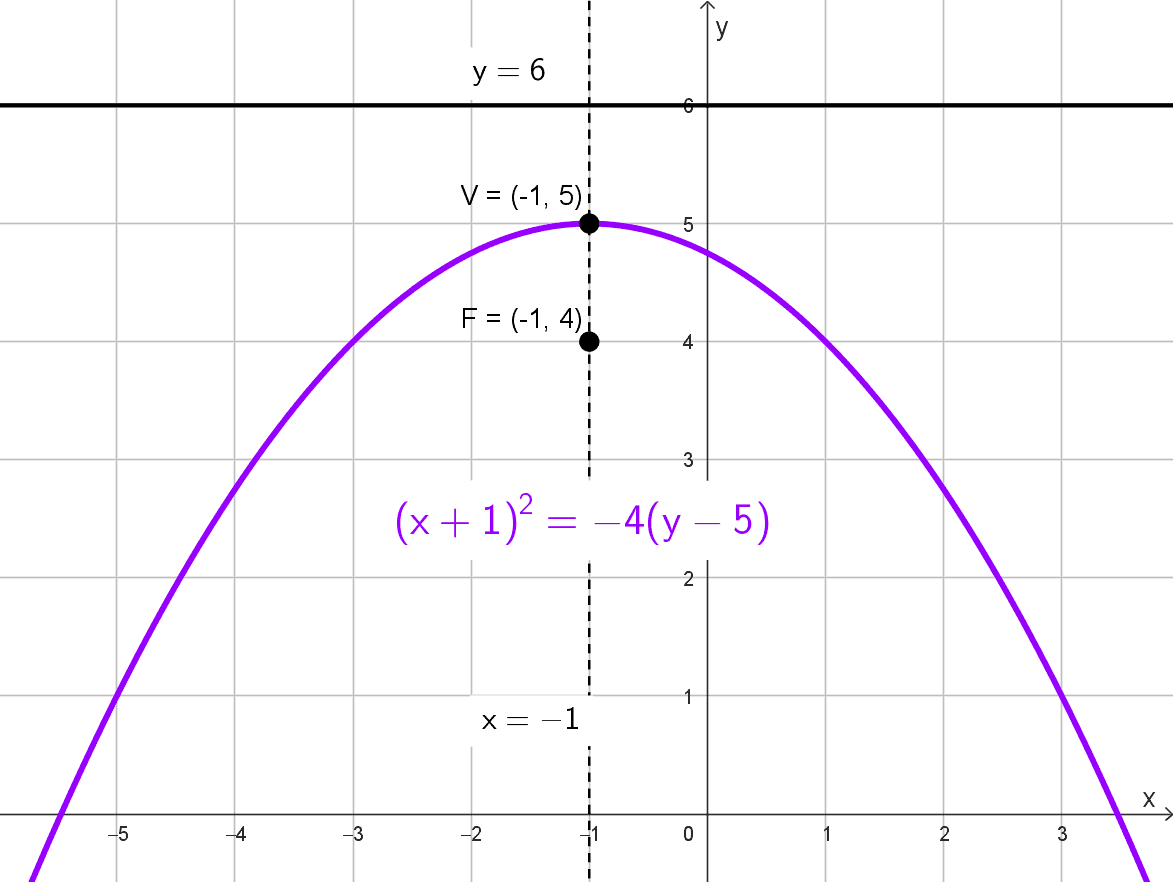
Para la ecuación \((y-2)^2=8 (x+1),\) identificamos una parábola horizontal con vértice fuera del origen, en \((-1, 2).\) Comparando con la forma estándar \((y-k)^2=4p (x-h),\) hallamos que \(4p=8,\) por lo que \(p=2.\) Como el parámetro es positivo, la parábola abre hacia la derecha.
Calculamos el foco en \((h+p, k)=(-1+2, 2)=(1, 2).\) La directriz es la recta vertical \(x=h-p,\) es decir, \(x=-1-2=-3.\) La longitud del lado recto es \(|4p|=8.\) El eje de simetría es paralelo al eje \(x\) y pasa por el vértice, con ecuación \(y=2.\)
- Vértice: \((-1, 2)\)
- Foco: \((1, 2)\)
- Directriz: \(x=-3\)
- Lado recto: \(L_R=8\)
- Eje de simetría: \(y=2\)
Solución 6
La ecuación \((x+4)^2=16 (y+2)\) corresponde a una parábola vertical con vértice en \((-4, -2).\) Al compararla con \((x-h)^2=4p (y-k),\) determinamos que \(4p=16,\) de donde \(p=4.\) Como p es positivo, la parábola abre hacia arriba.
El foco se ubica en \((h, k+p)=(-4, -2+4)=(-4, 2).\) La directriz es la recta horizontal \(y=k-p,\) es decir, \(y=-2-4=-6.\) La longitud del lado recto es \(|4p|=16.\) El eje de simetría es paralelo al eje \(y,\) con ecuación \(x=-4.\)
- Vértice: \((-4, -2)\)
- Foco: \((-4, 2)\)
- Directriz: \(y=-6\)
- Lado recto: \(L_R=16\)
- Eje de simetría: \(x=-4\)
Solución 7
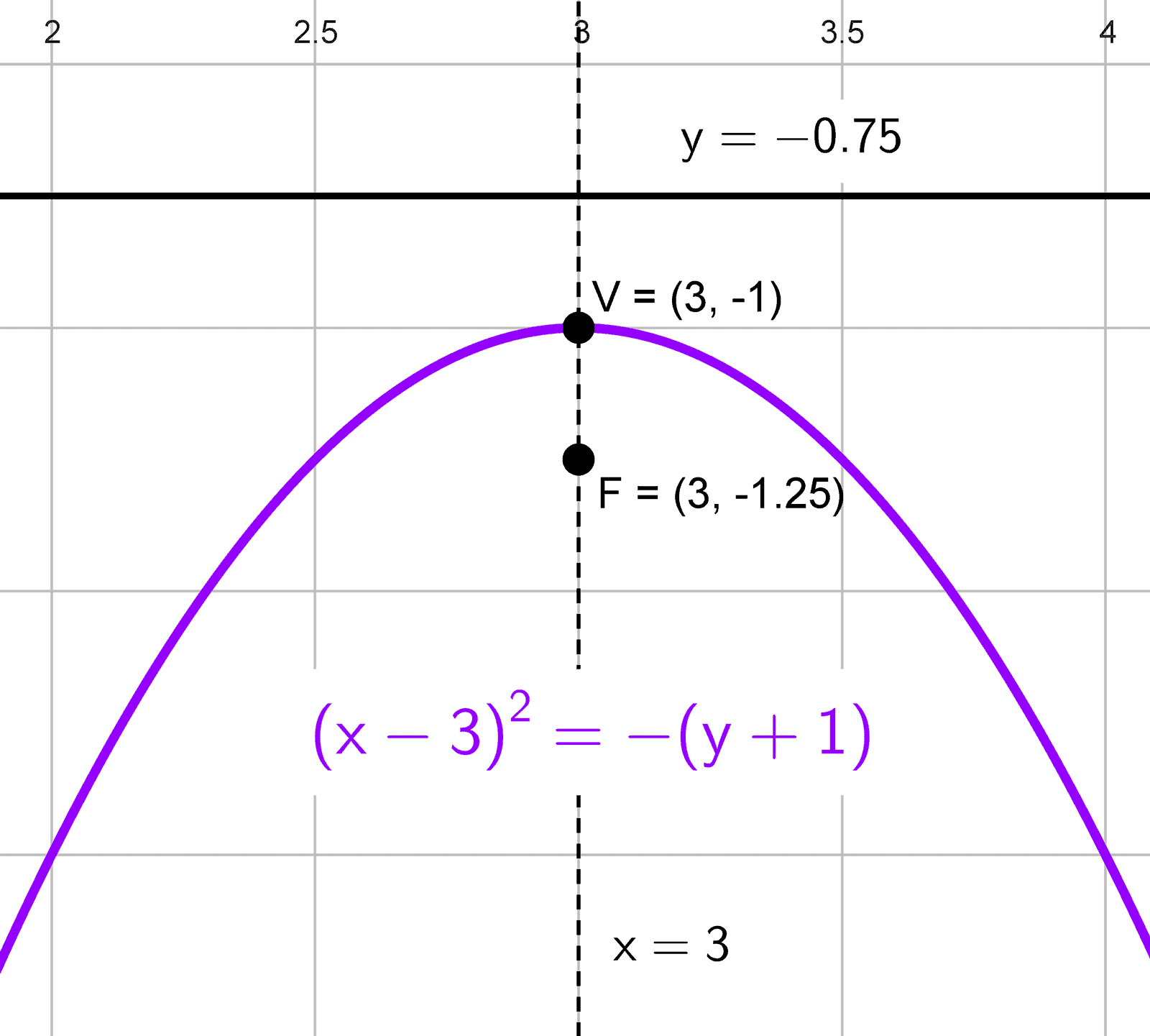
En la ecuación \((x-3)^2=-(y+1),\) reconocemos una parábola vertical que abre hacia abajo, con vértice en \((3, -1).\) Comparando con \((x-h)^2=4p (y-k),\) obtenemos \(4p=-1,\) lo que implica \(p=-0, 25.\) Como p es negativo, confirmamos que la apertura es hacia abajo.
El foco está en \((h, k+p)=(3, -1-0, 25)=(3;-1, 25).\) La directriz es \(y=k-p,\) es decir, \(y=-1-(-0, 25)=-0, 75.\) La longitud del lado recto es \(|4p|=1.\) El eje de simetría es \(x=3.\)
- Vértice: \((3, -1)\)
- Foco: \((3;-1, 25)\)
- Directriz: \(y=-0, 75\)
- Lado recto: \(L_R=1\)
- Eje de simetría: \(x=3\)
Solución 8
La ecuación \((y+1)^2=-4 (x-2)\) representa una parábola horizontal con vértice en \((2, -1).\) Al compararla con \((y-k)^2=4p (x-h),\) sacamos que \(4p=-4,\) por lo que \(p=-1.\) Dado que \(p<0,\) la apertura es hacia la izquierda.
El foco se encuentra en \((h+p, k)=(2-1, -1)=(1, -1).\) La directriz es \(x=h-p,\) es decir, \(x=2-(-1)=3.\) La longitud del lado recto es \(|4p|=4.\) El eje de simetría es \(y=-1.\)
- Vértice: \((2, -1)\)
- Foco: \((1, -1)\)
- Directriz: \(x=3\)
- Lado recto: \(L_R=4\)
- Eje de simetría: \(y=-1\)
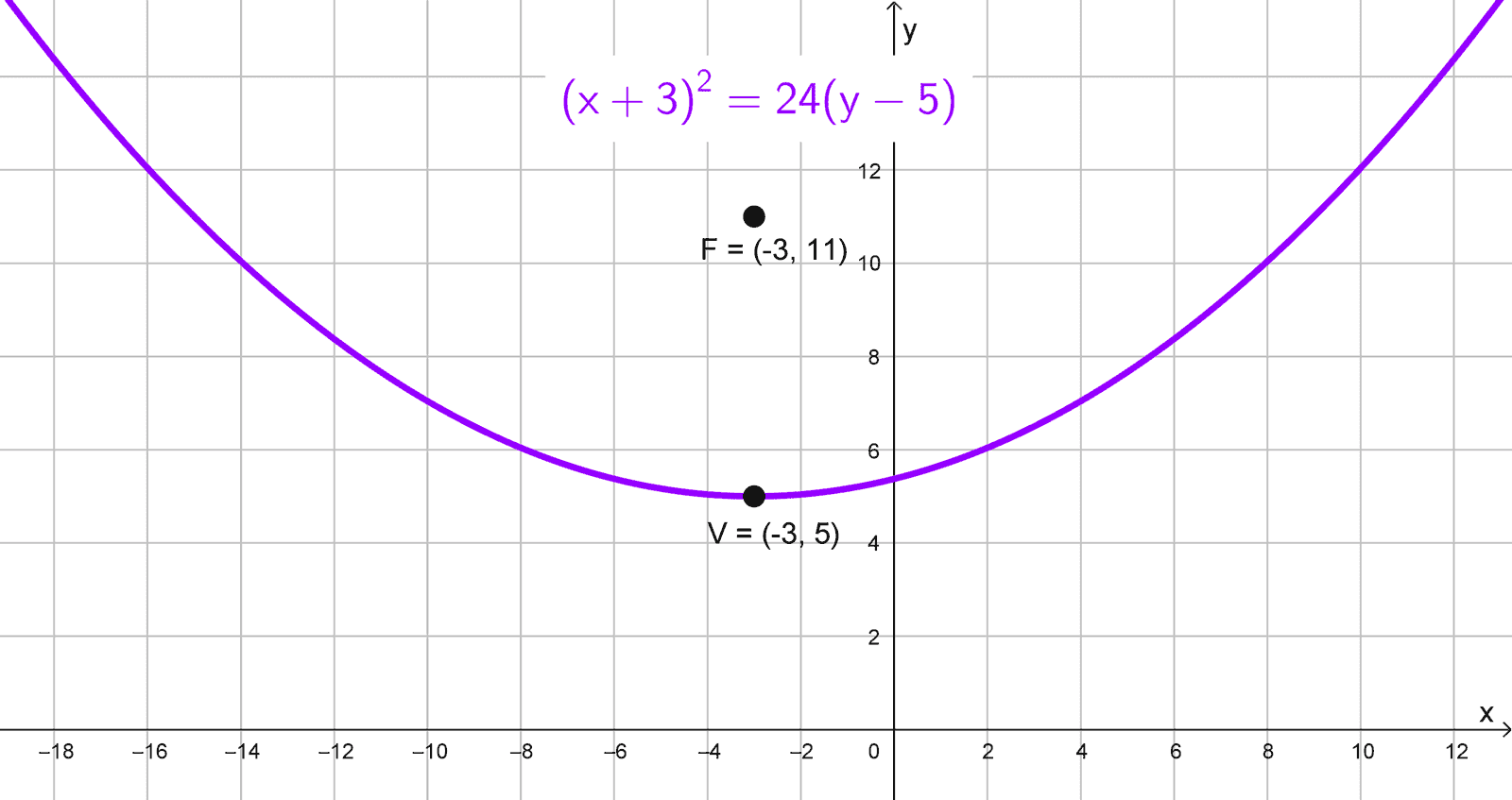
Solución 9
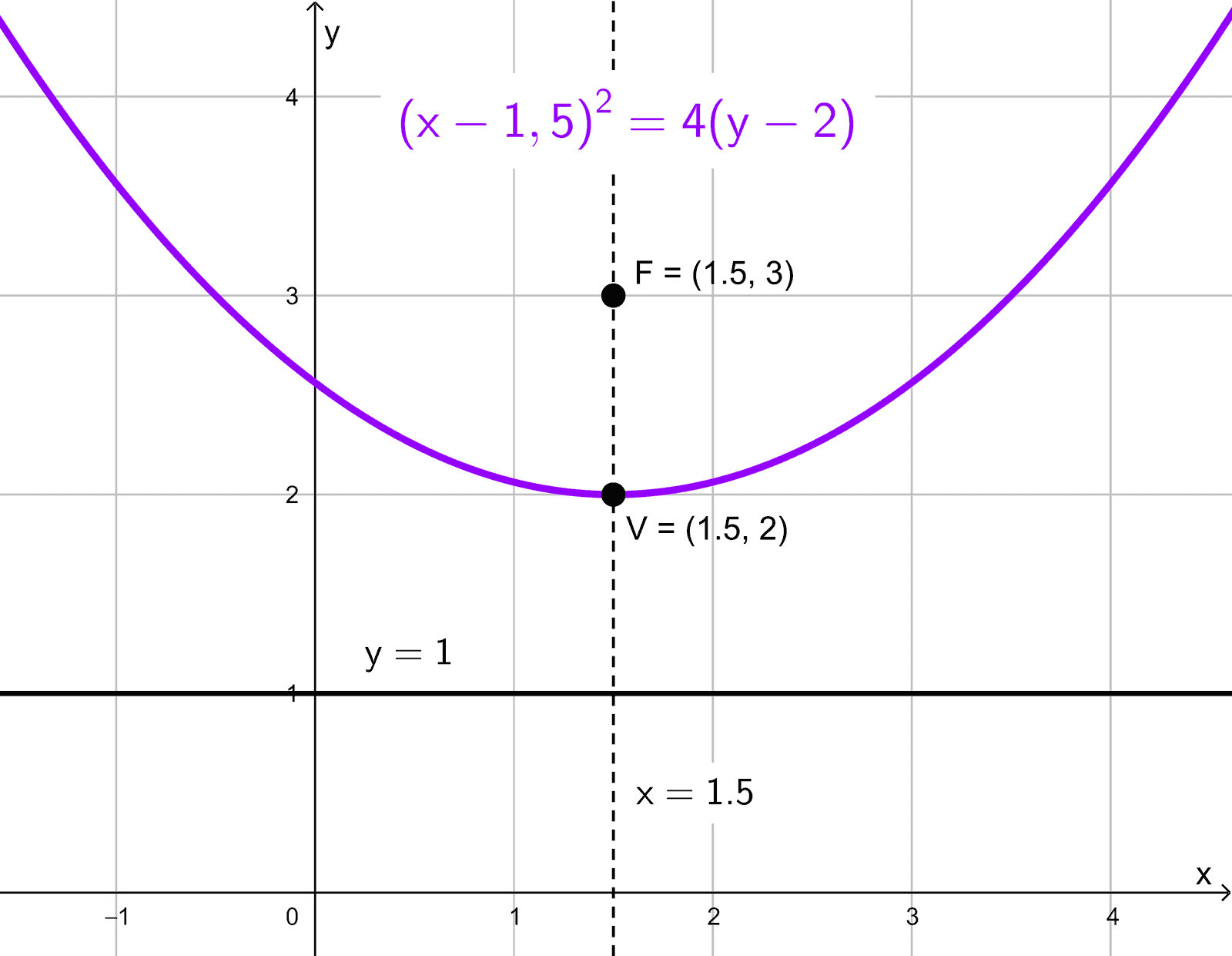
La ecuación dada es: \(4x^2-12x-16y+41=0.\) No está en forma canónica, así que es necesario completar los cuadrados y reacomodarla para poder analizarla. El procedimiento completo está en los ejercicios de pasar de la ecuación general a la canónica. Realizando el proceso, la ecuación obtenida es: \((x-1,5)^2=4 (y-2).\)
Esta ecuación corresponde a una parábola vertical con vértice en \((1,5; 2).\) Al compararla con la forma estándar \((x-h)^2=4p (y-k),\) identificamos que \(4p=4,\) por lo que \(p=1.\) Como \(p\) es positivo, la parábola abre hacia arriba.
El foco se encuentra en \((h, k+p)=(1,5; 2+1)=(1,5; 3).\) La directriz es la recta horizontal \(y=k-p,\) es decir, \(y=2-1=1.\) La longitud del lado recto es \(|4p|=4.\) El eje de simetría es paralelo al eje \(y,\) con ecuación \(x=1,5.\)
Elementos:
- Vértice: \((1,5; 2)\)
- Foco: \((1,5; 3)\)
- Directriz: \(y=1\)
- Lado recto: \(L_R=4\)
- Eje de simetría: \(x=1,5\)
Solución 10
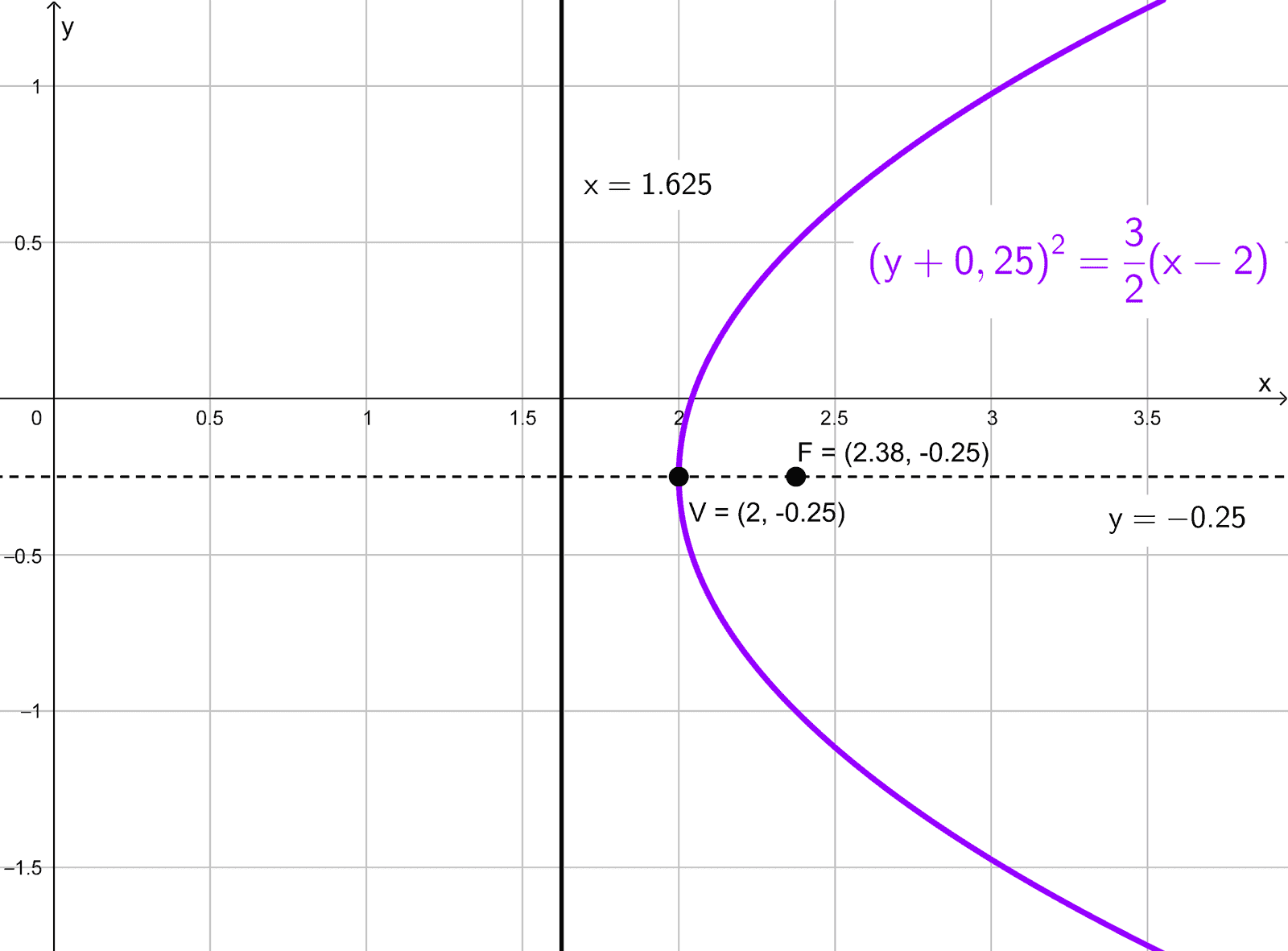
La ecuación dada es \(16y^2+8y-24x+49=0.\) Completando los cuadrados se obtiene la forma canónica \((y+0,25)^2=\dfrac{3}{2}(x-2).\)
Esta ecuación representa una parábola horizontal con vértice en \((2;-0,25).\) Comparando con \((y-k)^2=4p (x-h),\) obtenemos \(4p=\dfrac{3}{2},\) lo que implica \(p=\dfrac{3}{8}.\) Como \(p\) es positivo, la parábola abre hacia la derecha.
El foco está en \((h+p, k)=(2+\dfrac{3}{8};-0,25)=(2,375;-0,25).\) La directriz es la recta vertical \(x=h-p,\) es decir, \(x=2-\dfrac{3}{8}=1,625.\) La longitud del lado recto es \(|4p|=\dfrac{3}{2}.\) El eje de simetría es paralelo al eje \(x,\) con ecuación \(y=-0,25.\)
Elementos:
- Vértice: \((2;-0,25)\)
- Foco: \((2,375;-0,25)\)
- Directriz: \(x=1,625\)
- Lado recto: \(L_R=\dfrac{3}{2}\)
- Eje de simetría: \(y=-0,25\)
Solución 11
La ecuación proporcionada es \(x^2+2x=-4y+19. \)Completando los cuadrados se obtiene la forma canónica equivalente \((x+1)^2=-4 (y-5).\)
Esta ecuación describe una parábola vertical con vértice en \((-1; 5).\) Comparándola con \((x-h)^2=4p (y-k),\) hallamos \(4p=-4,\) de donde \(p=-1.\) El signo negativo de \(p\) indica que la parábola abre hacia abajo.
El foco se ubica en \((h, k+p)=(-1; 5-1)=(-1; 4).\) La directriz es \(y=k-p,\) es decir, \(y=5-(-1)=6.\) La longitud del lado recto es \(|4p|=4.\) El eje de simetría es \(x=-1.\)
Elementos:
- Vértice: \((-1; 5)\)
- Foco: \((-1; 4)\)
- Directriz: \(y=6\)
- Lado recto: \(L_R=4\)
- Eje de simetría: \(x=-1\)
Solución 12
La ecuación del ejercicio es \(8y+56=-y^2-20x.\) Si acomodamos y completamos cuadrados, la ecuación es \((y+4)^2=-20 (x+2).\)
Esta ecuación corresponde a una parábola horizontal con vértice en \((-2;-4).\) Al compararla con \((y-k)^2=4p (x-h),\) obtenemos \(4p=-20,\) por lo que \(p=-5.\) El valor negativo de \(p\) indica que la parábola abre hacia la izquierda.
El foco está en \((h+p, k)=(-2-5;-4)=(-7;-4).\) La directriz es \(x=h-p,\) es decir, \(x=-2-(-5)=3.\) La longitud del lado recto es \(|4p|=20.\) El eje de simetría es \(y=-4.\)
Elementos:
- Vértice: \((-2;-4)\)
- Foco: \((-7;-4)\)
- Directriz: \(x=3\)
- Lado recto: \(L_R=20\)
- Eje de simetría: \(y=-4\)
Pasar de ecuación general a ecuación canónica
Convertir las siguientes ecuaciones de parábolas a su forma canónica:
- \(4x^2-12x-16y+41=0\)
- \(16y^2+8y-24x+49=0\)
- \(x^2+2x=-4y+19\)
- \(8y+56=-y^2-20x\)
Soluciones
Solución 1
Partimos de la ecuación \(4x^2-12x-16y+41=0.\) Primero agrupamos los términos en \(x\) y completamos el cuadrado:
\(4x^2-12x=4(x^2-3x)\)
Para completar el cuadrado, sumamos y restamos \(\left (\dfrac{3}{2}\right)^2=2, 25\) dentro del paréntesis:
\(4\left(x^2-3x+2,25-2,25\right)=4\left((x-1,5)^2-2,25\right)=4(x-1,5)^2-9\)
Sustituyendo en la ecuación original:
\(4(x-1,5)^2-9-16y+41=0 → 4(x-1,5)^2-16y+32=0\)
Despejamos el término en \(y:\)
\(4(x-1,5)^2+32=16y → y=\dfrac{1}{4}(x-1,5)^2+2\)
La forma canónica es:
\((x-1,5)^2=4(y-2)\)
donde el vértice está en \((1, 5; 2)\) y \(4p=4\) implica \(p=1.\)
Solución 2
Dada la ecuación \(16y^2+8y-24x+49=0,\) agrupamos los términos en \(y\) y completamos el cuadrado:
\(16y^2+8y=16\left(y^2+0,5y\right)\)
Sumamos y restamos \(\left (\dfrac{0, 5}{2}\right)^2=0, 0625:\)
\(16\left(y^2+0,5y+0,0625-0,0625\right)=16\left((y+0,25)^2-0,0625\right)=16(y+0,25)^2-1\)
Sustituyendo en la ecuación original:
\(16(y+0,25)^2-1-24x+49=0 → 16(y+0,25)^2-24x+48=0\)
Despejamos el término en \(x:\)
\(16(y+0,25)^2+48=24x → x=\dfrac{2}{3}(y+0,25)^2+2\)
La forma canónica es:
\((y+0,25)^2=\dfrac{3}{2}(x-2)\)
con vértice en \((2;-0, 25)\) y \(4p=\dfrac{3}{2}\) implica \(p=\dfrac{3}{8}.\)
Solución 3
La ecuación \(x^2+2x=-4y+19\) se reordena como \(x^2+2x+4y-19=0.\) Completamos el cuadrado en \(x:\)
\(x^2+2x=(x^2+2x+1)-1=(x+1)^2-1\)
Sustituyendo:
\((x+1)^2-1+4y-19=0 → (x+1)^2+4y-20=0\)
Despejamos \(y:\)
\((x+1)^2=-4y+20 → (x+1)^2=-4(y-5)\)
La forma canónica muestra un vértice en \((-1; 5)\) y \(4p=-4\) implica \(p=-1.\)
Solución 4
Reorganizamos \(8y+56=-y^2-20x\) como \(y^2+8y+20x+56=0.\) Completamos el cuadrado en \(y:\)
\(y^2+8y=(y^2+8y+16)-16=(y+4)^2-16\)
Sustituyendo:
\((y+4)^2-16+20x+56=0 → (y+4)^2+20x+40=0\)
Despejamos \(x:\)
\((y+4)^2=-20x-40 → (y+4)^2=-20(x+2)\)
La forma canónica tiene vértice en \((-2;-4)\) y \(4p=-20\) implica \(p=-5.\)
Pasar de ecuación canónica a ecuación general
Convertir las siguientes ecuaciones de parábolas a su forma general:
- \((y-2)^2=8(x+1)\)
- \((x+4)^2=16(y+2)\)
- \((x-3)^2=-(y+1)\)
- \((y+1)^2=-4(x-2)\)
Soluciones
Solución 1
Partimos de la ecuación \((y-2)^2=8 (x+1).\) Para convertirla a su forma general, expandimos el cuadrado del binomio y distribuimos los términos:
\(y^2-4y+4=8x+8\)
Luego, trasladamos todos los términos a un lado de la ecuación para igualar a cero:
\(y^2-4y+4-8x-8=0\)
Simplificamos los términos constantes:
\(y^2-8x-4y-4=0\)
Ordenamos la ecuación:
\(y^2-4y-8x-4=0\)
Solución 2
Comenzamos con \((x+4)^2=16 (y+2).\) Expandimos el cuadrado del binomio:
\(x^2+8x+16=16y+32\)
Movemos todos los términos a un lado:
\(x^2+8x+16-16y-32=0\)
Reducimos los términos constantes:
\(x^2+8x-16y-16=0\)
La forma general queda:
\(x^2+8x-16y-16=0\)
Solución 3
Analizamos \((x-3)^2=-(y+1).\) Expandimos el cuadrado:
\(x^2-6x+9=-y-1\)
Trasladamos todos los términos:
\(x^2-6x+9+y+1=0\)
Simplificamos:
\(x^2-6x+y+10=0\)
La forma general es:
\(x^2-6x+y+10=0\)
Solución 4
Partimos de \((y+1)^2=-4 (x-2).\) Expandimos el binomio:
\(y^2+2y+1=-4x+8\)
Agrupamos todos los términos:
\(y^2+2y+1+4x-8=0\)
Simplificamos:
\(y^2+4x+2y-7=0\)
Ordenamos la ecuación:
\(y^2+2y+4x-7=0\)
Problemas de la vida real
A continuación, veremos problemas de aplicación de las parábolas en la vida real y en ciencias.
Ejercicio 1
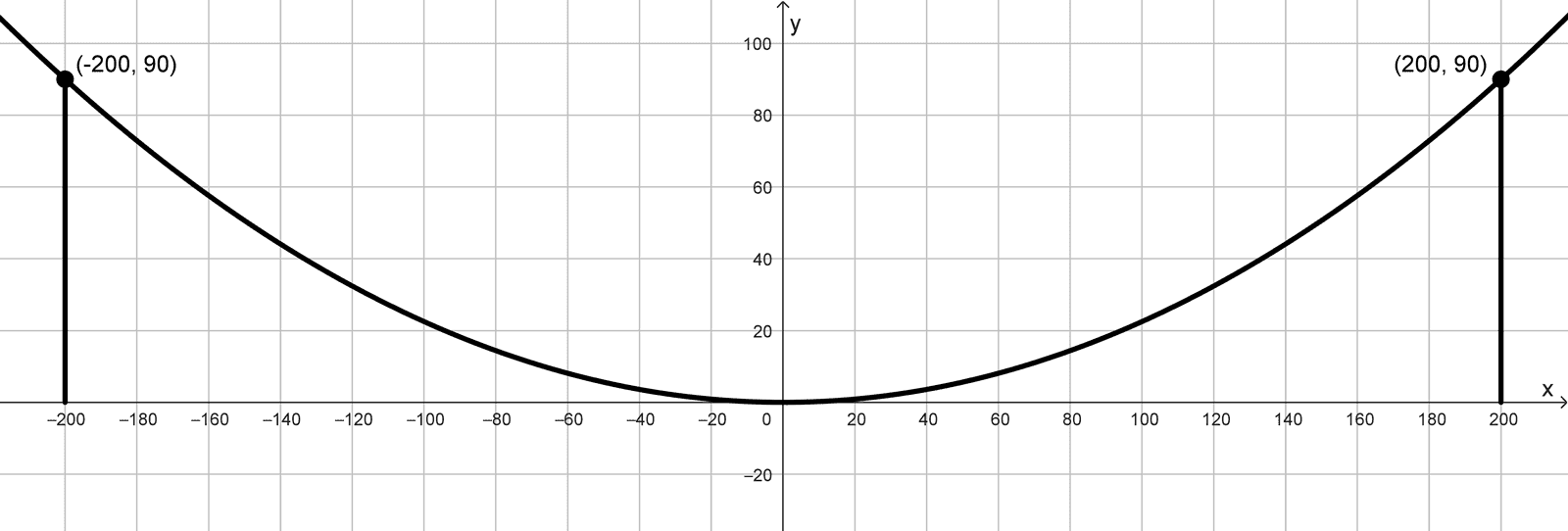
Las dos torres de soporte de un puente colgante están separadas por una distancia de 400 metros y se elevan 90 metros por encima de la plataforma. El cable principal (que sigue la forma de una parábola) es tangente a la plataforma en el punto central del puente. Determinar la altura del cable sobre la plataforma a 30 metros y también a 75 metros del centro del puente. (Suponer que la plataforma es horizontal).
Solución
Para modelar la situación, colocamos el sistema de coordenadas con el origen en el punto central del puente, donde el cable es tangente a la plataforma. La parábola tendrá su vértice en \((0; 0)\) y se abrirá hacia arriba, por lo que su ecuación general es:
\(y=ax^2\)
Dado que las torres están separadas por 400 metros, cada torre se ubica en \(x=200\) y \(x=-200.\) La altura de las torres es de 90 metros, lo que significa que los puntos \((200; 90)\) y \((-200; 90)\) pertenecen a la parábola. Sustituyendo uno de estos puntos en la ecuación:
\(90=a(200)^2 → a=\dfrac{90}{40000}=\dfrac{9}{4000}\)
Así, la ecuación del cable es:
\(y=\dfrac{9}{4000}x^2\)
Para hallar la altura del cable a 30 metros del centro, sustituimos \(x=30:\)
\(y=\dfrac{9}{4000}(30)^2=\dfrac{9 \times 900}{4000}=\dfrac{8100}{4000}=2,025 \text{ metros}\)
Para \(x=75\) metros:
\(y=\dfrac{9}{4000}(75)^2=\dfrac{9 \times 5625}{4000}=\dfrac{50625}{4000}=12,65625 \text{ metros}\)
Respuesta final:
- A 30 metros del centro: \(\boxed{2, 03 \text{ metros}}\) (redondeado a centésimas).
- A 75 metros del centro: \(\boxed{12, 66 \text{ metros}}\) (redondeado a centésimas).
Ejercicio 2
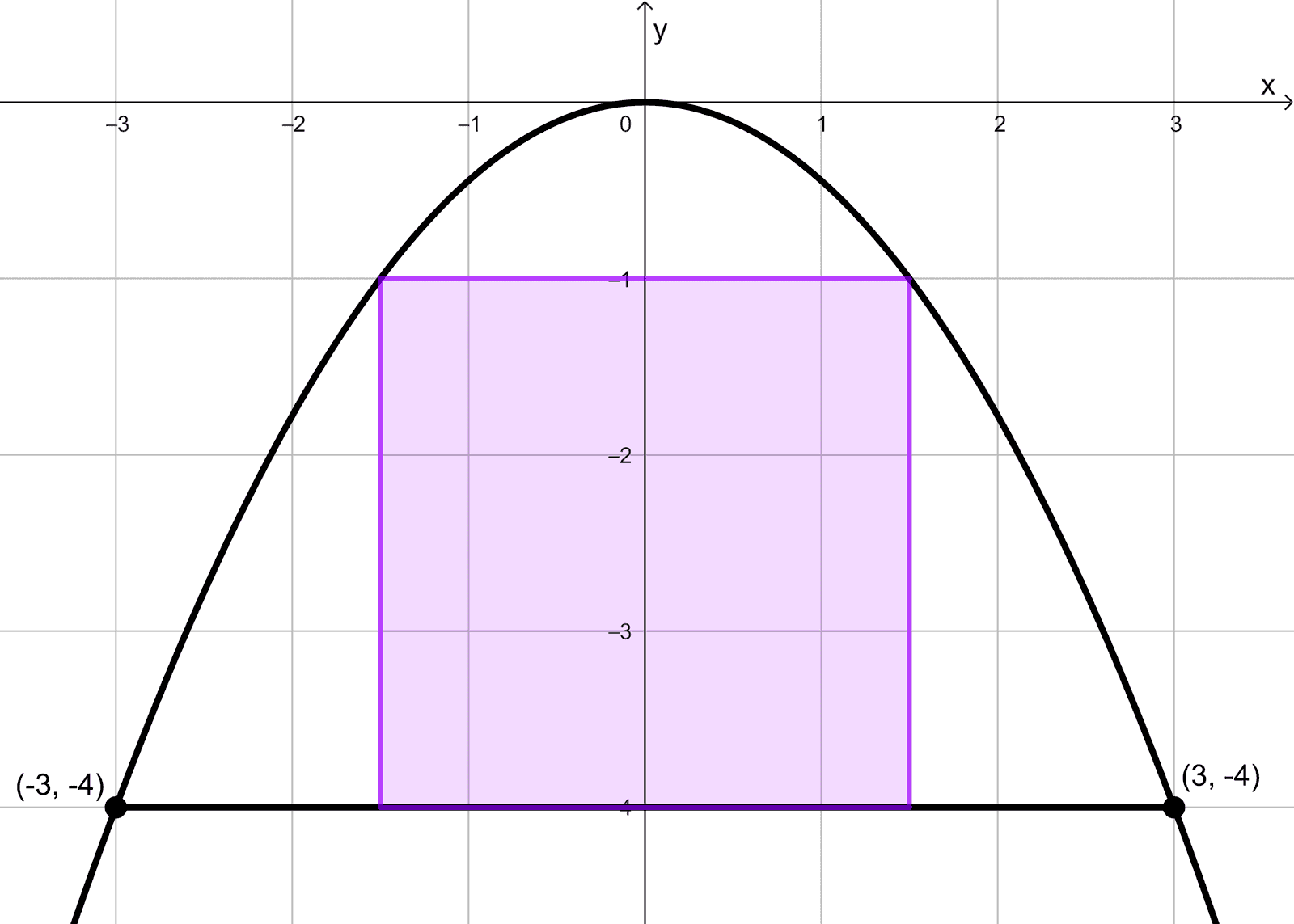
La entrada de un depósito tiene forma de arco parabólico. La altura en el punto central de la entrada es de 4 metros, y el ancho en la base es de 6 metros. Se desea introducir un contenedor rectangular en el depósito. Si el contenedor tiene una altura de 3 metros, ¿cuál es el máximo ancho posible que puede tener el contenedor para que pueda pasar por la entrada?
Solución
Para modelar el arco parabólico de la entrada, colocamos el sistema de coordenadas con el origen en el vértice de la parábola (punto más alto del arco). Dado que la altura máxima es de 4 metros y el ancho en la base es de 6 metros, los extremos de la base están en \((-3;-4)\) y \((3;-4),\) ya que el ancho total es 6 metros (3 metros a cada lado).
La ecuación general de una parábola con vértice en \((0; 0)\) y que abre hacia abajo es:
\(y=ax^2~~\text{donde~~} a<0\)
Como la parábola pasa por \((3;-4),\) sustituimos para hallar \(a:\)
\(-4=a(3)^2 → a=-\dfrac{4}{9}\)
Entonces, la ecuación del arco es:
\(y=-\dfrac{4}{9}x^2\)
El contenedor tiene una altura de 3 metros. Para encontrar su máximo ancho, debemos determinar a qué distancia horizontal (\(x\)) del centro la altura del arco es igual a \(-1\) metro (ya que el vértice está en \(y=0\) y la base en \(y=-4,\) y el contenedor ocupa 3 metros de altura, dejando \(4-3=1\) metro de espacio en la parte superior).
Sustituyendo \(y=-1\) en la ecuación:
\(-1=-\dfrac{4}{9}x^2 → x^2=\dfrac{9}{4} → x=\pm \dfrac{3}{2}\)
Esto significa que los puntos donde el contenedor tocaría el arco están en \(x=-1, 5\) y \(x=1, 5.\) Por lo tanto, el ancho máximo del contenedor es:
\(2 \times 1,5=3 \text{ metros}\)
Ejercicio 3
El diámetro de una antena parabólica es de 1.5 metros y su profundidad es de 25 centímetros. ¿A qué altura se debe colocar el receptor?
Solución
Una antena parabólica está diseñada para reflejar las ondas incidentes hacia un punto específico. Esto se debe a la propiedad geométrica de las parábolas: cualquier rayo paralelo al eje de simetría que incide sobre la superficie parabólica se reflejará directamente hacia el foco. Por lo tanto, el receptor debe colocarse en el foco para captar eficientemente todas las ondas reflejadas.
Para determinar la altura a la que se debe ubicar el receptor, modelamos la antena como una parábola. Supongamos que el vértice de la parábola está en el origen \((0, 0)\) y que la parábola abre hacia arriba. La ecuación estándar de una parábola en esta posición es:
\(y=\dfrac{1}{4p}x^2\)
donde \(p\) es la distancia del vértice al foco.
Datos del problema:
- Diámetro de la antena: 1,5 metros → radio (semidiámetro) = 0,75 metros.
- Profundidad: 25 centímetros = 0,25 metros.
La profundidad corresponde al valor de \(y\) cuando \(x=0,75\) (el borde de la antena). Sustituyendo en la ecuación:
\(0,25=\dfrac{1}{4p}(0,75)^2\)
Resolviendo para \(p:\)
\(0,25=\dfrac{0,5625}{4p} \quad → \quad 4p=\dfrac{0,5625}{0,25}=2,25 \quad → \quad p=\dfrac{2,25}{4}=0,5625 \text{ metros}\)
Por lo tanto, el receptor debe colocarse a 56,25 centímetros de altura desde el vértice de la antena.
Problemas avanzados
Los ejercicios anteriores son de parábolas horizontales y verticales, los siguientes artículos contienen un tipo de problema más general de Geometría Analítica donde el eje de la parábola puede estar inclinado con respecto a los ejes coordenados, resultando en una parábola rotada:
Bibliografía
- Engler, A., Müller, D., Vrancken, S. y Hecklein, M. (2020). Geometría analítica. Universidad Nacional del Litoral.
- Fuller, G. y Tarwater, D. (1995). Geometría analítica (7.ª ed.). Pearson Educación.
- Lehmann, C. (1989). Geometría analítica. Limusa.
- Leithold. L. (1992). Álgebra y trigonometría con geometría analítica. Oxford University Press.
- Márquez, A., Vázquez, F., Ruiz, H., Villegas, M. y Figueroa, M. (2009). Geometría analítica. Prentice Hall.
- Raichman, S. y Totter, E. (2016). Geometría analítica para ciencias e ingeniería. Universidad Nacional de Cuyo.
- Sullivan, M. (2006). Álgebra y trigonometría. Pearson Educación.
- Swokowski, E. y Cole, J. (2009). Álgebra y trigonometría con geometría analítica. Cengage Learning.
¿Te ha servido este contenido? ¡Califícalo!
0,0 / 5 — 0 votos
CÓMO CITAR ESTE ARTÍCULO
Machado, D. (2025, 2 de mayo). Ejercicios de parábola. Exponty. https://exponty.com/ejercicios-parabola
Deja una respuesta

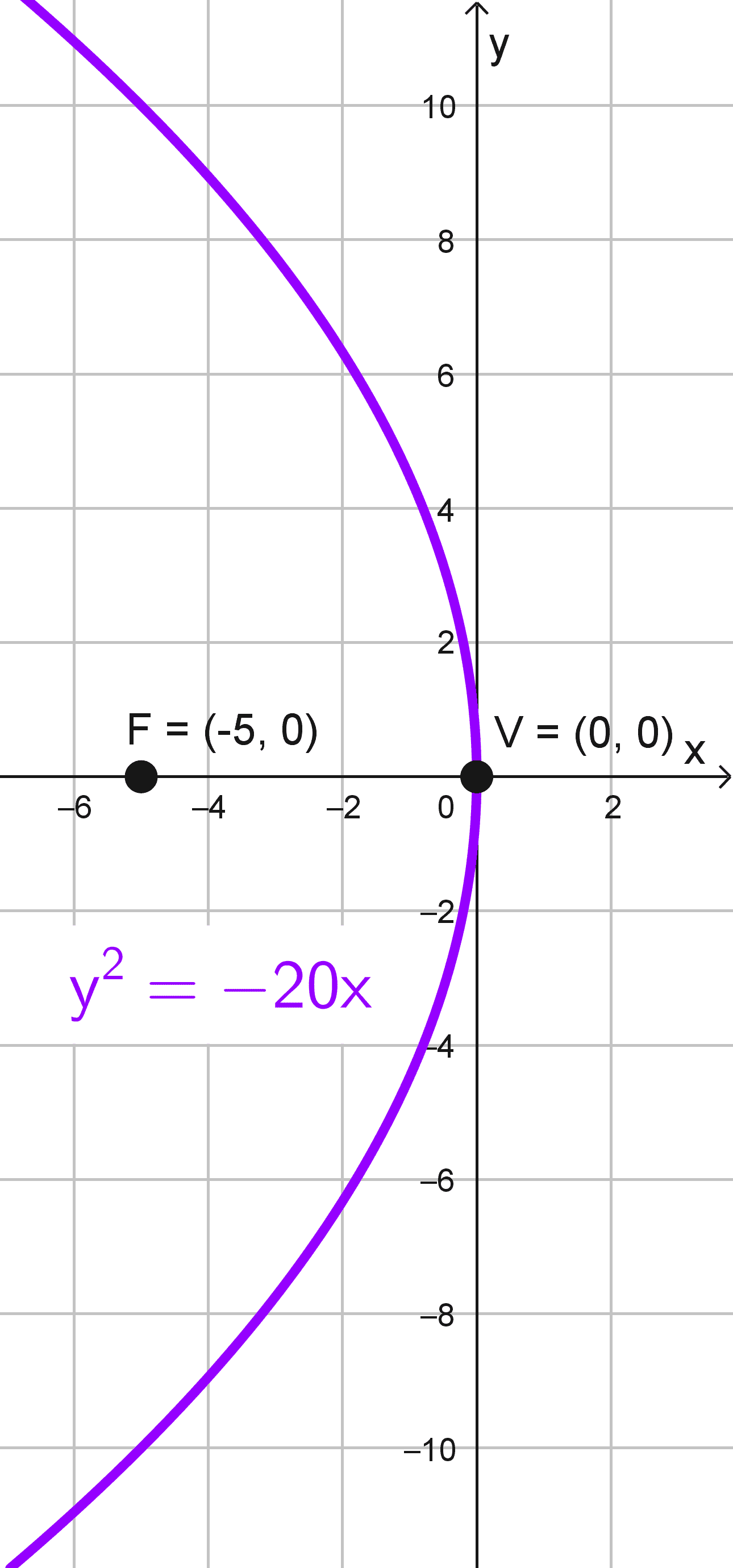
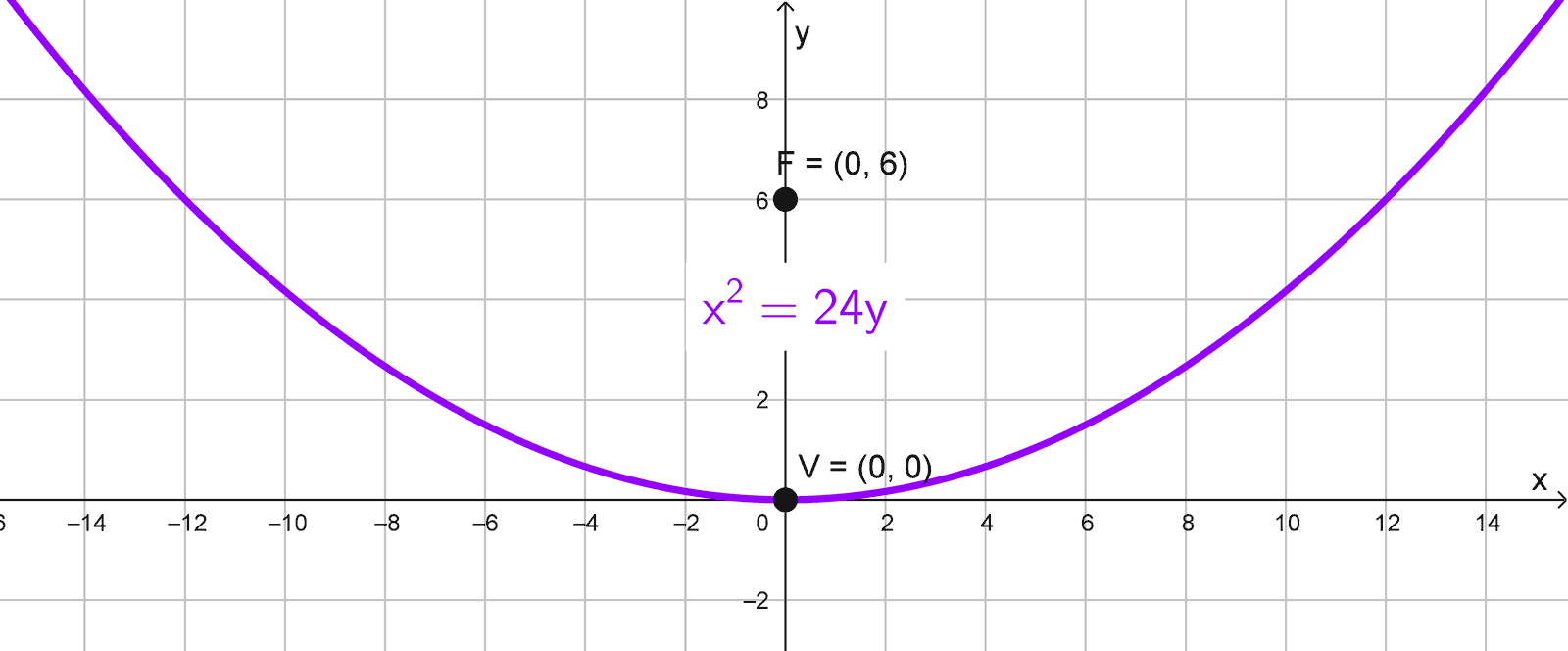
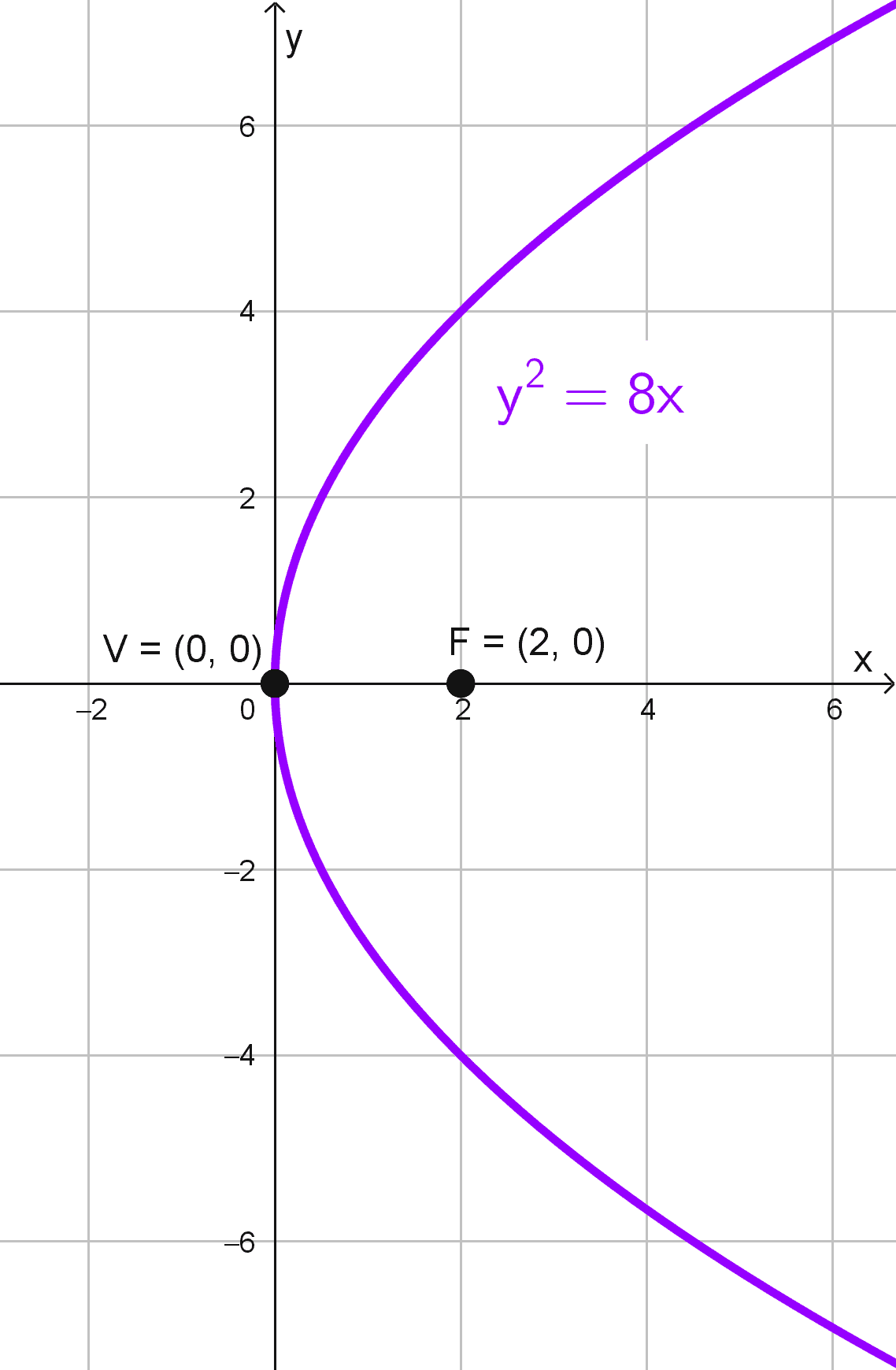

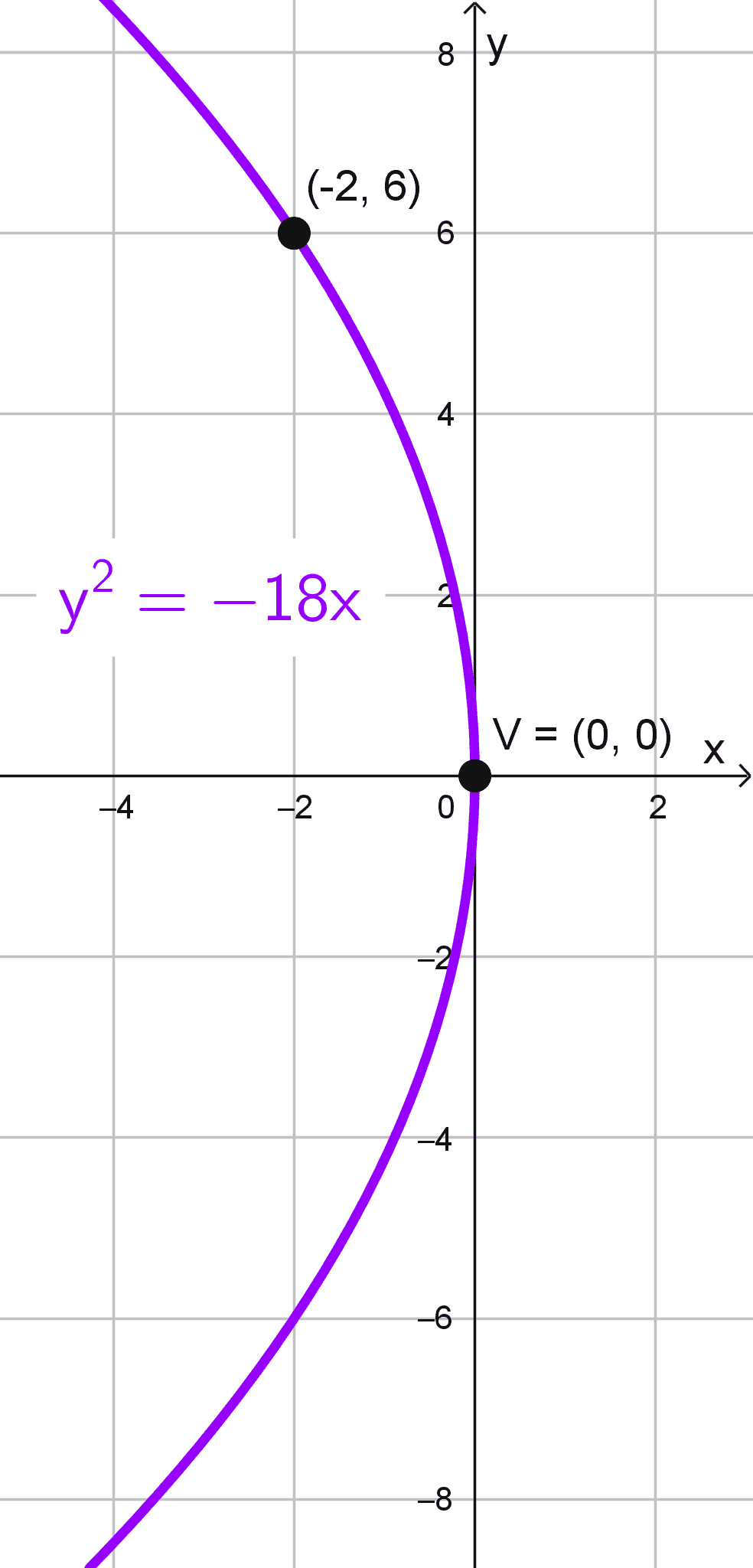
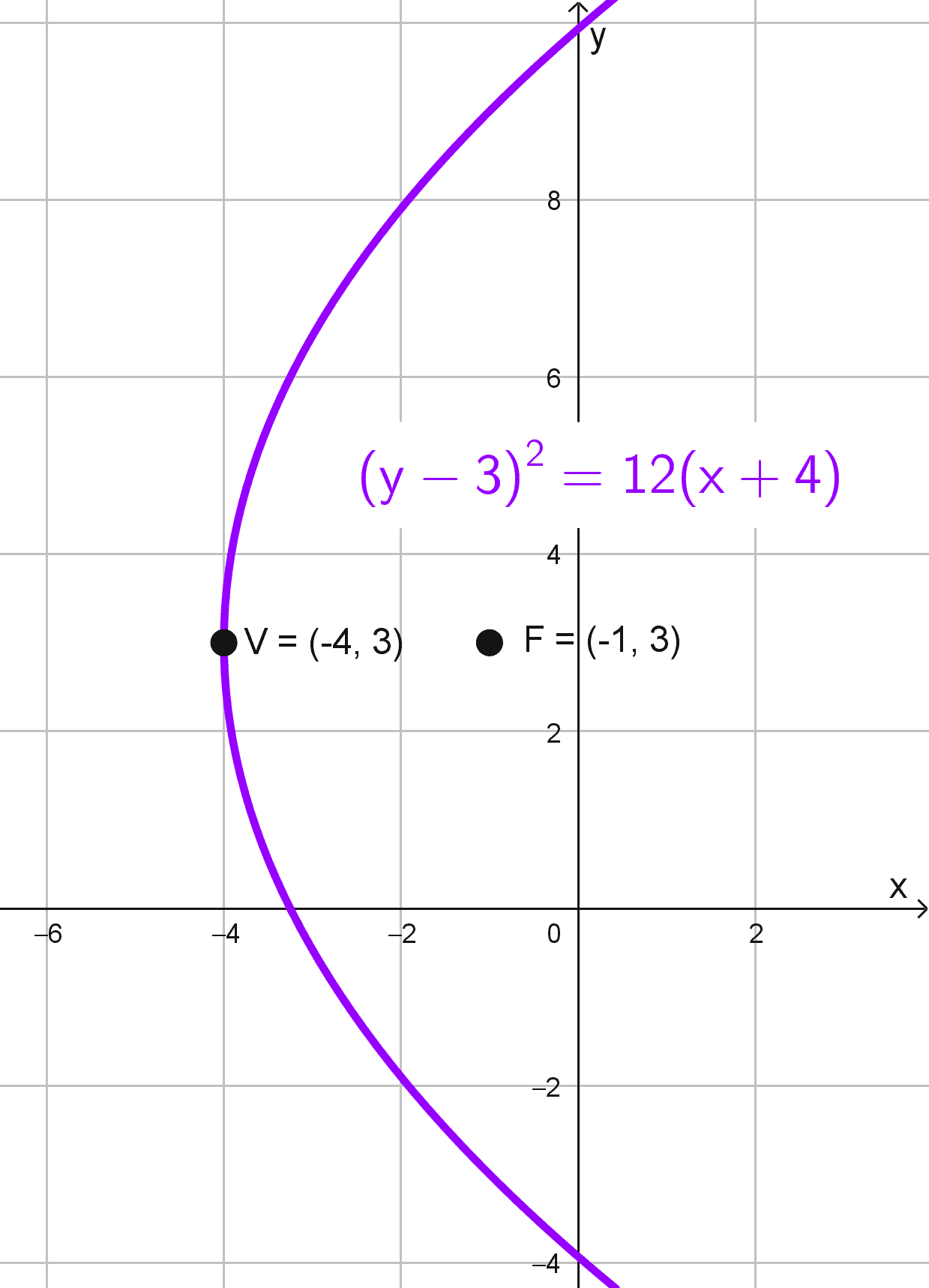
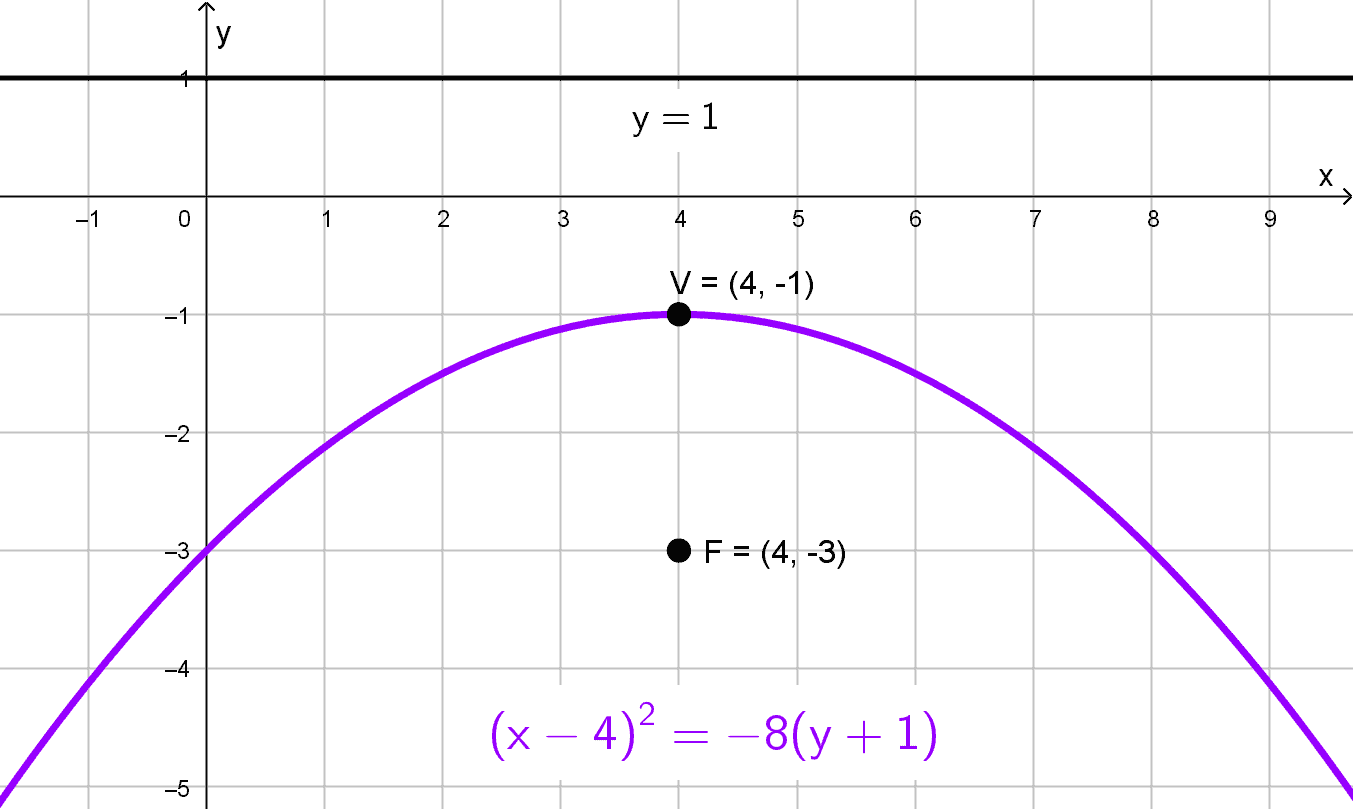
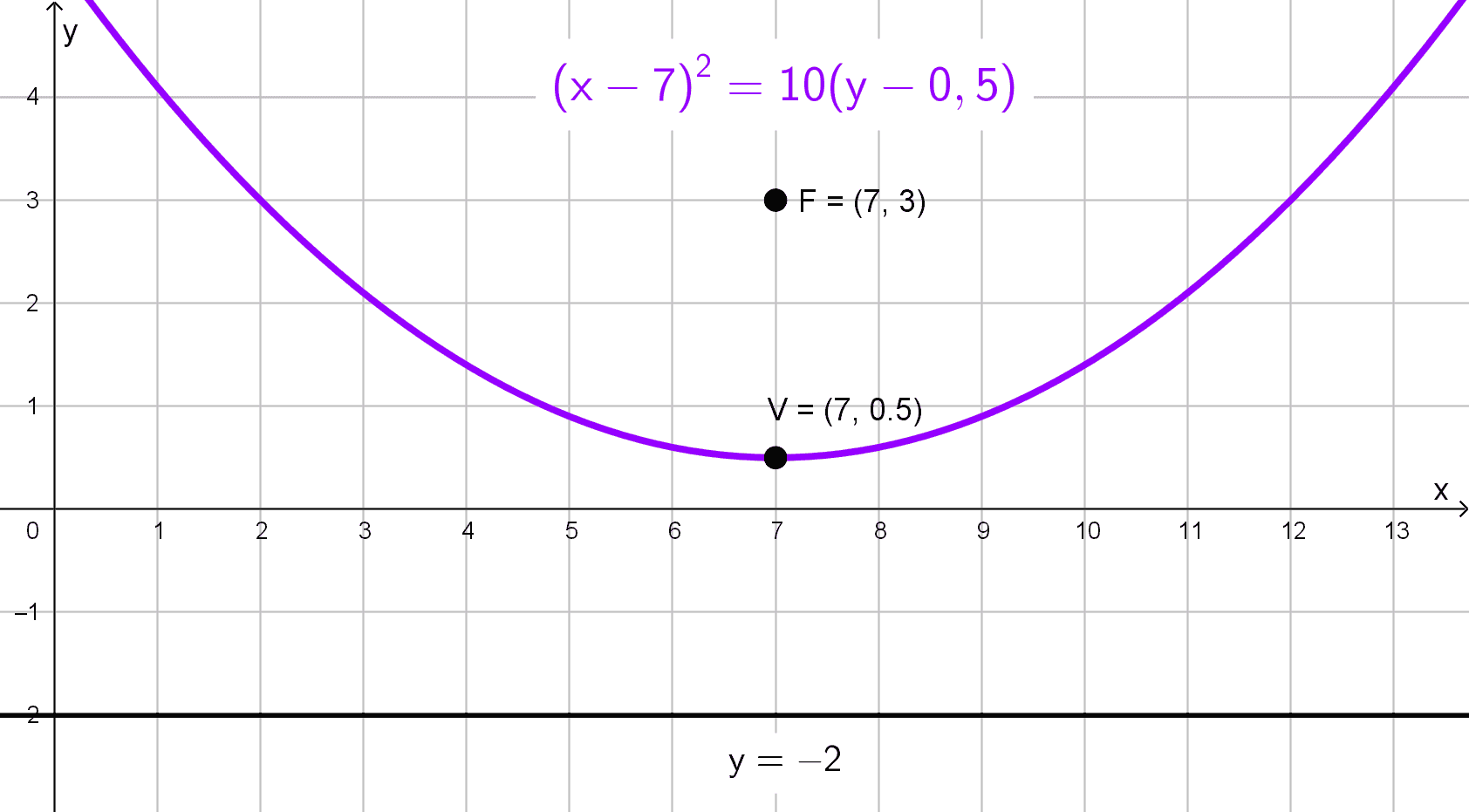
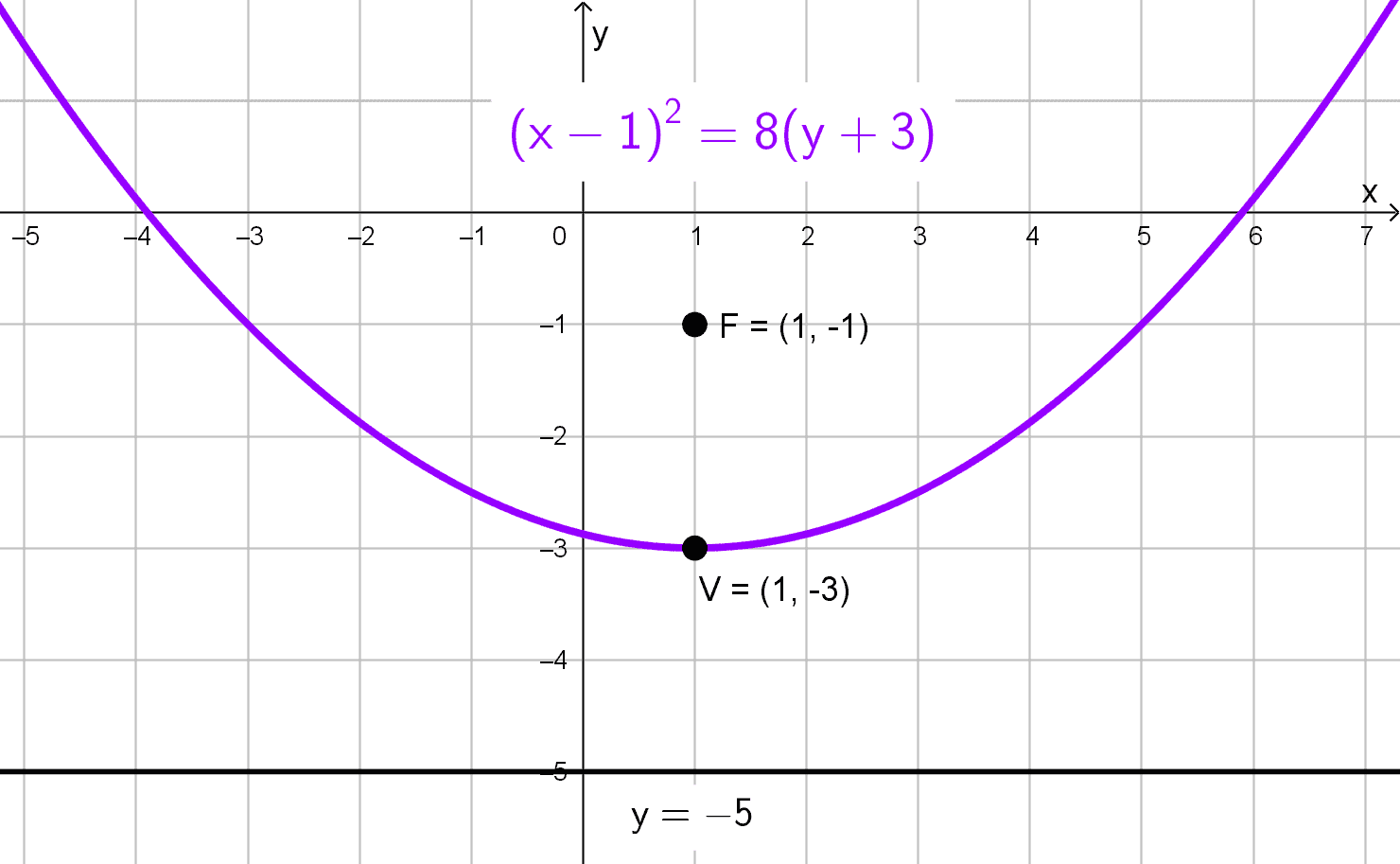
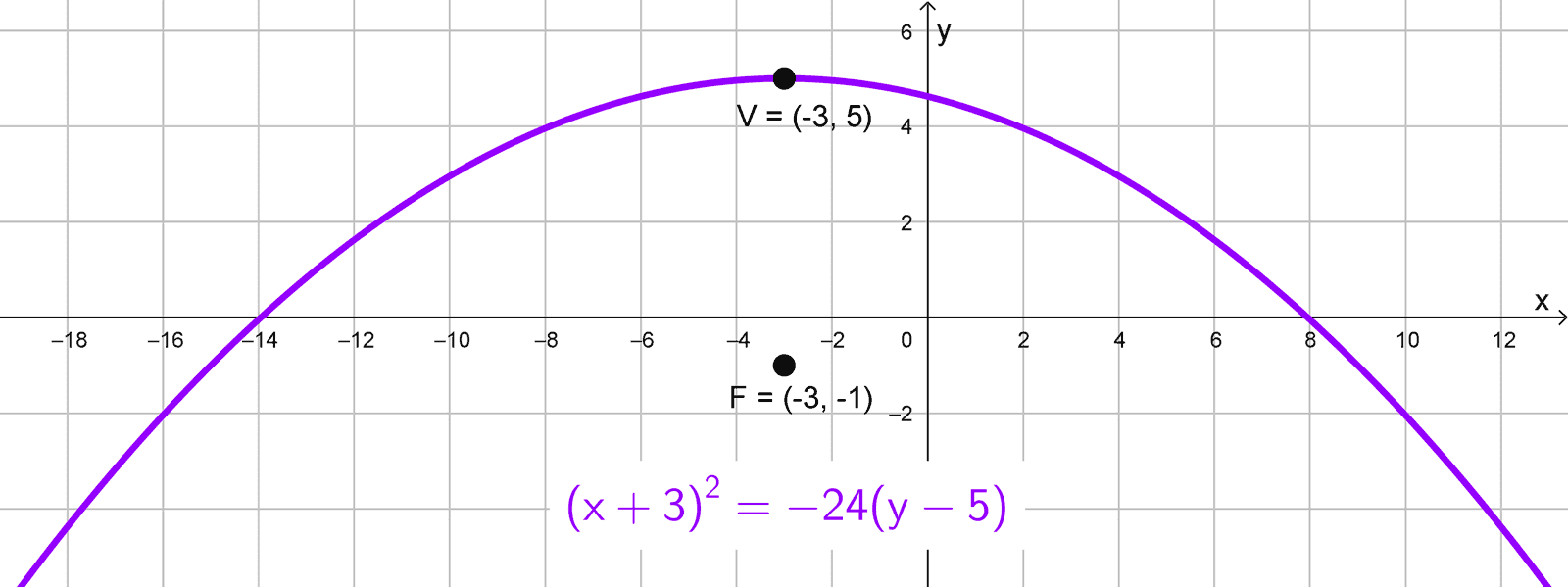
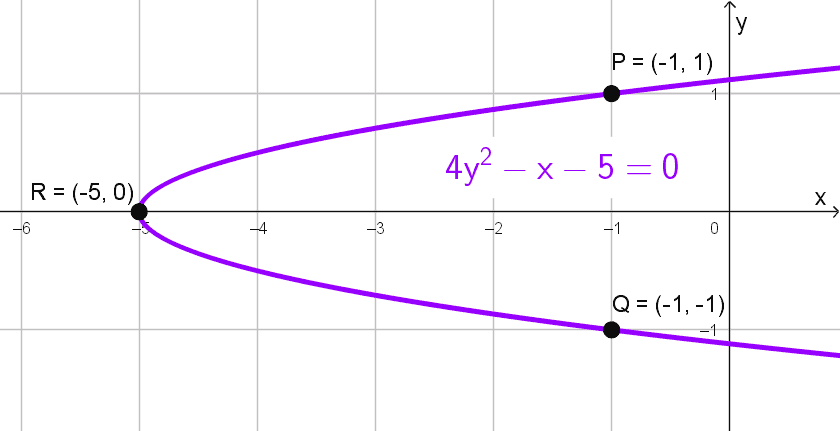
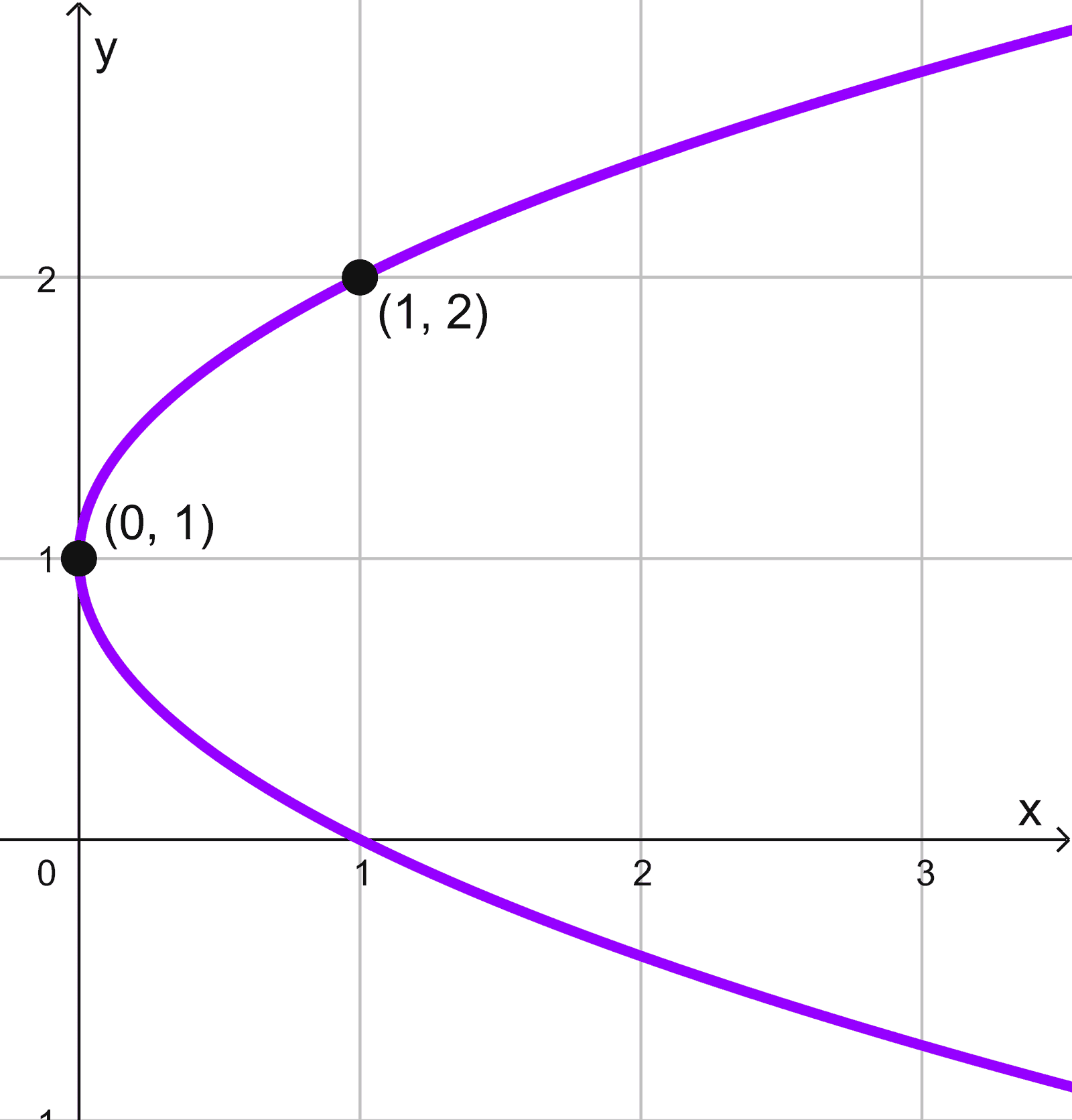
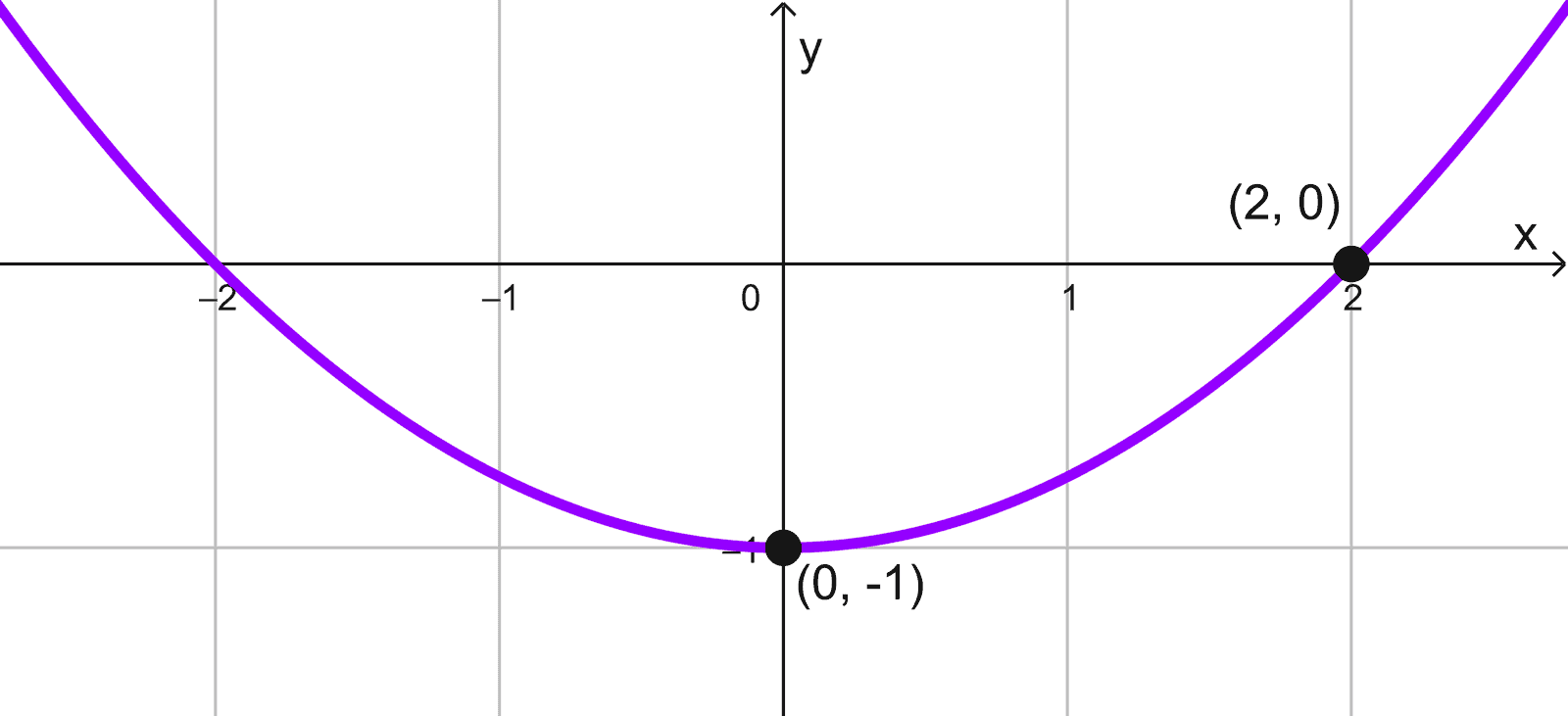

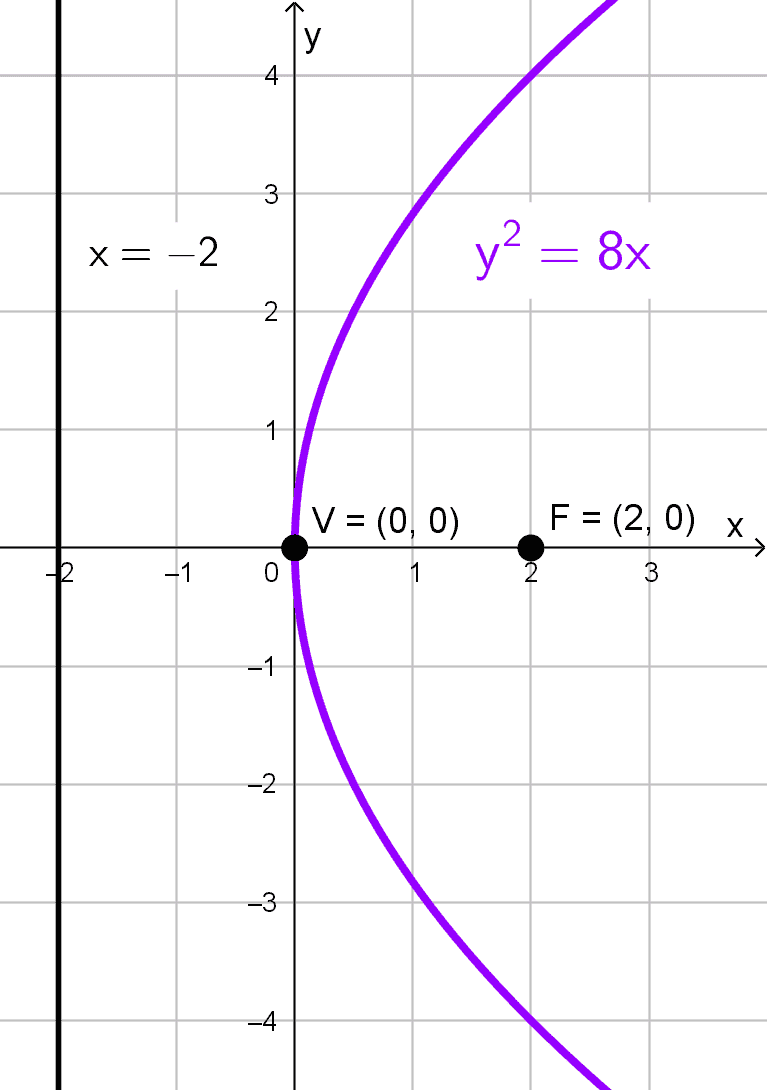
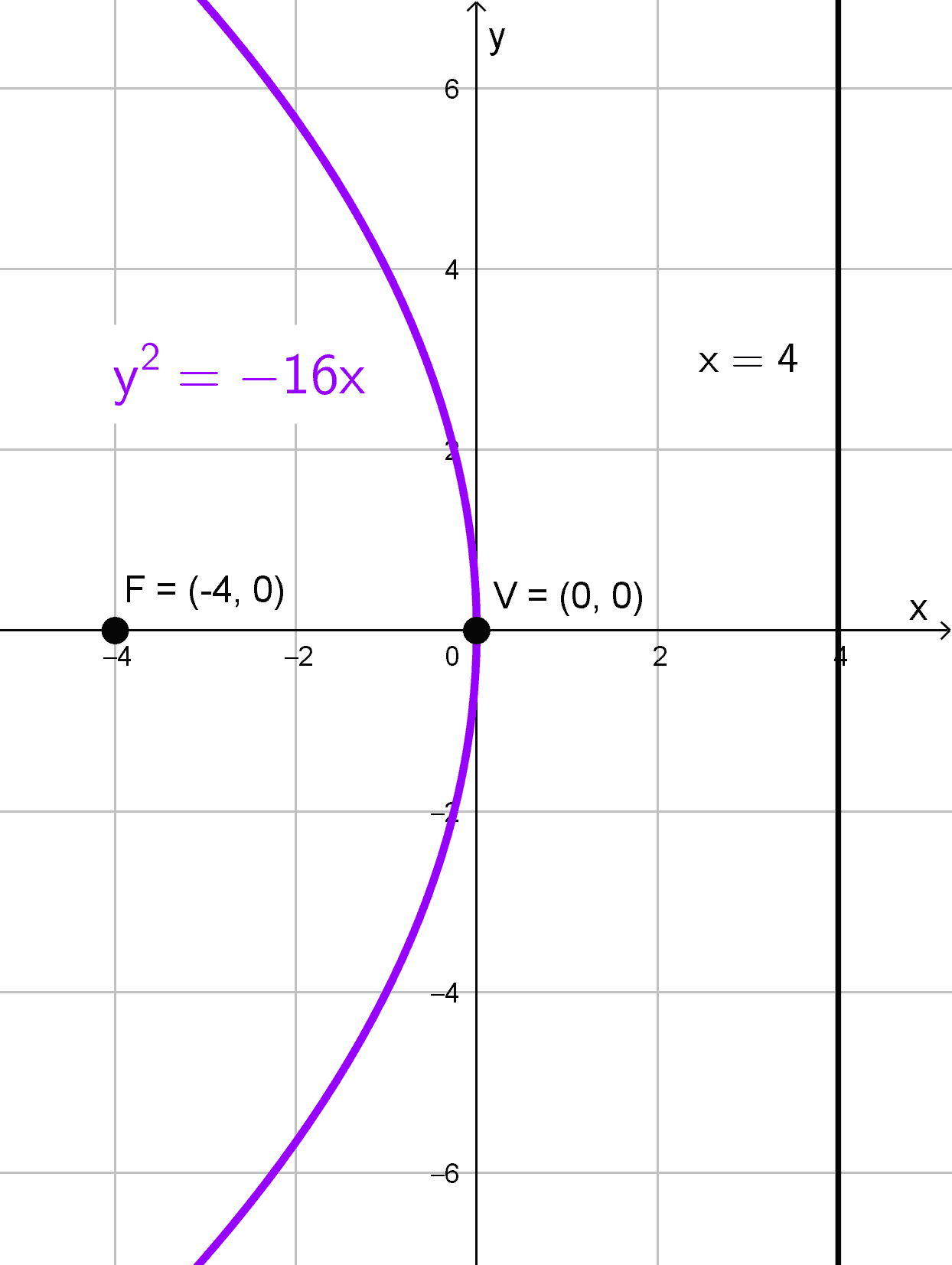


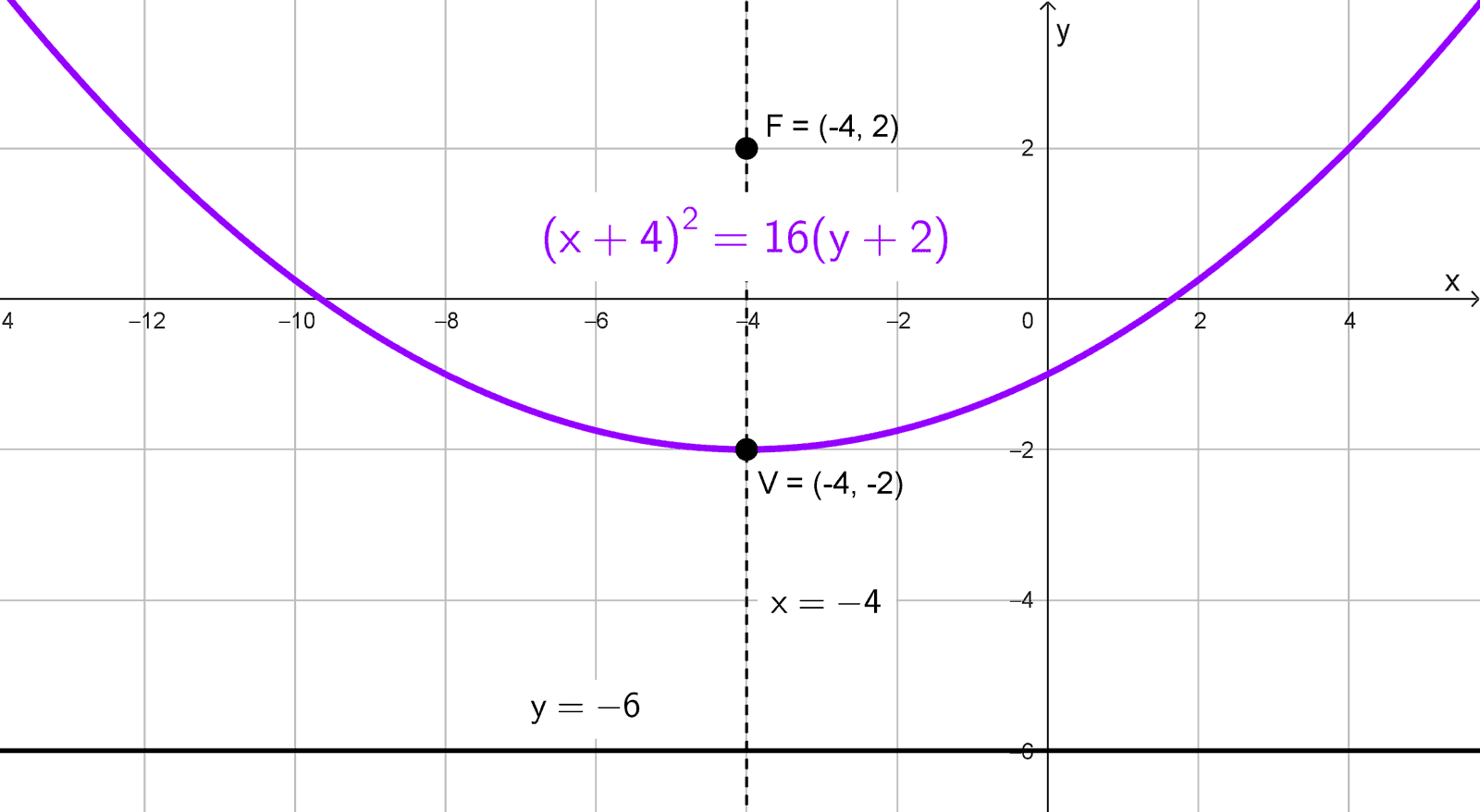
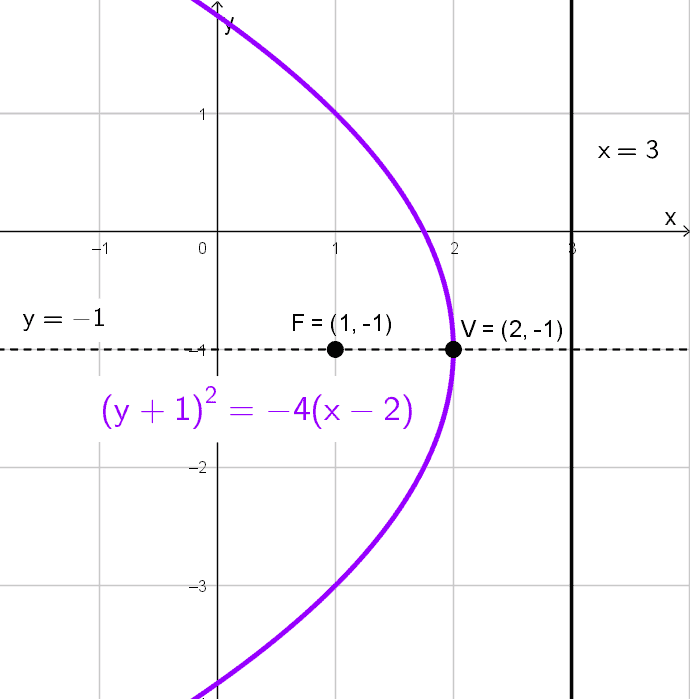
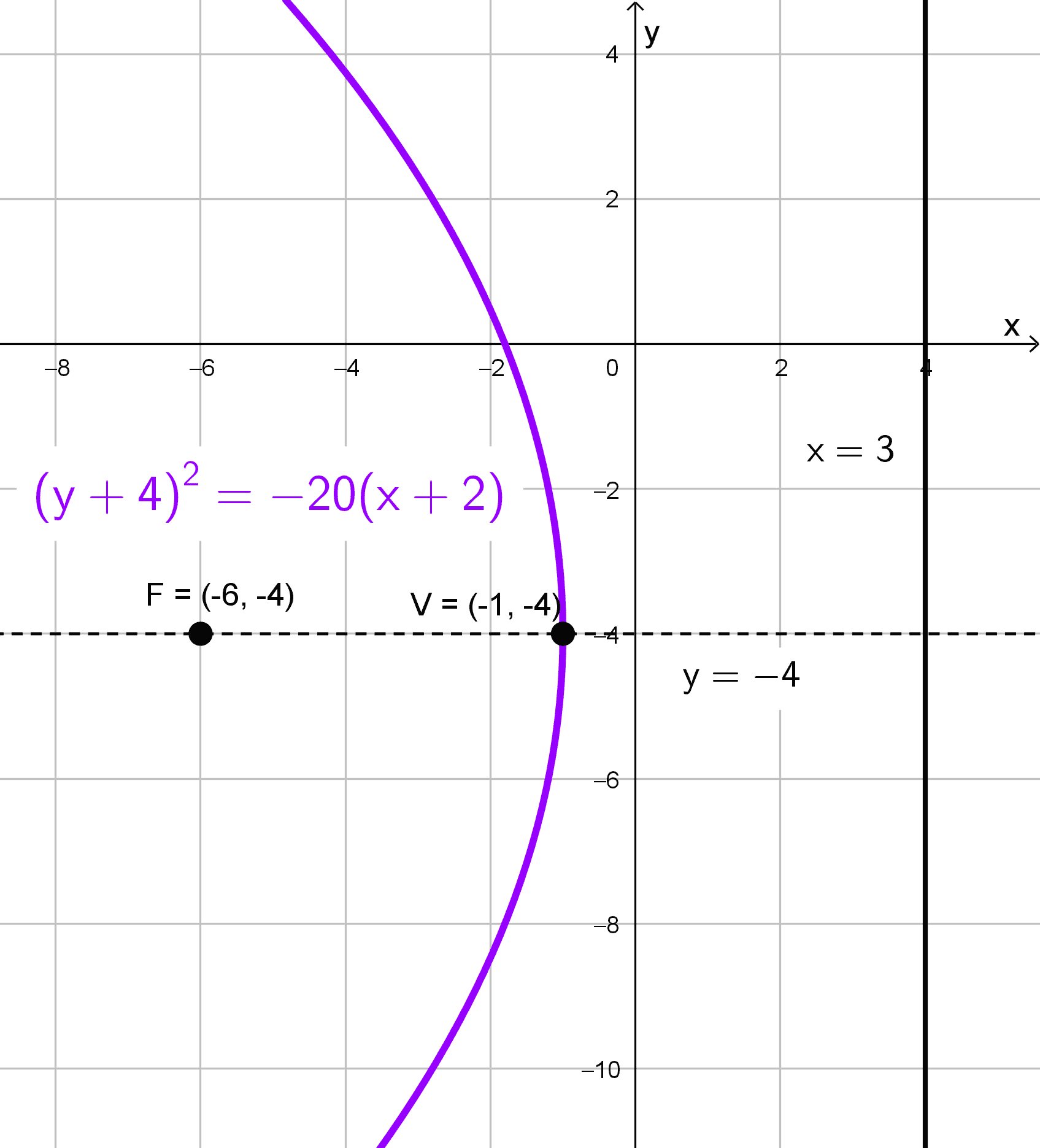


Otros artículos que pueden interesarte