Rotación de secciones cónicas
En este artículo explicamos qué es y cómo realizar una rotación de ejes coordenados de secciones cónicas. Además, veremos cómo encontrar el ángulo adecuado para eliminar el término mixto de la ecuación general.
Índice
¿Qué es la rotación?
La rotación es una transformación geométrica que implica un cambio en el sistema de coordenadas en el cual se describe la cónica. A diferencia de la traslación, donde los ejes del nuevo sistema siguen siendo paralelos a los ejes originales, en una rotación los ejes del sistema se giran respecto a un ángulo específico alrededor del origen de coordenadas (0, 0).
Este giro modifica la orientación de la cónica, pero no altera su forma ni sus propiedades. Al realizar la rotación, los términos de su ecuación original se reorganizan, lo que puede resultar en la introducción o eliminación de términos mixtos, aquellos que incluyen el producto de xy. Recordemos que estos términos cruzados indican que los ejes de la cónica no son paralelos a los ejes coordenados.
En este artículo veremos que es posible encontrar un ángulo adecuado de rotación que permita eliminar el término mixto de la ecuación de una cónica.
Fórmulas de rotación
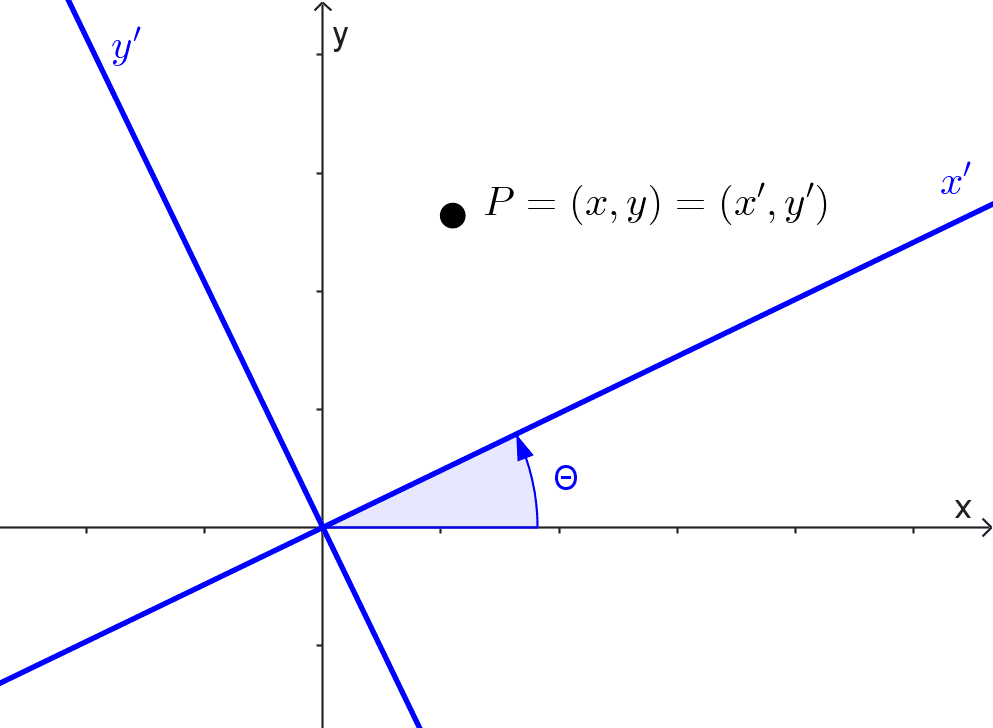
Consideremos un punto genérico P(x, y) ubicado en el plano. Al aplicar una rotación, este punto sigue estando en la misma posición del plano, pero sus coordenadas cambian, siendo ahora P (x’, y’).
Podemos relacionar las coordenadas originales (x, y) con las nuevas (x', y') utilizando un conjunto de fórmulas que dependen del ángulo de rotación θ:
*x=x'\cosθ-y'\sinθ*
*y=x'\sinθ+y'\cosθ*
Estas relaciones nos permitirán conocer las nuevas ecuaciones de las cónicas luego de efectuar un giro de ejes.
Cómo hallar el ángulo de rotación adecuado
Es posible remover el término mixto (el que contiene el producto xy) de una ecuación de segundo grado mediante una rotación de ejes, para esto se necesita encontrar el ángulo de rotación adecuado.
Partimos de la ecuación general de segundo grado:
*Ax^2+Bxy+Cy^2+Dx+Ey+F=0*
Aplicando una rotación de ejes con un ángulo θ, la ecuación resultante tendrá la forma:
*A'x'^2+B'x'y'+C'y'^2+D'x'+E'y'+F'=0*
en donde:
*A'=A\cos^2\theta+B\sin\theta\cos\theta+C\sin^2\theta *
*B'=B\cos 2\theta-(A-C)\sin 2\theta *
*C'=A\sin^2\theta-B\sin\theta\cos\theta+C\cos^2\theta *
*D'=D\cos\theta+E\sin\theta *
*E'=E\cos\theta-D\sin\theta*
*F'=F*
Para que el término B'x'y' se anule, necesitamos que su coeficiente sea igual a cero. Es decir, debe ocurrir que B’=0, o sea:
*B\cos 2\theta-(A-C)\sin 2\theta=0*
Si A ≠ C, la solución es:
*\tan 2\theta=\dfrac{B}{A-C}*
Esta expresión determina el ángulo de rotación θ en términos de los coeficientes de la ecuación original cuando A ≠ C. Sin embargo, cuando A=C, la ecuación se transforma en:
*B\cos 2\theta=0*
*\cos 2\theta=0*
*2\theta=90°*
*\theta=45°*
Resumimos los resultados en el siguiente cuadro.
La ecuación de segundo grado
*Ax^2+Bxy+Cy^2+Dx+Ey+F=0*
donde B ≠ 0 se puede transformar a otra de la forma
*A'x'^2+C'y'^2+D'x'+E'y'+F'=0*
realizando una rotación de ángulo θ obtenido a partir de la ecuación:
*\tan 2\theta=\dfrac{B}{A-C},* si A ≠ C
o bien
*\theta=45°,* si A = C
Ahora bien, las fórmulas de rotación incluyen senos y cosenos. Para evitar errores por aproximación, será necesario utilizar las siguientes identidades trigonométricas:
*\cos(2\theta)=\dfrac{1}{\sqrt{\tan^2(2\theta)+1}}*
*\sin\theta=\sqrt{\dfrac{1-\cos(2\theta)}{2}}*
*\cos\theta=\sqrt{\dfrac{1+\cos(2\theta)}{2}}*
Se debe tomar a cos(2θ) con el mismo signo de tan(2θ).
Ejercicios resueltos
Ejercicio 1
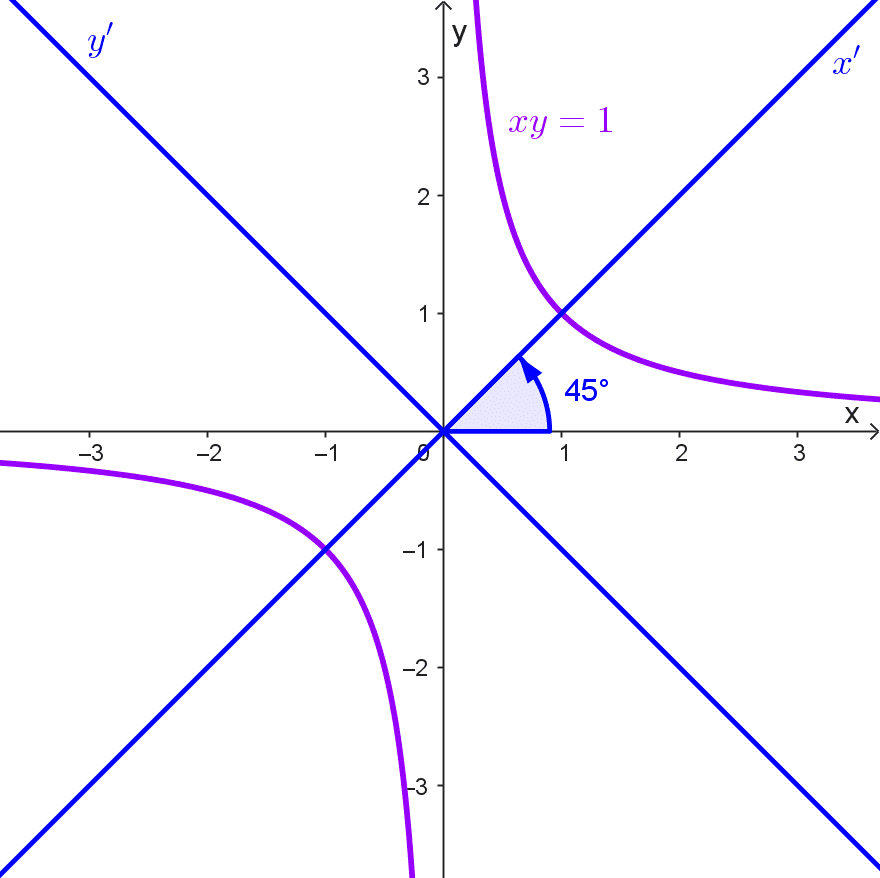
Encuentre la ecuación de la cónica *xy=1* luego de realizar una rotación de ejes con un ángulo de 45°
Solución: para expresar la ecuación xy=1 en términos de nuevas coordenadas x' y y' al girar los ejes un ángulo de 45°, seguimos estos pasos.
Primero, recordamos los valores de las funciones trigonométricas para 45°:
*\cos 45^\circ=\dfrac{\sqrt{2}}{2} \quad \text{y} \quad \sin 45^\circ=\dfrac{\sqrt{2}}{2}*
Utilizando estas expresiones, reescribimos las nuevas coordenadas x y y en términos de x' y y':
*x=x' \cos 45^\circ-y' \sin 45^\circ=x' \dfrac{\sqrt{2}}{2}-y' \dfrac{\sqrt{2}}{2}=\dfrac{\sqrt{2}}{2}(x'-y')*
*y=x' \sin 45^\circ+y' \cos 45^\circ=x' \dfrac{\sqrt{2}}{2}+y' \dfrac{\sqrt{2}}{2}=\dfrac{\sqrt{2}}{2}(x'+y')*
Sustituyendo estas expresiones en la ecuación xy=1:
*\left(\dfrac{\sqrt{2}}{2}(x'-y')\right)\left(\dfrac{\sqrt{2}}{2}(x'+y')\right)=1*
Simplificando, tenemos:
*\dfrac{\sqrt{2}}{2} \cdot \dfrac{\sqrt{2}}{2} \cdot (x'-y')(x'+y')=1*
*\dfrac{1}{2}(x'^2-y'^2)=1*
Distribuyendo:
*\dfrac{x'^2}{2}-\dfrac{y'^2}{2}=1*
Esta es la ecuación de una hipérbola con centro en (0, 0) y eje transversal paralelo al eje x'. Los vértices están en *(\pm \sqrt{2},0)* sobre el eje x', y las asíntotas son *y'=x'* y *y'=-x',* que corresponden a los ejes x e y originales.
Nótese que la ecuación *xy=1* se puede reescribir como *y=\dfrac{1}{x},* la cual es conocida como la función de proporcionalidad inversa o función recíproca.
Ejercicio 2
Realice una rotación para eliminar el término xy de la ecuación *3x^2+3xy-y^2=9*
Solución: comenzamos identificando los coeficientes relevantes: A=3, B=3, y C=-1. La primera etapa es calcular el ángulo de rotación α que nos permitirá eliminar el término mixto. Utilizamos la fórmula para la tangente doble del ángulo:
*\tan(2\alpha)=\dfrac{B}{A-C}=\dfrac{3}{3-(-1)}=\dfrac{3}{4}*
Con este resultado, ahora calculamos *\cos(2\alpha):*
*\cos(2\alpha)=\dfrac{1}{\sqrt{\tan^2(2\alpha)+1}}=\dfrac{1}{\sqrt{\left(\dfrac{3}{4}\right)^2+1}}=\dfrac{1}{\sqrt{\dfrac{9}{16}+1}}=\dfrac{1}{\sqrt{\dfrac{25}{16}}}=\dfrac{4}{5}*
Una vez que tenemos este valor, calculamos los valores de *\sin\alpha* y *\cos\alpha* usando las identidades trigonométricas:
*\sin\alpha=\sqrt{\dfrac{1-\cos(2\alpha)}{2}}=\sqrt{\dfrac{1-\dfrac{4}{5}}{2}}=\sqrt{\dfrac{\dfrac{1}{5}}{2}}=\sqrt{\dfrac{1}{10}}=\dfrac{1}{\sqrt{10}}*
*\cos\alpha=\sqrt{\dfrac{1+\cos(2\alpha)}{2}}=\sqrt{\dfrac{1+\dfrac{4}{5}}{2}}=\sqrt{\dfrac{\dfrac{9}{5}}{2}}=\sqrt{\dfrac{9}{10}}=\dfrac{3}{\sqrt{10}}*
Ahora aplicamos la rotación de ejes utilizando las fórmulas de transformación de coordenadas:
*x=x'\cos\alpha-y'\sin\alpha=x'\left(\dfrac{3}{\sqrt{10}}\right)-y'\left(\dfrac{1}{\sqrt{10}}\right)=\dfrac{3x'-y'}{\sqrt{10}}*
*y=x'\sin\alpha+y'\cos\alpha=x'\left(\dfrac{1}{\sqrt{10}}\right)+y'\left(\dfrac{3}{\sqrt{10}}\right)=\dfrac{x'+3y'}{\sqrt{10}}*
Sustituyendo estas expresiones en la ecuación original *3x^2+3xy-y^2=9,* desarrollamos y simplificamos las operaciones. Primero, reemplazamos x y y en la ecuación de la cónica:
*3\left(\dfrac{3x'-y'}{\sqrt{10}}\right)^2+3\left(\dfrac{3x'-y'}{\sqrt{10}}\right)\left(\dfrac{x'+3y'}{\sqrt{10}}\right)-\left(\dfrac{x'+3y'}{\sqrt{10}}\right)^2=9*
Al expandir y simplificar los términos cuadráticos y mixtos, se reorganizan los coeficientes para obtener la forma simplificada:
*7x'^2-3y'^2=18*
La ecuación resultante corresponde a una hipérbola, ya que presenta términos cuadrados con signos opuestos. Para llevarla a su forma canónica en los nuevos ejes, dividimos toda la ecuación por 18:
*\dfrac{7x'^2}{18}-\dfrac{3y'^2}{18}=1*
Simplificando, obtenemos la forma canónica de la hipérbola en los nuevos ejes:
*\dfrac{x'^2}{\dfrac{18}{7}}-\dfrac{y'^2}{6}=1*
Lo cual indica que los ejes de la hipérbola están alineados con los ejes transformados x' e y', con semiejes *\sqrt{\dfrac{18}{7}}* y *\sqrt{6},* respectivamente.

Este ejercicio fue extraído del artículo de ecuación general de las cónicas:
Ejercicio 3
Simplifique la siguiente ecuación mediante una rotación de coordenadas:
*73x^2-72xy+52y^2+100x-200y+100=0*
Solución: primero se transforma la ecuación, de modo que el término producto x'y' desaparezca. Para encontrar el ángulo de rotación, usamos:
*\tan 2\theta=\dfrac{B}{A-C}=\dfrac{-72}{73-52}=\dfrac{-24}{7}*
con ello calculamos:
*\cos 2\theta=\dfrac{-7}{25}*
por tanto:
*\sin \theta=\sqrt{\dfrac{1-\cos 2\theta}{2}}=\dfrac{4}{5} *
*\cos \theta=\sqrt{\dfrac{1+\cos 2\theta}{2}}=\dfrac{3}{5}*
Entonces, las fórmulas de rotación son
*x=\dfrac{3x'-4y'}{5} \quad \text{y} \quad y=\dfrac{4x'+3y'}{5}*
Al sustituir para x e y en la ecuación dada y simplificar, se obtiene
*x'^2+4y'^2-4x'-8y'+4=0*
Completando los cuadrados en los términos x' y y':
*(x'-2)^2+4(y'-1)^2-4=0*
Reordenando y dividiendo entre 4:
*(x'-2)^2+4(y'-1)^2=4*
*\dfrac{(x'-2)^2}{4}+(y'-1)^2=1*
Que es una elipse con centro en (2, 1), semieje mayor a = 2 y semieje menor b = 1.
Ejercicio 4
Reducir la siguiente ecuación a su forma canónica por transformación de coordenadas.
*5x^2+4xy+2y^2-24x-12y+29=0*
Solución: para suprimir el término en xy, hacemos girar los ejes coordenados un ángulo θ tal que:
*\tan 2\theta=\dfrac{B}{A-C}=\dfrac{4}{5-2}=\dfrac{4}{3}*
De *\tan 2\theta* podemos obtener *\cos 2\theta* por la relación
*\cos 2\theta=\dfrac{1}{\sqrt{\text{tan}^2 2\theta+1}}*
de donde,
*\cos 2\theta=\dfrac{1}{\sqrt{(4/3)^2+1}}=\dfrac{3}{5}*
De este valor de *\cos 2\theta* podemos obtener los valores de *\sin \theta* y *\cos \theta* por medio de las fórmulas trigonométricas:
*\sin \theta=\sqrt{\dfrac{1-\cos 2\theta}{2}}=\sqrt{\dfrac{1-(3/5)}{2}}=\dfrac{1}{\sqrt{5}}*
*\cos \theta=\sqrt{\dfrac{1+\cos 2\theta}{2}}=\sqrt{\dfrac{1+(3/5)}{2}}=\dfrac{2}{\sqrt{5}}*
Las ecuaciones de transformación por rotación son entonces
*x=x'\cos\theta-y'\sin\theta=\dfrac{2x'-y'}{\sqrt{5}}*
*y=x'\sin\theta+y'\cos\theta=\dfrac{x'+2y'}{\sqrt{5}}*
Sustituyendo estos valores de x y y en la ecuación original, obtenemos
*5\left(\dfrac{2x'-y'}{\sqrt{5}}\right)^2+4\left(\dfrac{2x'-y'}{\sqrt{5}}\right)\left(\dfrac{x'+2y'}{\sqrt{5}}\right)+2\left(\dfrac{x'+2y'}{\sqrt{5}}\right)^2 *
*-24\left(\dfrac{2x'-y'}{\sqrt{5}}\right)-12\left(\dfrac{x'+2y'}{\sqrt{5}}\right)+29=0*
la cual toma la forma:
*6x'^2+y'^2-12\sqrt{5}x'+29=0*
Completando los cuadrados:
*6(x'-\sqrt{5})^2+y'^2=1*
*\dfrac{(x'-\sqrt{5})^2}{1/6}+y'^2=1*
Que es la ecuación de una elipse con centro en *(\sqrt{5}, 0),* con semieje mayor *a = 1* y semieje menor *b = \sqrt{1/6} ≈ 0,41.*
Puedes ver ejercicios de rotación combinada con traslación en este artículo:
Puntos clave
Las fórmulas de rotación de ejes coordenados con un ángulo θ son:
x = x' cos θ - y' sin θ
y = x' sin θ + y' cos θ
La fórmula para encontrar ángulo de rotación de una cónica de modo que se elimine el término mixto es:
tan (2θ) = B / (A - C), si A ≠ C
o bien θ = 45°, si A = C
Bibliografía
- Barco, V., Caraballo, L. y Murinigo, A. (2015). Estudio de la ecuación general de segundo grado. Universidad Nacional de Rosario.
- Escobar, J. y Ávila, H. (2018). Ecuación general de segundo grado en dos y tres variables. Instituto Tecnológico Metropolitano.
- Fuller, G. y Tarwater, D. (1995). Geometría Analítica (7ma edición). Pearson Educación.
- Hurtado Cruz, E. (s.f.). Rotación de Cónicas en R2. Facultad de Ciencias UNAM.
- Lehmann, C. (1989). Geometría Analítica. Limusa.
- Márquez, A. y otros. (2009). Geometría Analítica. Prentice Hall.
- Raichman, S. y Totter, E. (2016). Geometría Analítica para Ciencias e Ingeniería. Universidad Nacional de Cuyo.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta


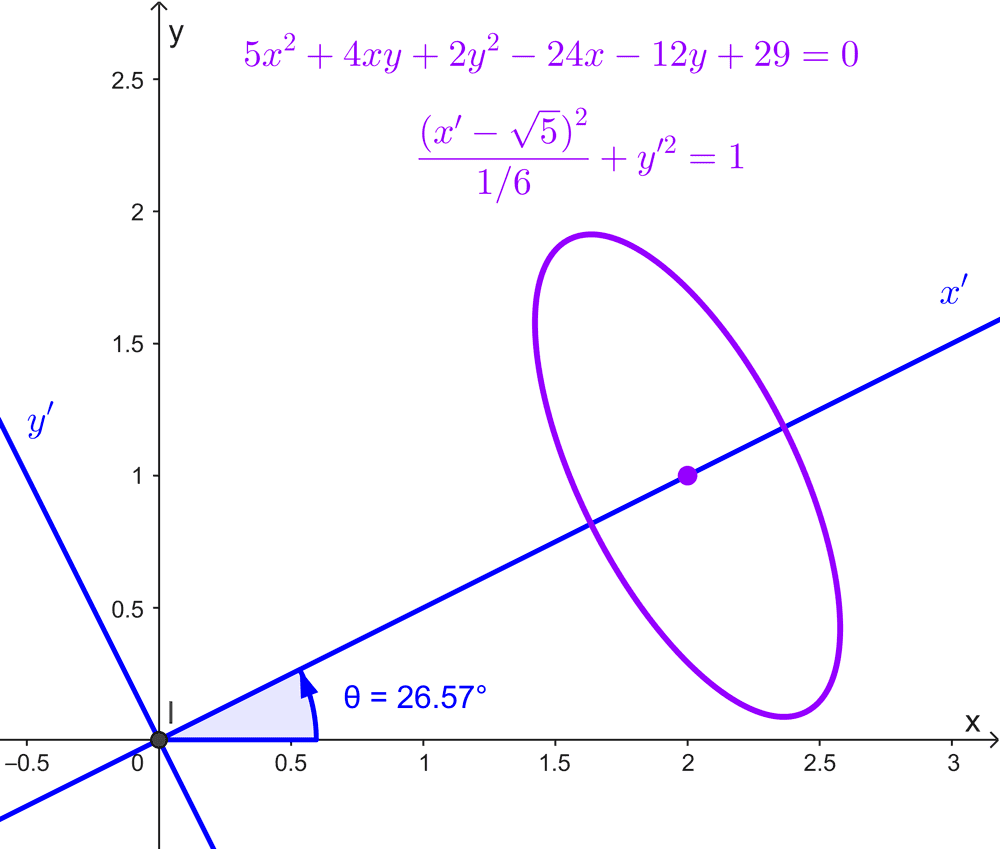
Otros artículos que pueden interesarte