Cónicas en coordenadas polares
En este artículo explicamos las ecuaciones de las secciones cónicas en coordenadas polares y cómo identificar y graficar una cónica a partir de su ecuación polar con ejercicios resueltos.
Índice
Coordenadas polares
En un sistema de coordenadas cartesianas (también llamadas rectangulares) podemos ubicar cualquier punto del plano mediante números x e y llamados coordenadas, las cuales representan las distancias (con signo) desde los ejes.
La coordenada x indica cuánto hay que alejarse del eje y horizontalmente, es decir, hacia la derecha o hacia la izquierda. La coordenada y indica cuánto hay que alejarse del eje x verticalmente, es decir, hacia abajo o hacia arriba. Por ejemplo, el punto (2, -5) está alejado del eje y dos unidades horizontalmente hacia la derecha y cinco unidades alejado del eje x verticalmente hacia abajo.
Las coordenadas polares son otra forma de ubicar un punto en un plano, pero en vez de usar distancias horizontales y verticales, utilizamos un ángulo y una distancia al origen.
Un punto P en el plano se describe mediante dos valores en el sistema de coordenadas polares:
- Radio (r): es la distancia del punto al origen (también llamado polo), siempre es un valor no negativo.
- Ángulo (θ): es el ángulo que forma el segmento que une el origen con el punto con el semieje positivo de x. Este ángulo se mide en radianes o grados sexagesimales. Al eje x se le llama eje polar.
Las coordenadas polares se pueden convertir a coordenadas cartesianas mediante las siguientes fórmulas:
x = r ⋅ cos(θ)
y = r ⋅ sin(θ)
Inversamente, para convertir de coordenadas cartesianas a polares:
*r = \sqrt{x^2+y^2}*
*θ=\arctan(y/x)* (teniendo en cuenta el cuadrante en el que se encuentra el punto para determinar el ángulo correcto).
Las secciones cónicas pueden escribirse en coordenadas polares, pero primero es necesario utilizar una definición diferente de ellas.
Definición general de una cónica
Hemos visto que la parábola se define como el conjunto de puntos que están a igual distancia de una recta llamada directriz y un punto fijo llamado foco. Esta definición que involucra una recta y un punto es en realidad aplicable a cualquier cónica, de modo que podemos definir una elipse, una hipérbola o una parábola en función de una directriz y un foco.
Definición: una cónica es el lugar geométrico de los puntos en el plano cuya distancia a un punto fijo, llamado foco, guarda una proporción constante con su distancia a una recta fija, denominada directriz. Esa proporción se denomina excentricidad, y según su valor determinamos qué tipo de cónica se describe.
Es decir, dada una directriz D y un punto fijo F, una cónica es la colección de puntos P para los que:
*\dfrac{d(F,P)}{d(D,P)}=e*
- Si e = 1, la cónica es una parábola.
- Si e < 1, la cónica es una elipse.
- Si e > 1, la cónica es una hipérbola.
Nótese que cuando e=1, se tiene que *d(F,P)=d(D,P),* lo cual coincide con la definición de parábola vista anteriormente.
Ecuación polar de una cónica
Las cónicas pueden describirse fácilmente en coordenadas polares utilizando la definición vista antes. Al igual que cuando usamos coordenadas cartesianas, en las polares también se elige una posición conveniente para el foco F y la directriz D. El foco F se coloca en el polo (centro) y la directriz D es paralela o perpendicular al eje polar.
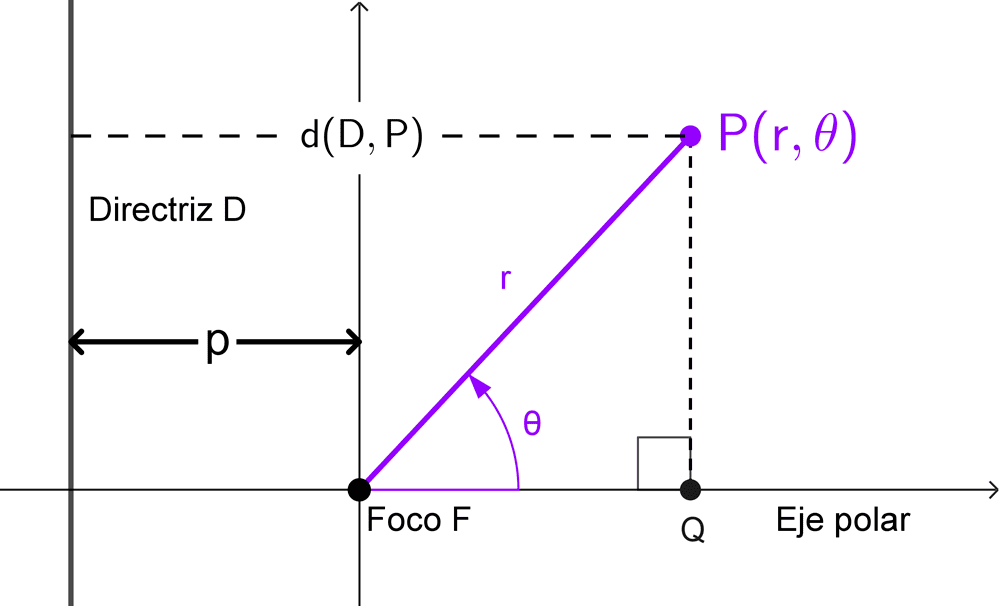
Comenzamos con una directriz D perpendicular al eje polar ubicada a una distancia de p unidades a la izquierda del polo, punto que será el foco F. Si P=(r, θ) es cualquier punto de la cónica, se tiene que, usando la definición anterior:
*\dfrac{d(F, P)}{d(D,P)}=e~* o *~d(F,P)=e\cdot d(D,P)*
Ahora utilizamos el punto Q obtenido de proyectar P sobre el eje polar para calcular d(D, P).
*d(D,P)=p+d(O,Q)=p+r \cos θ*
Retomando la primera ecuación:
*d(F,P)=e\cdot d(D,P)*
*r=e(p+r \cos θ)*
*r=ep + er \cos θ*
*r-er \cosθ=ep*
*r(1-e \cosθ)=ep*
*r=\dfrac{ep}{1-e \cos θ}*
Con esto llegamos a la ecuación polar de la cónica.
La ecuación polar de una cónica con foco en el polo, excentricidad e y directriz perpendicular al eje polar a una distancia p a la izquierda del polo es:
*r=\dfrac{ep}{1-e \cos θ}*
Si, en cambio, se considera que la directriz es perpendicular al eje polar pero está ubicada a una distancia de p unidades a la derecha del polo, en la ecuación polar cambia el signo de un término del denominador, quedando:
*r=\dfrac{ep}{1+e \cos \theta}*
Al usar una directriz paralela al eje polar se mantiene una lógica parecida, solo que en lugar de coseno de θ aparece el seno de θ. El término e⋅sin θ es positivo cuando la directriz está por encima del polo y es negativo cuando la directriz está por debajo. Las ecuaciones se resumen en la siguiente tabla:
| Ecuación | Descripción |
|---|---|
| *r=\dfrac{ep}{1-e \cos \theta}* | Directriz perpendicular al eje polar a una distancia de p unidades a la izquierda del polo. |
| *r=\dfrac{ep}{1+e \cos \theta}* | Directriz perpendicular al eje polar a una distancia de p unidades a la derecha del polo. |
| *r=\dfrac{ep}{1-e \sin \theta}* | Directriz paralela al eje polar a una distancia de p unidades debajo del polo. |
| *r=\dfrac{ep}{1+e \sin \theta}* | Directriz paralela al eje polar a una distancia de p unidades arriba del polo. |
| Excentricidad | Cónica |
|---|---|
| e = 1 | La cónica es una parábola; el eje de simetría es perpendicular a la directriz. |
| e < 1 | La cónica es una elipse; el eje mayor es perpendicular a la directriz. |
| e > 1 | La cónica es una hipérbola; el eje transversal es perpendicular a la directriz. |
Ecuaciones polares de cada cónica
A continuación veremos la forma general y ejemplos de las ecuaciones de cada cónica en forma polar.
Circunferencia
La ecuación polar de una circunferencia es r = k, donde k es el radio de la circunferencia, un número real positivo. Es una ecuación muy sencilla ya que no aparece el ángulo como variable, sino únicamente el radio.
Ejemplos
- r = 1 es una circunferencia de radio 1, también llamada circunferencia unitaria.
- r = 4 es una circunferencia de radio 4.
- r = 1/2 es una circunferencia de radio 1/2.
- r = √2 es una circunferencia de radio √2.
Elipse
La ecuación polar de una elipse con directriz perpendicular al eje polar a p unidades a la derecha o izquierda del polo es:
*r=\dfrac{ep}{1±e \cos \theta}*
Si la directriz es paralela al eje polar y está a p unidades arriba o abajo del polo entonces la ecuación es:
*r=\dfrac{ep}{1±e \sin \theta}*
La excentricidad e está entre 0 y 1 (0 ≤ e < 1) por tratarse de una elipse.
Ejemplos
- *r=\dfrac{1}{1+\frac{1}{2} \cos θ}*
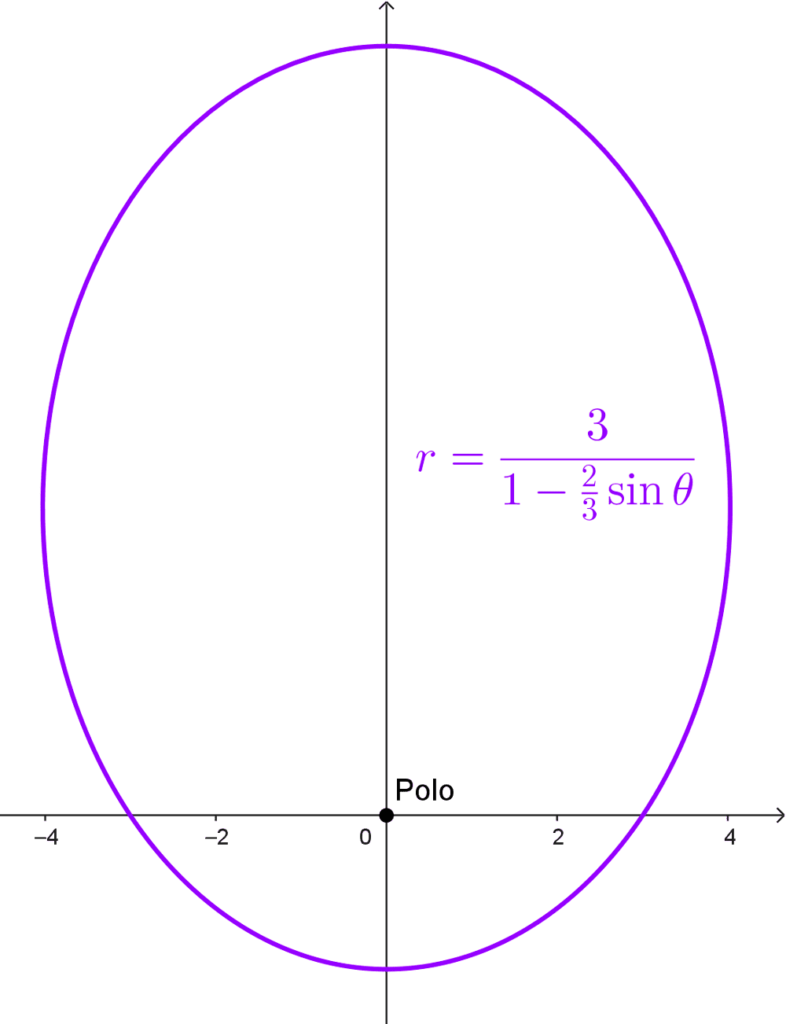
- *r=\dfrac{3}{1-\frac{2}{3} \sin θ}*
- *r=\dfrac{35}{7-\cos θ}*
- *r(4+\sin θ)=4*
Hipérbola
La ecuación polar de una hipérbola con directriz perpendicular al eje polar a p unidades a la derecha o izquierda del polo es:
*r=\dfrac{ep}{1±e \cos \theta}*
Si la directriz es paralela al eje polar y está a p unidades arriba o abajo del polo entonces la ecuación es:
*r=\dfrac{ep}{1±e \sin \theta}*
La excentricidad e es mayor que 1 (e > 1) por tratarse de una hipérbola.
Ejemplos
- *r=\dfrac{1}{1+2\cos θ}*
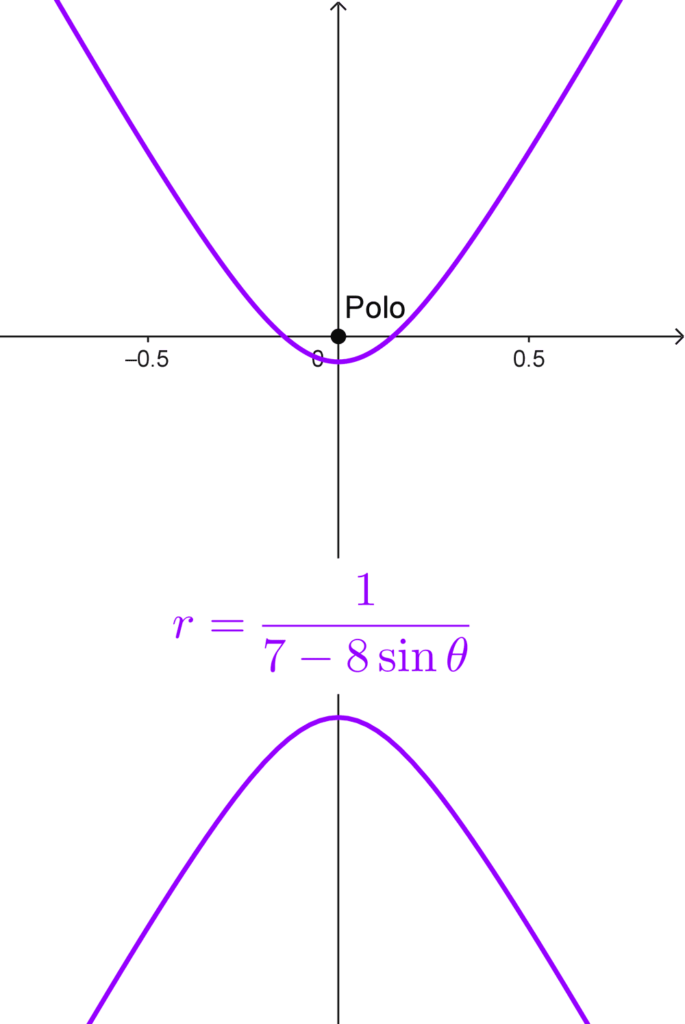
- *r=\dfrac{1}{7-8\sin θ}*
- *r=\dfrac{6}{1-3\cosθ}*
- *r(4\cos θ+3)=2*
Parábola
La ecuación polar de una parábola con directriz perpendicular al eje polar a p unidades a la derecha o izquierda del polo es:
*r=\dfrac{p}{1±\cos \theta}*
Si la directriz es paralela al eje polar y está a p unidades arriba o abajo del polo entonces la ecuación es:
*r=\dfrac{p}{1±\sin \theta}*
Nótese que la excentricidad no aparece en la ecuación porque es igual a 1 (e = 1), debido a que se trata de una parábola.
Ejemplos
- *r=\dfrac{1}{1+\cos θ}*
- *r=\dfrac{2}{2-2\sin θ}*
- *r=\dfrac{5}{1-\cos θ}*
- *r(\sin θ+1)=10*
Nota: es importante destacar que en coordenadas polares las ecuaciones de las cónicas no son únicas, esto es porque existen infinitas formas de expresar un mismo ángulo. Por ejemplo, la ecuación *r=\dfrac{1}{1+\cos θ}* representa la misma cónica que la ecuación *r=\dfrac{1}{1+\cos (θ+360°)}.*
Cómo identificar y graficar una cónica dada en forma polar
Nos encontramos en la situación de querer graficar una cónica dada en forma polar, para poder realizar esto primero debemos identificar el tipo de cónica a través de la excentricidad, la posición de la directriz (paralela o perpendicular al eje polar) y la distancia del polo a la directriz.
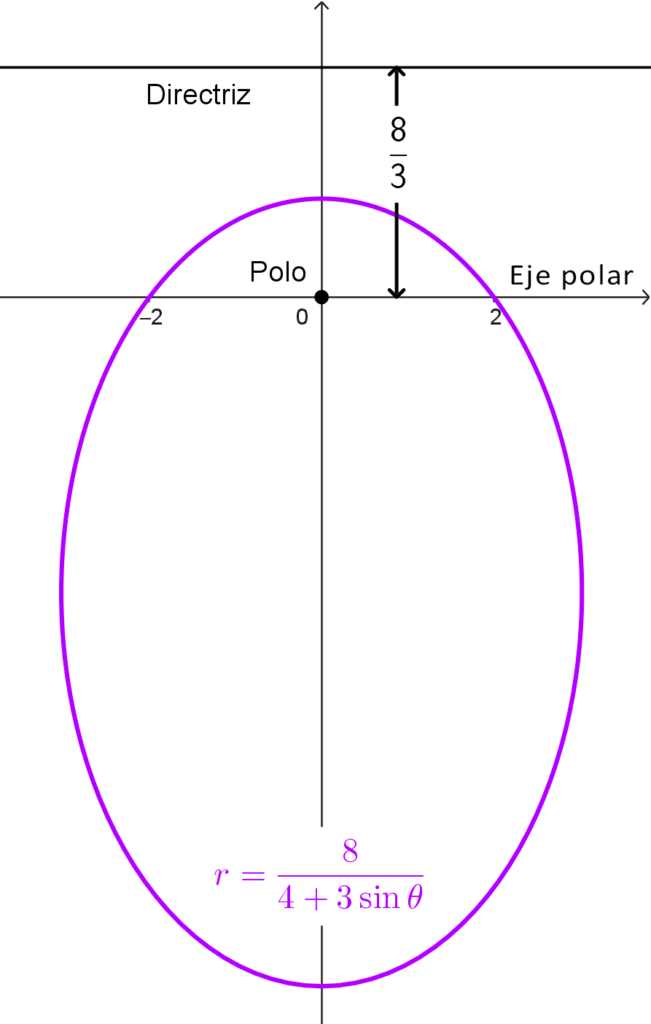
Por ejemplo, queremos analizar la ecuación polar *r=\dfrac{8}{4+3\sin θ}*
Para empezar no tenemos una forma estándar, necesitamos lograr una ecuación de la forma *r=\dfrac{ep}{1±e\sin θ}. *
En el denominador de la ecuación *r=\dfrac{8}{4+3\sin θ}* no aparece un 1 como término independiente. Podemos conseguir que aparezca un 1 dividiendo numerador y denominador entre el término independiente del denominador, en este caso es 4. Así:
*r=\dfrac{\frac{8}{4}}{\frac{4+3\sin θ}{4}}*
*r=\dfrac{\frac{8}{4}}{\frac{4}{4}+\frac{3\sin θ}{4}}*
*r=\dfrac{2}{1+\frac{3}{4}\sin θ}*
Ahora hemos conseguido un 1 como término independiente del denominador. Podemos extraer la excentricidad como el número que multiplica a la función trigonométrica, en este caso tenemos que:
*e=\dfrac{3}{4}*
Como 3/4 es un número menor que 1, la ecuación representa a una elipse.
Aún necesitamos extraer el parámetro p, lo haremos desde el numerador. Usaremos el dato de la excentricidad:
*ep=2*
*\dfrac{3}{4}p=2*
*p=2\cdot \dfrac{4}{3}*
*p=\dfrac{8}{3}*
Ya tenemos suficiente para trazar la gráfica de la ecuación polar. Con los datos obtenidos podemos saber que:
- Es una elipse, porque la excentricidad es e = 3/4 que es menor a 1.
- La directriz es paralela al eje polar porque la forma estándar tiene en el denominador una función seno. Esto significa que la elipse tiene orientación vertical.
- La directriz se encuentra a 8/3 unidades del polo, pues p es igual a esa cantidad.
- La directriz está por encima del polo porque la función seno tiene coeficiente positivo.
Pasos para identificar una cónica dada en forma polar
1) Si la ecuación no está en la forma estándar, se debe manipular algebraicamente para obtener una de las formas siguientes formas:
*r=\dfrac{ep}{1±e \cos \theta}*
*r=\dfrac{ep}{1±e \sin \theta}*
Esto generalmente se logra dividiendo el numerador y denominador entre el término independiente del denominador.
2) Una vez se consiga una forma estándar, extraer la excentricidad, el cual es el número que multiplica al seno o el coseno que aparece en el denominador. Si e < 1, se trata de una elipse; si e > 1, se trata de una hipérbola; si no aparece nada, entonces la excentricidad es 1, tratándose de una parábola.
3) Extraer el parámetro p igualando el numerador a ep y despejando p.
Ejemplo 1
Identificar y graficar la cónica con ecuación polar: *r=\dfrac{12}{4+8\sinθ}*
Solución: primero convertimos a la forma estándar *r=\dfrac{ep}{1±e\sinθ}.*
En este caso, no tenemos un 1 como término independiente en el denominador, así que dividimos tanto el numerador como el denominador entre el término independiente, que es 4:
*r=\dfrac{\frac{12}{4}}{\frac{4+8\sinθ}{4}}*
*r=\dfrac{3}{1+2\sinθ}*
Ahora que la ecuación está en la forma estándar *r=\dfrac{ep}{1+e\sinθ},* podemos extraer la excentricidad. El número que multiplica a sin θ es 2, por lo que:
*e=2*
Como e > 1, sabemos que la cónica es una hipérbola.
Como tercer paso extraemos el parámetro p, el cual se obtiene desde el numerador. Sabemos que ep=3, entonces:
*2p=3*
*p=\dfrac{3}{2}*
Conclusión:
- La ecuación representa una hipérbola porque e=2 que es mayor a 1.
- La directriz es paralela al eje polar ya que la función trigonométrica involucrada es sin θ, la hipérbola tiene orientación vertical.
- La directriz está a 3/2 unidades del polo.
- Como el coeficiente de sin θ es positivo, la directriz está por encima del polo.
Ejemplo 2
Dada la ecuación polar *r=\dfrac{3}{4-2\cosθ}* identificar qué cónica representa y graficarla.
Solución: queremos obtener una ecuación de la forma estándar *r=\dfrac{ep}{1±e\cosθ},* así que dividimos numerador y denominador entre el término independiente del denominador, que es 4:
*r=\dfrac{\frac{3}{4}}{\frac{4-2\cosθ}{4}}*
*r=\dfrac{\frac{3}{4}}{1-\frac{2}{4}\cosθ}*
*r=\dfrac{\frac{3}{4}}{1-\frac{1}{2}\cosθ}*
El número que multiplica a cos θ en el denominador es 1/2, por lo que la excentricidad es:
*e=\dfrac{1}{2}*
Como e < 1, sabemos que la cónica es una elipse.
El parámetro p se obtiene desde el numerador. Sabemos que *ep=\dfrac{3}{4},* entonces:
*\dfrac{1}{2}p=\dfrac{3}{4}*
*p=2\cdot\dfrac{3}{4}=\dfrac{3}{2}*
Conclusiones:
- La ecuación representa una elipse porque e = 1/2, es decir, e<1.
- La directriz es perpendicular al eje polar, ya que la función trigonométrica involucrada es cos θ. La elipse tiene una orientación horizontal.
- La directriz está a 3/2 unidades del polo.
- Como el coeficiente de cos θ es negativo, la directriz está a la izquierda del polo.
Ejemplo 3
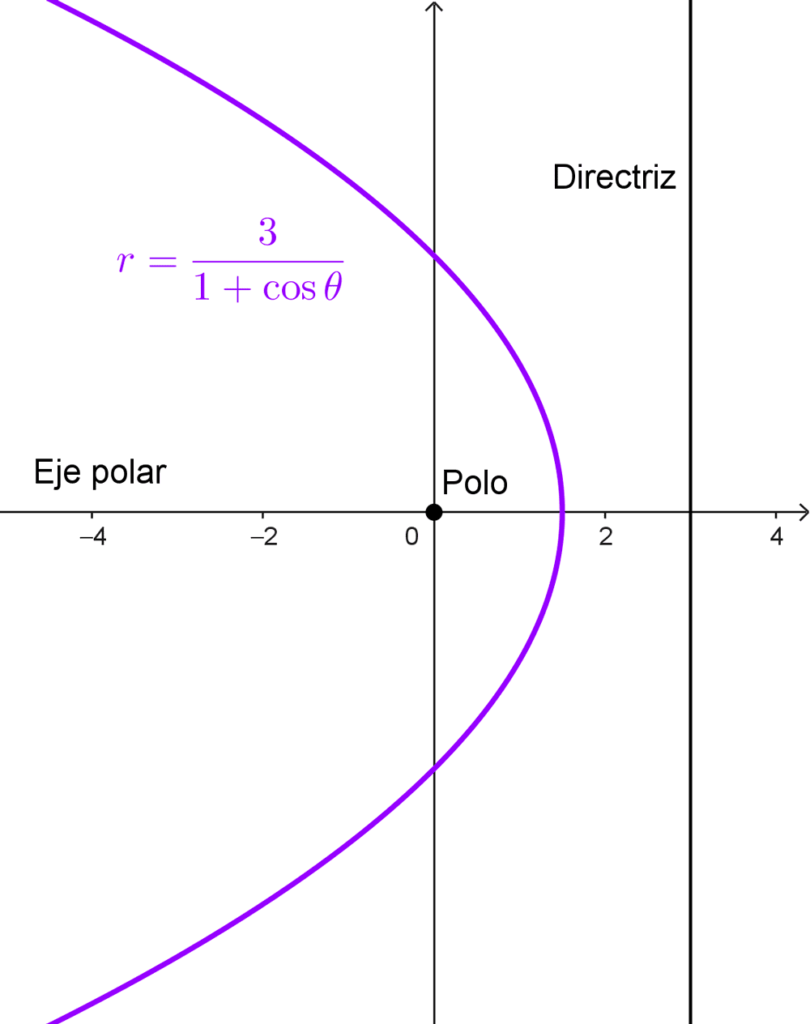
Identificar y graficar la siguiente ecuación: *r=\dfrac{3}{1+\cosθ}*
Solución: en este caso, la ecuación ya está en la forma estándar *r=\dfrac{ep}{1+e\cosθ},* así que no es necesario hacer ninguna manipulación adicional.
El número que multiplica a cos θ es 1, por lo que la excentricidad es:
*e=1*
Dado que e = 1, la cónica es una parábola.
El parámetro p se obtiene desde el numerador. Sabemos que ep = 3, y como e = 1, entonces:
*p=3*
Conclusiones:
- La ecuación representa una parábola porque e = 1.
- La directriz es perpendicular al eje polar, ya que la función trigonométrica involucrada es cos θ. La parábola tiene una orientación horizontal.
- La directriz está a 3 unidades del polo.
- Como el coeficiente de cos θ es positivo, la directriz está a la derecha del polo.
Transformación de coordenadas polares a rectangulares
Es posible convertir la ecuación de una cónica dada en coordenadas polares (con variables r, θ) a la forma general dada en coordenadas rectangulares (con variables x, y). Para esto tenemos que usar las siguientes ecuaciones de conversión:
*r^2=x^2+y^2 → r=\sqrt{x^2+y^2}*
*x= r\cdot \cos θ → \cos θ=\dfrac{x}{r}=\dfrac{x}{\sqrt{x^2+y^2}}*
*y= r\cdot \sin θ → \sin θ=\dfrac{y}{r}=\dfrac{y}{\sqrt{x^2+y^2}}*
Comenzamos con la ecuación en forma estándar:
*r=\dfrac{ep}{1±e \cos \theta}*
Multiplicamos ambos miembros por el denominador del segundo miembro y aplicamos propiedad distributiva:
*r(1±e \cos \theta)=ep*
*r±r e\cos \theta = ep*
Sustituimos las expresiones r y cos θ por sus equivalentes:
*\sqrt{x^2+y^2}±\sqrt{x^2+y^2}\cdot \dfrac{ex}{\sqrt{x^2+y^2}}=ep*
*\sqrt{x^2+y^2}±ex=ep*
Aislamos la raíz cuadrada y sacamos factor común:
*\sqrt{x^2+y^2}=ep±ex*
*\sqrt{x^2+y^2}=e(p±x)*
Elevamos ambos miembros al cuadrado:
*x^2+y^2=e^2 (p±x)^2*
Esta expresión se puede seguir desarrollando hasta obtener la ecuación general de una cónica donde aparecen la excentricidad e y el parámetro p y representará una cónica con eje focal sobre el eje x.
Si en lugar de comenzar con la ecuación con coseno se comienza con la que lleva seno, se llega a:
*x^2+y^2=e^2 (p±y)^2*
Esta representa una cónica con eje focal sobre el eje y.
Puntos clave
1) Las ecuaciones de las cónicas en coordenadas polares son las siguientes:
*r=\dfrac{ep}{1±e \cos \theta}*
*r=\dfrac{ep}{1±e \sin \theta}*
Donde p es la distancia del polo a la directriz y e es la excentricidad de la cónica.
2) La excentricidad determina el tipo de cónica:
- Si e = 1, es una parábola.
- Si e < 1, es una elipse.
- Si e > 1, es una hipérbola.
3) La diferencia entre las cónicas en coordenadas cartesianas y en coordenadas polares radica en que en la primera las variables son x e y, distancias medidas de forma paralela a los ejes; en cambio, en las coordenadas polares las variables son r y θ, siendo el primero la distancia del origen a un punto y la segunda el ángulo que se forma con el eje polar.
4) Para graficar una cónica en coordenadas polares primero debemos identificar el tipo de cónica a través de la excentricidad, la posición de la directriz (paralela o perpendicular al eje polar) y la distancia del polo a la directriz.
Recursos adicionales
Con el siguiente recurso puedes modificar la excentricidad y el parámetro p para ver cómo cambia una cónica en tiempo real:
Lecturas recomendadas:
- Lehmann, C. (1989). Geometría Analítica. Limusa.
- Sullivan, M. (2006). Álgebra y Trigonometría. Pearson Educación.
- Swokowski, E. y Cole, J. (2009). Álgebra y Trigonometría con Geometría Analítica. Cengage Learning.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta




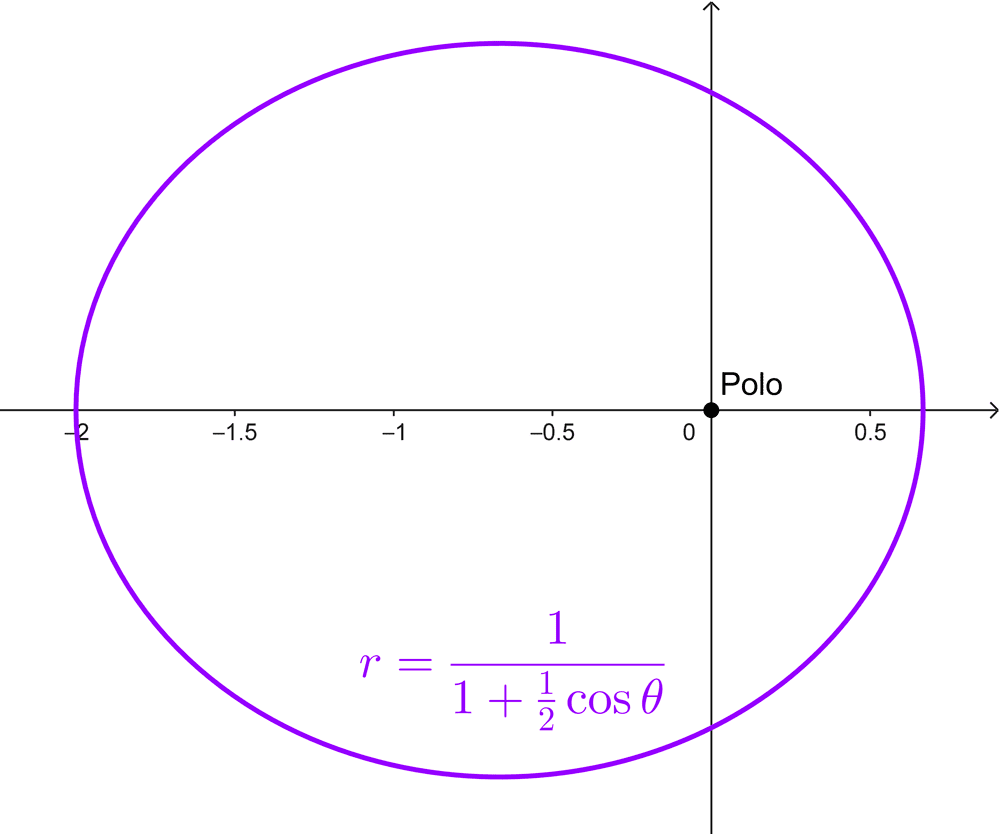





Otros artículos que pueden interesarte