Parábola vertical

Una parábola vertical es aquella cuyo eje de simetría es paralelo o coincidente con el eje y. Sus ramas pueden abrir hacia arriba (parábola convexa) o hacia abajo (parábola cóncava).

La ecuación canónica de una parábola vertical con vértice en el origen es:

x² = 4py

siendo |p| es la distancia del vértice al foco. Si p tiene signo positivo, las ramas de la parábola se abren hacia arriba; si p es negativo, las ramas abren hacia abajo.

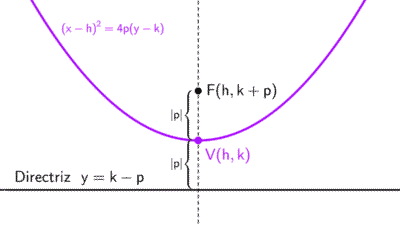
Si el vértice no está en el origen sino en un punto (h, k), la ecuación canónica es:

(x - h)² = 4p (y - k)

Del mismo modo que antes, el signo de p indica hacia donde abren las ramas.

Podemos reconocer la ecuación de una parábola con eje vertical fijándonos cuál variable está elevada al cuadrado. En las parábolas verticales es la variable x, mientras que en las parábolas horizontales es la variable y.

Es común trabajar con la ecuación de la parábola vertical de la siguiente forma:

y = ax² + bx + c

Aquí, el signo de “a” es el que determina si la parábola abre hacia arriba (cuando a es positivo) o abre hacia abajo (cuando a es negativo). Esto ocurre porque a = 1 / 4p.

Parábola vertical positiva que abre hacia arriba con vértice en el origen de coordenadas — Parábola vertical que abre hacia arriba con vértice en (0, 0)

Parábola vertical negativa que abre hacia abajo con vértice en el origen de coordenadas — Parábola vertical que abre hacia abajo con vértice en (0, 0)

Parábola convexa con vértice fuera del origen de coordenadas en (h, k) — Parábola vertical que abre hacia arriba con vértice en (h, k)

Parábola cóncava con vértice fuera del origen de coordenadas en (h, k) — Parábola vertical que abre hacia abajo con vértice en (h, k)

Nota: aquí nos enfocamos solo en un tipo de parábola. Para comprenderlo mejor, es conveniente que antes repases el artículo principal sobre esta cónica, donde abordamos su teoría básica:

Índice

Elementos

Las ecuaciones junto con los elementos de las parábolas verticales se resumen en la siguiente tabla:

Ecuación	Vértice	Apertura	Eje de simetría	Foco	Directriz
x² = 4py	(0, 0)	Hacia arriba si p > 0 Hacia abajo si p < 0	x = 0	(0, p)	y = -p
(x - h)² = 4p (y - k)	(h, k)	Hacia arriba si p > 0 Hacia abajo si p < 0	x = h	(h, k + p)	y = k - p

Ejemplos

Los siguientes son ejemplos de ecuaciones de parábolas con eje focal vertical:

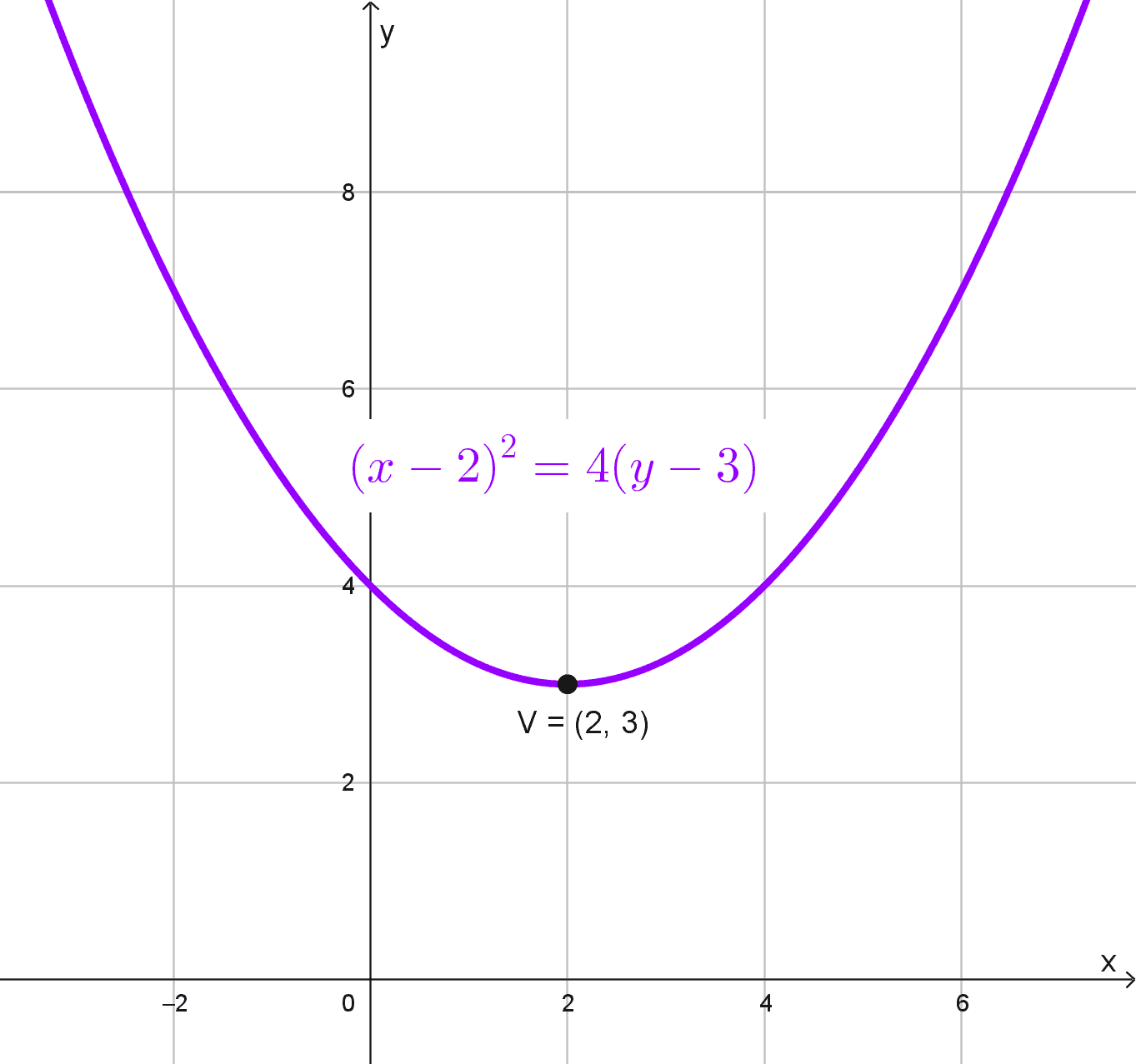
*(x-2)^2=4(y-3)*
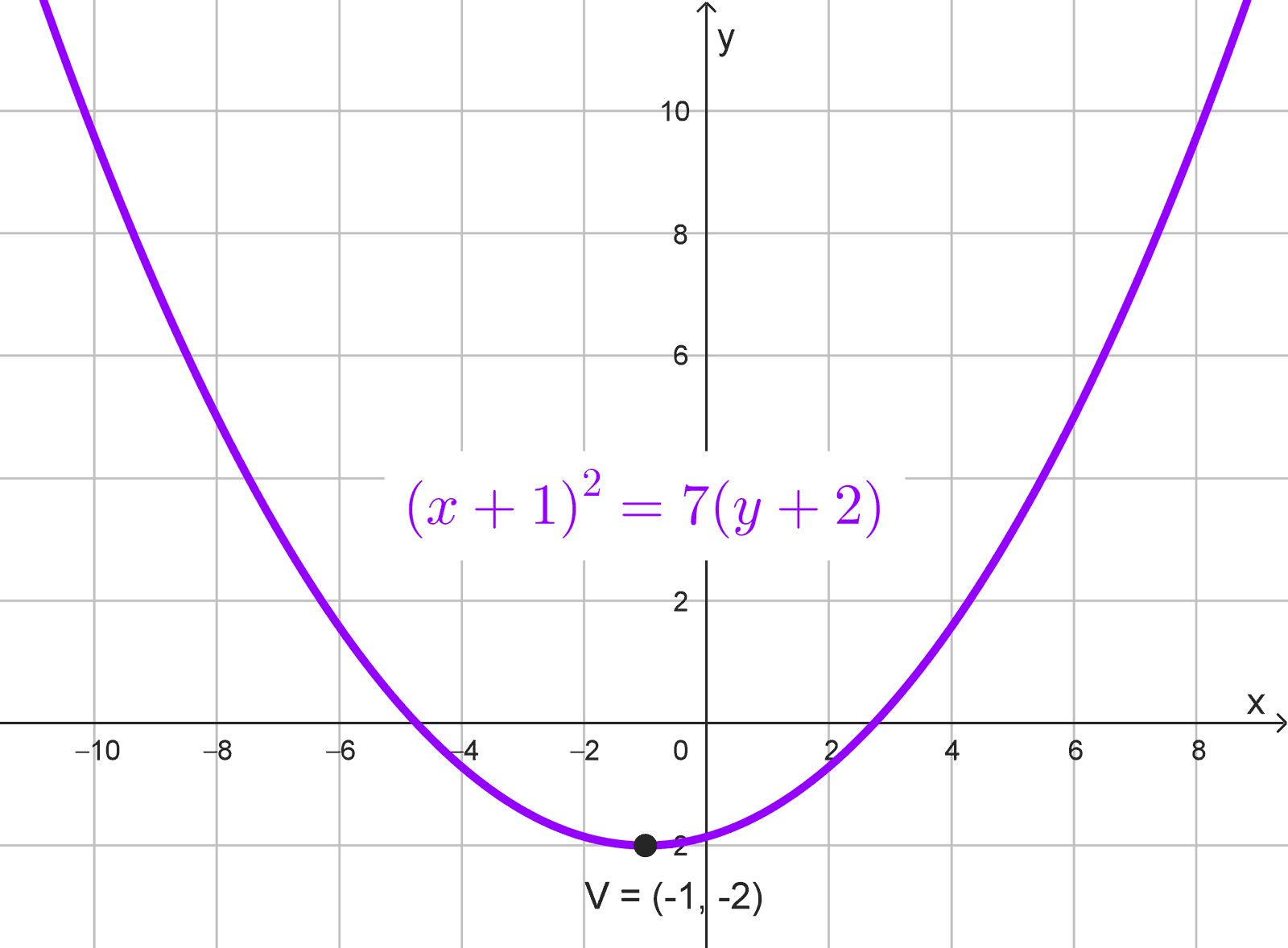
*(x+1)^2=7(y+2)*
*-8 (y-4)=(x+3)^2*
*(x+2)^2=-6y*

Gráfica de la parábola vertical del ejemplo 1 — Gráfica de la parábola 1

Gráfica de la parábola vertical del ejemplo 2 — Gráfica de la parábola 2

Gráfica de la parábola vertical del ejemplo 3 — Gráfica de la parábola 3

Gráfica de la parábola vertical del ejemplo 4 — Gráfica de la parábola 4

Ecuación general

La ecuación general de una parábola vertical es:

Ax² + Dx + Ey + F = 0

A diferencia de una parábola horizontal, la variable elevada al cuadrado es x.

Se puede llegar a esta forma a partir de la ecuación canónica:

*(x-h)^2=4p (y-k)*

*x^2-2hx+h^2=4py-4pk*

*x^2-2hx+h^2-4py+4pk=0*

*x^2-2hx-4py+(h^2+4pk)=0*

donde se ve que:

*A=1*
*D=-2h*
*E=-4p*
*F=h^2+4pk*

Ejemplos

Las siguientes son ecuaciones generales de parábolas verticales:

*x^2+4x-6y+4=0*
*-4y+x^2+28=0*
*x^2-2x+8y+25=0*
*y=2x^2-6x+3*

Relación con la función cuadrática

Las parábolas verticales son funciones cuadráticas, esto es porque tienen una ecuación que puede desarrollarse para despejar la variable y:

*(x-h)^2=4p(y-k)*

*x^2-2hx+h^2=4p(y-k)*

*\dfrac{x^2-2hx+h^2}{4p}=y-k*

*y=\dfrac{x^2-2hx+h^2}{4p}+k*

*y=\dfrac{1}{4p}x^2-\dfrac{2h}{4p}x+\dfrac{h^2}{4p}+k*

*y=\left(\dfrac{1}{4p}\right)x^2+\left(-\dfrac{h}{2p}\right)x+\left(\dfrac{h^2}{4p}+k\right)*

Aquí hacemos:

*a=\dfrac{1}{4p}*
*b=-\dfrac{h}{2p}*
*c=\dfrac{h^2}{4p}+k*

Entonces, una parábola vertical puede expresarse como:

*y=ax^2+bx+c*

Esta no es otra cosa que una función de segundo grado, también llamada función cuadrática, donde la variable independiente es x y la variable dependiente es y. Otra forma de expresarlo, con notación de funciones, es:

*f(x)=ax^2+bx+c*

Recordemos que esto no ocurre si el eje de simetría es horizontal, pues las parábolas horizontales no son funciones por el hecho de no cumplir el postulado de unicidad.

Al estudiar las funciones cuadráticas nos interesan las coordenadas del vértice y los cortes con los ejes cartesianos. El vértice (h, k) es un máximo o mínimo de la función *f(x)=ax^2+bx+c* y se puede determinar con la siguiente fórmula:

*h=\dfrac{-b}{2a}*

*k=f(h)*

El corte con el eje y se da en *f(0)=c* y es único. Los cortes con el eje x pueden ser hasta dos o no existir ninguno, los valores de x donde *f(x)=0* se llaman raíces. Las raíces de la función pueden obtenerse con la fórmula de Bhaskara:

*x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}*

Bibliografía

Engler, A. y otros. (2020). Geometría Analítica. Universidad Nacional del Litoral.
Lehmann, C. (1989). Geometría Analítica. Limusa.
Leithold. L. (1992). Álgebra y Trigonometría con Geometría Analítica. Oxford University Press.
Sullivan, M. (2006). Álgebra y Trigonometría. Pearson Educación.
Swokowski, E. y Cole, J. (2009). Álgebra y Trigonometría con Geometría Analítica. Cengage Learning.