
¿Cómo saber cuándo una parábola es horizontal o vertical?
Para saber si una parábola es horizontal o vertical hay que mirar qué variable está elevada al cuadrado en la ecuación, ya sea la canónica o la general:
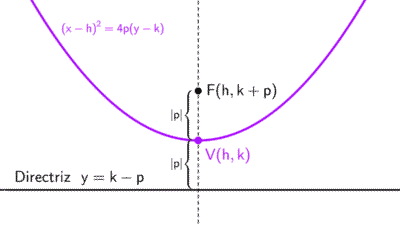
- Si la variable x aparece elevada al cuadrado, la parábola es vertical.
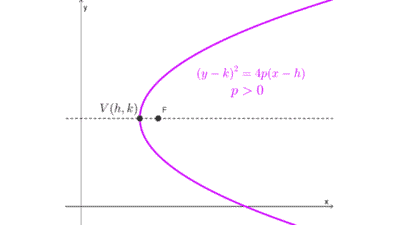
- Si la variable y está elevada al cuadrado, la parábola es horizontal.
Ejemplos
- La parábola *x^2-4x-4y+16=0* es vertical porque la variable x aparece elevada al cuadrado.
- La parábola *(y-5)^2=12(x-4)* es horizontal porque la variable y está elevada a la segunda potencia.
La variable elevada al cuadrado nos dice a cuál eje cartesiano es paralela la directriz. Por otro lado, la variable que no está elevada al cuadrado nos dice a qué eje cartesiano es paralelo el eje de simetría de la parábola.
Una vez que sabemos la orientación de la parábola también interesa saber hacia dónde abren sus ramas, esto lo podemos saber encontrando la forma canónica y mirando el signo de p o despejando la variable que no está al cuadrado y fijándonos en el signo del coeficiente principal. A continuación veremos unos ejemplos.
Importante: en este artículo nos enfocamos solo en determinar la orientación de una parábola. Si no estás familiarizado con los fundamentos de esta cónica, te sugiero leer primero el artículo general donde los desarrollamos a fondo:
Ejercicios resueltos
Indicar si las siguientes parábolas son horizontales o verticales y hacia donde abren.
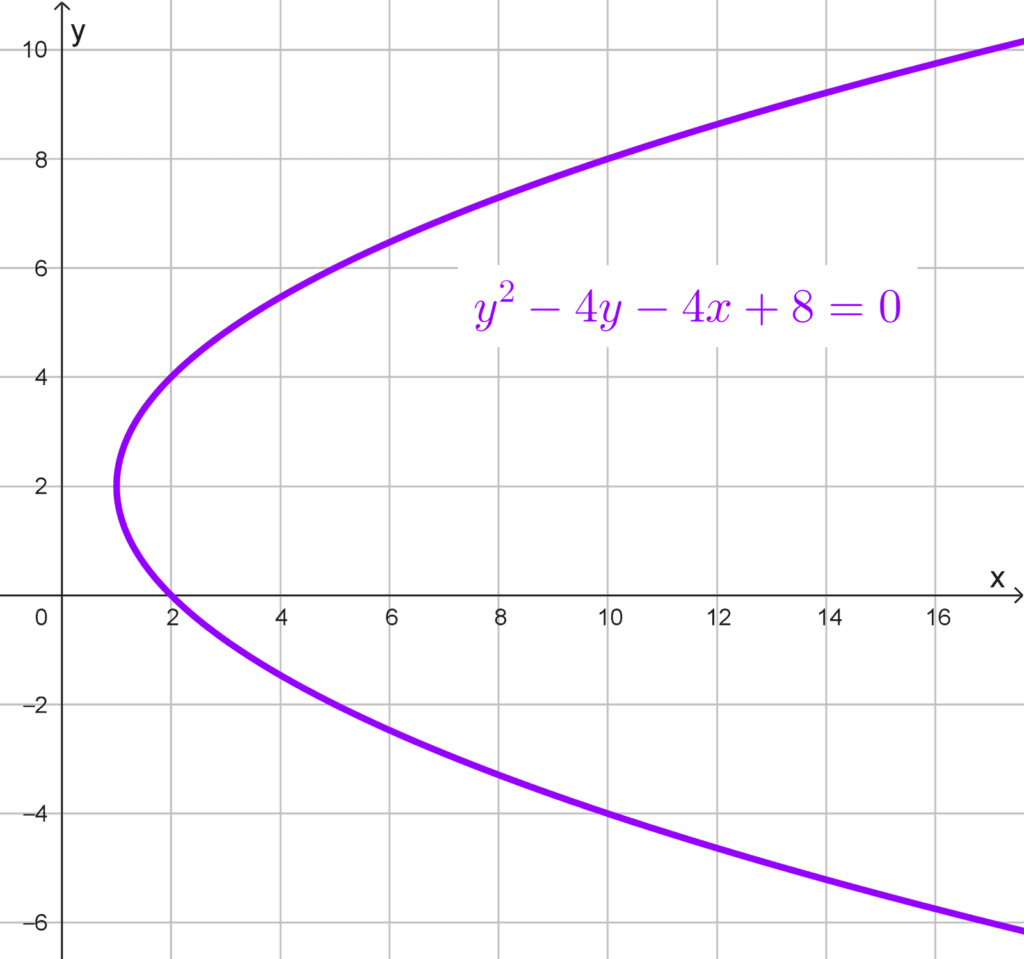
- *y^2-4y-4x+8=0*
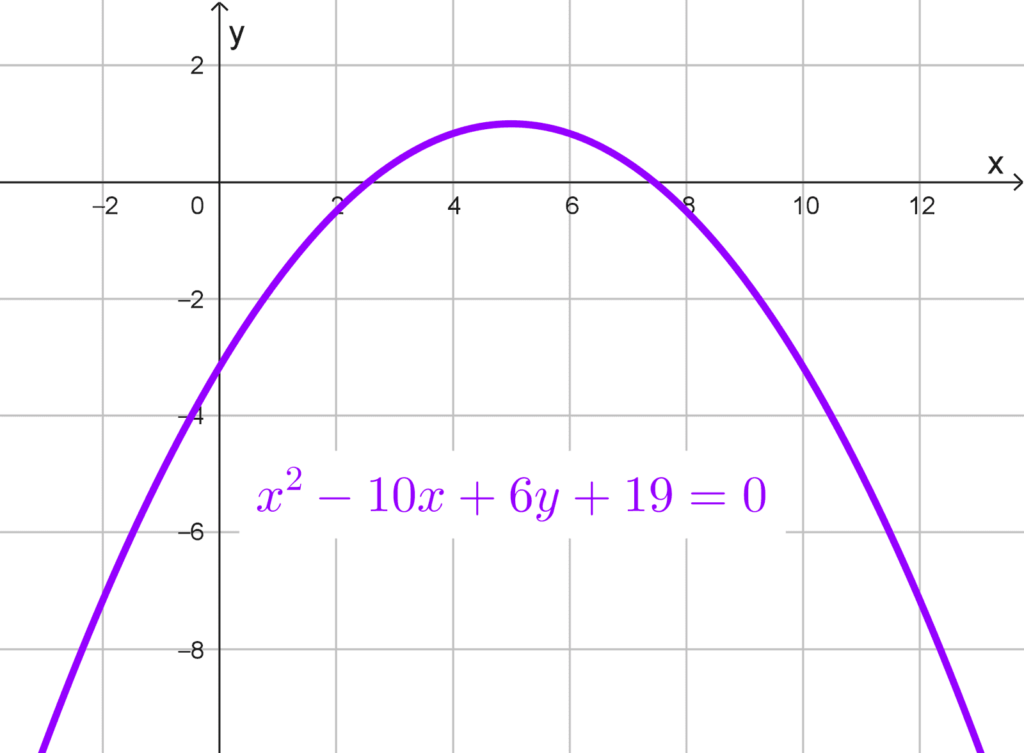
- *x^2-10x+6y+19=0*
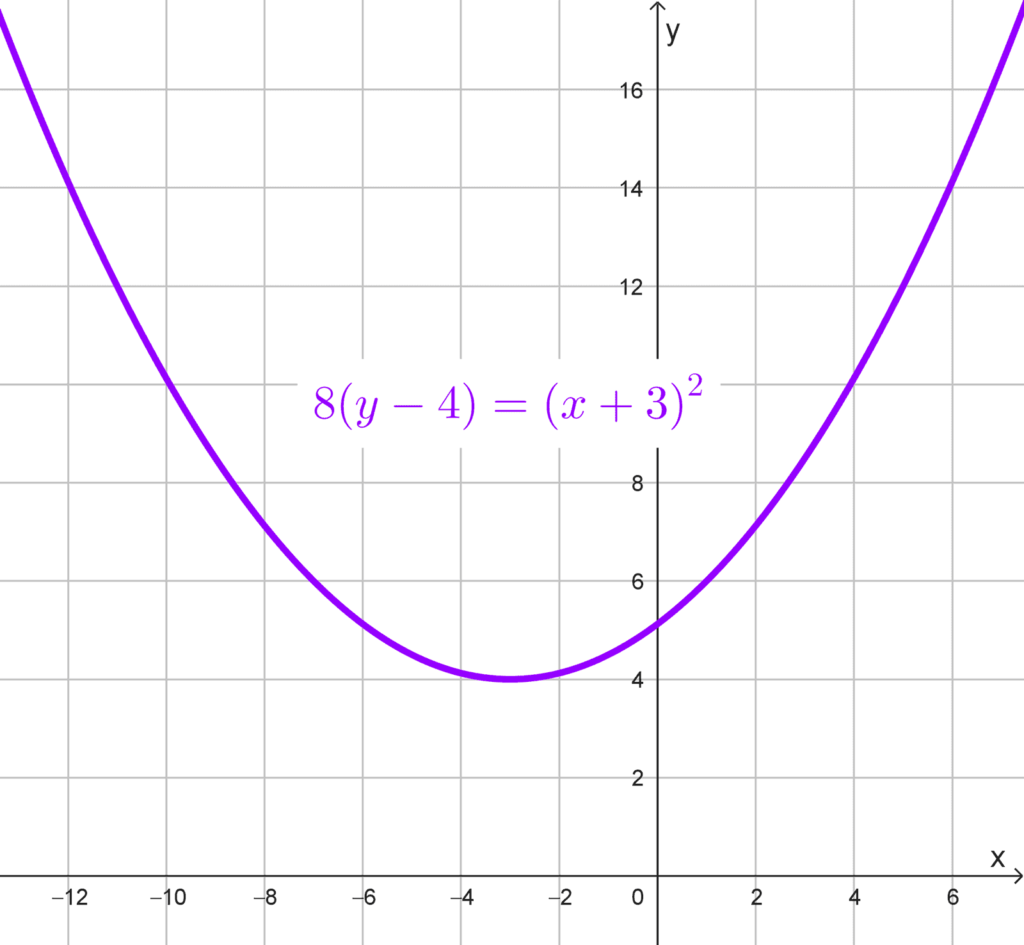
- *8(y-4)=(x+3)^2*
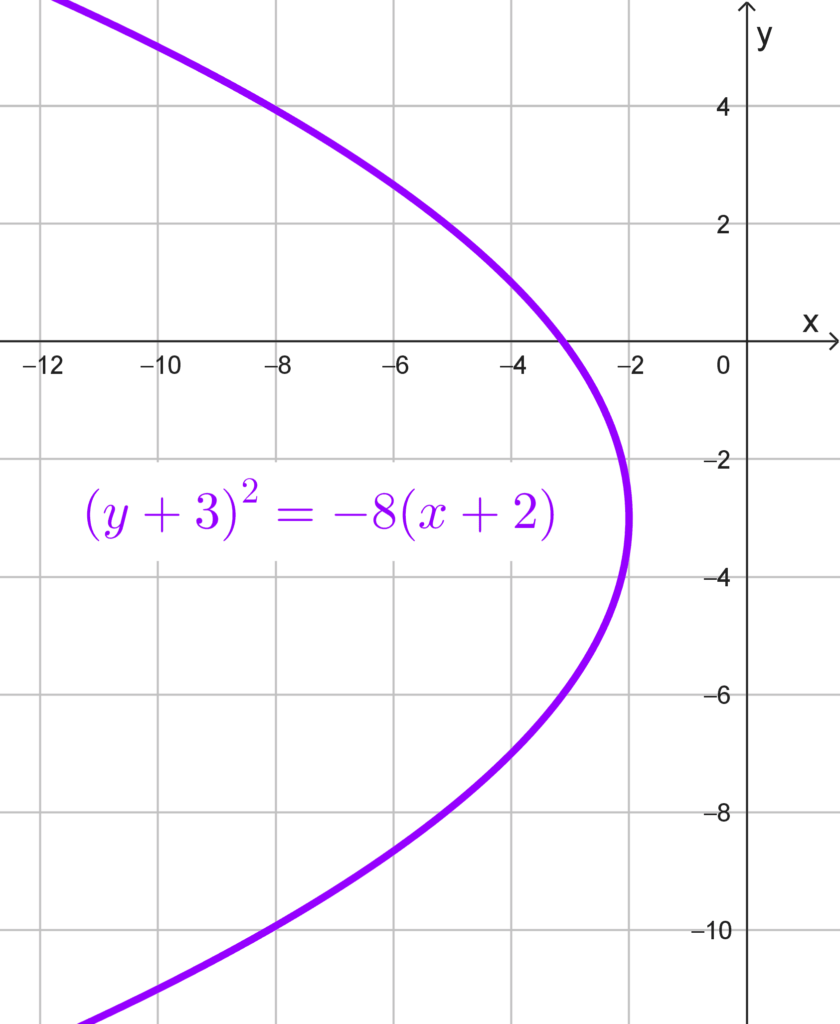
- *(y+3)^2=-8(x+2)*
- *-6x+x^2+10y+19=0*
Solución 1
La ecuación dada es: *y^2-4y-4x+8=0.* Como la variable “y” está elevada al cuadrado, podemos decir que se trata de una parábola horizontal.
Para averiguar si abre hacia la izquierda o la derecha tenemos dos caminos: encontrar la ecuación canónica y fijarnos en el signo del parámetro p (positivo para derecha y negativo para izquierda) o despejar la variable que no está elevada al cuadrado y mirar el signo del coeficiente principal.
Hallar la forma canónica requiere completar los cuadrados, así que seguiremos el segundo camino. La variable que no está elevada al cuadrado es x, así que la despejamos en la ecuación:
*y^2-4y-4x+8=0*
Aislamos el término con x a un lado de la ecuación:
*-4x=-y^2+4y-8*
Dividimos toda la ecuación entre -4 para despejar x:
*x=\dfrac{-y^2}{-4}+\dfrac{4y}{-4}-\dfrac{8}{-4}*
Simplificamos:
*x=\dfrac{1}{4}y^2-y+2*
El coeficiente principal es el número que multiplica a y2, en este caso es 1/4. Como se trata de un número positivo, la parábola abre hacia la derecha.
Solución 2
La ecuación proporcionada es: *x^2-10x+6y+19=0.* Observamos que la variable x está elevada al cuadrado, lo cual nos indica que se trata de una parábola vertical.
Para determinar si abre hacia arriba o hacia abajo, podemos optar por dos métodos: encontrar la ecuación canónica y analizar el signo del parámetro p (positivo para arriba y negativo para abajo), o despejar la variable que no está elevada al cuadrado y examinar el coeficiente principal.
En este caso, despejaremos la variable *y,* ya que no está elevada al cuadrado. Partiendo de la ecuación original:
*x^2-10x+6y+19=0*
Aislamos los términos en *x* y el término independiente:
*6y=-x^2+10x-19*
Dividimos toda la ecuación por 6 para despejar *y:*
*y=-\dfrac{1}{6}x^2+\dfrac{10}{6}x-\dfrac{19}{6}*
Simplificamos los coeficientes:
*y=-\dfrac{1}{6}x^2+\dfrac{5}{3}x-\dfrac{19}{6}*
El coeficiente principal es el número que multiplica a x2, que en este caso es -1/6. Dado que es negativo, concluimos que la parábola abre hacia abajo.
De manera alternativa, si completamos el cuadrado para obtener la forma canónica, partimos de la ecuación original:
*x^2-10x=-6y-19*
Completamos el cuadrado en *x:*
*x^2-10x+25=-6y-19+25*
*(x-5)^2=-6y+6*
Factorizamos el lado derecho:
*(x-5)^2=-6(y-1)*
Esta es la forma canónica *(x-h)^2=4p(y-k),* donde *4p=-6→p=-6/4=-3/2.* Como p es negativo, la parábola abre hacia abajo, confirmando nuestro resultado anterior.
Solución 3
Analizando la ecuación dada *8 (y-4)=(x+3)^2,* observamos que está escrita en una forma que se asemeja a la ecuación canónica de una parábola. Primero, reescribimos la ecuación en su forma estándar con el término cuadrático al lado izquierdo:
*(x+3)^2=8(y-4)*
Podemos identificar que corresponde a una parábola vertical, ya que la variable x está elevada al cuadrado. La ecuación está en la forma *(x-h)^2=4p (y-k),* donde *4p=8→p=2* es positivo, por tanto la parábola abre hacia arriba.
Solución 4
La ecuación dada *(y+3)^2=-8 (x+2)* ya está en su forma canónica, la cual corresponde a una parábola horizontal porque la variable y está al cuadrado. La estructura general de esta forma es *(y-k)^2=4p (x-h),* donde *(h, k)* es el vértice. Dado que *4p=-8→p=-2* es negativo, la parábola se abre hacia la izquierda.
Solución 5
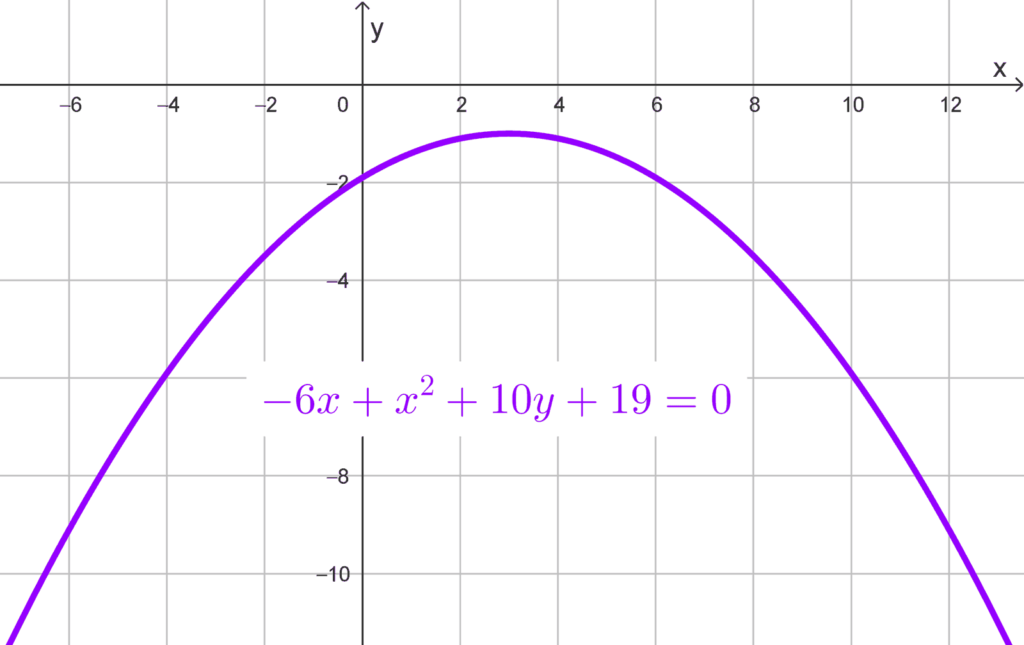
Analizamos la ecuación dada: *-6x+x^2+10y+19=0*
Como la variable x está elevada al cuadrado, se trata de una parábola vertical (abre hacia arriba o hacia abajo). Para determinar su dirección, podemos despejar y o completar el cuadrado en x. Usaremos el primer método.
Aislamos los términos en y:
*10y=-x^2+6x-19*
Dividimos toda la ecuación entre 10:
*y=-\dfrac{1}{10}x^2+\dfrac{6}{10}x-\dfrac{19}{10}*
Simplificamos:
*y=-\dfrac{1}{10}x^2+\dfrac{3}{5}x-\dfrac{19}{10}*
El coeficiente principal es -1/10, que es negativo, lo que indica que la parábola abre hacia abajo.
Bibliografía
- Engler, A. y otros. (2020). Geometría Analítica. Universidad Nacional del Litoral.
- Lehmann, C. (1989). Geometría Analítica. Limusa.
- Leithold. L. (1992). Álgebra y Trigonometría con Geometría Analítica. Oxford University Press.
- Sullivan, M. (2006). Álgebra y Trigonometría. Pearson Educación.
- Swokowski, E. y Cole, J. (2009). Álgebra y Trigonometría con Geometría Analítica. Cengage Learning.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta





Otros artículos que pueden interesarte