Ejercicios de secciones cónicas
En este artículo veremos ejercicios de cónicas en Geometría Analítica resueltos paso a paso para todos los niveles educativos. Si aún no conoces la teoría de cada cónica te recomiendo revisar primero los siguientes artículos:

Índice
Ejercicios de cada cónica
Los siguientes artículos contienen ejercicios resueltos de cada sección cónica.
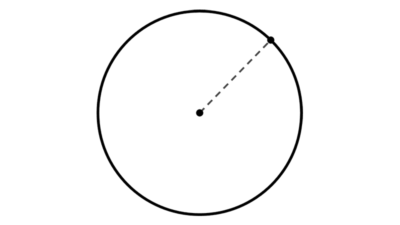
Circunferencia
Determinar la ecuación ordinaria de la circunferencia que cumple las condiciones dadas en cada caso y graficarla.
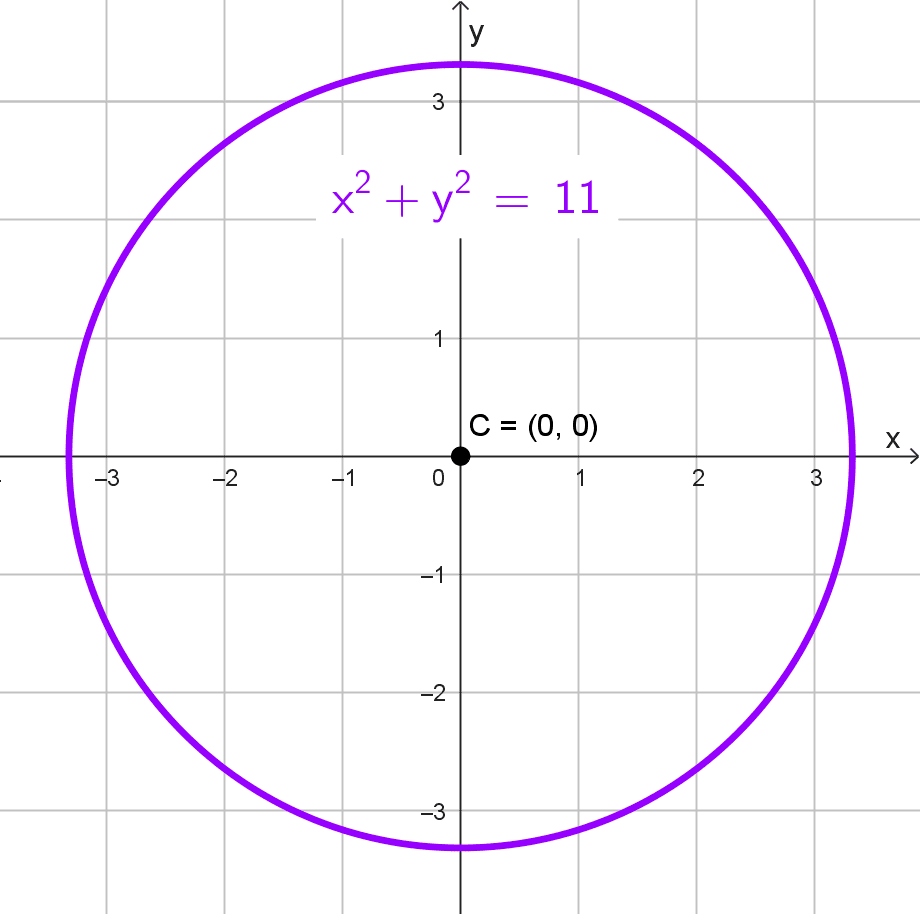
- Centro en el origen y diámetro 2√11.
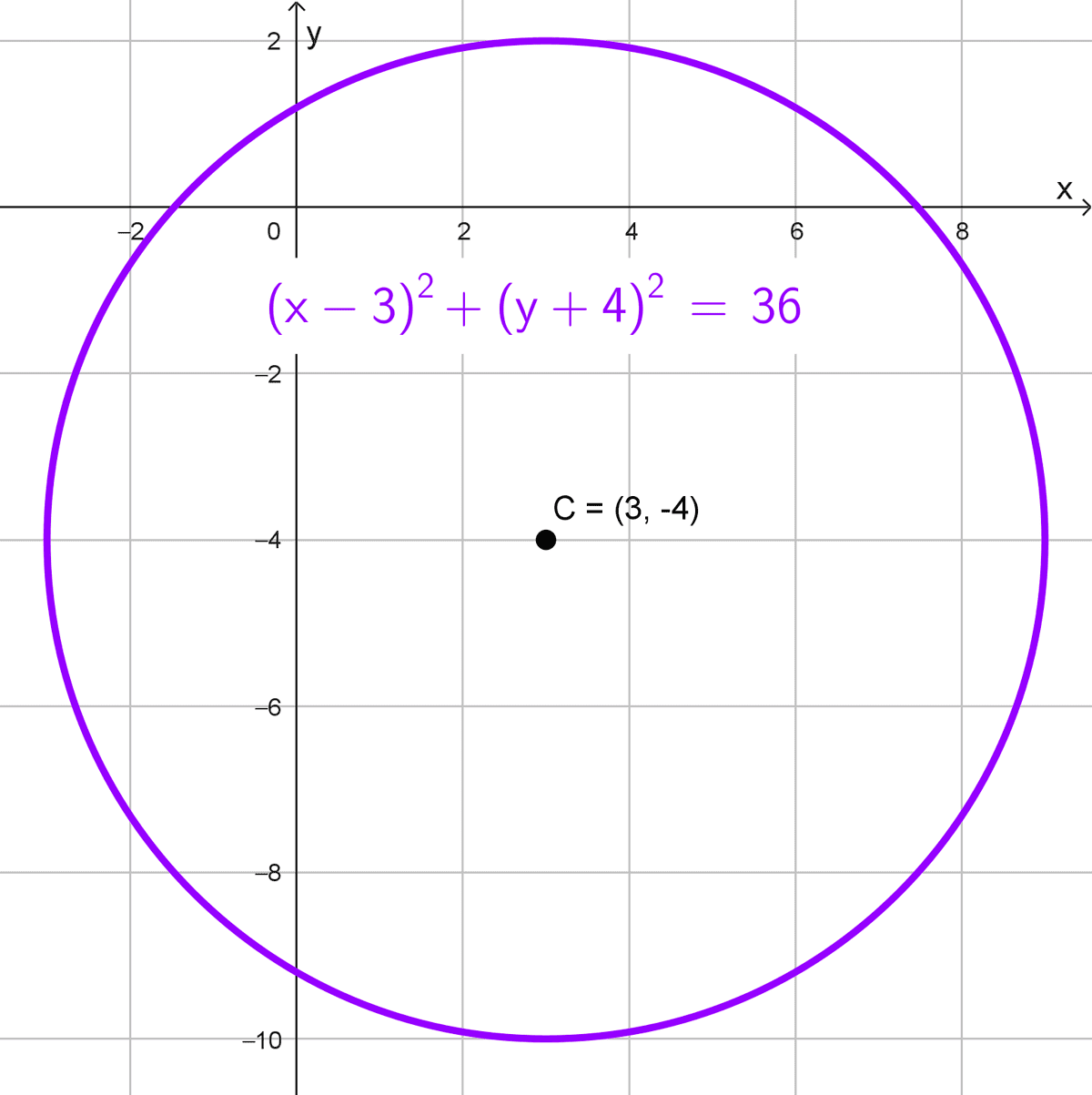
- Centro (3, -4), radio 6.
Soluciones
Solución 1
La ecuación ordinaria de una circunferencia con centro en el origen (0, 0) es \(x^2+y^2=r^2,\) donde r es el radio. Dado que el diámetro es \(2\sqrt{11},\) el radio es la mitad de este valor:
\(r=\dfrac{2\sqrt{11}}{2}=\sqrt{11}\)
Sustituyendo en la ecuación, obtenemos:
\(x^2+y^2=(\sqrt{11})^2 → x^2+y^2=11\)
Solución 2
Para una circunferencia con centro en \((h, k)=(3,-4)\) y radio \(r=6,\) la ecuación ordinaria es:
\((x-h)^2+(y-k)^2=r^2\)
Reemplazando los valores dados:
\((x-3)^2+(y+4)^2=6^2\)
\((x-3)^2+(y+4)^2=36\)
Los ejercicios y soluciones fueron extraídos del artículo de ejercicios de circunferencia.
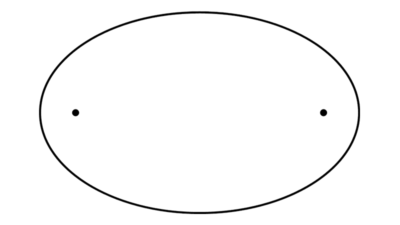
Elipse
A partir de los siguientes datos encontrar la ecuación de la elipse, todos sus elementos y graficarla.
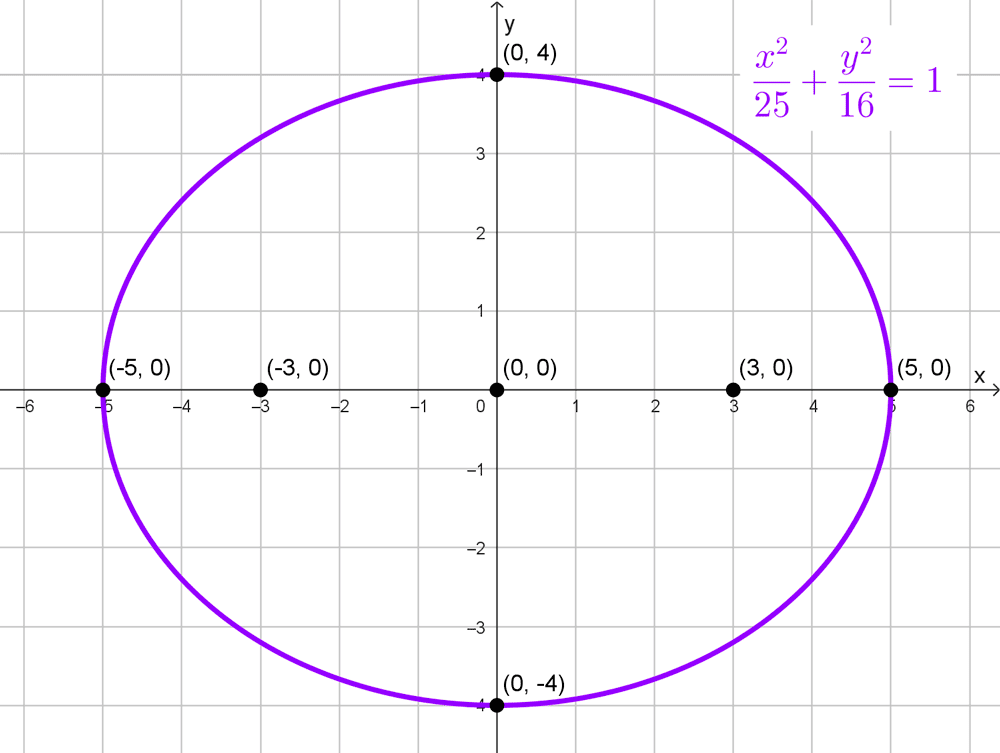
- Centro en el origen, foco en el punto (0, 3) y semieje mayor igual a 5.
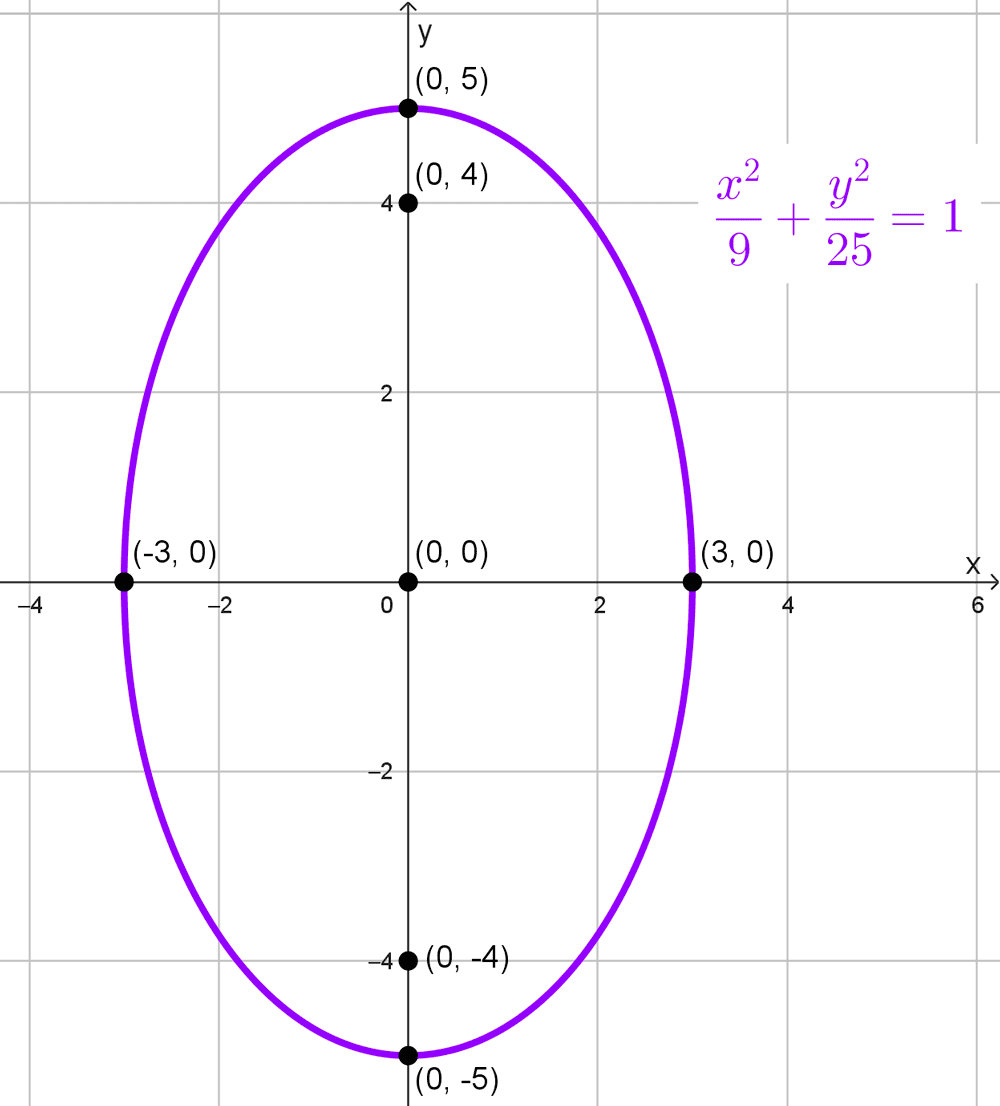
- Eje mayor sobre el eje y, tiene un vértice principal en (0, 5), un vértice secundario en (3, 0) y tiene centro en el origen de coordenadas.
Soluciones
Solución del ejercicio 1
Datos del problema:
- Centro: (0, 0)
- Foco: (0, 3)
- Semieje mayor: a = 5
Como el centro y el foco están sobre el eje x, la elipse es horizontal, lo que significa que tendrá una ecuación de la forma:
\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\)
Conocemos un semieje, obtendremos el otro mediante la relación fundamental. Primero necesitamos la semidistancia focal c, la cual es la distancia entre el centro y el foco, en este caso c = 3.
Ahora aplicamos la relación fundamental
\(c^2=a^2-b^2→b^2=a^2-c^2\)
Así:
\(b^2=5^2-3^2=25-9=16\)
Conociendo estos datos podemos armar la ecuación canónica de la elipse:
\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\)
\(\dfrac{x^2}{25}+\dfrac{y^2}{16}=1\)
Conociendo las medidas a, b y c se pueden obtener los demás elementos de la elipse.
Elementos de la elipse:
- Focos: (0, 3) y (0, -3)
- Centro: (0, 0)
- Semiejes: a = 5, b = 4
- Distancia focal: 2c = 6
- Vértices principales: (5, 0) y (-5, 0)
- Vértices secundarios: (0, 4) y (0, -4)
- Lado recto: \(L_R=\dfrac{2b^2}{a}=\dfrac{2\cdot 16}{5}=6,4\)
- Excentricidad: \(e=\dfrac{c}{a}=\dfrac{3}{5}=0,6\)
Solución del ejercicio 2
Datos iniciales:
- Centro: (0, 0)
- Vértice principal: (0, 5)
- Vértice secundario: (3, 0)
- Eje mayor sobre el eje y.
El eje mayor está sobre el eje y, por lo que la ecuación canónica de la elipse será:
\(\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1\)
donde a es el semieje mayor y b el semieje menor.
El vértice principal (0,5) nos indica que la longitud del semieje mayor es a = 5.
El vértice secundario (3,0) nos indica que la longitud del semieje menor es b = 3.
Usamos la relación fundamental para las elipses:
\(c^2=a^2-b^2\)
Sustituyendo los valores:
\(c^2=5^2-3^2=25-9=16\)
Por lo tanto:
\(c=\sqrt{16}=4\)
Con \(a^2=25\) y \(b^2=9,\) la ecuación canónica de la elipse será:
\(\dfrac{x^2}{9}+\dfrac{y^2}{25}=1\)
Elementos de la elipse:
- Centro: (0, 0)
- Focos: (0, 4) y (0, -4), ya que c = 4 y están sobre el eje y.
- Semiejes: a = 5, b = 3
- Vértices principales: (0, 5) y (0, -5)
- Vértices secundarios: (3, 0) y (-3, 0)
- Distancia focal: 2c = 8
- Lado recto: \(L_R=\dfrac{2b^2}{a}=\dfrac{2\cdot9}{5}=\dfrac{18}{5}=3,6\)
- Excentricidad: \(e=\dfrac{c}{a}=\dfrac{4}{5}=0,8 \)
Los ejercicios y soluciones fueron extraídos del artículo de ejercicios de elipse.
Hipérbola
Determinar las ecuaciones de las hipérbolas que cumplen las siguientes características, todos sus elementos y graficarlas.
- C(4, -1); foco (7, -1); vértice (6, -1).
- Focos en (3, 7) y (7, 7), vértice en (6, 7).
Solución del problema 1
Solución del problema 1
Datos proporcionados:
- Centro de la hipérbola: C (4, -1)
- Foco: (7, -1)
- Vértice: (6, -1)
Observamos que tanto el centro, el foco y el vértice tienen la misma coordenada y, lo que indica que la hipérbola está orientada horizontalmente. Por lo tanto, la ecuación canónica de la hipérbola es:
\(\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1\)
donde (h, k) es el centro de la hipérbola.
El centro es C (4, -1), por lo que \(h=4\) y \(k=-1.\)
La distancia entre el centro y el vértice es a. El vértice es (6, -1), entonces:
\(a=6-4=2\)
La distancia entre el centro y el foco es c. El foco es (7, -1), entonces:
\(c=7-4=3\)
Para una hipérbola, se cumple que:
\(c^2=a^2+b^2\)
Sustituyendo los valores conocidos:
\(3^2=2^2+b^2 → 9=4+b^2 → b^2=5 → b=\sqrt{5}\)
Sustituyendo los valores de h, k, a y b en la ecuación:
\(\dfrac{(x-4)^2}{4}-\dfrac{(y+1)^2}{5}=1\)
Para una hipérbola horizontal, las ecuaciones de las asíntotas son:
\(y-k=\pm \dfrac{b}{a}(x-h)\)
Sustituyendo los valores conocidos:
\(y+1=\pm \dfrac{\sqrt{5}}{2}(x-4)\)
La excentricidad e de una hipérbola se calcula como:
\(e=\dfrac{c}{a}\)
Sustituyendo los valores conocidos:
\(e=\dfrac{3}{2}=1,5\)
El lado recto LR de una hipérbola se calcula como:
\(L_R=\dfrac{2b^2}{a}\)
Sustituyendo los valores conocidos:
\(L_R=\dfrac{2 \cdot 5}{2}=5\)
Elementos de la hipérbola:
- Centro: (4, -1)
- Focos: (7, -1) y (1, -1)
- Vértices: (6, -1) y (2, -1)
- Semieje transversal: \(a=2\)
- Semieje conjugado: \(b=\sqrt{5}\)
- Asíntotas: \(y+1=\pm \dfrac{\sqrt{5}}{2}(x-4)\)
- Excentricidad: \(e=1, 5\)
- Lado recto: \(L_R=5\)
Ecuación: \(\dfrac{(x-4)^2}{4}-\dfrac{(y+1)^2}{5}=1\)
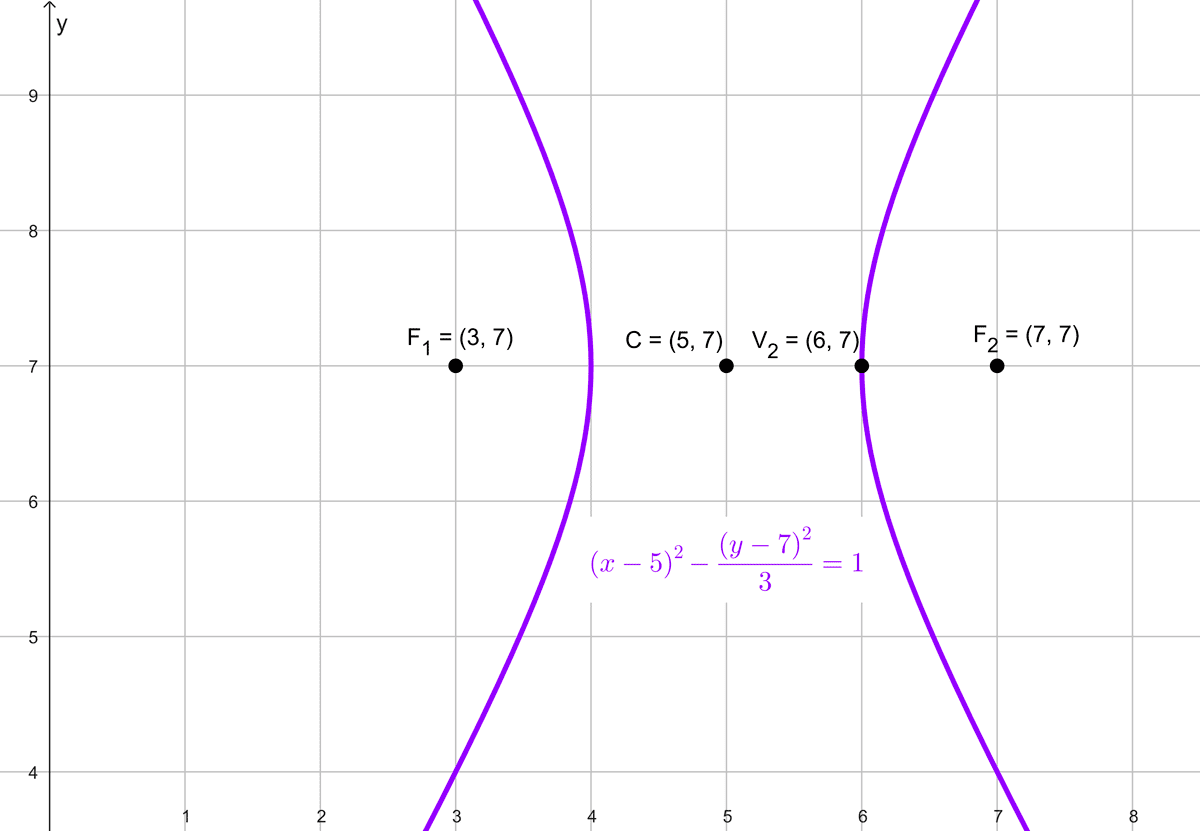
Solución del problema 2
Solución del problema 2
Datos proporcionados:
- Focos: (3, 7) y (7, 7).
- Vértice: (6, 7).
Observamos que tanto los focos como el vértice tienen la misma coordenada y = 7, lo que indica que la hipérbola está orientada horizontalmente. Por lo tanto, la ecuación reducida de la hipérbola es:
\(\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1\)
donde (h, k) es el centro de la hipérbola.
El centro de la hipérbola es el punto medio entre los focos. Dados los focos (3, 7) y (7, 7), el centro se calcula como:
\(h=\dfrac{3+7}{2}=5, \quad k=\dfrac{7+7}{2}=7\)
Por lo tanto, el centro es C (5, 7).
La distancia entre el centro y el vértice es a. El vértice es (6, 7), y el centro es (5, 7), entonces:
\(a=6-5=1\)
La distancia entre el centro y uno de los focos es c. El foco es (7, 7), y el centro es (5, 7), entonces:
\(c=7-5=2\)
Para una hipérbola, se cumple que \(c^2=a^2+b^2.\) Sustituyendo los valores conocidos:
\(2^2=1^2+b^2 → 4=1+b^2 → b^2=3 → b=\sqrt{3}\)
Sustituyendo los valores de \(h=5, k=7, a=1\) y \(b=\sqrt{3}\) en la ecuación, obtenemos:
\(\dfrac{(x-5)^2}{1}-\dfrac{(y-7)^2}{3}=1\)
Simplificando, la ecuación queda:
\((x-5)^2-\dfrac{(y-7)^2}{3}=1\)
Para una hipérbola horizontal, las ecuaciones de las asíntotas son:
\(y-k=\pm \dfrac{b}{a}(x-h)\)
Sustituyendo los valores conocidos:
\(y-7=\pm \dfrac{\sqrt{3}}{1}(x-5) → y-7=\pm \sqrt{3}(x-5)\)
La excentricidad de la hipérbola es:
\(e=\dfrac{c}{a}=\dfrac{2}{1}=2\)
El lado recto de la hipérbola es:
\(L_R=\dfrac{2b^2}{a}=\dfrac{2 \cdot 3}{1}=6\)
Elementos de la hipérbola:
- Centro: (5, 7)
- Focos: (7, 7) y (3, 7)
- Vértices: (6, 7) y (4, 7)
- Semieje transversal: \(a=1\)
- Semieje conjugado: \(b=\sqrt{3}\)
- Asíntotas: \(y-7=\pm \sqrt{3}(x-5)\)
- Excentricidad: \(e=2\)
- Lado recto: \(L_R=6\)
Ecuación: \((x-5)^2-\dfrac{(y-7)^2}{3}=1\)
Los ejercicios y soluciones fueron extraídos del artículo de ejercicios de hipérbola.
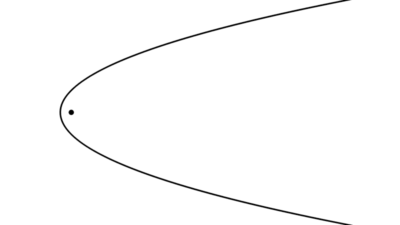
Parábola
Encontrar las ecuaciones de las parábolas con los datos dados y graficarlas:
- Vértice en (3, 1) y foco en (3, -1).
- V(-4, 3) y F(-1, 3).
Soluciones
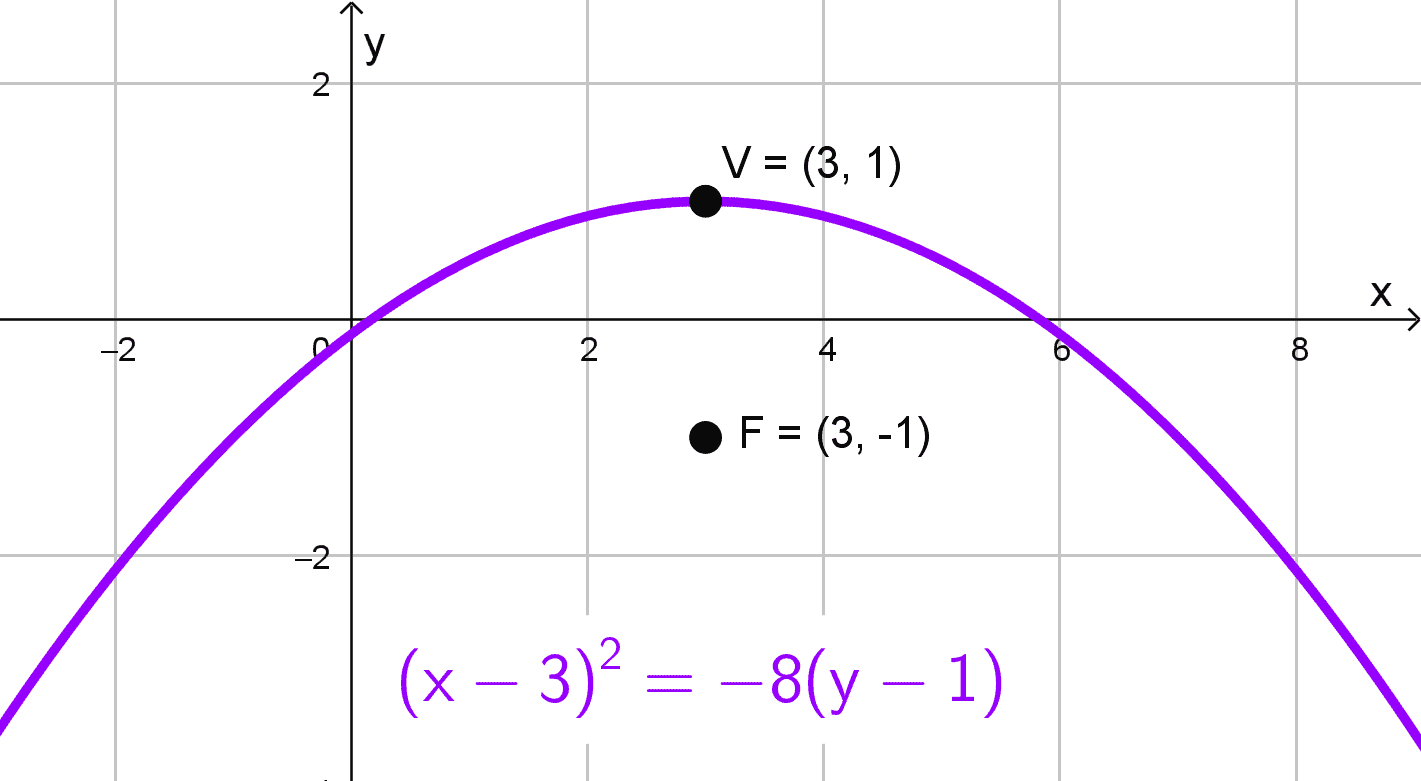
Solución 1
Como primer paso, identificamos las coordenadas del vértice V (3, 1) y del foco F (3, -1). Observamos que ambos puntos comparten la misma abscisa, lo que indica que el eje de la parábola es vertical. Calculamos el parámetro \(p\) como la diferencia entre las ordenadas del foco y el vértice:
\(p=-1-1=-2\)
Dado que \(p\) es negativo, la parábola abre hacia abajo. También nos damos cuenta de esto viendo que el foco está por debajo del vértice. Utilizando la forma canónica de una parábola con eje vertical:
\((x-h)^2=4p (y-k)\)
donde \((h, k)\) es el vértice, sustituimos los valores:
\((x-3)^2=4 (-2)(y-1)\)
Simplificando, obtenemos la ecuación:
\((x-3)^2=-8 (y-1)\)
Solución 2
En este caso, el vértice está en \(V (-4, 3)\) y el foco en \(F (-1, 3).\) Ambos puntos tienen la misma ordenada, por lo que el eje de la parábola es horizontal. Hallamos el parámetro \(p\) como la diferencia entre las abscisas del foco y el vértice:
\(p=-1-(-4)=3\)
Como \(p\) es positivo, la parábola abre hacia la derecha. La forma canónica para una parábola con eje horizontal es:
\((y-k)^2=4p (x-h)\)
Sustituyendo los valores conocidos:
\((y-3)^2=4 (3)(x-(-4))\)
Simplificando, llegamos a:
\((y-3)^2=12 (x+4)\)
Los ejercicios y soluciones fueron extraídos del artículo de ejercicios de parábola.
Identificar cónica a partir de ecuación general
Analizar las siguientes ecuaciones y determinar a qué tipo de cónica corresponden o si no representan ningún lugar geométrico real:
- \(x^2+y^2-2x-2y=0\)
- \(5x^2-2y^2-10x+8y-13=0\)
- \(y^2+9x+9=0\)
- \(x^2+y^2+4x+5=0\)
- \(16x^2+9y^2-64x-54y+1=0\)
- \(-7x^2+12y^2+28x+72y-4=0\)
- \(x^2+y^2-6x-8y+40=0\)
- \(x^2+6x-8y+41=0\)
Soluciones
Solución 1
Empezamos analizando la ecuación \(x^2+y^2-2x-2y=0.\) Observamos que contiene términos cuadráticos en \(x\) e \(y\) con coeficientes iguales para \(x^2\) y \(y^2,\) lo cual sugiere que podría tratarse de una circunferencia. Para confirmarlo, completamos cuadrados en ambas variables.
Agrupamos los términos en \(x\) e \(y:\)
\(x^2-2x+y^2-2y=0\)
Completamos cuadrados para \(x:\)
\(x^2-2x=(x^2-2x+1)-1=(x-1)^2-1\)
Hacemos lo mismo para \(y:\)
\(y^2-2y=(y^2-2y+1)-1=(y-1)^2-1\)
Sustituimos en la ecuación original:
\((x-1)^2-1+(y-1)^2-1=0\)
Simplificamos sumando las constantes:
\((x-1)^2+(y-1)^2-2=0 → (x-1)^2+(y-1)^2=2\)
Esta es la ecuación de una circunferencia con centro en \((1; 1)\) y radio \(\sqrt{2}.\) Por lo tanto, la cónica representada es una circunferencia real.
Solución 2
Analizamos la ecuación \(5x^2-2y^2-10x+8y-13=0.\) Observamos que contiene términos cuadráticos en \(x\) e \(y\) con coeficientes de signos opuestos (\(5\) y \(-2\)), lo cual sugiere que podría tratarse de una hipérbola. Para confirmarlo, completamos cuadrados en ambas variables.
Agrupamos los términos en \(x\) e \(y:\)
\(5x^2-10x-2y^2+8y=13\)
Factorizamos el coeficiente de \(x^2\) y \(y^2:\)
\(5(x^2-2x)-2(y^2-4y)=13\)
Completamos cuadrados para \(x:\)
\(x^2-2x=(x^2-2x+1)-1=(x-1)^2-1\)
Para \(y:\)
\(y^2-4y=(y^2-4y+4)-4=(y-2)^2-4\)
Sustituimos en la ecuación:
\(5[(x-1)^2-1]-2[(y-2)^2-4]=13\)
Simplificamos:
\(5(x-1)^2-5-2(y-2)^2+8=13\)
\(5(x-1)^2-2(y-2)^2+3=13\)
\(5(x-1)^2-2(y-2)^2=10\)
Dividimos toda la ecuación por 10 para obtener la forma estándar:
\(\dfrac{(x-1)^2}{2}-\dfrac{(y-2)^2}{5}=1\)
Esta es la ecuación de una hipérbola con centro en \((1; 2),\) eje transversal paralelo al eje \(x,\) donde \(a^2=2\) y \(b^2=5.\)
Solución 3
Examinamos la ecuación \(y^2+9x+9=0.\) Notamos que solo hay un término cuadrático (\(y^2\)) y un término lineal en \(x,\) lo cual indica que se trata de una parábola. Reorganizamos la ecuación para expresarla en su forma estándar:
\(y^2=-9x-9\)
\(y^2=-9(x+1)\)
Esta es la ecuación de una parábola que abre hacia la izquierda, con vértice en \((-1; 0)\) y parámetro \(p=-\dfrac{9}{4}.\)
Solución 4
Analizamos la ecuación \(x^2+y^2+4x+5=0.\) Observamos que contiene términos cuadráticos en \(x\) e \(y\) con coeficientes iguales (ambos 1), lo cual sugiere que podría tratarse de una circunferencia. Para verificarlo, completamos cuadrados en la variable \(x\) (ya que no hay término lineal en \(y\)):
Agrupamos los términos en \(x:\)
\(x^2+4x+y^2=-5\)
Completamos cuadrados para \(x:\)
\(x^2+4x=(x^2+4x+4)-4=(x+2)^2-4\)
Sustituimos en la ecuación:
\((x+2)^2-4+y^2=-5\)
\((x+2)^2+y^2=-1\)
Esta ecuación implica que la suma de dos cuadrados es igual a \(-1,\) lo cual es imposible en los números reales. Por lo tanto, la ecuación no representa ningún lugar geométrico real.
Solución 5
Estudiamos la ecuación \(16x^2+9y^2-64x-54y+1=0.\) Los coeficientes de \(x^2\) e \(y^2\) son positivos y diferentes, lo que sugiere una elipse. Completamos cuadrados para confirmar:
Agrupamos términos en \(x\) e \(y:\)
\(16x^2-64x+9y^2-54y=-1\)
Factorizamos los coeficientes:
\(16(x^2-4x)+9(y^2-6y)=-1\)
Completamos cuadrados para \(x:\)
\(x^2-4x=(x^2-4x+4)-4=(x-2)^2-4\)
Para \(y:\)
\(y^2-6y=(y^2-6y+9)-9=(y-3)^2-9\)
Sustituimos en la ecuación:
\(16[(x-2)^2-4]+9[(y-3)^2-9]=-1\)
\(16(x-2)^2-64+9(y-3)^2-81=-1\)
\(16(x-2)^2+9(y-3)^2-145=-1\)
\(16(x-2)^2+9(y-3)^2=144\)
Dividimos por 144 para obtener la forma estándar:
\(\dfrac{(x-2)^2}{9}+\dfrac{(y-3)^2}{16}=1\)
Esta es la ecuación de una elipse con centro en \((2; 3),\) semieje mayor \(a=4\) (paralelo al eje \(y\)) y semieje menor \(b=3.\)
Solución 6
Analizamos la ecuación \(-7x^2+12y^2+28x+72y-4=0.\) Los términos cuadráticos tienen coeficientes de signos opuestos, indicando una hipérbola. Completamos cuadrados:
Reorganizamos la ecuación:
\(-7x^2+28x+12y^2+72y=4\)
Factorizamos coeficientes:
\(-7(x^2-4x)+12(y^2+6y)=4\)
Completamos cuadrados para \(x:\)
\(x^2-4x=(x^2-4x+4)-4=(x-2)^2-4\)
Para \(y:\)
\(y^2+6y=(y^2+6y+9)-9=(y+3)^2-9\)
Sustituimos en la ecuación:
\(-7[(x-2)^2-4]+12[(y+3)^2-9]=4\)
\(-7(x-2)^2+28+12(y+3)^2-108=4\)
\(-7(x-2)^2+12(y+3)^2-80=4\)
\(-7(x-2)^2+12(y+3)^2=84\)
Dividimos por 84 y reorganizamos:
\(\dfrac{(y+3)^2}{7}-\dfrac{(x-2)^2}{12}=1\)
Esta es la ecuación de una hipérbola con centro en \((2;-3),\) eje transversal paralelo al eje \(y,\) donde \(a^2=7\) y \(b^2=12.\)
Solución 7
Estudiamos la ecuación \(x^2+y^2-6x-8y+40=0.\) Los términos cuadráticos tienen coeficientes iguales (1 para \(x^2\) e \(y^2\)), lo que indica una posible circunferencia. Completamos cuadrados en ambas variables:
Agrupamos términos en \(x\) e \(y:\)
\(x^2-6x+y^2-8y=-40\)
Completamos cuadrados para \(x:\)
\(x^2-6x=(x^2-6x+9)-9=(x-3)^2-9\)
Para \(y:\)
\(y^2-8y=(y^2-8y+16)-16=(y-4)^2-16\)
Sustituimos en la ecuación:
\((x-3)^2-9+(y-4)^2-16=-40\)
\((x-3)^2+(y-4)^2-25=-40\)
\((x-3)^2+(y-4)^2=-15\)
La suma de cuadrados es igual a un número negativo (-15), lo cual no tiene solución en los reales. Por lo tanto, esta ecuación no representa ningún lugar geométrico real.
Solución 8
Examinamos la ecuación \(x^2+6x-8y+41=0.\) Solo hay un término cuadrático (\(x^2\)) y un término lineal en \(y,\) lo que sugiere una parábola. Reorganizamos la ecuación:
\(x^2+6x=8y-41\)
Completamos cuadrados para \(x:\)
\(x^2+6x=(x^2+6x+9)-9=(x+3)^2-9\)
Sustituimos:
\((x+3)^2-9=8y-41\)
\((x+3)^2=8y-32\)
\((x+3)^2=8(y-4)\)
Esta es la ecuación de una parábola que abre hacia arriba, con vértice en \((-3; 4)\) y parámetro \(p=2.\)
Ejercicios de traslación y rotación
Estos artículos contienen explicaciones y ejercicios resueltos sobre traslación y rotación de secciones cónicas en el plano cartesiano.
Bibliografía
- Engler, A., Müller, D., Vrancken, S. y Hecklein, M. (2020). Geometría analítica. Universidad Nacional del Litoral.
- Fuller, G. y Tarwater, D. (1995). Geometría analítica (7.ª ed.). Pearson Educación.
- Lehmann, C. (1989). Geometría analítica. Limusa.
- Leithold. L. (1992). Álgebra y trigonometría con geometría analítica. Oxford University Press.
- Márquez, A., Vázquez, F., Ruiz, H., Villegas, M. y Figueroa, M. (2009). Geometría analítica. Prentice Hall.
- Raichman, S. y Totter, E. (2016). Geometría analítica para ciencias e ingeniería. Universidad Nacional de Cuyo.
- Sullivan, M. (2006). Álgebra y trigonometría. Pearson Educación.
- Swokowski, E. y Cole, J. (2009). Álgebra y trigonometría con geometría analítica. Cengage Learning.
¿Te ha servido este contenido? ¡Califícalo!
5,0 / 5 — 1 votos
CÓMO CITAR ESTE ARTÍCULO
Machado, D. (2025, 13 de julio). Ejercicios de secciones cónicas. Exponty. https://exponty.com/ejercicios-conicas
Deja una respuesta



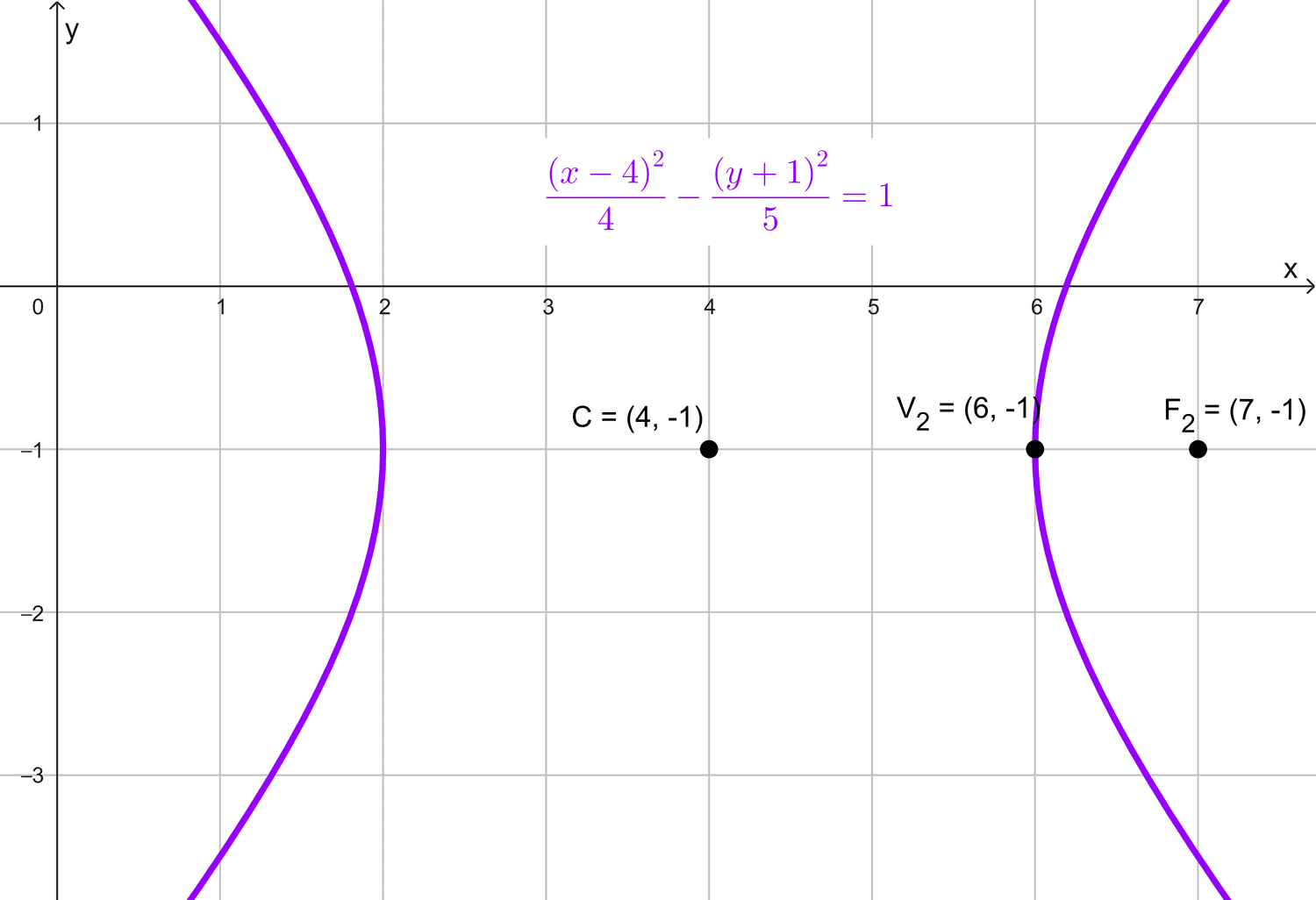
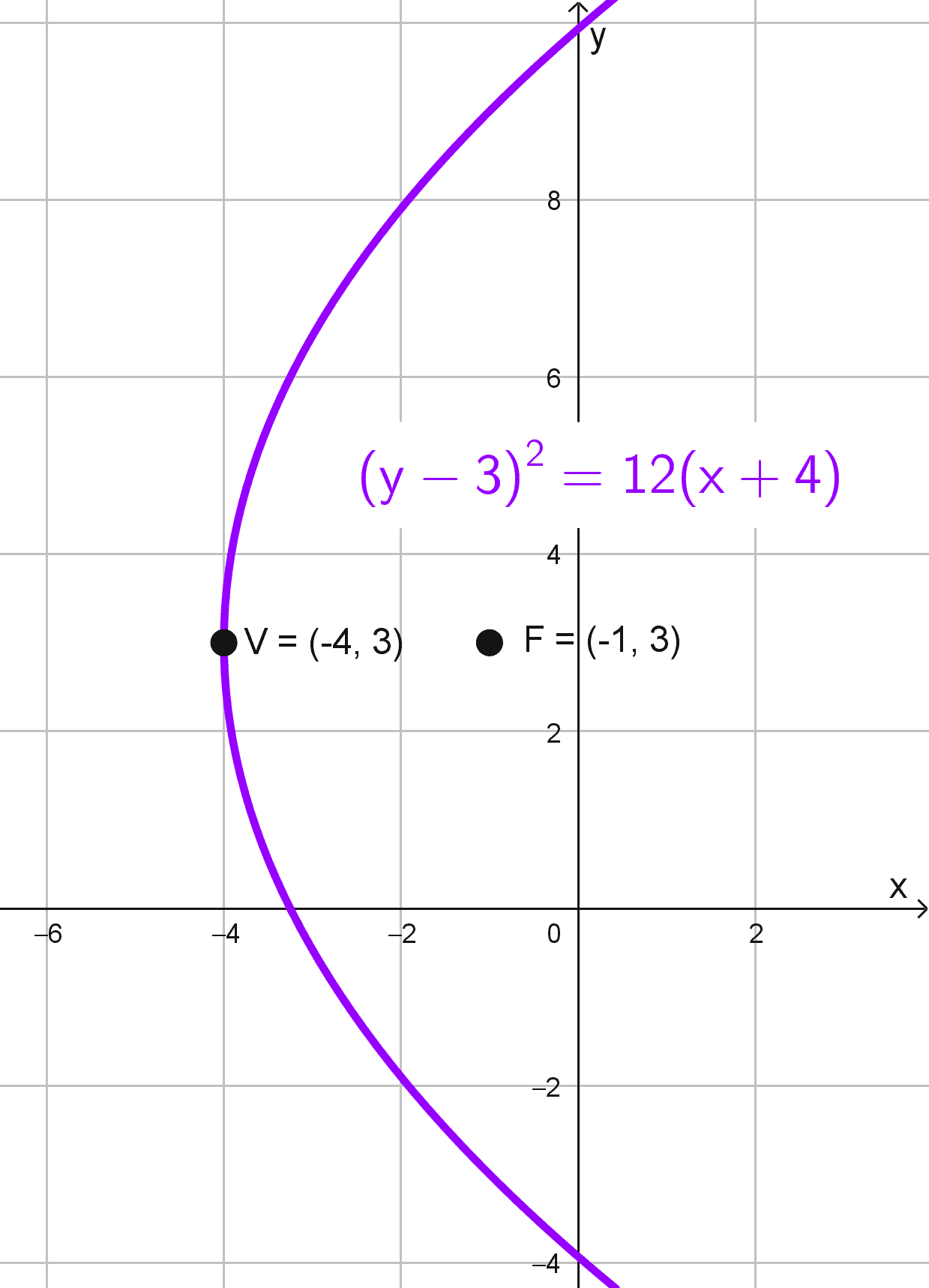
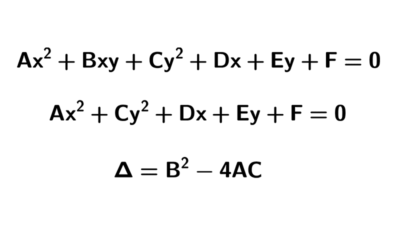

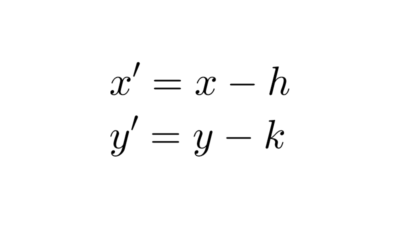
Otros artículos que pueden interesarte