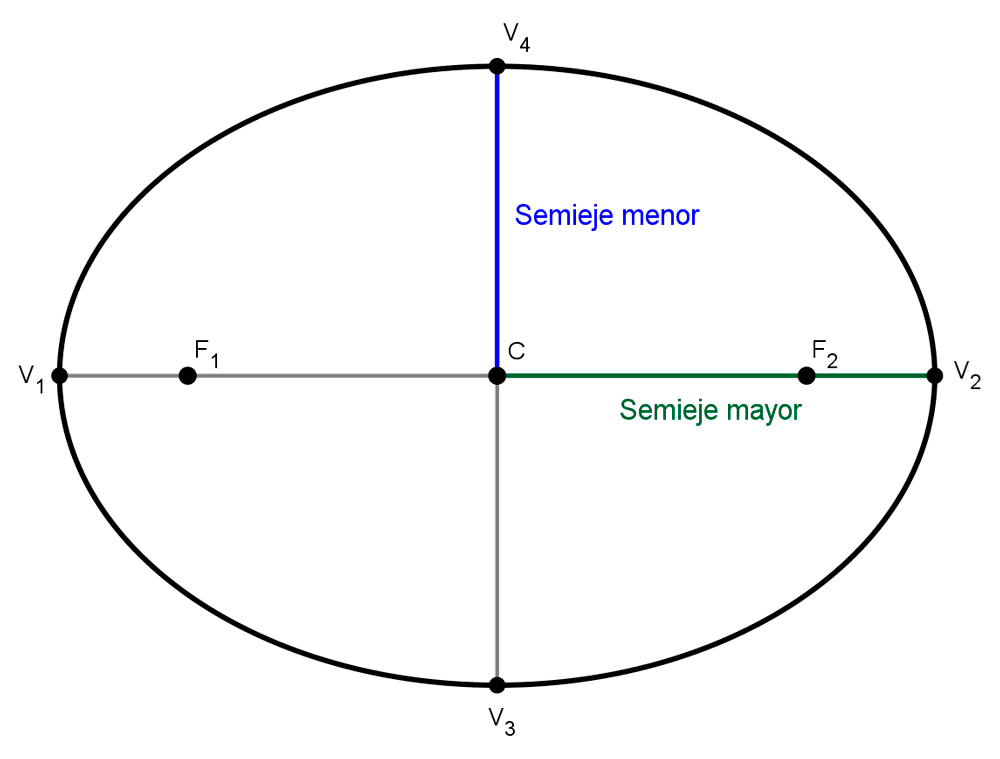
Ejes y semiejes de una elipse

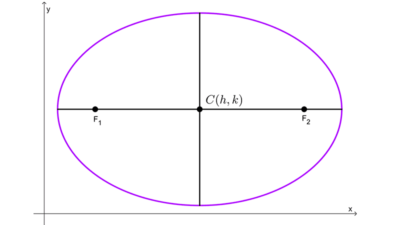
Los ejes de una elipse son dos segmentos que unen los vértices principales y los secundarios, pasando por el centro. Existen dos ejes principales: el eje mayor, que tiene como extremos a los vértices principales pasando por los focos y el centro; y el eje menor, que es perpendicular al eje mayor, tiene como extremos a los vértices secundarios y pasa por el centro. 

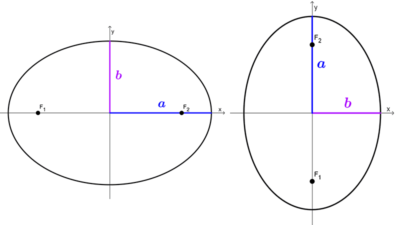
A la mitad del eje mayor se le llama semieje mayor y su longitud se simboliza con la letra "a"; de modo similar, a la mitad del eje menor se le llama semieje menor y su longitud se simboliza como "b". Por esto, el eje mayor mide 2a y el eje menor 2b.

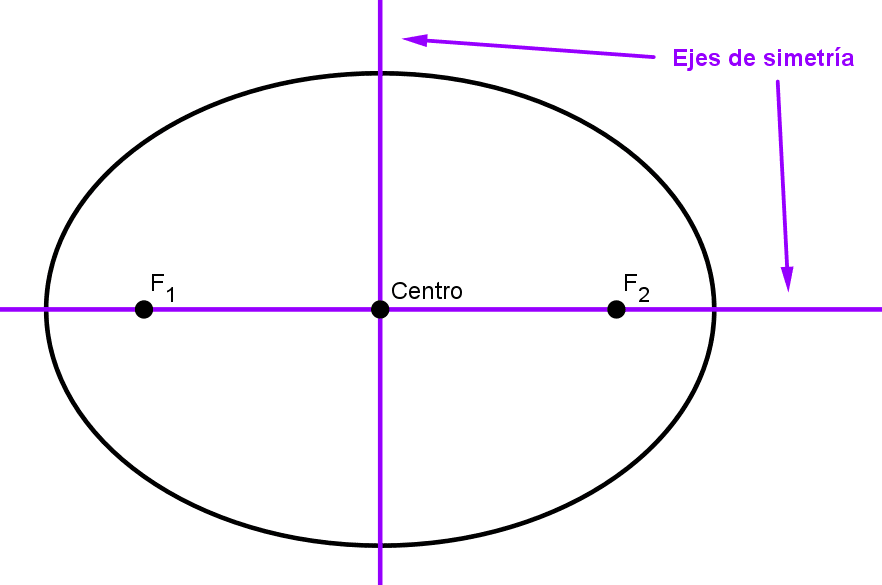
Dependiendo de la orientación del eje mayor, la elipse es horizontal, si el eje mayor es paralelo al eje x, o vertical, si el eje mayor es paralelo al eje y. El eje mayor también podría ser oblicuo, resultando en una elipse rotada, pero este caso no se tratará en este artículo.

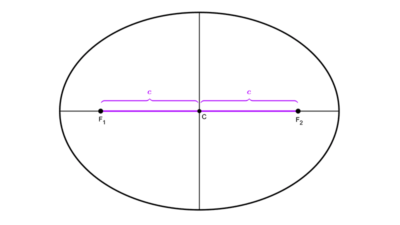
Existe una propiedad que relaciona a las longitudes de los semiejes con la semidistancia focal (distancia desde el centro hasta un foco), esta nos dice que el cuadrado de la semidistancia focal es igual a la diferencia entre los cuadrados de las longitudes de los semiejes y se expresa con la siguiente fórmula:

c² = a² - b²

Los semiejes pueden tener la misma longitud, en tal caso la elipse es una circunferencia y los semiejes pasan a ser radios de la misma. En este artículo trataremos los casos donde a > b. 

La elipse también tiene dos ejes de simetría, que son las rectas que contienen al eje mayor y al eje menor. Al eje de simetría que contiene al eje mayor también se le suele llamar eje focal, ya que contiene a los focos. 

A continuación, veremos ejemplos de cómo encontrar las longitudes de los ejes y semiejes a partir de la ecuación.

Cómo calcular los ejes de una elipse

Las longitudes de los semiejes aparecen en la ecuación canónica de la elipse elevados al cuadrado y como los denominadores de las variables.

Orientación	Ecuación canónica	Ejes y semiejes	Ejes de simetría
Elipse horizontal	*\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1*	El semieje mayor es a, el semieje menor es b. El eje mayor mide 2a y el eje menor 2b.	x = h y = k
Elipse vertical	*\dfrac{(x-h)^2}{b^2}+\dfrac{(y-k)^2}{a^2}=1*	El semieje mayor es a, el semieje menor es b. El eje mayor mide 2a y el eje menor 2b.	x = h y = k

El denominador más grande indica la longitud del semieje mayor, representado como a:

• Si el denominador más grande es el del término que tiene x, entonces el eje mayor es paralelo al eje x, resultado en una elipse horizontal.
• Si el denominador más grande es el del término que tiene y, entonces el eje mayor es paralelo al eje y, produciendo una elipse vertical.

De modo similar, el denominador más pequeño permite extraer la longitud del semieje menor, b. Para obtener cuánto miden los ejes, basta con multiplicar los valores de a y b por dos. 

Ejercicios resueltos

A continuación, resolvemos algunos ejercicios del cálculo de ejes y semiejes.

Ejercicio 1

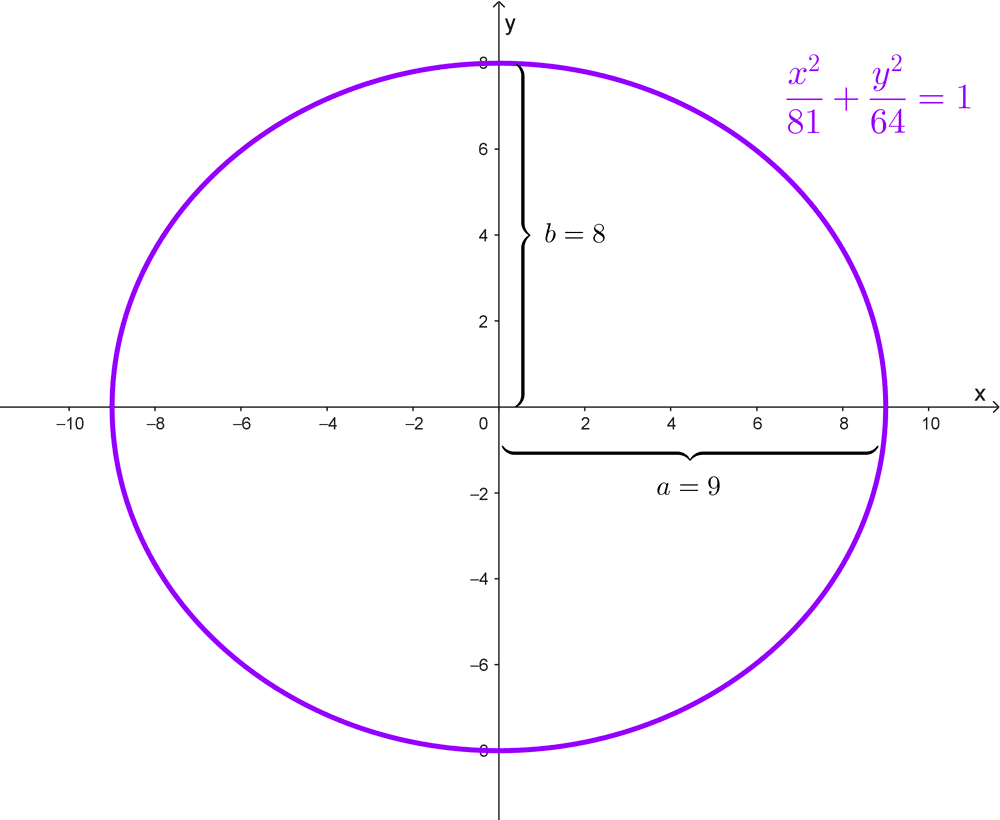
Dada la elipse *\dfrac{x^2}{81}+\dfrac{y^2}{64}=1* calcular sus ejes.

Solución: la ecuación está en forma canónica así que podemos extraer los datos necesarios.

El denominador más grande es 81, por tanto *a^2=81 → a=\sqrt{81}=9.*

El denominador más pequeño es 64, por tanto *b^2=64→b=\sqrt{64}=8.*

Tenemos entonces que el semieje mayor es a = 9 y el semieje menor es b = 8. Con estos datos obtenemos las longitudes de sus ejes multiplicando por dos:

• Eje mayor: *2a=2\cdot 9=18*
• Eje menor: *2b=2\cdot 8=16*

Ejercicio 2

Determinar los ejes principales de la elipse *\dfrac{(x-3)^2}{4}+\dfrac{(y+4)^2}{36}=1*

Solución: la ecuación está en forma canónica así que podemos extraer los datos que necesitamos.

*a^2=36→a=\sqrt{36}=6*

*b^2=4→b=\sqrt{4}=2*

El semieje mayor es a = 6 y el menor es b = 2, obtenemos los ejes multiplicando por dos:

• Eje mayor: *2a=2\cdot 6=12*
• Eje menor: *2b=2\cdot 2=4*

Si quisiéramos hallar los ejes de simetría, es suficiente con encontrar el centro y escribir las ecuaciones de las rectas. De la ecuación identificamos que el centro es (3, -4), por tanto los ejes de simetría son las siguientes rectas:

x = 3
y = -4

Ejercicio 3

Obtener los ejes de la elipse con ecuación *16x^2+25y^2=100*

Solución: la ecuación no está en forma canónica así que no se pueden extraer directamente los datos. Sin embargo, es posible manipular algebraicamente la ecuación para que tome la siguiente forma:

*\dfrac{x^2}{25/4}+\dfrac{y^2}{4}=1*

En esta forma sí podemos extraer los semiejes y con ellos los ejes:

*a^2=\dfrac{25}{4}→a=\sqrt{\dfrac{25}{4}}=\dfrac{5}{2}*

*b^2=4→b=\sqrt{4}=2*

Entonces:

• Eje mayor: *2a=2\cdot \dfrac{5}{2}=5*
• Eje menor: *2b=2\cdot 2=4*

Ejercicio 4

Hallar los ejes y semiejes de la elipse *2x^2+4x+7y^2-28y-40=0*

Solución: al igual que en el ejemplo anterior, la ecuación no está en forma canónica, sin embargo, se pueden completar los cuadrados para obtener una forma equivalente:

*\dfrac{(x+1)^2}{35}+\dfrac{(y-2)^2}{10}=1*

De aquí se saca que:

*a^2=35→a=\sqrt{35}*

*b^2=10→b=\sqrt{10}*

Por tanto:

• Eje mayor: *2a=2\sqrt{35}≈11,83*
• Eje menor: *2b=2\sqrt{10}≈6,32*

Bibliografía

• Engler, A. y otros. (2020). Geometría Analítica. Universidad Nacional del Litoral.
• Fuller, G. y Tarwater, D. (1995). Geometría Analítica (7ma edición). Pearson Educación.
• Lehmann, C. (1989). Geometría Analítica. Limusa.
• Leithold. L. (1992). Álgebra y Trigonometría con Geometría Analítica. Oxford University Press.
• Mora, W., y Figueroa, G. (2009). Cónicas. Revista Digital Matemática, Educación e Internet.
• Márquez, A. y otros. (2009). Geometría Analítica. Prentice Hall.
• Raichman, S. y Totter, E. (2016). Geometría Analítica para Ciencias e Ingeniería. Universidad Nacional de Cuyo.
• Sullivan, M. (2006). Álgebra y Trigonometría. Pearson Educación.
• Swokowski, E. y Cole, J. (2009). Álgebra y Trigonometría con Geometría Analítica. Cengage Learning.