Centro de la hipérbola

En este artículo explicamos qué es el centro de una hipérbola y cómo hallarlo dependiendo de los datos con los que se cuente.

¿Qué es el centro?

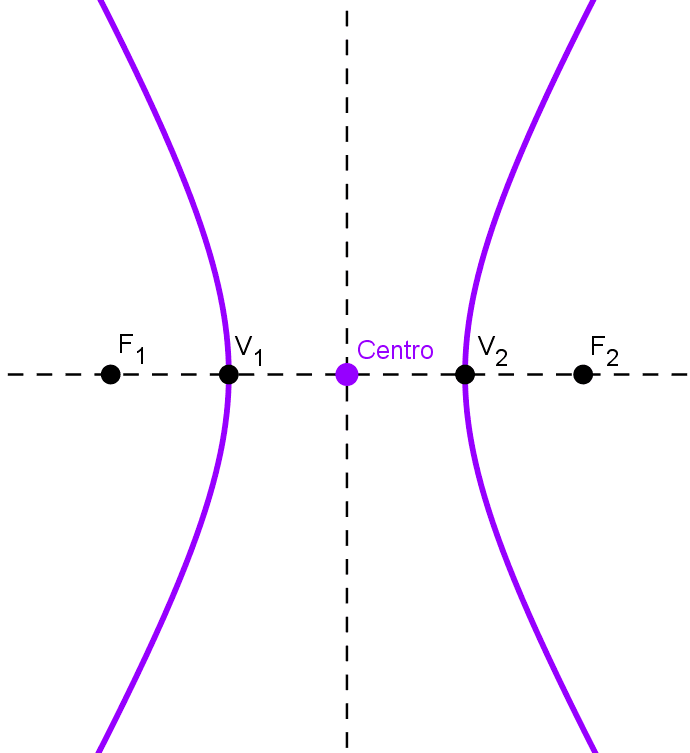
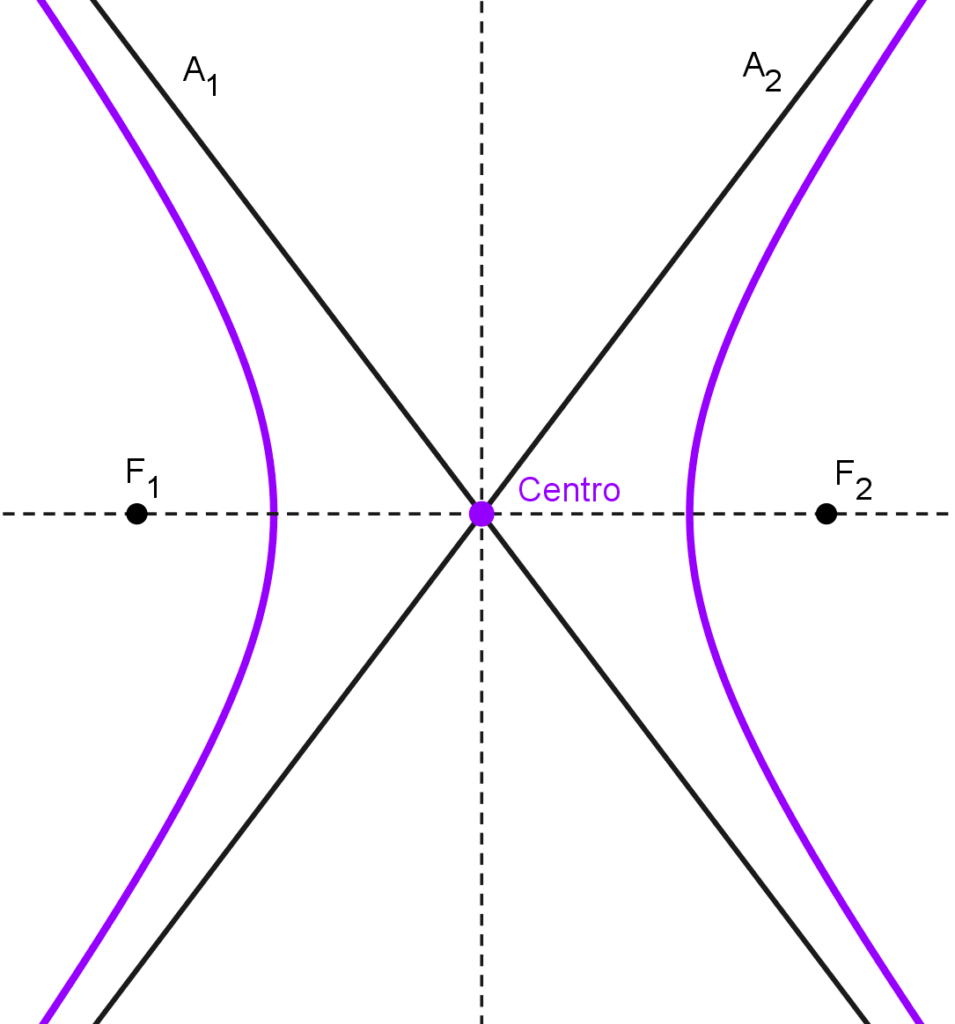
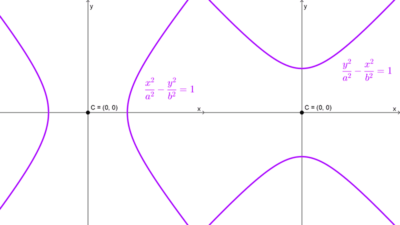
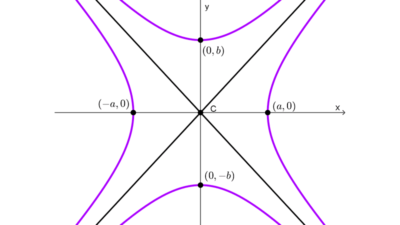
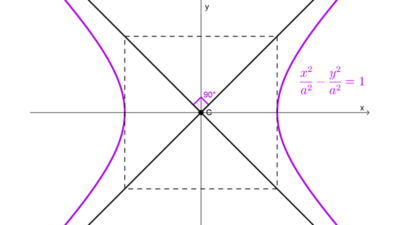
El centro de la hipérbola es el punto medio entre sus focos, también el punto medio entre sus vértices y la intersección del eje transversal y el eje conjugado (y de los ejes focal e imaginario). Es también el punto donde se cruzan las asíntotas de la curva. 

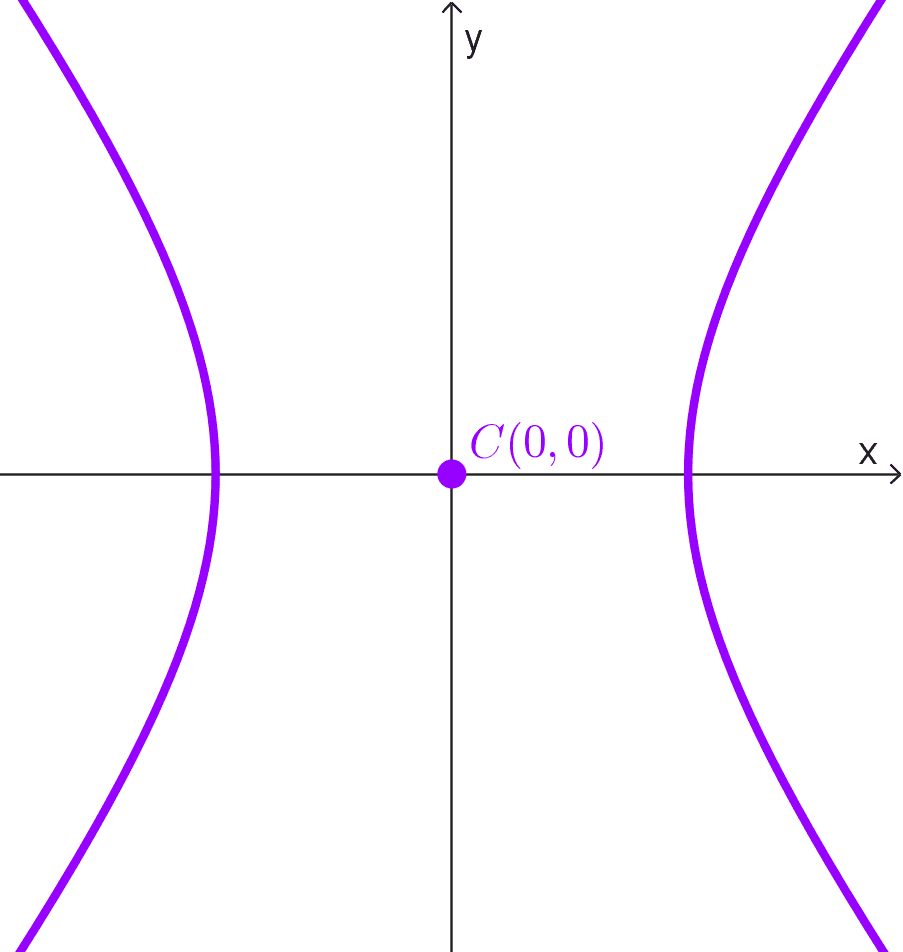
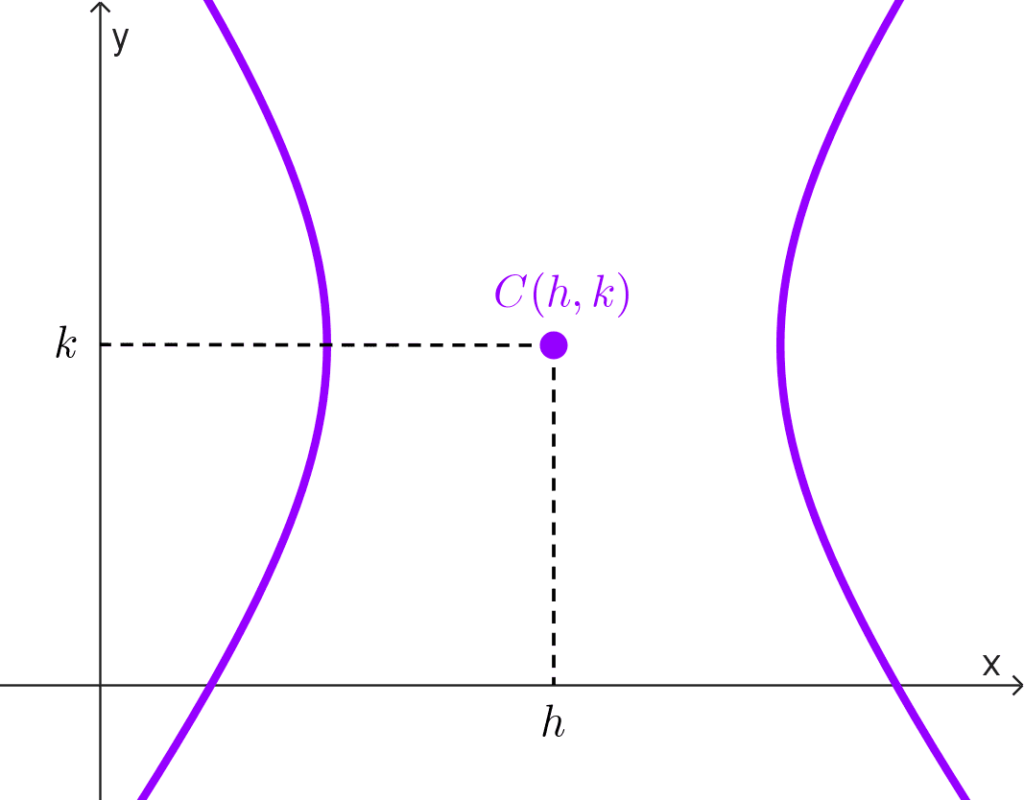
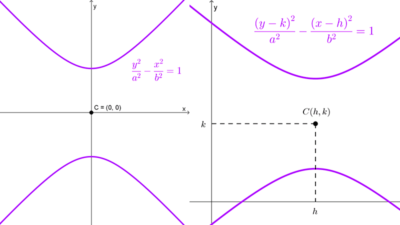
El centro puede estar en el origen de coordenadas (0, 0) o cualquier otro punto del plano denotado genéricamente con (h, k). 

Para conocer el centro de una hipérbola, podemos fijarnos en la ecuación canónica, en ella aparecen explícitamente las coordenadas del centro. La ecuación cuando el centro es el origen es más sencilla que cuando el centro es otro punto. Esto también puede verse en la ecuación general, donde se introducen términos lineales Dx e Ey en el segundo caso.

Centro	Ecuación canónica u ordinaria	Ecuación general
En el origen, punto (0, 0)	*\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1* *\dfrac{y^2}{a^2}-\dfrac{x^2}{b^2}=1*	*Ax^2+Cy^2+F=0* A y C tienen signos opuestos.
Fuera del origen, punto (h, k)	*\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1* *\dfrac{(y-k)^2}{a^2}-\dfrac{(x-h)^2}{b^2}=1*	*Ax^2+Cy^2+Dx+Ey+F=0* A y C tienen signos opuestos.

En la ecuación ordinaria de la hipérbola con centro en el origen las variables x e y aparecen elevadas al cuadrado, mientras que si el centro es (h, k), dichas coordenadas aparecen cambiadas de signo junto con la variable correspondiente. 

¿Cómo hallar el centro?

Existen varias formas de determinar las coordenadas del centro de una hipérbola dependiendo de la información que se tiene:

1. Si se tiene la ecuación canónica, podemos hacer un análisis de la misma para extraer las coordenadas del centro. Si tenemos la ecuación general, podemos operar algebraicamente para conseguir la forma ordinaria.
2. Si se tienen las coordenadas de los focos, el centro se obtiene como el punto medio entre ellos. Lo mismo podemos hacer si contamos con las coordenadas de los vértices.
3. Si se tiene la gráfica, el centro es la intersección de las asíntotas o de los ejes transverso y conjugado.

Ejercicios resueltos

Veremos a continuación ejemplos de la obtención del centro de una hipérbola.

Ejercicio 1

Obtener el centro de la hipérbola *\dfrac{x^2}{4}-\dfrac{y^2}{9}=1*

Solución: identificamos que la ecuación está en forma canónica. Como las variables no aparecen dentro de un paréntesis acompañadas de ningún número, el centro de esta hipérbola es el origen de coordenadas, el punto C(0, 0). 

Ejercicio 2

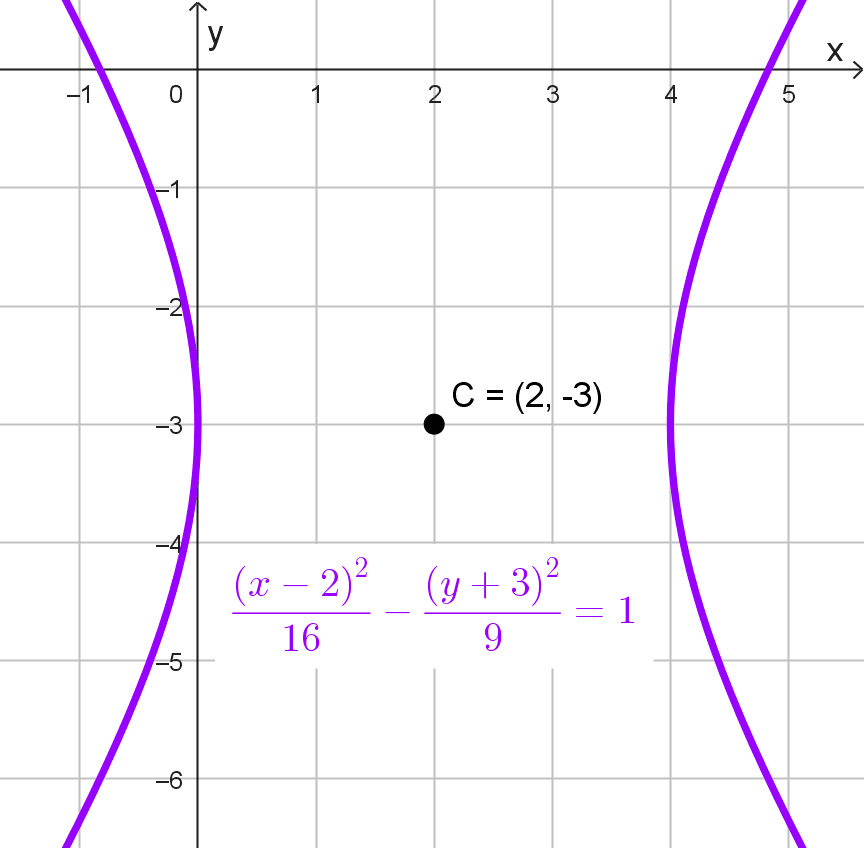
Calcular el centro de la hipérbola con ecuación *\dfrac{(x-2)^2}{16}-\dfrac{(y+3)^2}{9}=1*

Solución: comenzamos identificando la forma estándar. La ecuación de una hipérbola en esta forma es:

*\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1*

donde (h, k) representa las coordenadas del centro de la hipérbola. Comparando la ecuación dada con la forma estándar, podemos observar que:

*h = 2,* ya que el término asociado a x es *(x-2)*

*k = -3,* ya que el término asociado a y es *(y+3)*

Por lo tanto, el centro de la hipérbola es: C(2, -3).

Ejercicio 3

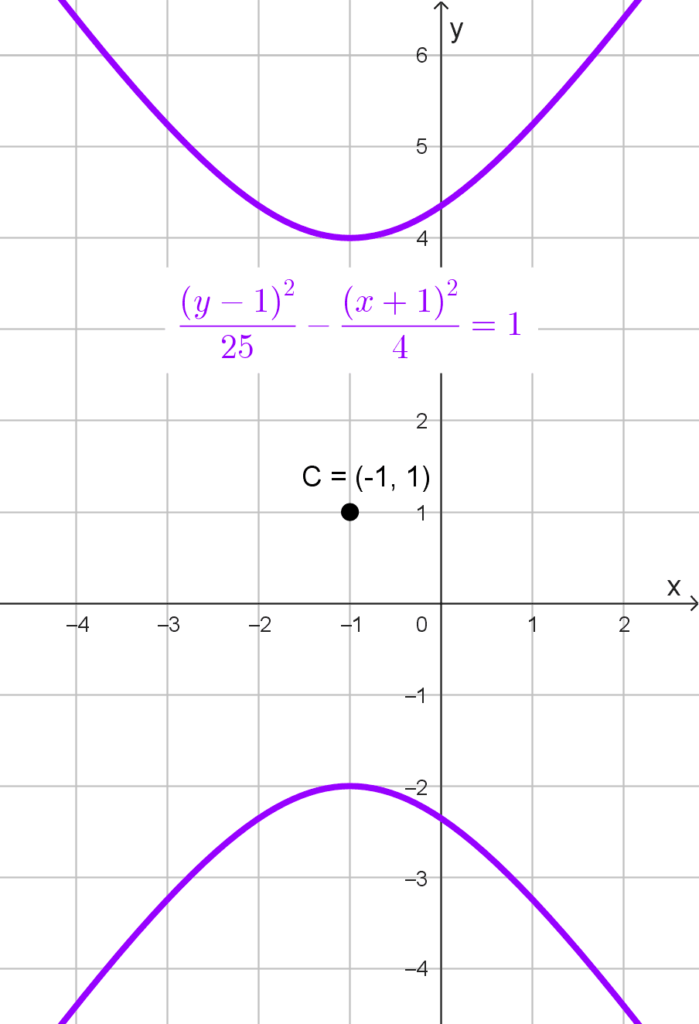
Hallar el centro de *\dfrac{(y-1)^2}{25}-\dfrac{(x+1)^2}{4}=1*

Solución: comparamos la ecuación dada con la forma canónica de una hipérbola vertical centrada en (h, k):

*\dfrac{(y-k)^2}{a^2}-\dfrac{(x-h)^2}{b^2}=1*

De aquí identificamos que, en la ecuación dada:

*y-k=y-1→k=1*

*x-h=x+1→h=-1*

Por lo tanto, el centro de la hipérbola es el punto *(h, k) = (-1, 1)*

Ejercicio 4

Dada la hipérbola *-7x^2+12y^2+28x+72y-4=0* encontrar su centro.

Solución: en este caso la ecuación no está en forma canónica, pero podemos completar los cuadrados para obtener una forma equivalente:

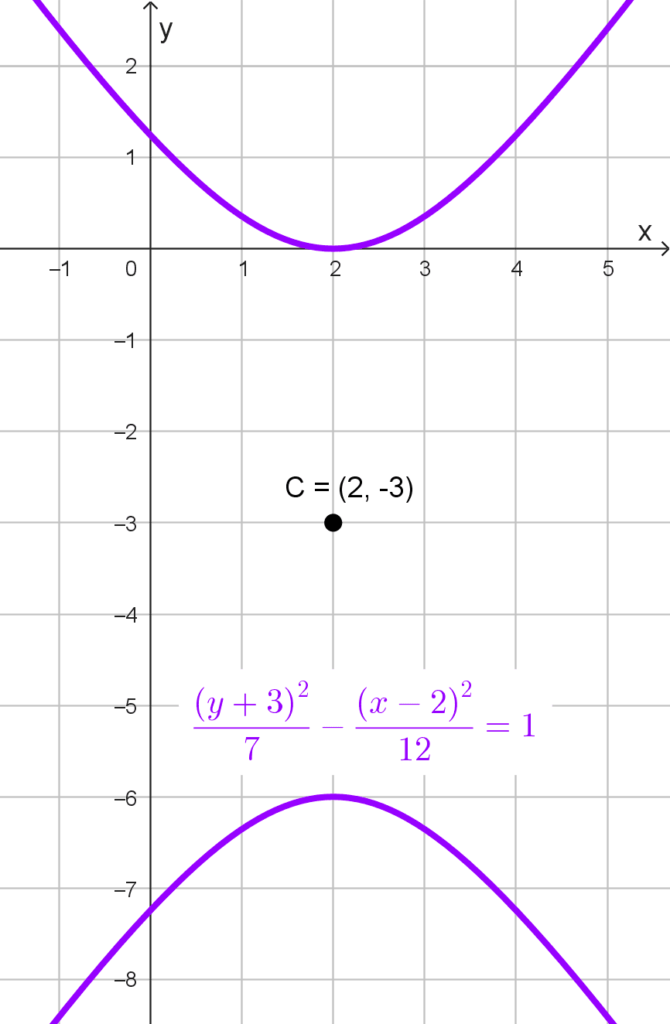
*\dfrac{(y+3)^2}{7}-\dfrac{(x-2)^2}{12}=1*

Aquí identificamos que es la ecuación de una hipérbola vertical centrada fuera del origen. Sacamos las coordenadas del centro de los binomios entre paréntesis, cambiando de signo al número que aparece junto a la variable correspondiente, así:

*k=-3*

*h=-(-2)=2*

Por tanto, el centro es el punto C(2, -3).

Ejercicio 5

Determinar el centro de una hipérbola cuyos focos son los puntos F₁(-5, 3) y F₂(2, 3)

Solución: sabemos que el centro es el punto medio entre los focos de una hipérbola, así que usamos la fórmula del punto medio para encontrarlo:

*(h,k)=\left( \dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2} \right)*

Sustituyendo las coordenadas de *F_1(-5, 3) ~~y~~ F_2(2, 3):*

*(h,k)=\left(\dfrac{-5+2}{2},  \dfrac{3+3}{2} \right)=\left(-\dfrac{3}{2}, \dfrac{6}{2} \right)=\left(\dfrac{-3}{2}; 3\right)*

Como -3/2 = -1,5, el centro de la hipérbola es: C(-1,5 ; 3).