
Hipérbolas con centro en el origen y fuera del origen
En este artículo explicamos las ecuaciones de las hipérbolas con centro en (0, 0) y en (h, k) con gráficas, ejemplos y elementos.
Índice
Hipérbola con centro en el origen
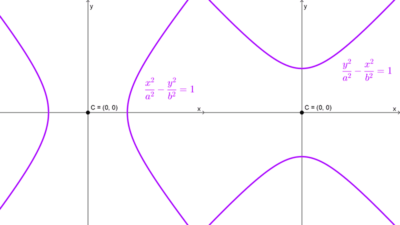
La ecuación canónica de una hipérbola centrada en el origen de coordenadas cambia según si el eje focal es horizontal o vertical:
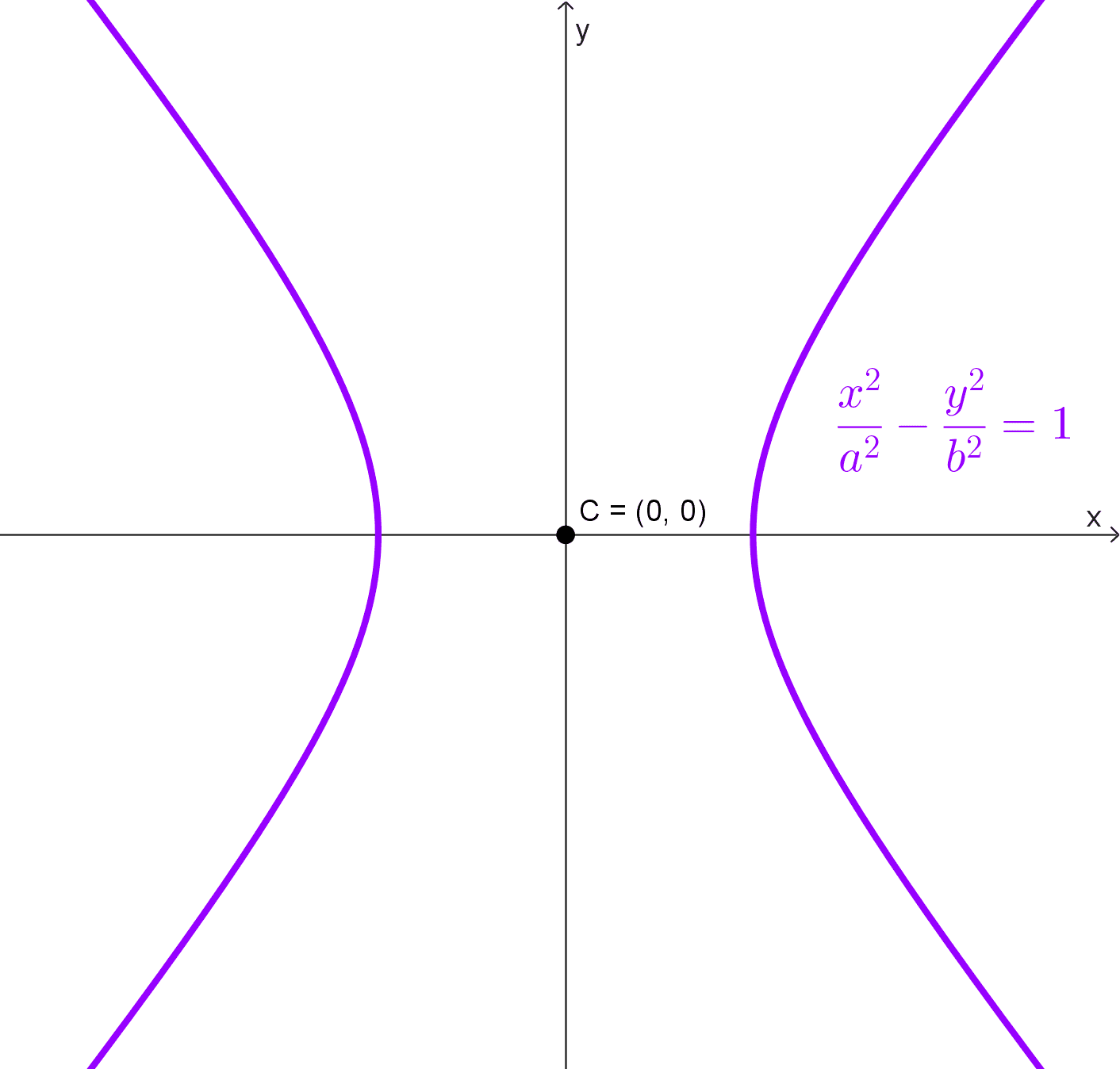
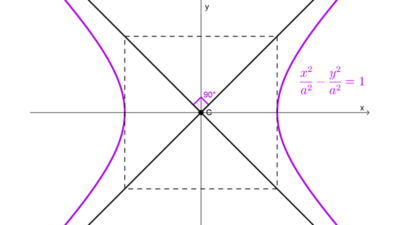
Hipérbola horizontal: \(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\)
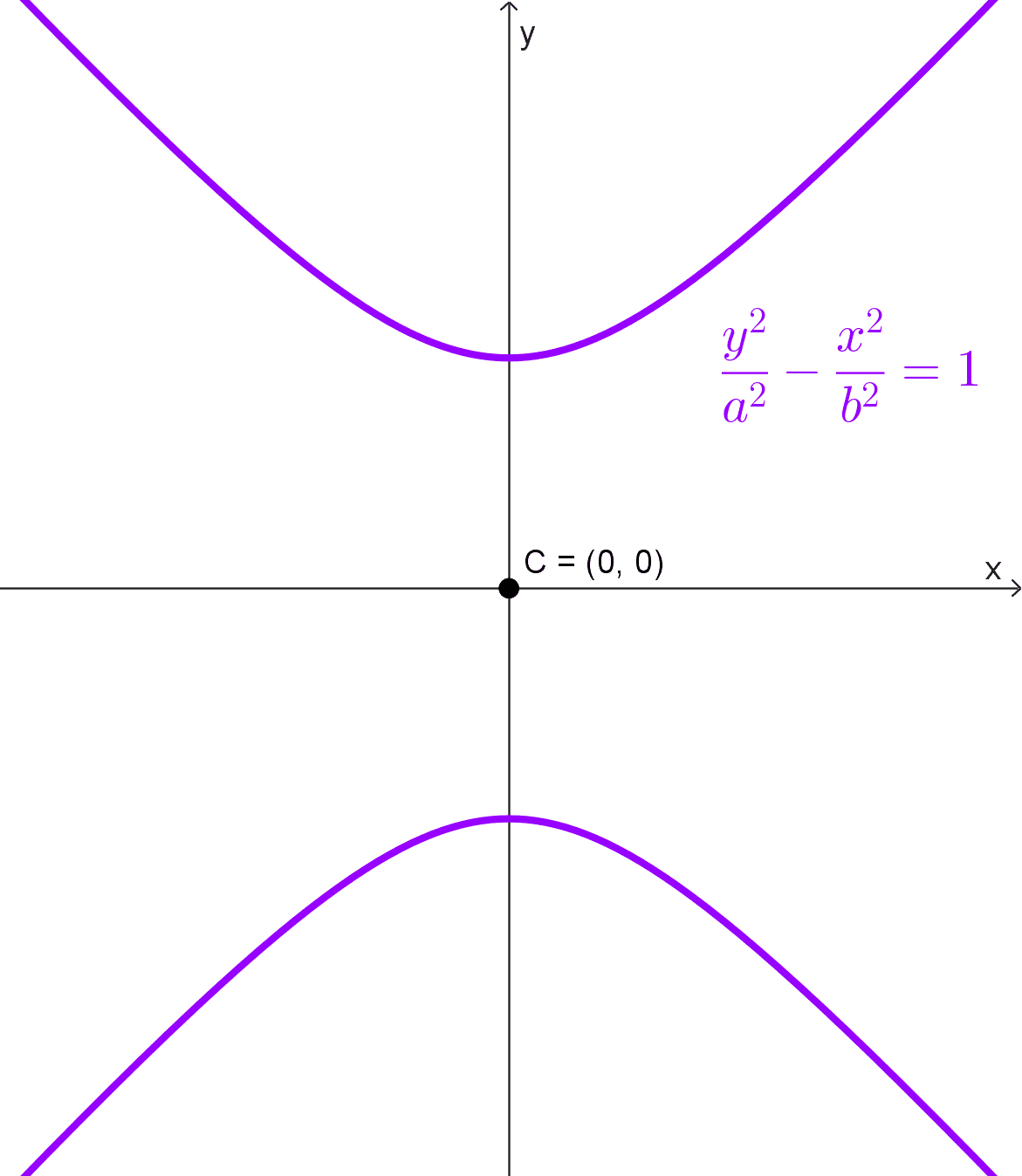
Hipérbola vertical: \(\dfrac{y^2}{a^2}-\dfrac{x^2}{b^2}=1\)
donde el semieje transversal es a y el semieje conjugado es b.
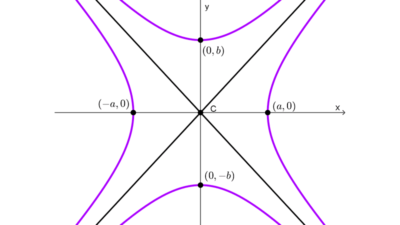
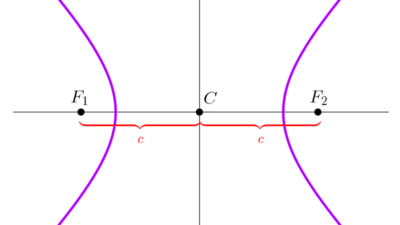
Si el centro es el origen, los focos y los vértices de la hipérbola están sobre los ejes cartesianos: sobre el eje x si la hipérbola es horizontal y sobre el eje y si la hipérbola es vertical.
Los elementos de la hipérbola pueden extraerse de la fórmula ordinaria:
| Ecuación canónica | Eje transverso | Centro | Focos | Vértices | Extremos del eje conjugado | Asíntotas |
|---|---|---|---|---|---|---|
| \(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\) | Sobre el eje x | (0, 0) | (±c, 0) c = √(a² + b²) | (±a, 0) | (0, ±b) | y = ± (b / a) x |
| \(\dfrac{y^2}{a^2}-\dfrac{x^2}{b^2}=1\) | Sobre el eje y | (0, 0) | (0, ±c) c = √(a² + b²) | (0, ±a) | (±b, 0) | y = ± (a / b) x |
La ecuación general de una hipérbola con centro en (0, 0) es:
Ax2 + Cy2 + F = 0
donde A y C tienen signos opuestos.
No aparecen términos lineales (Dx y Ey) porque los mismos indicarían un desplazamiento del origen.
Ejemplos
Las siguientes son ecuaciones de hipérbolas con centro en (0, 0):
- \(\dfrac{x^2}{4}-\dfrac{y^2}{9}=1\)
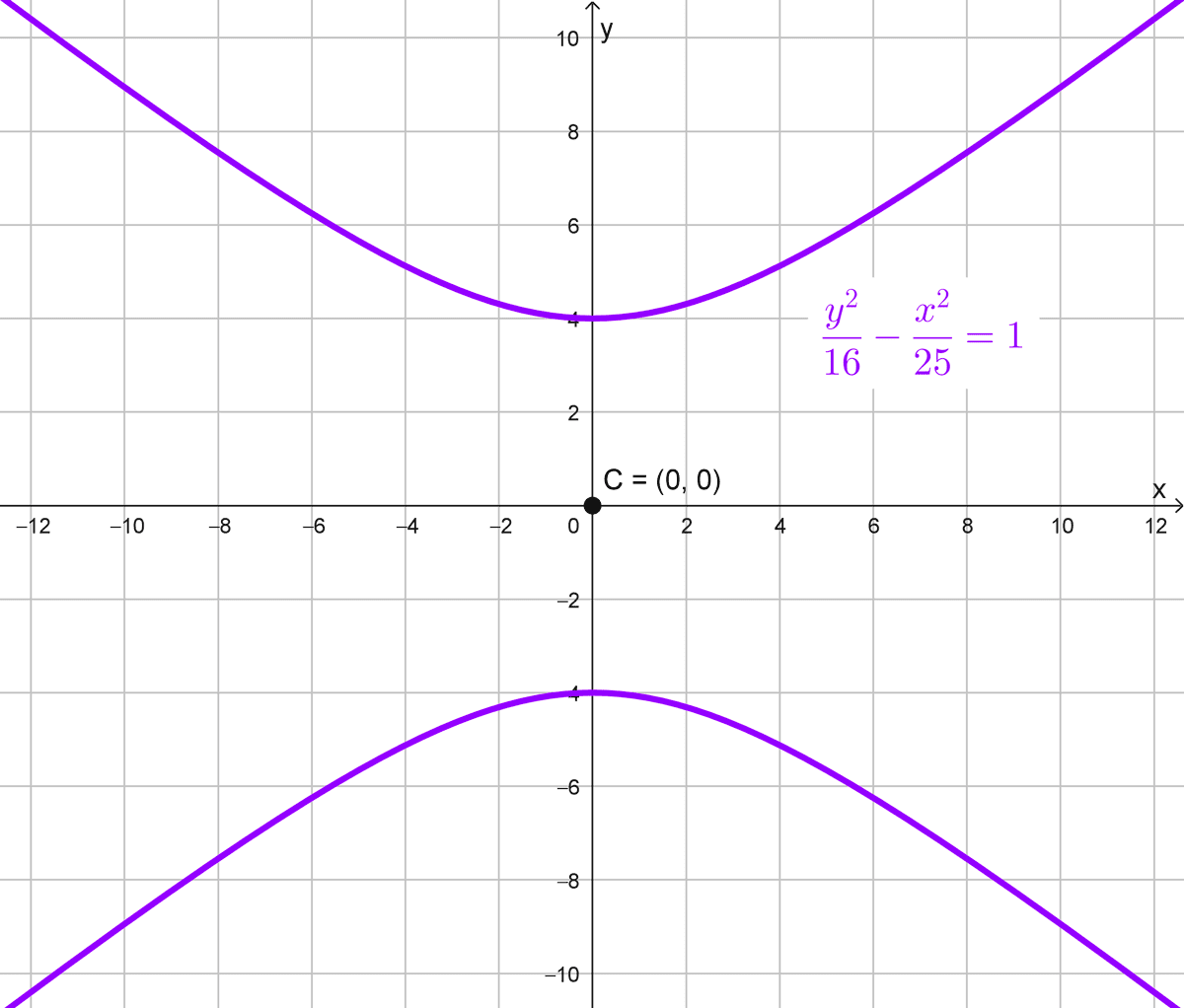
- \(\dfrac{y^2}{16}-\dfrac{x^2}{25}=1\)
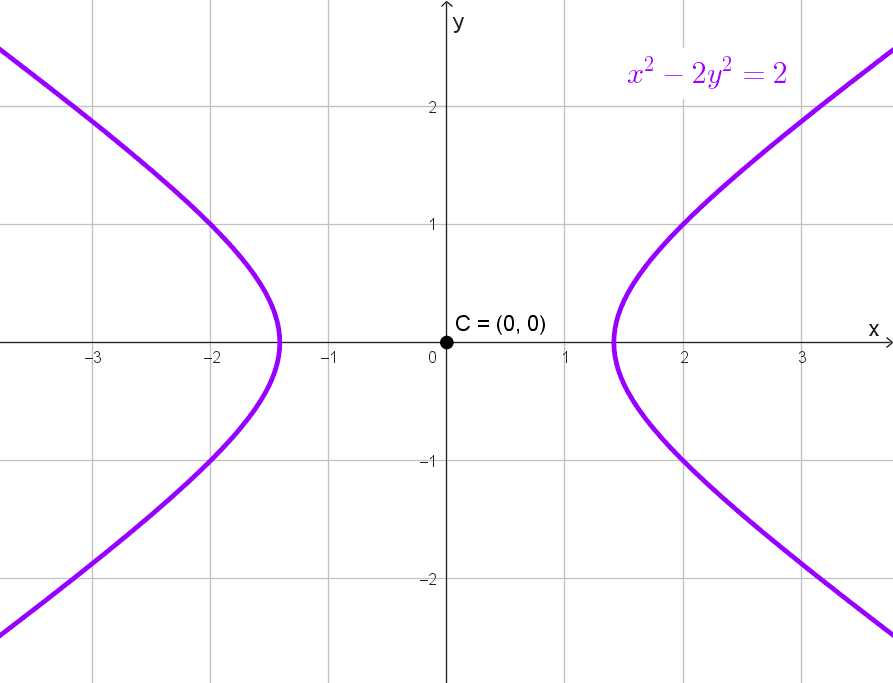
- \(x^2-2y^2=2\)
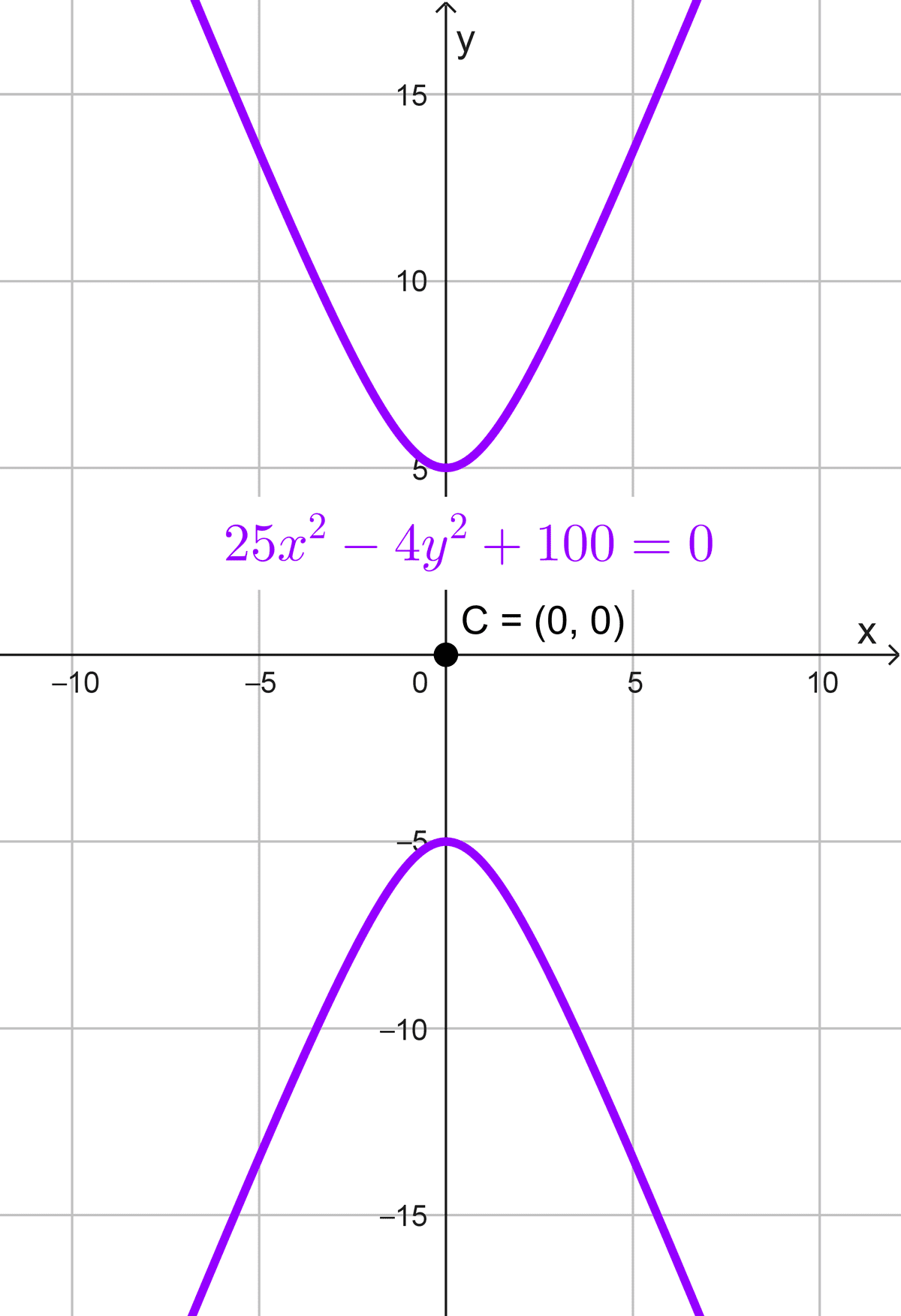
- \(25x^2-4y^2+100=0\)
Hipérbola con centro fuera del origen
De la misma forma que antes, la ecuación canónica de una hipérbola centrada fuera del origen en un punto (h, k) varía dependiendo de la orientación:
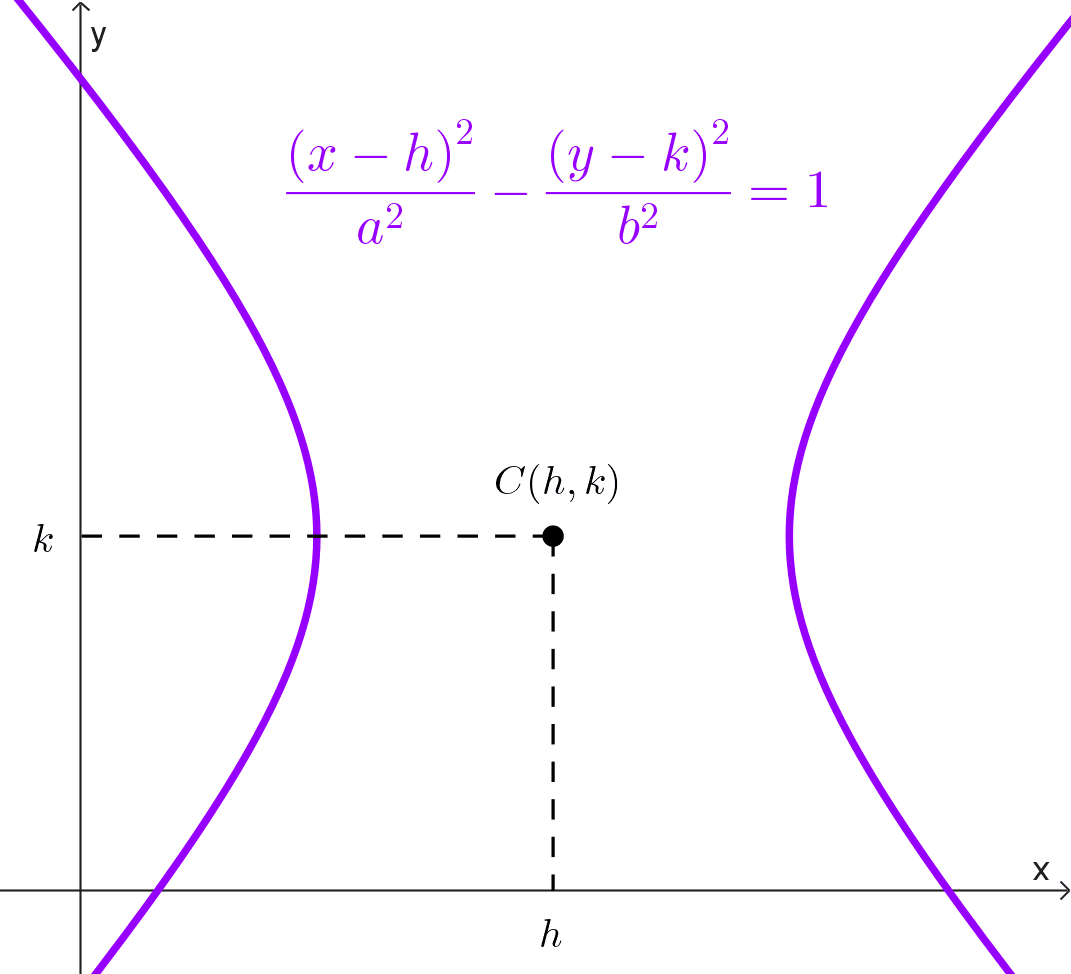
Hipérbola horizontal: \(\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1\)
Hipérbola vertical: \(\dfrac{(y-k)^2}{a^2}-\dfrac{(x-h)^2}{b^2}=1\)
donde el semieje transversal es a y el semieje conjugado es b.
Si el centro no es el origen, los focos y los vértices de la hipérbola están sobre la recta x = h si la orientación es vertical y sobre la recta y = k si la orientación es horizontal.
De modo similar a lo antes visto, los elementos de la hipérbola pueden extraerse de la fórmula canónica:
| Ecuación canónica | Eje transverso | Centro | Focos | Vértices | Extremos del eje conjugado | Asíntotas |
|---|---|---|---|---|---|---|
| \(\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1\) | Paralelo al eje x | (h, k) | (h ± c, k) c = √(a² + b²) | (h ± a, k) | (h, k ± b) | y - k = ± (b / a) (x - h) |
| \(\dfrac{(y-k)^2}{a^2}-\dfrac{(x-h)^2}{b^2}=1\) | Paralelo al eje y | (h, k) | (h, k ± c) c = √(a² + b²) | (h, k ± a) | (h ± b, k) | y - k = ± (a / b) (x - h) |
La ecuación general de una hipérbola con centro fuera del origen es:
Ax2 + Cy2 + Dx + Ey + F = 0
donde A y C tienen signos diferentes.
Nótese que en este caso aparecen los términos lineales Dx y Ey que indican un desplazamiento del origen de coordenadas.
Ejemplos
Las siguientes son ecuaciones de hipérbolas con centro en (h, k):
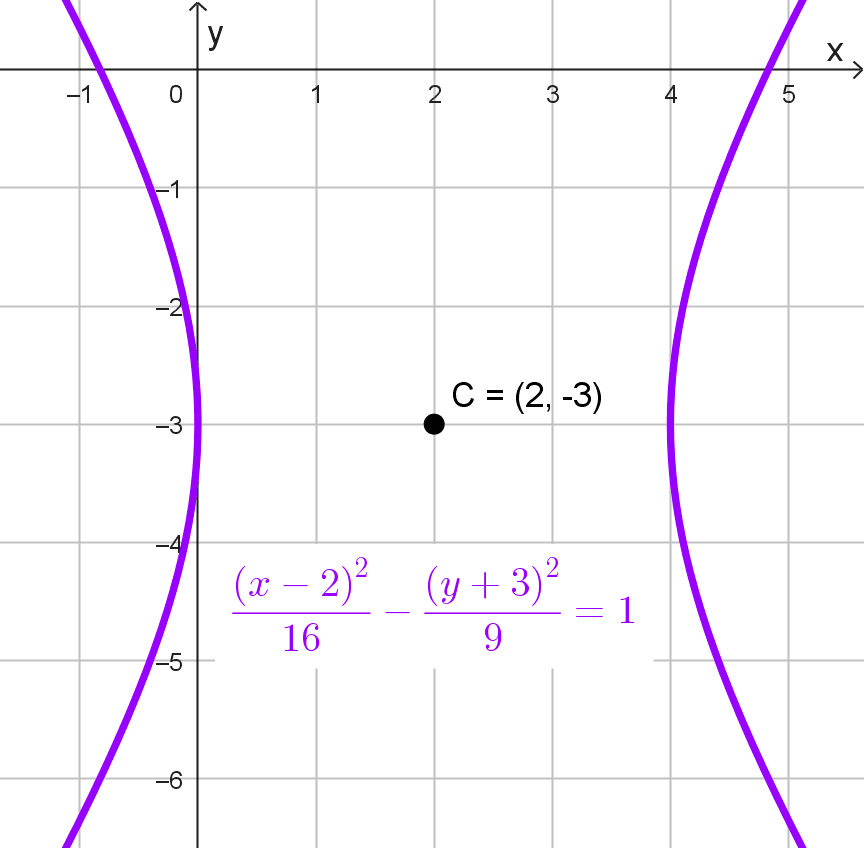
- \(\dfrac{(x-2)^2}{16}-\dfrac{(y+3)^2}{9}=1\) tiene centro en (2, -3).
- \(\dfrac{(y-1)^2}{25}-\dfrac{(x+1)^2}{4}=1\) está centrado en (-1, 1).
- \(-7x^2+12y^2+28x+72y-4=0\) en forma canónica es \(\dfrac{(y+3)^2}{7}-\dfrac{(x-2)^2}{12}=1,\) aquí se obtiene que su centro es (2, -3).
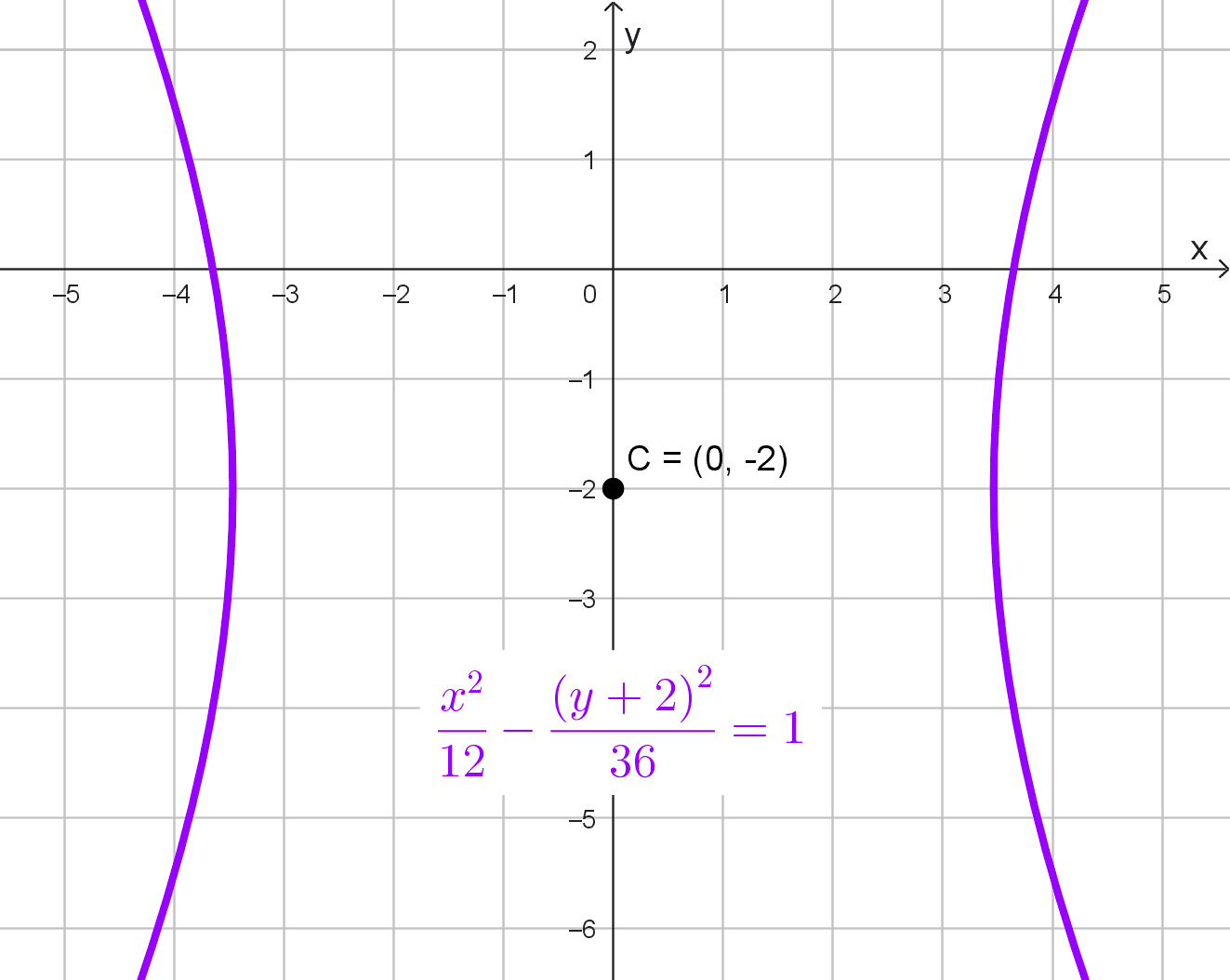
- \(3x^2-y^2-4y-40=0\) completando cuadrados es \(\dfrac{x^2}{12}-\dfrac{(y+2)^2}{36}=1,\) cuyo centro está en (0, -2).
Ejercicios resueltos
A continuación, resolvemos algunos ejercicios sobre cómo construir ecuaciones en base a datos. Los ejercicios de encontrar el centro de una hipérbola están en este artículo:
Ejercicio 1
Encontrar la ecuación de la hipérbola centrada en el origen con vértices en (±3, 0) y focos en (±4, 0).
Solución
Sabemos que la hipérbola está centrada en el origen, con los vértices y los focos alineados sobre el eje x. Esto implica que la ecuación tendrá la forma:
\(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\)
Los vértices están a una distancia a = 3 del centro. Por otro lado, la distancia entre el centro y los focos es c = 4. La relación entre a, b y c para una hipérbola es:
\(c^2=a^2+b^2\)
Sustituyendo los valores de a y c:
\(4^2=3^2+b^2 → 16=9+b^2 → b^2=7\)
Así, la ecuación de la hipérbola es:
\(\dfrac{x^2}{9}-\dfrac{y^2}{7}=1\)
Ejercicio 2
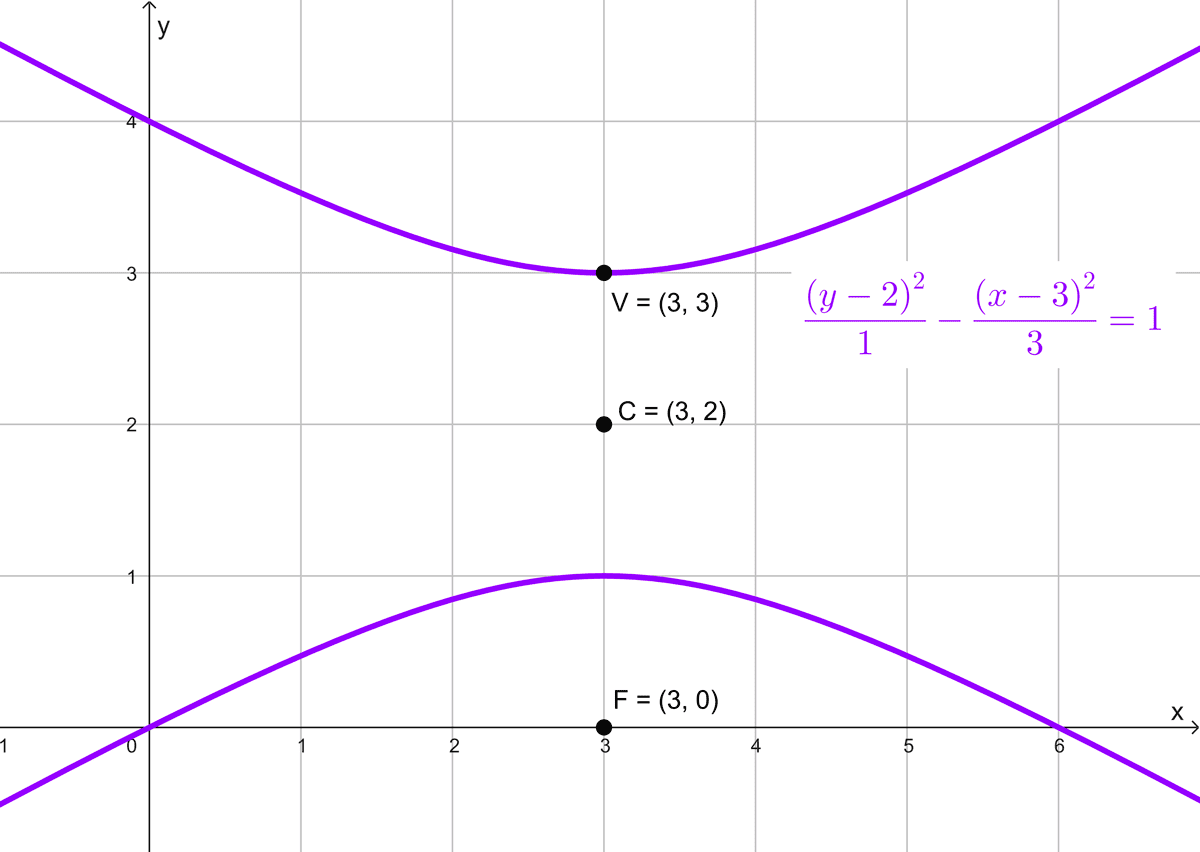
Determinar la ecuación ordinaria de una hipérbola con centro en (3, 2), un vértice está en (3, 3) y un foco en (3, 0).
Solución
La hipérbola tiene su centro en (3, 2), y los vértices están alineados verticalmente (el eje focal es paralelo al eje y). La ecuación general será de la forma:
\(\dfrac{(y-k)^2}{a^2}-\dfrac{(x-h)^2}{b^2}=1\)
donde (h, k) = (3, 2).
La distancia entre el centro y el vértice es a = 1, de (3, 2) a (3, 3). La distancia entre el centro y el foco es c = 2, de (3, 2) a (3, 0).
De nuevo usamos la relación:
\(c^2=a^2+b^2\)
Sustituyendo los valores:
\(2^2=1^2+b^2 → 4=1+b^2 → b^2=3\)
Por lo tanto, la ecuación de la hipérbola es:
\(\dfrac{(y-2)^2}{1}-\dfrac{(x-3)^2}{3}=1\)
o simplemente:
\(\dfrac{(y-2)^2}{1}-\dfrac{(x-3)^2}{3}=1\)
Ejercicio 3
Hallar la fórmula canónica de una hipérbola con centro en el origen, vértice en (-5, 0) y asíntota \(y=\dfrac{6}{5}x.\)
Solución
Dado que la hipérbola tiene el vértice en (-5, 0), su eje transverso es horizontal. Esto nos indica que la ecuación será de la forma:
\(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\)
La distancia del centro al vértice es a = 5. Para determinar b, usamos la pendiente de las asíntotas, que en una hipérbola horizontal es:
\(\text{Pendiente}=\pm \dfrac{b}{a}\)
Aquí, la pendiente de la asíntota es \(\dfrac{6}{5},\) por lo que:
\(\dfrac{b}{a}=\dfrac{6}{5} → b=6\)
Por lo tanto, \(a^2=25\) y \(b^2=36.\) La ecuación de la hipérbola es:
\(\dfrac{x^2}{25}-\dfrac{y^2}{36}=1\)
Ejercicio 4
Obtener la ecuación de una hipérbola con centro en (-2, 1), foco en (-2, 5) y vértice en (-2, 4).
Solución
La hipérbola tiene su centro en (-2, 1) y su eje focal es vertical (ya que los vértices y focos están alineados verticalmente). La ecuación será:
\(\dfrac{(y-k)^2}{a^2}-\dfrac{(x-h)^2}{b^2}=1\)
donde (h, k) = (-2, 1).
La distancia entre el centro y el vértice es a = 3, de (-2, 1) a (-2, 4). La distancia entre el centro y el foco es c = 4, de (-2, 1) a (-2, 5).
De nuevo, usamos la relación:
\(c^2=a^2+b^2\)
Sustituyendo los valores:
\(4^2=3^2+b^2 → 16=9+b^2 → b^2=7\)
Por lo tanto, la ecuación de la hipérbola es:
\(\dfrac{(y-1)^2}{9}-\dfrac{(x+2)^2}{7}=1\)
Bibliografía consultada
- Engler, A., Müller, D., Vrancken, S. y Hecklein, M. (2020). Geometría analítica. Universidad Nacional del Litoral.
- Lehmann, C. (1989). Geometría analítica. Limusa.
- Leithold. L. (1992). Álgebra y trigonometría con geometría analítica. Oxford University Press.
- Sullivan, M. (2006). Álgebra y trigonometría. Pearson Educación.
- Swokowski, E. y Cole, J. (2009). Álgebra y trigonometría con geometría analítica. Cengage Learning.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta


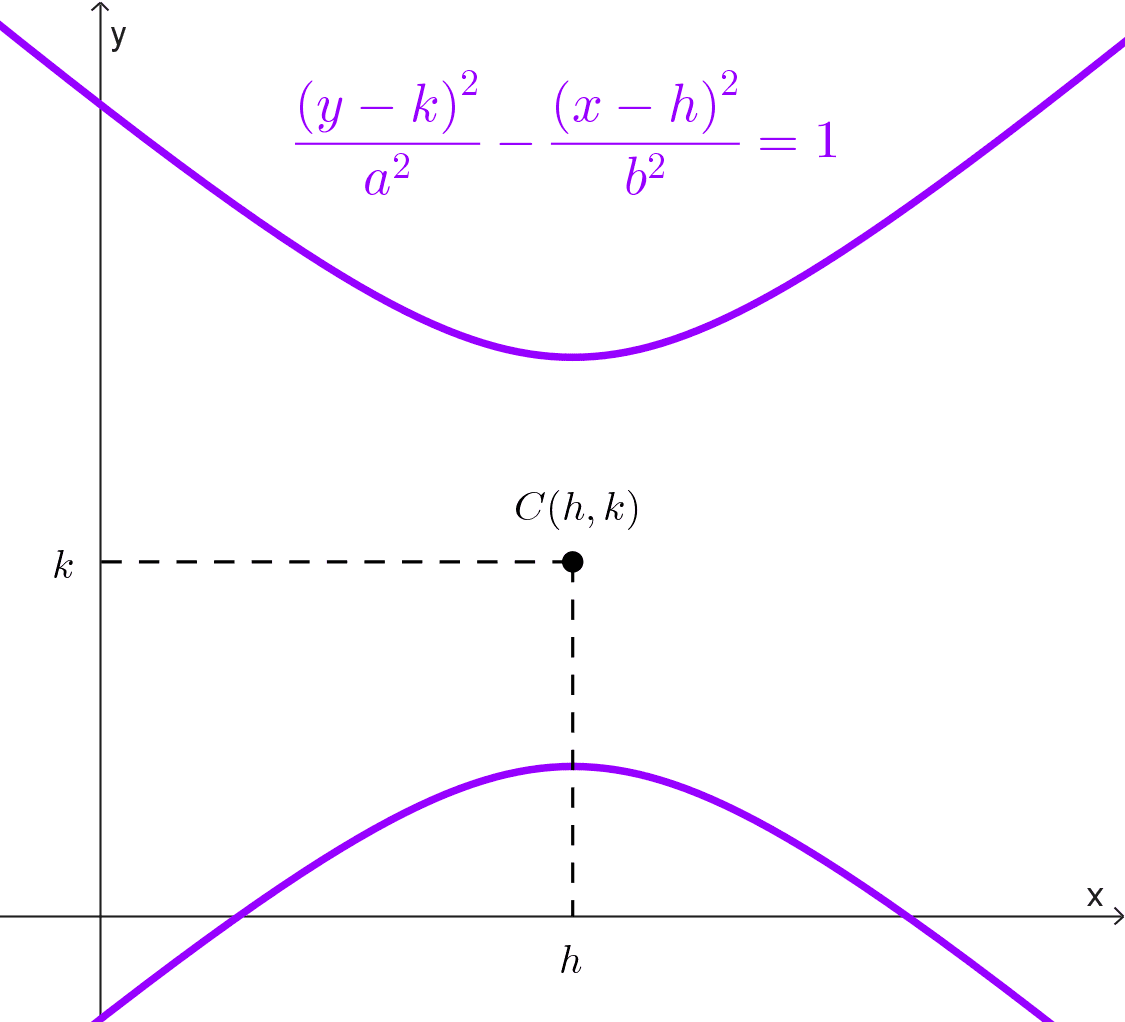
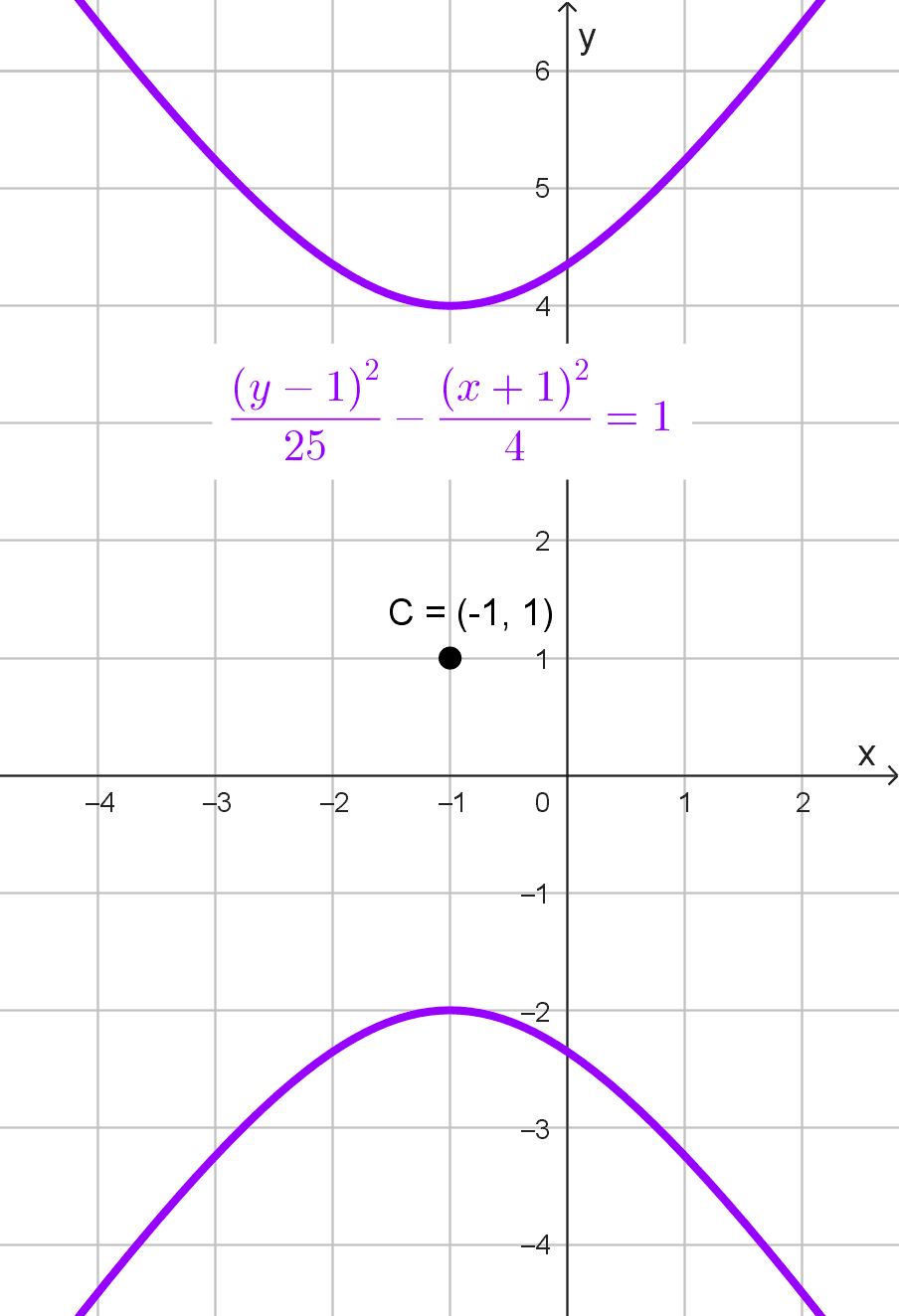
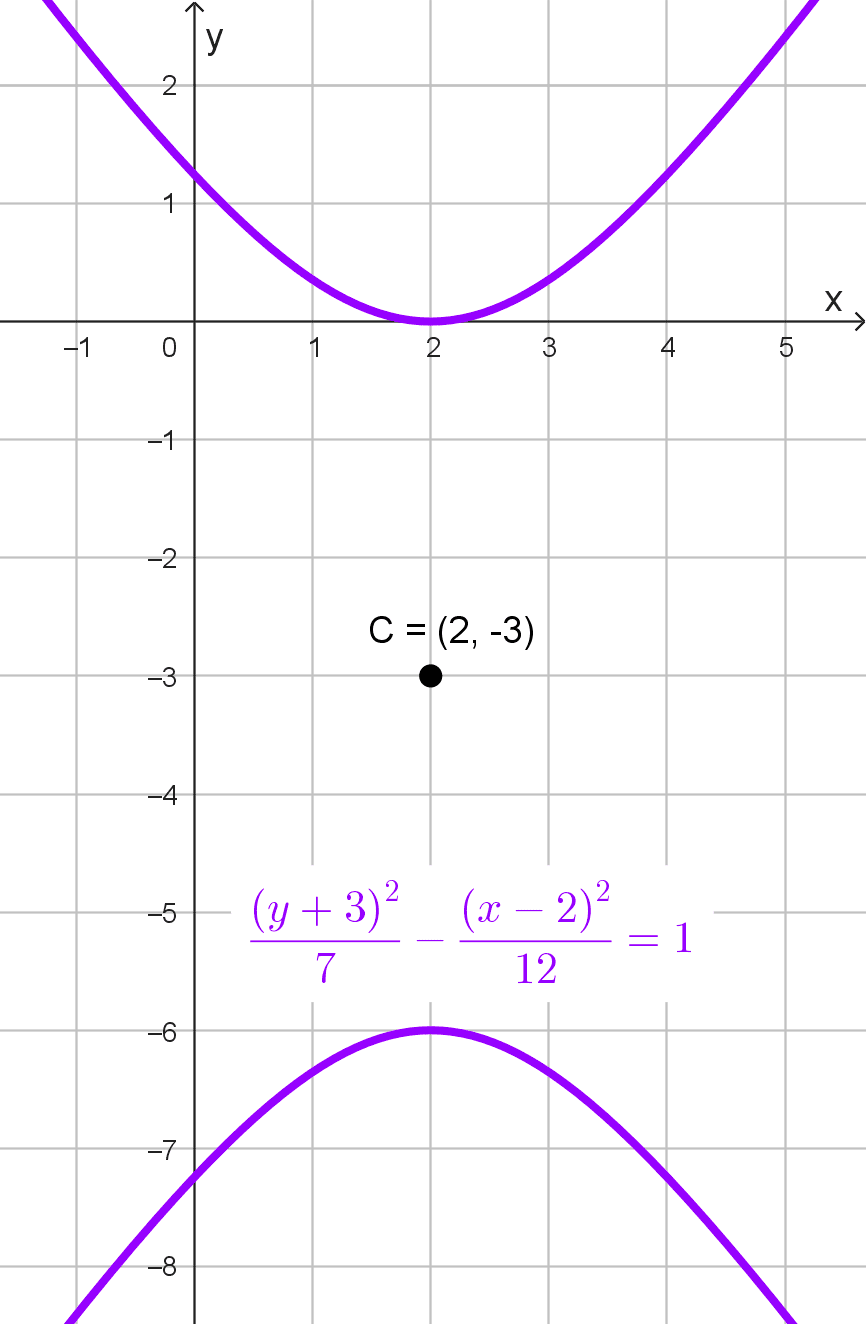
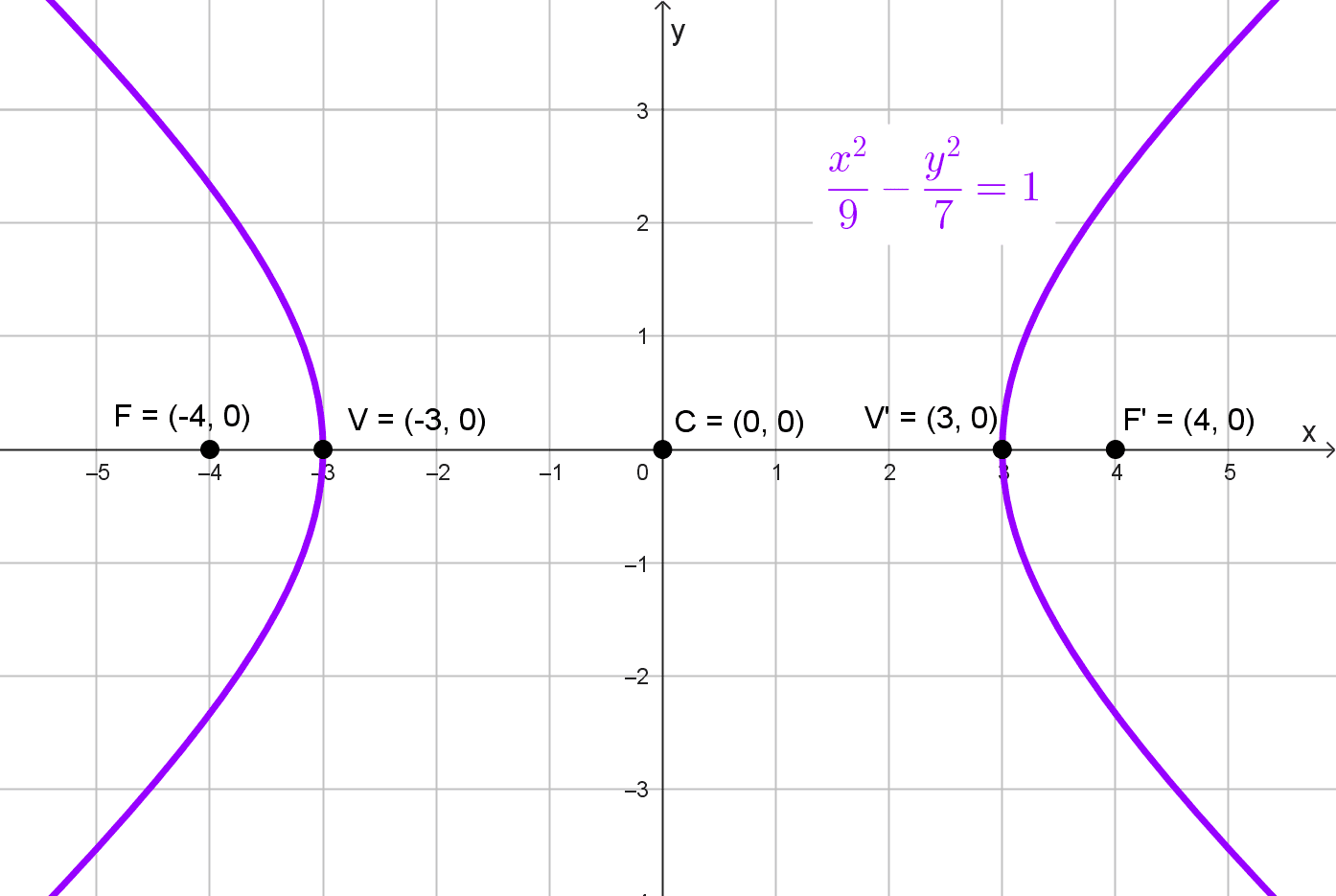
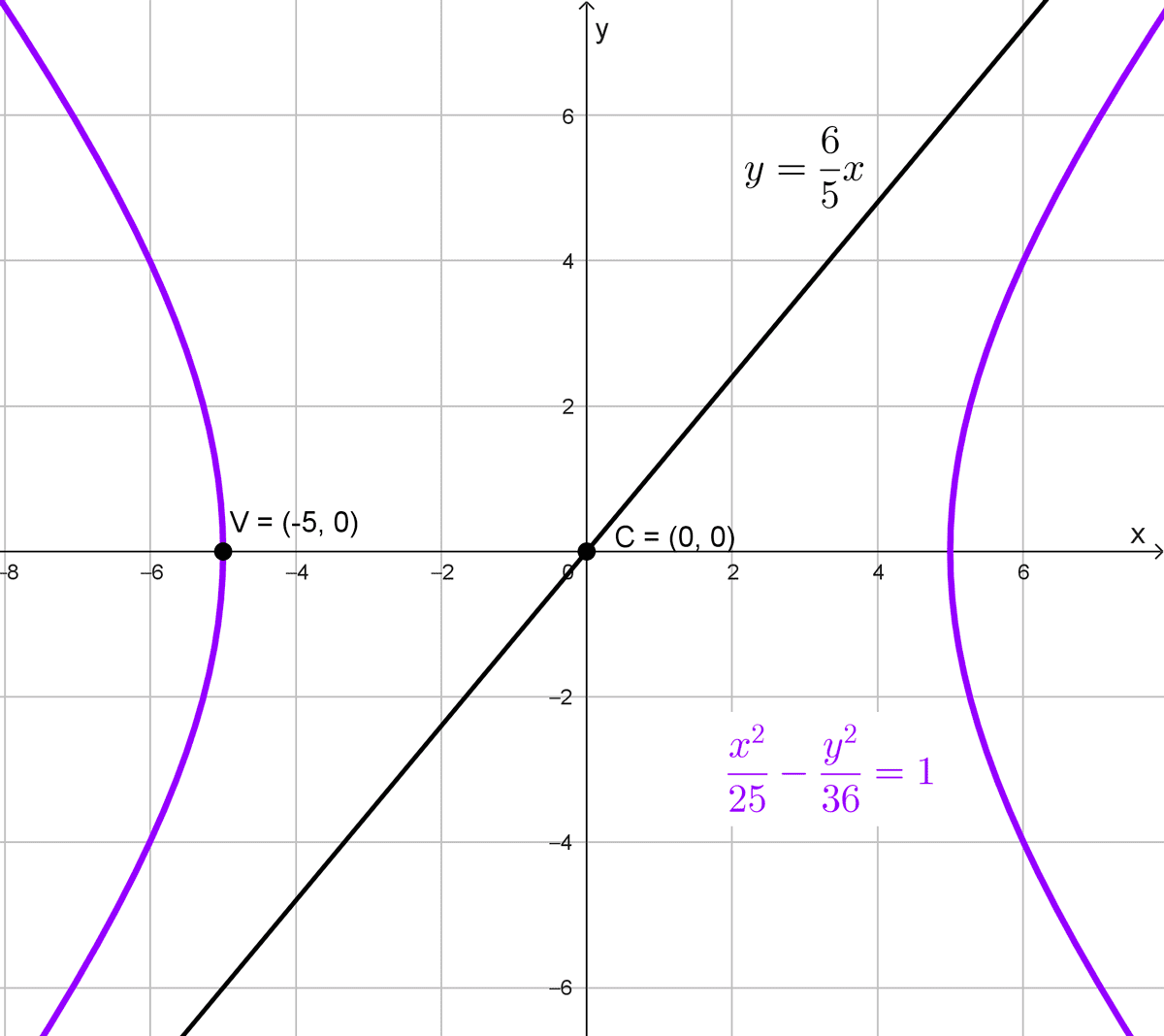
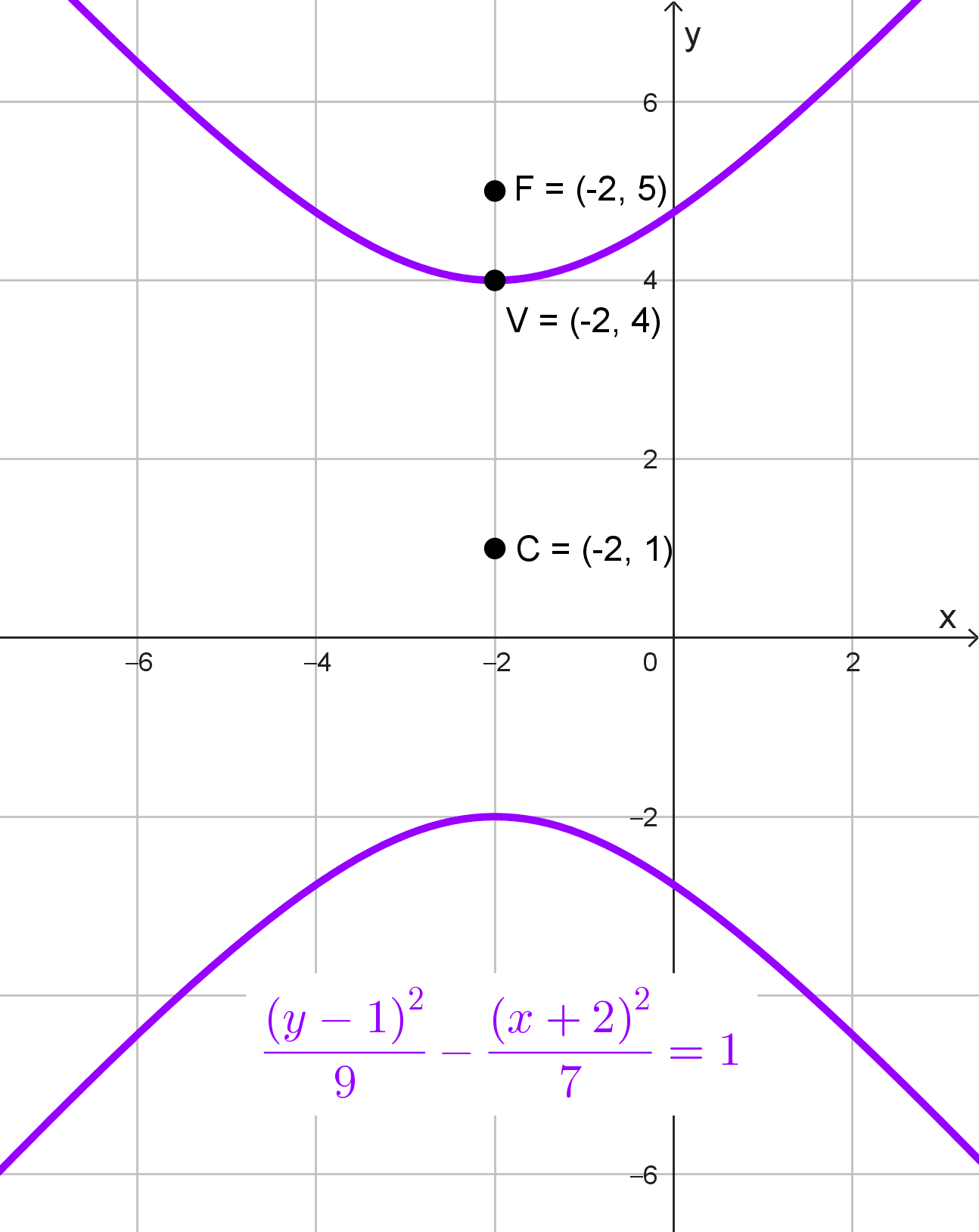
Otros artículos que pueden interesarte