Asíntotas de la hipérbola

En este artículo explicamos qué son las asíntotas de una hipérbola, sus ecuaciones, las formas de calcularlas y un método para trazarlas con ejercicios resueltos paso a paso.

¿Qué son las asíntotas?

Las asíntotas de una hipérbola son líneas rectas a las cuales la curva se aproxima cuando las variables crecen en valor absoluto, pero nunca llegan a cortarla. Toda hipérbola tiene dos asíntotas que se cruzan en el centro, estas sirven como guía para graficar y entender cómo se comporta la hipérbola en sus extremos.

Ecuaciones de las asíntotas

Las fórmulas que describen a las asíntotas de la hipérbola se pueden obtener si se conocen el centro y las longitudes de los semiejes transversal (a) y conjugado (b).

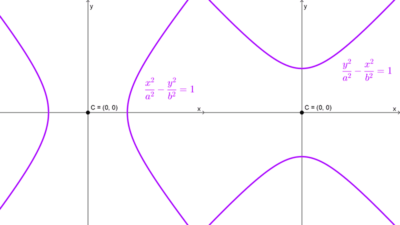
Hipérbolas con centro en (0, 0)

Cuando el centro es el origen de coordenadas, las ecuaciones de las asíntotas varían dependiendo de la orientación de la hipérbola:

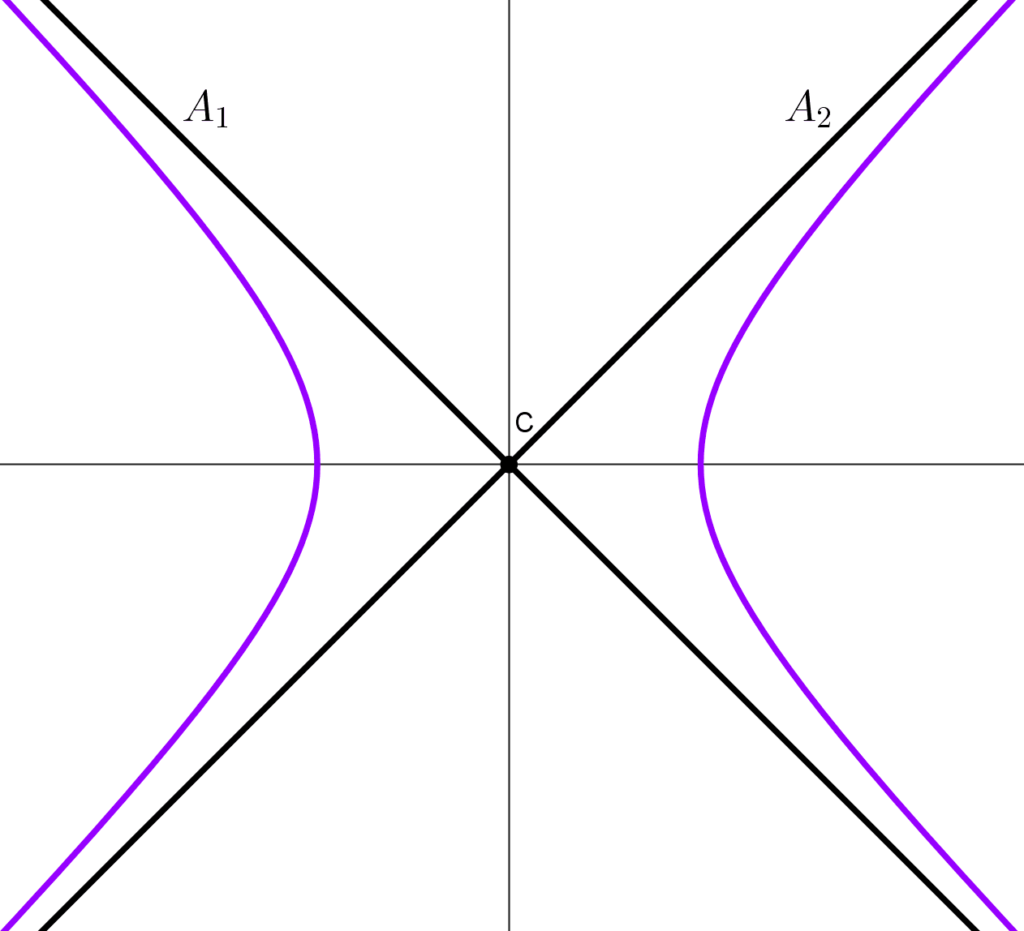
Hipérbola horizontal: *y=\dfrac{b}{a}x~~~~\text{y}~~~~y=-\dfrac{b}{a}x*

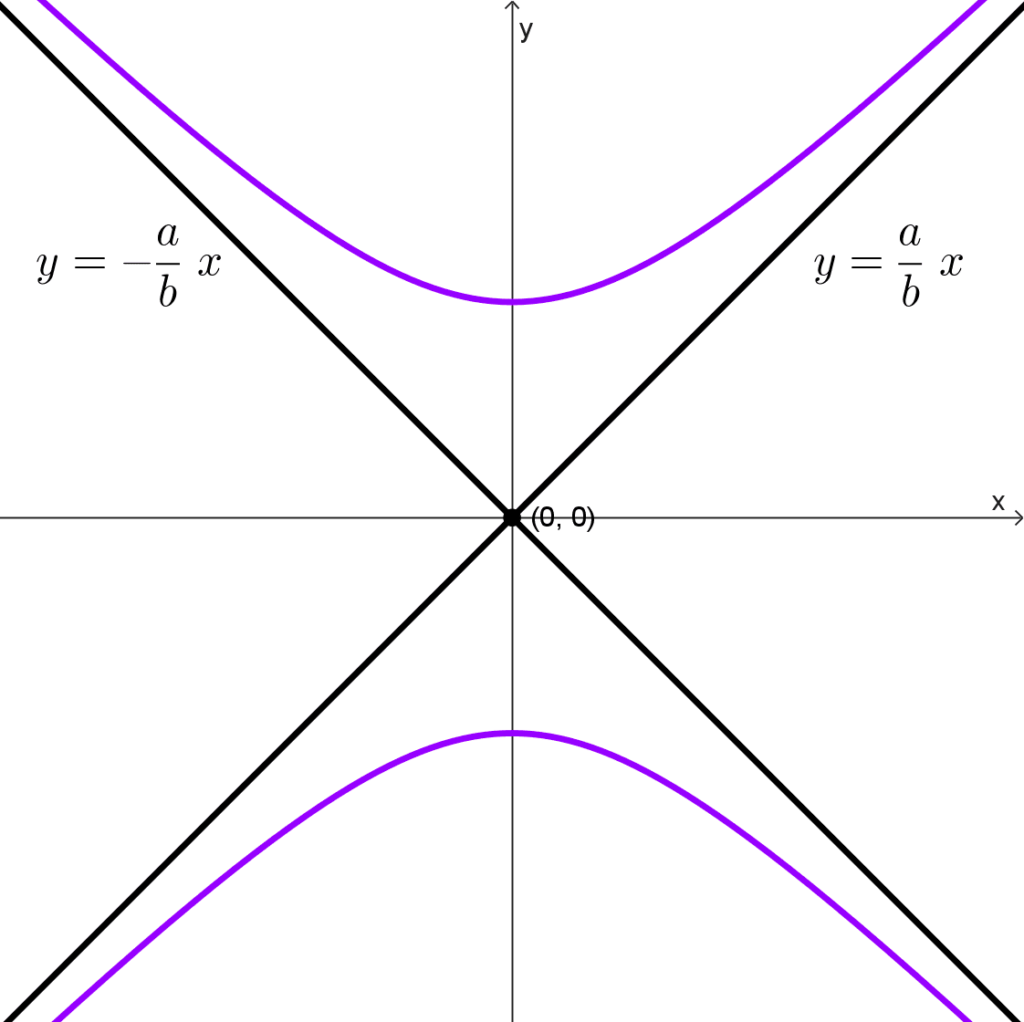
Hipérbola vertical: *y=\dfrac{a}{b}x~~~~\text{y}~~~~y=-\dfrac{a}{b}x*

Hipérbolas con centro en (h, k)

Cuando el centro no es el origen de coordenadas, las ecuaciones de las asíntotas se obtienen restando los números h y k a las variables correspondientes.

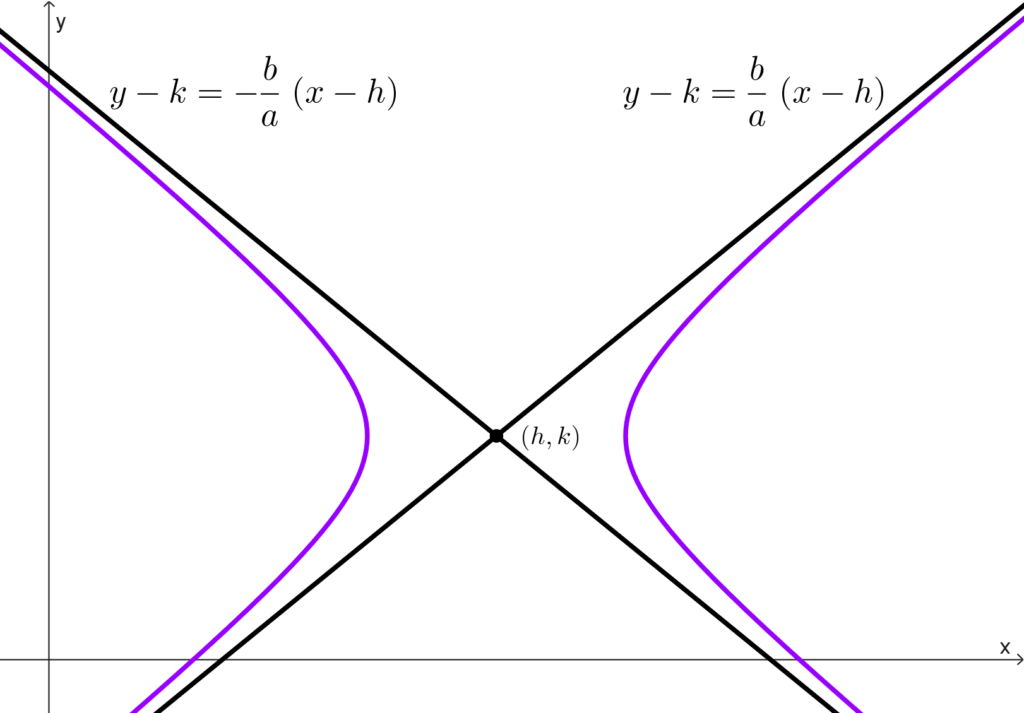
Hipérbola horizontal: *y-k=\dfrac{b}{a}(x-h)~~~~\text{y}~~~~y-k=-\dfrac{b}{a}(x-h)*

Hipérbola vertical: *y-k=\dfrac{a}{b}(x-h)~~~~\text{y}~~~~y-k=-\dfrac{a}{b}(x-h)*

Las ecuaciones se resumen en la siguiente tabla.

Ecuación canónica	Eje transversal	Centro	Asíntotas
*\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1*	Sobre el eje x	(0, 0)	*y=±\dfrac{b}{a}x*
*\dfrac{y^2}{a^2}-\dfrac{x^2}{b^2}=1*	Sobre el eje y	(0, 0)	*y=±\dfrac{a}{b}x*
*\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1*	Paralelo al eje x	(h, k)	*y-k=±\dfrac{b}{a}(x-h)*
*\dfrac{(y-k)^2}{a^2}-\dfrac{(x-h)^2}{b^2}=1*	Paralelo al eje y	(h, k)	*y-k=±\dfrac{a}{b}(x-h)*

Demostración

Se comienza por despejar "y" en la ecuación de la hipérbola.

*\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1*

*\dfrac{y^2}{b^2}=\dfrac{x^2}{a^2}-1*

*y^2=b^2\left(\dfrac{x^2}{a^2}-1\right)*

Como x ≠ 0, se reordena el lado derecho en la forma:

*y^2=\dfrac{b^2x^2}{a^2}\left(1-\dfrac{a^2}{x^2}\right)*

*y=±\dfrac{bx}{a}\sqrt{1-\dfrac{a^2}{x^2}}*

Ahora, cuando *x → ∞* o cuando *x → -∞* (dicho de otro modo: x se hace muy grande en valor absoluto), el término *a^2/x^2* tiende a cero, por lo que la expresión con radical tiende a 1. Esto significa que cuando x crece, el valor de y tiende a *±\dfrac{bx}{a};* es decir, la gráfica de la hipérbola tiende a las rectas:

*y=-\dfrac{b}{a}x~~~\text{y}~~~y=\dfrac{b}{a}x*

Estas rectas son las asíntotas oblicuas de la hipérbola. Estas no forman parte de la gráfica, pero sirven de guía para graficarla.

Cómo calcular las asíntotas

Una forma de encontrar las asíntotas de una hipérbola es usando las fórmulas vistas en la tabla anterior, para lo cual se deben conocer el centro y las longitudes de los semiejes. Estos datos se obtienen de la ecuación canónica de la hipérbola.

Otra forma consiste en partir de la ecuación canónica, reemplazar el segundo miembro por cero y despejar y. De este modo se obtienen las ecuaciones de las asíntotas.

Por ejemplo, partimos de la ecuación de una hipérbola horizontal centrada en el origen:

*\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1*

Reemplazamos el segundo miembro por cero:

*\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=0*

Despejamos y:

*\dfrac{y^2}{b^2}=\dfrac{x^2}{a^2}*

*y^2=\dfrac{b^2x^2}{a^2}*

Sacamos raíz cuadrada a ambos miembros:

*\sqrt{y^2}=\sqrt{\dfrac{b^2x^2}{a^2}}*

*y=±\dfrac{b}{a}x*

O sea, *y=\dfrac{b}{a}x~~* o *~~y=-\dfrac{b}{a}x,* que son las ecuaciones de las asíntotas de la hipérbola dada.

Si el centro es otro punto, este método funciona igual. Por ejemplo, probemos con una hipérbola vertical centrada en (h, k):

*\dfrac{(y-k)^2}{a^2}-\dfrac{(x-h)^2}{b^2}=1*

Reemplazamos el segundo miembro por cero y despejamos y:

*\dfrac{(y-k)^2}{a^2}-\dfrac{(x-h)^2}{b^2}=0*

*(y-k)^2=\dfrac{a^2(x-h)^2}{b^2}*

*y-k=±\dfrac{a}{b}(x-h)*

Otra forma es una equivalente en la que se sustituye el segundo miembro por cero y se factoriza por diferencia de cuadrados:

*\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=0*

*\left(\dfrac{x}{a}+\dfrac{y}{b}\right)\left(\dfrac{x}{a}-\dfrac{y}{b}\right)=0*

por propiedad de los números reales, esto equivale a las ecuaciones

*\dfrac{x}{a}+\dfrac{y}{b}=0~~~ o~~~ \dfrac{x}{a}-\dfrac{y}{b}=0*

Despejando y en cada caso se obtiene

*y=\dfrac{b}{a}x~~~ y~~~ y=-\dfrac{b}{a}x*

Cómo graficar las asíntotas

Una vez se tienen las ecuaciones de las asíntotas se puede usar cualquier método para graficar rectas y trazarlas en el plano cartesiano, sin embargo, existe una forma más sencilla para hacerlo. 

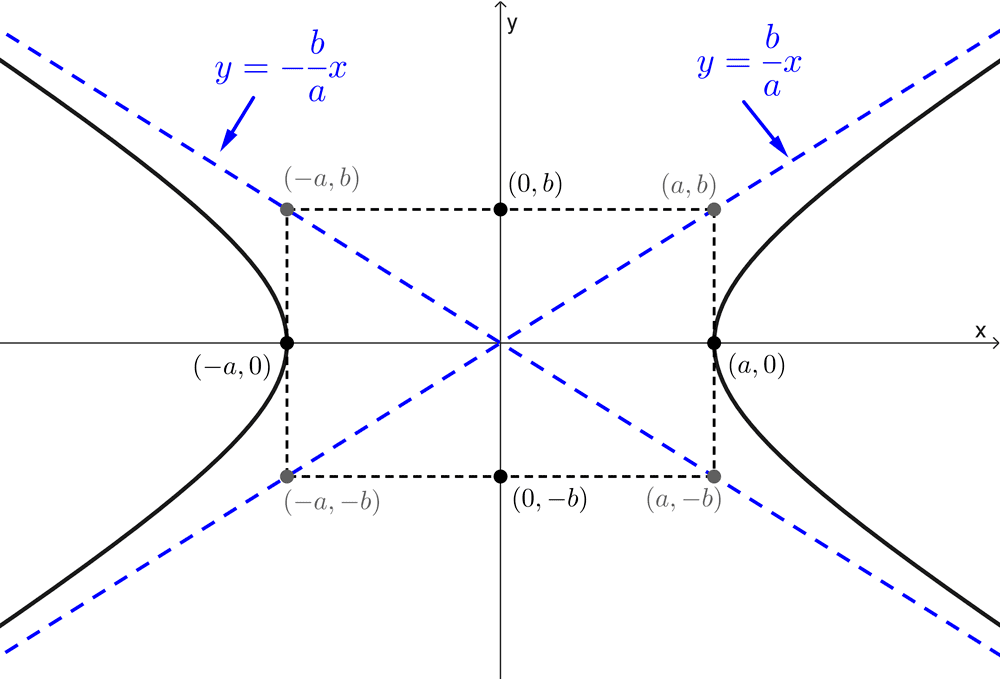
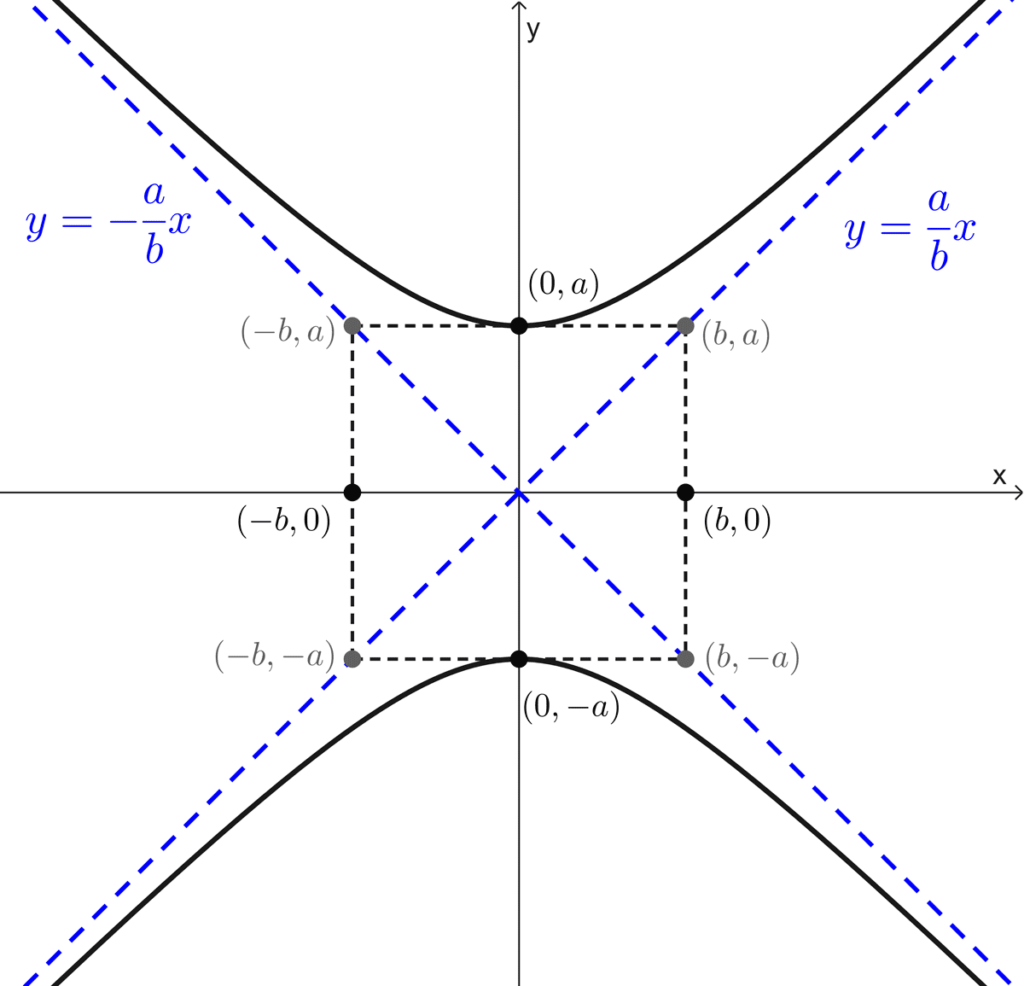
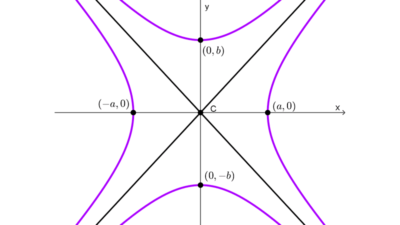
Consideraremos el caso de una hipérbola horizontal centrada en el origen. Conociendo los semiejes a y b podemos localizar los vértices V(a, 0), V’(-a, 0) que son los extremos del eje transverso y los puntos B(0, b), B’(0, -b) que son los extremos del eje conjugado. Los puntos B y B’ no pertenecen a la hipérbola, pero permiten dibujar un rectángulo que los contiene a ellos y a los vértices, este se conoce como rectángulo auxiliar.

Las diagonales del rectángulo auxiliar tienen pendientes b/a y -b/a, las mismas que las de las asíntotas. En consecuencia, al extender estas diagonales obtenemos las asíntotas y = ±(b / a) x. Una vez trazadas, se puede graficar la hipérbola usando las asíntotas como guías.  Esto también funciona si la hipérbola tiene centro en (h, k) y si el eje transverso es vertical.

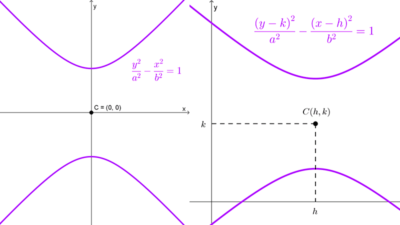
Los siguientes gráficos muestran el rectángulo auxiliar y las asíntotas en los diferentes casos:

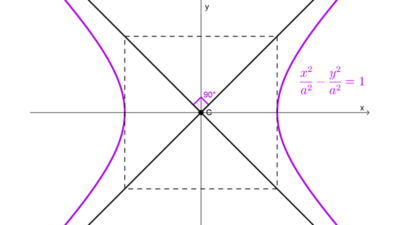
En el caso de una hipérbola equilátera, es decir, aquella en la que sus ejes transverso y conjugado son de igual longitud, el rectángulo auxiliar es un cuadrado, resultando en que las asíntotas son perpendiculares entre sí. 

Ejercicios resueltos

Ejercicio 1

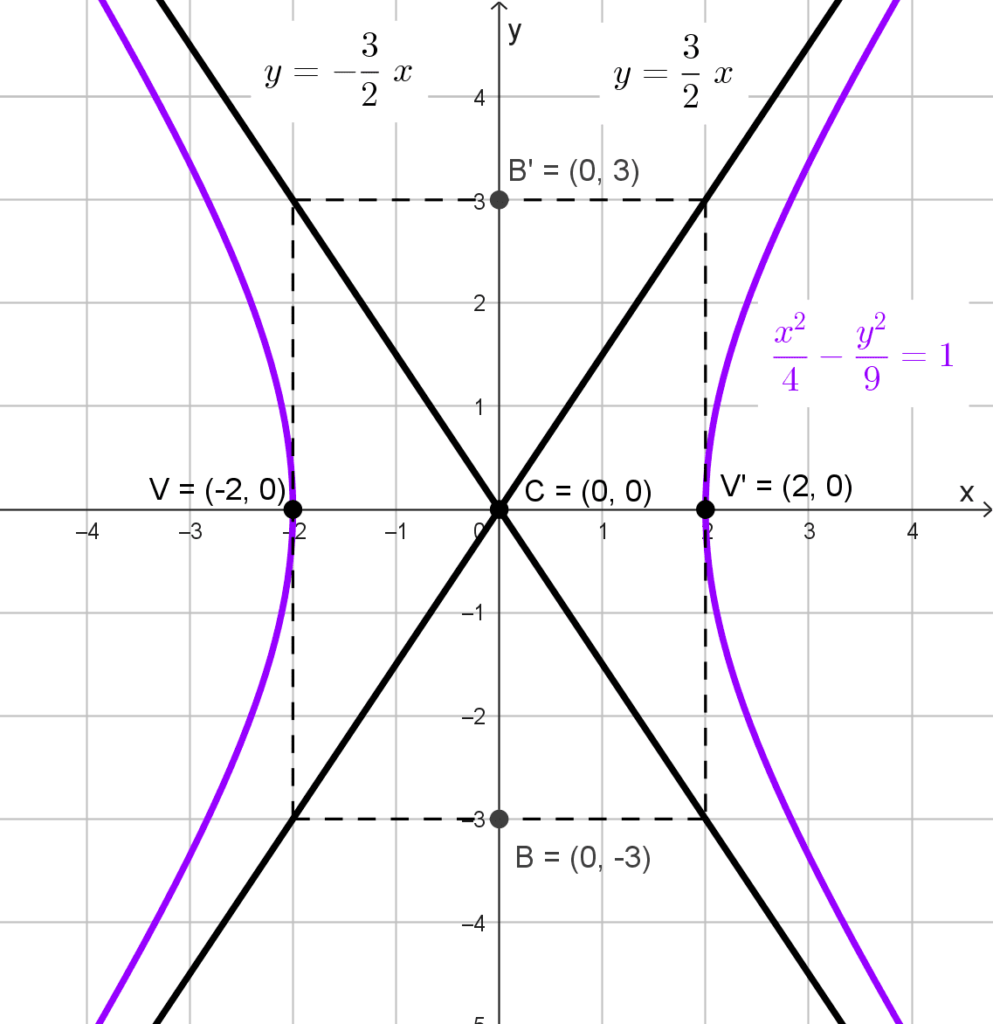
Calcular las asíntotas de la hipérbola *\dfrac{x^2}{4}-\dfrac{y^2}{9}=1*

Solución: identificamos que la ecuación representa una hipérbola horizontal porque el término positivo está asociado a x², además, el centro es el origen de coordenadas.

De la fórmula de la tabla sabemos que en este caso las asíntotas tienen por ecuación *y=±\dfrac{b}{a}x,* donde a y b son las longitudes del semieje transverso y conjugado, respectivamente. Estos valores los extraemos de los denominadores de la ecuación:

*a^2=4→a=\sqrt{4}=2*

*b^2=9→b=\sqrt{9}=3*

Entonces, reemplazando en la fórmula de las asíntotas:

*y=±\dfrac{3}{2}x*

Es decir, las asíntotas de la hipérbola son:

*y=\dfrac{3}{2}x~~~~y~~~~y=-\dfrac{3}{2}x*

Ejercicio 2

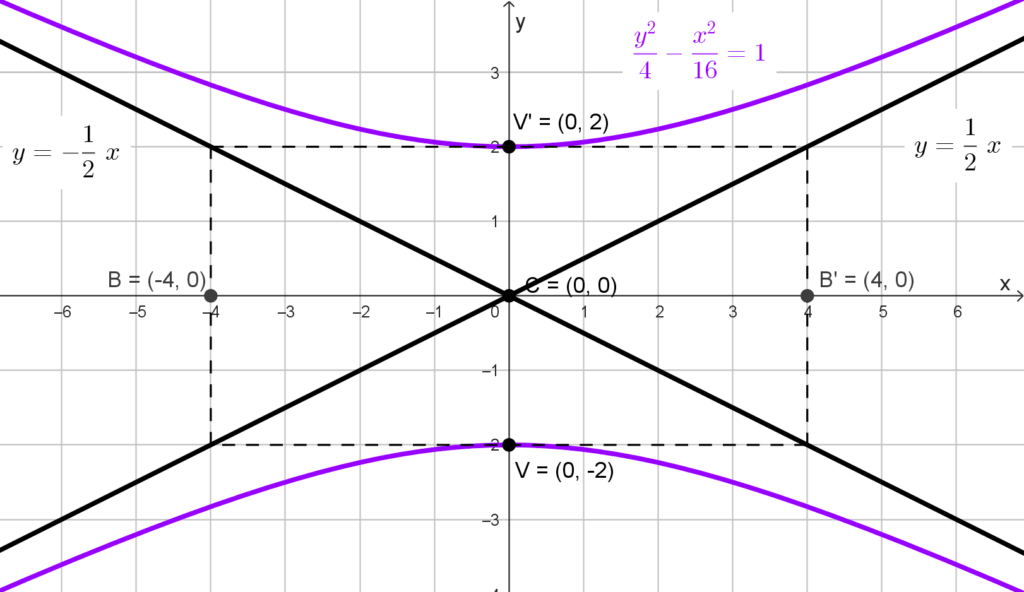
Encontrar las ecuaciones de las asíntotas de la hipérbola *\dfrac{y^2}{4}-\dfrac{x^2}{16}=1*

Solución: identificamos que la ecuación representa una hipérbola vertical, ya que el término positivo está asociado a  y². Además, el centro de la hipérbola está en el origen de coordenadas.

De la fórmula de la tabla sabemos que, en el caso de una hipérbola vertical, las asíntotas tienen por ecuación:

*y=\pm \dfrac{a}{b}x*

donde  a  y  b  son las longitudes de los semiejes transversal y conjugado, respectivamente. Estos valores se obtienen de los denominadores de la ecuación:

*a^2=4 → a=\sqrt{4}=2*

*b^2=16 → b=\sqrt{16}=4*

Sustituyendo estos valores en la fórmula de las asíntotas, obtenemos:

*y=\pm \dfrac{2}{4}x → y=\pm \dfrac{1}{2}x*

Por lo tanto, las asíntotas de la hipérbola son:

*y=\dfrac{1}{2}x~~~~ y~~~~ y=-\dfrac{1}{2}x*

Ejercicio 3

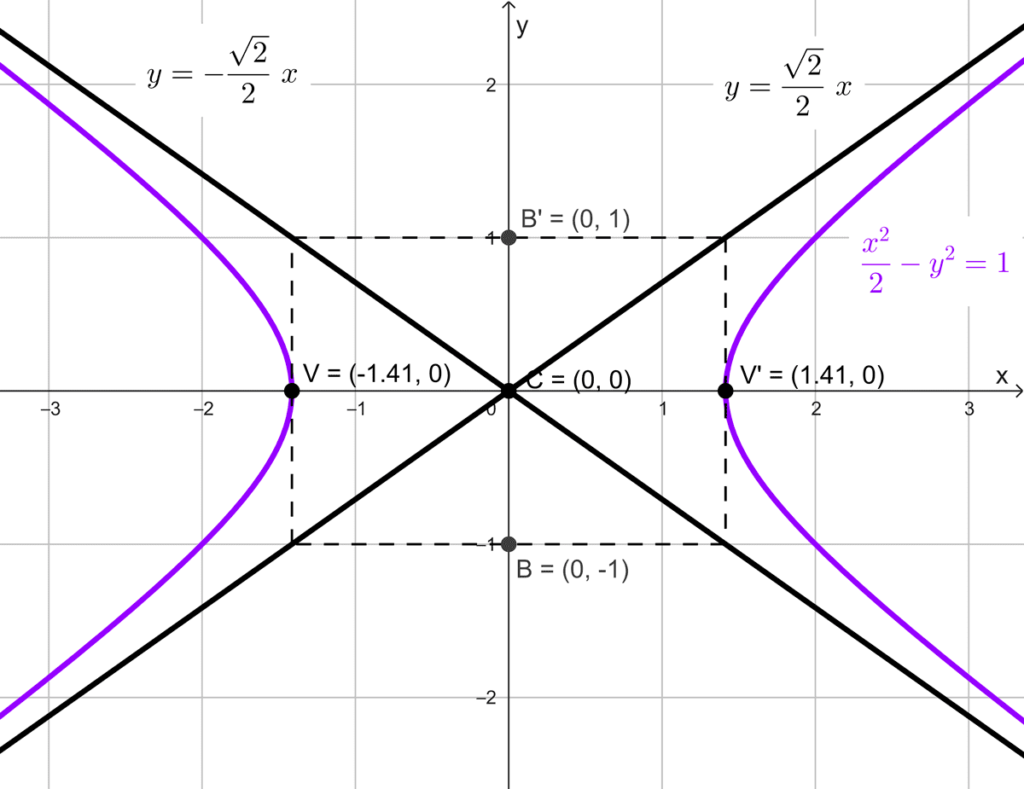
Determinar las asíntotas de la hipérbola *x^2-2y^2=2*

Solución: la ecuación no está en forma canónica, sin embargo, si dividimos ambos miembros entre dos obtenemos esta forma:

*\dfrac{x^2}{2}-y^2=1*

Utilizaremos un procedimiento distinto al anterior, primero reemplazamos el segundo miembro por cero:

*\dfrac{x^2}{2}-y^2=0*

Despejamos y²:

*y^2=\dfrac{x^2}{2}*

Aplicamos raíz cuadrada a ambos lados de la ecuación:

*\sqrt{y^2}=\sqrt{\dfrac{x^2}{2}}*

Esto nos da:

*y=\pm \dfrac{\sqrt{x^2}}{\sqrt{2}}*

Simplificando, obtenemos:

*y=\pm \dfrac{1}{\sqrt{2}}x*

Racionalizamos el denominador:

*y=\pm \dfrac{\sqrt{2}}{2}x*

Por lo tanto, las ecuaciones de las asíntotas son:

*y=\dfrac{\sqrt{2}}{2}x~~~~ y~~~~ y=-\dfrac{\sqrt{2}}{2}x*

En este caso, no fue necesario identificar si la hipérbola es horizontal o vertical, ya que el procedimiento para calcular las asíntotas es general y no depende de esa clasificación.

Ejercicio 4

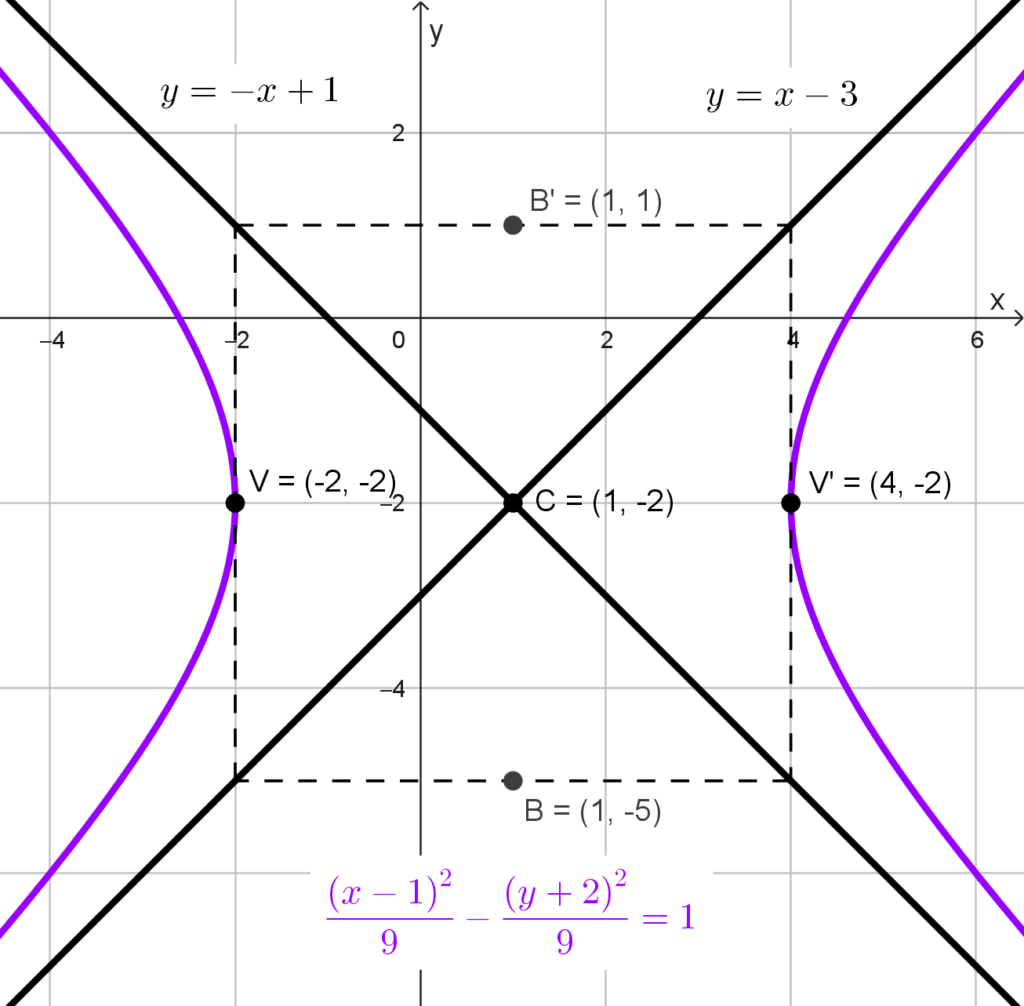
Dada la hipérbola *\dfrac{(x-1)^2}{9}-\dfrac{(y+2)^2}{9}=1,* hallar sus asíntotas.

Solución: primero, identificamos las características de la hipérbola. Observamos que el término positivo está asociado a *(x-1)^2,* lo que indica que se trata de una hipérbola horizontal. El centro de la hipérbola es (h, k)=(1, -2).

De la fórmula general de las asíntotas para una hipérbola horizontal:

*y-k=\pm \dfrac{b}{a}(x-h)*

necesitamos determinar los valores de a y b, que corresponden a las raíces cuadradas de los denominadores de los términos del primer miembro. En este caso:

*a^2=9 → a=\sqrt{9}=3*

*b^2=9 → b=\sqrt{9}=3*

Sustituyendo a, b, h y k en la fórmula, las ecuaciones de las asíntotas son:

*y-(-2)=\pm \dfrac{3}{3}(x-1)*

Simplificamos:

*y+2=\pm (x-1)*

De esta forma, despejamos y para escribir las ecuaciones en su forma estándar:

Para la pendiente positiva (+):

*y+2=x-1 → y=x-3*

Para la pendiente negativa (-):

*y+2=-(x-1) → y=-x+1*

En conclusión, las asíntotas de la hipérbola son las rectas:

*y=x-3~~~ y~~~ y=-x+1*

Nótese que en este caso los semiejes tienen la misma longitud (a = b), por lo que se trata de una hipérbola equilátera. Esto resulta en que la pendiente de las asíntotas es ±1, el ángulo entre ellas es de 90° y el rectángulo auxiliar es un cuadrado. 

Ejercicio 5

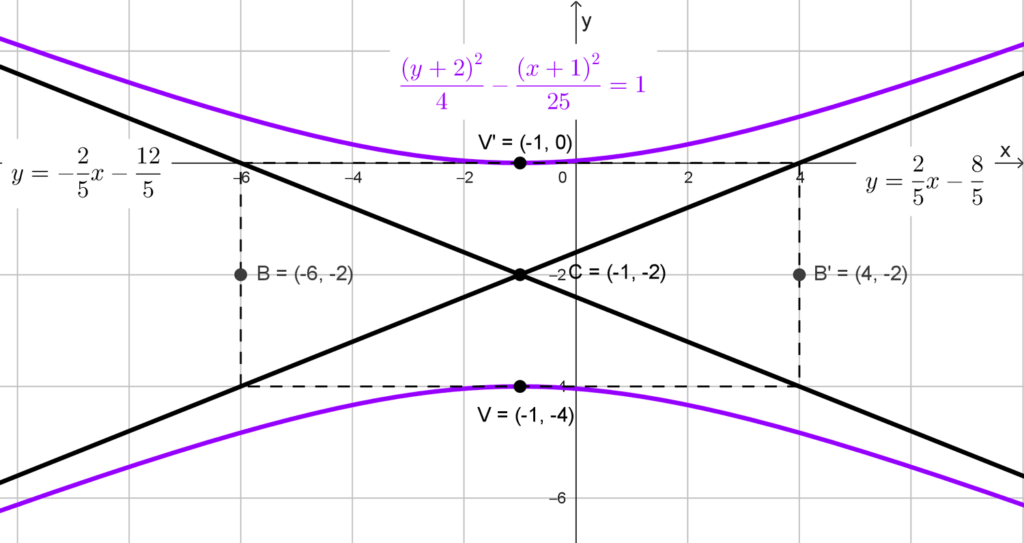
Calcular las asíntotas de la hipérbola de ecuación *\dfrac{(y+2)^2}{4}-\dfrac{(x+1)^2}{25}=1*

Solución: identificamos que el término positivo está asociado a *(y+2)^2,* lo que indica que se trata de una hipérbola vertical. El centro de la hipérbola es (h, k) = (-1, -2).

De la fórmula general de las asíntotas para una hipérbola vertical:

*y-k=\pm \dfrac{a}{b}(x-h)*

necesitamos determinar los valores de a y b, que corresponden a las raíces cuadradas de los denominadores de los términos del primer miembro. En este caso:

*a^2=4 → a=\sqrt{4}=2*

*b^2=25 → b=\sqrt{25}=5*

Sustituyendo a, b, h y k en la fórmula, las ecuaciones de las asíntotas son:

*y-(-2)=\pm \dfrac{2}{5}(x-(-1))*

Simplificamos:

*y+2=\pm \dfrac{2}{5}(x+1)*

Finalmente, despejamos y para sacar las ecuaciones en su forma estándar:

Para la pendiente positiva (+):

*y+2=\dfrac{2}{5}(x+1) → y=\dfrac{2}{5}x+\dfrac{2}{5}-2 → y=\dfrac{2}{5}x-\dfrac{8}{5}*

Para la pendiente negativa (-):

*y+2=-\dfrac{2}{5}(x+1) → y=-\dfrac{2}{5}x-\dfrac{2}{5}-2 → y=-\dfrac{2}{5}x-\dfrac{12}{5}*

En conclusión, las asíntotas de la hipérbola son las rectas:

*y=\dfrac{2}{5}x-\dfrac{8}{5}~~~ y~~~ y=-\dfrac{2}{5}x-\dfrac{12}{5}*

Ejercicio 6

Obtener las ecuaciones de las asíntotas de *-7x^2+12y^2+28x+72y-4=0*

Solución: no tenemos la forma canónica sino la ecuación general de la hipérbola, pero completando cuadrados se obtiene una forma equivalente:

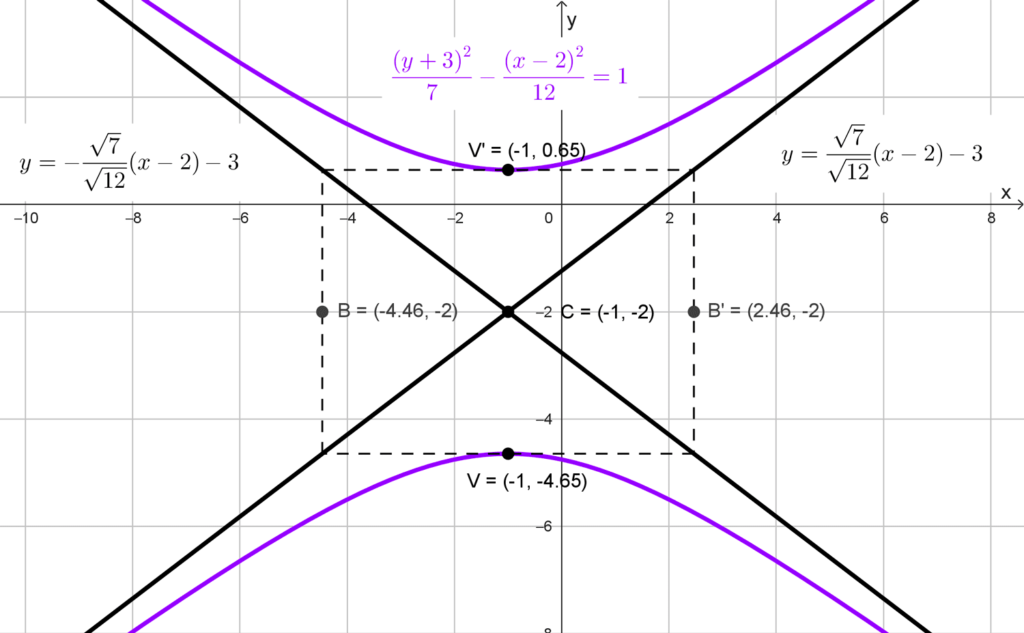
*\dfrac{(y+3)^2}{7}-\dfrac{(x-2)^2}{12}=1*

Utilizaremos un procedimiento sin fórmulas. Para comenzar, sustituimos el segundo miembro por cero para trabajar con las asíntotas:

*\dfrac{(y+3)^2}{7}-\dfrac{(x-2)^2}{12}=0*

Reescribimos esta ecuación como una diferencia de cuadrados y factorizamos:

*\left( \dfrac{y+3}{\sqrt{7}}+\dfrac{x-2}{\sqrt{12}} \right)\left( \dfrac{y+3}{\sqrt{7}}-\dfrac{x-2}{\sqrt{12}} \right)=0*

Por propiedad de los números reales, esto equivale a resolver las dos ecuaciones:

*\dfrac{y+3}{\sqrt{7}}+\dfrac{x-2}{\sqrt{12}}=0~~~ o~~~ \dfrac{y+3}{\sqrt{7}}-\dfrac{x-2}{\sqrt{12}}=0*

Despejamos y en cada caso:

De *\dfrac{y+3}{\sqrt{7}}+\dfrac{x-2}{\sqrt{12}}=0:*

*\dfrac{y+3}{\sqrt{7}}=-\dfrac{x-2}{\sqrt{12}}*

*y+3=-\dfrac{\sqrt{7}}{\sqrt{12}}(x-2)*

*y=-\dfrac{\sqrt{7}}{\sqrt{12}}(x-2)-3*

De *\dfrac{y+3}{\sqrt{7}}-\dfrac{x-2}{\sqrt{12}}=0:*

*\dfrac{y+3}{\sqrt{7}}=\dfrac{x-2}{\sqrt{12}}*

*y+3=\dfrac{\sqrt{7}}{\sqrt{12}}(x-2)*

*y=\dfrac{\sqrt{7}}{\sqrt{12}}(x-2)-3*

Finalmente, las ecuaciones de las asíntotas son:

*y=\dfrac{\sqrt{7}}{\sqrt{12}}(x-2)-3~~~ y~~~ y=-\dfrac{\sqrt{7}}{\sqrt{12}}(x-2)-3*

Bibliografía consultada

Para respaldar la información de este artículo, se ha recurrido a las siguientes obras.

• Engler, A. y otros. (2020). Geometría Analítica. Universidad Nacional del Litoral.
• Fuller, G. y Tarwater, D. (1995). Geometría Analítica (7ma edición). Pearson Educación.
• Lehmann, C. (1989). Geometría Analítica. Limusa.
• Leithold. L. (1992). Álgebra y Trigonometría con Geometría Analítica. Oxford University Press.
• Sullivan, M. (2006). Álgebra y Trigonometría. Pearson Educación.
• Swokowski, E. y Cole, J. (2009). Álgebra y Trigonometría con Geometría Analítica. Cengage Learning.