Hipérbolas conjugadas

Daniel Machado · Actualizado el 03/02/2025

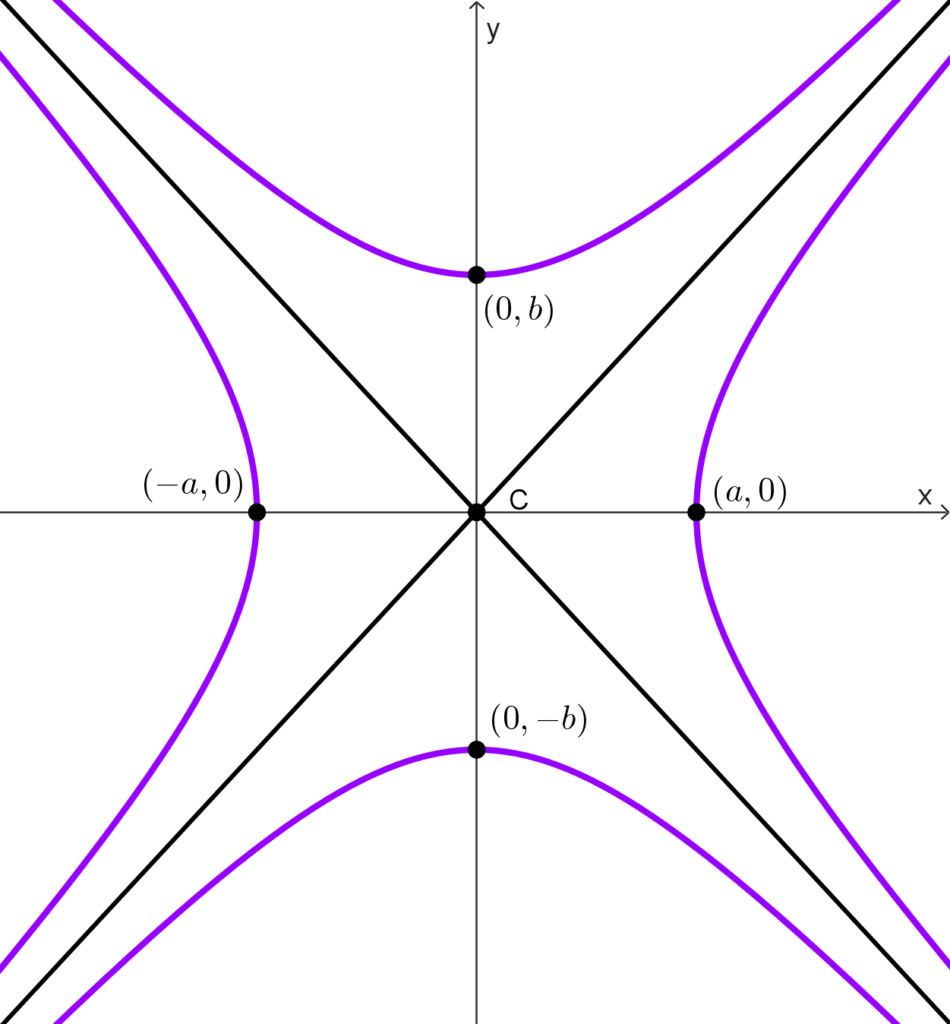
Dos hipérbolas son conjugadas una de la otra si el eje transversal de cada una es el eje conjugado de la otra. Las hipérbolas conjugadas tienen las mismas asíntotas y el mismo centro, los cuatro focos están a la misma distancia del centro.

Gráfica de hipérbolas conjugadas en el plano cartesiano — Gráfica de dos hipérbolas conjugadas

A continuación, veremos cómo encontrar las ecuaciones de las hipérbolas conjugadas. Si aún no conoces el significado de la hipérbola en matemáticas, te recomiendo revisar antes el artículo principal donde explicamos su concepto, definición, fórmulas y propiedades.

Índice

Ecuaciones

Si la ecuación de una hipérbola es

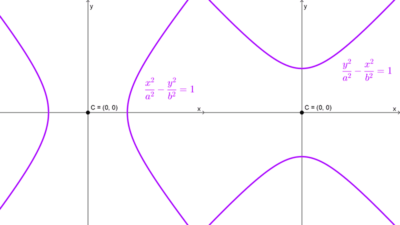
*\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1*

entonces, de acuerdo a la definición, su hipérbola conjugada tiene por ecuación

*\dfrac{y^2}{b^2}-\dfrac{x^2}{a^2}=1*

Nótese que la ecuación de la hipérbola conjugada puede obtenerse cambiando de signo los términos del primer miembro en la ecuación canónica.

Hipérbola original	Hipérbola conjugada	Centro
\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1	\dfrac{y^2}{b^2}-\dfrac{x^2}{a^2}=1	(0, 0)
\dfrac{y^2}{a^2}-\dfrac{x^2}{b^2}=1	\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1	(0, 0)
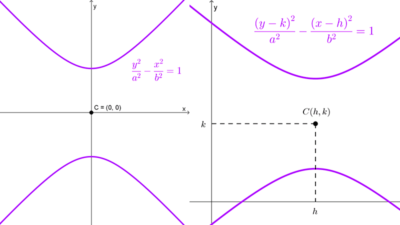
\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1	\dfrac{(y-k)^2}{b^2}-\dfrac{(x-h)^2}{a^2}=1	(h, k)
\dfrac{(y-k)^2}{b^2}-\dfrac{(x-h)^2}{a^2}=1	\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1	(h, k)

Si una hipérbola es horizontal, su conjugada es vertical; del mismo modo, si la original es vertical, su conjugada es horizontal.

Ejemplos

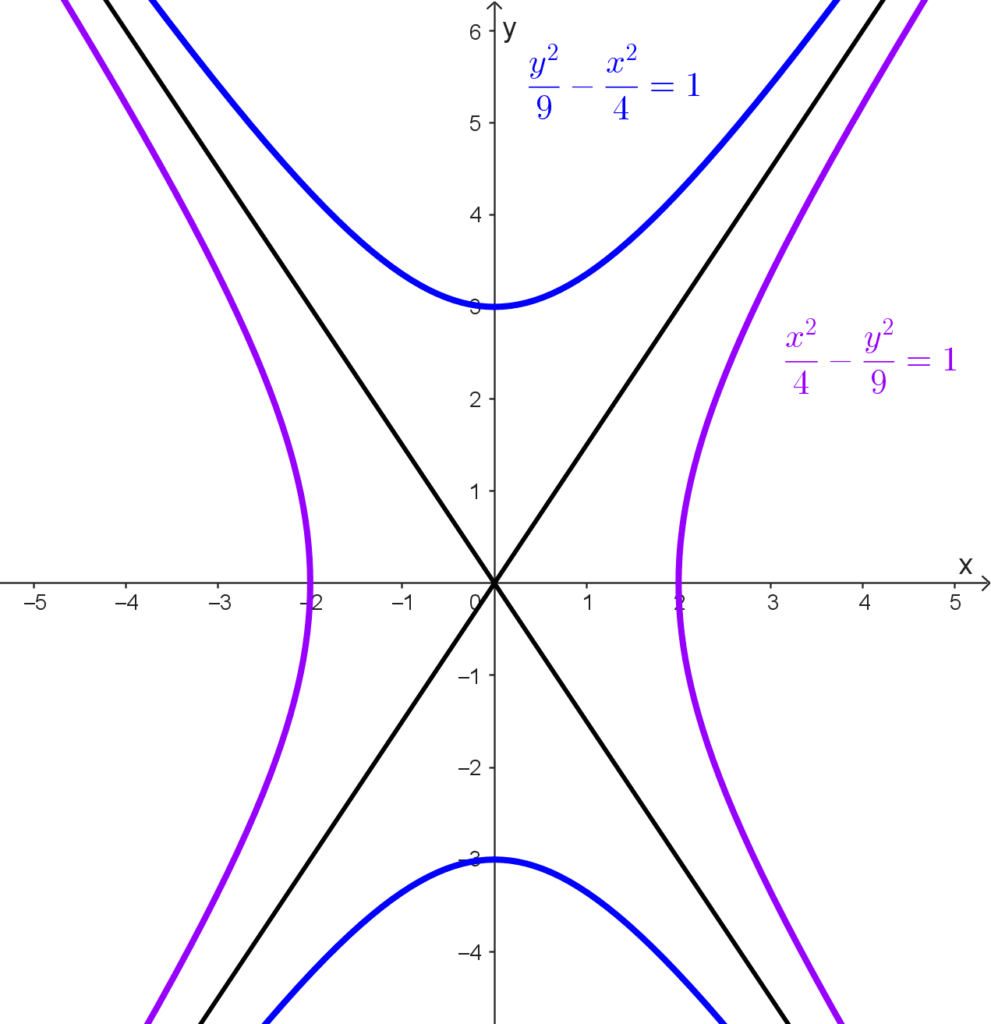
La hipérbola conjugada de *\dfrac{x^2}{4}-\dfrac{y^2}{9}=1* es *\dfrac{y^2}{9}-\dfrac{x^2}{4}=1.*
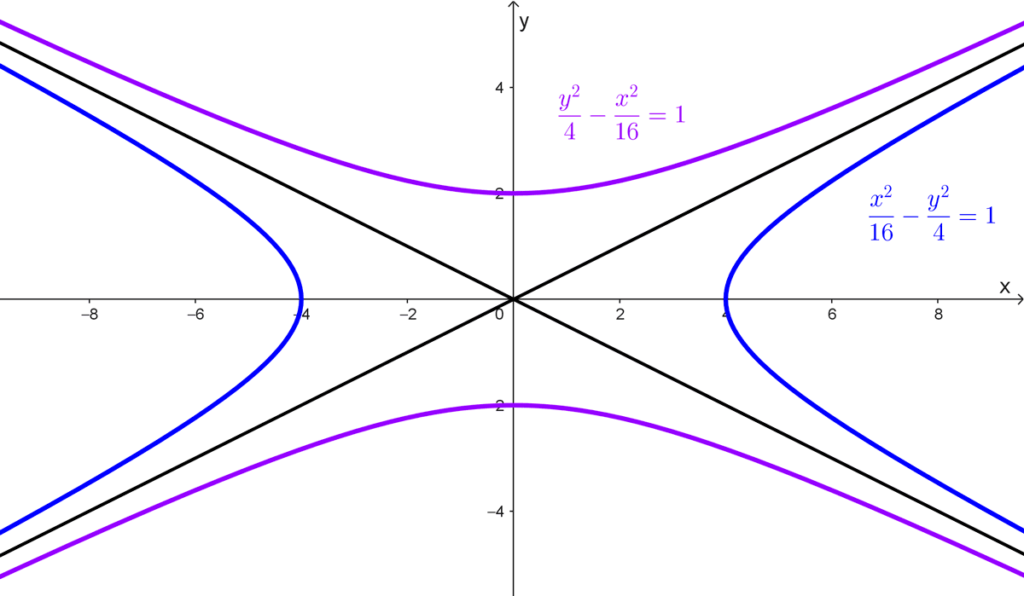
Dada la ecuación de la hipérbola *\dfrac{y^2}{4}-\dfrac{x^2}{16}=1,* su conjugada es *\dfrac{x^2}{16}-\dfrac{y^2}{4}=1.*
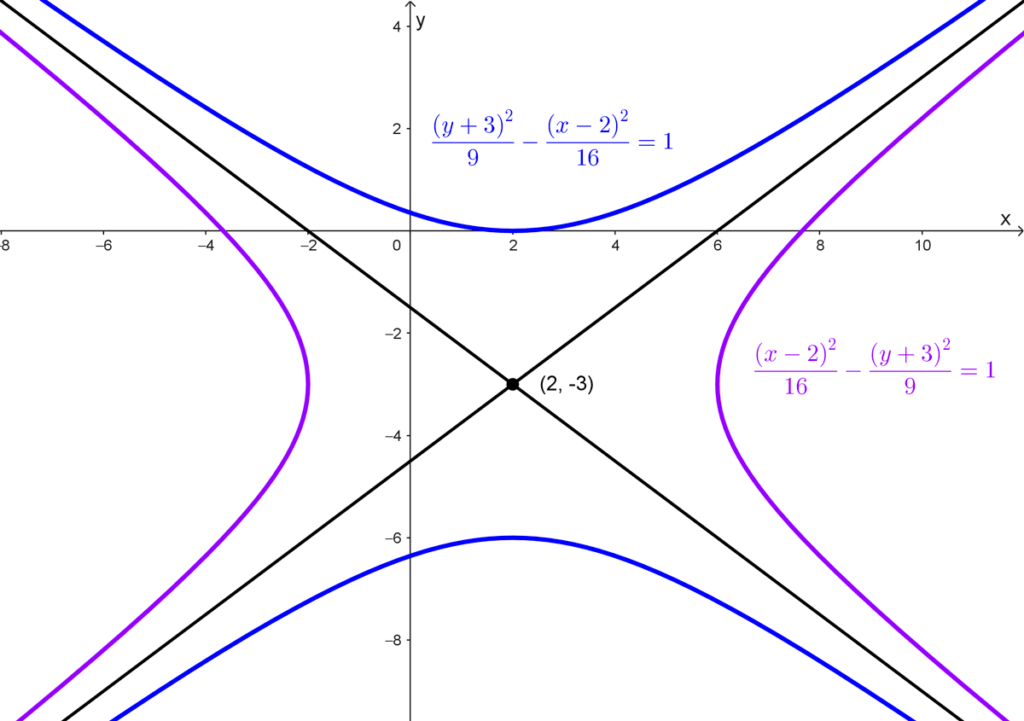
La conjugada de la hipérbola *\dfrac{(x-2)^2}{16}-\dfrac{(y+3)^2}{9}=1* es *\dfrac{(y+3)^2}{9}-\dfrac{(x-2)^2}{16}=1.*
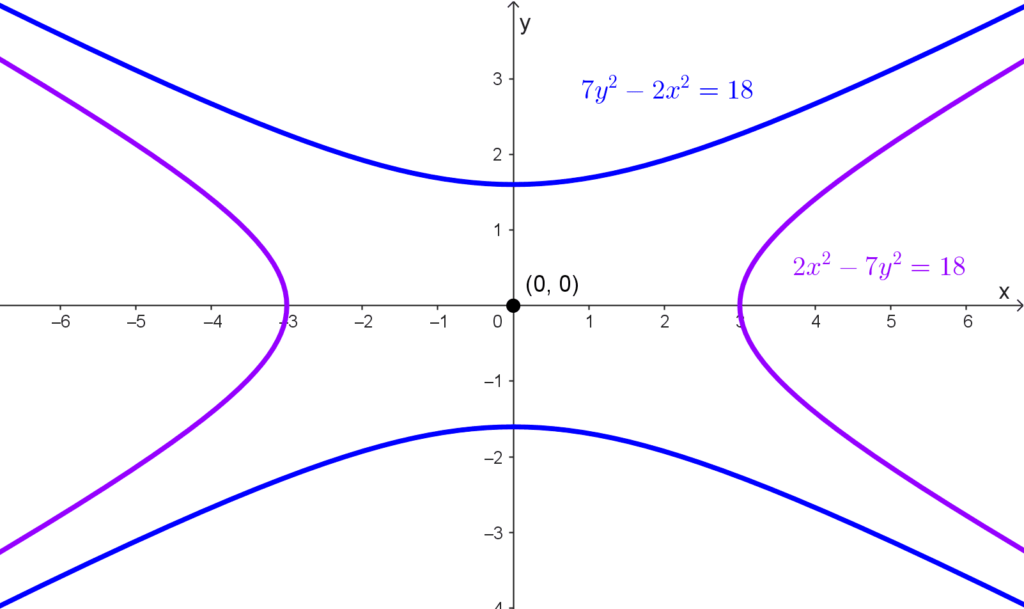
Si la ecuación de una hipérbola es *2x^2-7y^2=18,* entonces su hipérbola conjugada tiene por ecuación a *7y^2-2x^2=18.*

hipérbolas conjugadas con centro en (0, 0) — Gráficas del ejemplo 1

hipérbolas conjugadas con centro en el origen — Gráficas del ejemplo 2

hipérbolas conjugadas con centro fuera del origen — Gráficas del ejemplo 3

Características

Las siguientes son las propiedades de las hipérbolas conjugadas:

Dos hipérbolas conjugadas tienen las mismas asíntotas y el mismo centro.
La distancia focal de dos hipérbolas conjugadas es la misma.
Los focos de un par de hipérbolas conjugadas están sobre una circunferencia.
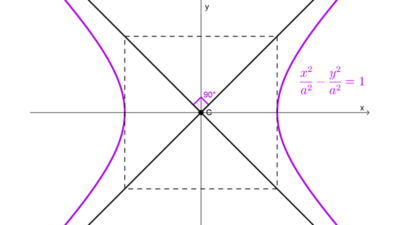
Si una hipérbola es equilátera, su hipérbola conjugada también es equilátera. Además, la excentricidad es la misma en ambas: *e=\sqrt{2}.* La excentricidad es la misma solo cuando se trata de hipérbolas equiláteras.