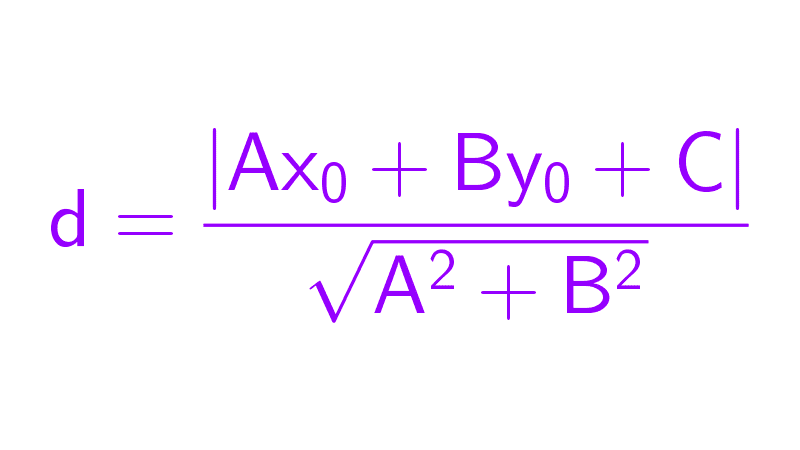
Distancia entre dos rectas
La distancia entre dos rectas en el plano es una medida que caracteriza su separación mínima. Si dos rectas son secantes (se cortan en un punto) o coincidentes (son la misma recta), la distancia entre ellas es cero, ya que tienen al menos un punto en común.
Sin embargo, cuando las rectas son paralelas y no coincidentes, la distancia se define como la longitud del segmento perpendicular trazado desde cualquier punto de una recta hasta la otra recta, y es una cantidad positiva constante.
Dadas dos rectas paralelas en su forma general: r: Ax + By + C1 = 0 y s: Ax + By + C2 = 0 donde los coeficientes A y B son idénticos (condición de paralelismo), la distancia entre ellas está dada por la siguiente fórmula:
\(d(r, s)=\dfrac{|C_2-C_1|}{\sqrt{A^2+B^2}}\)
Esta expresión se obtiene tomando un punto cualquiera de una recta y calculando su distancia a la otra recta. Es importante saber que esta expresión sólo es aplicable cuando las rectas están expresadas con los mismos coeficientes para x e y; si las ecuaciones no están en esta forma, primero deben manipularse algebraicamente para lograr dicha estructura.
Índice
Ejemplos
Realizaremos primero un ejemplo detallado explicando el procedimiento geométrico que da origen a la fórmula de la distancia, en los siguientes ejemplos practicaremos la aplicación de la fórmula que se dio al principio.
Ejemplo 1
Calcular la distancia entre las rectas r: 15x + 8y + 68 = 0 y s: 15x + 8y - 51 = 0.
Solución
Observamos primero que los coeficientes de x e y en ambas ecuaciones son iguales: 15 y 8, respectivamente. Esto nos indica de inmediato que las rectas son paralelas, ya que sus pendientes son idénticas. No son coincidentes, pues el término independiente es diferente en cada ecuación.
Para hallar la distancia entre ellas podemos usar un procedimiento geométrico que consiste en tomar un punto cualquiera perteneciente a una de las rectas y luego calcular su distancia a la otra recta. Para simplificar los cálculos, es conveniente elegir un punto de coordenadas sencillas. Una estrategia frecuente es hacer x = 0 en la ecuación de una de las rectas y despejar el valor correspondiente de y.
Tomemos la primera recta, \(r: 15x+8y+68=0.\) Sustituyendo \(x=0,\) la ecuación se reduce a \(8y+68=0.\) Despejamos y: \(8y=-68,\) lo que nos da
\(y=-\dfrac{68}{8}=-\dfrac{17}{2}\)
Así, hemos obtenido el punto \(P\left(0,-\dfrac{17}{2}\right),\) que pertenece a la primera recta.
Ahora, la distancia entre las dos rectas paralelas será exactamente la distancia desde este punto P hasta la segunda recta, dada por 15x + 8y - 51 = 0. Es decir, d(r, s) = d(P, s). Para calcularlo, aplicamos la fórmula de distancia de un punto a una recta, que recordamos es:
\(d=\dfrac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}\)
donde (x0, y0) son las coordenadas del punto y Ax + By + C = 0 es la ecuación de la recta.
Identificamos los coeficientes de la segunda recta: A = 15, B = 8 y C = -51. Sustituimos las coordenadas de P(0, -17/2):
\(d(P, s)=\dfrac{\left| 15(0)+8\left(-\dfrac{17}{2}\right)-51 \right|}{\sqrt{15^2+8^2}}\)
Realizamos las operaciones:
\(d(P, s)=\dfrac{\left| 15(0)+8\left(-\dfrac{17}{2}\right)-51 \right|}{\sqrt{15^2+8^2}}=\dfrac{\left| 0-68-51 \right|}{\sqrt{225+64}}=\dfrac{|-119|}{\sqrt{289}}=\dfrac{119}{17}=7\)
Por lo tanto, la distancia entre las dos rectas paralelas dadas es de 7 unidades.
Este procedimiento, basado en elegir un punto de una recta y medir su distancia a la otra, es la esencia de la deducción de la fórmula general \(d=\dfrac{|C_2-C_1|}{\sqrt{A^2+B^2}},\) que utilizaremos de forma directa en los siguientes ejemplos.
Ejemplo 2
Determinar la distancia entre las rectas 2x + 6y - 5 = 0 y 6x + 18y + 45 = 0.
Solución
Observamos primero que los coeficientes de x e y en ambas ecuaciones no son directamente iguales, pero notamos que la segunda ecuación podría ser un múltiplo de la primera. Para verificarlo, dividimos entre 3 en la segunda ecuación:
\(\dfrac{6x+18y+45}{3}=\dfrac{0}{3}→2x+6y+15=0\)
Vemos entonces que la ecuación resultante tiene los mismos coeficientes A = 2 y B = 6 que la primera recta, confirmando que son paralelas. Además, el término independiente es diferente: la primera tiene C1 = -5 y esta equivalente tiene C2 = 15. Así, podemos aplicar la fórmula de distancia para rectas paralelas con A = 2, B = 6, C1 = -5 y C2 = 15.
Calculamos la distancia usando la fórmula:
\(d=\dfrac{|C_2-C_1|}{\sqrt{A^2+B^2}}=\dfrac{|15-(-5)|}{\sqrt{2^2+6^2}}=\dfrac{|15+5|}{\sqrt{4+36}}=\dfrac{20}{\sqrt{40}}=\dfrac{20}{2\sqrt{10}}=\dfrac{10}{\sqrt{10}}\)
Racionalizando:
\(d=\dfrac{10}{\sqrt{10}}=\sqrt{10}\)
Por lo tanto, la distancia entre las rectas es \(\sqrt{10}\) unidades, aproximadamente 3,16 unidades.
Los pasos para calcular la distancia entre dos líneas rectas en el plano se pueden resumir así:
1) Confirmar el paralelismo y la no coincidencia: dos rectas son paralelas si sus pendientes son iguales. En la forma general Ax + By + C = 0, esto se traduce en que los coeficientes A y B de ambas ecuaciones sean proporcionales. Es decir, debe cumplirse que \(\frac{A_1}{A_2}=\frac{B_1}{B_2}.\) Si, además, los términos independientes también guardan la misma proporción (\(\frac{A_1}{A_2}=\frac{B_1}{B_2}=\frac{C_1}{C_2}\)), las rectas son coincidentes y la distancia es cero.
Si la ecuaciones están en forma explícita, las pendientes deben ser iguales (m1 = m2) y las ordenadas al origen distintas (b1 ≠ b2).
2) Estandarizar los coeficientes lineales: si las ecuaciones no tienen los mismos coeficientes A y B (aunque sean proporcionales), debemos manipular algebraicamente una de ellas para que coincidan. Esto se logra multiplicando o dividiendo toda la ecuación por una constante adecuada. Es importante saber que esta operación sí modifica el término independiente.
3) Identificar los coeficientes y términos independientes y aplicar la fórmula: una vez que ambas ecuaciones tengan exactamente los mismos valores para A y B, las escribimos en la forma Ax + By + C1 = 0 y Ax + By + C2 = 0. Extraemos los valores de A, B, C1 y C2, y aplicamos la fórmula de distancia:
\(d=\dfrac{|C_2-C_1|}{\sqrt{A^2+B^2}}\)
El resultado puede expresarse en forma exacta (con radicales o fracciones) o, si se requiere, como una aproximación decimal. La distancia obtenida es siempre un número no negativo, expresado en las mismas unidades de longitud que las coordenadas.
Ejemplo 3
Hallar la distancia que separa las rectas x + y + 3 = 0 y 2x + 2y - 5 = 0.
Solución
Notamos que la segunda ecuación, \(2x+2y-5=0,\) puede simplificarse dividiendo toda la ecuación entre 2, obteniendo:
\(x+y-\dfrac{5}{2}=0\)
Ahora ambas rectas tienen la misma forma con coeficientes \(A=1\) y \(B=1,\) lo que confirma que son paralelas. Identificamos los términos independientes: para la primera recta, \(C_1=3;\) para la segunda recta equivalente, \(C_2=-\dfrac{5}{2}.\) Aplicamos la fórmula:
\(d=\dfrac{|C_2-C_1|}{\sqrt{A^2+B^2}}=\dfrac{\left|-\dfrac{5}{2}-3 \right|}{\sqrt{1^2+1^2}}=\dfrac{\left|-\dfrac{5}{2}-\dfrac{6}{2} \right|}{\sqrt{1+1}}=\dfrac{\left|-\dfrac{11}{2} \right|}{\sqrt{2}}=\dfrac{\dfrac{11}{2}}{\sqrt{2}}=\dfrac{11}{2\sqrt{2}}=\dfrac{11\sqrt{2}}{4}\)
La distancia es \(\dfrac{11\sqrt{2}}{4}≈3,89\) unidades.
Ejemplo 4
Calcular la distancia entre las rectas 3x - 4y = 0 y 3x + 4y + 3 = 0.
Solución
A simple vista, los coeficientes de x son iguales (3) y los de y son opuestos (-4 y 4). Esto no garantiza paralelismo. Para comprobarlo, despejamos la pendiente de cada recta.
De la primera, \(3x-4y=0,\) obtenemos \(y=\dfrac{3}{4}x,\) con pendiente \(m_1=\dfrac{3}{4}.\)
De la segunda, \(3x+4y+3=0,\) obtenemos \(y=-\dfrac{3}{4}x-\dfrac{3}{4},\) con pendiente \(m_2=-\dfrac{3}{4}.\)
Como las pendientes son distintas (\(\frac{3}{4} ≠-\frac{3}{4}\)), las rectas no son paralelas, sino que son secantes. Cuando dos rectas se cortan, la distancia entre ellas es cero, pues existe al menos un punto en común. Por lo tanto, no se aplica la fórmula de distancia entre rectas paralelas y el resultado es directamente d = 0.
Ejemplo 5
Obtener la distancia entre las rectas y = 2x + 3 y y = 2x - 7.
Solución
Ambas rectas están dadas en forma pendiente-ordenada y comparten la misma pendiente m = 2, lo cual las hace paralelas, además, sus ordenadas son diferentes. Para usar la fórmula general, primero las escribimos en la forma Ax + By + C = 0. La primera recta es 2x - y + 3 = 0 y la segunda es 2x - y - 7 = 0. Identificamos A = 2, B = -1, C1 = 3 y C2 = -7. Aplicamos la fórmula:
\(d=\dfrac{|C_2-C_1|}{\sqrt{A^2+B^2}}=\dfrac{|(-7)-3|}{\sqrt{2^2+(-1)^2}}=\dfrac{|-10|}{\sqrt{4+1}}=\dfrac{10}{\sqrt{5}}=2\sqrt{5}\)
La distancia entre las rectas es \(2\sqrt{5}≈4,47\) unidades.
¿Te está sirviendo este artículo? ¡Por favor, califícalo!
Ejemplo 6
Encontrar la distancia entre las rectas 4x + y = 6 y 12x + 3y = 14.
Solución
Observamos que la segunda ecuación es múltiplo de la primera si dividimos entre 3: \(12x+3y=14\) se convierte en \(4x+y=\dfrac{14}{3}\)
Ahora ambas rectas tienen los coeficientes \(A=4\) y \(B=1.\) Escribiéndolas en la forma general, la primera es \(4x+y-6=0\) (con \(C_1=-6\)) y la segunda equivalente es \(4x+y-\dfrac{14}{3}=0\) (con \(C_2=-14/3\)). Calculamos la distancia:
\(d=\dfrac{|C_2-C_1|}{\sqrt{A^2+B^2}}=\dfrac{\left|-\dfrac{14}{3}-(-6) \right|}{\sqrt{4^2+1^2}}=\dfrac{\left|-\dfrac{14}{3}+6 \right|}{\sqrt{16+1}}=\dfrac{\left|-\dfrac{14}{3}+\dfrac{18}{3} \right|}{\sqrt{17}}=\dfrac{\left| \dfrac{4}{3} \right|}{\sqrt{17}}=\dfrac{4}{3\sqrt{17}}=\dfrac{4\sqrt{17}}{51}\)
La distancia es \(\dfrac{4\sqrt{17}}{51}≈0,32\) unidades.
Ejemplo 7
Calcular la distancia que separa las rectas x - y + 7 = 0 y x - y + 11 = 0.
Solución
Aquí, los coeficientes de x e y son idénticos en ambas ecuaciones (A = 1, B = -1), confirmando que son paralelas. Los términos independientes son C1 = 7 y C2 = 11. Aplicamos directamente la fórmula:
\(d=\dfrac{|C_2-C_1|}{\sqrt{A^2+B^2}}=\dfrac{|11-7|}{\sqrt{1^2+(-1)^2}}=\dfrac{4}{\sqrt{1+1}}=\dfrac{4}{\sqrt{2}}=2\sqrt{2}\)
La distancia entre las rectas es \(2\sqrt{2}≈2,83\) unidades.
Ejemplo 8
Determinar la distancia entre las rectas -x + 3y = 5 y 5x - 15y = -8.
Solución
Para verificar el paralelismo, manipulamos las ecuaciones. La primera recta, \(-x+3y=5,\) tiene coeficientes \(A=-1\), \(B=3.\) La segunda, \(5x-15y=-8,\) podemos dividirla entre -5 para igualar los coeficientes, obteniendo:
\(-x+3y=\dfrac{8}{5}\)
que acomodando es:
\(-x+3y-\dfrac{8}{5}=0\)
Así, obtenemos una ecuación equivalente con los mismos coeficientes \(A=-1\), \(B=3.\) Confirmamos que son paralelas, con \(C_1=-5\) (de \(-x+3y-5=0\)) y \(C_2=-\dfrac{8}{5}\). Aplicamos la fórmula:
\(d=\dfrac{|C_2-C_1|}{\sqrt{A^2+B^2}}=\dfrac{\left|-\dfrac{8}{5}-(-5) \right|}{\sqrt{(-1)^2+3^2}}=\dfrac{\left|-\dfrac{8}{5}+5 \right|}{\sqrt{1+9}}=\dfrac{\left|-\dfrac{8}{5}+\dfrac{25}{5} \right|}{\sqrt{10}}=\dfrac{\left| \dfrac{17}{5} \right|}{\sqrt{10}}=\dfrac{17}{5\sqrt{10}}=\dfrac{17\sqrt{10}}{50}\)
La distancia es \(\dfrac{17\sqrt{10}}{50}≈1,08\) unidades.
Demostración
Consideremos dos rectas paralelas y distintas en el plano cartesiano, dadas en su forma general:
r: Ax + By + C1 = 0
s: Ax + By + C2 = 0
donde A y B no son simultáneamente cero. La igualdad de estos coeficientes asegura que las rectas tienen la misma pendiente, es decir, son paralelas. Asumimos C1 ≠ C2, pues si fueran iguales las rectas serían coincidentes y su distancia sería cero.
La distancia d(r, s) entre dos rectas paralelas se define como la longitud del segmento perpendicular común, y es constante. Equivalentemente, podemos calcularla tomando cualquier punto P perteneciente a una de las rectas (por ejemplo, r) y hallando su distancia a la otra recta (s).
Sea entonces P(x0, y0) un punto cualquiera de la recta r. Por pertenecer a ella, satisface:
\(Ax_0+By_0+C_1=0 \quad → \quad Ax_0+By_0=-C_1\)
Ahora, aplicamos la fórmula de distancia de un punto a una recta para calcular d(P, s), donde la ecuación de s es Ax + By + C2 = 0:
\(d(P, s)=\dfrac{|Ax_0+By_0+C_2|}{\sqrt{A^2+B^2}}\)
Sustituimos \(Ax_0+By_0=-C_1\) en el numerador:
\(d(P, s)=\dfrac{|(-C_1)+C_2|}{\sqrt{A^2+B^2}}=\dfrac{|C_2-C_1|}{\sqrt{A^2+B^2}}\)
Dado que P es un punto arbitrario de r, este resultado no depende de la elección particular del punto, confirmando que la distancia entre las rectas es constante. Por lo tanto, hemos demostrado que la distancia entre dos rectas paralelas Ax + By + C1 = 0 y Ax + By + C2 = 0 está dada por la expresión:
\(d(r, s)=\dfrac{|C_2-C_1|}{\sqrt{A^2+B^2}}\)
Bibliografía
- Engler, A., Müller, D., Vrancken, S. y Hecklein, M. (2020). Geometría analítica. Universidad Nacional del Litoral.
- Fuller, G. y Tarwater, D. (1995). Geometría analítica (7.ª ed.). Pearson Educación.
- Oteyza, E., Lam, E., Hernández, C., Carrillo, Á. y Ramírez, A. (2011). Geometría analítica (3.ª ed.). Pearson Educación.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta

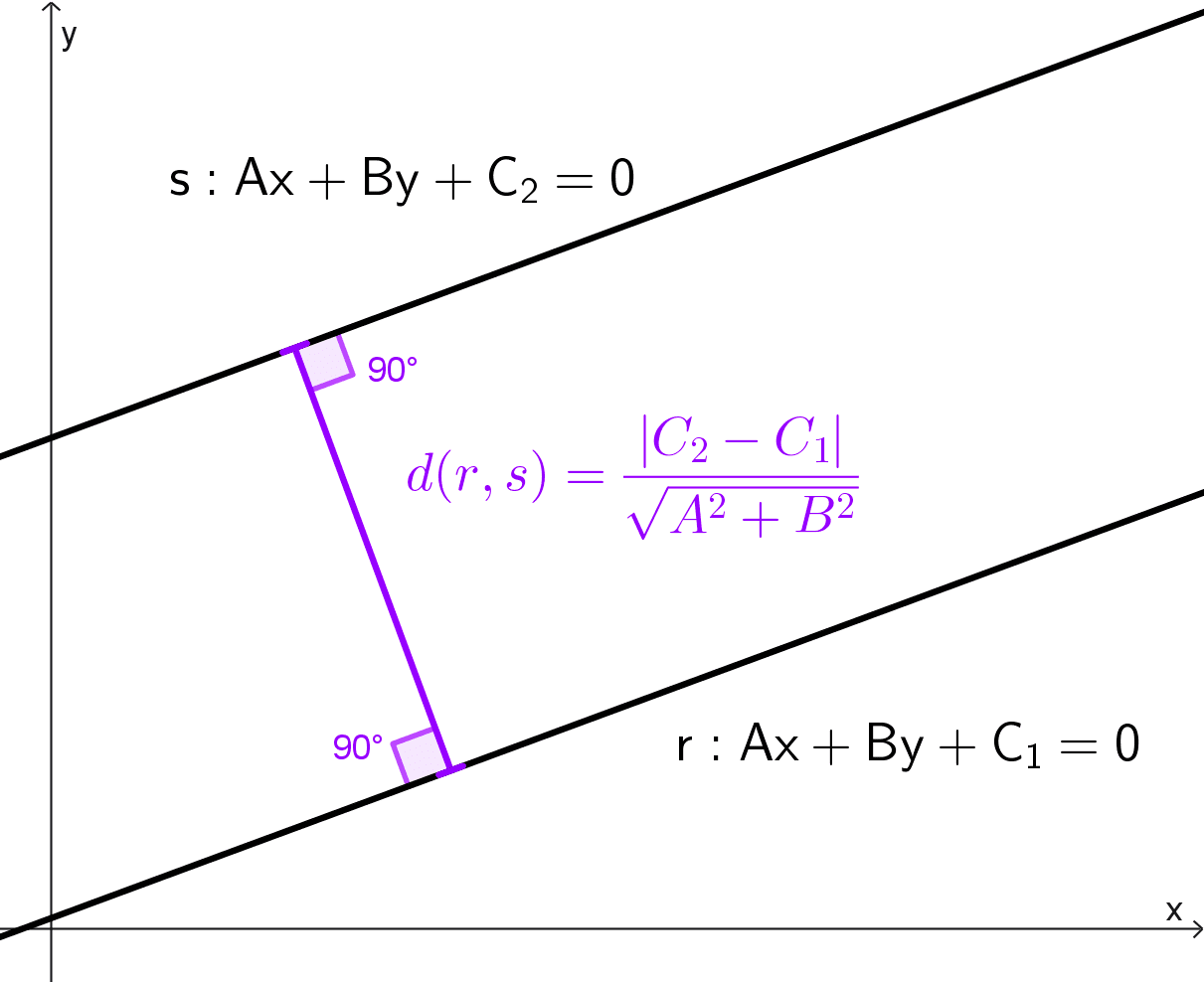
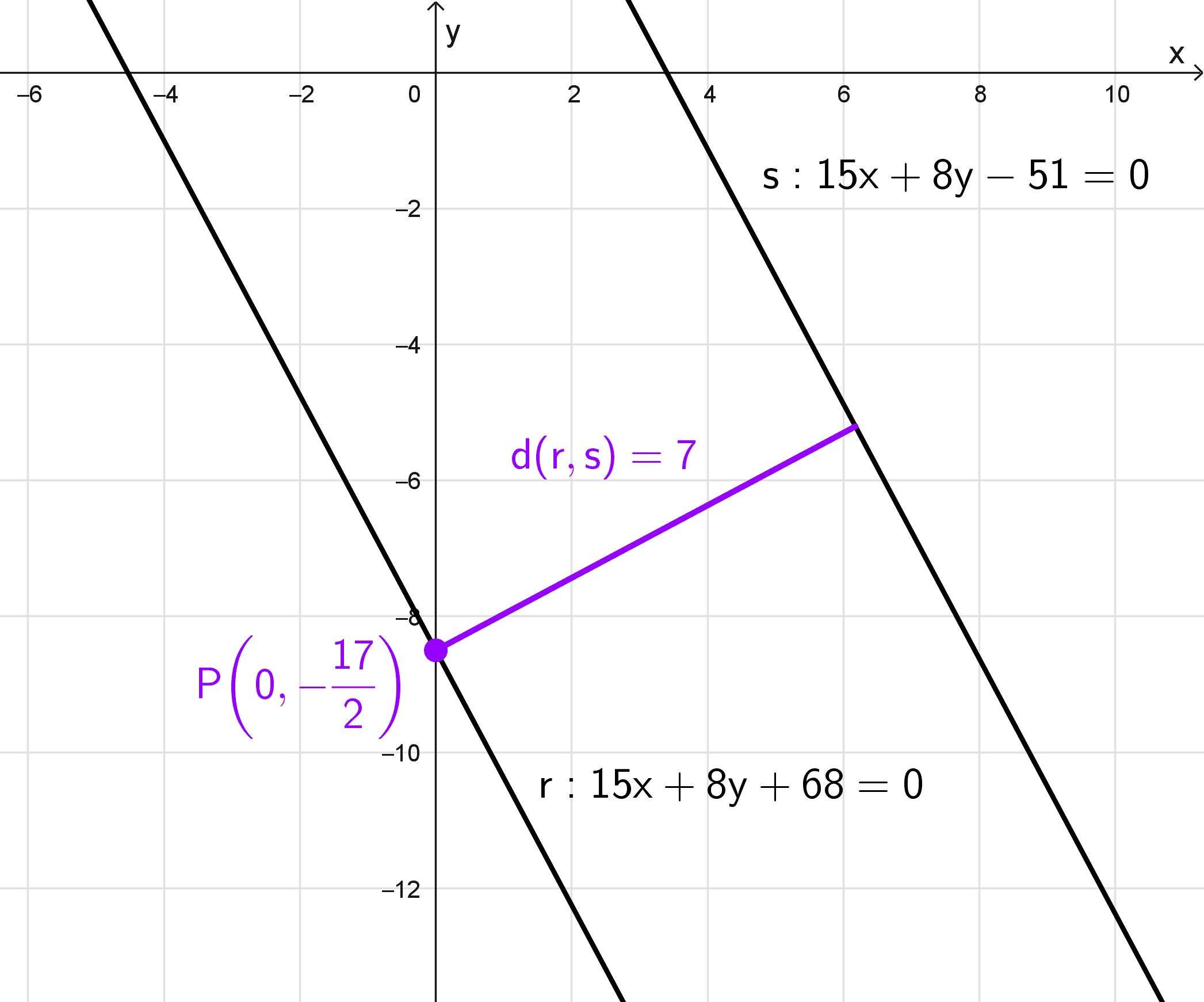
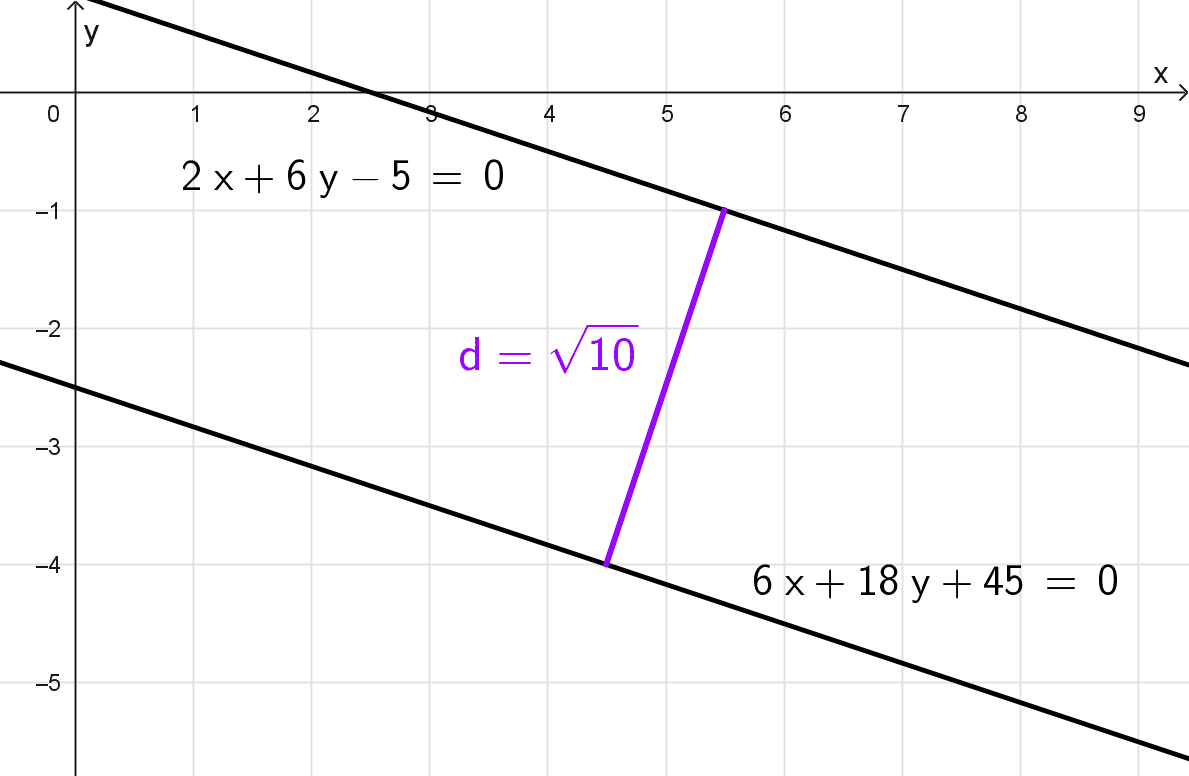
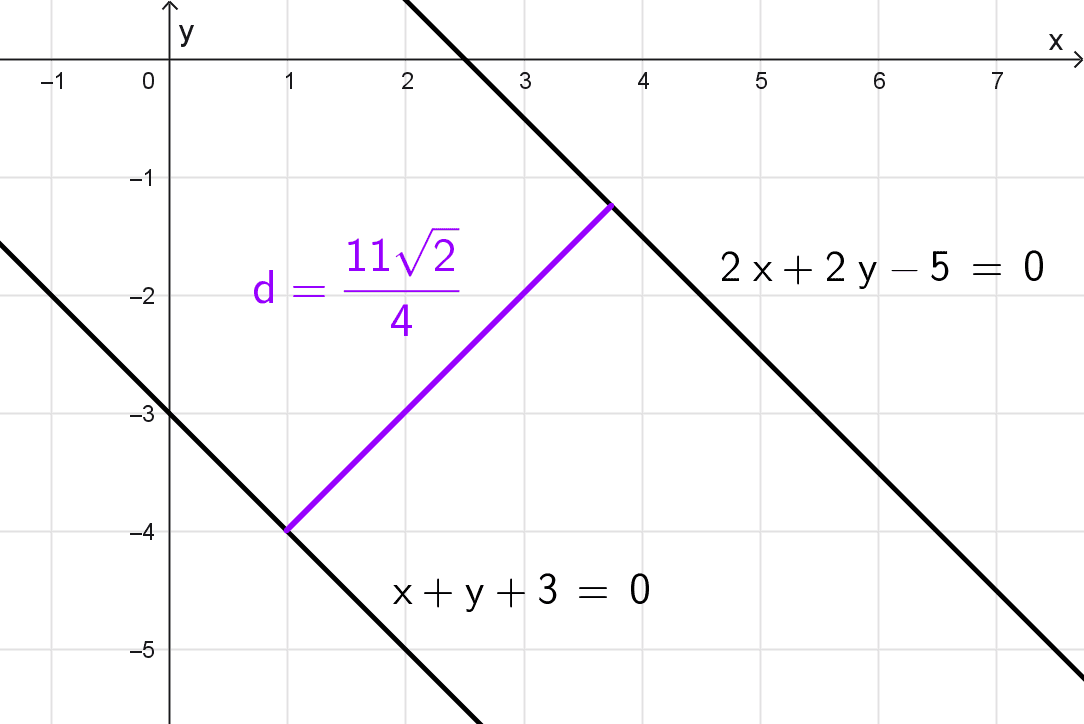
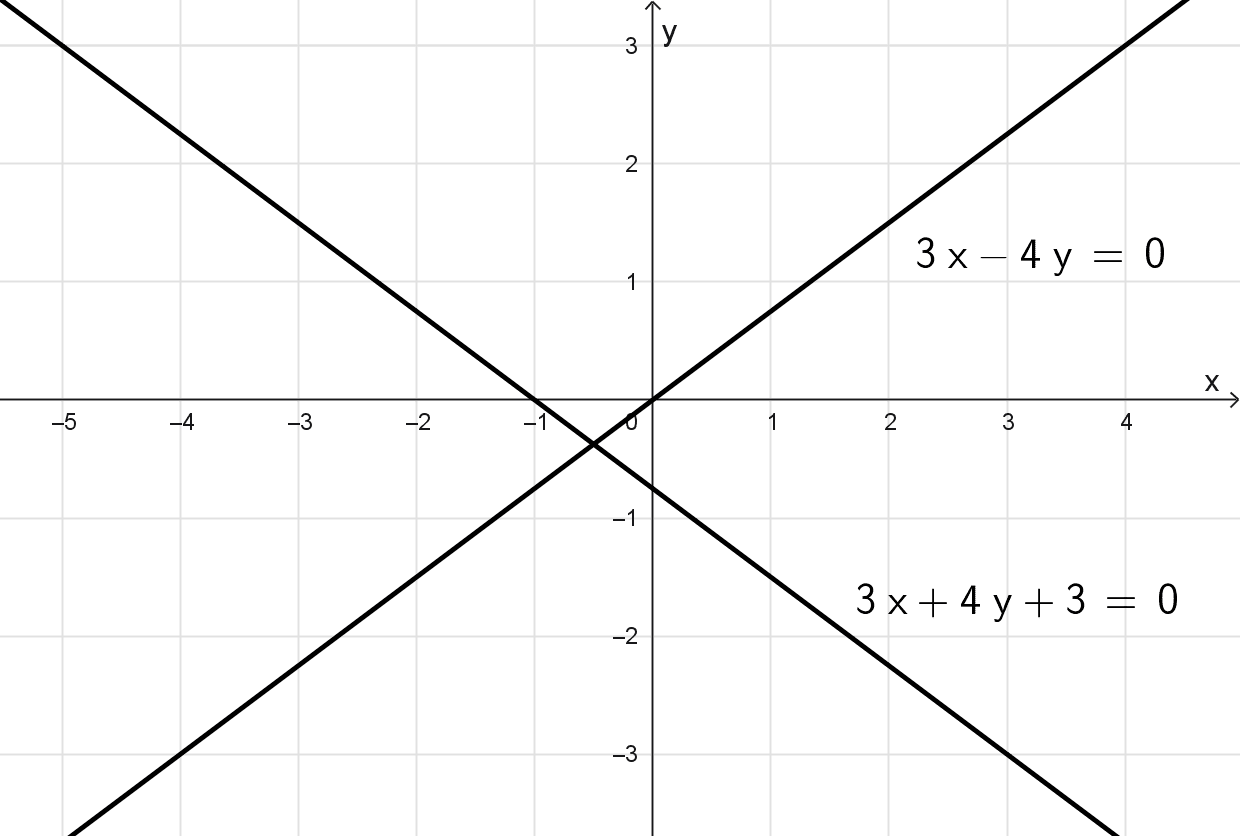
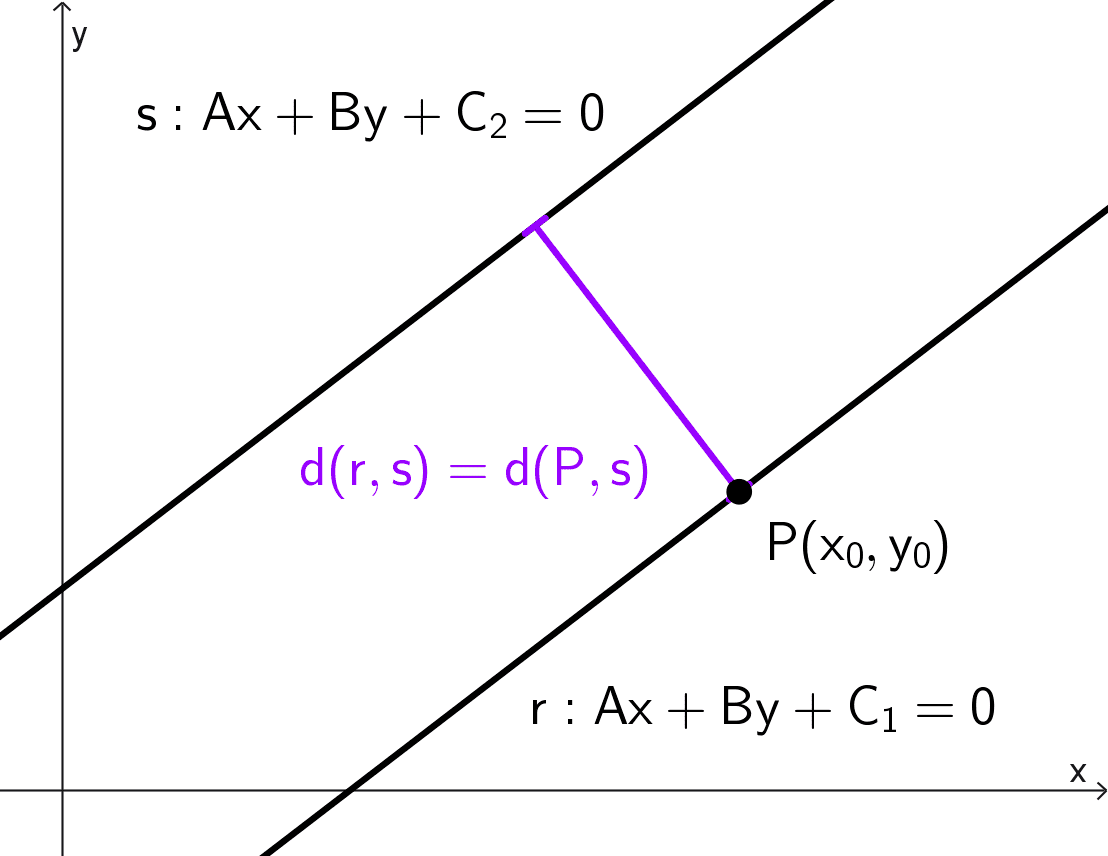
Otros artículos que pueden interesarte