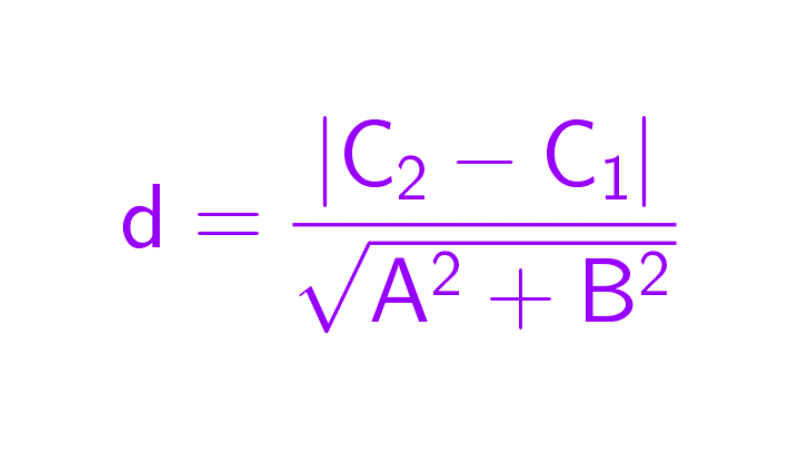
Distancia de un punto a una recta
La distancia de un punto a una recta es la longitud del segmento perpendicular que une ese punto con la recta. Esta es una cantidad no negativa y representa la mínima separación posible entre el punto y la línea.
La fórmula general para calcular la distancia d de un punto P(x0, y0) a una recta L expresada en su forma general, Ax + By + C = 0, es:
\(d=\dfrac{|Ax_0+By_0+C|}{\sqrt{A^{2}+B^{2}}}\)
Para aplicar esta fórmula, primero debemos identificar las coordenadas del punto P(x0, y0) y los coeficientes A, B y C de la ecuación general de la recta. El procedimiento consiste en sustituir las coordenadas del punto en la ecuación de la recta; luego, tomamos el valor absoluto de ese resultado para garantizar una magnitud no negativa. Finalmente, este valor lo dividimos entre la raíz cuadrada de la suma de los cuadrados de los coeficientes A y B.
Aunque desde un punto dado se pueden trazar infinitos segmentos hasta una recta, la distancia se define específicamente como la longitud del segmento perpendicular (u ortogonal), es decir, el que forma un ángulo de 90° con la recta. Esto es porque se puede demostrar que constituye el camino más corto entre el punto y la línea.
Índice
Ejemplos
Haremos primero un ejemplo detallado explicando el procedimiento geométrico que da origen a la fórmula de la distancia, en los siguientes ejemplos practicaremos la aplicación directa de la fórmula. Realizaremos la demostración general más adelante en este artículo.
Ejemplo 1
Encontrar la distancia del punto P(2, 3) a la recta \(y=\dfrac{3}{4}x+1.\)
Solución
Tenemos que encontrar la longitud del segmento perpendicular a la recta donde uno de sus extremos es el punto P. Una de las formas de lograr esto es seguir este procedimiento:
- Encontrar la recta perpendicular a la dada que pase por el punto P, para esto tenemos que conocer la pendiente de dicha recta.
- Determinar el punto de intersección Q entre ambas rectas, para ello igualamos ambas ecuaciones en forma explícita y resolvemos.
- Calcular la distancia entre P y Q usando la fórmula de distancia, este resultado nos dirá la separación entre P y la recta.
Primero, identificamos la pendiente de la recta dada, que es \(m_r=3/4.\) Para trazar la recta perpendicular que pasa por P, necesitamos su pendiente. Recordamos que el producto de las pendientes de dos rectas perpendiculares es -1, es decir:
\(m_r \cdot m_p=-1\)
Despejando, calculamos la pendiente perpendicular:
\(m_p=-\dfrac{1}{m_r}=-\dfrac{1}{\dfrac{3}{4}}=-\dfrac{4}{3}\)
Conocido el punto P(2, 3) y la pendiente perpendicular \(m_p=-4/3,\) escribimos la ecuación de la recta perpendicular. Utilizamos la forma punto-pendiente:
\(y-y_1=m(x-x_1)\)
Sustituyendo los datos, obtenemos:
\(y-3=-\dfrac{4}{3}(x-2)\)
Desarrollamos esta ecuación para llevarla a una forma conveniente para resolver el sistema:
\(y=-\dfrac{4}{3}x+\dfrac{8}{3}+3=-\dfrac{4}{3}x+\dfrac{17}{3}\)
El siguiente paso es encontrar el punto de intersección Q entre la recta original y la recta perpendicular, ya que este será el pie de la perpendicular. Para ello, resolvemos el sistema de ecuaciones formado por \(y=\dfrac{3}{4}x+1\) y \(y=-\dfrac{4}{3}x+\dfrac{17}{3}.\)
Igualamos las expresiones para y:
\(\dfrac{3}{4}x+1=-\dfrac{4}{3}x+\dfrac{17}{3}\)
Para eliminar fracciones, multiplicamos toda la ecuación por 12 (el mínimo común múltiplo de 4 y 3), resultando en:
\(9x+12=-16x+68\)
Agrupamos los términos:
\(9x+16x=68-12\)
\(25x=56\)
Por tanto, la coordenada x del punto de intersección es \(x=\dfrac{56}{25}.\)
Sustituimos este valor en cualquiera de las dos ecuaciones originales para hallar la coordenada y. Usamos la recta dada:
\(y=\dfrac{3}{4} \cdot \dfrac{56}{25}+1=\dfrac{42}{25}+1=\dfrac{42}{25}+\dfrac{25}{25}=\dfrac{67}{25}\)
Así, el punto de intersección (el pie de la perpendicular) es \(Q\left(\dfrac{56}{25}, \dfrac{67}{25}\right).\)
Finalmente, calculamos la distancia entre el punto original P(2, 3) y el punto Q utilizando la fórmula de distancia entre dos puntos:
\(d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
Sustituyendo las coordenadas, tenemos:
\(d=\sqrt{\left(\dfrac{56}{25}-2\right)^2+\left(\dfrac{67}{25}-3\right)^2}=\sqrt{\left(\dfrac{6}{25}\right)^2+\left(-\dfrac{8}{25}\right)^2}\)
\(=\sqrt{\dfrac{36}{625}+\dfrac{64}{625}}=\sqrt{\dfrac{100}{625}}=\dfrac{\sqrt{100}}{\sqrt{625}}=\dfrac{10}{25}=\dfrac{2}{5}\)
Por lo tanto, la distancia del punto P(2, 3) a la recta \(y=\dfrac{3}{4}x+1\) es 2/5 unidades.
En los siguientes ejemplos aplicaremos directamente la fórmula que se dio al inicio.
Ejemplo 2
Calcular la distancia del punto \(P\left(-4, \dfrac{7}{2}\right)\) a la línea recta \(y=\dfrac{x}{2}-1.\)
Solución
Para poder aplicar la fórmula de distancia, escribimos la ecuación de la recta en la forma general \(Ax+By+C=0.\) Partimos de \(y=\dfrac{x}{2}-1,\) multiplicamos ambos miembros por 2 para eliminar la fracción:
\(2y=x-2\)
Pasamos todos los términos al mismo lado:
\(x-2y-2=0\)
Identificamos los coeficientes: \(A=1\), \(B=-2\), \(C=-2.\)
La fórmula de la distancia de un punto \((x_0, y_0)\) a una recta es:
\(d=\dfrac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}\)
Aplicamos la fórmula de distancia con \(x_0=-4\), \(y_0=\dfrac{7}{2}:\)
\(d=\dfrac{\left| 1(-4)+(-2)\left(\dfrac{7}{2}\right)+(-2) \right|}{\sqrt{1^2+(-2)^2}}=\dfrac{\left|-4-7-2 \right|}{\sqrt{1+4}}=\dfrac{\left|-13 \right|}{\sqrt{5}}=\dfrac{13}{\sqrt{5}}\)
Racionalizamos la expresión:
\(d=\dfrac{13\sqrt{5}}{5}\)
La distancia exacta es \(\dfrac{13\sqrt{5}}{5}\) unidades, aproximadamente 5,81 unidades.
Podemos resumir así los pasos para calcular la distancia de un punto a una recta usando la fórmula general:
- Escribir la ecuación de la recta en su forma general, esta es la forma Ax + By + C = 0. Si la recta está dada en otra forma (como punto-pendiente o pendiente-ordenada), debemos realizar las operaciones algebraicas necesarias para reordenar todos los términos a un lado de la igualdad, dejando el otro lado igual a cero.
- Identificar los coeficientes y el punto: extraemos los valores de los coeficientes A, B y C, y las coordenadas del punto P(x0, y0), con su respectivo signo.
- Sustituir en la fórmula y desarrollar: \(d=\dfrac{|Ax_0+By_0+C|}{\sqrt{A^{2}+B^{2}}}\)
Ejemplo 3
Obtener la distancia entre la recta de ecuación 4x - 6y = 12 y el punto P(4, 5).
Solución
Primero expresamos la ecuación de la recta en la forma general \(Ax+By+C=0.\) Tomamos \(4x-6y=12\) y pasamos todos los términos al mismo lado:
\(4x-6y-12=0\)
Identificamos los coeficientes: \(A=4\), \(B=-6\), \(C=-12.\)
Sustituimos las coordenadas \(x_0=4\), \(y_0=5\) en la fórmula de distancia:
\(d=\dfrac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}=\dfrac{|4(4)+(-6)(5)+(-12)|}{\sqrt{4^2+(-6)^2}}\)
Realizamos las operaciones:
\(d=\dfrac{|16-30-12|}{\sqrt{16+36}}=\dfrac{|-26 |}{\sqrt{52}}=\dfrac{26}{2\sqrt{13}}=\dfrac{13}{\sqrt{13}}=\dfrac{13\sqrt{13}}{13}=\sqrt{13}\)
Por tanto, la distancia buscada es \(\sqrt{13}≈3,61\) unidades.
Ejemplo 4
Hallar la menor distancia que separa el punto P(1, -5) y la línea recta y + 1 = -x.
Solución
Llevamos la ecuación de la recta a la forma general \(Ax+By+C=0.\) De \(y+1=-x\) pasamos todos los términos a un lado:
\(x+y+1=0\)
Identificamos \(A=1\), \(B=1\), \(C=1.\)
Sustituimos en la fórmula con \(x_0=1\), \(y_0=-5:\)
\(d=\dfrac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}=\dfrac{|1(1)+1(-5)+1|}{\sqrt{1^2+1^2}}\)
Realizamos las operaciones:
\(d=\dfrac{|1-5+1|}{\sqrt{2}}=\dfrac{|-3 |}{\sqrt{2}}=\dfrac{3}{\sqrt{2}}=\dfrac{3\sqrt{2}}{2}\)
La distancia mínima entre el punto y la recta es \(\dfrac{3\sqrt{2}}{2}≈2,12\) unidades.
¿Te está sirviendo este artículo? ¡Por favor, califícalo!
Ejemplo 5
Determinar la distancia del punto P(-2, 1) a la recta 5x - 12y = -3.
Solución
Primero escribimos la ecuación en la forma general \(Ax+By+C=0:\)
\(5x-12y+3=0\)
Tenemos \(A=5\), \(B=-12\), \(C=3.\)
Aplicamos la fórmula de distancia con \(x_0=-2\), \(y_0=1:\)
\(d=\dfrac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}=\dfrac{|5(-2)+(-12)(1)+3|}{\sqrt{5^2+(-12)^2}}\)
Desarrollamos:
\(d=\dfrac{|-10-12+3 |}{\sqrt{25+144}}=\dfrac{|-19 |}{\sqrt{169}}=\dfrac{19}{13}\)
La distancia es \(\dfrac{19}{13}≈1,46\) unidades.
Ejemplo 6
Obtener la distancia del punto P(-1, 2) a la recta \(y=\dfrac{1}{2}x+5.\)
Solución
Transformamos la ecuación a la forma general \(Ax+By+C=0.\) De \(y=\dfrac{1}{2}x+5,\) multiplicamos por 2:
\(2y=x+10\)
Pasamos todos los términos al mismo lado:
\(x-2y+10=0\)
Entonces \(A=1\), \(B=-2\), \(C=10.\)
Sustituimos en la fórmula de distancia con \(x_0=-1\), \(y_0=2:\)
\(d=\dfrac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}=\dfrac{|1(-1)+(-2)(2)+10|}{\sqrt{1^2+(-2)^2}}\)
Realizamos las operaciones y simplificamos:
\(d=\dfrac{|-1-4+10 |}{\sqrt{1+4}}=\dfrac{| 5 |}{\sqrt{5}}=\dfrac{5}{\sqrt{5}}=\sqrt{5}\)
La distancia es \(\sqrt{5}≈2,24\) unidades.
Ejemplo 7
Determinar la distancia del punto P(-3, -4) a la recta 5y = -7x + 3.
Solución
Llevamos la ecuación a la forma general. De \(5y=-7x+3\) pasamos todo al mismo lado:
\(7x+5y-3=0\)
Tenemos \(A=7\), \(B=5\), \(C=-3.\)
Sustituimos en la fórmula de distancia con \(x_0=-3\), \(y_0=-4:\)
\(d=\dfrac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}=\dfrac{|7(-3)+5(-4)+(-3)|}{\sqrt{7^2+5^2}}\)
Desarrollamos:
\(d=\dfrac{|-21-20-3 |}{\sqrt{49+25}}=\dfrac{|-44 |}{\sqrt{74}}=\dfrac{44}{\sqrt{74}}=\dfrac{44\sqrt{74}}{74}=\dfrac{22\sqrt{74}}{37}\)
La distancia es \(\dfrac{22\sqrt{74}}{37}≈5,11\) unidades.
Ejemplo 8
Hallar la distancia del punto P(1, 5) a la línea recta \(\dfrac{x}{4}+\dfrac{y}{-5}=1.\)
Solución
Transformamos la ecuación a la forma general \(Ax+By+C=0.\) Partimos de \(\dfrac{x}{4}-\dfrac{y}{5}=1\) y multiplicamos todo por 20 (mínimo común múltiplo de 4 y 5):
\(5x-4y=20\)
Pasamos todos los términos al mismo lado:
\(5x-4y-20=0\)
Entonces \(A=5\), \(B=-4\), \(C=-20.\)
Sustituimos en la fórmula con \(x_0=1\), \(y_0=5:\)
\(d=\dfrac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}=\dfrac{|5(1)+(-4)(5)+(-20)|}{\sqrt{5^2+(-4)^2}}\)
Realizamos las operaciones:
\(d=\dfrac{| 5-20-20 |}{\sqrt{25+16}}=\dfrac{|-35 |}{\sqrt{41}}=\dfrac{35}{\sqrt{41}}=\dfrac{35\sqrt{41}}{41}\)
La distancia es \(\dfrac{35\sqrt{41}}{41}≈5,47\) unidades.
Casos especiales
Existen casos particulares donde es más sencillo calcular la distancia entre un punto y una línea recta.
Distancia a una recta horizontal o vertical
Cuando la recta a la que se desea calcular la distancia es paralela a uno de los ejes coordenados, el cálculo se simplifica notablemente y puede resolverse directamente con las coordenadas del punto, sin necesidad de aplicar la fórmula general.
Para una recta vertical, cuya ecuación es de la forma x = h, la distancia desde cualquier punto P(x0, y0) hasta ella es simplemente el valor absoluto de la diferencia entre la abscisa del punto y la constante h. Geométricamente, esta distancia es la longitud del segmento horizontal que une el punto con la recta, calculándose como:
d = |x0 - h|
De manera análoga, para una recta horizontal con ecuación y = k, la distancia desde el punto P(x0, y0) corresponde al valor absoluto de la diferencia entre su ordenada y la constante k. En este caso, la distancia es la longitud del segmento vertical entre el punto y la recta, dada por:
d = |y0 - k|
Ejemplo 1
Encuentre la distancia de la recta y - 6 = 0 al punto (5, 3).
Solución
La ecuación dada, y - 6 = 0, puede reescribirse como y = 6, lo que corresponde a la ecuación de una recta horizontal.
Para calcular la distancia desde cualquier punto (x0, y0) hasta una recta horizontal y = k, aplicamos la fórmula simplificada d = |y0 - k|.
En este caso, las coordenadas del punto son x0 = 5 e y0 = 3, y la constante de la recta es k = 6. Sustituyendo estos valores, obtenemos:
d = |3 - 6| = |-3| = 3
Por lo tanto, la distancia requerida es de 3 unidades.
Ejemplo 2
Obtener la distancia entre el punto (-1, -4) y la línea recta de ecuación x + 3 = 0.
Solución
La ecuación de la recta, x + 3 = 0, es equivalente a x = -3, identificándose así como una recta vertical. La distancia desde un punto (x0, y0) a una recta vertical x = h se calcula directamente con la expresión d = |x0 - h|.
Para el punto dado, x0 = -1 e y0 = -4, mientras que el valor de la constante en la ecuación es h = -3. Al realizar la sustitución, el cálculo es:
d = |-1 - (-3)| = |-1 + 3| = |2| = 2
Por lo tanto, la distancia es de 2 unidades.
Distancia de una recta al origen de coordenadas
Sabemos que la fórmula general para la distancia desde un punto \((x_0, y_0)\) a una recta con ecuación general \(Ax+By+C=0\) es:
\(d=\dfrac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}\)
Si ese punto es el origen de coordenadas (0, 0), debemos sustituir \(x_0=0\) e \(y_0=0\):
\(d=\dfrac{|A(0)+B(0)+C|}{\sqrt{A^2+B^2}}=\dfrac{|C|}{\sqrt{A^2+B^2}}\)
Es decir, la fórmula de distancia de una recta al origen de coordenadas es:
\(d=\dfrac{|C|}{\sqrt{A^2+B^2}}\)
Ejemplo
Encuentre la distancia desde la recta 3x - 4y + 10 = 0 hasta el origen de coordenadas.
Solución
La ecuación dada, \(3x-4y+10=0,\) ya se encuentra en la forma general \(Ax+By+C=0,\) donde \(A=3\), \(B=-4\) y \(C=10.\) Para calcular la distancia de esta recta al origen (0, 0), aplicamos la fórmula específica:
\(d=\dfrac{|C|}{\sqrt{A^2+B^2}}\)
Sustituyendo los valores identificados, procedemos con el cálculo:
\(d=\dfrac{|10|}{\sqrt{(3)^2+(-4)^2}}=\dfrac{10}{\sqrt{9+16}}=\dfrac{10}{\sqrt{25}}=\dfrac{10}{5}=2\)
Por lo tanto, la distancia desde la recta hasta el origen es de 2 unidades.
Demostración de la fórmula
La demostración de la fórmula de la distancia de un punto a una recta en el plano cartesiano puede abordarse desde varias perspectivas, siendo una de las más intuitivas el uso de vectores. Sin embargo, en este desarrollo nos centraremos en un enfoque puramente algebraico y geométrico basado en la construcción de una recta perpendicular, siguiendo el mismo principio utilizado en el primer ejemplo.
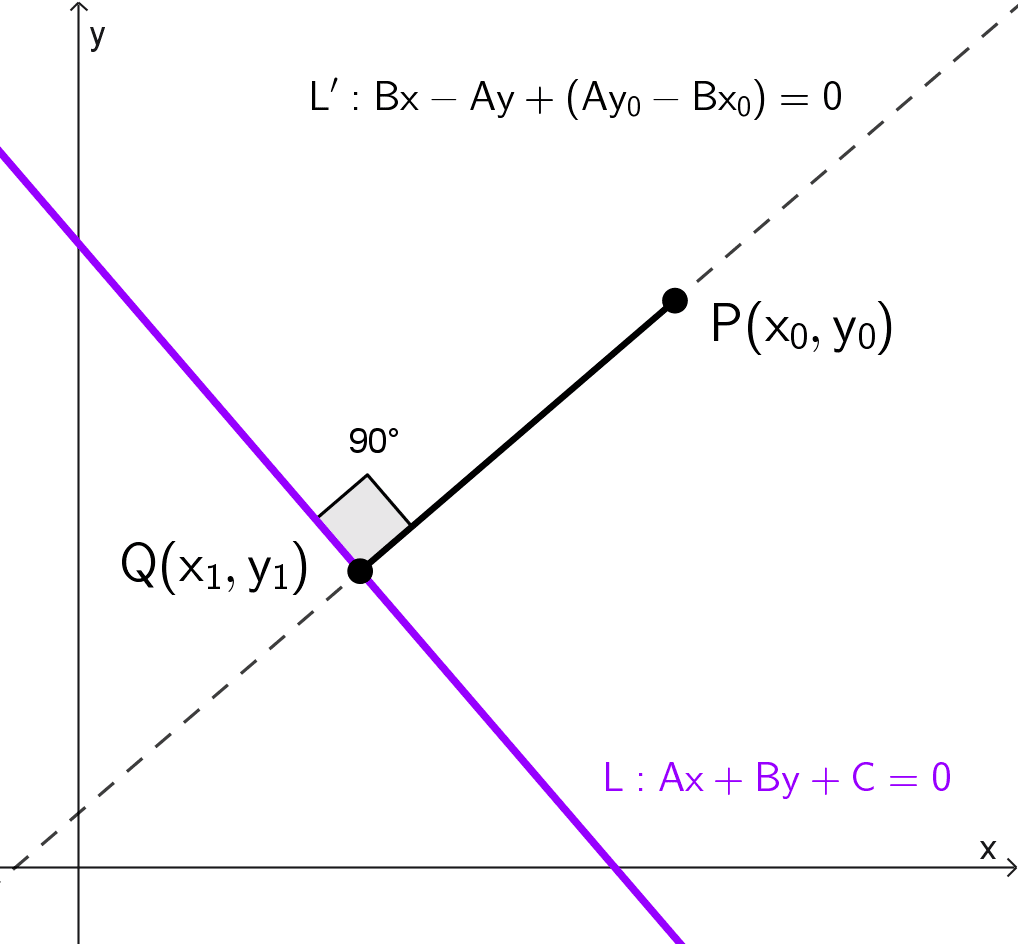
Consideremos una recta L dada en su forma general Ax + By + C = 0 y un punto P(x0, y0) fuera de ella, del cual queremos calcular su distancia más corta a L. Este segmento de mínima longitud corresponde a la perpendicular trazada desde P hasta L, cuya intersección llamaremos Q(x1, y1). Si ocurriera que P pertenece a la recta, su distancia a ella es cero, por eso consideramos el caso en que no pertenece.
El primer paso consiste en determinar la ecuación de la recta L' que pasa por P y es perpendicular a L. Para ello, partimos de la pendiente de L. Si despejamos la ecuación general de L a la forma explícita, suponiendo B ≠ 0, obtenemos:
\(y=-\dfrac{A}{B}x-\dfrac{C}{B}\)
donde la pendiente de L es \(m_L=-\dfrac{A}{B}.\) Dado que las rectas perpendiculares cumplen que el producto de sus pendientes es -1, la pendiente de la recta perpendicular L' será:
\(m_{L'}=\dfrac{B}{A}\)
Con esta pendiente y el punto P(x0, y0), escribimos la ecuación de L' en forma punto-pendiente:
\(y-y_0=\dfrac{B}{A}(x-x_0)\)
Para facilitar los cálculos posteriores, la reescribimos en su forma general. Multiplicamos ambos lados por A:
\(A(y-y_0)=B(x-x_0)\)
y reagrupamos términos:
\(Bx-Ay+(Ay_0-Bx_0)=0\)
Ahora tenemos un sistema de dos ecuaciones lineales: la recta original \(L: Ax+By+C=0\) y la recta perpendicular \(L': Bx-Ay+(Ay_0-Bx_0)=0.\) El punto de intersección \(Q(x_1, y_1)\) (también conocido como pie de la perpendicular) es la solución de este sistema. Para encontrarlo, podemos resolver por igualación o sustitución. Despejamos \(x\) de la ecuación de \(L':\)
\(Bx=Ay-Ay_0+Bx_0 \quad → \quad x=\dfrac{Ay-Ay_0+Bx_0}{B}\)
Sustituyendo esta expresión en la ecuación de L:
\(A\left(\dfrac{Ay-Ay_0+Bx_0}{B}\right)+By+C=0\)
Multiplicamos toda la ecuación por B para eliminar el denominador:
\(A(Ay-Ay_0+Bx_0)+B^2y+BC=0\)
Desarrollamos y agrupamos los términos con y:
\(A^2y-A^2y_0+ABx_0+B^2y+BC=0\)
\((A^2+B^2)y+(ABx_0-A^2y_0+BC)=0\)
Despejamos y:
\((A^2+B^2)y=A^2y_0-ABx_0-BC\)
\(y_1=\dfrac{A^2y_0-ABx_0-BC}{A^2+B^2}\)
Un proceso análogo, despejando y de L' y sustituyendo en L, nos permite hallar x1:
\(x_1=\dfrac{B^2x_0-ABy_0-AC}{A^2+B^2}\)
Habiendo determinado las coordenadas del pie de la perpendicular Q(x1, y1), aplicamos la fórmula de la distancia entre dos puntos para calcular la longitud del segmento PQ:
\(d=\sqrt{(x_1-x_0)^2+(y_1-y_0)^2}\)
Sustituimos las expresiones de x1 e y1:
\(d=\sqrt{\left(\dfrac{B^2x_0-ABy_0-AC}{A^2+B^2}-x_0 \right)^2+\left(\dfrac{A^2y_0-ABx_0-BC}{A^2+B^2}-y_0 \right)^2 }\)
Para simplificar, escribimos cada diferencia como una sola fracción. Para la coordenada x:
\(\dfrac{B^2x_0-ABy_0-AC}{A^2+B^2}-x_0=\dfrac{B^2x_0-ABy_0-AC-A^2x_0-B^2x_0}{A^2+B^2}=\dfrac{-A(Ax_0+By_0+C)}{A^2+B^2}\)
Para la coordenada y:
\(\dfrac{A^2y_0-ABx_0-BC}{A^2+B^2}-y_0=\dfrac{A^2y_0-ABx_0-BC-A^2y_0-B^2y_0}{A^2+B^2}=\dfrac{-B(Ax_0+By_0+C)}{A^2+B^2}\)
Ahora, la distancia al cuadrado es:
\(d^2=\left(\dfrac{-A(Ax_0+By_0+C)}{A^2+B^2} \right)^2+\left(\dfrac{-B(Ax_0+By_0+C)}{A^2+B^2} \right)^2\)
Factorizamos el término común \((Ax_0+By_0+C)^2/(A^2+B^2)^2:\)
\(d^2=\dfrac{(Ax_0+By_0+C)^2}{(A^2+B^2)^2} (A^2+B^2)\)
Simplificamos \((A^2+B^2)\) en el numerador y denominador:
\(d^2=\dfrac{(Ax_0+By_0+C)^2}{A^2+B^2}\)
Finalmente, tomamos la raíz cuadrada para obtener la fórmula de la distancia. Dado que la distancia es un valor no negativo y el numerador está elevado al cuadrado, tomamos su valor absoluto para garantizar este resultado:
\(d=\dfrac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}\)
Esta es la expresión general y compacta para calcular la distancia de un punto (x0, y0) a la recta Ax + By + C = 0.
Nota: aunque en la demostración se supuso que la recta no es horizontal ni vertical (al usar los valores A y B en denominadores se asume que no son cero), la fórmula funciona también en esos casos.
Ejercicios resueltos
A continuación veremos algunos problemas de aplicación resueltos paso a paso.
Ejercicio 1
Una línea de gas se puede representar en un plano cartesiano con la ecuación 2x + y = 2. Una fábrica localizada en (6, 7) se conectará perpendicularmente con la línea de gas. Encuentra la longitud de la tubería requerida, si las unidades son kilómetros.
Solución
Primero identificamos que la línea de gas está representada por la recta 2x + y = 2. La fábrica está ubicada en el punto P(6, 7). La conexión debe ser perpendicular a la línea de gas, por lo que la longitud de la tubería coincide con la distancia desde el punto a la recta.
La fórmula para la distancia de un punto \((x_0,y_0)\) a una recta \(Ax+By+C=0\) es
\(d=\dfrac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}\)
Para la recta dada, escribimos \(2x+y-2=0,\) de modo que \(A=2\), \(B=1\), \(C=-2.\) Sustituimos \(x_0=6\), \(y_0=7:\)
\(d=\dfrac{|2\cdot 6+1\cdot 7-2|}{\sqrt{2^2+1^2}}=\dfrac{|12+7-2|}{\sqrt{4+1}}=\dfrac{|17|}{\sqrt{5}}=\dfrac{17}{\sqrt{5}}=\dfrac{17\sqrt{5}}{5}\)
Por tanto, la longitud de tubería necesaria es \(\dfrac{17\sqrt{5}}{5}≈7,60\) kilómetros.
Ejercicio 2
Sea la recta 4x + 3y - 1 = 0 y el punto (-1, k). Determina el valor de k de modo que la distancia del punto a la recta sea 2.
Solución
Usamos la fórmula de distancia punto-recta con \(x_0=-1, y_0=k, A=4, B=3, C=-1:\)
\(d=\dfrac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}=\dfrac{|4(-1)+3k-1|}{\sqrt{4^2+3^2}}=2\)
Desarrollando, la ecuación queda como:
\(\dfrac{|3k-5|}{5}=2\)
Multiplicamos ambos miembros por 5:
\(|3k-5|=10\)
Al eliminar el valor absoluto obtenemos dos casos:
\(3k-5=10 \quad \text{o} \quad 3k-5=-10\)
Resolviendo el primero: \(3k=15\) → \(k=5.\)
Resolviendo el segundo: \(3k=-5\) → \(k=-\dfrac{5}{3}.\)
Por lo tanto, los valores de \(k\) que hacen que la distancia sea 2 son \(k=5\) y \(k=-\dfrac{5}{3}.\) Es decir, existen dos puntos con abscisa -1 cuya distancia a la recta dada es 2, ellos son (-1, 5) y (-1, -5/3).
Ejercicio 3
Calcula el valor de k para que la distancia del origen de coordenadas a la recta 4x + ky - 5 = 0 sea 1.
Solución
Queremos que la distancia del origen \((0,0)\) a la recta \(4x+ky-5=0\) sea igual a 1.
Aplicamos la fórmula de distancia:
\(\dfrac{|4\cdot 0+k\cdot 0-5|}{\sqrt{4^2+k^2}}=1\)
Desarrollando obtenemos:
\(\dfrac{5}{\sqrt{16+k^2}}=1\)
Multiplicamos ambos lados por \(\sqrt{16+k^2}:\)
\(5=\sqrt{16+k^2}\)
Elevamos al cuadrado:
\(25=16+k^2\)
Restamos 16:
\(k^2=9\)
Tomando raíz cuadrada:
\(k=3 \quad \text{o} \quad k=-3\)
Por lo tanto, los valores de \(k\) que cumplen la condición son \(k=3\) y \(k=-3.\) Es decir, las ecuaciones de las rectas pueden ser 4x + 3y - 5 = 0 o 4x - 3y - 5 = 0.
Ejercicio 4
Un punto P(x, y) equidista de los puntos A(3, 7) y B(6, 6). La distancia de P a la recta que pasa por A y tiene pendiente 2 es \(\dfrac{4}{\sqrt{5}}.\) Encuentra las coordenadas de P.
Solución
Primero, la condición de que P equidista de A y B implica que \(d(P, A)=d(P, B).\) Usando la fórmula de distancia, escribimos:
\(\sqrt{(x-3)^2+(y-7)^2}=\sqrt{(x-6)^2+(y-6)^2}\)
Elevamos al cuadrado ambos miembros:
\((x-3)^2+(y-7)^2=(x-6)^2+(y-6)^2\)
Desarrollamos los cuadrados:
\(x^2-6x+9+y^2-14y+49=x^2-12x+36+y^2-12y+36\)
Simplificamos cancelando \(x^2\) e \(y^2,\) y reagrupamos términos:
\(-6x-14y+58=-12x-12y+72\)
Pasamos todos los términos al lado izquierdo:
\(6x-2y-14=0\)
Dividimos entre \(2:\)
\(3x-y-7=0. \quad \text{(1)}\)
Ahora, la recta que pasa por \(A(3,7)\) con pendiente \(2\) tiene ecuación \(y-7=2(x-3),\) que simplificamos a \(y=2x+1,\) o en forma general:
\(2x-y+1=0\)
La distancia de un punto \((x_0, y_0)\) a la recta \(Ax+By+C=0\) es \(\dfrac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}.\) En nuestro caso, la distancia de \(P(x, y)\) a esta recta es \(\dfrac{4}{\sqrt{5}}.\) Sustituimos:
\(\dfrac{|2x-y+1|}{\sqrt{4+1}}=\dfrac{4}{\sqrt{5}}\)
Multiplicamos ambos lados por \(\sqrt{5}:\)
\(|2x-y+1|=4\)
Esto nos da dos ecuaciones posibles:
\(2x-y+1=4 \quad \text{o} \quad 2x-y+1=-4\)
Simplificamos:
\(2x-y=3, \quad \text{(2)}\)
\(2x-y=-5. \quad \text{(3)}\)
Ahora resolvemos el sistema con (1) en cada caso.
Primero, con (1) y (2):
De (1): \(y=3x-7.\) Sustituimos en (2):
\(2x-(3x-7)=3 \quad → \quad-x+7=3 \quad → \quad x=4\)
Entonces \(y=3(4)-7=5.\) Un posible punto es \(P_1(4,5).\)
Segundo, con (1) y (3):
De (1): \(y=3x-7.\) Sustituimos en (3):
\(2x-(3x-7)=-5 \quad → \quad-x+7=-5 \quad → \quad x=12\)
Entonces \(y=3(12)-7=29.\) El otro punto es \(P_2(12, 29).\)
Por lo tanto, las coordenadas de P pueden ser (4, 5) o (12, 29).
Ejercicio 5
Los puntos A(x, 4) y B(5, y) se encuentran ambos a una distancia de \(20/\sqrt{130}\) de la recta que pasa por los puntos P(-3, 2) y Q(8, 5). Encuentra los posibles valores para la abscisa de A y la ordenada de B.
Solución
Primero hallamos la ecuación de la recta que pasa por \(P(-3, 2)\) y \(Q(8, 5).\) La pendiente es:
\(m=\dfrac{5-2}{8-(-3)}=\dfrac{3}{11}\)
Usamos la forma punto-pendiente con \(P:\)
\(y-2=\dfrac{3}{11}(x+3)\)
Multiplicamos por 11:
\(11y-22=3x+9\)
Llevamos todo a un lado:
\(3x-11y+31=0. \quad \text{(1)}\)
La distancia de un punto \((x_0, y_0)\) a esta recta es:
\(\dfrac{|3x_0-11y_0+31|}{\sqrt{9+121}}=\dfrac{|3x_0-11y_0+31|}{\sqrt{130}}\)
Para \(A(x, 4),\) esta distancia debe ser \(\dfrac{20}{\sqrt{130}}:\)
\(\dfrac{|3x-11(4)+31|}{\sqrt{130}}=\dfrac{20}{\sqrt{130}}\)
Multiplicamos por \(\sqrt{130}:\)
\(|3x-44+31|=20 \quad → \quad |3x-13|=20\)
Esto da dos ecuaciones:
\(3x-13=20 \quad → \quad 3x=33 \quad → \quad x=11\)
\(3x-13=-20 \quad → \quad 3x=-7 \quad → \quad x=-\dfrac{7}{3}\)
Así, la abscisa de \(A\) puede ser \(11\) o \(-\dfrac{7}{3}.\)
Ahora para \(B(5, y),\) usamos la misma fórmula de distancia con la recta (1):
\(\dfrac{|3(5)-11y+31|}{\sqrt{130}}=\dfrac{20}{\sqrt{130}}\)
Multiplicamos por \(\sqrt{130}:\)
\(|15-11y+31|=20 \quad → \quad |46-11y|=20\)
Esto da:
\(46-11y=20 \quad → \quad-11y=-26 \quad → \quad y=\dfrac{26}{11}\)
\(46-11y=-20 \quad → \quad-11y=-66 \quad → \quad y=6\)
Por lo tanto, la ordenada de \(B\) puede ser \(\dfrac{26}{11}\) o \(6.\)
Ejercicio 6
Sea m < 0 y b un número real, la recta L de ecuación y = mx + b pasa por el punto (3, 1), determina m y b si se sabe que la distancia del punto (-1, 1) a L es \(2\sqrt{2}.\)
Solución
Como \(L\) pasa por \((3, 1),\) sustituimos en \(y=mx+b:\)
\(1=3m+b \quad → \quad b=1-3m. \quad \text{(1)}\)
La forma general de \(L\) es \(m x-y+b=0.\) Sustituyendo \(b\) de (1):
\(mx-y+1-3m=0\)
La distancia del punto \((-1, 1)\) a esta recta es:
\(\dfrac{|m(-1)-1+1-3m|}{\sqrt{m^2+1}}=\dfrac{|-m-3m|}{\sqrt{m^2+1}}=\dfrac{|-4m|}{\sqrt{m^2+1}}\)
Como \(m<0\), \(|-4m|=-4m\) (esto porque \(-4m\) es positivo, así que el valor absoluto lo deja igual). Esta distancia debe ser \(2\sqrt{2}:\)
\(\dfrac{-4m}{\sqrt{m^2+1}}=2\sqrt{2}\)
Multiplicamos ambos lados por \(\sqrt{m^2+1}:\)
\(-4m=2\sqrt{2} \sqrt{m^2+1}\)
Dividimos entre \(2:\)
\(-2m=\sqrt{2} \sqrt{m^2+1}\)
Elevamos al cuadrado:
\(4m^2=2(m^2+1) \quad → \quad 4m^2=2m^2+2\)
Restamos \(2m^2:\)
\(2m^2=2 \quad → \quad m^2=1\)
Como \(m<0,\) tomamos \(m=-1.\) Sustituimos en (1):
\(b=1-3(-1)=4\)
Por lo tanto, \(m=-1\) y \(b=4.\) La recta es \(y=-x+4.\)
Bibliografía
- Cotrina, J. y Escudero, P. (2021). Introducción a la geometría analítica. Universidad del Pacífico.
- Engler, A., Müller, D., Vrancken, S. y Hecklein, M. (2020). Geometría analítica. Universidad Nacional del Litoral.
- Márquez, A., Vázquez, F., Ruiz, H., Villegas, M. y Figueroa, M. (2009). Geometría analítica. Prentice Hall.
- Oteyza, E., Lam, E., Hernández, C., Carrillo, Á. y Ramírez, A. (2011). Geometría analítica (3.ª ed.). Pearson Educación.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta

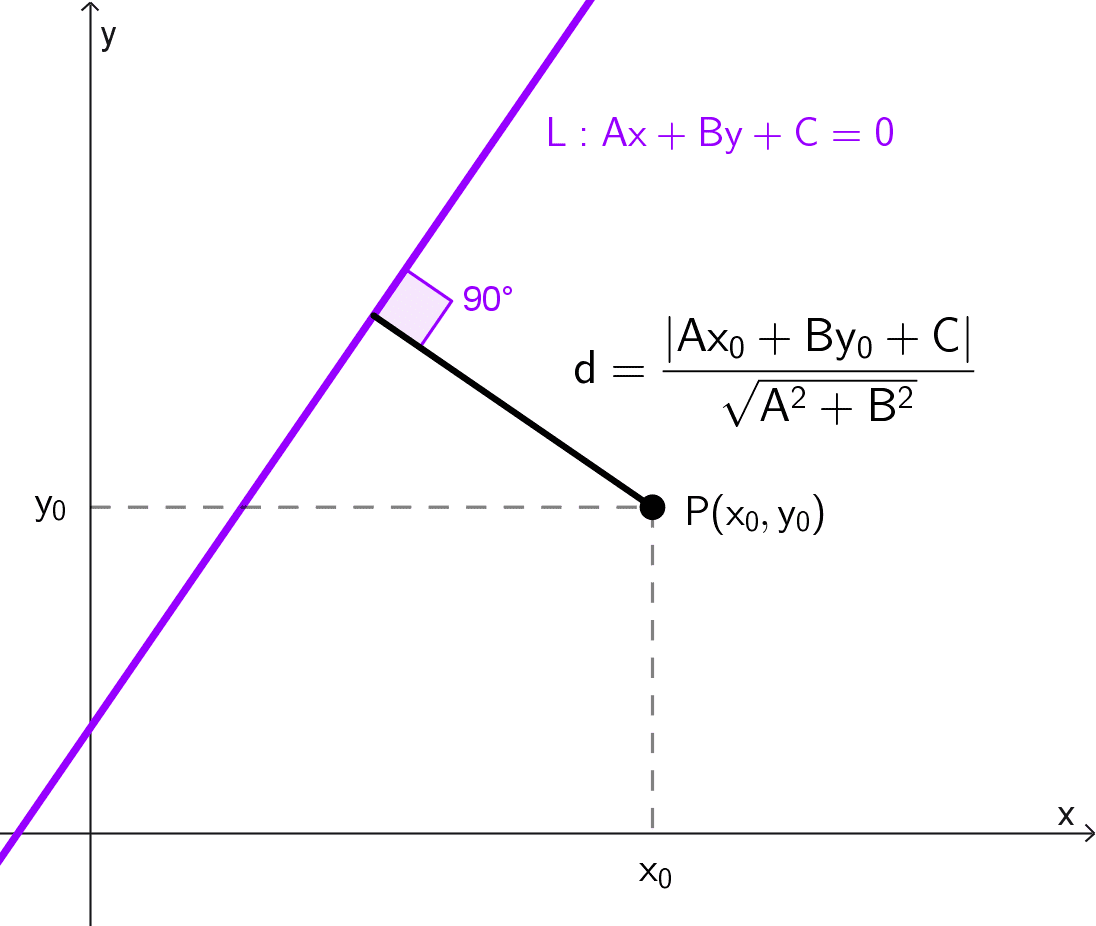
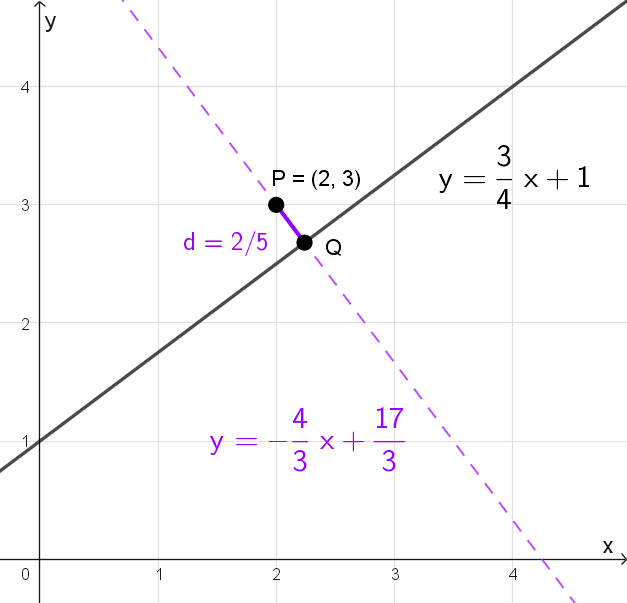
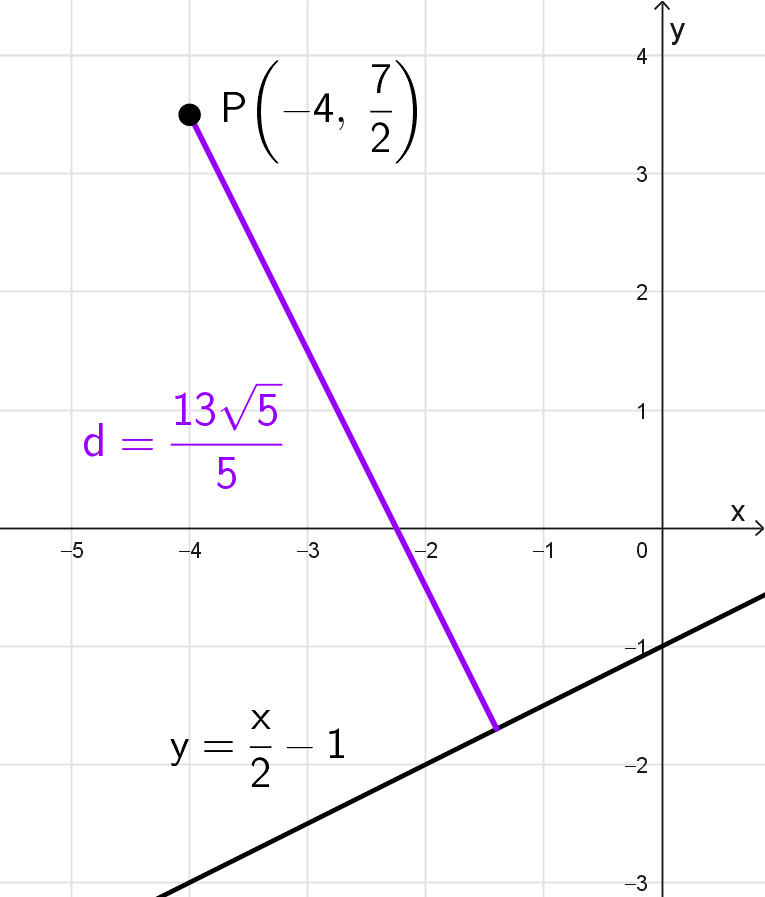
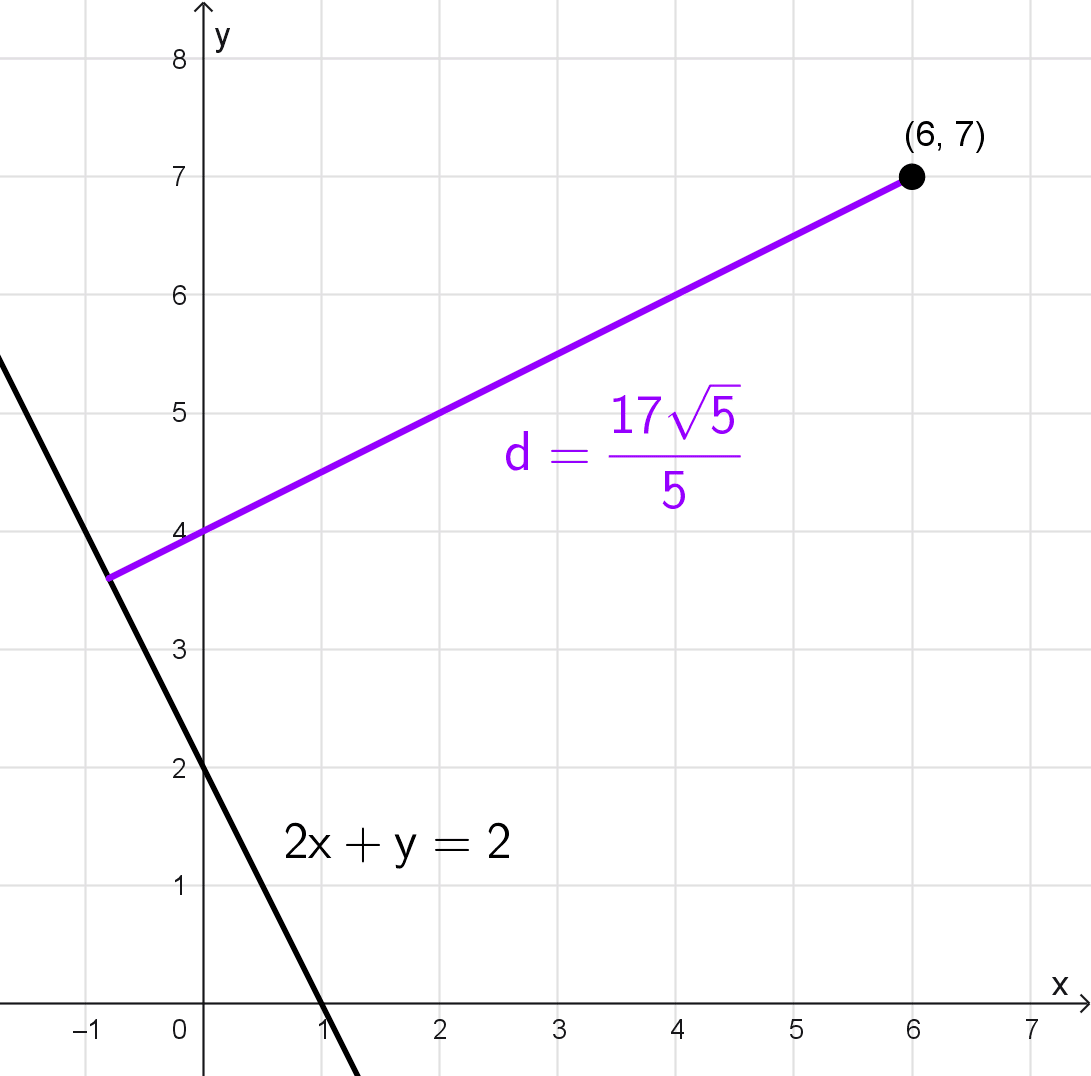
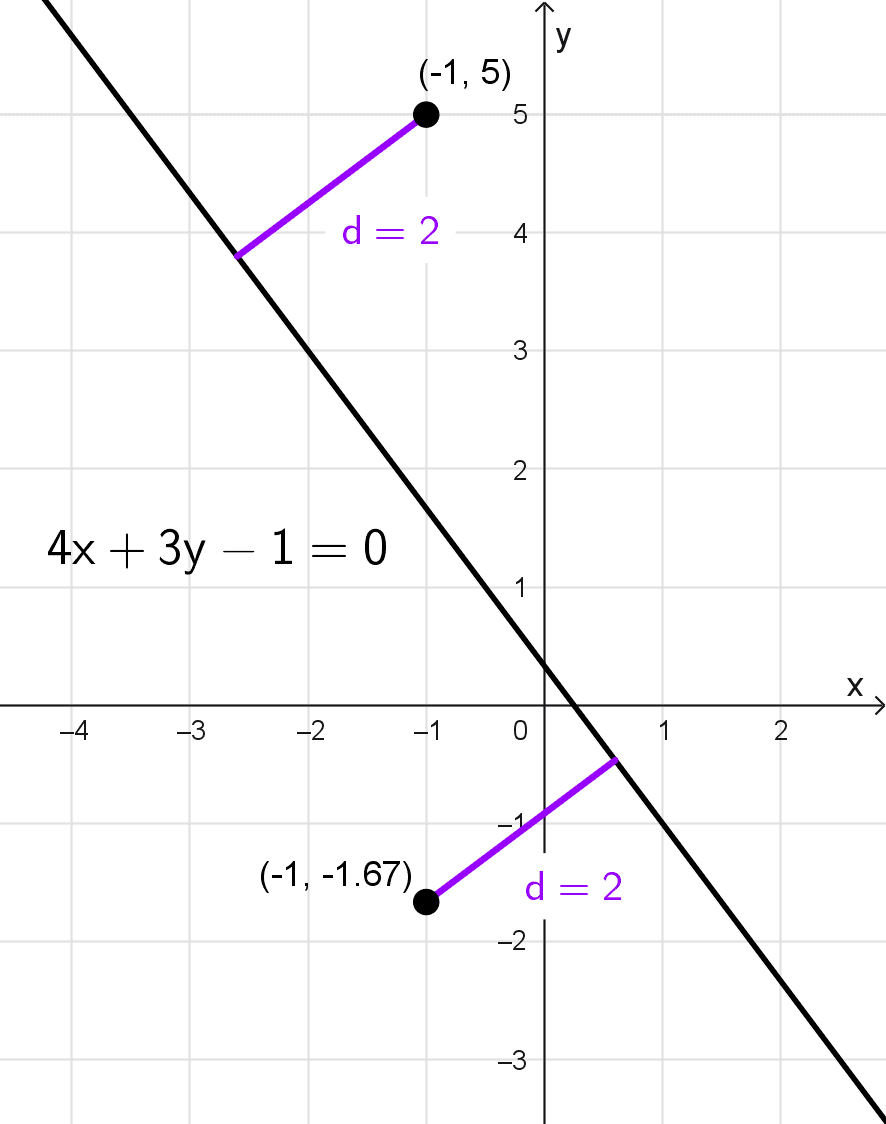
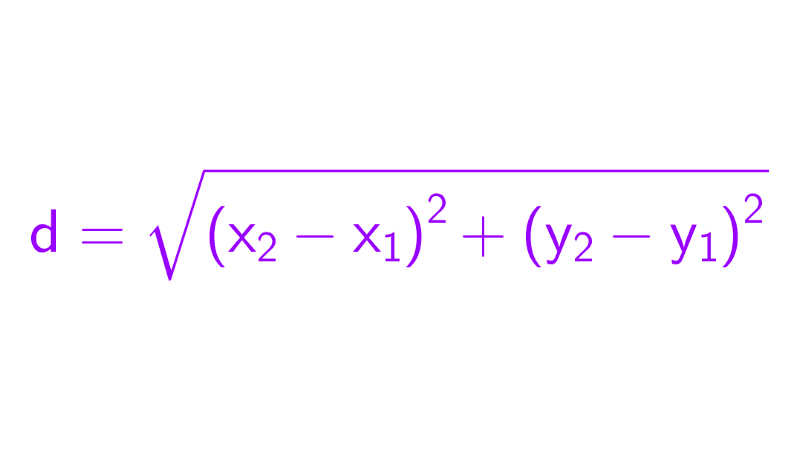
Otros artículos que pueden interesarte