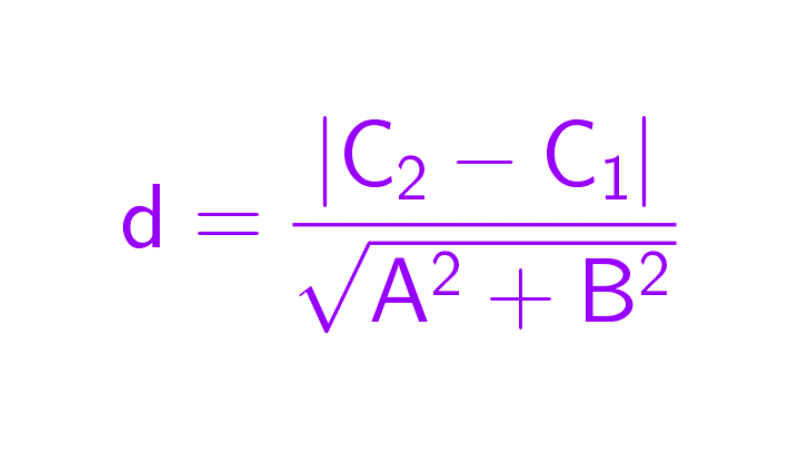
Distancia entre dos puntos
La distancia entre dos puntos en el plano cartesiano es la longitud del segmento de recta que los une. Es siempre un número no negativo y representa el camino más corto entre ambas ubicaciones.
La fórmula general o euclidiana para calcular la distancia entre dos puntos A(x1, y1) y B(x2, y2) es:
\(d(A,B)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
Esta expresión se lee como la raíz cuadrada de la suma de los cuadrados de las diferencias de las coordenadas correspondientes. Es decir, para obtener la distancia entre dos puntos se calculan primero la diferencia horizontal (x2 - x1) y la diferencia vertical (y2 - y1). Luego, cada diferencia se eleva al cuadrado, se suman ambos resultados y, finalmente, se extrae la raíz cuadrada de dicha suma.
Una forma común de denotar las variaciones es mediante la notación delta, donde Δx = x2 - x1 y Δy = y2 - y1. De esta manera, la fórmula también puede expresarse como:
\(d=\sqrt{(\Delta x)^2+(\Delta y)^2}\)
En otras palabras, la distancia es igual a la raíz cuadrada de la suma de los cuadrados de la variación horizontal y la variación vertical entre los puntos.
La fórmula tiene su origen en el teorema de Pitágoras, ya que las diferencias en las coordenadas x e y definen los catetos de un triángulo rectángulo cuya hipotenusa es la distancia que queremos hallar, como se puede ver en la imagen de arriba. Más adelante en este artículo veremos la demostración completa.
Índice
Ejemplos
Realizaremos primero un ejemplo detallado explicando el procedimiento que da origen a la fórmula de distancia, los siguientes ejemplos serán para practicar la aplicación de la fórmula.
Ejemplo 1
Calcular la distancia entre los puntos A(3, 1) y B(7, 4).
Solución
La distancia entre dos puntos debe medir qué tan separados están, y debe hacerlo de la manera más corta posible. No es una convención arbitraria: si no exigimos que sea el camino más corto, entonces cualquier trayectoria curva o quebrada serviría para definir una "distancia", y el concepto perdería su sentido único y objetivo. Por ello, en geometría, la distancia entre dos puntos se define siempre como la longitud del segmento recto que une ambos puntos, ya que se puede demostrar que esta es la más corta posible.
En el plano cartesiano, los puntos dados A(3, 1) y B(7, 4) representan los extremos de un segmento oblicuo, es decir, que no es paralelo a ninguno de los ejes coordenados, como se ve en la figura de abajo.
Trazamos segmentos paralelos a los ejes desde cada uno de los puntos hasta que se intersecten, construyendo un triángulo rectángulo auxiliar. En este triángulo, la hipotenusa es exactamente el segmento AB, cuya longitud deseamos calcular.
Podemos notar que los catetos de este triángulo corresponden a los desplazamientos horizontal y vertical entre los puntos; es decir, sus longitudes son las diferencias entre las coordenadas correspondientes. Así, la longitud del cateto horizontal es 7 - 3 = 4 unidades, y la del cateto vertical es 4 - 1 = 3 unidades.
Aquí es donde aplicamos el teorema de Pitágoras, que establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Por lo tanto, si llamamos d a la distancia (la hipotenusa), tenemos:
\(d^2=4^2+3^2\)
Calculamos los cuadrados:
\(d^2=16+9=25\)
Finalmente, para hallar d, extraemos la raíz cuadrada positiva, ya que una distancia es siempre un valor no negativo:
\(d=\sqrt{25}=5\)
Así, la distancia entre los puntos A(3, 1) y B(7, 4) es de 5 unidades.
Este procedimiento, basado en la construcción geométrica de un triángulo rectángulo y el teorema de Pitágoras, es la esencia de la deducción de la fórmula general para la distancia entre dos puntos, la cual haremos más adelante.
Ejemplo 2
Determinar la distancia entre los puntos del plano C(-2, 1) y D(5, -3).
Solución
Observamos que las coordenadas de C son \(x_1=-2, y_1=1,\) y las de D son \(x_2=5, y_2=-3.\) Para calcular la distancia, aplicamos la fórmula de distancia euclidiana entre dos puntos en el plano:
\(d(C, D)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
Sustituyendo los valores, obtenemos:
\(d(C, D)=\sqrt{(5-(-2))^2+((-3)-1)^2}=\sqrt{(5+2)^2+(-3-1)^2}=\sqrt{7^2+(-4)^2}\)
Realizamos las operaciones:
\(d(C, D)=\sqrt{49+16}=\sqrt{65}\)
Como no se trata de una raíz exacta, expresamos el resultado en su forma radical. La distancia entre C y D es \(\sqrt{65}\) unidades, aproximadamente 8,06 unidades.
Nota: al usar la fórmula, da lo mismo cuál punto tomemos como el primero, ya que siempre la distancia de un punto A a un punto B es igual a la de B hasta A: d(A, B) = d(B, A).
El orden de la sustracción dentro de cada diferencia no afecta el resultado final, ya que las diferencias se elevan al cuadrado; por ejemplo, (x2 - x1)2 es idéntico a (x1 - x2)2. Además, los puntos pueden estar ubicados en cualquier cuadrante.
Lo que sí es importante es restar coordenadas homólogas: la abscisa de un punto debe restarse con la abscisa del otro, y la ordenada con la ordenada. Nunca se debe, por ejemplo, restar la coordenada x de un punto con la coordenada y del otro.
Ejemplo 3
Hallar la distancia que separa los puntos E(-2, -1) y F(3, -2).
Solución
Identificamos las coordenadas: \(x_1=-2, y_1=-1, x_2=3, y_2=-2.\) Utilizamos la fórmula de distancia:
\(d(E, F)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}=\sqrt{(3-(-2))^2+((-2)-(-1))^2}=\sqrt{(3+2)^2+(-2+1)^2}\)
Simplificamos dentro de los paréntesis:
\(d(E, F)=\sqrt{5^2+(-1)^2}=\sqrt{25+1}=\sqrt{26}\)
Por lo tanto, la distancia entre E y F es \(\sqrt{26}≈5,1\) unidades.
Ejemplo 4
Calcular la distancia entre los puntos G(6, 3) y H(-1, -1).
Solución
Tomamos \(x_1=6, y_1=3, x_2=-1, y_2=-1\) y aplicamos la fórmula:
\(d(G, H)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}=\sqrt{(-1-6)^2+(-1-3)^2}=\sqrt{(-7)^2+(-4)^2}\)
Elevamos al cuadrado y sumamos:
\(d(G, H)=\sqrt{49+16}=\sqrt{65}\)
Así, la distancia entre G y H resulta ser \(\sqrt{65}\) unidades, coincidiendo numéricamente con la del ejemplo 2, aunque los puntos son diferentes.
Ejemplo 5
Encontrar la distancia entre los puntos P(2, 3) y Q(-1, 0).
Solución
Las coordenadas son \(x_1=2, y_1=3, x_2=-1, y_2=0.\) Sustituyendo en la fórmula:
\(d(P, Q)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}=\sqrt{(-1-2)^2+(0-3)^2}=\sqrt{(-3)^2+(-3)^2}\)
Operamos:
\(d(P, Q)=\sqrt{9+9}=\sqrt{18}=\sqrt{9 \cdot 2}=3\sqrt{2}\)
Simplificamos el radical para expresar el resultado como \(3\sqrt{2} ≈ 4,24\) unidades.
Ejemplo 6
Determinar la distancia entre los puntos \(R\left(-\dfrac{1}{4}, \dfrac{1}{6}\right)\) y \(S\left(\dfrac{1}{2},-\dfrac{5}{6}\right).\)
Solución
En este caso hay coordenadas con fracciones, las trabajamos de igual forma que en los demás casos. Identificamos \(x_1=-\dfrac{1}{4}, y_1=\dfrac{1}{6}, x_2=\dfrac{1}{2}, y_2=-\dfrac{5}{6}.\) Aplicamos la fórmula de distancia euclidiana:
\(d(R, S)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}=\sqrt{\left(\dfrac{1}{2}-\left(-\dfrac{1}{4}\right) \right)^2+\left(-\dfrac{5}{6}-\dfrac{1}{6} \right)^2}\)
Operamos:
\(d(R, S)=\sqrt{\left(\dfrac{3}{4} \right)^2+\left(-1 \right)^2}=\sqrt{ \dfrac{9}{16}+1 }=\sqrt{\dfrac{9}{16}+\dfrac{16}{16}}=\sqrt{ \dfrac{25}{16} }=\dfrac{\sqrt{25}}{\sqrt{16}}=\dfrac{5}{4}\)
Por lo tanto, la distancia entre los puntos R y S es 5/4 unidades, equivalente a 1,25 en notación decimal.
Ejemplo 7
Obtener la distancia entre los puntos \(A(-1, \sqrt{2})\) y \(B(3,-\sqrt{2}).\)
Solución
Observamos que hay coordenadas que contienen números irracionales. Identificamos \(x_1=-1, y_1=\sqrt{2}, x_2=3, y_2=-\sqrt{2}.\) Aplicamos la fórmula:
\(d(A, B)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}=\sqrt{(3-(-1))^2+(-\sqrt{2}-\sqrt{2})^2}\)
\(=\sqrt{(4)^2+(-2\sqrt{2})^2}=\sqrt{16+4 \cdot 2}=\sqrt{16+8}=\sqrt{24}=\sqrt{4 \cdot 6}=2\sqrt{6}\)
La distancia entre A y B es \(2\sqrt{6} ≈ 4,9\) unidades.
Ejemplo 8
Calcular la distancia entre P1(4,136; -2,394) y P2(-8,419; 2,843).
Solución
Aquí las coordenadas están dadas en notación decimal.
Tomamos \(x_1=4,136, y_1=-2,394, x_2=-8,419, y_2=2,843.\) Usamos la fórmula:
\(d(P_1, P_2)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}=\sqrt{(-8,419-4,136)^2+(2,843-(-2,394))^2}\)
\(=\sqrt{(-12,555)^2+(5,237)^2}=\sqrt{157,628025+27,426169}=\sqrt{185,054194}≈ 13,60\)
La distancia entre los puntos dados es aproximadamente 13,60 unidades.
¿Te está sirviendo este artículo? ¡Por favor, califícalo!
Casos especiales
Existen casos particulares donde calcular la distancia entre puntos se vuelve más sencillo.
Segmentos horizontales
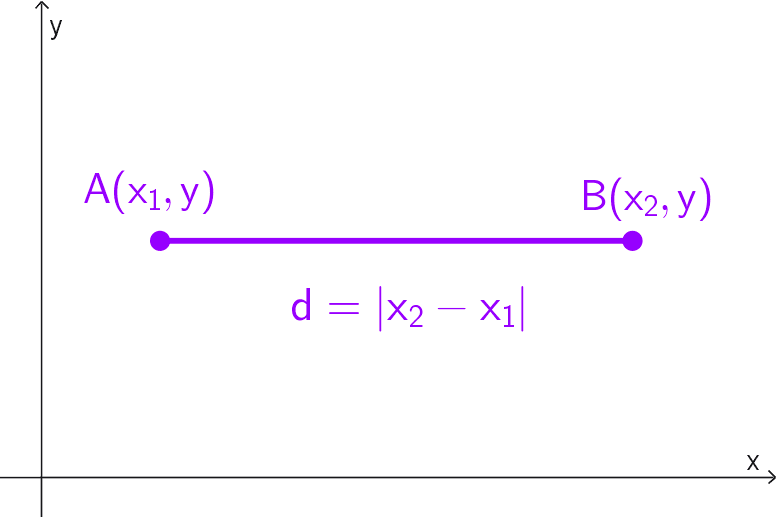
Cuando dos puntos comparten la misma coordenada en el eje vertical, es decir, tienen idéntica ordenada, se ubican en una línea paralela al eje de las abscisas. En esta situación, la distancia entre ellos se reduce al valor absoluto de la diferencia entre sus coordenadas en el eje x, simplificándose la fórmula general a:
d = |x2 - x1|
Esto ocurre porque el término (y2 - y1)2 se vuelve cero al ser iguales los valores de y.
Ejemplo
Para calcular la distancia entre los puntos A(-3, 4) y B(5, 4), basta con restar sus abscisas:
d = |5 - (-3)| = |8| = 8
Por tanto, la distancia que los separa es de 8 unidades.
Segmentos verticales
Un caso análogo ocurre cuando los puntos comparten la misma coordenada en el eje horizontal, presentando una abscisa común. Esto significa que están alineados verticalmente, formando un segmento paralelo al eje de las ordenadas.
En este caso, la distancia se calcula considerando únicamente la diferencia absoluta entre sus coordenadas y, ya que el término (x2 - x1)2 de la fórmula general se anula. La expresión se simplifica a:
d = |y2 - y1|
Ejemplo
Tomemos los puntos C(2, -2) y D(2, 7), su distancia es la diferencia entre sus ordenadas:
d = |7 - (-2)| = |9| = 9
Por tanto, la distancia entre ellos es de 9 unidades.
Distancia al origen
Cuando uno de los puntos es el origen de coordenadas (0, 0), la fórmula de la distancia se simplifica notablemente. Si tomamos un punto genérico A(x, y), la distancia d desde A hasta el origen es:
\(d=\sqrt{(x-0)^2+(y-0)^2}=\sqrt{x^2+y^2}\)
Ejemplo
Para hallar la distancia del punto Q(-6, 8) al origen, aplicamos esta expresión:
\(d=\sqrt{(-6)^2+(8)^2}=\sqrt{36+64}=\sqrt{100}=10\)
Es decir, la distancia del punto Q al origen es de 10 unidades.
Demostración de la fórmula
Supongamos que tenemos dos puntos en el plano: A(x1, y1) y B(x2, y2).
Si trazamos segmentos paralelos a los ejes coordenados desde cada punto, se forma un triángulo rectángulo cuya hipotenusa es el segmento que une A y B, cuya longitud llamamos d y es la que queremos determinar.
Las longitudes de los catetos de este triángulo son fáciles de determinar: la distancia horizontal entre los puntos es |x2 - x1| y la distancia vertical es |y2 - y1|. Tomamos valor absoluto para evitar resultados negativos.
Aplicando el teorema de Pitágoras, que establece que en un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos, obtenemos la siguiente relación:
\(d^2=(x_2-x_1)^2+(y_2-y_1)^2\)
El valor absoluto desaparece por estar elevado al cuadrado (propiedad |a|2 = a2). Para finalizar, simplemente despejamos d tomando la raíz cuadrada positiva, ya que la distancia es una magnitud siempre no negativa. Esto nos lleva a la fórmula general válida para cualquier par de puntos en el plano:
\(d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
Nota: no es necesario memorizar la fórmula de la distancia entre dos puntos. Lo fundamental es recordar el procedimiento geométrico que la origina: dados dos puntos, construir el triángulo rectángulo cuyos catetos son las diferencias de sus coordenadas y luego aplicar el teorema de Pitágoras. Si comprendemos este proceso, podemos deducir la fórmula en cualquier momento.
Distancia en tres dimensiones
La extensión del concepto de distancia al espacio tridimensional sigue un principio lógico similar al del plano. En lugar de dos coordenadas, ahora trabajamos con tres: un punto A se define como (x1, y1, z1) y un punto B como (x2, y2, z2).
La fórmula de la distancia entre dos puntos en el espacio tridimensional, derivada de dos aplicaciones consecutivas del teorema de Pitágoras, es una generalización natural de la fórmula bidimensional. Se expresa como:
\(d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}\)
Ejemplo
Calcular la distancia entre A(1, -2, 3) y B(4, 1, 0).
Solución
Primero, calculamos las diferencias de las coordenadas: \(x_2-x_1=4-1=3\), \(y_2-y_1=1-(-2)=3,\) y \(z_2-z_1=0-3=-3.\)
Luego, sustituimos estos valores en la fórmula:
\(d=\sqrt{(3)^2+(3)^2+(-3)^2}=\sqrt{9+9+9}=\sqrt{27}=3\sqrt{3}\)
Por lo tanto, la distancia entre los puntos A y B es \(3\sqrt{3}\) unidades.
Ejercicios resueltos
A continuación veremos algunos ejercicios de aplicación resueltos paso a paso.
Ejercicio 1
En una carta de navegación, el origen se sitúa en un puerto. Un barco se encuentra en el punto (-5, 6) y otro en el (2, 3). ¿Qué distancia hay entre ellos si las unidades de la carta corresponden a kilómetros?
Solución
Para hallar la distancia entre dos puntos en el plano cartesiano usamos la fórmula de distancia euclidiana. Asignamos el primer barco al punto (-5, 6) y el segundo al punto (2, 3).
\(d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}=\sqrt{(2-(-5))^2+(3-6)^2}=\sqrt{7^2+(-3)^2}=\sqrt{49+9}=\sqrt{58}\)
En conclusión, la distancia entre los dos barcos es \(\sqrt{58}\) kilómetros, que aproximadamente equivale a 7,62 km.
Ejercicio 2
Halle él o los valores de a para que el punto (a, 3) esté a cinco unidades del punto (-2, -1).
Solución
Planteamos la condición de distancia igual a 5 entre los puntos \((a, 3)\) y \((-2,-1).\) Usando la fórmula de distancia:
\(\sqrt{(a-(-2))^2+(3-(-1))^2}=5\)
Simplificamos las expresiones dentro del paréntesis:
\(\sqrt{(a+2)^2+4^2}=5\)
\(\sqrt{(a+2)^2+16}=5\)
Para eliminar la raíz cuadrada, elevamos ambos miembros al cuadrado:
\((a+2)^2+16=25\)
Restamos 16 en ambos lados:
\((a+2)^2=9\)
Extraemos la raíz cuadrada, recordando que hay dos soluciones posibles:
\(a+2=3 \quad \text{o} \quad a+2=-3\)
Resolvemos cada caso. En el primero, \(a+2=3\) implica \(a=1.\) En el segundo, \(a+2=-3\) implica \(a=-5.\)
Por lo tanto, los valores de a que satisfacen la condición son a = 1 y a = -5. Esto significa que tanto el punto (1, 3) como el punto (-5, 3) están a 5 unidades del punto (-2, -1).
Ejercicio 3
Dados los puntos de coordenadas A(-3, 5) y B(x, -1), halle el valor de x sabiendo que la longitud del segmento que determinan es \(\sqrt{61}.\)
Solución
La distancia entre los puntos \(A(-3, 5)\) y \(B(x,-1)\) es \(\sqrt{61}.\) Aplicamos la fórmula de distancia:
\(\sqrt{(x-(-3))^2+(-1-5)^2}=\sqrt{61}\)
Esto se simplifica a:
\(\sqrt{(x+3)^2+(-6)^2}=\sqrt{61}\)
\(\sqrt{(x+3)^2+36}=\sqrt{61}\)
Elevamos al cuadrado ambos miembros:
\((x+3)^2+36=61\)
Restamos 36 en ambos lados de la ecuación:
\((x+3)^2=25\)
Tomamos raíz cuadrada en ambos lados, considerando las dos posibilidades:
\(x+3=5 \quad \text{o} \quad x+3=-5\)
Resolviendo, en el primer caso x = 2, y en el segundo x = -8. Así, hay dos valores de x que cumplen la condición, es decir, dos puntos puntos posibles B(2, -1) y B(-8, -1). Ambos hacen que la distancia entre A y B sea \(\sqrt{61}.\)
Ejercicio 4
Dados los puntos M(2, -1) y S(6, y), calcule el valor de y de tal manera que la longitud del segmento que ellos determinan sea 5.
Solución
La distancia entre \(M(2,-1)\) y \(S(6, y)\) debe ser igual a 5. Escribimos la fórmula de distancia correspondiente:
\(\sqrt{(6-2)^2+(y-(-1))^2}=5\)
Realizamos las operaciones algebraicas dentro de los paréntesis:
\(\sqrt{4^2+(y+1)^2}=5\)
\(\sqrt{16+(y+1)^2}=5\)
Elevamos al cuadrado para eliminar la raíz:
\(16+(y+1)^2=25\)
Restamos 16 en ambos lados:
\((y+1)^2=9\)
Obtenemos las dos soluciones posibles al tomar raíz cuadrada:
\(y+1=3 \quad \text{o} \quad y+1=-3\)
Del primer caso, \(y=2;\) del segundo caso, \(y=-4.\) Por tanto, existen dos puntos \(S\) que cumplen la condición: \(S(6, 2)\) y \(S(6, -4).\) Ambos están a 5 unidades del punto \(M(2, -1).\)
Ejercicio 5
Halle el valor de b de tal manera que la distancia que separa los puntos P(b, 7) y Q(-4, 2) sea 13.
Solución
Aplicamos esta fórmula de distancia con los datos dados:
\(\sqrt{(-4-b)^2+(2-7)^2}=13\)
Realizamos las operaciones dentro del paréntesis:
\(\sqrt{(-4-b)^2+(-5)^2}=13\)
Esto se simplifica a:
\(\sqrt{(b+4)^2+25}=13\)
Elevamos al cuadrado ambos miembros para eliminar la raíz cuadrada:
\((b+4)^2+25=169\)
Restamos 25 en ambos lados de la ecuación:
\((b+4)^2=144\)
Tomamos raíz cuadrada, recordando que hay dos posibles soluciones:
\(b+4=12 \quad \text{o} \quad b+4=-12\)
Resolvemos cada ecuación. De la primera obtenemos \(b=8,\) y de la segunda \(b=-16.\) Por lo tanto, los valores de \(b\) que hacen que la distancia entre \(P\) y \(Q\) sea 13 son \(b=8\) y \(b=-16.\)
Ejercicio 6
La abscisa de un punto es -3 y su distancia al punto P(1, -2) es \(\sqrt{52}.\) Encuentre la ordenada del punto.
Solución
Denotamos al punto buscado como \(A(-3, y),\) donde la abscisa es \(-3\) y la ordenada \(y\) es desconocida. La distancia entre \(A\) y \(P(1,-2)\) es \(\sqrt{52}.\) Aplicamos la fórmula de distancia:
\(\sqrt{(1-(-3))^2+(-2-y)^2}=\sqrt{52}\)
Esto se simplifica a:
\(\sqrt{(4)^2+(-2-y)^2}=\sqrt{52}\)
Elevamos al cuadrado ambos lados para eliminar las raíces:
\(16+(y+2)^2=52\)
Restamos 16 en ambos miembros:
\((y+2)^2=36\)
Tomamos raíz cuadrada, considerando ambas posibilidades:
\(y+2=6 \quad \text{o} \quad y+2=-6\)
Resolviendo, del primer caso obtenemos \(y=4,\) y del segundo \(y=-8.\) Así, existen dos puntos que satisfacen la condición: \((-3, 4)\) y \((-3,-8),\) ambos a \(\sqrt{52}\) unidades de \(P(1,-2).\)
Ejercicio 7
La distancia del punto P(2, y) a R(5, -1) es la mitad de la distancia a S(-6, 9). Calcule el valor de la ordenada del punto P.
Solución
Planteamos la condición dada. Primero calculamos la distancia entre \(P(2, y)\) y \(R(5,-1):\)
\(d(P, R)=\sqrt{(5-2)^2+(-1-y)^2}=\sqrt{9+(y+1)^2}\)
Luego, la distancia entre \(P(2, y)\) y \(S(-6, 9):\)
\(d(P, S)=\sqrt{(-6-2)^2+(9-y)^2}=\sqrt{(-8)^2+(9-y)^2}=\sqrt{64+(y-9)^2}\)
La condición establece que \(d(P, R)=\dfrac{1}{2} d(P, S).\) Escribimos la ecuación:
\(\sqrt{9+(y+1)^2}=\dfrac{1}{2} \sqrt{64+(y-9)^2}\)
Para simplificar, elevamos al cuadrado ambos miembros:
\(9+(y+1)^2=\dfrac{1}{4} \left[ 64+(y-9)^2 \right]\)
Multiplicamos toda la ecuación por 4 para eliminar el denominador:
\(36+4(y+1)^2=64+(y-9)^2\)
\(36+4y^2+8y+4=64+y^2-18y+81\)
Simplificamos términos semejantes:
\(4y^2+8y+40=y^2-18y+145\)
Pasamos todos los términos a un lado:
\(3y^2+26y-105=0\)
Resolvemos esta ecuación cuadrática usando la fórmula general:
\(y_{1,2}=\dfrac{-26±\sqrt{26^2-4(3)(-105)}}{2(3)}=\dfrac{-26±\sqrt{676+1260}}{6}=\dfrac{-26±\sqrt{1936}}{6}\)
Dado que \(\sqrt{1936}=44,\) tenemos:
\(y_1=\dfrac{-26+44}{6}=\dfrac{18}{6}=3\)
\(y_2=\dfrac{-26-44}{6}=\dfrac{-70}{6}=-\dfrac{35}{3}\)
Los valores de la ordenada \(y\) que cumplen la condición son \(y_1=3\) y \(y_2=-\dfrac{35}{3}.\)
Ejercicio 8
Obtenga el valor de la ordenada de M(1, y) sabiendo que su distancia al punto A(-1, -3) es el doble que su distancia al origen de coordenadas.
Solución
El origen de coordenadas es \(O(0, 0).\) Calculamos la distancia de \(M(1, y)\) a \(A(-1,-3):\)
\(d(M, A)=\sqrt{(-1-1)^2+(-3-y)^2}=\sqrt{4+(y+3)^2}\)
La distancia de \(M\) al origen es:
\(d(M, O)=\sqrt{(1-0)^2+(y-0)^2}=\sqrt{1+y^2}\)
La condición dada es \(d(M, A)=2 \cdot d(M, O).\) Planteamos la ecuación:
\(\sqrt{4+(y+3)^2}=2 \sqrt{1+y^2}\)
Elevamos al cuadrado ambos miembros:
\(4+(y+3)^2=4(1+y^2)\)
Desarrollamos el cuadrado y simplificamos:
\(4+y^2+6y+9=4+4y^2\)
\(y^2+6y+13=4+4y^2\)
Pasamos todos los términos a un lado:
\(3y^2-6y-9=0\)
Dividimos toda la ecuación por 3 para simplificar:
\(y^2-2y-3=0\)
Factorizamos:
\((y-3)(y+1)=0\)
Las soluciones son \(y=3\) y \(y=-1.\) Por lo tanto, la ordenada de \(M\) puede tomar los valores \(y=3\) o \(y=-1.\)
Ejercicio 9
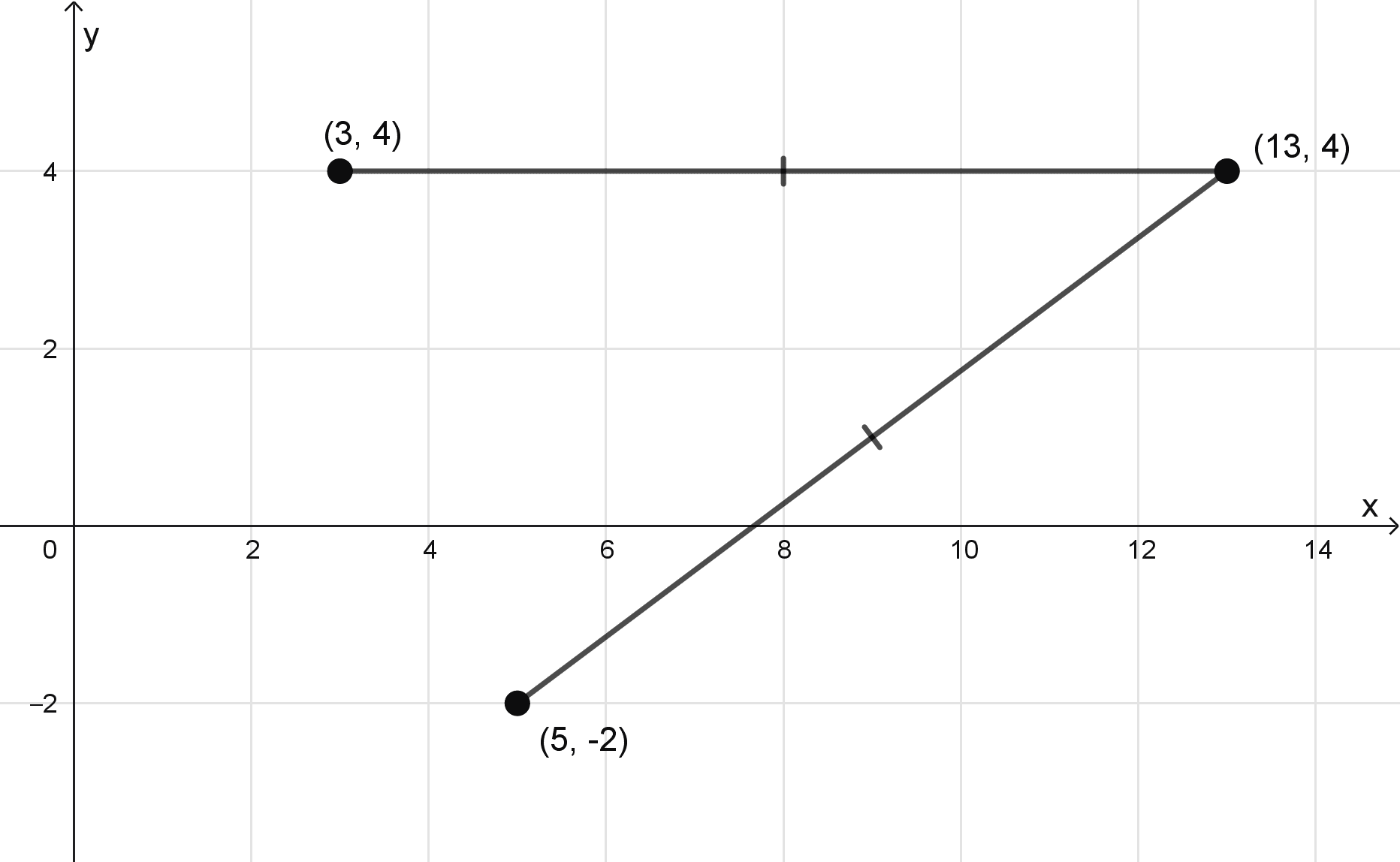
Si (x, 4) equidista de (5, -2) y (3, 4), encuentre x.
Solución
Para que un punto equidiste de otros dos, las distancias a cada uno deben ser iguales. Calculamos la distancia entre \(P(x, 4)\) y \(A(5,-2),\) y la igualamos a la distancia entre \(P(x, 4)\) y \(B(3, 4).\)
Aplicamos la fórmula de distancia entre dos puntos:
\(\sqrt{(5-x)^2+(-2-4)^2}=\sqrt{(3-x)^2+(4-4)^2}\)
Simplificamos las expresiones dentro de los radicales:
\(\sqrt{(5-x)^2+36}=\sqrt{(3-x)^2}\)
Elevamos al cuadrado ambos miembros para eliminar las raíces:
\((5-x)^2+36=(3-x)^2\)
Desarrollamos los cuadrados:
\(25-10x+x^2+36=9-6x+x^2\)
Cancelamos \(x^2\) en ambos lados y simplificamos los términos numéricos:
\(61-10x=9-6x\)
Pasamos los términos con \(x\) a un lado y los independientes al otro:
\(-10x+6x=9-61\)
\(-4x=-52\)
Dividimos entre \(-4\) para obtener el valor de la abscisa:
\(x=13\)
Por lo tanto, el punto que equidista de (5, -2) y (3, 4) con ordenada 4 es (13, 4).
Ejercicio 10
Si (-3, y) equidista de (2, 6) y (7, -2), encuentre y.
Solución
Establecemos la condición de equidistancia entre el punto \(P(-3, y)\) y los puntos dados \(A(2, 6)\) y \(B(7,-2).\) Igualamos las distancias:
\(d(P,A)=d(P,B)\)
\(\sqrt{(2+3)^2+(6-y)^2}=\sqrt{(7+3)^2+(-2-y)^2}\)
\(\sqrt{25+(6-y)^2}=\sqrt{100+(-2-y)^2}\)
Elevamos al cuadrado para eliminar las raíces:
\(25+(6-y)^2=100+(-2-y)^2\)
Desarrollamos los cuadrados:
\(25+36-12y+y^2=100+4+4y+y^2\)
Cancelamos \(y^2\) en ambos lados y combinamos términos numéricos:
\(61-12y=104+4y\)
Pasamos los términos con \(y\) a un lado:
\(-12y-4y=104-61\)
\(-16y=43\)
Dividimos entre \(-16\) para hallar la ordenada:
\(y=-\dfrac{43}{16}\)
Por lo tanto, el punto que cumple la condición es \(\left(-3,-\dfrac{43}{16}\right).\)
Ejercicio 11
Encuentre el punto sobre el eje y que equidista de (-4, -2) y (3, 1).
Solución
Todo punto sobre el eje \(y\) tiene coordenadas de la forma \((0, y).\) Planteamos que sus distancias a \(A(-4,-2)\) y \(B(3, 1)\) sean iguales:
\(\sqrt{(0+4)^2+(y+2)^2}=\sqrt{(0-3)^2+(y-1)^2}\)
Simplificamos:
\(\sqrt{16+(y+2)^2}=\sqrt{9+(y-1)^2}\)
Elevamos al cuadrado:
\(16+(y+2)^2=9+(y-1)^2\)
Desarrollamos los cuadrados:
\(16+y^2+4y+4=9+y^2-2y+1\)
Cancelamos \(y^2\) y simplificamos:
\(4y+20=-2y+10\)
Pasamos los términos con \(y\) a un lado:
\(4y+2y=10-20\)
\(6y=-10\)
Dividimos entre 6:
\(y=-\dfrac{5}{3}\)
El punto buscado sobre el eje \(y\) es \(\left(0,-\dfrac{5}{3}\right),\) aproximadamente (0; -1,67).
Ejercicio 12
Encuentre el punto sobre el eje x que equidista de (-2, 5) y (4, 1).
Solución
Los puntos sobre el eje \(x\) tienen coordenadas \((x, 0).\) Igualamos las distancias a \(A(-2, 5)\) y \(B(4, 1):\)
\(\sqrt{(x+2)^2+(0-5)^2}=\sqrt{(x-4)^2+(0-1)^2}\)
Simplificamos:
\(\sqrt{(x+2)^2+25}=\sqrt{(x-4)^2+1}\)
Elevamos al cuadrado:
\((x+2)^2+25=(x-4)^2+1\)
Desarrollamos los cuadrados:
\(x^2+4x+4+25=x^2-8x+16+1\)
Cancelamos \(x^2\) y simplificamos:
\(4x+29=-8x+17\)
Pasamos los términos con \(x\) a un lado:
\(4x+8x=17-29\)
\(12x=-12\)
Dividimos entre 12:
\(x=-1\)
El punto sobre el eje \(x\) que cumple la condición es \((-1, 0).\)
Ejercicio 13
Demostrar que los puntos \(A(3, 3)\), \(B(-3,-3)\) y \(C(-3\sqrt{3}, 3\sqrt{3})\) son vértices de un triángulo equilátero.
Solución
Para que un triángulo sea equilátero, las longitudes de sus tres lados deben ser iguales. Calculamos las distancias entre cada par de puntos usando la fórmula de distancia entre dos puntos.
Primero hallamos d(A, B):
\(d(A, B)=\sqrt{(-3-3)^2+(-3-3)^2}=\sqrt{(-6)^2+(-6)^2}=\sqrt{36+36}=\sqrt{72}=\sqrt{36 \cdot 2}=6\sqrt{2}\)
Ahora calculamos d(A, C):
\(d(A, C)=\sqrt{(-3\sqrt{3}-3)^2+(3\sqrt{3}-3)^2}=\sqrt{(3\sqrt{3}+3)^2+(3\sqrt{3}-3)^2}=\sqrt{(27+18\sqrt{3}+9)+(27-18\sqrt{3}+9)}=\sqrt{72}=\sqrt{36\cdot 2}=6\sqrt{2}\)
Finalmente, hallamos d(B, C):
\(d(B, C)=\sqrt{(-3\sqrt{3}+3)^2+(3\sqrt{3}+3)^2}=\sqrt{(3\sqrt{3}-3)^2+(3\sqrt{3}+3)^2}=\sqrt{(27-18\sqrt{3}+9)+(27+18\sqrt{3}+9)}=\sqrt{72}=\sqrt{36 \cdot 2}=6\sqrt{2}\)
Como \(d(A, B)=d(A, C)=d(B, C)=6\sqrt{2},\) los tres lados tienen la misma longitud. Así, A, B y C son los vértices de un triángulo equilátero.
Ejercicio 14
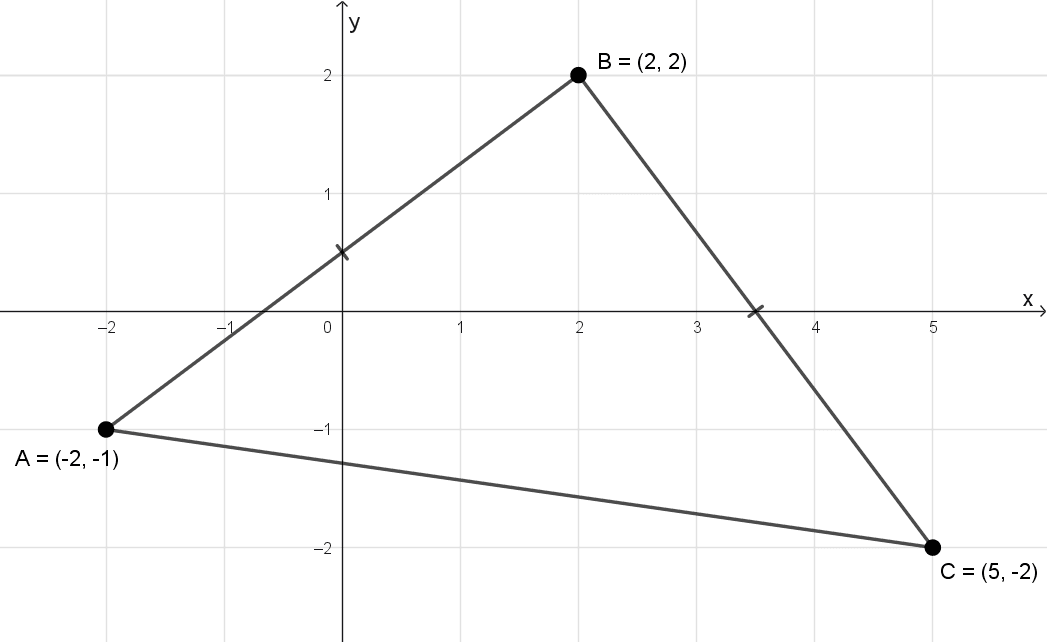
Probar que los puntos A(-2, -1), B(2, 2) y C(5, -2) son los vértices de un triángulo isósceles.
Solución
Un triángulo es isósceles si al menos dos de sus lados tienen igual longitud. Calculamos las distancias entre cada par de puntos.
Primero hallamos \(d(A, B)\) donde \(A(-2,-1)\) y \(B(2, 2):\)
\(d(A, B)=\sqrt{(2+2)^2+(2+1)^2}=\sqrt{4^2+3^2}=\sqrt{16+9}=\sqrt{25}=5\)
Ahora \(d(A, C)\) con \(C(5,-2):\)
\(d(A, C)=\sqrt{(5+2)^2+(-2+1)^2}=\sqrt{7^2+(-1)^2}=\sqrt{49+1}=\sqrt{50}\)
Finalmente \(d(B, C):\)
\(d(B, C)=\sqrt{(5-2)^2+(-2-2)^2}=\sqrt{3^2+(-4)^2}=\sqrt{9+16}=\sqrt{25}=5\)
Observamos que \(d(A, B)=d(B, C)=5,\) mientras que \(d(A, C)=\sqrt{50}.\) Por tanto, dos lados son iguales y el tercero es distinto, lo cual satisface la definición de triángulo isósceles.
Ejercicio 15
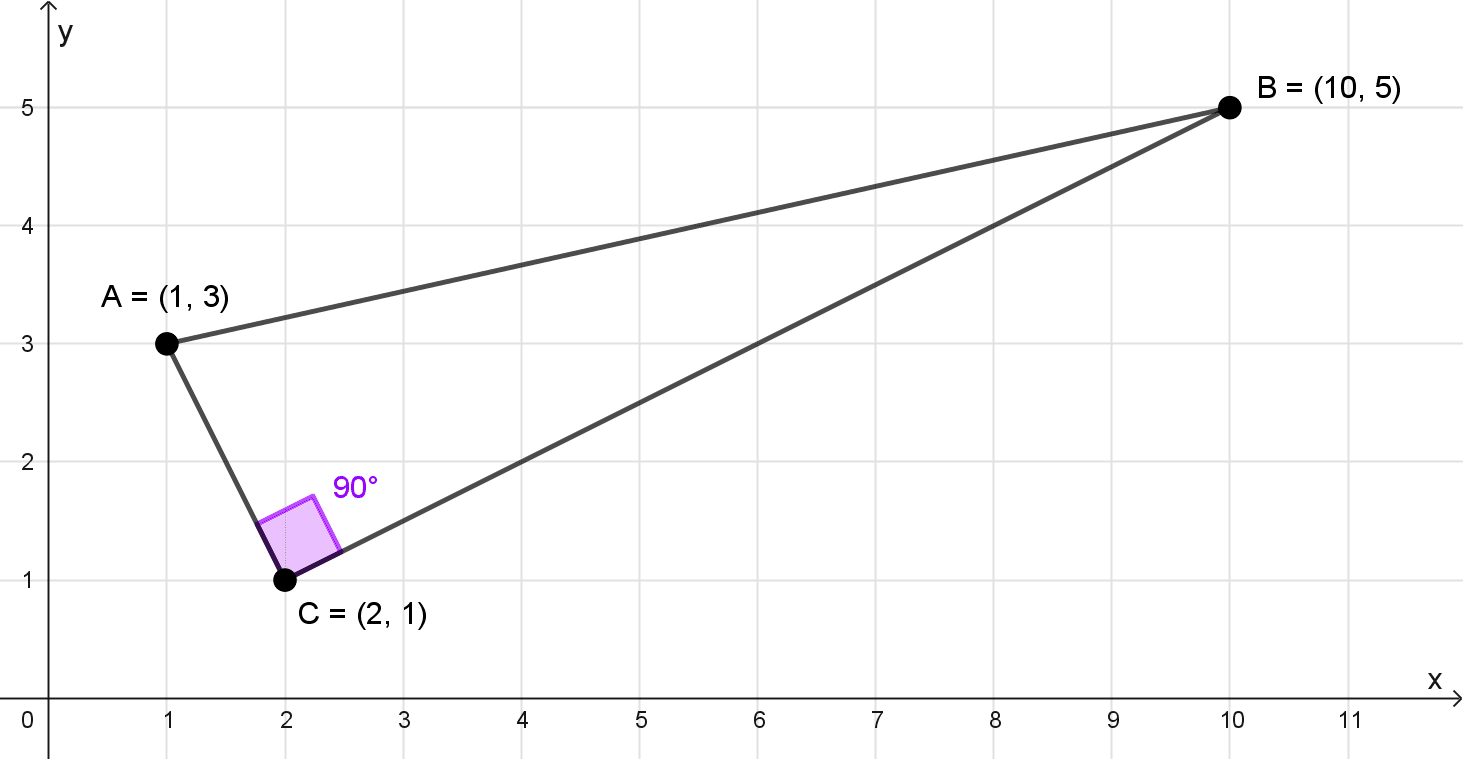
Muestre que los puntos A(1, 3), B(10, 5) y C(2, 1) son los vértices de un triángulo rectángulo.
Solución
Un triángulo es rectángulo si cumple el teorema de Pitágoras: la suma de los cuadrados de los dos lados más cortos es igual al cuadrado del lado más largo. Calculamos las longitudes de los tres lados.
\(d(A, B)=\sqrt{(10-1)^2+(5-3)^2}=\sqrt{81+4}=\sqrt{85}\)
\(d(B, C)=\sqrt{(2-10)^2+(1-5)^2}=\sqrt{64+16}=\sqrt{80}\)
\(d(C, A)=\sqrt{(1-2)^2+(3-1)^2}=\sqrt{1+4}=\sqrt{5}\)
Identificamos los valores numéricos de los cuadrados:
\([d(A, B)]^2=85, \quad [d(B, C)]^2=80, \quad [d(C, A)]^2=5\)
Observamos que los dos lados más cortos son \(d(B, C)\) y \(d(C, A).\) Sumamos sus cuadrados:
\(80+5=85\)
Esta suma es exactamente igual al cuadrado del lado restante \([d(A, B)]^2=85.\) Por tanto:
\([d(B, C)]^2+[d(C, A)]^2=[d(A, B)]^2\)
La relación pitagórica se cumple, lo que demuestra que el triángulo es rectángulo con el ángulo recto en el vértice \(C.\)
Ejercicio 16
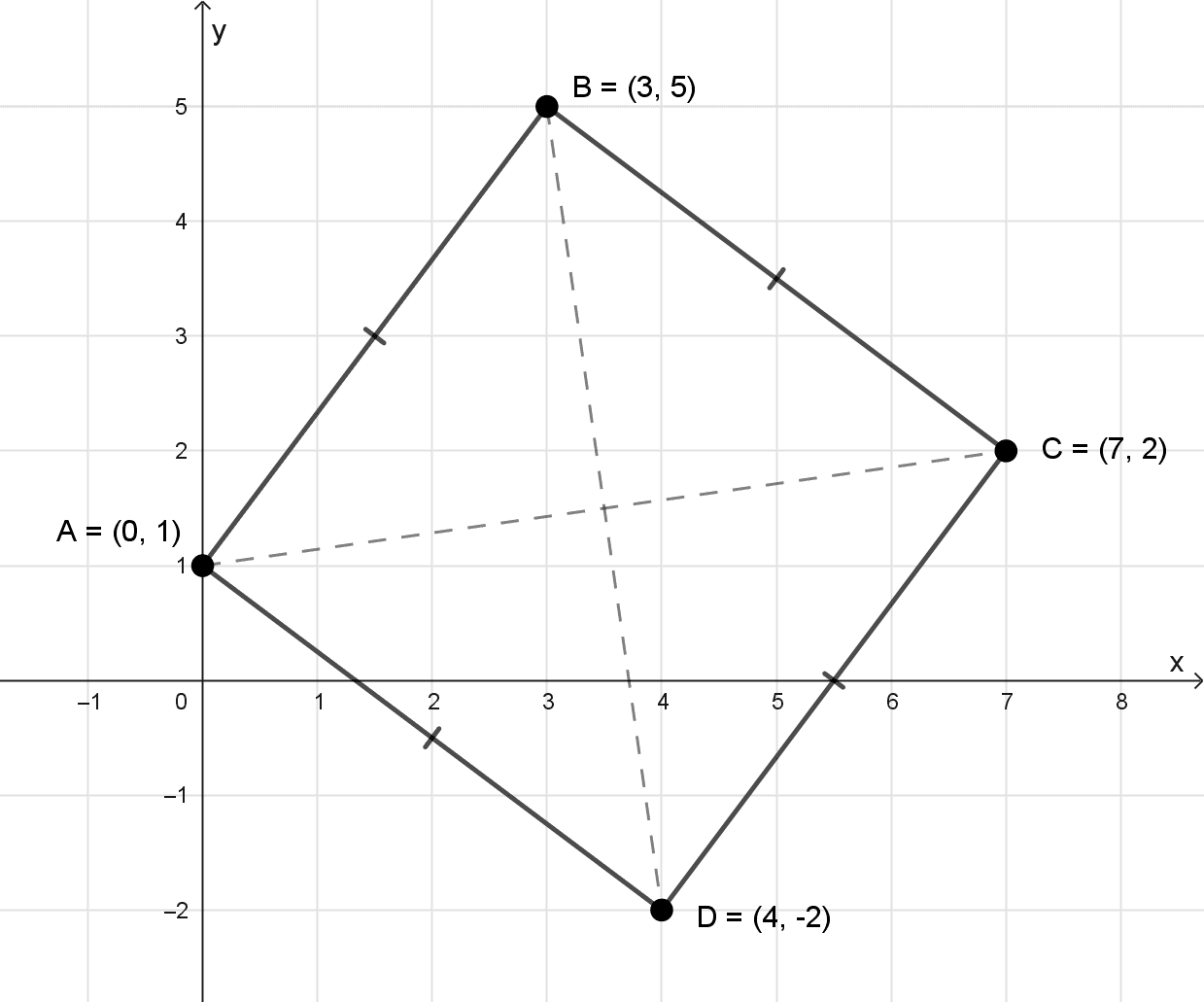
Demostrar que los puntos (0, 1), (3, 5), (7, 2), (4, -2) son los vértices de un cuadrado.
Solución
Para que cuatro puntos formen un cuadrado, todos los lados deben tener igual longitud y las diagonales también deben ser iguales entre sí (y además los lados deben ser perpendiculares, lo cual se verifica si se cumple la igualdad de lados y diagonales en un cuadrilátero con lados iguales consecutivos). Llamaremos \(A(0, 1)\), \(B(3, 5)\), \(C(7, 2)\) y \(D(4,-2).\)
Calculamos las longitudes de los lados:
\(d(A, B)=\sqrt{(3-0)^2+(5-1)^2}=\sqrt{9+16}=\sqrt{25}=5\)
\(d(B, C)=\sqrt{(7-3)^2+(2-5)^2}=\sqrt{16+9}=\sqrt{25}=5\)
\(d(C, D)=\sqrt{(4-7)^2+(-2-2)^2}=\sqrt{9+16}=\sqrt{25}=5\)
\(d(D, A)=\sqrt{(0-4)^2+(1+2)^2}=\sqrt{16+9}=\sqrt{25}=5\)
Todos los lados miden \(5,\) por lo que el cuadrilátero es un rombo. Ahora verificamos las diagonales:
\(d(A, C)=\sqrt{(7-0)^2+(2-1)^2}=\sqrt{49+1}=\sqrt{50}\)
\(d(B, D)=\sqrt{(4-3)^2+(-2-5)^2}=\sqrt{1+49}=\sqrt{50}\)
Las diagonales son iguales. En un rombo, si las diagonales son iguales, entonces es un cuadrado (pues los ángulos internos son rectos). Con esto queda demostrado que A, B, C, D son los vértices de un cuadrado.
Preguntas frecuentes
¿Cuál es la fórmula general para calcular la distancia entre dos puntos?
La fórmula general es: d = √[(x₂ - x₁)² + (y₂ - y₁)²]. Esta expresión es una aplicación directa del teorema de Pitágoras, donde (x₂ - x₁) e (y₂ - y₁) representan las longitudes de los catetos del triángulo rectángulo formado por los puntos. Es válida para cualquier par de coordenadas, sean enteras, fraccionarias o irracionales.
En la fórmula de distancia, ¿importa qué punto se elige como (x₁, y₁) y cuál como (x₂, y₂)?
No, el orden no importa. La resta (x₂ - x₁) y (y₂ - y₁) está al cuadrado, por lo que el signo negativo se elimina, dando siempre el mismo resultado positivo. Además, los puntos pueden estar en cualquier cuadrante del plano.
¿En qué unidades se expresa el resultado?
El resultado se expresa en las mismas unidades de longitud utilizadas para las coordenadas. Si las coordenadas se miden en centímetros, la distancia estará en centímetros; si son unidades arbitrarias, la distancia será en esas mismas unidades.
¿Qué hacer si el resultado no es una raíz exacta?
Si el resultado bajo la raíz cuadrada no es un cuadrado perfecto, podemos dejar la distancia expresada en forma radical simplificada (por ejemplo, √13) o, si el contexto lo requiere, proporcionar una aproximación decimal (por ejemplo, ≈ 3.606). Ambas formas son correctas.
¿Qué pasa si los dos puntos tienen la misma coordenada x o la misma coordenada y?
Si los puntos comparten la misma coordenada x, significa que están alineados verticalmente. La fórmula se simplifica a d = |y₂ - y₁|, que es simplemente la diferencia absoluta de sus coordenadas y. Análogamente, si tienen la misma coordenada y, están alineados horizontalmente y la distancia es d = |x₂ - x₁|.
¿Puede la distancia entre dos puntos ser negativa?
No, la distancia es una magnitud escalar que representa una longitud, por lo que siempre es un valor mayor o igual a cero. El cálculo mediante la fórmula siempre arroja un resultado no negativo debido a los cuadrados y a la raíz cuadrada principal.
¿Qué significa si la distancia calculada es 0?
Una distancia igual a 0 indica que los dos puntos son coincidentes, es decir, tienen exactamente las mismas coordenadas (x₁ = x₂ e y₁ = y₂). No hay separación entre ellos en el plano.
Bibliografía
- Cotrina, J. y Escudero, P. (2021). Introducción a la geometría analítica. Universidad del Pacífico.
- Engler, A., Müller, D., Vrancken, S. y Hecklein, M. (2020). Geometría analítica. Universidad Nacional del Litoral.
- Fuller, G. y Tarwater, D. (1995). Geometría analítica (7.ª ed.). Pearson Educación.
- Lehmann, C. (1989). Geometría analítica. Limusa.
- Márquez, A., Vázquez, F., Ruiz, H., Villegas, M. y Figueroa, M. (2009). Geometría analítica. Prentice Hall.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta

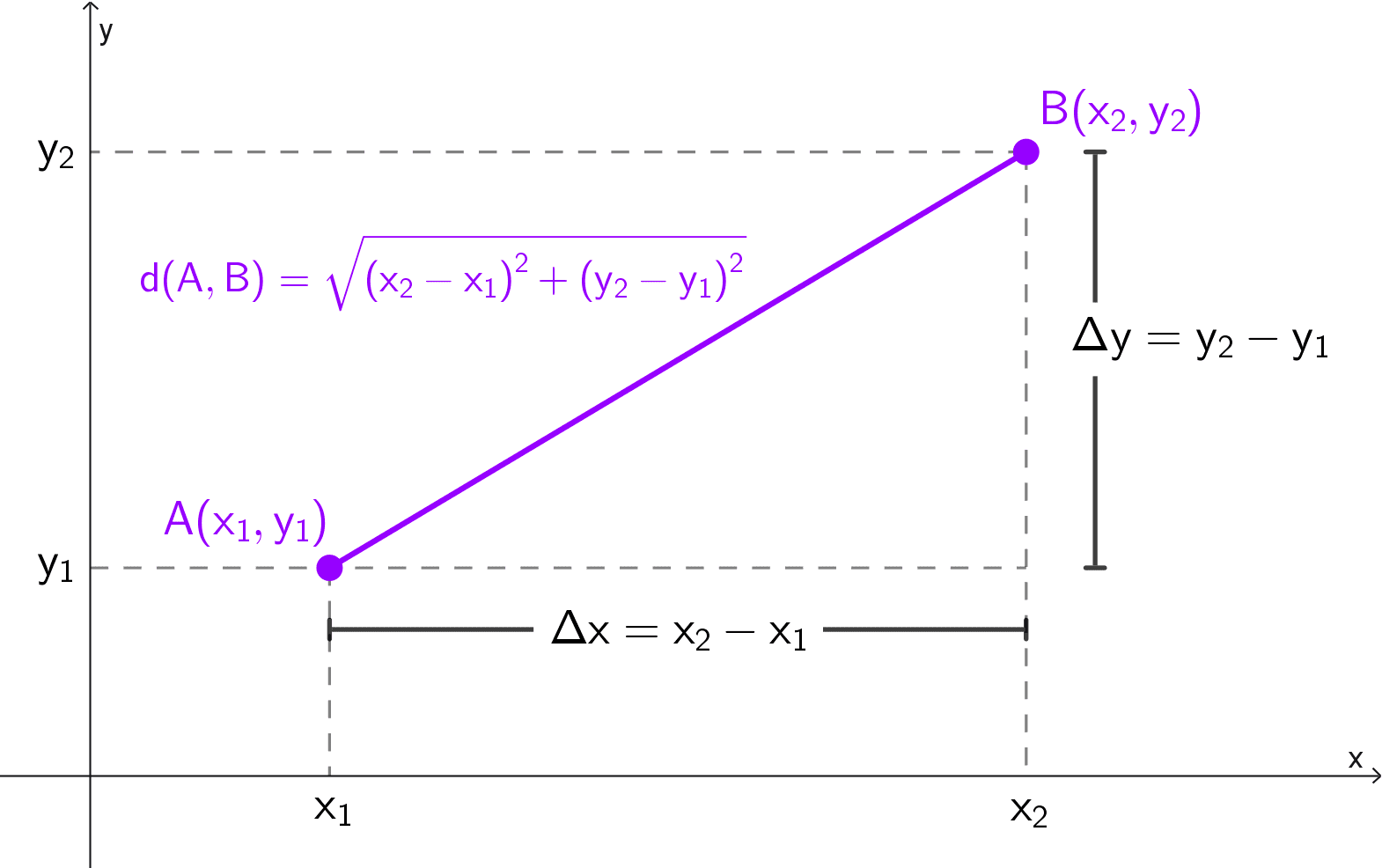
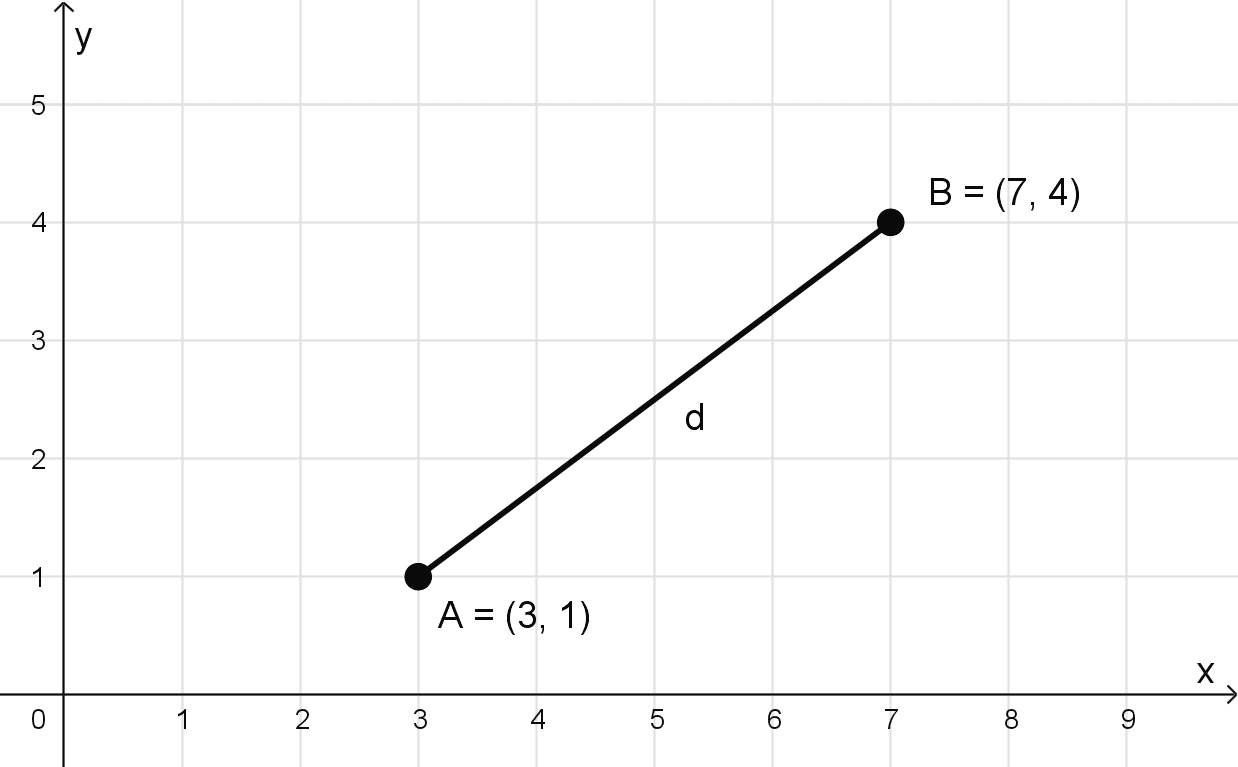
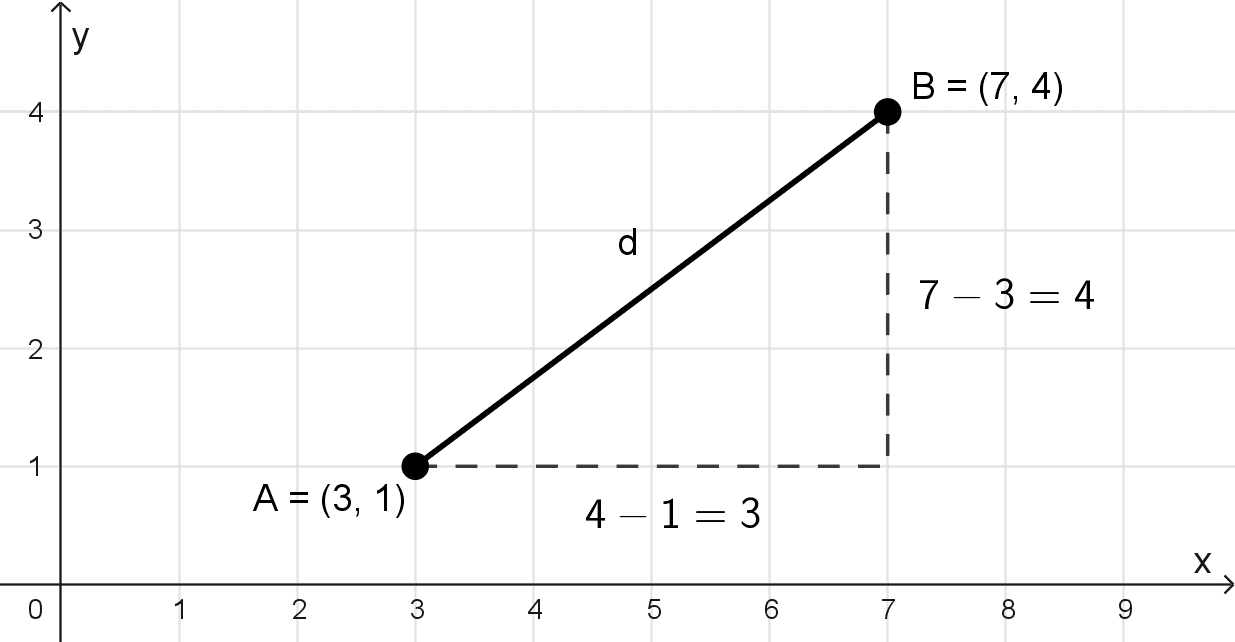
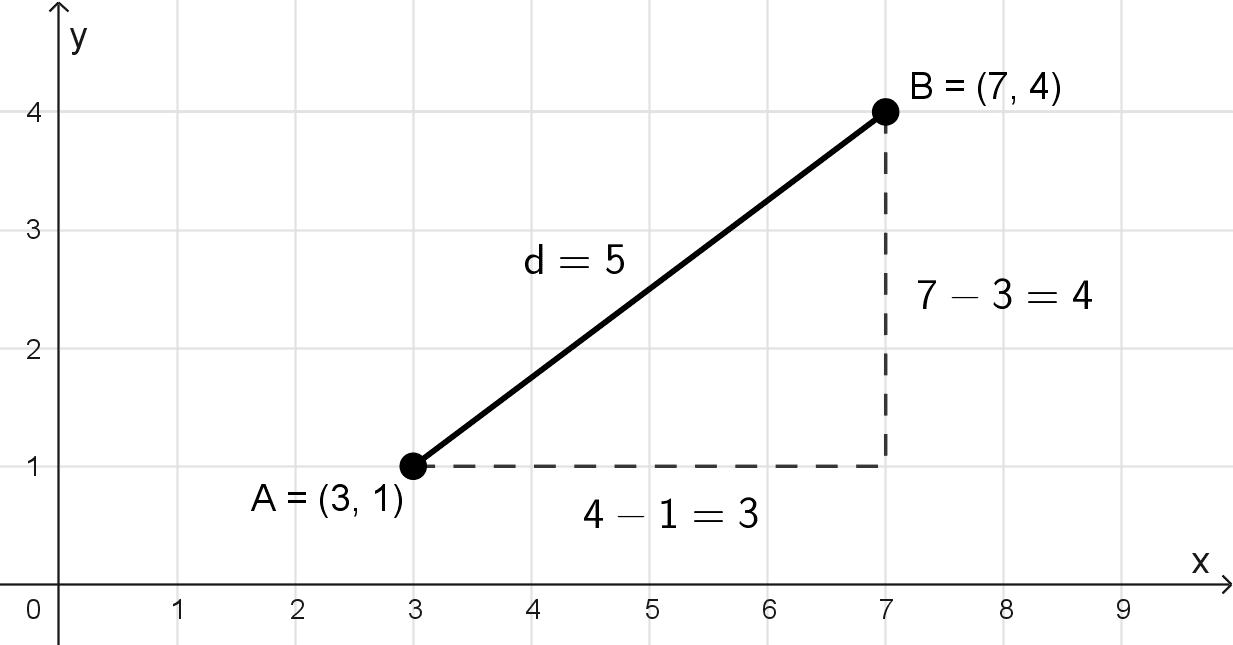
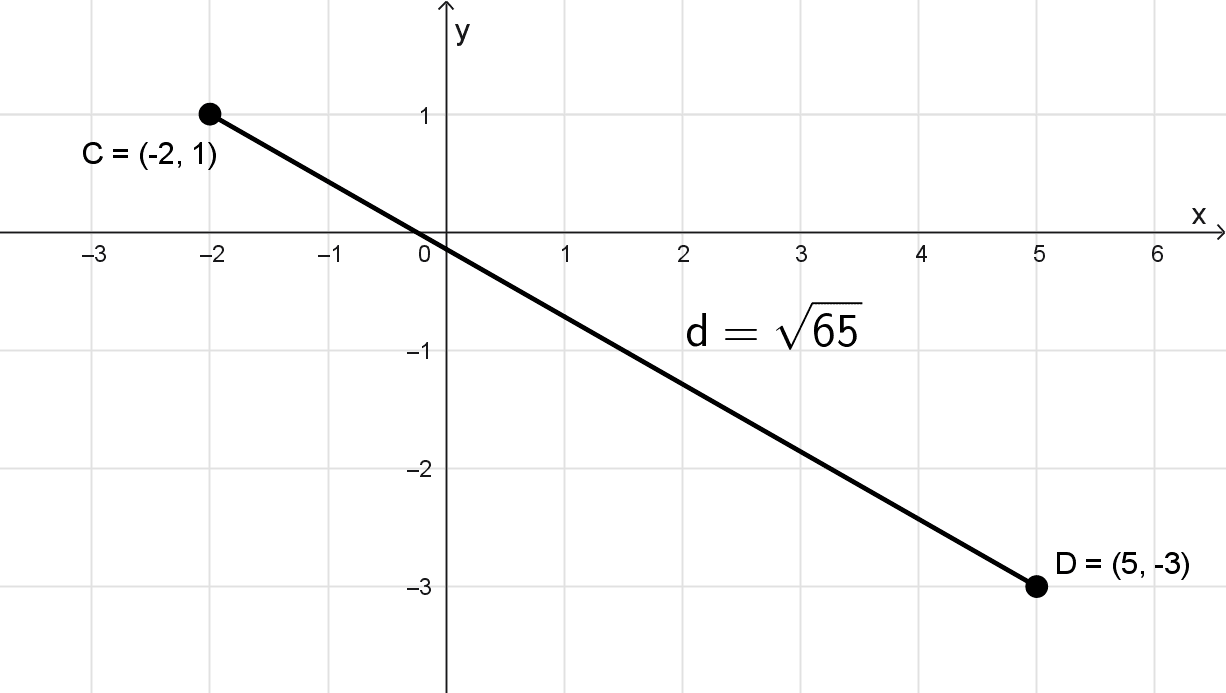
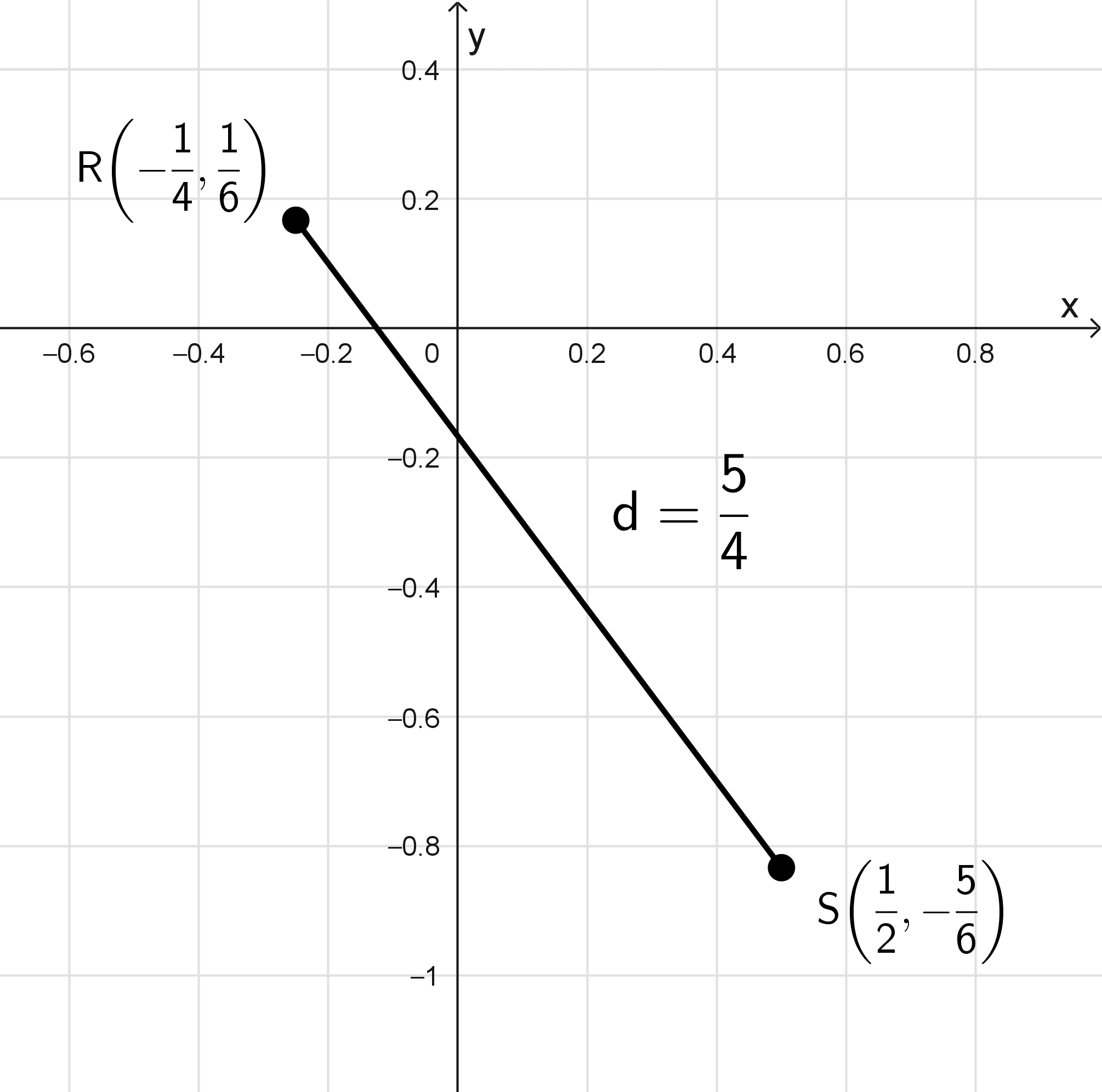
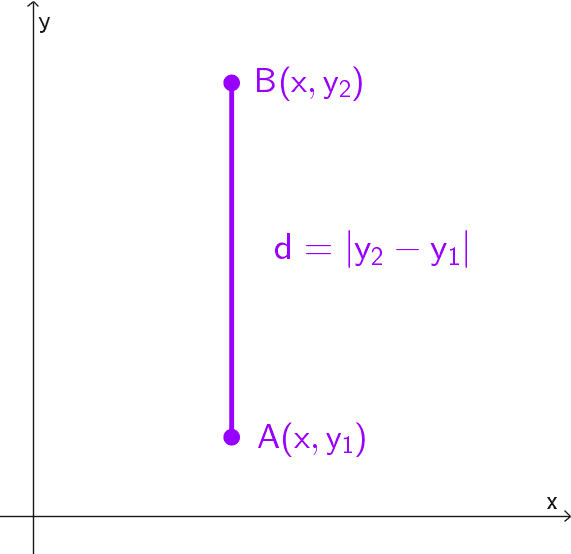
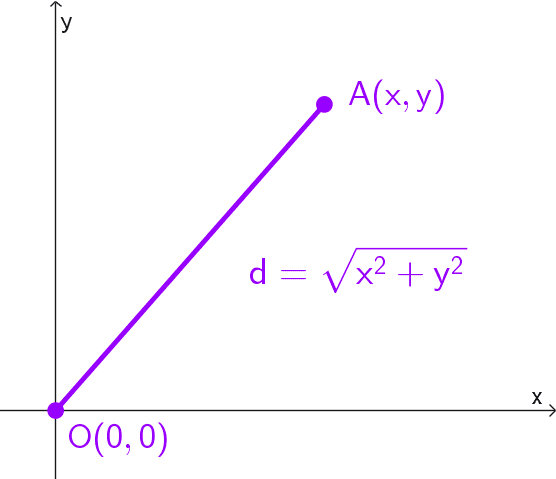
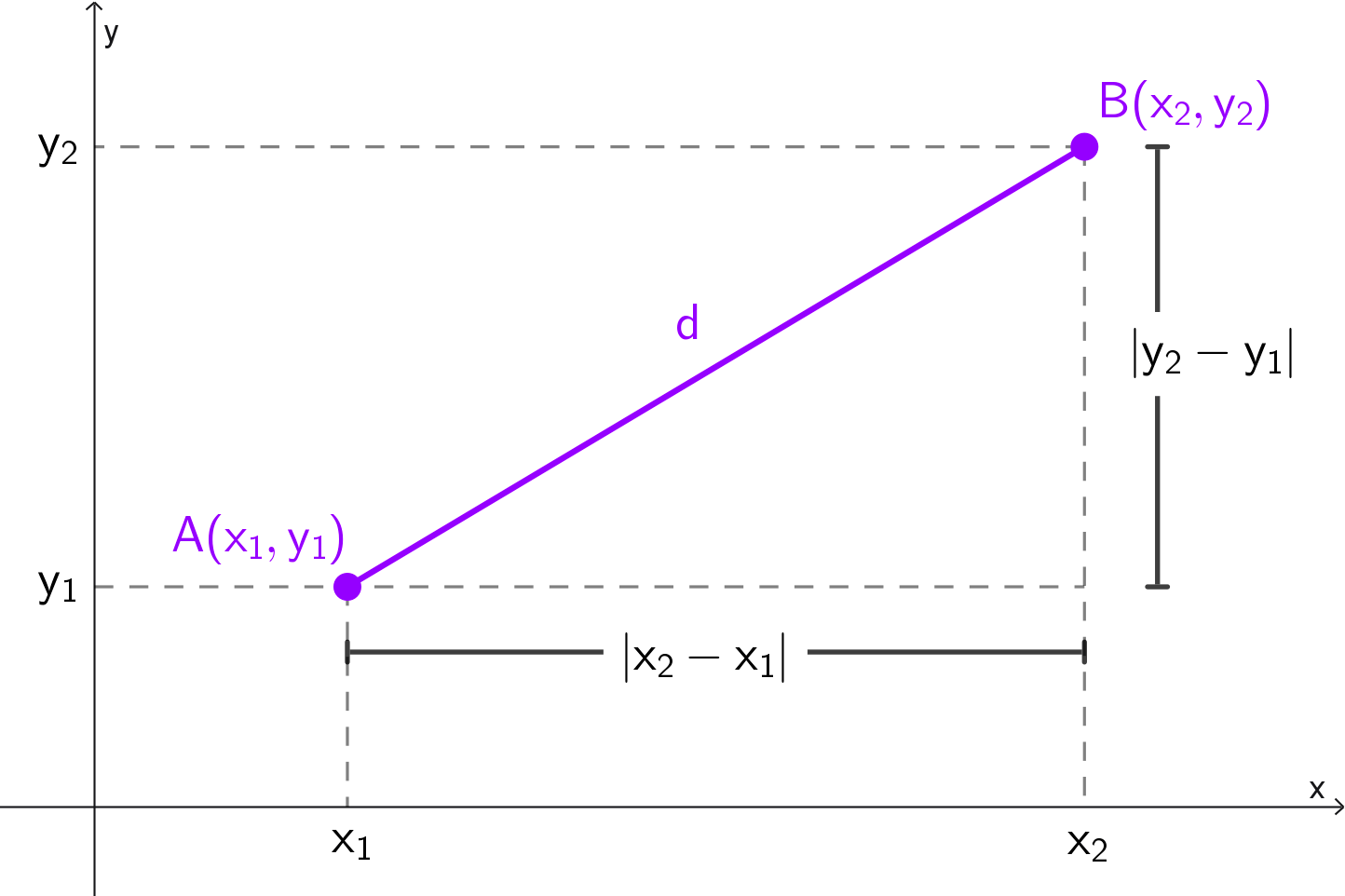
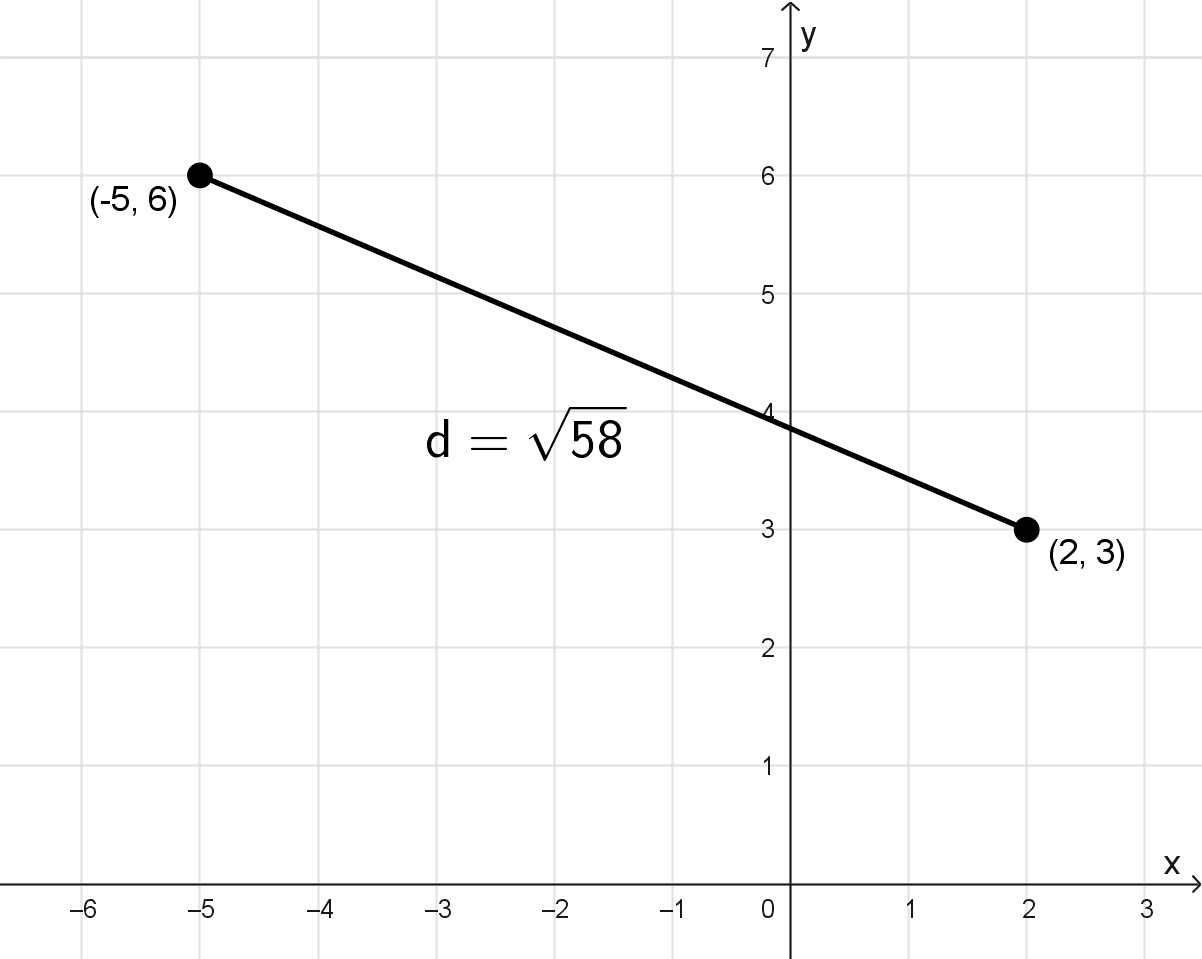
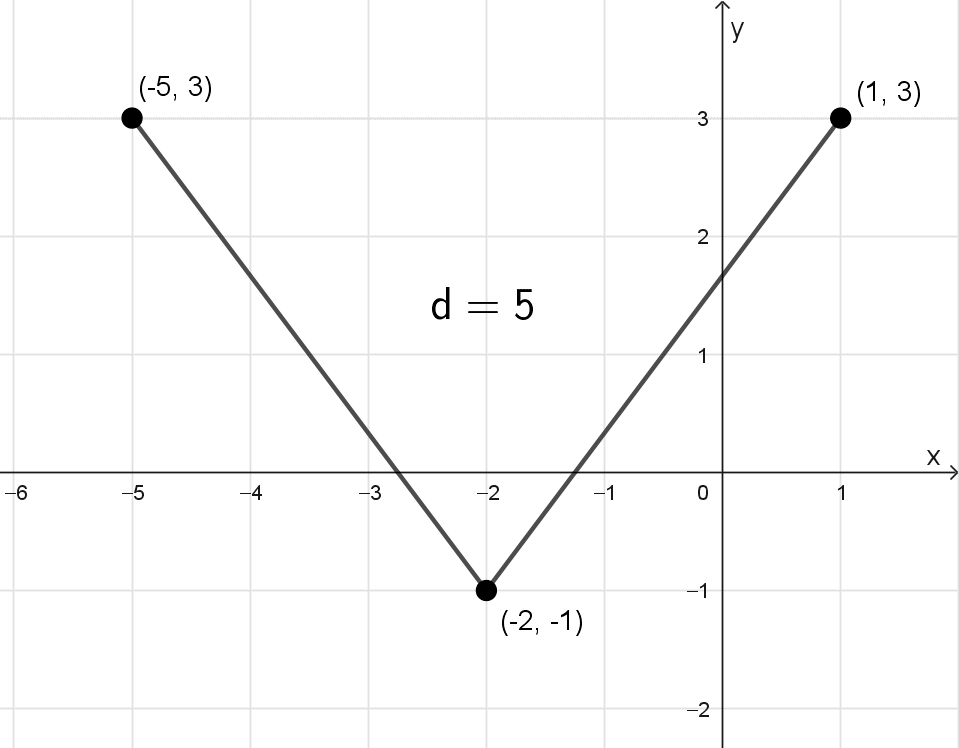
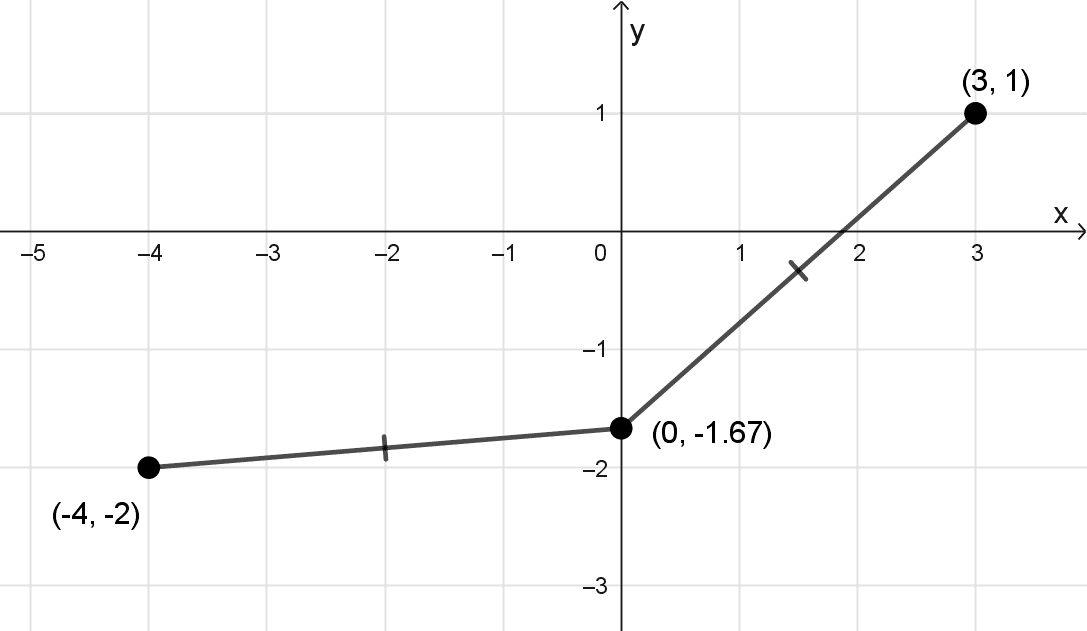
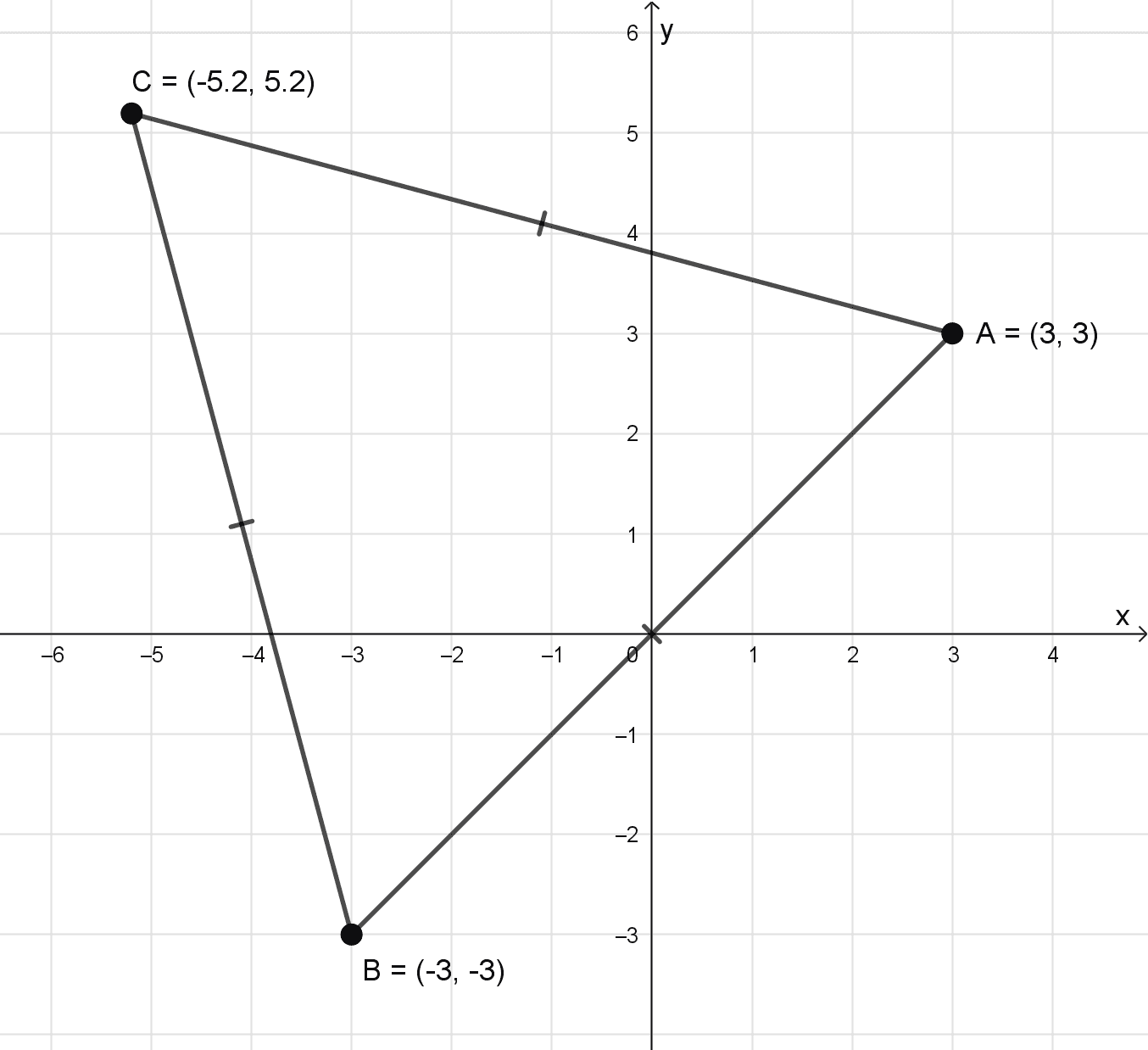
Otros artículos que pueden interesarte