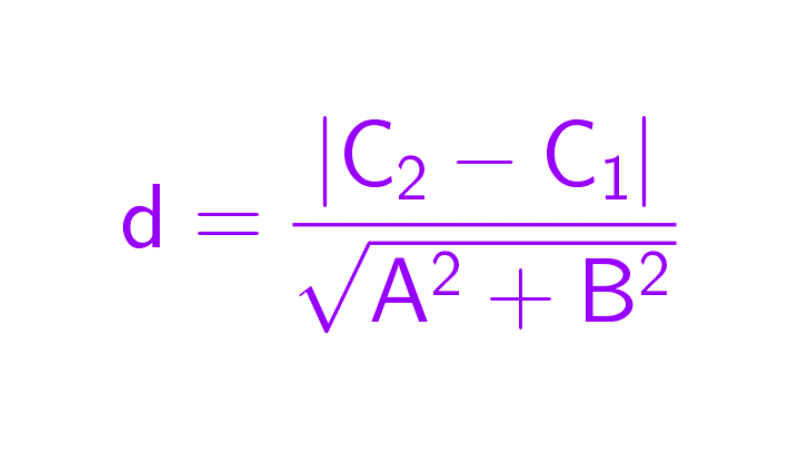
Plano cartesiano
El plano cartesiano es un sistema de referencia en matemáticas que nos permite ubicar cualquier punto en una superficie plana. Se compone de dos rectas numéricas perpendiculares que se cruzan en un punto llamado origen. La recta horizontal se llama eje de las abscisas o eje X, mientras que la recta vertical es el eje de las ordenadas o eje Y. La posición de un punto se define mediante un par ordenado de números (x, y), donde el primer valor (x) indica la distancia horizontal al origen y el segundo (y) la distancia vertical.
Este sistema lleva ese nombre por su creador: el filósofo y matemático francés René Descartes, cuyo nombre latinizado es Renatus Cartesius. Lo presentó en 1637 en su obra La Géométrie, anexa al famoso Discurso del método. Su gran aporte fue fusionar el álgebra con la geometría, dando origen a lo que hoy conocemos como geometría analítica.
La principal utilidad del sistema cartesiano es proporcionar un marco de referencia para la geometría analítica y otras ramas de la matemática. Gracias a él, es posible ubicar puntos y describir rectas, curvas y figuras geométricas mediante coordenadas. De este modo, las posiciones y formas geométricas pueden expresarse algebraicamente, lo que permite transformar problemas geométricos en problemas algebraicos y estudiarlos utilizando las herramientas del álgebra.
Índice
Elementos
A continuación veremos todas las partes del plano cartesiano.
Ejes
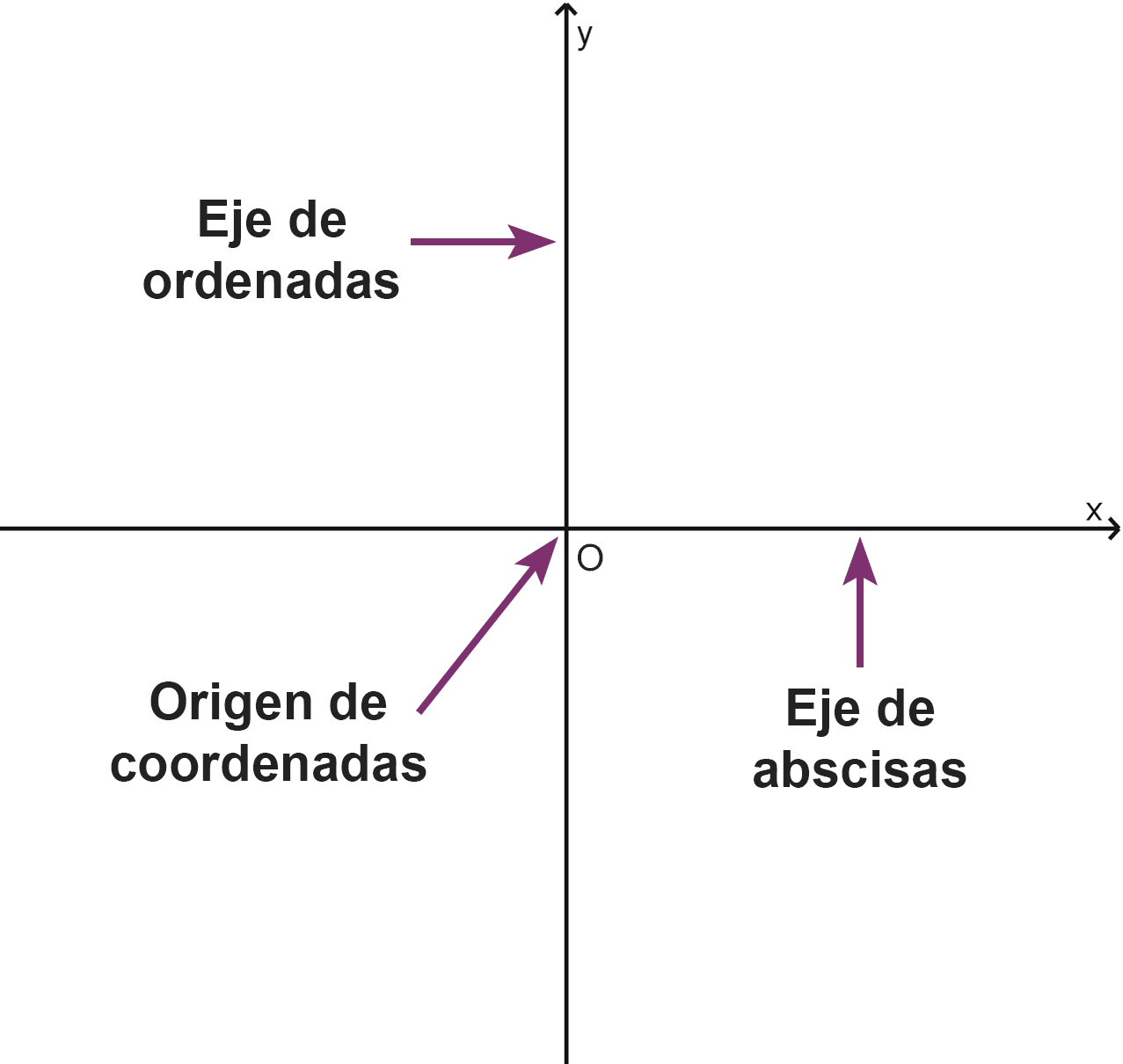
Los ejes cartesianos son las dos rectas numéricas perpendiculares (forman un ángulo de 90°) que se cruzan en un punto llamado origen, el cual corresponde al valor 0 en ambas rectas. La recta horizontal se denomina eje de las abscisas o eje X, mientras que la vertical recibe el nombre de eje de las ordenadas o eje Y.
Cada eje tiene una dirección positiva y otra negativa. En el eje X, los valores a la derecha del origen son positivos, mientras que los situados a la izquierda son negativos. En el eje Y, los valores por encima del origen son positivos y los que están por debajo son negativos. Esta dirección de crecimiento se indica convencionalmente con una flecha en el extremo positivo de cada eje, aunque en algunas representaciones se colocan flechas en los cuatro extremos.
Es fundamental etiquetar claramente cada eje en cualquier gráfico, normalmente con "x" para el horizontal e "y" para el vertical. Sin embargo, dependiendo del contexto, se pueden emplear otras letras, como "t" para representar el tiempo en el eje horizontal, "V" para la velocidad en el eje vertical, etc.
A partir del origen, cada eje se divide en dos semirrectas llamadas semiejes. Si consideramos estas divisiones, obtenemos cuatro semiejes en total:
- Semieje positivo de las abscisas (o eje X+): es la parte del eje X situada a la derecha del origen.
- Semieje negativo de las abscisas (o eje X-): es la parte del eje X situada a la izquierda del origen.
- Semieje positivo de las ordenadas (o eje Y+): es la parte del eje Y situada por encima del origen.
- Semieje negativo de las ordenadas (o eje Y-): es la parte del eje Y situada por debajo del origen.
Origen
El punto donde se cruzan los ejes cartesianos se denomina origen de coordenadas. Constituye el punto de referencia fundamental del sistema, ya que desde él se miden todas las distancias horizontales y verticales. Se representa habitualmente con la letra "O" o mediante el par ordenado (0, 0).
Cuadrantes
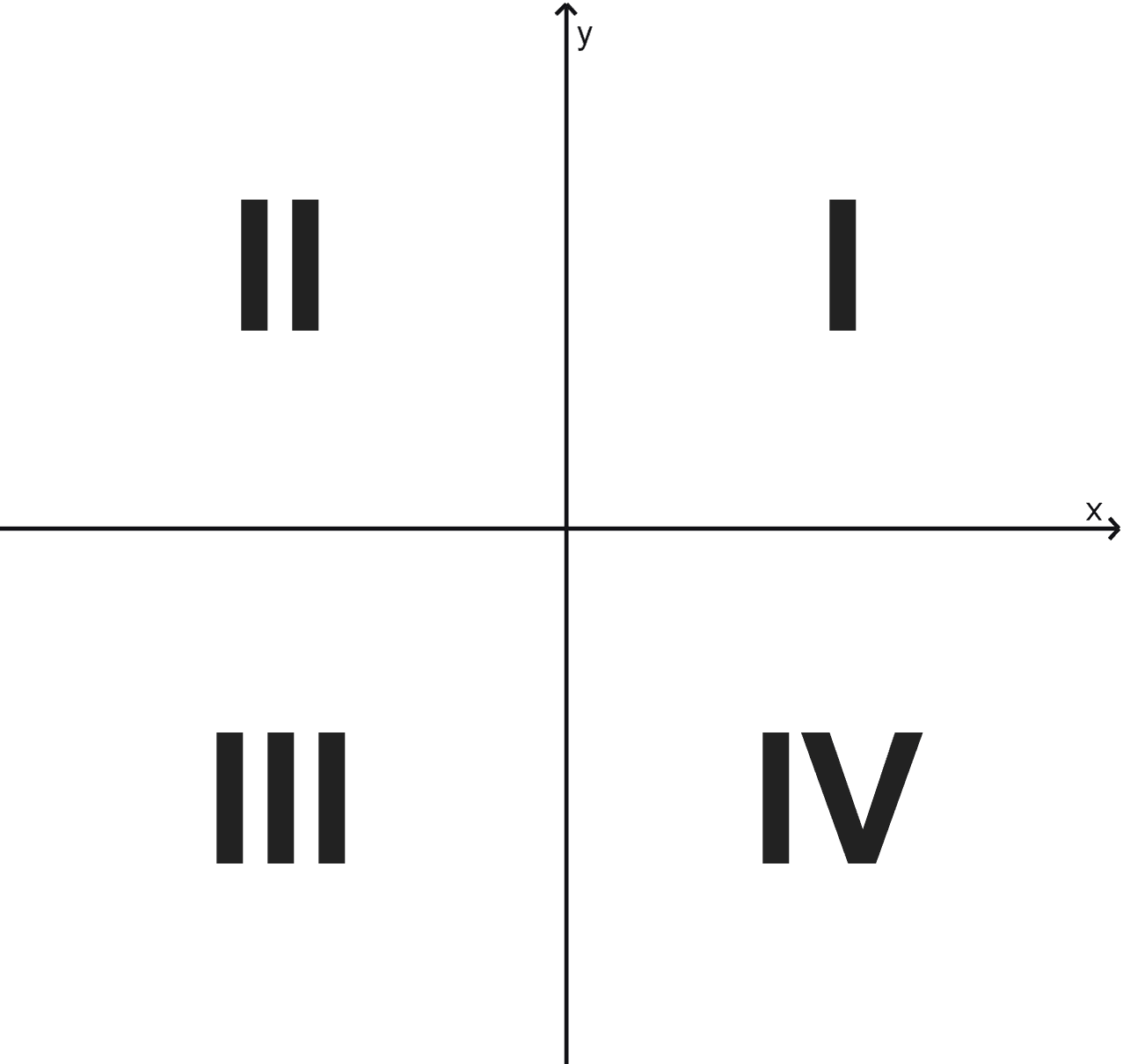
Los ejes, al cortarse, dividen el plano en cuatro regiones llamadas cuadrantes. Estos se numeran utilizando números romanos (I, II, III y IV) en sentido antihorario, comenzando por la región superior derecha.
- Primer cuadrante (I): es la zona delimitada por el semieje positivo de las abscisas y el semieje positivo de las ordenadas, la parte superior derecha del plano.
- Segundo cuadrante (II): es la zona entre el semieje negativo de las abscisas y el semieje positivo de las ordenadas, la parte superior izquierda del plano.
- Tercer cuadrante (III): corresponde a la región comprendida entre el semieje negativo de las abscisas y el semieje negativo de las ordenadas, la zona inferior izquierda del plano.
- Cuarto cuadrante (IV): ocupa el área entre el semieje positivo de las abscisas y el semieje negativo de las ordenadas, la región inferior derecha del plano.
Coordenadas de un punto
Cada punto en el plano se identifica con un par ordenado de números que se escriben entre paréntesis como (x, y), estos números son las coordenadas cartesianas del punto. El primer número se llama abscisa o coordenada x, el segundo se denomina ordenada o coordenada y.
Los valores de abscisa y ordenada son distancias dirigidas, lo que significa que pueden ser positivas o negativas. El signo de una coordenada nos dice en qué dirección movernos desde el origen: una abscisa positiva indica un desplazamiento horizontal hacia la derecha, mientras que una negativa, hacia la izquierda. Una ordenada positiva señala un desplazamiento vertical hacia arriba, y una negativa, hacia abajo.
Existe una correspondencia uno a uno entre los puntos del plano y los pares ordenados de números reales. Esto significa que a cada punto le corresponde un único par ordenado (x, y) y, recíprocamente, a cada par ordenado le corresponde un único punto en el plano. Por lo tanto, no hay dos puntos distintos que compartan las mismas coordenadas, ni dos pares ordenados diferentes que representen el mismo punto.
En la práctica, esta relación nos permite realizar dos acciones fundamentales. Dadas las coordenadas de un punto, podemos ubicarlo o trazarlo en el plano, proceso que se conoce como graficar el punto. Inversamente, dado un punto ya representado gráficamente, podemos determinar sus coordenadas observando su distancia dirigida respecto a los ejes cartesianos.
Ubicar puntos en el plano
Veremos a continuación ejemplos del proceso para localizar puntos en un plano coordenado.
Ejemplo 1
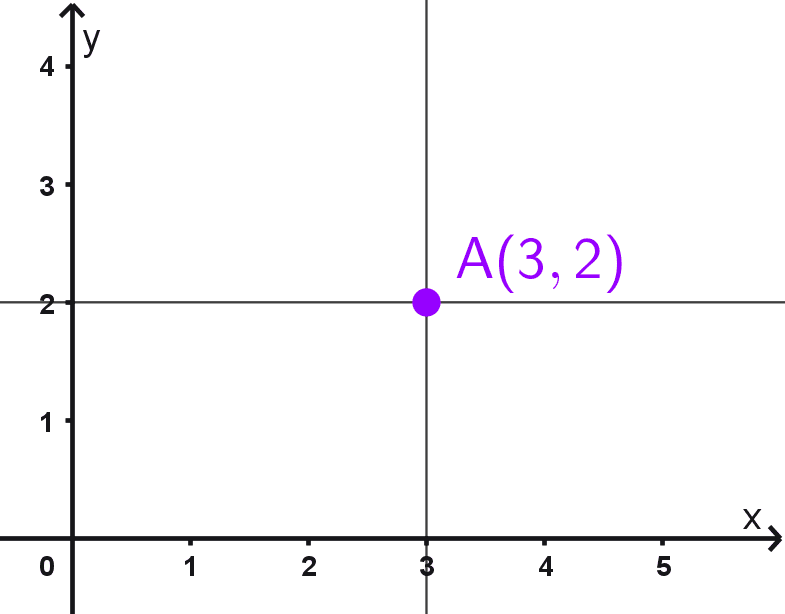
Graficar el punto A(3, 2) en el plano cartesiano.
Solución
Primero interpretamos las coordenadas: el par ordenado (3, 2) nos indica que la abscisa es 3 y la ordenada es 2. Ambas son positivas, por lo que el desplazamiento desde el origen será hacia la derecha y hacia arriba.
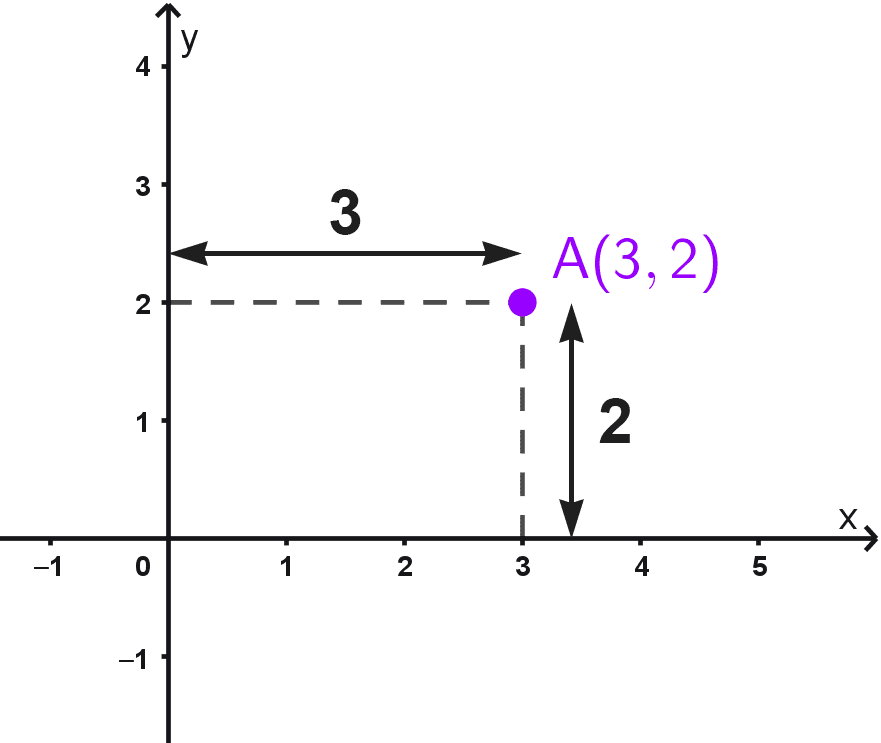
Iniciamos en el origen, el punto (0, 0). Comenzamos con el desplazamiento horizontal: nos movemos 3 unidades hacia la derecha a lo largo del eje x, hasta llegar a la marca correspondiente al 3. A partir de ese lugar sobre el eje x, realizamos el desplazamiento vertical: nos movemos 2 unidades hacia arriba, en dirección paralela al eje y. El lugar donde terminamos este recorrido es la ubicación exacta del punto A.
De manera equivalente, podemos visualizar este proceso trazando líneas perpendiculares: una línea vertical que pasa por el valor 3 del eje de abscisas y una línea horizontal que pasa por el valor 2 del eje de ordenadas. La intersección de estas dos líneas de referencia es el punto A(3, 2), como se muestra en el gráfico.
Al realizar este proceso en papel, es muy recomendable utilizar papel cuadriculado o milimetrado, ya que la cuadrícula facilita enormemente la tarea de contar y ubicar las unidades.
Importante: en un par ordenado (x, y) el orden sí importa. La primera componente siempre representa la abscisa (coordenada x) y la segunda, la ordenada (coordenada y). Por lo tanto, el punto (3, 2) es completamente distinto del punto (2, 3).
Dos puntos del plano (x1, y1) y (x2, y2) son iguales si sus coordenadas correspondientes son iguales. Es decir, cuando x1 = x2 y, simultáneamente, y1 = y2. Si una sola coordenada difiere, se trata de puntos distintos.
Ejemplo 2
Ubicar los siguientes puntos en un plano coordenado: A(4, 1), B(-4, 2), C(0, 1), D(-2, -2), E(-3, 0), F(2, -4).
Solución
La lógica es la misma para todos: partimos del origen (0, 0) y realizamos los desplazamientos indicados por sus coordenadas cartesianas, respetando el signo para la dirección. A continuación, detallamos el procedimiento para cada punto:
- Para el punto A(4, 1): nos desplazamos 4 unidades hacia la derecha y luego 1 unidad hacia arriba, por ser ambos valores positivos.
- Para el punto B(-4, 2): nos movemos 4 unidades hacia la izquierda (por el signo negativo en la abscisa) y luego 2 unidades hacia arriba.
- Para el punto C(0, 1): como la abscisa es 0, no hay desplazamiento horizontal; partiendo del origen, solo subimos 1 unidad, el punto se encuentra sobre el eje y.
- Para el punto D(-2, -2): nos desplazamos 2 unidades hacia la izquierda y, desde allí, 2 unidades hacia abajo, por ser ambas coordenadas negativas.
- Para el punto E(-3, 0): nos movemos 3 unidades hacia la izquierda. Como la ordenada es 0, no hay movimiento vertical, por lo que el punto queda ubicado sobre el eje x.
- Para el punto F(2, -4): nos desplazamos 2 unidades hacia la derecha y, desde esa posición, 4 unidades hacia abajo.
En el siguiente gráfico podemos ver todos los puntos ubicados:
Nota: al escribir un par ordenado, las coordenadas pueden separarse con una coma (abscisa, ordenada) o con un punto y coma (abscisa; ordenada). Ambas formas son válidas, pero se recomienda especialmente el uso del punto y coma cuando se trabaja con números decimales que utilizan la coma como separador decimal; por ejemplo, al escribir el punto (2,5; 3,2).
Signos de las coordenadas en cada cuadrante
El signo de las coordenadas cartesianas de un punto nos permite saber inmediatamente en qué cuadrante del plano se encuentra, sin necesidad de graficarlo:
- Primer cuadrante (I): la abscisa y la ordenada son positivas (x > 0, y > 0). Ejemplo: (3, 5).
- Segundo cuadrante (II): la abscisa es negativa y la ordenada es positiva (x < 0, y > 0). Ejemplo: (-4, 2).
- Tercer cuadrante (III): la abscisa y la ordenada son negativas (x < 0, y < 0). Ejemplo: (-1, -6).
- Cuarto cuadrante (IV): la abscisa es positiva y la ordenada es negativa (x > 0, y < 0). Ejemplo: (5, -2).
Un punto puede no estar situado en ningún cuadrante si cae sobre uno de los ejes. En ese caso, al menos una de sus coordenadas es cero. Si la coordenada x es cero (0, y), el punto está sobre el eje y; si la coordenada y es cero (x, 0), el punto está sobre el eje x. Finalmente, si ambas coordenadas son cero (0, 0), el punto es el origen de coordenadas, donde se intersectan ambos ejes.
¿Te está sirviendo este artículo? ¡Por favor, califícalo!
Cómo hacer un plano cartesiano
Para construir un plano cartesiano es muy recomendable usar papel cuadriculado, ya que facilita el trazado de líneas rectas y el conteo de unidades. Sin embargo, también puede realizarse en papel liso utilizando una regla.
Para crear el sistema cartesiano, puedes seguir estos pasos:
- Trazar los ejes: dibuja dos rectas perpendiculares (que formen un ángulo de 90°) que se corten en el centro de la hoja o de la zona que vas a utilizar. La línea horizontal será el eje x (eje de abscisas) y la vertical será el eje y (eje de ordenadas). Su punto de intersección es el origen de coordenadas (0, 0).
- Marcar la escala: en cada eje, elige una unidad de medida (por ejemplo, 1 centímetro en el papel equivaldrá a 1 unidad matemática) y marca intervalos regulares y equidistantes a partir del origen. Puedes utilizar el cuadriculado del papel como guía para asegurar que todas las marcas estén a la misma distancia.
- Numerar las marcas: a partir del origen, escribe los números que corresponden a cada marca. En la dirección positiva del eje x (derecha) y del eje y (arriba), coloca números positivos (1, 2, 3...). En las direcciones opuestas, coloca números negativos (-1, -2, -3...).
- Identificar los ejes: escribe la letra "x" junto al extremo derecho del eje horizontal y la letra "y" junto al extremo superior del eje vertical. En esos mismos extremos, dibuja una pequeña flecha para indicar claramente la dirección en la que crecen los valores.
Errores comunes
- Los ejes no son perpendiculares: si el ángulo entre los ejes no es de 90°, las coordenadas de los puntos y las formas geométricas se distorsionan. Usa una escuadra o la esquina de una hoja para trazar un ángulo recto.
- Olvidar indicar la dirección positiva: en geometría analítica, solo se indican con flechas las direcciones positivas de los ejes (hacia la derecha para x, hacia arriba para y). Las direcciones negativas se asumen como las opuestas. No es necesario colocar flechas en ambos sentidos.
- Escala no uniforme: la distancia entre marcas consecutivas debe ser exactamente la misma a lo largo de todo el eje. Es un error, por ejemplo, que los primeros 5 cm del eje representen 5 unidades (1 cm = 1 unidad) y los siguientes 5 cm representen 10 unidades (1 cm = 2 unidades). Esto deformaría completamente cualquier gráfica.
- Ejes sin identificar: un plano sin las letras "x" e "y" en los ejes carece de referencia. Además, es crucial escribir al menos un valor numérico en cada eje para que quien lo observe pueda entender la escala utilizada.
- Marcas sin unidades: es fácil dibujar las rayas de la escala pero olvidarse de escribir los números que representan. Recuerda que las marcas por sí solas no indican si representan 1, 10 o 0,5 unidades. Siempre numera al menos una de ellas en cada eje.
Consideraciones
Aunque no es un requisito matemático que las escalas de los ejes x e y sean iguales, en geometría analítica es una práctica altamente recomendable utilizar la misma escala para ambos. Si las escalas son diferentes, las figuras geométricas (como una circunferencia, un cuadrado o un triángulo) se representarán deformadas (una circunferencia se vería como una elipse), y las mediciones de distancias y ángulos en el dibujo no corresponderán a los valores matemáticos reales.
Para quienes prefieren trabajar de manera digital, existen herramientas en línea gratuitas para crear planos cartesianos interactivos, como GeoGebra y Desmos.
Aplicaciones
El plano cartesiano es la herramienta fundamental de la geometría analítica, ya que permite representar cualquier punto en dos dimensiones mediante sus coordenadas. Esta es la base para describir figuras geométricas más complejas, como las curvas.
En esencia, una curva no es más que un conjunto de puntos muy próximos entre sí, cada uno con sus propias coordenadas. La relación que vincula a todos estos puntos se expresa mediante una ecuación, que actúa como una regla o condición algebraica que deben cumplir sus coordenadas.
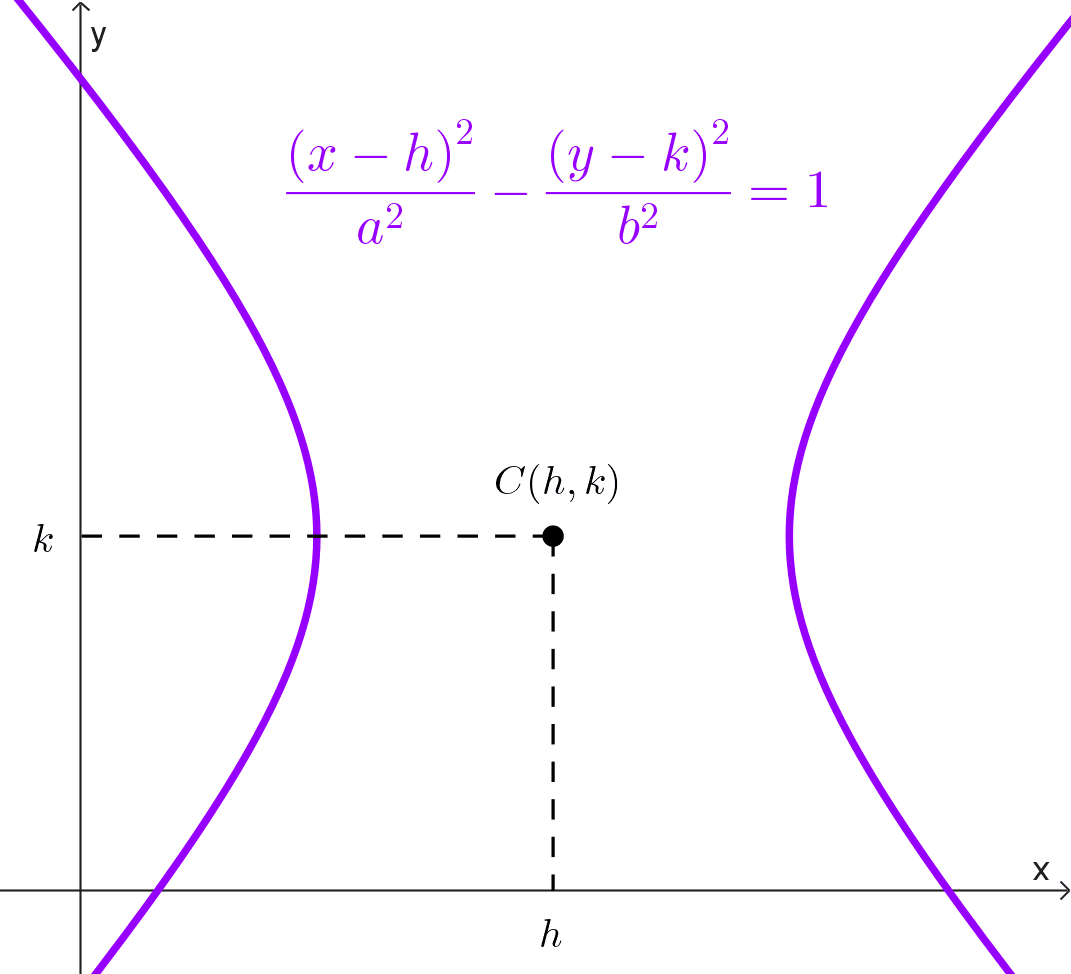
La principal utilidad del plano coordenado es transformar problemas puramente geométricos en problemas algebraicos, y viceversa. Gracias a este sistema, podemos realizar operaciones que van más allá de la simple ubicación, como calcular distancias entre puntos, encontrar puntos medios de segmentos, determinar las ecuaciones y propiedades de lugares geométricos como rectas, circunferencias, elipses, hipérbolas y parábolas, entre otros.
Un ejemplo fundamental es la fórmula de distancia entre dos puntos A(x1, y1) y B(x2, y2), que es una aplicación directa del teorema de Pitágoras en el plano. Al considerar la diferencia de sus coordenadas como los catetos de un triángulo rectángulo, la distancia d se obtiene como:
\(d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
De manera similar, las coordenadas del punto medio M del segmento AB, que geométricamente es su centro de equilibrio, se hallan calculando el promedio simple de las coordenadas de sus extremos:
\(M=\left(\dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2} \right)\)
Uno de los objetos más estudiados es la recta. Geométricamente, una recta queda definida por un punto y una dirección. Analíticamente, esta dirección se cuantifica con la pendiente m, que mide su inclinación. Con un punto conocido (x1, y1) y la pendiente, podemos escribir su ecuación en la forma punto-pendiente:
\(y-y_1=m(x-x_1)\)
Al simplificar, esta ecuación adopta la forma general Ax + By + C = 0 o la forma explícita y = mx + b, donde b representa la intersección con el eje vertical. Cada coeficiente en esta última ecuación tiene una interpretación geométrica directa: la pendiente dicta si la recta sube, baja o es horizontal, mientras que el término independiente señala dónde corta al eje y.
En resumen, el plano coordenado sentó las bases de esta disciplina al crear un puente entre la geometría y el álgebra: ahora, cualquier figura geométrica (un punto, una línea, una curva) puede describirse, estudiarse y analizarse a través de ecuaciones algebraicas.
Esta capacidad de representación no se limita a la geometría, el plano cartesiano también es esencial en otras áreas como el cálculo, física, ingeniería o astronomía, donde se utiliza para graficar funciones, visualizar la relación entre variables, analizar el comportamiento de fenómenos y representar datos, entre otras.
Bibliografía
- Cotrina, J. y Escudero, P. (2021). Introducción a la geometría analítica. Universidad del Pacífico.
- Fuller, G. y Tarwater, D. (1995). Geometría analítica (7.ª ed.). Pearson Educación.
- Lehmann, C. (1989). Geometría analítica. Limusa.
- Márquez, A. y otros. (2009). Geometría analítica. Prentice Hall.
- Matemática 1 ESO. (2011). Santillana Educación.
- Matemática 2 ESO. (2012). Santillana Educación.
- Raichman, S. y Totter, E. (2016). Geometría analítica para ciencias e ingeniería. Universidad Nacional de Cuyo.
- Wilches, L., Costa, R., Rincón, M., Acosta, M., Roa, J., Sulvara, J. y Jaime, D. (2013). Matemática 6. Editorial Santillana.
Preguntas frecuentes
¿Quién inventó el plano cartesiano y por qué se llama así?
El sistema de coordenadas que conocemos como plano cartesiano fue ideado por el filósofo y matemático francés René Descartes (1596-1650). Su desarrollo fundamental se publicó en 1637 en su obra La Géométrie, como un apéndice de su Discurso del método. El término cartesiano proviene del adjetivo latino Cartesianus, formado a partir de Cartesius, que es la latinización del apellido Descartes.
¿Qué otros nombres recibe el plano cartesiano?
Es común referirse al plano con varios nombres que destacan diferentes aspectos: sistema de coordenadas cartesianas (por su inventor), sistema de coordenadas rectangulares o ortogonales (debido al ángulo recto entre sus ejes), plano coordenado o simplemente plano xy. En un contexto más algebraico, también se le denomina espacio R² (R al cuadrado), que es la notación para el conjunto de todos los pares ordenados de números reales, o sistema de coordenadas bidimensional.
Al utilizar un plano cartesiano como referencia, ¿cuántas dimensiones usamos?
Un plano cartesiano estándar utiliza dos dimensiones: la horizontal (generalmente llamada x) y la vertical (y). Esto permite ubicar cualquier punto en un espacio plano mediante dos valores numéricos, su coordenada x y su coordenada y.
¿En un plano cartesiano cuál es x y cuál es y?
La convención establece que el eje horizontal es el eje de las abscisas, denominado eje X. El eje vertical es el eje de las ordenadas, denominado eje Y. Para escribir las coordenadas de un punto, siempre va primero la coordenada x (horizontal) y luego la y (vertical), en el formato (x, y).
¿Desde dónde se empieza el plano cartesiano?
El punto de inicio o referencia absoluta es la intersección de los dos ejes, llamado origen de coordenadas, sus coordenadas son (0, 0). Desde este punto, los números aumentan de valor (positivos) o disminuyen (negativos) a lo largo de cada eje, definiendo así la posición de todos los demás puntos del plano.
¿En cuántas partes se divide el plano cartesiano?
El plano cartesiano está dividido en cuatro regiones llamadas cuadrantes, que se numeran en sentido antihorario (contrario a las manecillas del reloj). El plano se forma a partir de dos ejes perpendiculares (el eje X y el eje Y) que se cortan en el origen.
¿Cuántos números forman una coordenada en el plano cartesiano?
Una coordenada para ubicar un punto específico en el plano cartesiano está formada por dos números reales, que corresponden a sus distancias dirigidas (con signo) respecto a los dos ejes. Por eso decimos que es un par ordenado, por ejemplo, (3, -5).
¿Cuál es la diferencia entre un punto y una coordenada?
Un punto es el concepto geométrico fundamental: una ubicación exacta en el plano, sin dimensión. La coordenada es la herramienta analítica o el "nombre" algebraico que le asignamos a ese punto dentro de un sistema de referencia (como el cartesiano). Es decir, la coordenada es la representación numérica del punto.
¿El orden de las coordenadas de un punto es importante?
Sí, el orden es importante y no es intercambiable. El formato es (x, y) y cambiar el orden implica referirse a otro lugar del plano. Por ejemplo, el par (2, 5) representa un punto completamente diferente al par (5, 2).
¿El plano cartesiano es infinito?
Sí, tanto el plano en sí como las líneas que forman los ejes se consideran infinitas. Los ejes X e Y se extienden indefinidamente en ambas direcciones (positiva y negativa), y el plano abarca todos los puntos posibles cuyas coordenadas (x, y) son números reales, sin límite alguno.
¿Existe el plano cartesiano en tres dimensiones?
Sí, la idea se extiende a tres dimensiones añadiendo un tercer eje perpendicular a los otros dos, comúnmente llamado eje Z. Esto crea un sistema de coordenadas cartesianas tridimensional o espacio R³. En él, un punto se localiza con tres números: (x, y, z).
¿Existe otro sistema para representar puntos que no sea el cartesiano?
Sí, existen varios sistemas de coordenadas alternativos. El más común es el sistema de coordenadas polares, donde un punto se define por su distancia al origen (radio r) y el ángulo (θ) que forma con una dirección de referencia, generalmente el eje X positivo. Otros sistemas incluyen las coordenadas cilíndricas y las esféricas, muy útiles en problemas de física y cálculo en tres dimensiones donde la simetría circular o esférica simplifica los análisis.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta

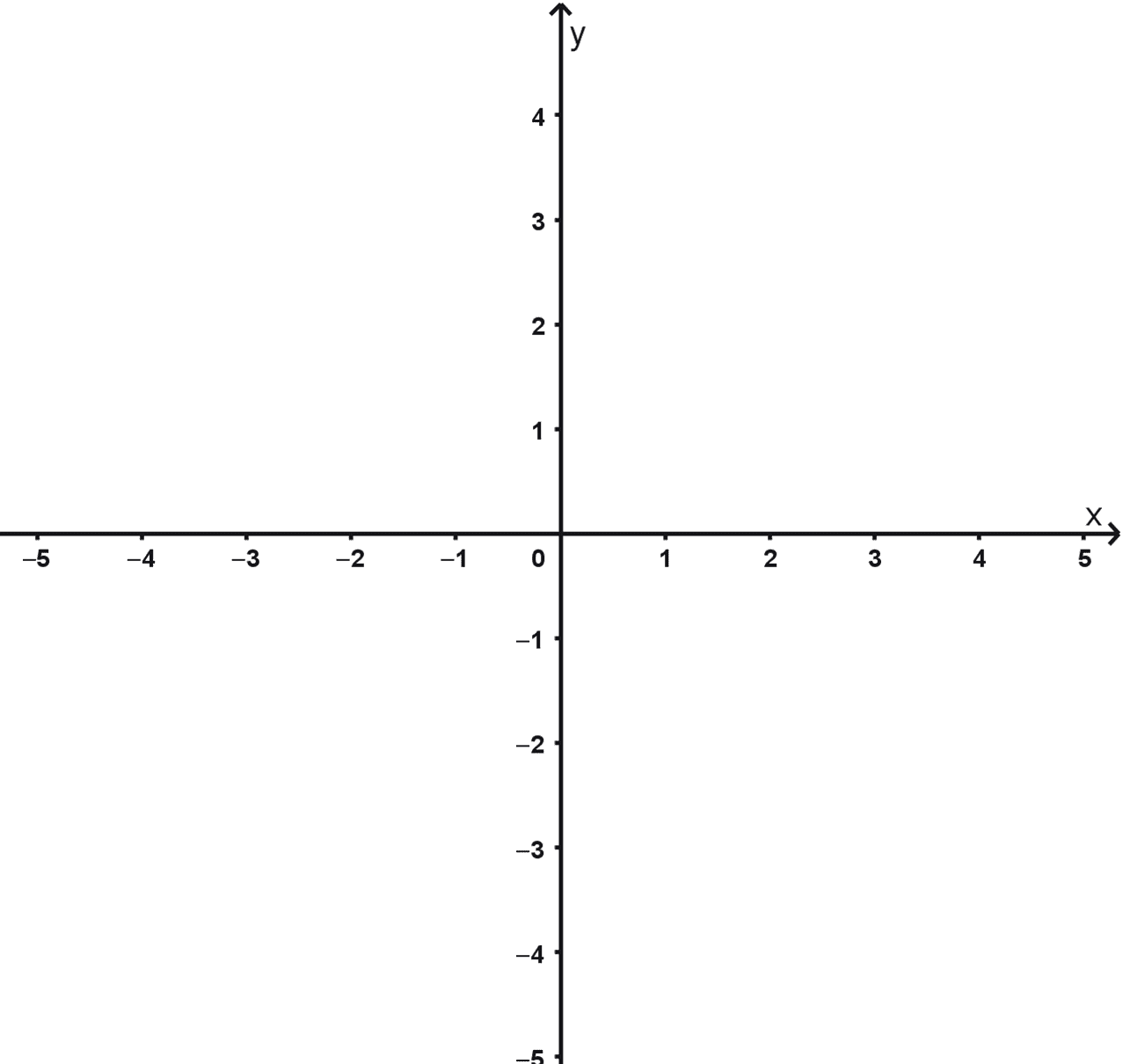
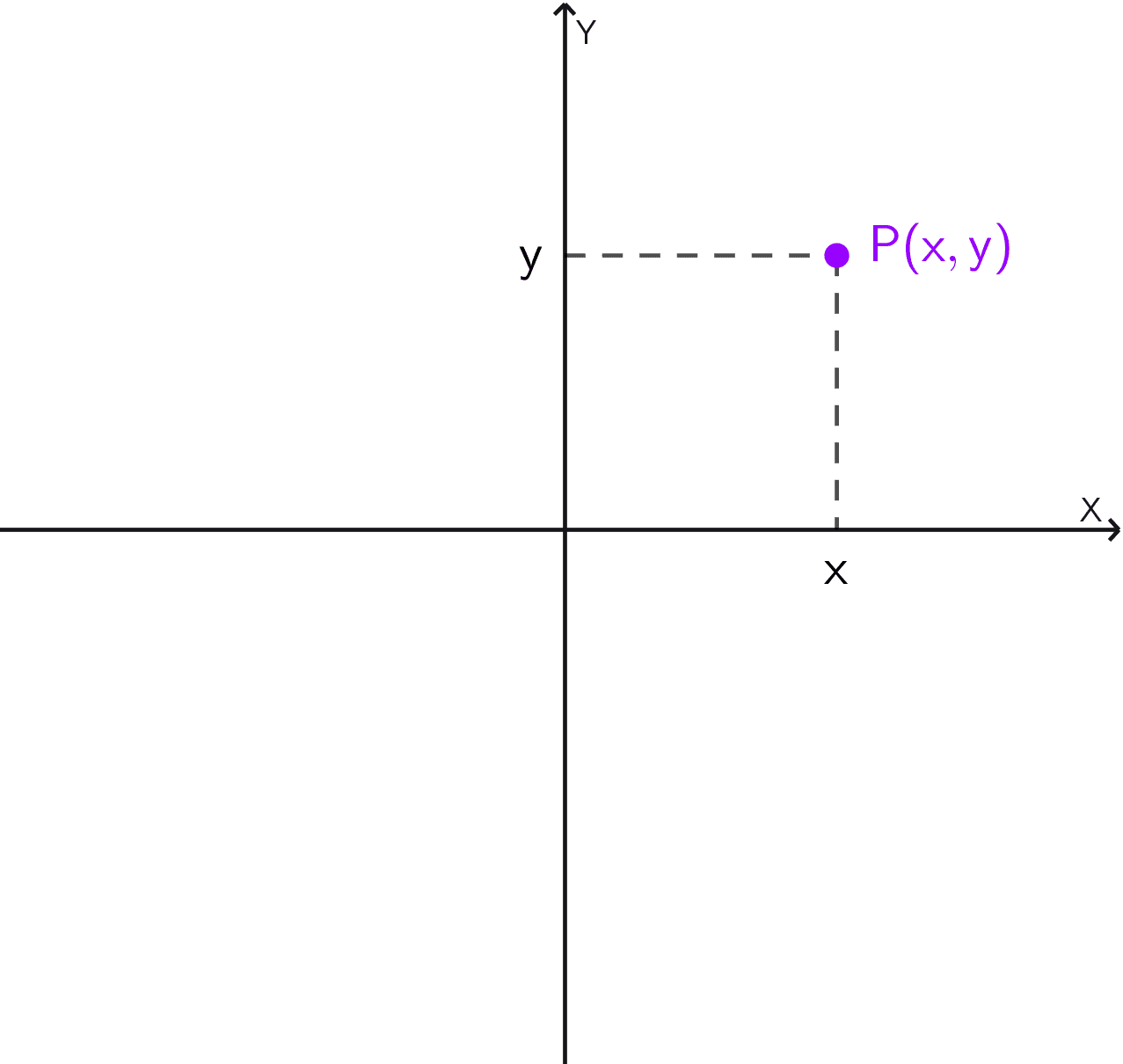
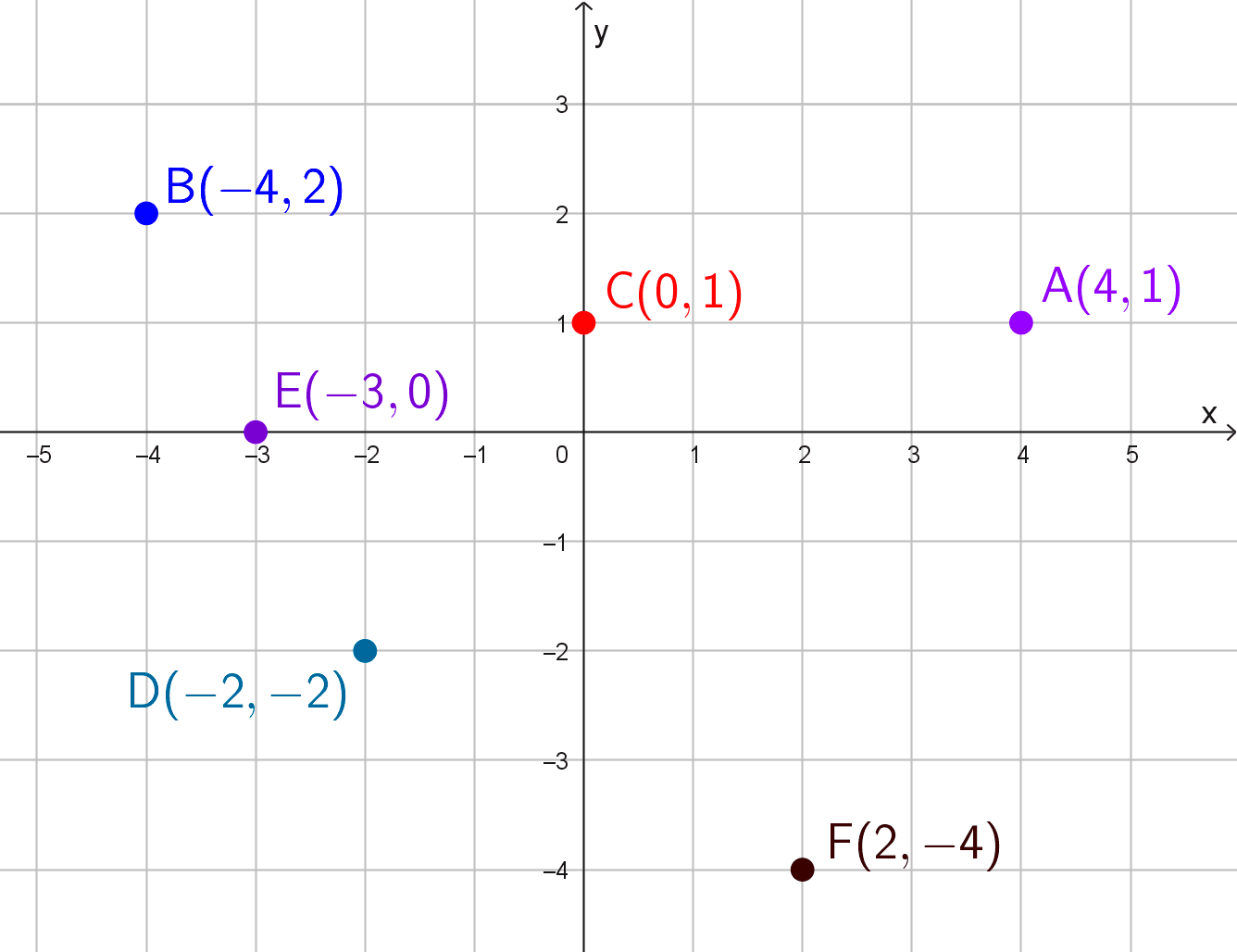
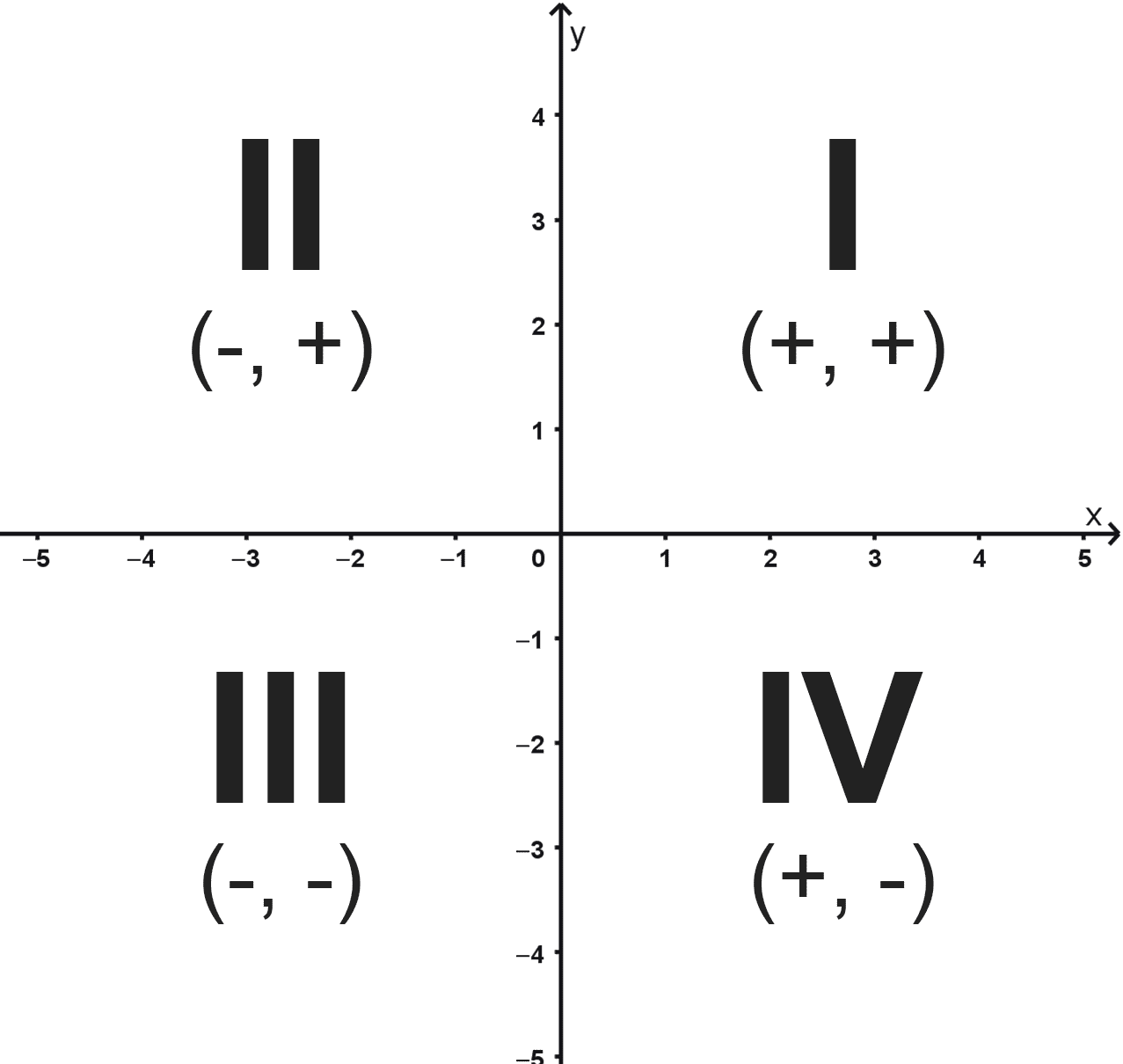
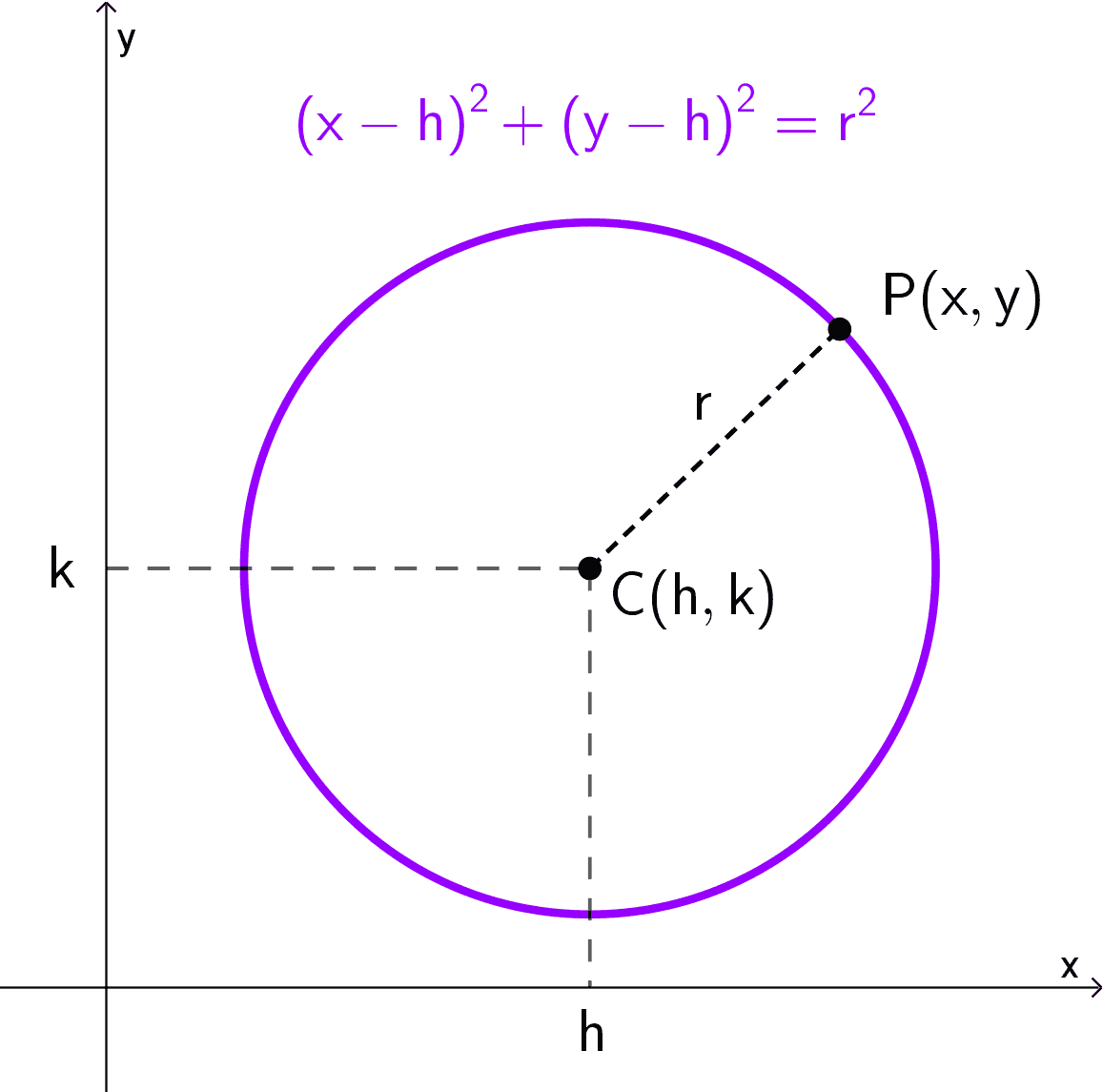
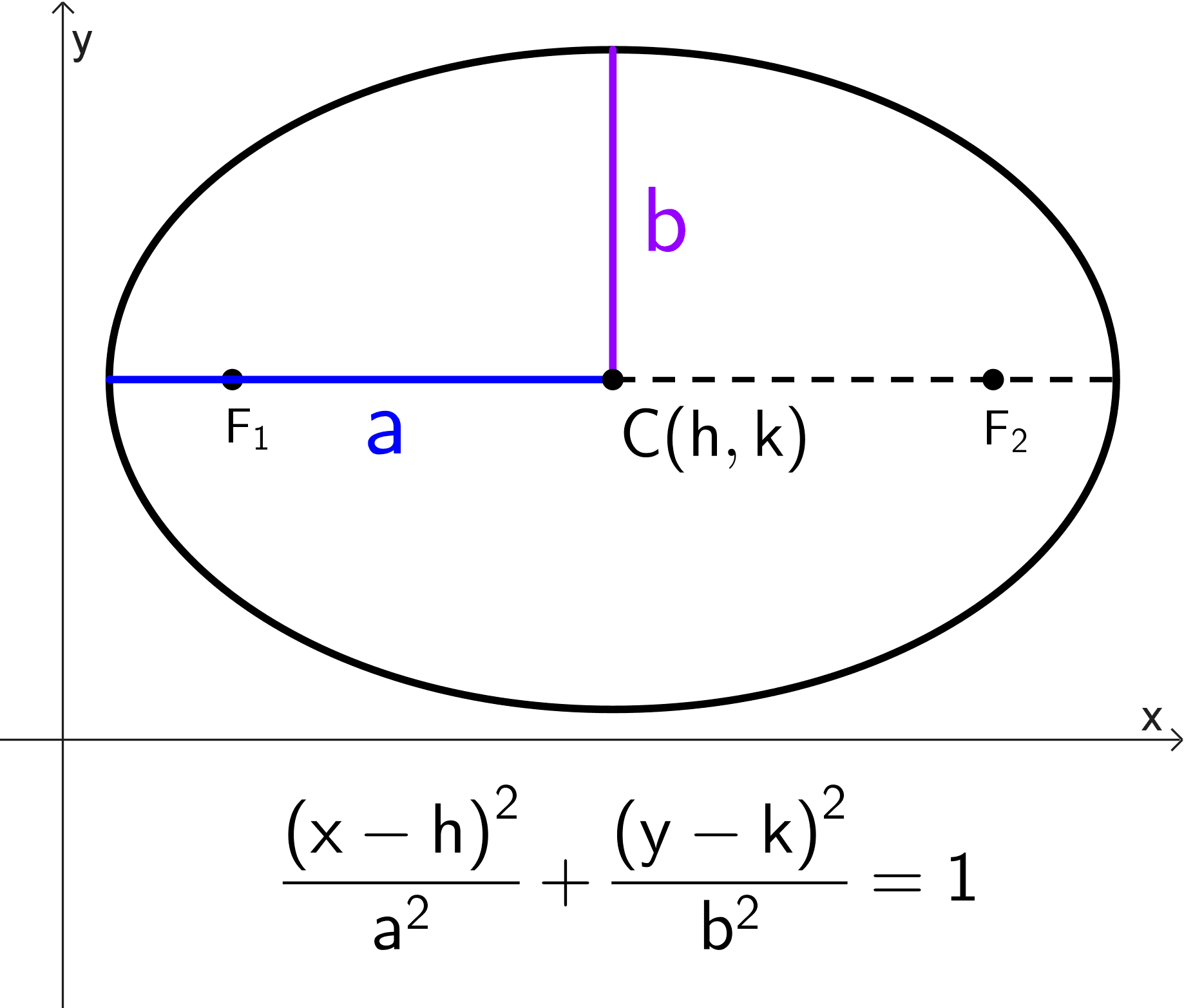

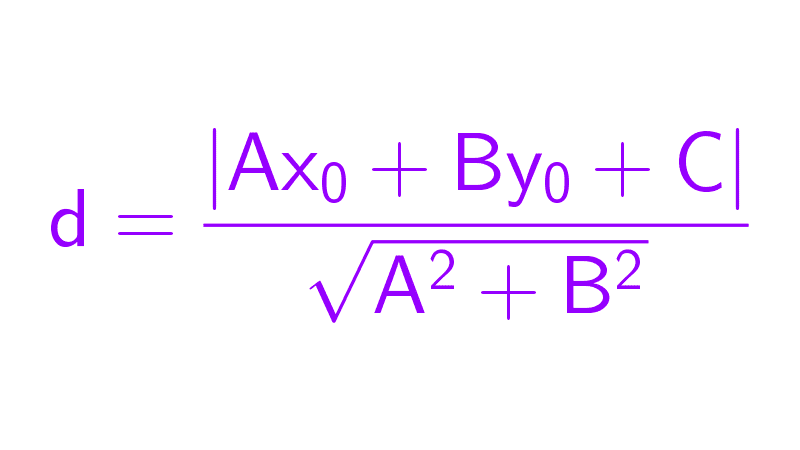
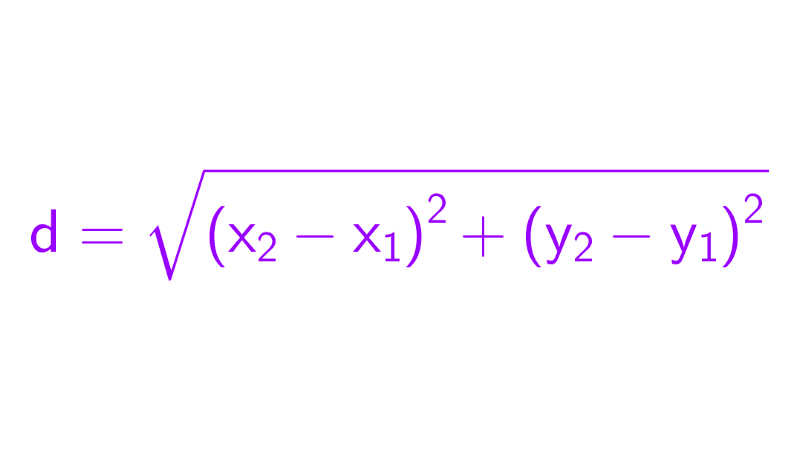
Otros artículos que pueden interesarte