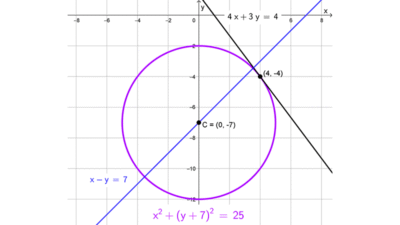
Circunferencia con centro en el origen y fuera del origen
La circunferencia es el lugar geométrico de los puntos del plano que están a una misma distancia de un punto fijo llamado centro. Dependiendo de la posición de este centro (en el origen de coordenadas o fuera de él), la ecuación de la circunferencia puede tomar diferentes formas. En este artículo explicaremos ambas situaciones, cómo se representan algebraicamente y qué diferencias presentan.
Índice
Centro en el origen
La ecuación canónica de una circunferencia con centro en el origen (0, 0) es x² + y² = r², donde “x” e “y” representan las coordenadas de cualquier punto de la circunferencia y “r” es el radio, es decir, la distancia desde el centro hasta cualquier punto de la curva.
Ejemplos
Los siguientes son ejemplos de circunferencias centradas en el origen:
- x2 + y2 = 4 es una circunferencia con radio *r=\sqrt{4}=2.*
- x2 + y2 = 1 tiene radio *r=\sqrt{1}=1,* este caso se conoce como circunferencia unitaria.
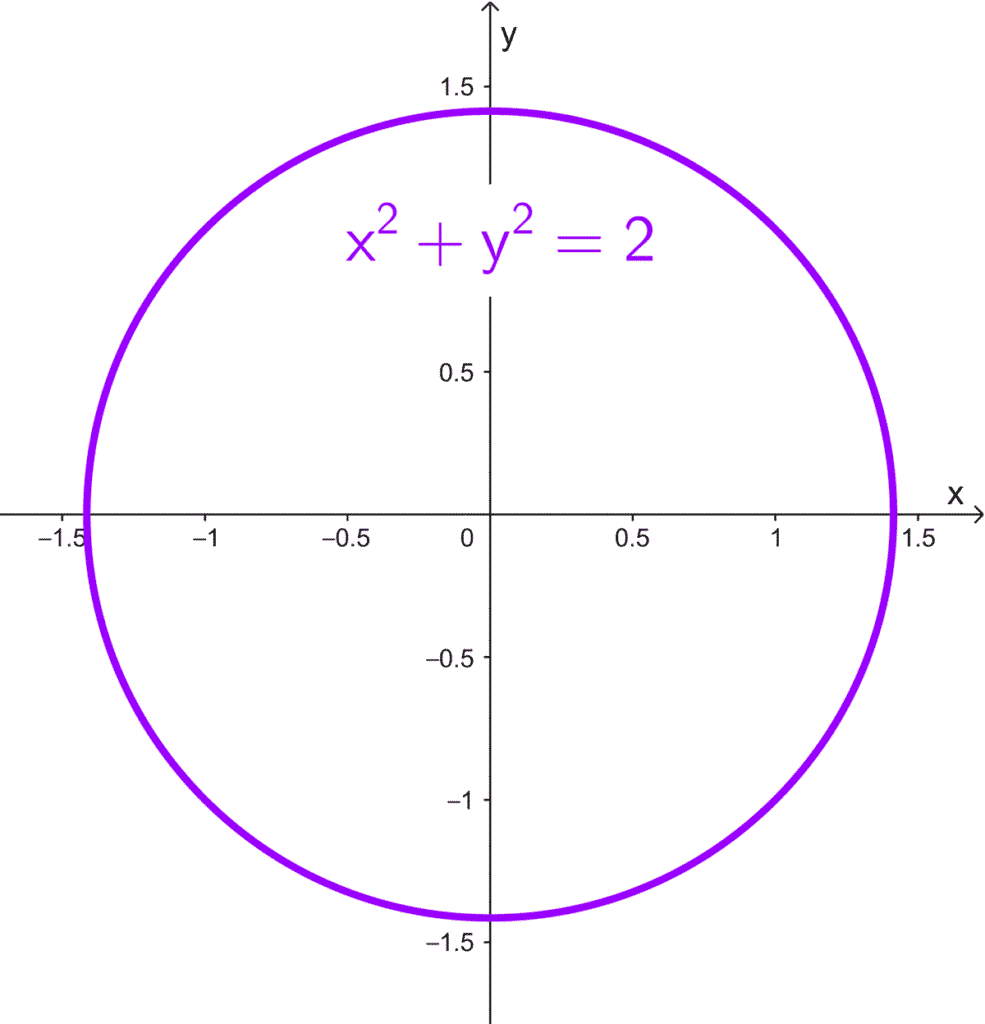
- x2 + y2 = 2 tiene un radio *r=\sqrt{2}≈1,41.*
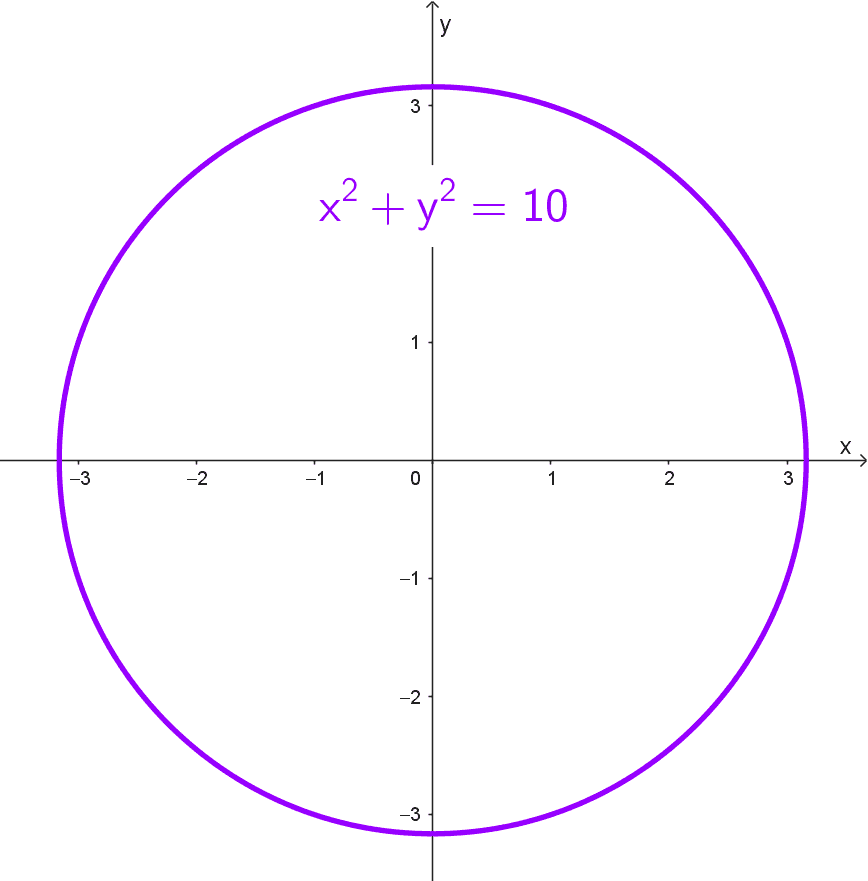
- x2 + y2 = 10 tiene radio *r=\sqrt{10}=3,16.*
Un problema común en geometría analítica es encontrar la ecuación de la circunferencia que cumple ciertas condiciones dadas. Cuando se sabe que el centro está en el origen, el procedimiento se simplifica bastante: solo es necesario conocer el valor del radio de la circunferencia y reemplazarlo en la ecuación ordinaria: x² + y² = r².
Ejercicios
Determinar la ecuación de la circunferencia con las siguientes condiciones:
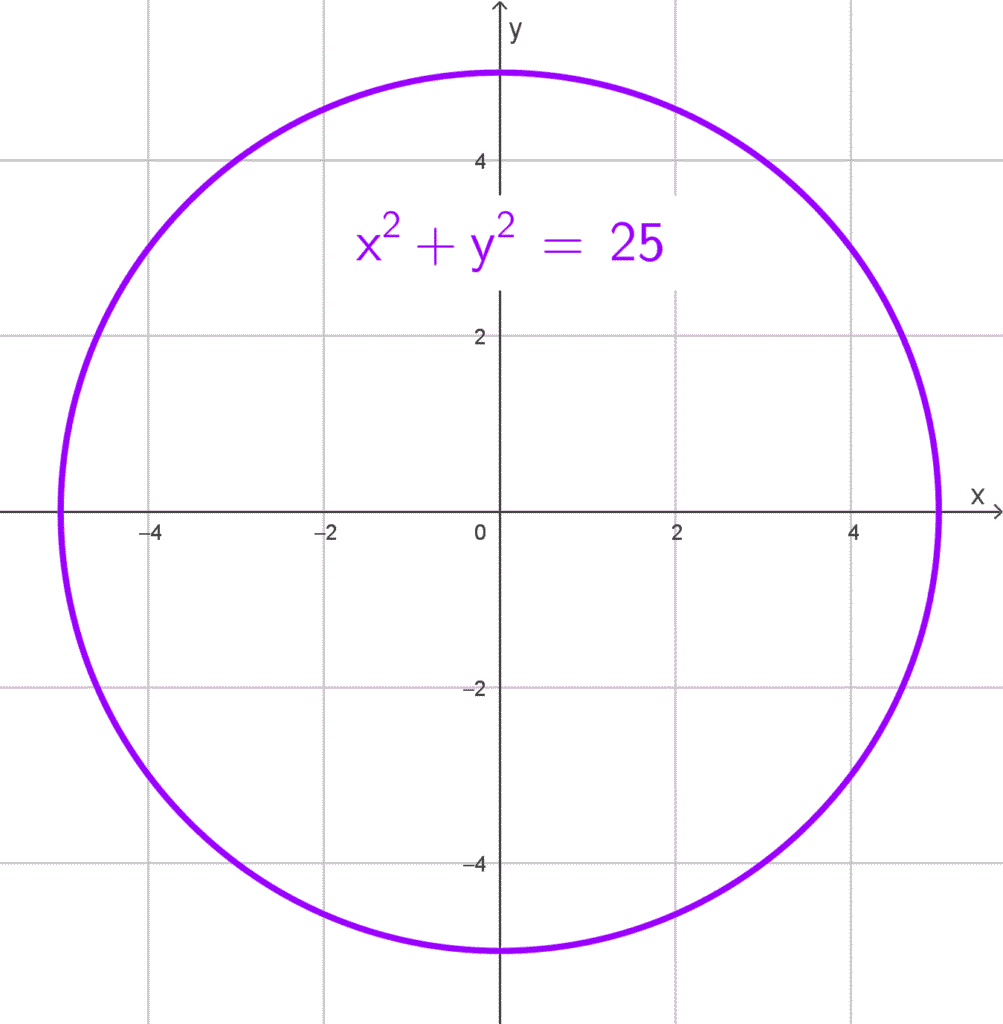
- Centro en el origen y radio igual a 5.
- Centro en (0, 0) y radio r = 7.
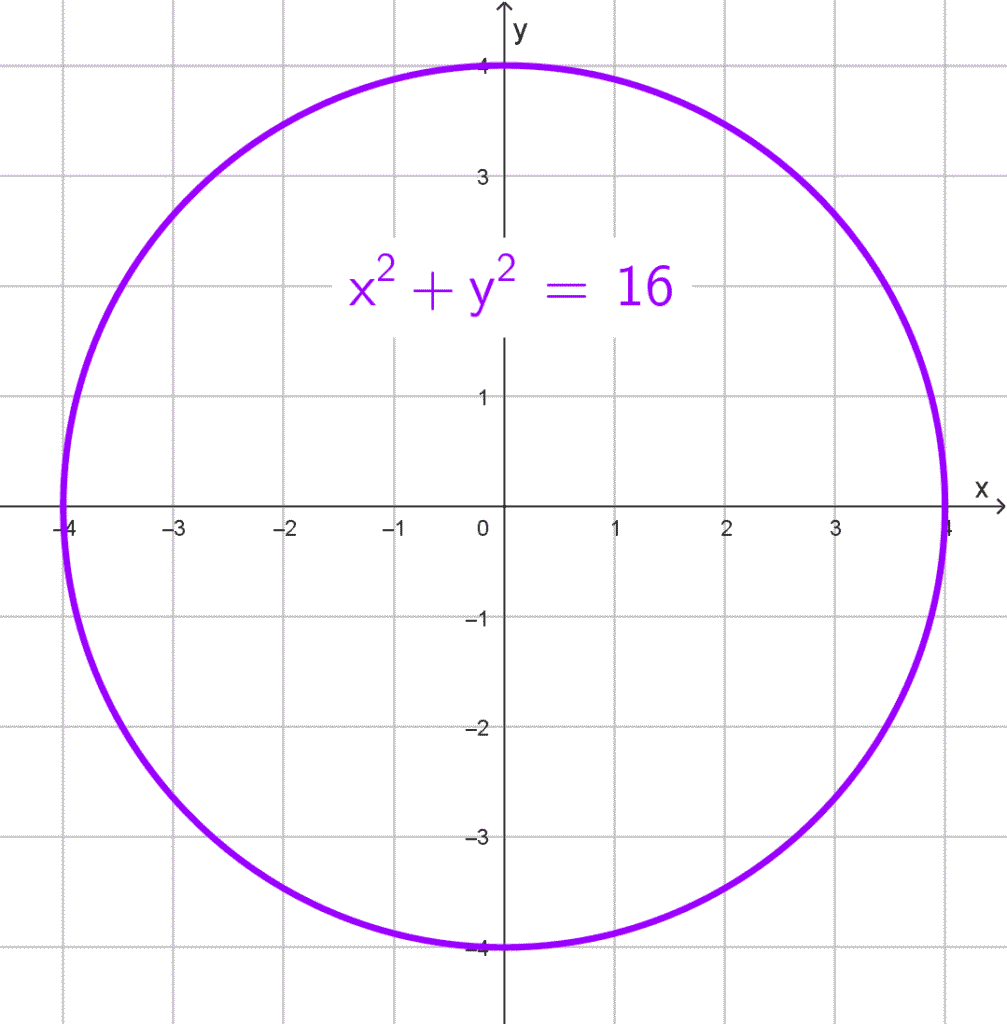
- Centro en el origen con radio de 4 unidades.
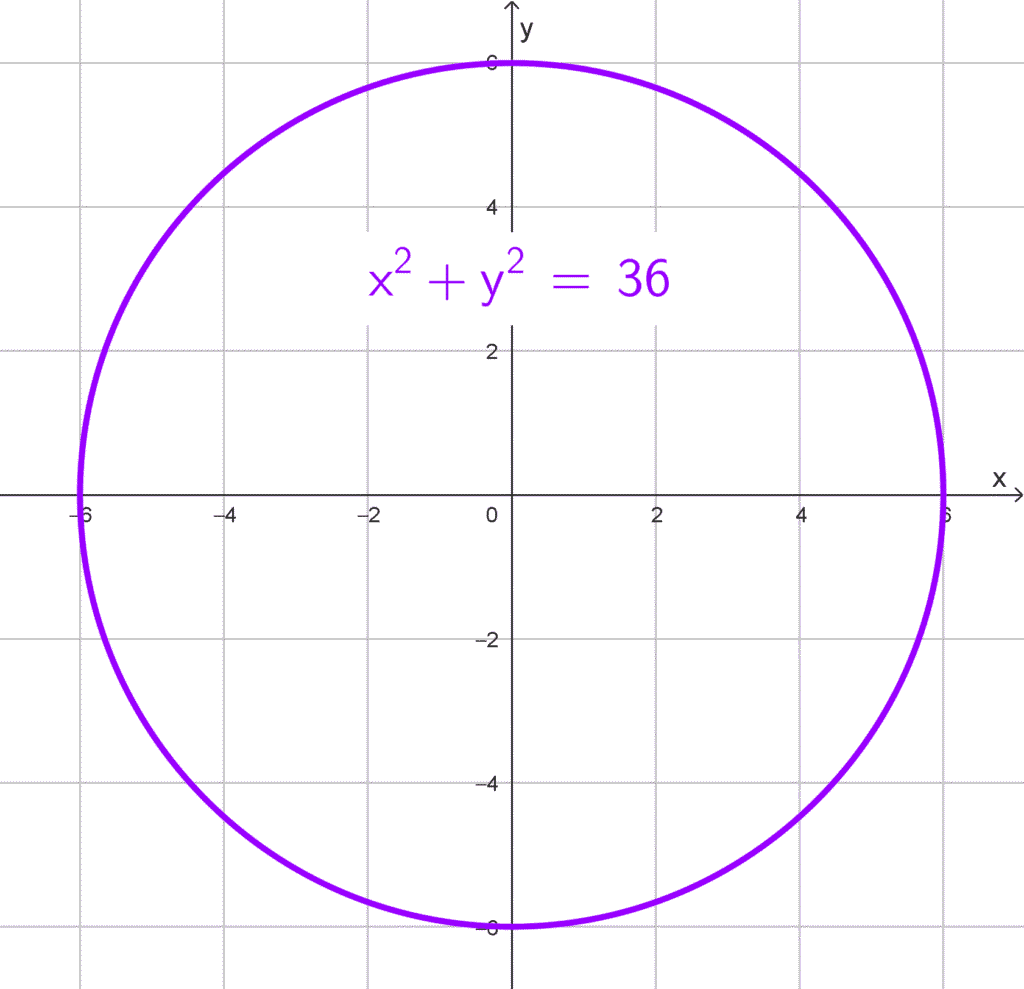
- Centro en el origen de coordenadas y diámetro igual a 12.
- Centro en (0, 0) y radio r = 3/5.
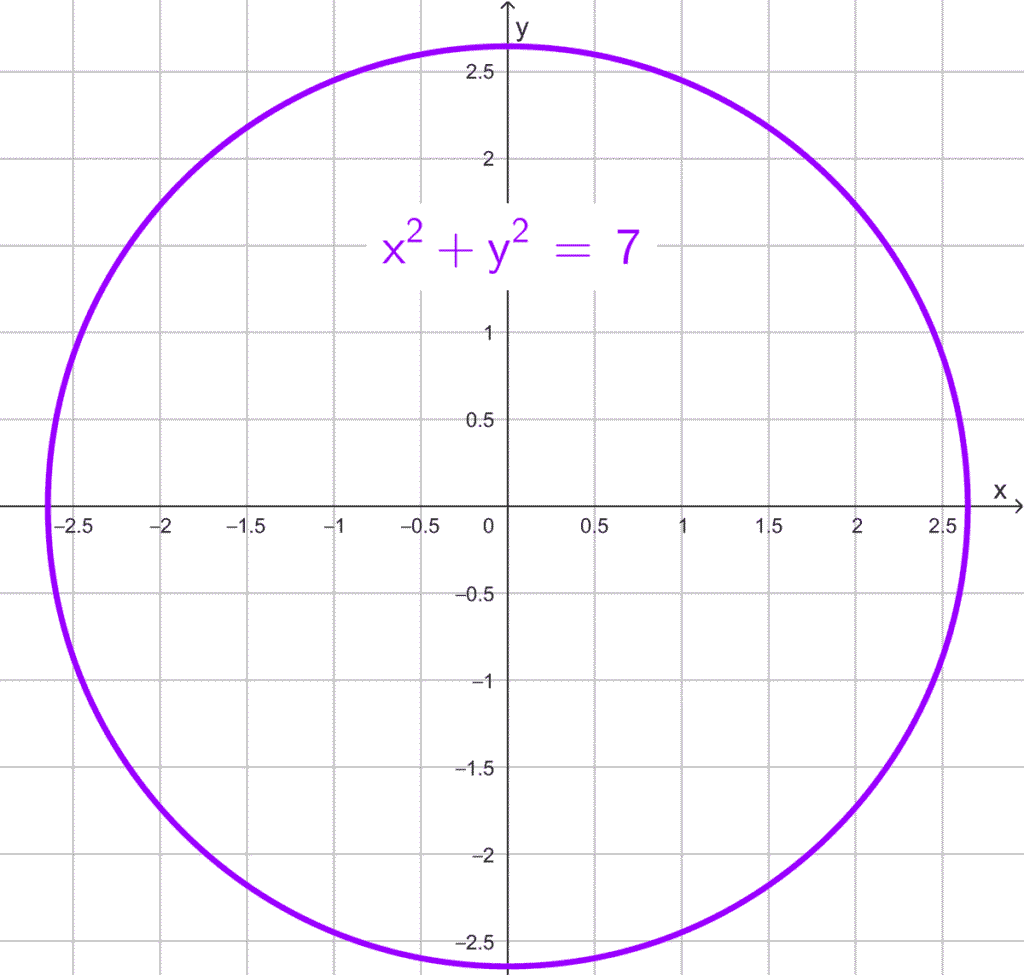
- C(0, 0), r = √7.
Soluciones
Solución 1
Dado que la circunferencia tiene su centro en el origen (0, 0) y un radio *r=5,* aplicamos directamente la ecuación ordinaria de la circunferencia centrada en el origen:
*x^2+y^2=r^2*
Sustituyendo el valor del radio y desarrollando la potencia:
*x^2+y^2=5^2*
*x^2+y^2=25*
Así, la ecuación buscada es *\boxed{x^2+y^2=25}*
Solución 5
Dado que la circunferencia tiene su centro en el origen (0, 0) y un radio *r=\dfrac{3}{5},* aplicamos la ecuación ordinaria de la circunferencia centrada en el origen:
*x^2+y^2=r^2*
Sustituyendo el valor del radio:
*x^2+y^2=\left(\dfrac{3}{5}\right)^2*
*x^2+y^2=\dfrac{9}{25}*
Por lo tanto, la ecuación buscada es *\boxed{x^2+y^2=\dfrac{9}{25}}*
La ecuación general de la circunferencia centrada en (0, 0) puede obtenerse reacomodando la fórmula ordinaria de modo que quede igualada a cero, así:
x2 + y2 - r2 = 0
De forma más general, una ecuación del tipo x2 + y2 + F = 0 representa a una circunferencia centrada en el origen si ocurre que F < 0. Nótese que no aparecen términos lineales (Dx y Ey) cuando el centro es (0, 0).
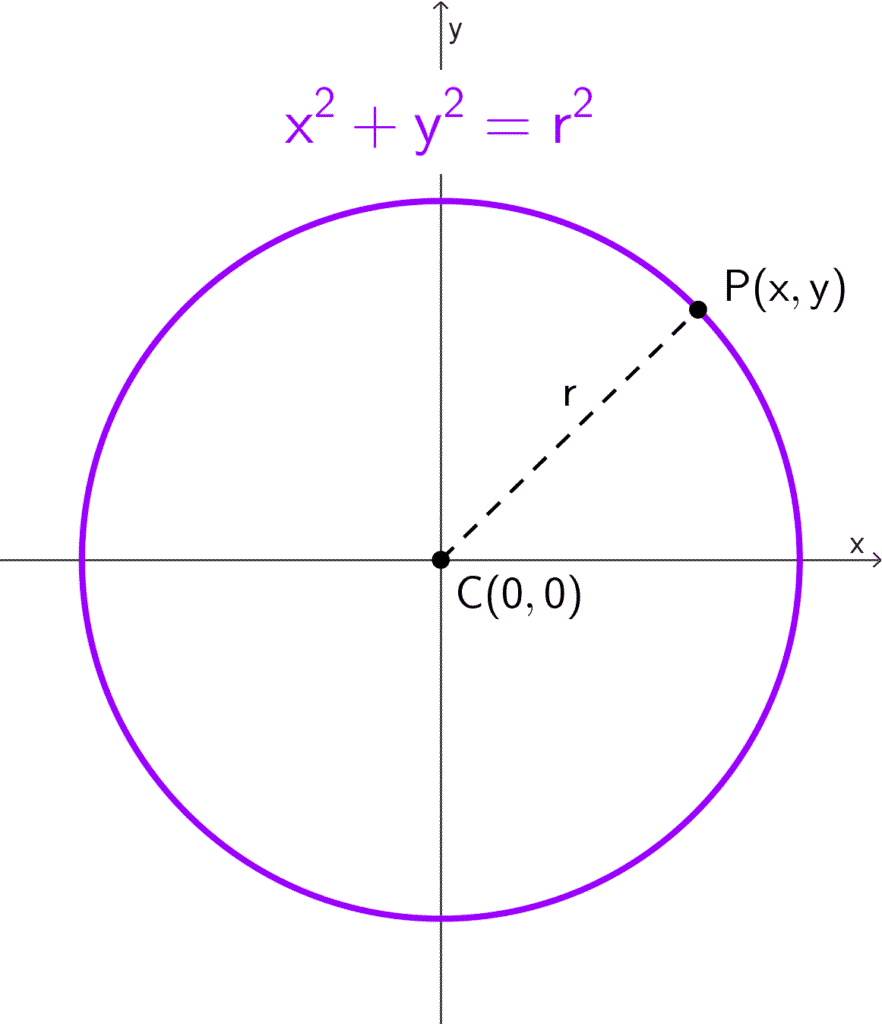
Demostración de la ecuación canónica
La ecuación de la circunferencia con centro en el origen se basa en la fórmula de distancia entre dos puntos en el plano. Consideramos:
- El centro de la circunferencia en el punto (0, 0).
- Un punto genérico (x, y) sobre la circunferencia.
La distancia entre estos dos puntos es:
*\sqrt{(x-0)^2+(y-0)^2}=\sqrt{x^2+y^2}*
Como esta distancia es igual al radio *r,* se cumple que:
*\sqrt{x^2+y^2}=r*
Elevando ambos lados al cuadrado para eliminar la raíz se obtiene la ecuación canónica:
*x^2+y^2=r^2*
Centro fuera del origen
Cuando el centro de la circunferencia no está en el origen, sino en un punto cualquiera del plano cartesiano, digamos (h, k), la fórmula se modifica para reflejar esa nueva posición. En este caso, la ecuación canónica es:
(x − h)² + (y − k)² = r²
donde x e y representan las coordenadas de cualquier punto de la circunferencia, h y k son las coordenadas del centro y r es el radio.
Ejemplos
Los siguientes son ejemplos de circunferencias centradas fuera del origen:
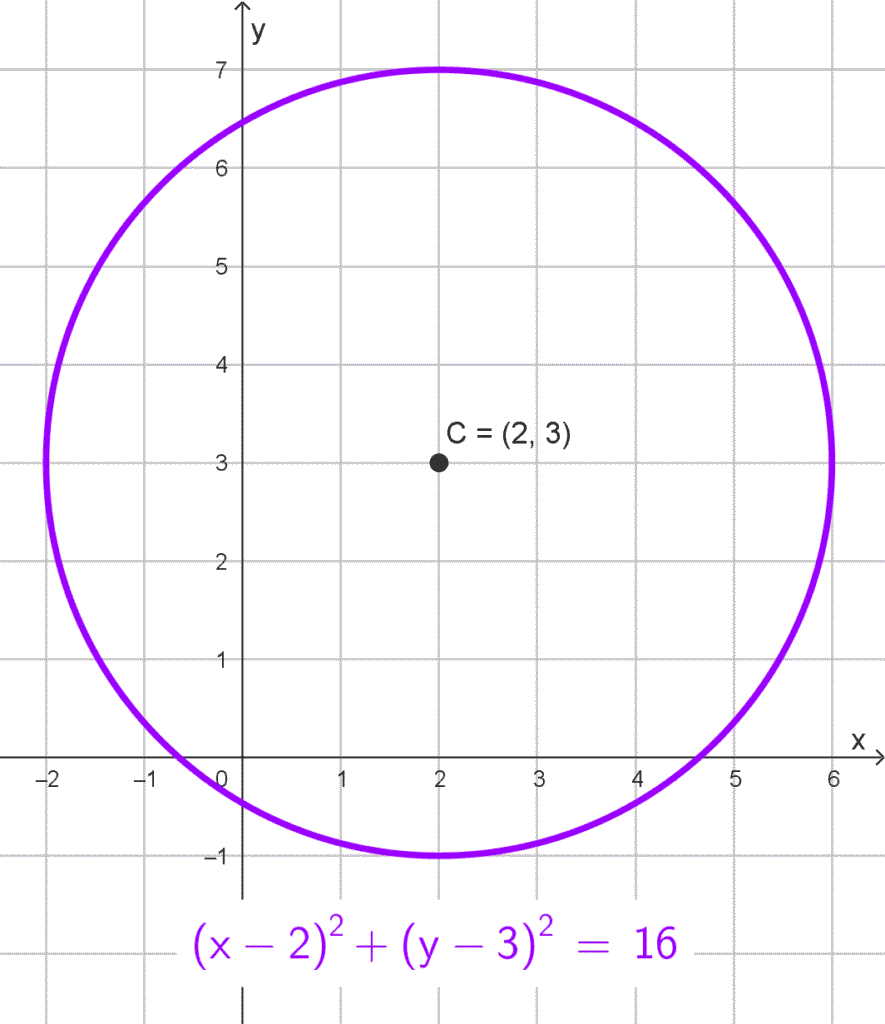
- *(x-2)^2+(y-3)^2=16* tiene centro en (2, 3) y radio *r=\sqrt{16}=4.*
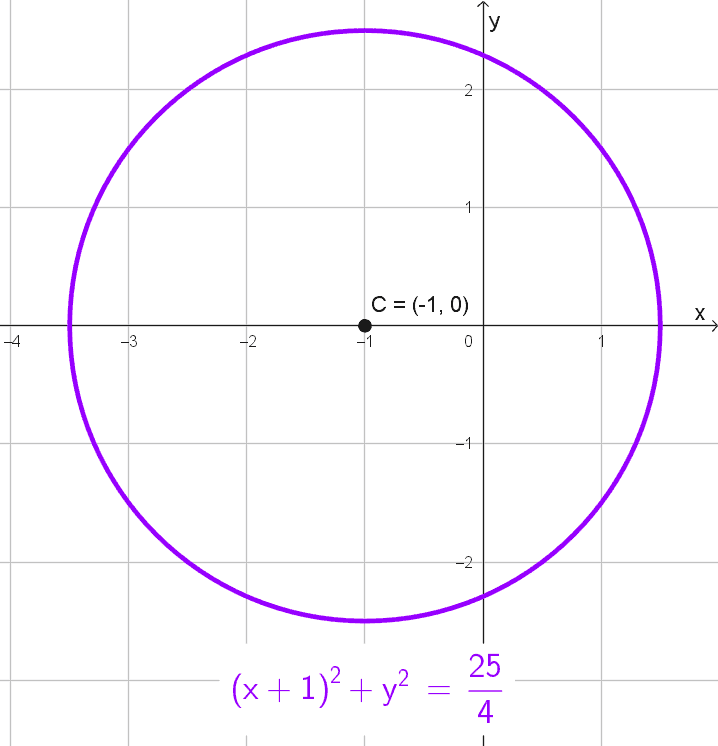
- *(x+1)^2+y^2=\dfrac{25}{4}* tiene su centro en (-1, 0) y radio *r=\sqrt{25/4}=5/2.*
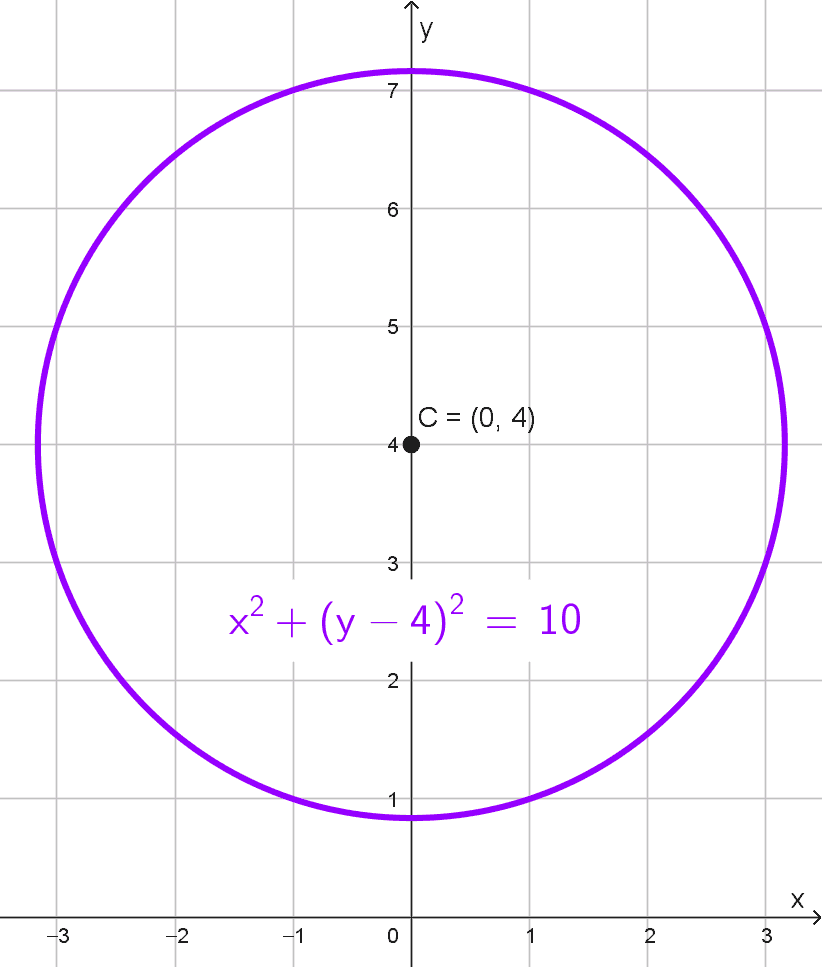
- *x^2+(y-4)^2=10* tiene centro en (0, 4) y radio *r=\sqrt{10}≈3,16.*
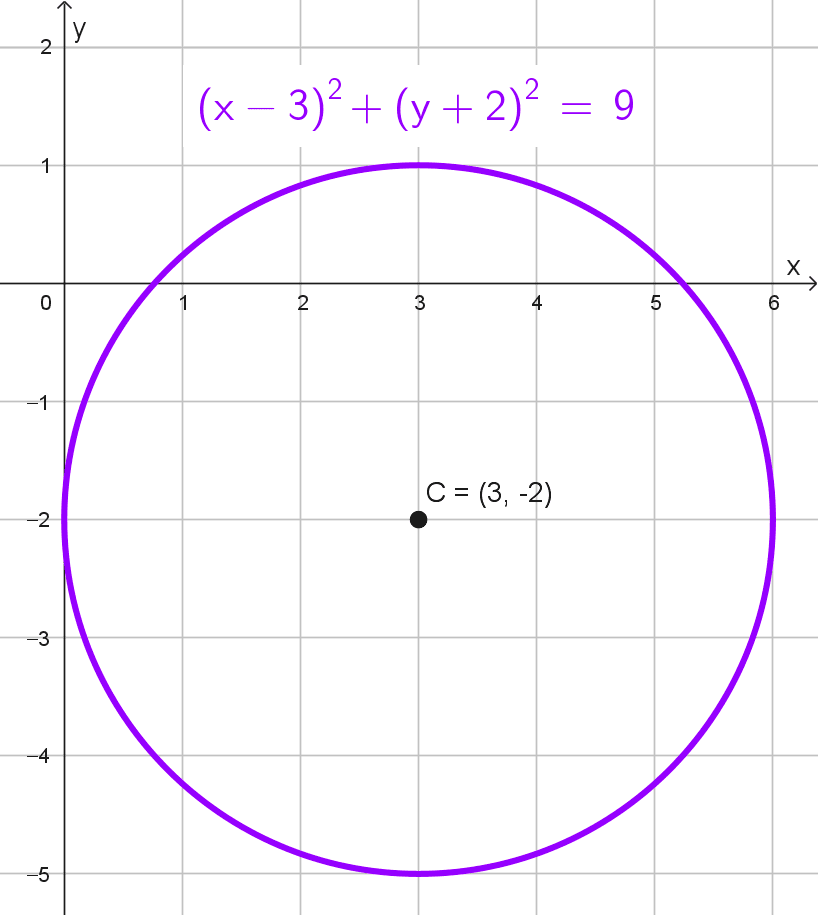
- *(x-3)^2+(y+2)^2=9* tiene centro en (3, -2) y radio *r=\sqrt{9}=3.*
Del mismo modo que antes, un problema común es encontrar la ecuación de la circunferencia cuando se conocen ciertos datos. Para resolverlos, es suficiente conocer el centro y el radio para sustituir estos datos en su lugar correspondiente de la ecuación.
Ejercicios
Hallar la ecuación de la circunferencia que cumple las siguientes condiciones:
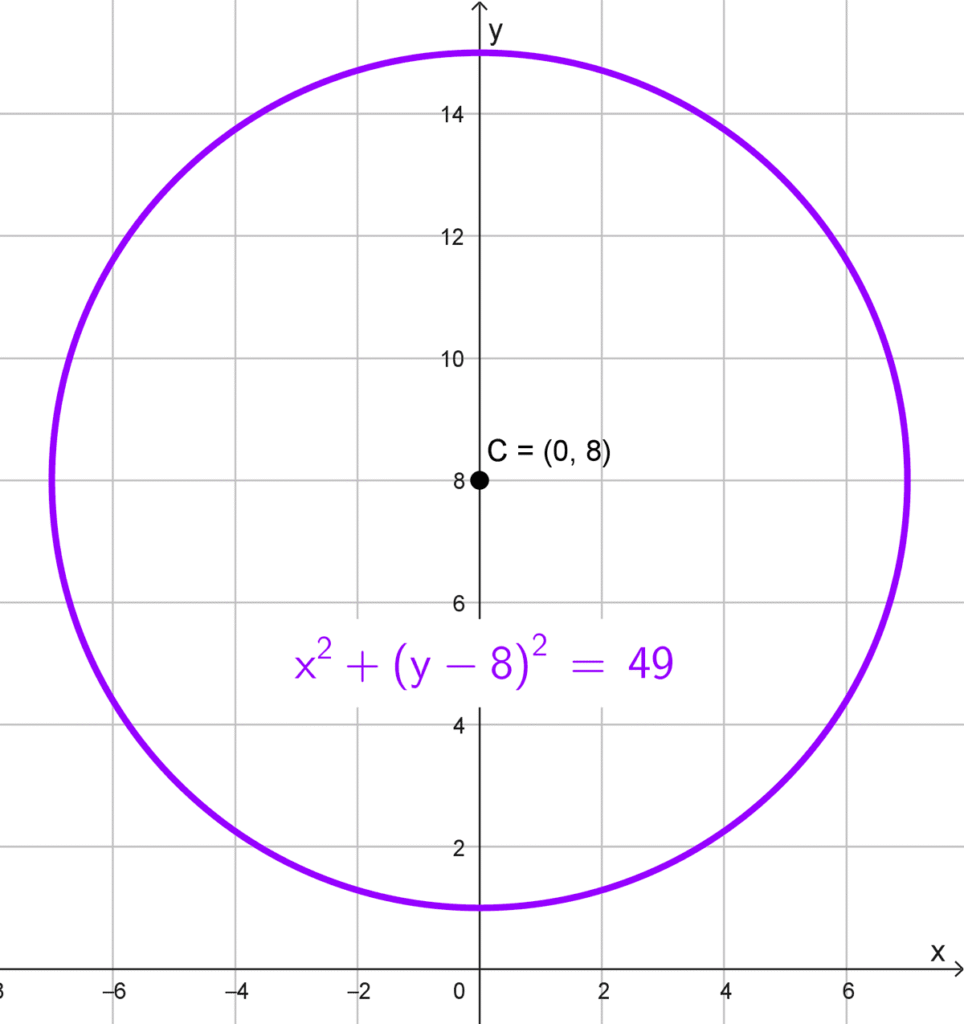
- Centro en (0, 8) y radio 7.
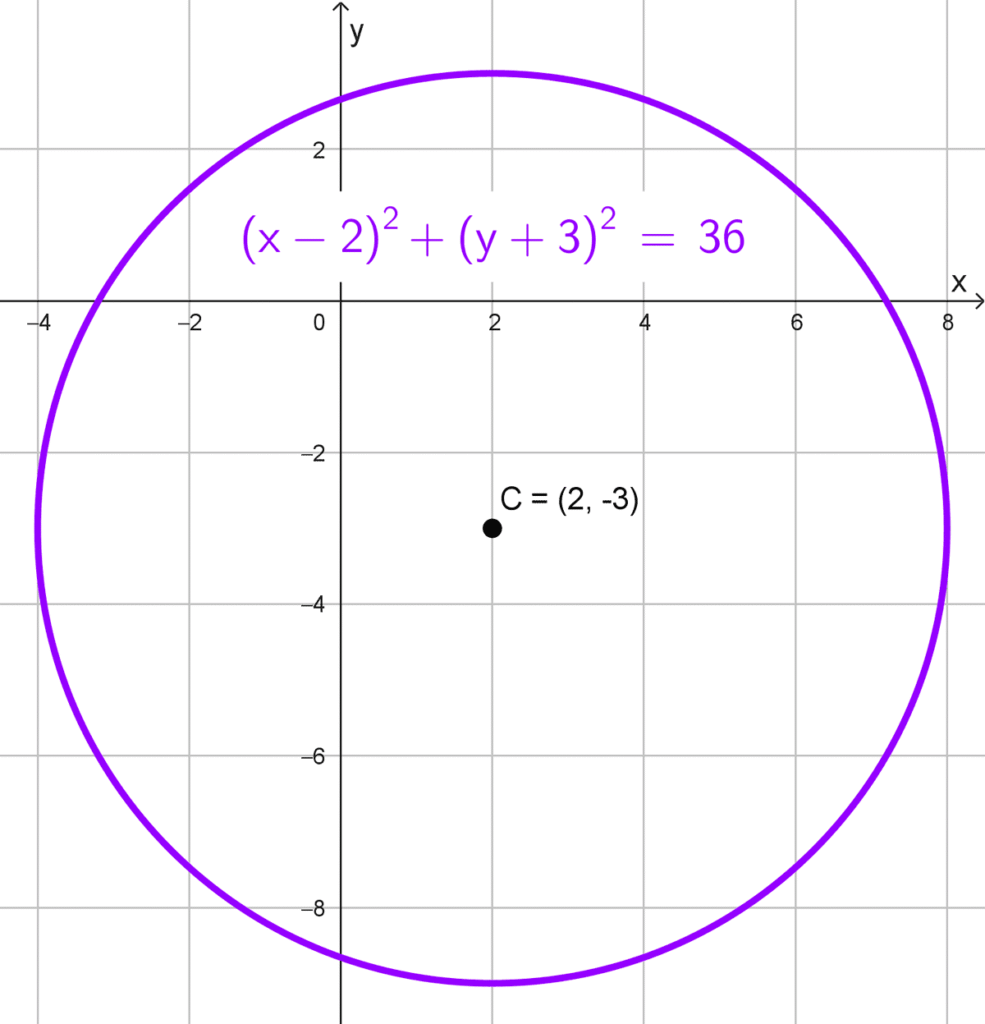
- C(2, -3) y diámetro 12.
- C(1, -4) y pasa por el punto P(7, 11).
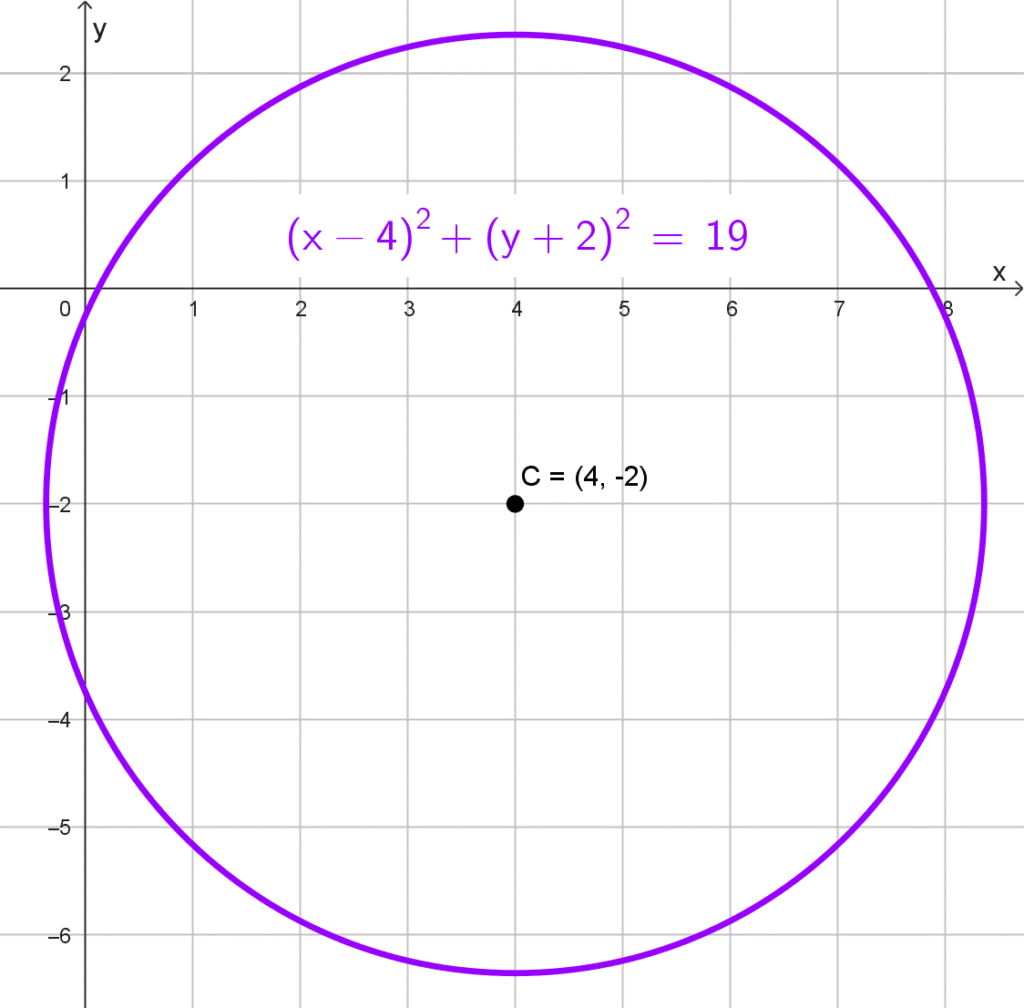
- C(4, -2) y radio de *\sqrt{19}.*
Solución 3
Sabiendo que el centro está en C(1, -4) y que la curva pasa por P(7, 11), determinamos el radio como la distancia entre estos puntos. Aplicamos la fórmula de distancia:
*r=\sqrt{(7-1)^2+(11-(-4))^2}*
*r=\sqrt{6^2+15^2}=\sqrt{36+225}=\sqrt{261}*
La ecuación reducida de la circunferencia queda:
*(x-1)^2+(y+4)^2=261*
La ecuación general de una circunferencia con centro fuera del origen es:
x2 + y2 + Dx + Ey + F = 0
donde se cumple que D2 + E2 - 4F > 0. Esta fórmula se obtiene desarrollando los cuadrados en la ecuación ordinaria. Nótese que en este caso sí aparecen términos lineales.
Ejemplos de ecuaciones generales
- *x^2+y^2-4x-6y-3=0*
- *x^2+y^2+2x-\dfrac{21}{4}=0*
- *x^2+y^2-8y+6=0*
- *x^2+y^2-6x+4y+4=0*
Para pasar de la fórmula general a la canónica es necesario realizar el proceso de completar los cuadrados.
Con el siguiente recurso de GeoGebra puedes cambiar la longitud del radio y las coordenadas del centro y ver cómo se modifica la gráfica y ecuación de la circunferencia:
Resumen de ecuaciones
| Circunferencia | Ecuación canónica | Ecuación general |
|---|---|---|
| Centro en el origen | x² + y² = r² | x² + y² + F = 0 donde F < 0 |
| Centro fuera del origen | (x − h)² + (y − k)² = r² | x² + y² + Dx + Ey + F = 0 donde D² + E² - 4F > 0 |
Bibliografía
- Engler, A. y otros. (2020). Geometría Analítica. Universidad Nacional del Litoral.
- Fuller, G. y Tarwater, D. (1995). Geometría Analítica (7ma edición). Pearson Educación.
- Lehmann, C. (1989). Geometría Analítica. Limusa.
- Márquez, A. y otros. (2009). Geometría Analítica. Prentice Hall.
- Raichman, S. y Totter, E. (2016). Geometría Analítica para Ciencias e Ingeniería. Universidad Nacional de Cuyo.
Deja una respuesta

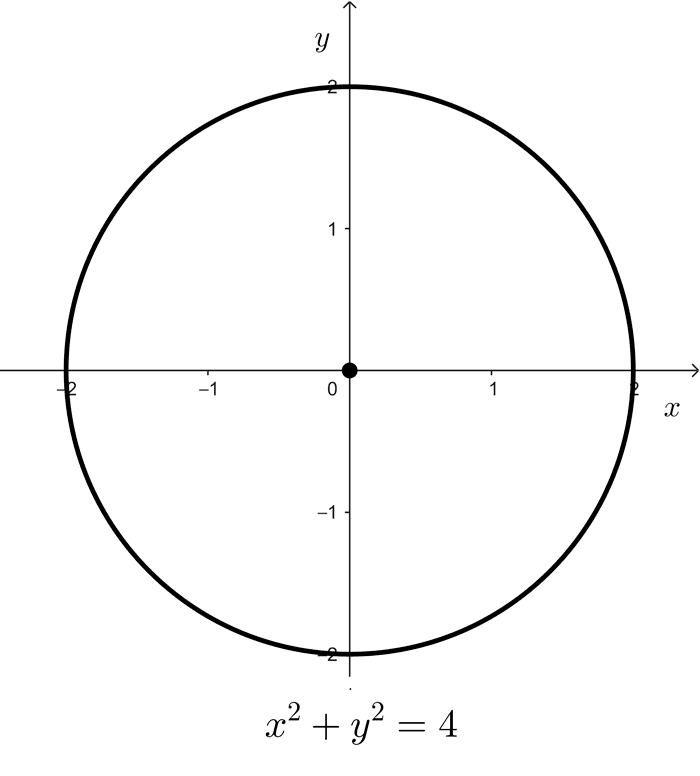
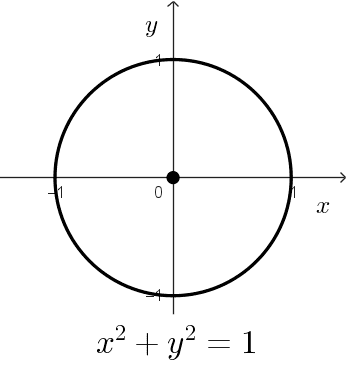
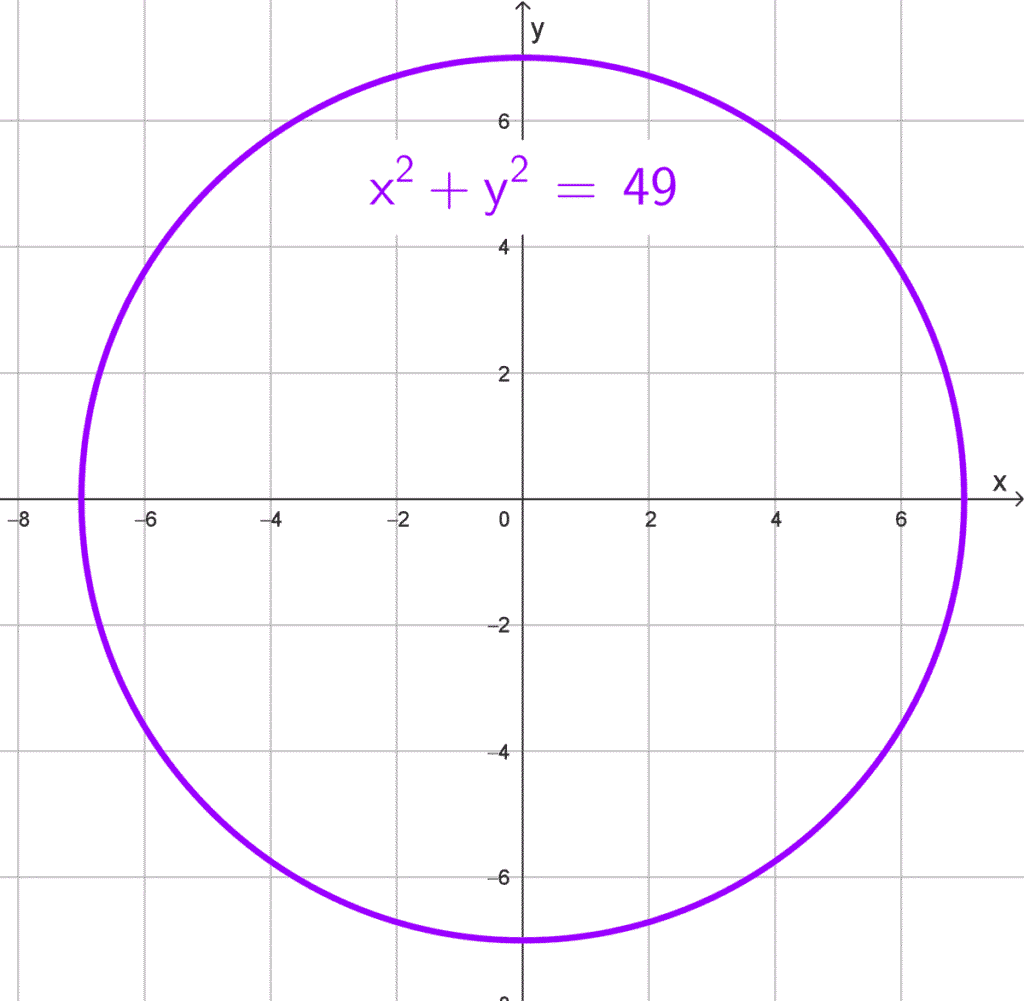
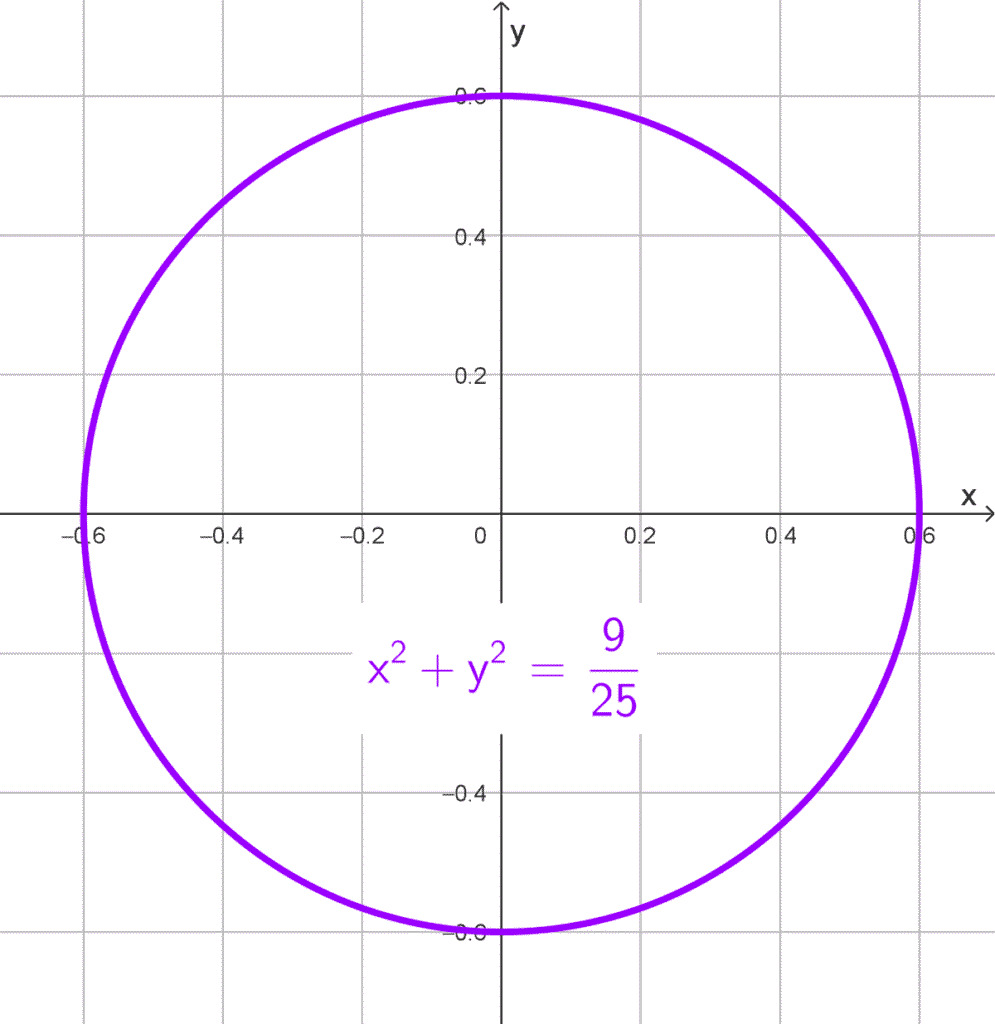
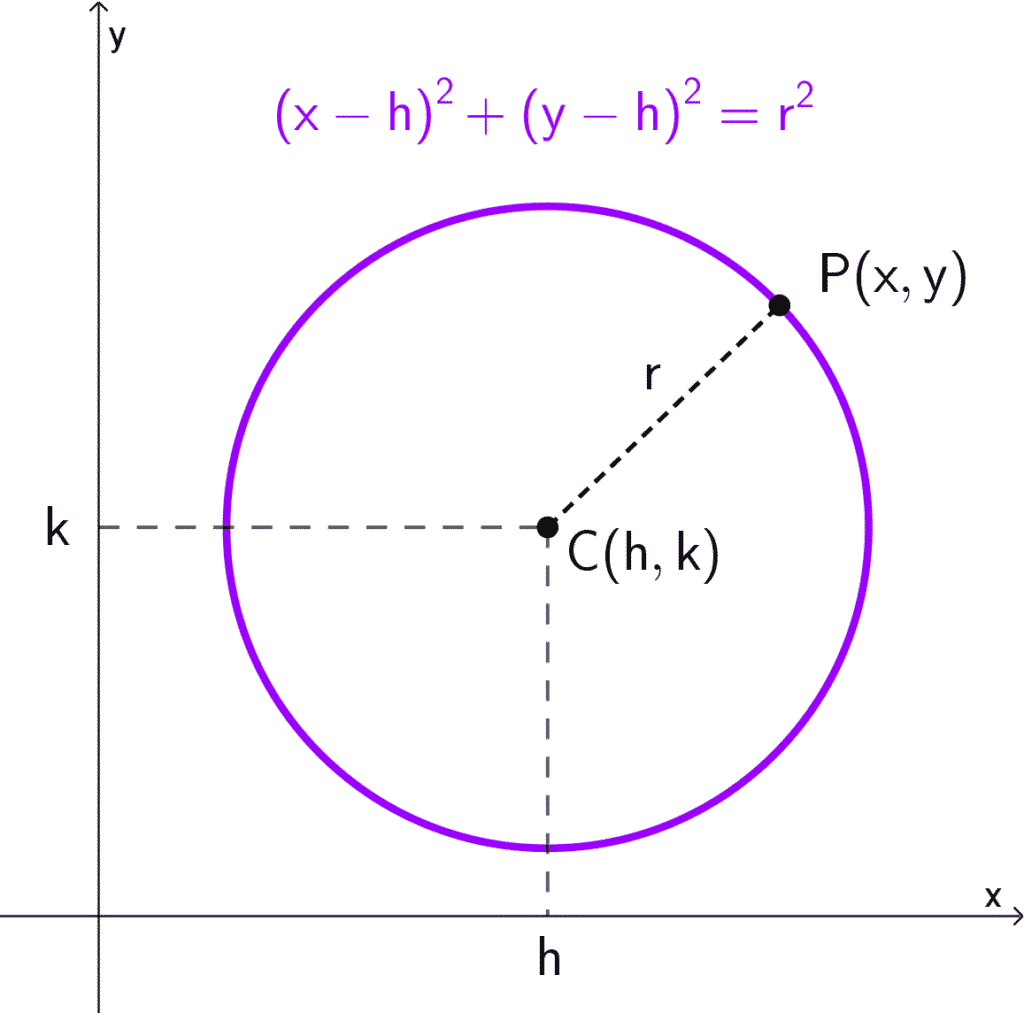
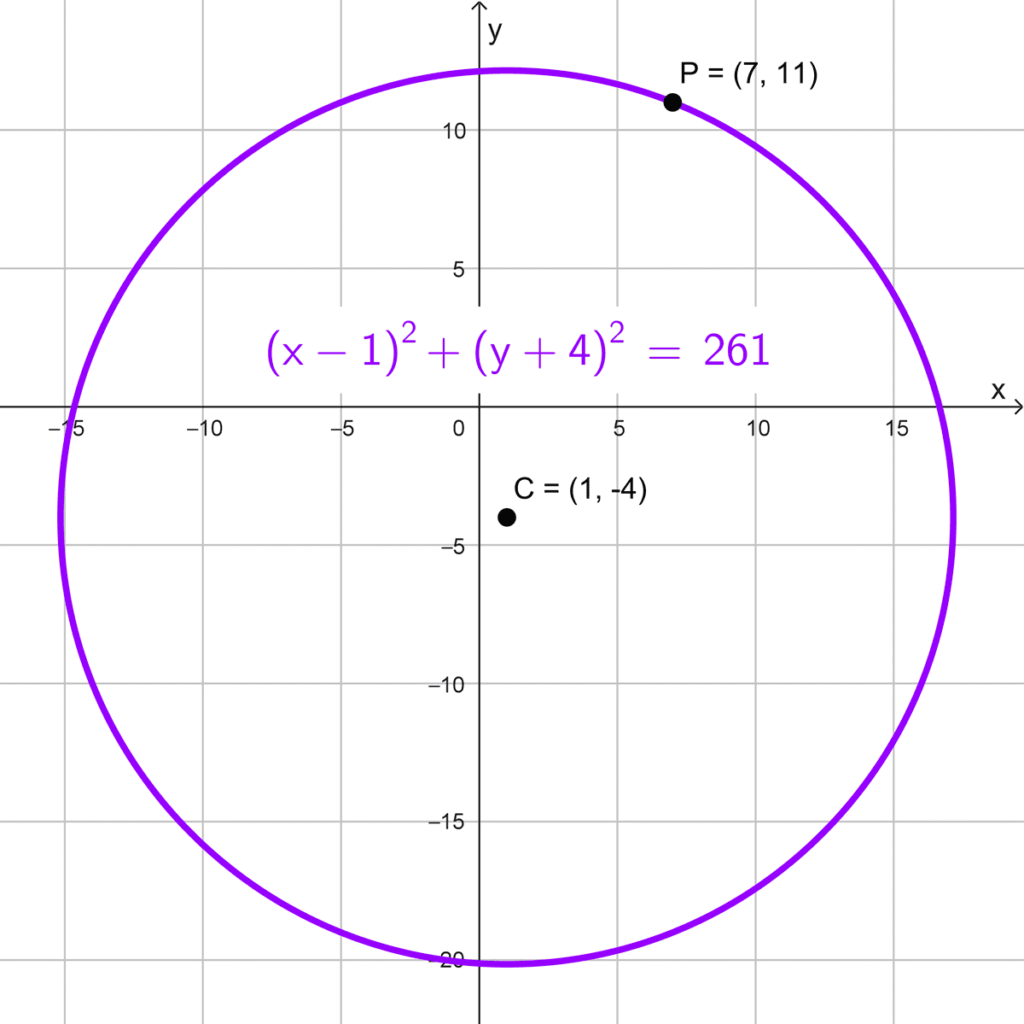



Otros artículos que pueden interesarte