
Parábolas con vértice en el origen y fuera del origen
Una parábola no tiene centro como las demás secciones cónicas, sin embargo, el vértice ocupa su lugar en la ecuación canónica, haciendo que esta varíe dependiendo de las coordenadas del vértice.
A continuación, veremos las ecuaciones y gráficos de parábolas con vértice en el origen y fuera del origen.
Nota: en este artículo nos enfocamos solo en un aspecto de la parábola. Para comprenderlo mejor, te recomiendo que antes revises el artículo principal sobre esta cónica, donde abordamos su teoría básica:
Índice
Parábolas con vértice en el origen
En estas parábolas, el vértice es el punto (0, 0), la ecuación canónica es simple y depende de si la orientación es horizontal o vertical.
Parábola horizontal: y2 = 4px
- Si p > 0, la parábola abre hacia la derecha (forma de ⊂).
- Si p < 0, la parábola abre hacia la izquierda (forma de ⊃).
Parábola vertical: x2 = 4py
- Si p > 0, la parábola abre hacia arriba (forma de U).
- Si p < 0, la parábola abre hacia abajo (forma de ∩).
Ejemplos
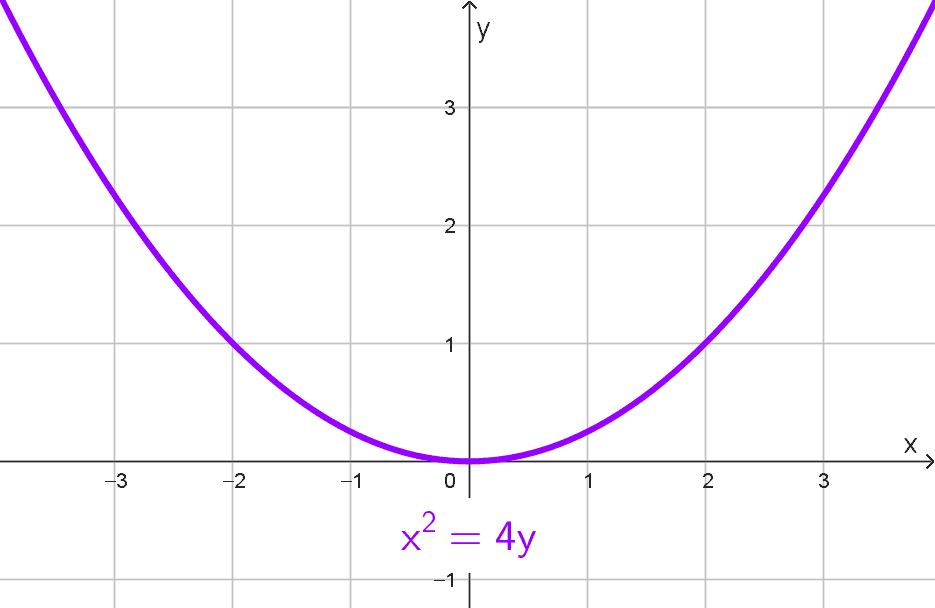
- \(x^2=4y\)
- \(y^2=-10x\)
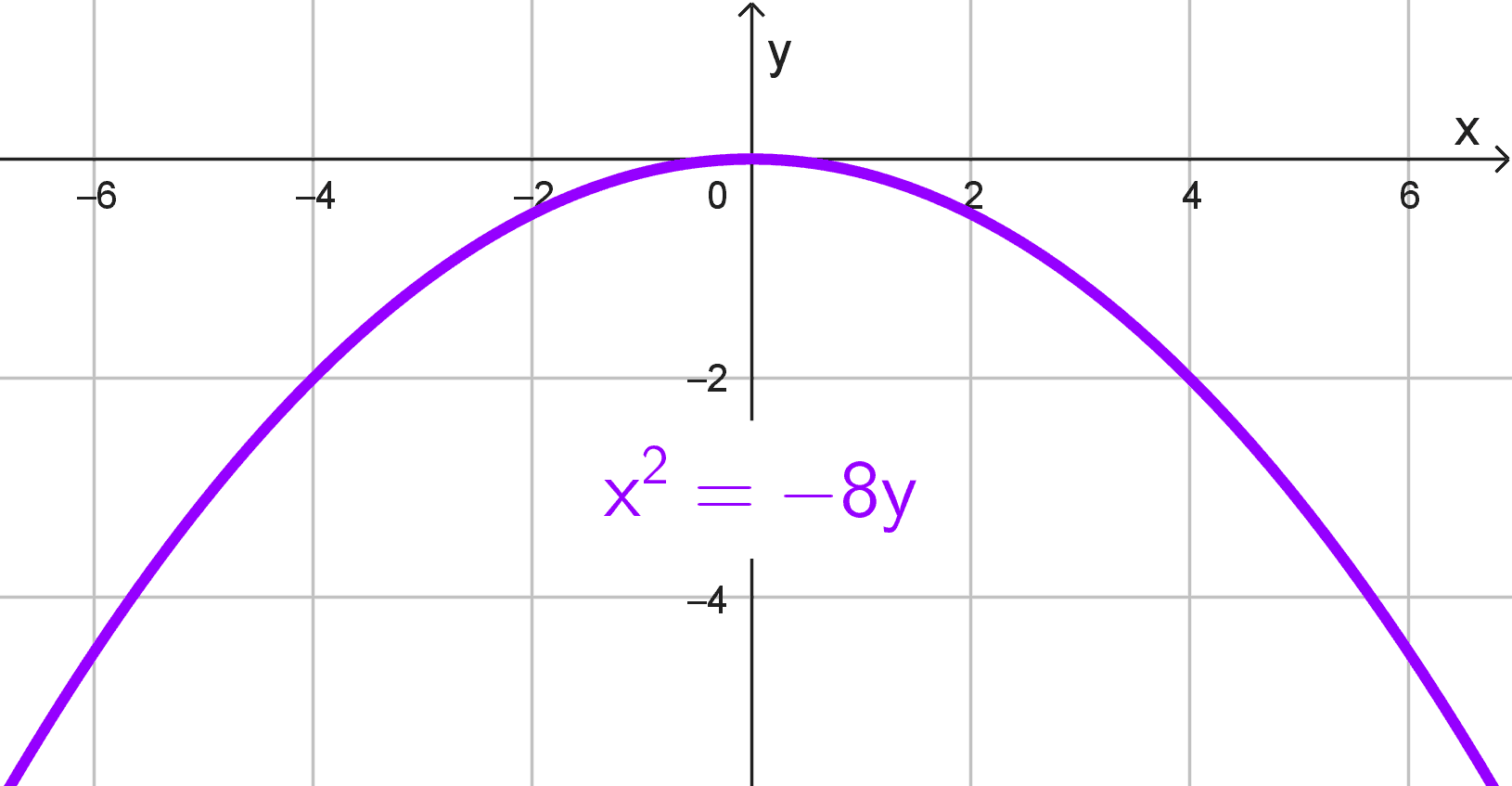
- \(x^2=-8y\)
- \(y^2=3x\)
¿Te está sirviendo este artículo? ¡Por favor, califícalo!
Elementos
Las características y elementos de las parábolas con vértice en el origen se resumen en la siguiente tabla.
| Ecuación | Vértice | Orientación | Directriz | Foco | Eje de simetría |
|---|---|---|---|---|---|
| y2 = 4px | (0, 0) | Horizontal | x = -p | (p, 0) | y = 0 |
| x2 = 4py | (0, 0) | Vertical | y = -p | (0, p) | x = 0 |
La ecuación general de una parábola con vértice en (0, 0) es:
- Para parábolas verticales: Ax2 + Ey = 0 donde A = 1 y E = -4p.
- Para parábolas horizontales: Cy2 + Dx = 0 donde C = 1 y D = -4p.
Otra forma común de expresar la ecuación es despejando la variable que no está elevada al cuadrado:
- Parábolas verticales: y = ax2 donde a = 1 / (4p).
- Parábolas horizontales: x = ay2 donde a = 1 / (4p).
Parábola con vértice fuera del origen
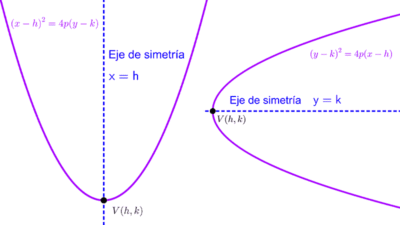
En este tipo de parábolas, el vértice no es el origen de coordenadas, sino otro punto (h, k) del plano cartesiano. La ecuación ordinaria es similar a las vistas anteriormente salvo que a la variable x se le resta el valor h y a la variable y se le resta el valor k.
Parábola horizontal: (y - k)2 = 4p (x - h)
- Si p > 0, la parábola abre hacia la derecha (forma de ⊂).
- Si p < 0, la parábola abre hacia la izquierda (forma de ⊃).
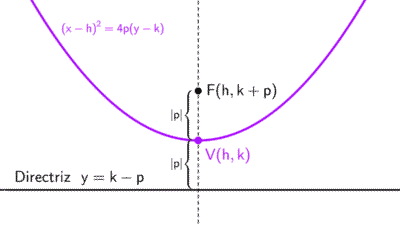
Parábola vertical: (x - h)2 = 4p (y - k)
- Si p > 0, la parábola abre hacia arriba (forma de U).
- Si p < 0, la parábola abre hacia abajo (forma de ∩).
Ejemplos
- \((y-2)^2=4(x-1)\)
- \((x+1)^2=7(y+3)\)
- \(y^2=-8(x-2)\)
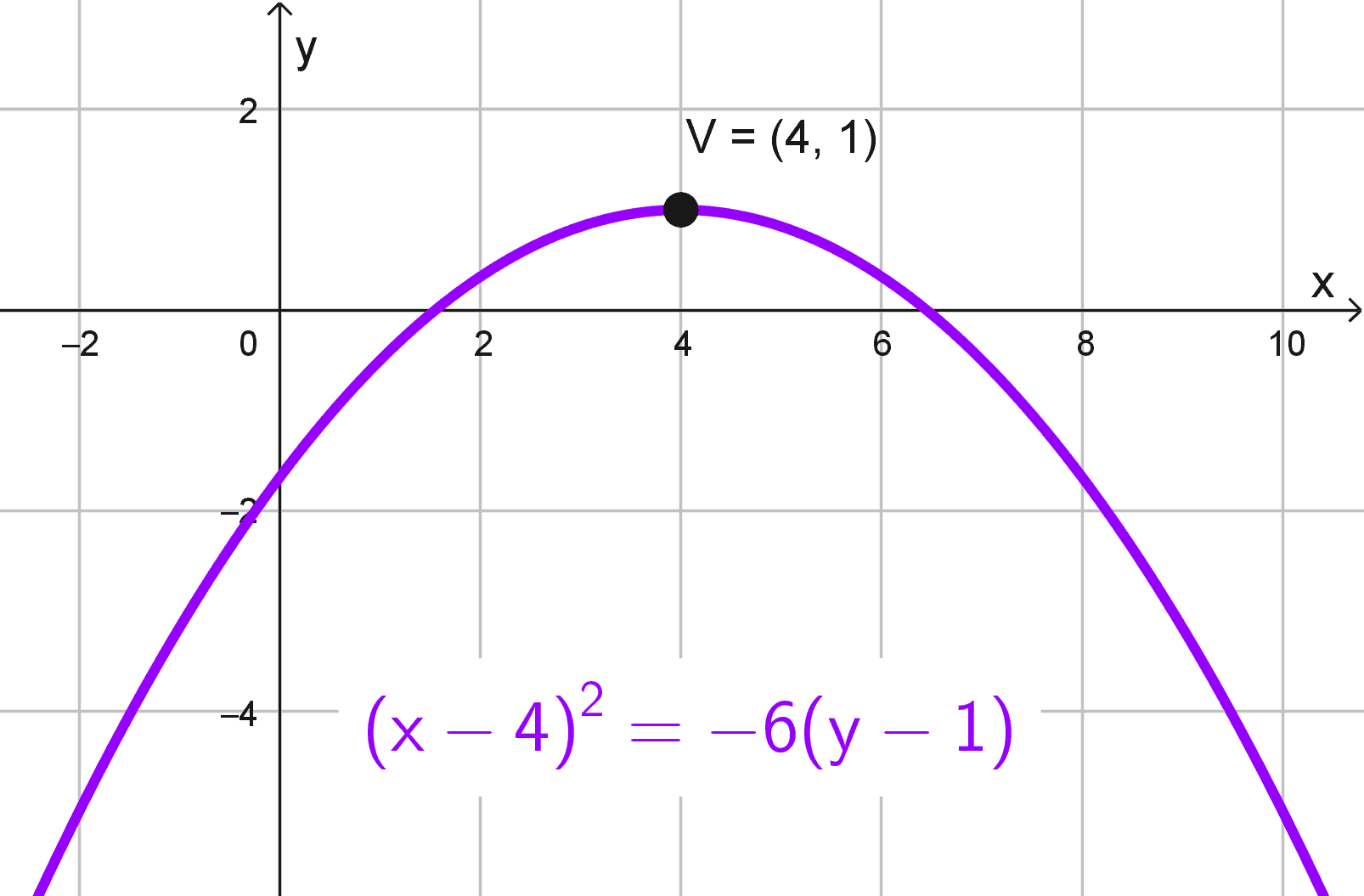
- \((x-4)^2=-6 (y-1)\)
Elementos
Las características y elementos de las parábolas con vértice en (h, k) se resumen en la siguiente tabla de fórmulas.
| Ecuación | Vértice | Orientación | Directriz | Foco | Eje de simetría |
|---|---|---|---|---|---|
| (y - k)2 = 4p (x - h) | (h, k) | Horizontal | x = h - p | (h + p, k) | y = k |
| (x - h)2 = 4p (y - k) | (h, k) | Vertical | y = k - p | (h, k + p) | x = h |
La ecuación general de una parábola con vértice en (h, k) es:
- Para parábolas verticales: Ax2 + Dx + Ey + F = 0.
- Para parábolas horizontales: Cy2 + Dx + Ey + F = 0.
Una forma muy usada de expresar la ecuación es despejando la variable que no está elevada al cuadrado:
- Parábolas verticales: y = ax2 + bx + c.
- Parábolas horizontales: x = ay2 + by + c.
Resumen de fórmulas
| Orientación | Vértice en (0, 0) | Vértice en (h, k) |
|---|---|---|
| Horizontal | y2 = 4px | (y - k)2 = 4p (x - h) |
| Vertical | x2 = 4py | (x - h)2 = 4p (y - k) |
Ejercicios resueltos
A continuación, haremos algunos ejercicios de armado de ecuaciones. Los ejercicios de encontrar el vértice los puedes ver en este artículo:
Ejercicio 1
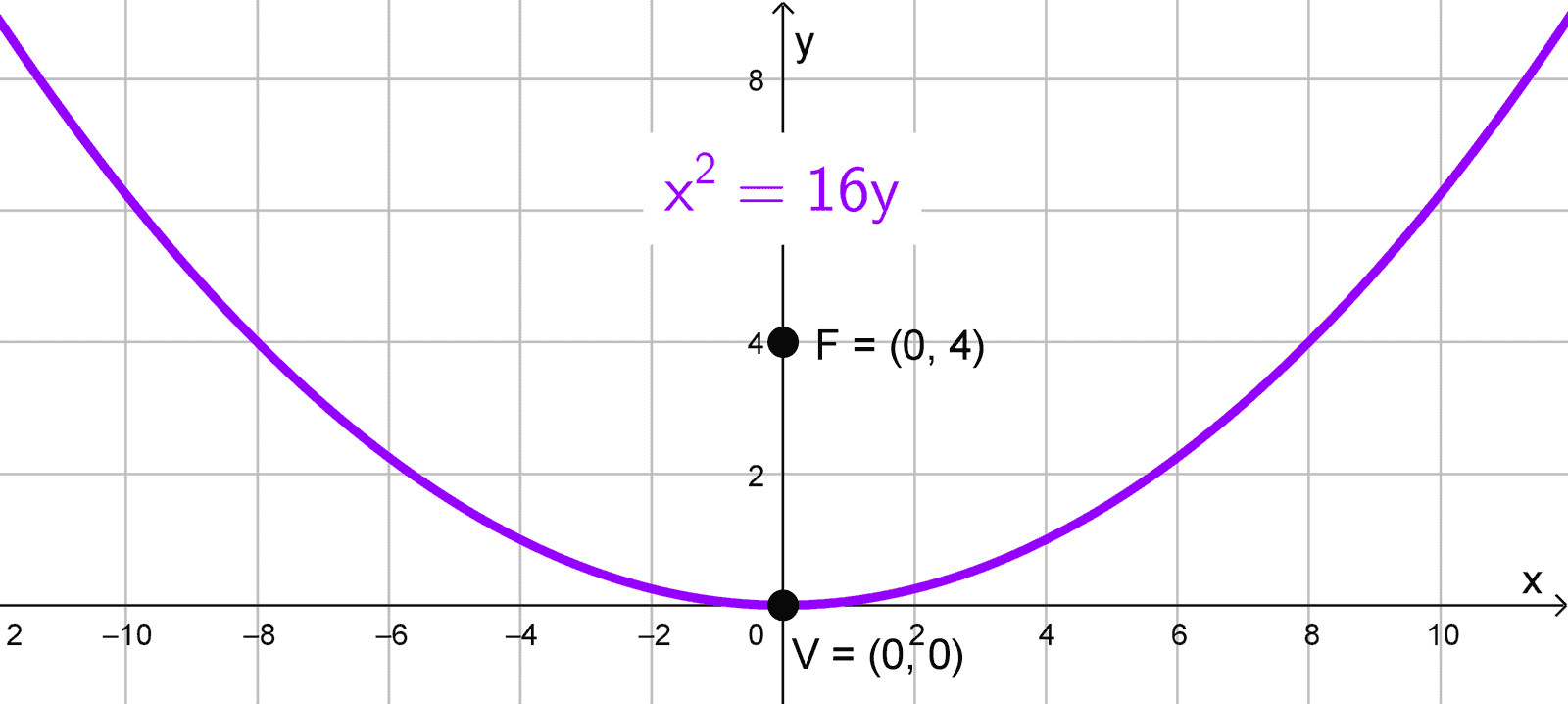
Hallar la ecuación de la parábola con vértice en el origen y foco (0, 4).
Solución
Dado que el foco está sobre el eje y por encima del vértice, la parábola se abre hacia arriba. La forma estándar de su ecuación es:
\(x^2=4py\)
Donde p es la coordenada y del foco, por tanto, p = 4. Sustituyendo en la ecuación, obtenemos:
\(x^2=4 \cdot 4 \cdot y → x^2=16y\)
Ejercicio 2
Escribe la ecuación de la parábola con vértice en el origen y foco F(2, 0).
Solución
En este caso, el foco está en (2, 0), lo que indica que la parábola abre hacia la derecha sobre el eje x. La forma estándar correspondiente es:
\(y^2=4px\)
El parámetro p es la coordenada x del foco: \(p=2.\) Reemplazandolo en la ecuación, sacamos:
\(y^2=4 \cdot 2 \cdot x → y^2=8x\)
Ejercicio 3
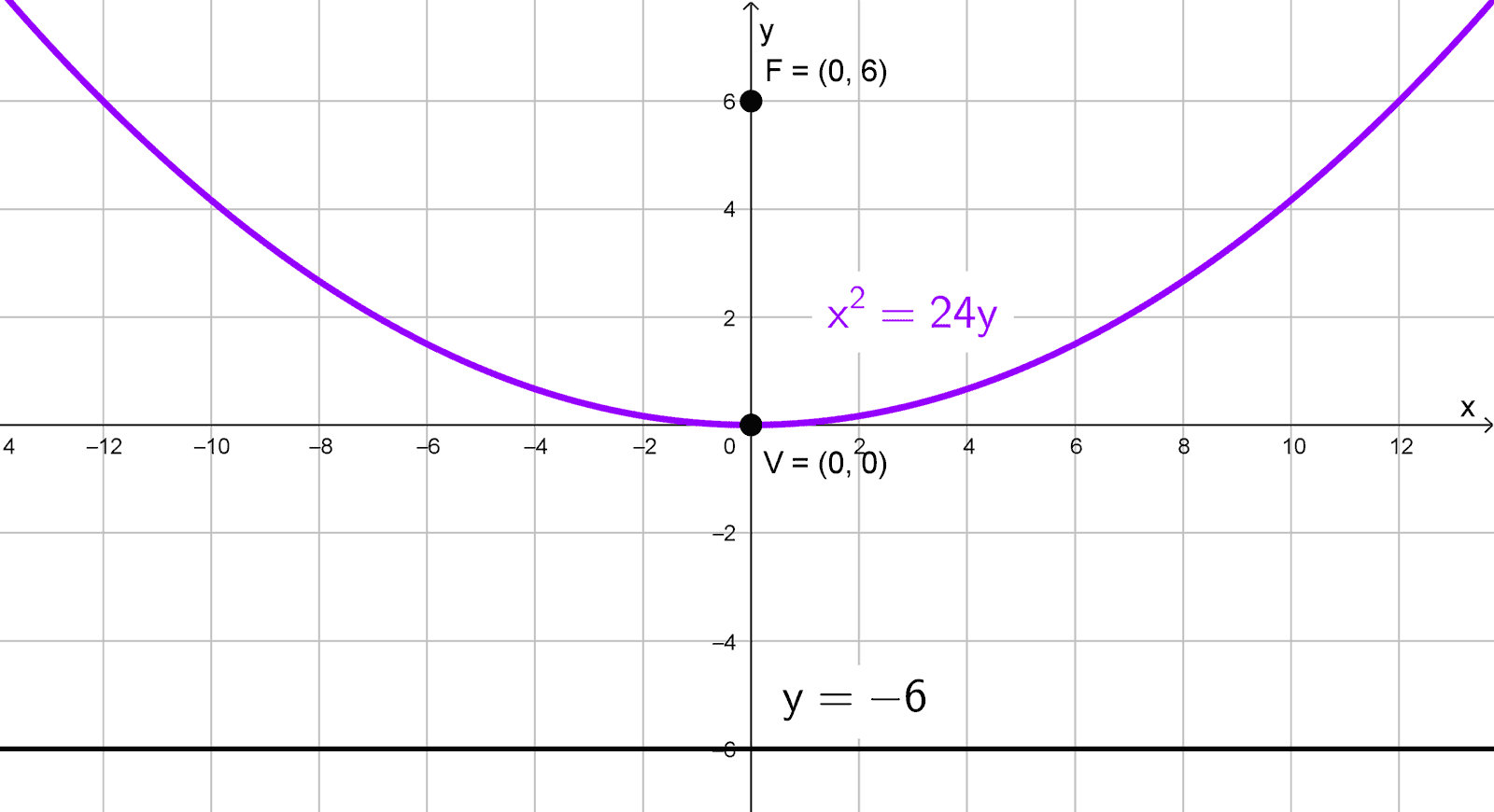
Determinar la ecuación de la parábola con vértice en el origen y directriz y = -6.
Solución
Primero, observamos que la directriz es horizontal y está por debajo del vértice, lo que significa que la parábola abre hacia arriba. Su ecuación estándar es:
\(x^2=4py\)
La directriz siempre tiene ecuación y = -p, lo que resulta en \(-p = -6→p=6\)
Sustituyendo \(p=6,\) encontramos:
\(x^2=4 \cdot 6 \cdot y → x^2=24y\)
Ejercicio 4
Encuentra la ecuación de la parábola con vértice en (2, -1) y foco en (2, 3).
Solución
Aquí, el vértice y el foco comparten la misma coordenada x, lo que indica que la parábola es vertical y abre hacia arriba porque el foco está por encima del vértice. La distancia |p| es la diferencia en las coordenadas y:
\(|p|=3-(-1)=4\)
Como la parábola se abre hacia arriba, p es positivo, así que p = 4. La forma estándar para una parábola vertical con vértice (h, k) es:
\((x-h)^2=4p(y-k)\)
Sustituyendo \(h=2,\) \(k=-1\) y \(p=4,\) determinamos:
\((x-2)^2=4 \cdot 4 \cdot (y+1) → (x-2)^2=16(y+1)\)
Ejercicio 5
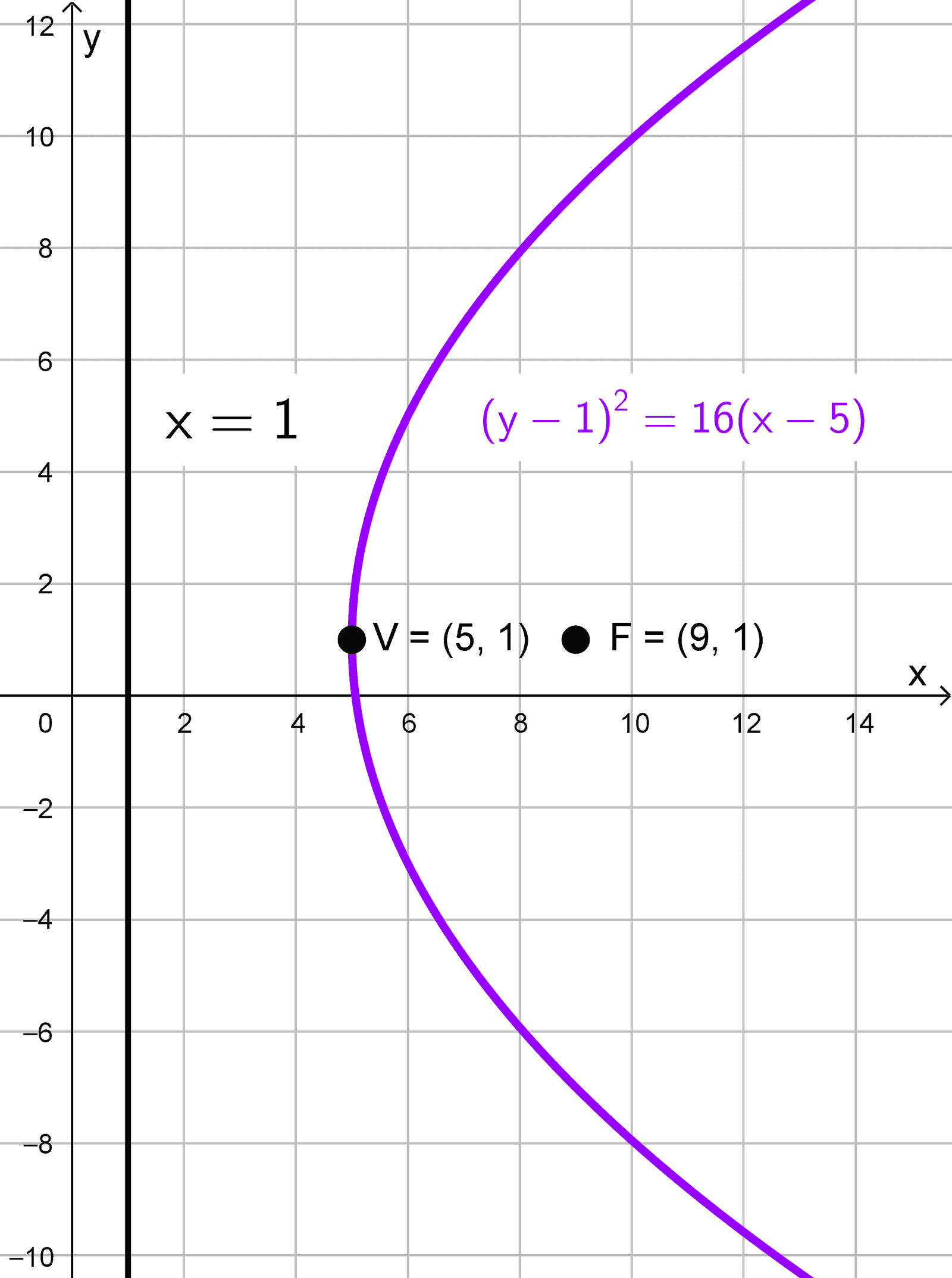
Escribe la ecuación de la parábola con vértice en (5, 1) y directriz x = 1.
Solución
La directriz es vertical y está a la izquierda del vértice, por lo que la parábola abre hacia la derecha. La distancia del vértice a la directriz es:
\(|p|=5-1=4\)
Como la apertura es hacia la derecha, utilizamos p con valor positivo, así que p = 4.
La forma estándar para una parábola horizontal con vértice (h, k) es:
\((y-k)^2=4p(x-h)\)
Reemplazando \(h=5,\) \(k=1\) y \(p=4,\) hallamos:
\((y-1)^2=4 \cdot 4 \cdot (x-5) → (y-1)^2=16(x-5)\)
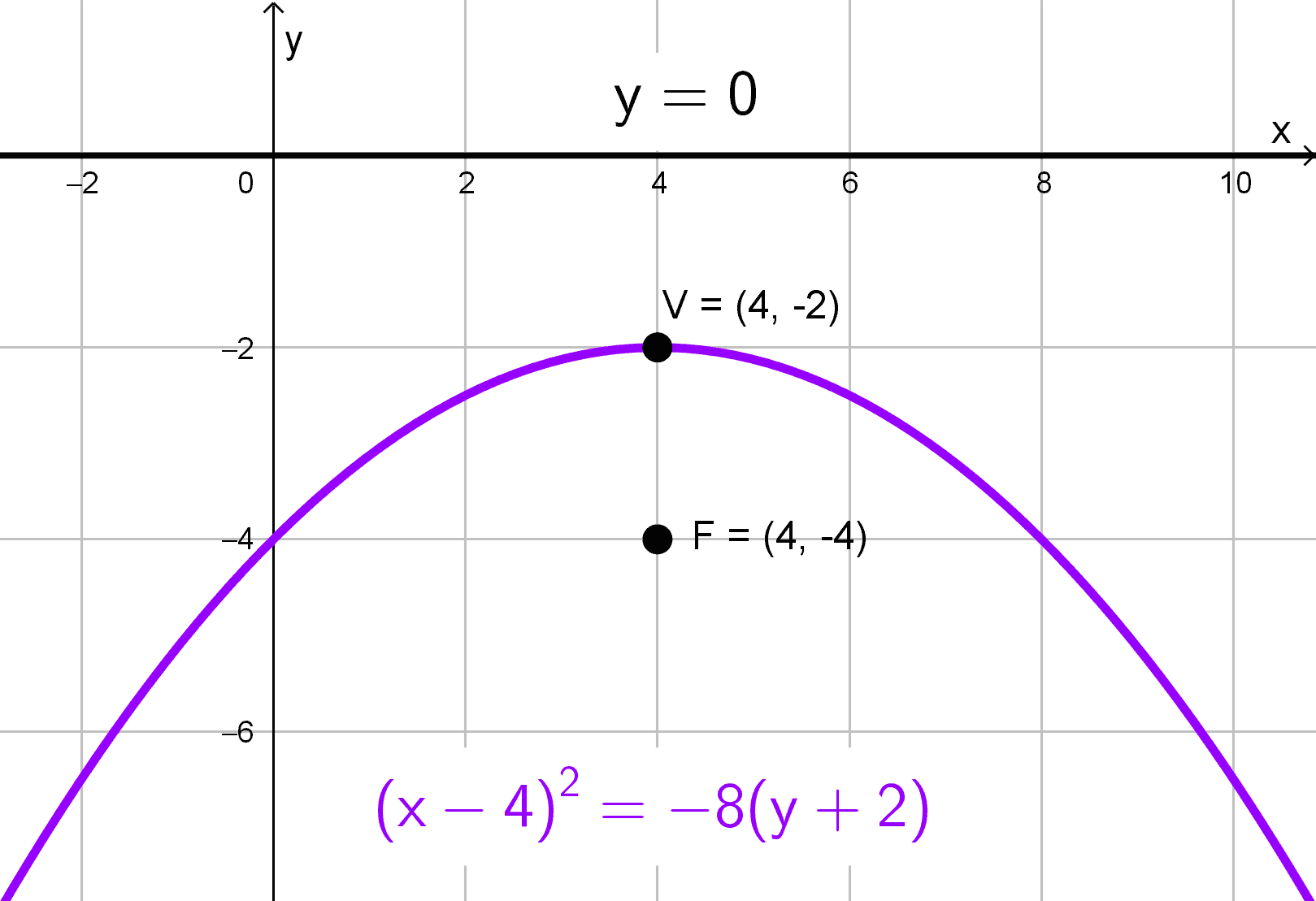
Ejercicio 6
Calcula la ecuación de la parábola cuyo vértice está en (4, -2) y su directriz es y = 0.
Solución
La directriz es horizontal y está por encima del vértice, lo que implica que la parábola abre hacia abajo. La distancia |p| es:
\(|p|=0-(-2)=2\)
Como la parábola abre hacia abajo, el parámetro p tiene valor negativo, así que \(p = -2.\)
La forma estándar para una parábola vertical con vértice (h, k) es:
\((x-h)^2=4p(y-k)\)
Sustituyendo \(h=4,\) \(k=-2\) y \(p=-2,\) obtenemos:
\((x-4)^2=4 \cdot (-2) \cdot (y+2) → (x-4)^2=-8(y+2)\)
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta





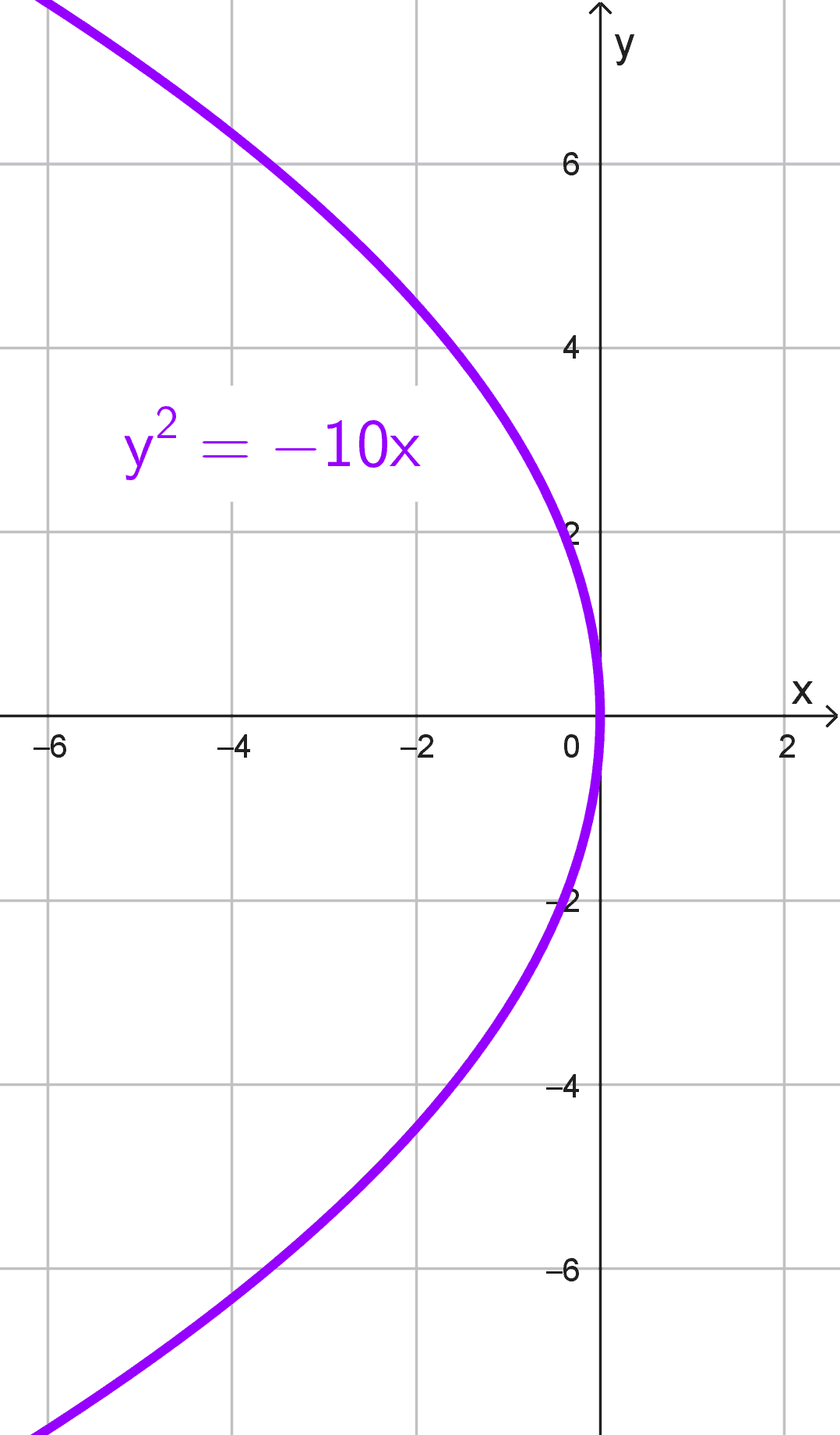
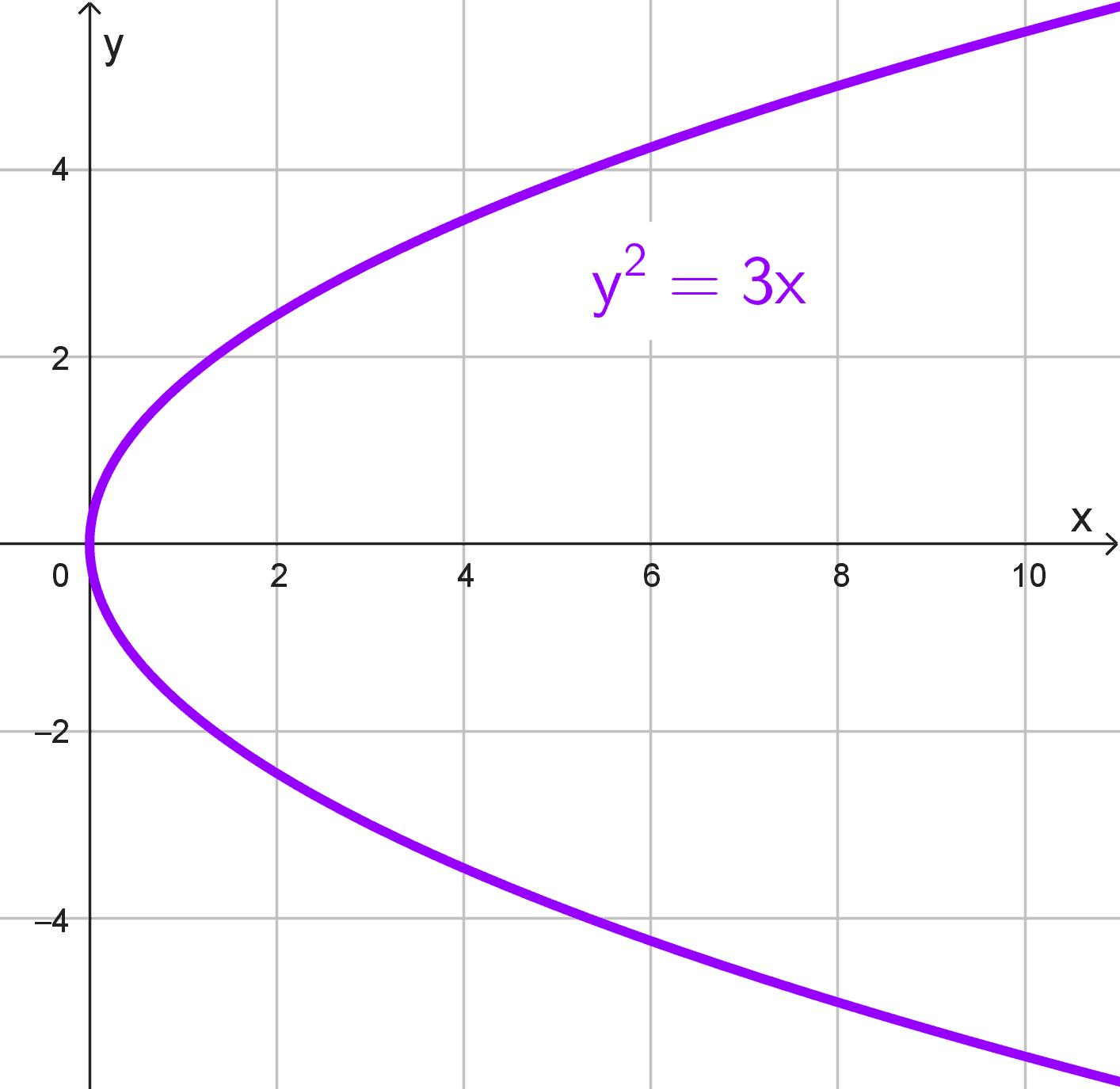




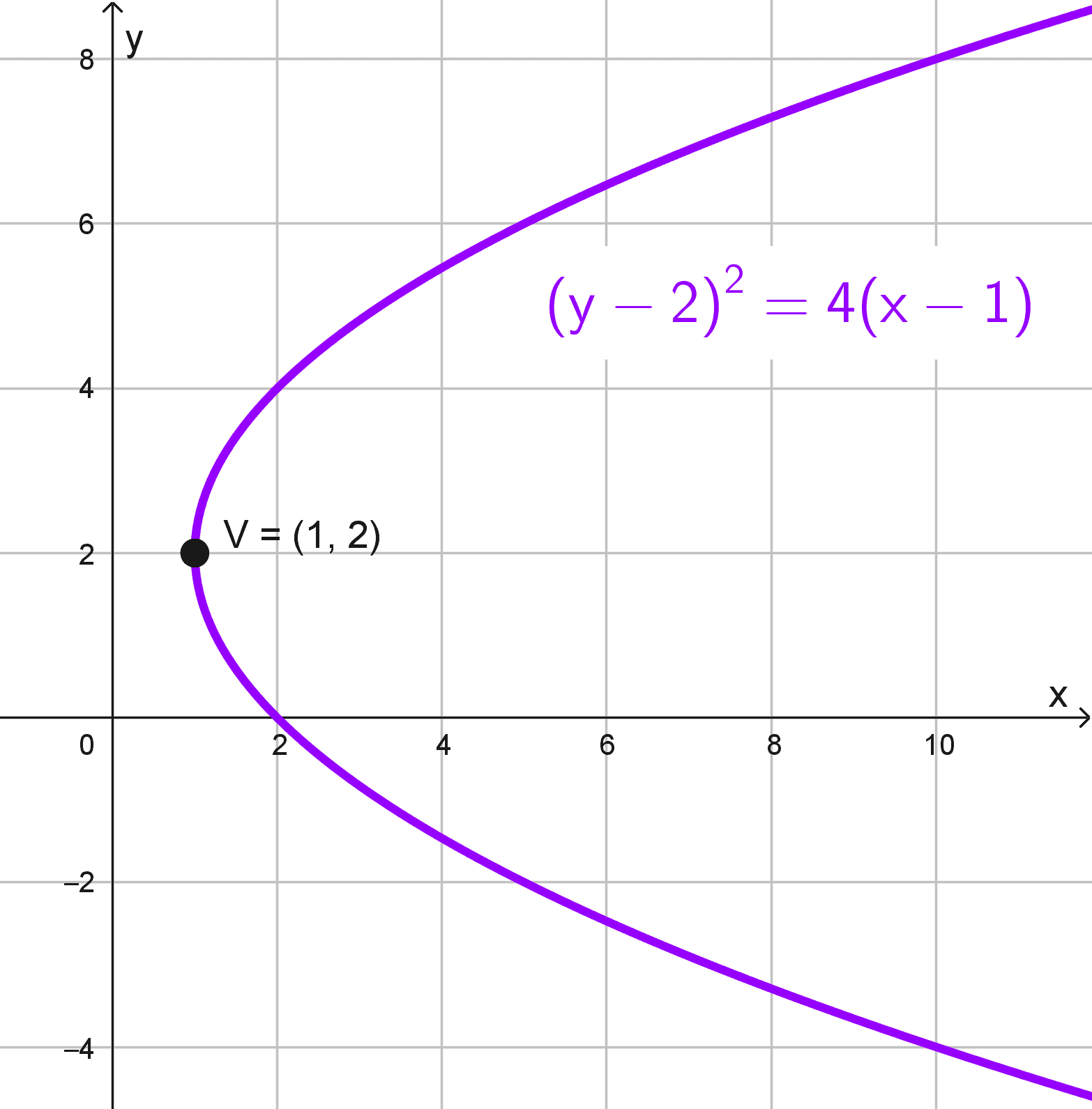
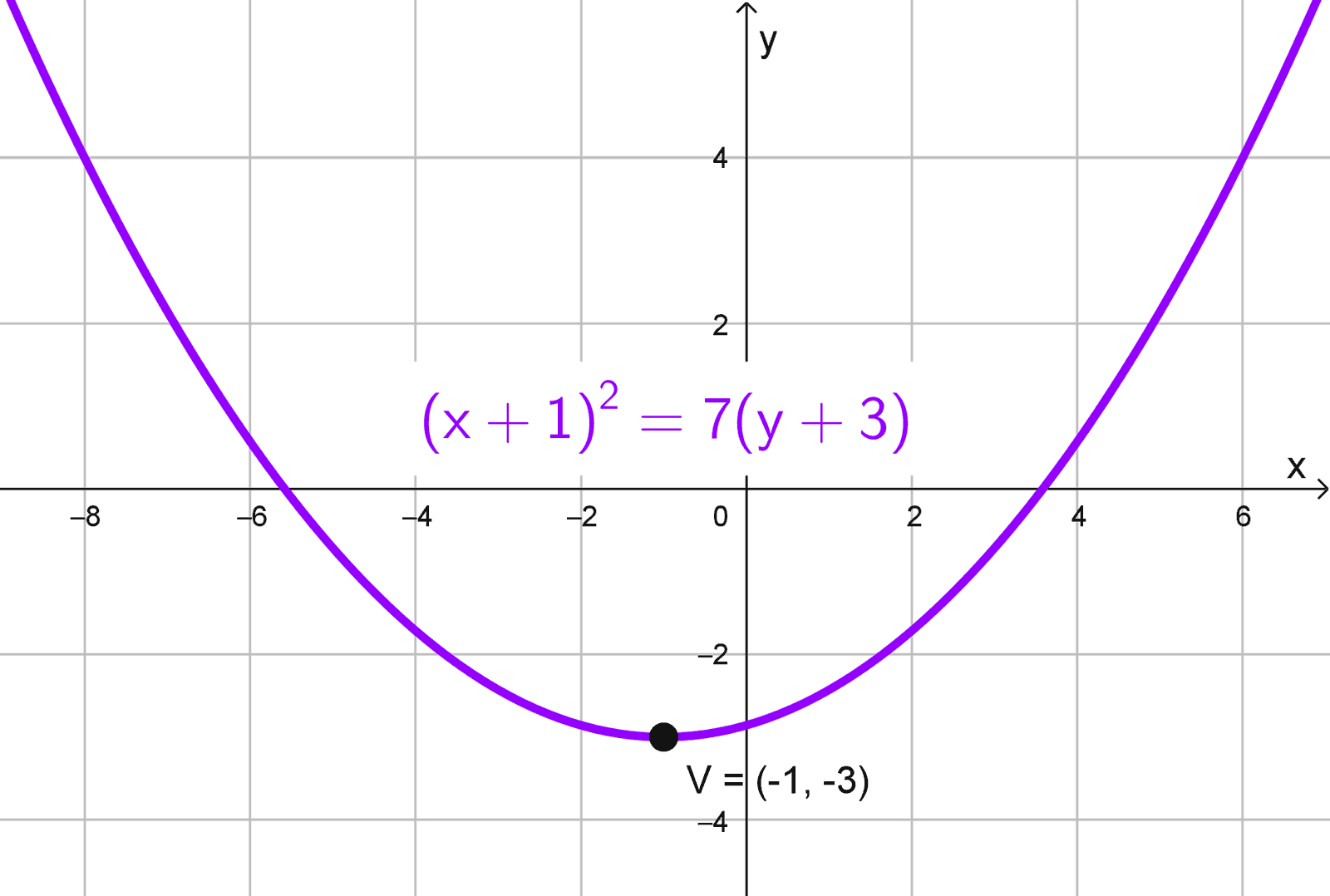
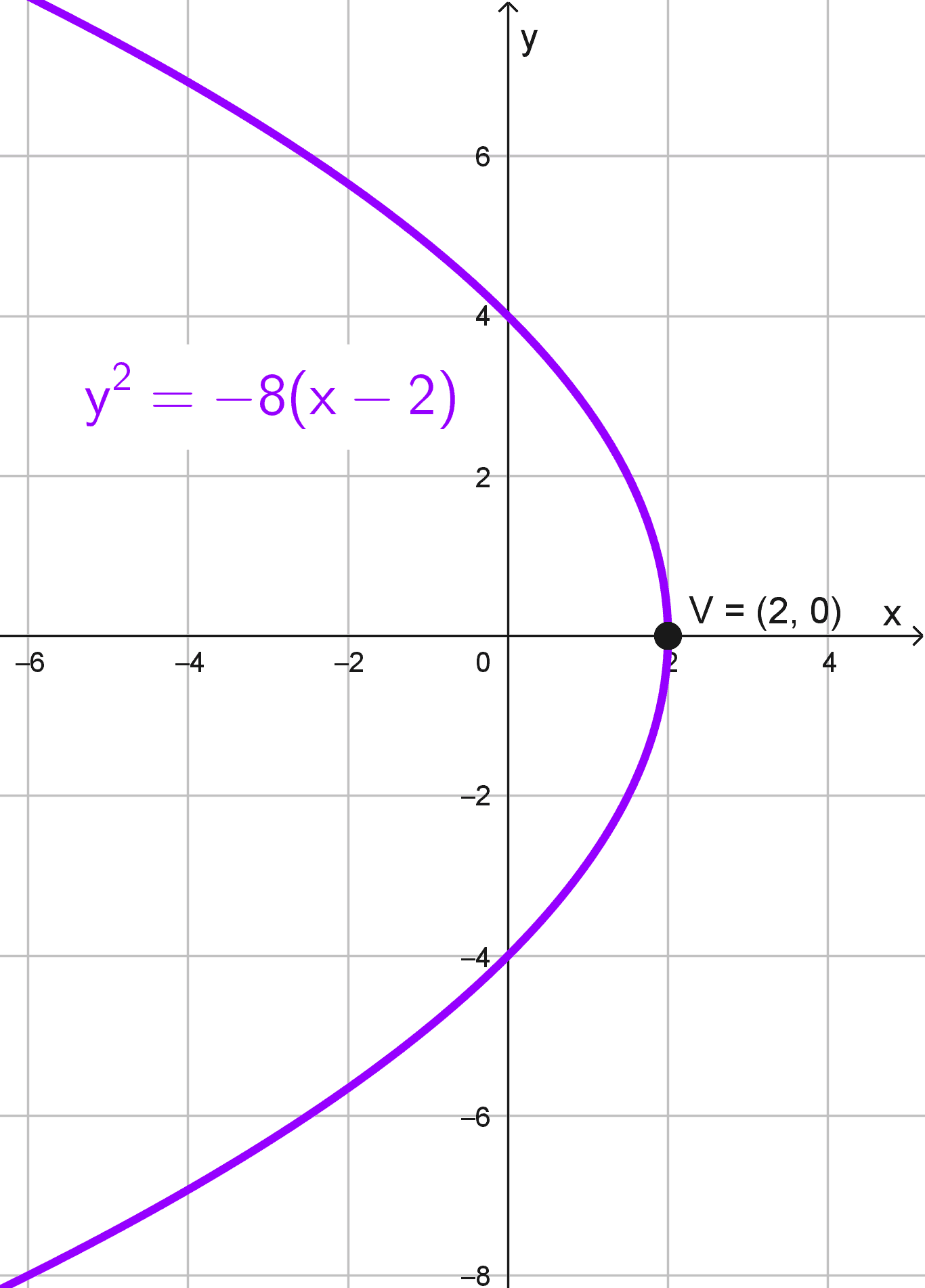
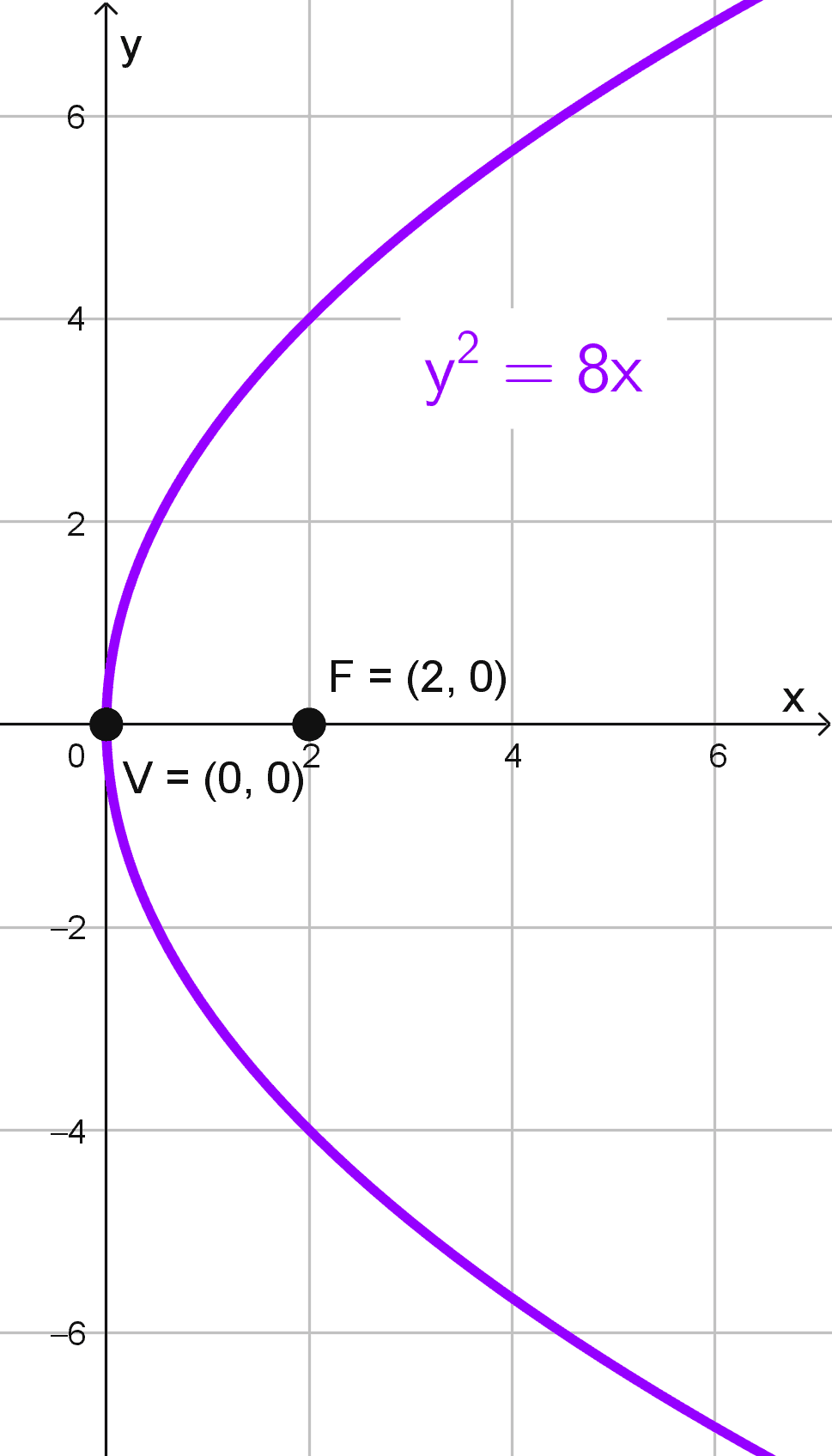
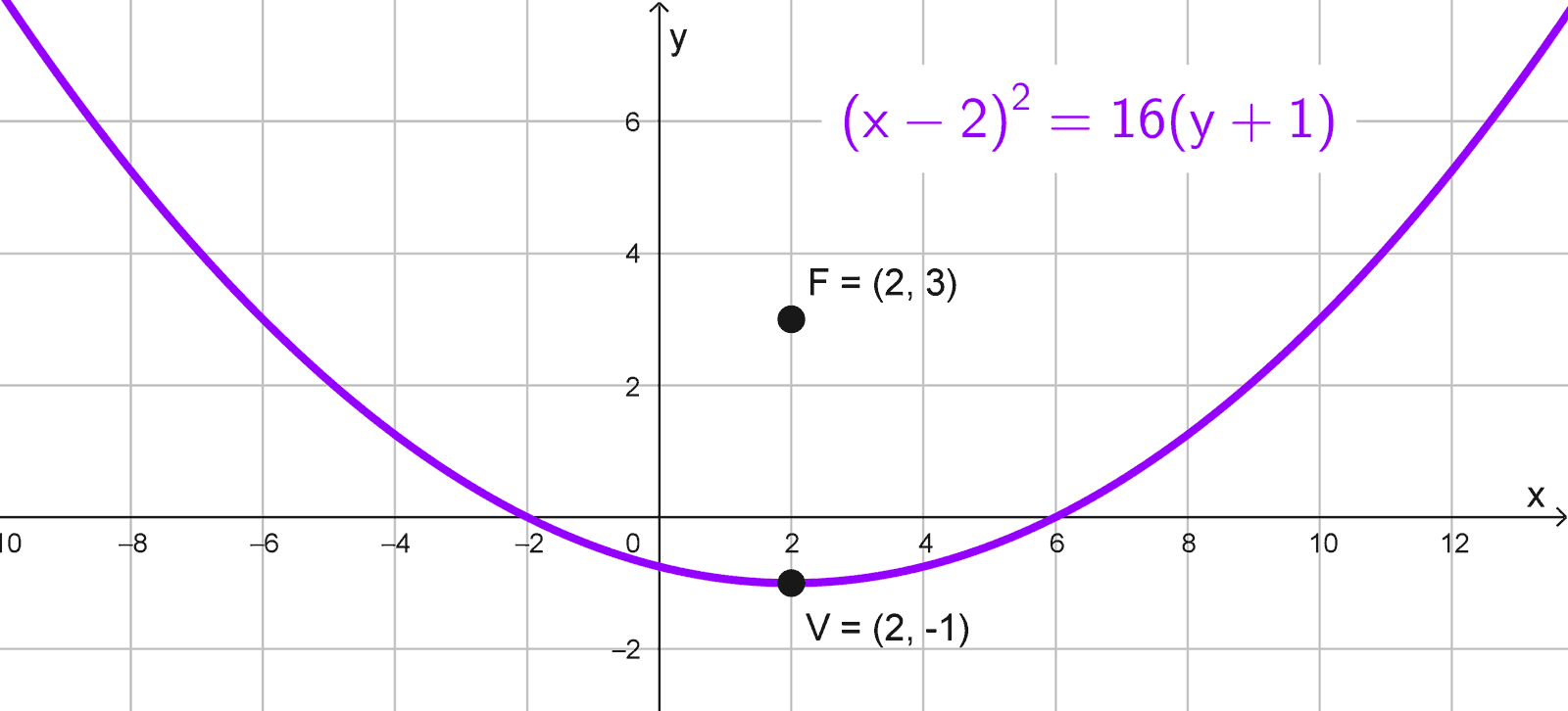


Otros artículos que pueden interesarte