
Eje de simetría de una parábola
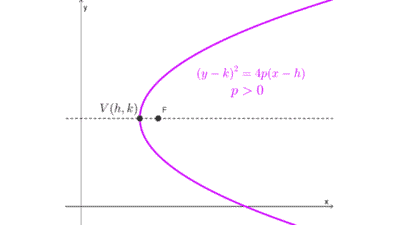
El eje de simetría es una línea recta que pasa por el vértice de la parábola, es perpendicular a la directriz y divide a la parábola en dos mitades idénticas. Otra forma de llamar a esta recta es como eje focal, ya que también pasa por el foco de la parábola.
El eje de simetría puede ser vertical u horizontal dependiendo de la orientación de la parábola. Debido a que pasa por el vértice, la coordenada x o y de éste aparece en la ecuación del eje de simetría:
- En parábolas verticales (que abren hacia arriba o hacia abajo) con vértice en el punto (h, k), el eje de simetría es una recta vertical con ecuación x = h.
- En parábolas horizontales (que se abren hacia la izquierda o la derecha) con vértice en (h, k), el eje de simetría es una recta horizontal con ecuación y = k.
Si el vértice está en el origen de coordenadas, la ecuación del eje de simetría es x = 0 (el eje y) para parábolas verticales e y = 0 (el eje x) para parábolas horizontales.
Nota: aquí nos enfocamos solo en un elemento de la parábola. Para comprenderlo mejor, es conveniente que antes repases el artículo principal sobre esta cónica, donde abordamos su teoría básica:
Índice
Ecuación del eje de simetría
Vimos que para conocer el eje de simetría hay que conocer primero el vértice de la parábola. Esto se puede conseguir de forma sencilla cuando la ecuación está en forma canónica. Los casos se resumen en la siguiente tabla:
| Ecuación de la parábola | Vértice | Orientación | Eje de simetría |
|---|---|---|---|
| y2 = 4px | (0, 0) | Horizontal | y = 0 |
| x2 = 4py | (0, 0) | Vertical | x = 0 |
| (y - k)2 = 4p (x - h) | (h, k) | Horizontal | y = k |
| (x - h)2 = 4p (y - k) | (h, k) | Vertical | x = h |
Ejemplos
Calcular el eje de simetría de las siguientes parábolas:
- \(y^2=8x\)
- \((x+1)^2=7(y+2)\)
- \((y-2)^2=4(x-1)\)
Solución 1
La ecuación dada es: \(y^2=8x\)
Como primer paso, observamos que es una parábola horizontal, ya que la variable y está al cuadrado y la variable x es lineal. Esto indica que la parábola se abre hacia la derecha o hacia la izquierda.
Ahora podemos identificar el vértice de la parábola. Dado que la ecuación no tiene términos adicionales que desplacen el vértice, este se encuentra en el origen de coordenadas (0, 0).
Teniendo esto en cuenta, recordamos que, para parábolas horizontales con vértice en (h, k), el eje de simetría es una recta horizontal con ecuación y = k. En este caso, como h = 0 y k = 0, el la ecuación del eje es \(y=0.\)
Solución 2
La ecuación dada es: \((x+1)^2=7(y+2)\)
Analizándola, observamos que es una parábola vertical, ya que la variable x está al cuadrado y la variable y es lineal. Esto indica que la parábola se abre hacia arriba o hacia abajo.
Ahora podemos obtener el vértice de la parábola. La ecuación está escrita en la forma estándar \((x-h)^2=4p (y-k),\) donde (h, k) es el vértice. Comparando, tenemos que el vértice está en el punto (-1, -2).
Teniendo esto en cuenta, recordamos que, para parábolas verticales con vértice en (h, k), el eje de simetría es una recta vertical con ecuación x = h. En este caso, como h = -1, la ecuación del eje es:
\(x=-1\)
Solución 3
Ecuación dada: \((y-2)^2=4(x-1)\)
Notamos que la variable y está elevada al cuadrado, mientras que x aparece linealmente, lo que nos indica que se trata de una parábola horizontal. Procedemos a identificar las coordenadas del vértice y concluimos que se ubica en (1, 2).
En parábolas horizontales, el eje focal (o eje de simetría) es una línea paralela al eje x que pasa por el vértice, su ecuación será de la forma y = k. En este caso, como k = 2, el eje focal está dado por:
\(y=2\)
Solución 4
Ecuación: \(x^2-8x+10y+66=0\)
La ecuación dada no está en forma ordinaria, sino general. Podemos completar los cuadrados y reacomodar la expresión para obtener la forma canónica:
\((x-4)^2=-10 (y+5)\)
Al observar que la variable x está elevada al cuadrado mientras que y aparece en forma lineal, reconocemos que se trata de una parábola vertical. Deducimos que el vértice se encuentra en el punto (4, -5).
Para una parábola vertical, el eje de simetría es una recta vertical que pasa por el vértice, es decir, una línea paralela al eje y con ecuación x = h. En este caso, como h = 4, la ecuación del eje es:
\(x=4\)
Si no se tiene la ecuación canónica, existen fórmulas para obtener el eje de simetría a partir de los coeficientes de la ecuación general, sin necesidad de completar los cuadrados. Veremos estos casos a continuación.
Parábolas verticales
El eje de simetría de una parábola vertical de la forma y = ax2 + bx + c tiene ecuación:
x = -b / (2a)
Esta ecuación es útil cuando se trabaja con la función cuadrática.
Ejemplos
Obtener la ecuación del eje de simetría de las siguientes parábolas verticales:
- \(y=2x^2+3x-5\)
- \(y=-3x^2+2x+7\)
- \(y=\dfrac{1}{2}x^2+x\)
- \(x^2+10x-y+25=0\)
Solución 1
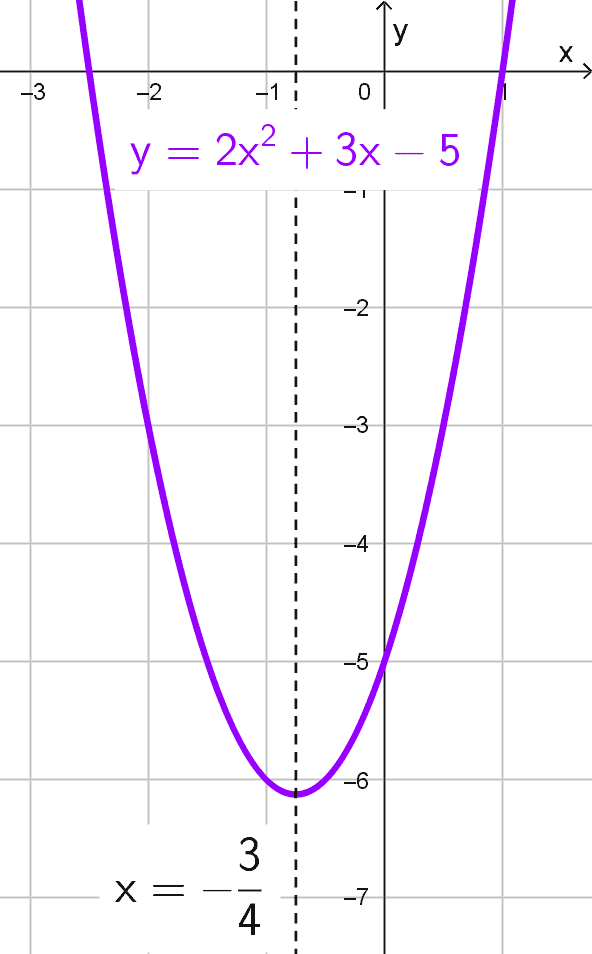
Ecuación: \(y=2x^2+3x-5\)
Como primer paso, identificamos los coeficientes de la ecuación dada \(y=2x^2+3x-5.\) En este caso, tenemos que \(a=2,\) \(b=3\) y \(c=-5.\)
Ahora podemos utilizar la fórmula para encontrar el eje de simetría de una parábola vertical, que está dada por x = -b / (2a). Sustituyendo los valores de a y b, obtenemos:
\(x=\dfrac{-3}{2 \times 2}=-\dfrac{3}{4}\)
Teniendo esto, concluimos que la ecuación del eje de simetría de la parábola \(y=2x^2+3x-5\) es:
\(x=-\dfrac{3}{4}\)
Solución 2
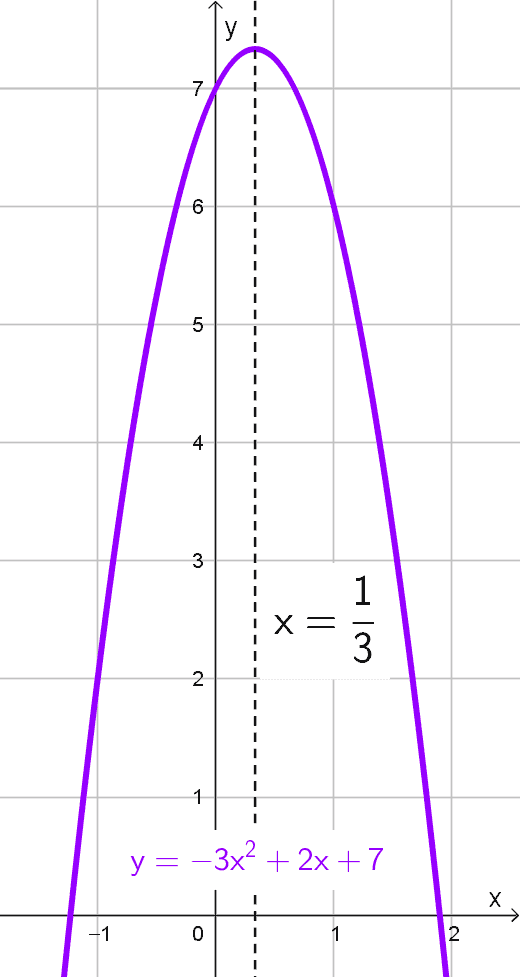
Ecuación: \(y=-3x^2+2x+7\)
Para resolver este problema, comenzamos por reconocer los coeficientes de la función cuadrática \(y=-3x^2+2x+7.\) Aquí observamos que \(a=-3,\) \(b=2\) y \(c=7.\)
A continuación, aplicamos la fórmula del eje de simetría para una parábola vertical. Sustituyendo los valores correspondientes, calculamos:
\(x=-\dfrac{b}{2a}=-\dfrac{2}{2 \times (-3)}=-\dfrac{2}{-6}=\dfrac{1}{3}\)
Solución 3
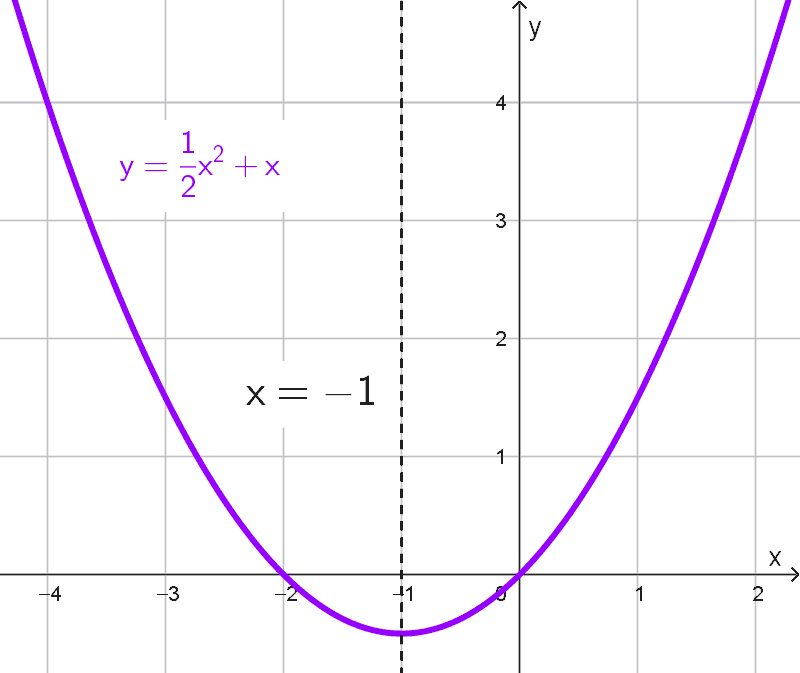
Ecuación: \(y=\dfrac{1}{2}x^2+x\)
Empezamos analizando la ecuación dada donde identificamos los coeficientes como a = 1/2, b = 1 y c = 0, aunque el término independiente no influye en el cálculo del eje.
Procedemos a sustituir los valores conocidos en la ecuación del eje de simetría:
\(x=-\dfrac{b}{2a}=-\dfrac{1}{2 \times (1/2)}=-\dfrac{1}{1}=-1\)
Por lo tanto, concluimos que el eje focal de la parábola es la recta vertical \(x=-1.\)
Solución 4
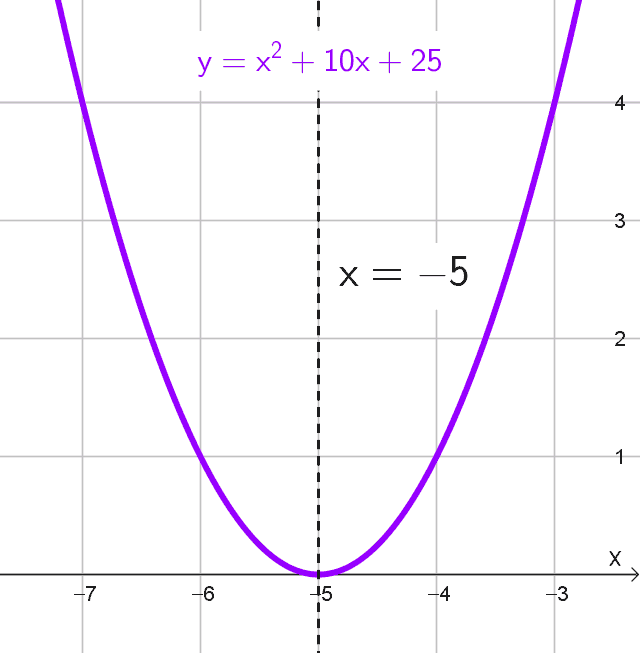
Ecuación: \(x^2+10x-y+25=0\)
Comencemos reescribiendo la ecuación dada para expresarla en términos de y. Despejamos y para llevarla a la forma estándar de una parábola vertical:
\(y=x^2+10x+25\)
Observamos que esta expresión puede simplificarse aún más, ya que \(x^2+10x+25\) es un trinomio cuadrado perfecto:
\(y=(x+5)^2\)
Al tener la ecuación en su forma canónica \(y=(x+h)^2,\) sabemos que el vértice está en (-5, 0) y el eje de simetría coincide con la recta vertical que pasa por el vértice. Por lo tanto, el eje de simetría es:
\(x=-5\)
Nota: también podríamos haber aplicado directamente la fórmula \(x=-b/(2a)\) a la forma \(y=x^2+10x+25,\) donde \(a=1\) y \(b=10,\) obteniendo el mismo resultado: \(x=-\dfrac{10}{2}=-5.\)
Parábolas horizontales
El eje de simetría de una parábola horizontal de la forma x = ay2 + by + c tiene ecuación:
y = -b / (2a)
Ejemplos
Determinar el eje de simetría de las siguientes parábolas horizontales:
- \(x=y^2+2y-3\)
- \(x=\dfrac{1}{2}y^2-3y+5\)
- \(3y^2-x+6y=0\)
Solución 1
Ecuación: \(x=y^2+2y-3\)
Como primer paso, identificamos los coeficientes de la ecuación, la cual tiene la forma general \(x=ay^2+by+c.\) En este caso, los coeficientes son \(a=1,\) \(b=2\) y \(c=-3.\)
Ahora podemos aplicar la fórmula del eje de simetría para una parábola horizontal, que está dada por \(y=-\dfrac{b}{2a}.\) Sustituyendo los valores de a y b, obtenemos:
\(y=-\dfrac{2}{2 \cdot 1}=-1\)
Concluimos que el eje de simetría de la parábola es la recta horizontal \(y=-1.\)
Solución 2
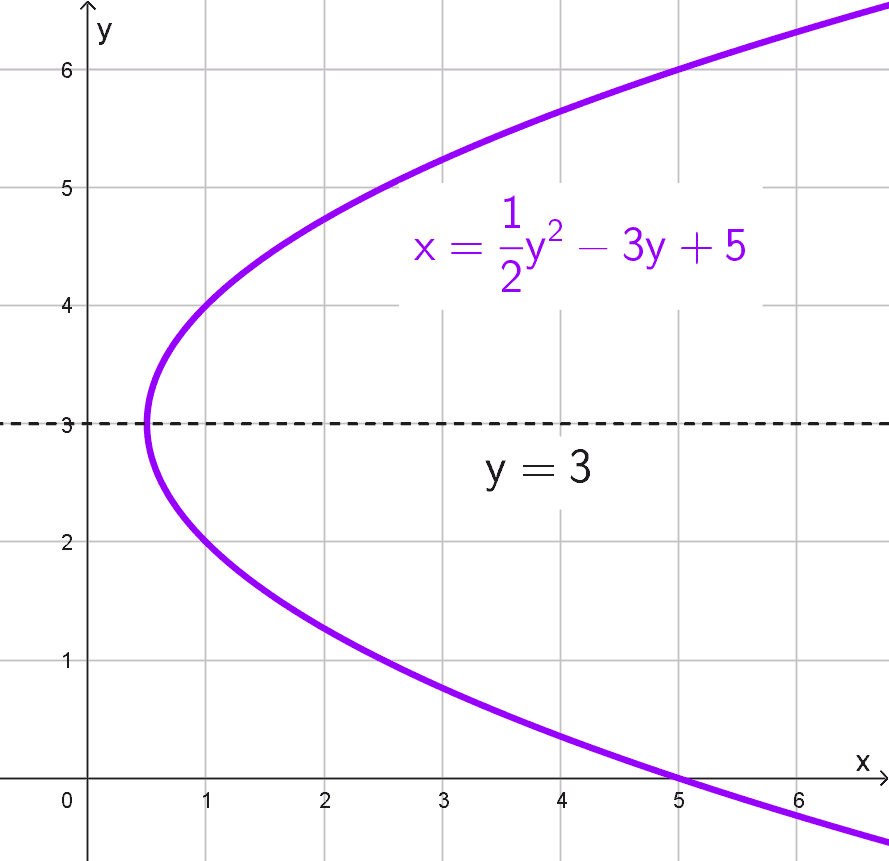
Ecuación: \(x=\dfrac{1}{2}y^2-3y+5\)
Observamos primero que la ecuación sigue la estructura general donde los coeficientes son \(a=\dfrac{1}{2},\) \(b=-3\) y \(c=5.\)
Aplicando la fórmula del eje de simetría para una parábola horizontal, sustituimos los valores identificados:
\(y=-\dfrac{b}{2a}=-\dfrac{-3}{2 \cdot (1/2)}=\dfrac{3}{1}=3\)
De esta manera, concluimos que el eje de simetría es la recta horizontal \(y=3.\)
Solución 3
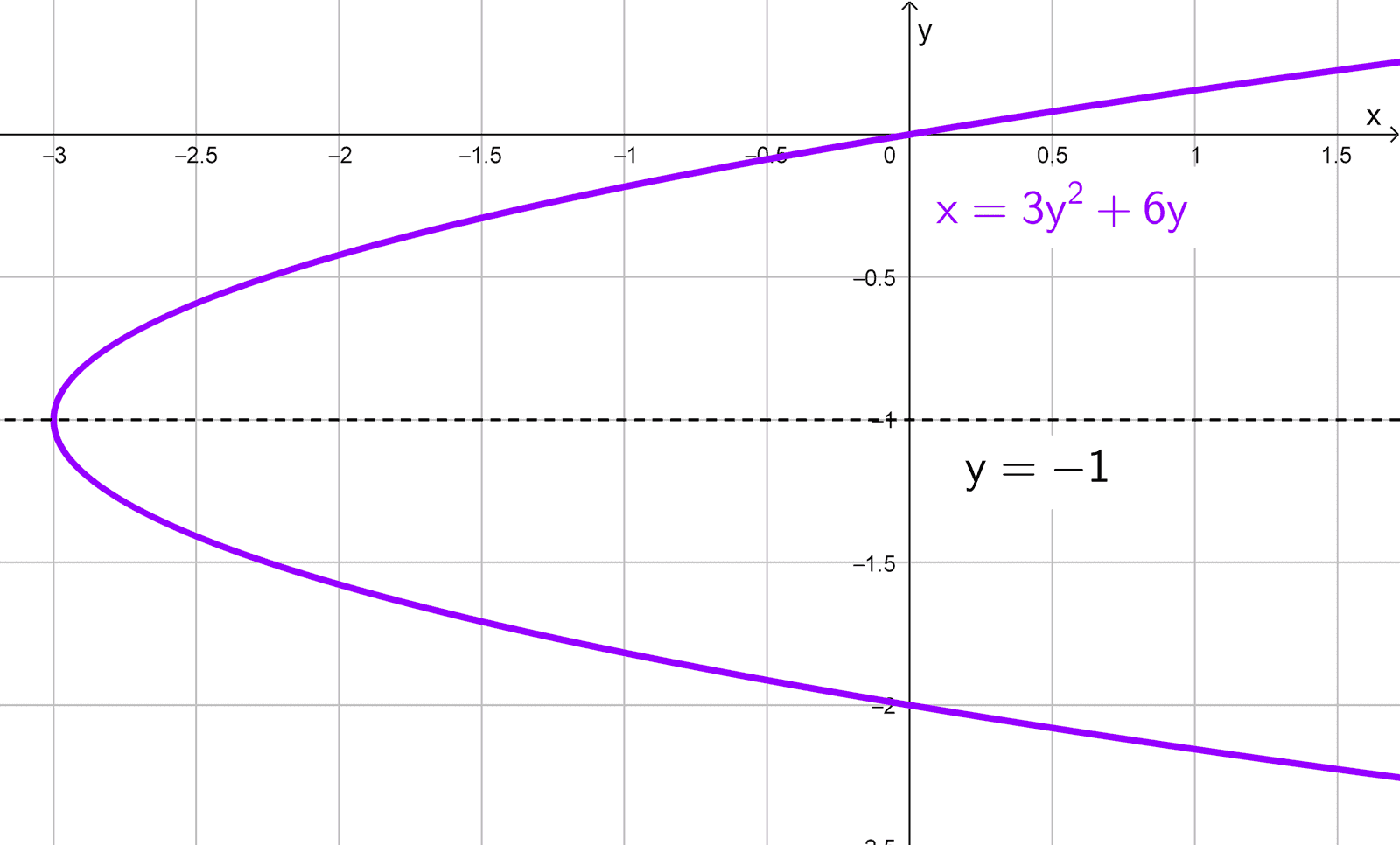
Ecuación: \(3y^2-x+6y=0\)
Primero debemos despejar la variable x para expresarla en la forma estándar de una parábola horizontal.
\(x=3y^2+6y\)
Así, identificamos los coeficientes: \(a=3,\) \(b=6\) y \(c=0.\) Ahora, aplicamos la fórmula del eje de simetría para una parábola horizontal:
\(y=-\dfrac{b}{2a}=-\dfrac{6}{2 \cdot 3}=-\dfrac{6}{6}=-1\)
Por lo tanto, el eje de simetría de esta parábola es la recta horizontal \(y=-1.\)
Resumen de ecuaciones
Las fórmulas y ecuaciones para hallar el eje de simetría se resumen en la siguiente tabla:
| Ecuación de la parábola | Orientación | Eje de simetría |
|---|---|---|
| y = ax2 + bx + c | Vertical | x = -b / (2a) |
| x = ay2 + by + c | Horizontal | y = -b / (2a) |
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta



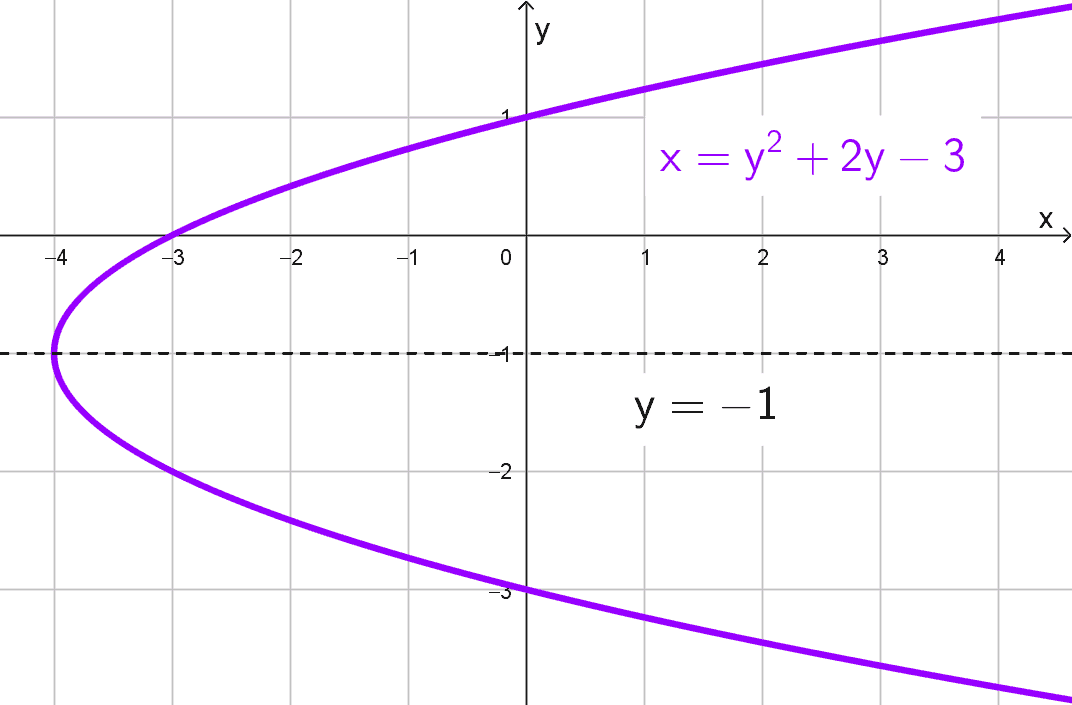


Otros artículos que pueden interesarte